En este capítulo, el estudio de la superficie de la Tierra sirve para introducir una primera clase de fractales; las curvas conexas de dimensión superior a 1. Aprovechamos además la ocasión para regular algunas cuestiones de aplicabilidad más general.

Tomando un trozo de costa marítima en una región accidentada, trataremos de medir su longitud efectiva. Es evidente que dicha longitud es mayor o igual que la distancia en línea recta entre los extremos de nuestro pedazo de curva; que, si la costa fuera recta, este primer paso daría la solución del problema; en fin, que una costa salvaje de verdad es sumamente sinuosa y, por consiguiente, más larga que dicha distancia en línea recta. Esto puede ser tenido en cuenta de diversas maneras pero, en cualquier caso, la longitud final resultará ser tan grande que, a fines prácticos, se la puede considerar infinita.

Cuando queramos comparar a continuación los «contenidos» de costas distintas, no podremos evitar introducir distintas formas de un concepto matemático que nadie había creído que tuviera aplicación concreta alguna, se trata del concepto de dimensión fractal.

He aquí un primer método: se pasea sobre la costa un compás de abertura dada η, comenzando cada paso donde termina el anterior. El valor de η multiplicado por el número de pasos nos dará una longitud aproximada L(η). Si se repite la operación reduciendo cada vez más la abertura del compás, se encuentra que L(η) tiende a aumentar sin límite. Antes de discutir esta comprobación, podemos observar que el principio en que se basa el procedimiento comentado consiste de entrada en reemplazar el objeto a medir, que es demasiado irregular, por una curva más manejable, arbitrariamente suavizada o «regularizada». La idea general se ilustra bien (recordemos la imagen utilizada por Jean Perrin) por un papel de estaño que envuelve una esponja sin seguir verdaderamente su contorno.

Aunque tal regularización resulta inevitable, puede hacerse igualmente de otras maneras: así, por ejemplo, se puede imaginar un hombre que anda a lo largo de una costa siguiendo el camino más corto posible sin separarse de ella más de una cierta distancia establecida η; luego, se repite haciendo cada vez más pequeña dicha distancia máxima del hombre a la costa. Después de esto se sustituye al hombre por un ratón, después por una mosca, y así sucesivamente. Cuanto más cerca de la costa se quiera uno mantener, tanto mayor será, inevitablemente, la distancia a recorrer.

Un método más: para evitar la asimetría entre tierra firme y agua establecida por el segundo método, se pueden considerar todos los puntos de una y otra que disten a lo más η de la costa. Así pues, se imagina que la costa está recubierta a la perfección por una banda de anchura 2η; se mide la superficie de dicha banda y se divide por 2η, como si fuera un rectángulo. Y finalmente, un cuarto procedimiento: se imagina un mapa dibujado por un pintor puntillista, que utiliza «puntos gruesos» de radio η; en otras palabras, se recubre la costa con círculos de radio menor o igual que η.

Ya debe de haber quedado claro que cuando se hace que n sea cada vez menor, todas las longitudes aproximadas aumentan. Siguen aumentando incluso cuando η es del orden del metro, sin significado geográfico alguno.

Antes de plantearse otras cuestiones acerca de la regla que rige esta tendencia, asegurémonos del significado de lo que acabamos de establecer. Para ello, repitamos las mismas medidas substituyendo la costa salvaje de Brest del año 1000 por la de 1975, domada por el hombre. El argumento de más arriba se podría aplicar en otro tiempo, pero hoy en día se ha de modificar; todas las maneras de medir la longitud con una «aproximación η» dan un resultado que aumenta hasta que la unidad disminuye hasta unos 20 metros; pero a continuación se encuentra una zona en la que L(η) varía muy poco, y no vuelve a aumentar hasta los n menores que 20 centímetros, es decir, tan pequeños que la longitud empieza a tener en cuenta las irregularidades de las piedras. Así pues, si se traza una gráfica de la longitud L(η) en función del paso η, aparece en la actualidad una especie de meseta, que no aparecía en el pasado. Ahora bien, cada vez que se quiere agarrar un objeto que no para de moverse es bueno precipitarse sobre él desde el preciso momento en que se detiene, pues no durará más que un instante; diremos, así pues, de muy buena gana que, para el Brest de hoy, un cierto grado de precisión en la medida de las longitudes de las costas se ha hecho intrínseco.

Pero este «intrínseco» es del todo antropocéntrico, pues es el tamaño de las mayores piedras que el hombre puede desplazar, o de los bloques de cemento que le gusta hacer. La situación no era muy diferente en el pasado, ya que la mejor η para medir la costa no era ni la del ratón ni la de la mosca, sino la de un hombre adulto. El antropocentrismo intervenía ya entonces, aunque de un modo distinto; por lo tanto, de un modo u otro, el concepto aparentemente inofensivo de la extensión longitudinal geográfica no es del todo «objetivo», ni lo ha sido jamás. El observador interviene en su definición de manera inevitable.

La variación de la longitud aproximada L(η) fue estudiada empíricamente por Richardson 1961. Veremos en el Capítulo 15 que Lewis Fry Richardson fue un sabio admirable, aunque a menudo su originalidad se tomara por excentricidad, y no haya alcanzado la celebridad que merecía. En el Capítulo 8 veremos que son debidas a él ideas profundas referentes a la naturaleza de la turbulencia. Rehuía los formalismos, sin vacilar en emplear conceptos finos y precisos allí donde él los creía útiles. Entre los papeles que dejó a su muerte, se han encontrado las gráficas reproducidas en la Figura 41, que inducen a concluir que L(η) es proporcional a η^−α.El valor de α depende de la costa elegida, y distintos tramos de la misma costa, considerados separadamente, dan a menudo distintos valores de α. A los ojos de Richardson, α era un mero exponente, sin ningún significado particular. Pero su valor parece ser independiente del método elegido para estimar la longitud y, por lo tanto, el parámetro merece ser considerado con detenimiento.

Mi primera contribución a este dominio, cuando Mandelbrot 19675 —por así decirlo— el trabajo de Richardson de una colección en la que hubiera podido permanecer perdido por siempre jamás, consistió en interpretar el exponente 1 + α como una «dimensión fractal». Vamos pues a denotarla por D. Reconozco, en efecto, que cada uno de los procedimientos para evaluar L(η), enumerados hace un instante, corresponde a una definición de la dimensión, definición ya utilizada en matemática pura, pero que nadie había pensado nunca que pudiera también aplicarse a lo concreto.

Por ejemplo, la definición que se basa en recubrir la costa por puntos gruesos de radio η es precisamente la utilizada por Pontrjagin y Schnirelman 1932 para definir la dimensión de recubrimiento; la idea de la definición basada en el recubrimiento por una banda de anchura 2η fue utilizada por Minkowski 1901; otras definiciones están relacionadas con la épsilon-entropía de Kolmogorov y Tihomirov 1959-1961. Pero estas definiciones, estudiadas en el Capítulo 14, son demasiado formales para ser verdaderamente explícitas. Vamos ahora a examinar con más detalle un concepto análogo pero mucho «más rico» desde el punto de vista geométrico: el de dimensión de Hausdorff-Besicovitch, así como el concepto sencillo y explícito de dimensión de homotecia.

Una tarea más fundamental consiste en representar y explicar la forma de las costas por medio de un valor D que satisfaga la desigualdad D > 1. Abordaremos esto en el Capítulo 7. Baste avanzar que encontraremos, en primera aproximación, D = 1,5, valor demasiado grande para explicar bien los hechos, pero más que suficiente para establecer que es «natural» que la dimensión sea superior a D = 1.

Señalemos finalmente que, incluso aquél que no acepte mis razones para considerar D > 1 para una costa, no sabría volver a la situación ingenua en la que aceptaba D = 1 sin mayor reflexión; quienquiera que crea que éste es el caso estará, en lo sucesivo, obligado a justificar su posición.

Si se admite que diversas costas naturales tienen «en realidad» una longitud infinita, y que sus longitudes antropocéntricas no dan más que una idea sumamente parcial, ¿cómo se pueden comparar dichas longitudes? Dado que el infinito es igual a cuatro veces el infinito, se puede decir que cualquier costa es cuatro veces más larga que cada uno de sus cuartos, pero éste es un resultado que carece de verdadero interés. ¿Cómo, pues, expresar la idea fuertemente arraigada de que toda curva tiene un «contenido» cuatro veces mayor que cada uno de sus cuartos? Para este fin existe un procedimiento, debido a Hausdorff, que vamos a examinar a continuación.

Su motivación intuitiva pate de los hechos siguientes: un contenido lineal se calcula sumando pasos η no transformados, es decir, elevados a la potencia 1, que es la dimensión de la recta, y el contenido de una superficie formada por cuadritos pequeños se calcula sumando los lados de estos cuadrados elevados a la potencia 2, que es la dimensión del plano. Procedamos igual en el caso de la forma aproximada de una costa que está implícita en el primer método de medida de longitudes. Es una línea quebrada, formada de pequeños segmentos de longitud η y enteramente recubierta por la reunión de los círculos de radio η, centrados en los puntos utilizados para la medida. Si se elevan estos pasos a la potencia D, obteniendo de este modo un «contenido aproximado en dimensión D», se constata que dicho contenido varía poco al variar η. En otras palabras, constatamos que la dimensión definida formalmente más arriba se comporta como de costumbre: el contenido calculado en cualquier dimensión d menor que D es infinito, pero si d es superior a D, el contenido se anula, y se comporta razonablemente para d = D. La definición precisa del «contenido», debida a Hausdorff (1919) y elaborada por Besicovitch, es necesariamente bastante más delicada, pero sus complicaciones (esbozadas en el Capítulo 14) no nos conciernen ahora.

Hemos insistido hasta aquí en la complicación y el desorden que caracterizan las costas consideradas como figuras geométricas. Examinemos ahora un orden que les es subyacente: de hecho, aunque las costas son muy irregulares, los grados de irregularidad que corresponden a distintas escalas son, grosso modo, iguales. Es, en efecto, asombroso que cuando una bahía o una península que estaban representadas en un mapa a escala 1/100.000, se examinan de nuevo en un mapa a 1/10.000, se observa que sus contornos están formados por innumerables sub-bahías y sub-penínsulas. En un mapa a 1/1.000, se ven aparecer también sub-sub-bahías y sub-sub-penínsulas, y así sucesivamente. Esta iteración no se puede continuar indefinidamente, pero se puede ir muy lejos, y se encontrará que, aunque los distintos mapas correspondientes a los sucesivos niveles de análisis sean completamente diferentes en lo que tienen de específico, tienen el mismo carácter global, los mismos rasgos genéricos. En otras palabras, que todo induce a creer que, a excepción de la escala, el mismo mecanismo hubiera podido engendrar tanto los pequeños detalles de las costas como los grandes.

Se puede pensar en este mecanismo como una especie de cascada, o más bien como un fuego de artificio por etapas, en el que cada etapa engendra detalles más pequeños que la que la que la precede. Cuando, hablando estadísticamente, cada pedazo de costa es homotético al todo —salvo detalles de los que decidimos no ocuparnos— se dirá que la costa posee una homotecia interna.

Al ser este ultimo concepto fundamental pero delicado, empezaremos afinándolo mediante una figura más regular que los matemáticos nos habían ya preparado sin saber para qué iba a servir. Veremos a continuación cómo sirve para medir el grado de irregularidad de las curvas por la intensidad relativa de los grandes y los pequeños detalles, y fin de cuentas —por una dimensión de homotecia.

Modelo basto de la costa de una isla: la curva en forma de copo de nieve de von Koch

La cascada geométrica de una costa puede simplificarse, como indican las Figuras 42 y 43. Supongamos que un trozo de costa trazada de un modo simplificado a escala 1/1.000.000 es, así a lo tonto, un triángulo equilátero. Que el nuevo detalle visible en un mapa a 3/1.000.000 sea el resultado de substituir el tercio central de cada lado por un promontorio en forma de triángulo equilátero, es decir, que cada lado se convierta en una figura formada por cuatro segmentos iguales. Que el nuevo detalle que aparece al 9/1.000.000 consista en substituir cada uno de estos cuatro segmentos por cuatro sub-segmentos de la misma forma, pero menores, guardando una proporción de un tercio y formando sub-promontorios. Continuando así hasta el infinito, se llega a un límite denominado curva de von Koch 1904. Se trata de una figura célebre que Cesàro 1905 describe en los términos extáticos siguientes: «Es esta similitud entre el todo y sus partes, incluso las infinitesimales, lo que nos lleva a considerar la curva de von Koch como una línea verdaderamente maravillosa entre las líneas. Si estuviera viva, no sería posible aniquilarla sin suprimirla de golpe, pues renacería sin cesar de las profundidades de sus triángulos, como la vida en el universo».

Se trata claramente de una curva y, en particular, su área es nula, pero cada etapa de su construcción aumenta, con toda evidencia, la longitud total en un factor 4/3, con lo que la curva de von Koch tiene una longitud infinita —exactamente igual que una costa—. Además, y esto es importante, es una curva continua, aunque no tenga tangente en prácticamente ninguno de sus puntos; es un objeto geométrico emparentado con las funciones continuas sin derivada.

Cualquier tratado de matemáticas que hable de ella subraya en seguida que es necesariamente un monstruo que carece de interés concreto. Y el físico que lee eso no puede evitar estar de acuerdo con ello. Aquí, sin embargo, no se permite sacar esta conclusión por cuanto ¡la curva de von Koch ha sido introducida precisamente como modelo simplificado de una costa! Si, de hecho, este modelo es inaceptable, no es en absoluto porque sea demasiado irregular, sino porque —en comparación con una costa— su irregularidad es demasiado sistemática. ¡Su desorden no es excesivo, sino insuficiente!

Nos quedan por citar a este respecto dos grandes matemáticos que, a pesar de no haber contribuido personalmente a la ciencia empírica, tenían un agudo sentido de lo concreto. Lévy 1970 escribía: «Sin duda que nuestra intuición preveía que la falta de tangentes y la longitud infinita de la curva están relacionados con recodos infinitamente pequeños que es impensable dibujar. (Insisto en este papel que juega la intuición porque siempre me ha sorprendido oír decir que la intuición geométrica conducía fatalmente a pensar que toda función continua era derivable. Desde mi primer encuentro con el concepto de derivada, mi experiencia personal me había probado lo contrario). Pero uno se queda confuso ante la impotencia de nuestra imaginación para ir tan siquiera más allá de las primeras etapas de la construcción de estos recodos infinitamente pequeños».

En la misma línea, resumiendo un estudio apasionante (que no llegó, sin embargo, hasta el concepto de dimensión), Steinhaus 1954 escribía: «Nos reconciliamos con la realidad al considerar que la mayoría de los arcos que se encuentran en la naturaleza son no rectificables. Esta afirmación es contraria a la creencia de que los arcos no rectificables son una invención de los matemáticos, y que los arcos naturales son rectificables; lo cierto es precisamente lo contrario».

Menudo contraste entre mis argumentos y citas y la célebre invectiva de Charles Hermite (1822-1901), que no se preocupaba sino por el rigor y por una cierta idea de pureza que él había inventado, y que declaraba (en una carta a Stieltjes) que «abandonaba con espanto y horror esta plaga lamentable de las funciones que no tienen derivada». (Nos gustaría creer que esta frase era irónica, pero un recuerdo de Henri Lebesgue sugiere lo contrario: «había enviado a M. Picard una nota acerca de las superficies aplicables sobre el plano: Hermite intentó oponerse a su inserción en los Comptes Rendus de l’Académie, esto ocurría más o menos en la época en que escribía…» …sigue el texto citado hace un momento).

El concepto de dimensión de homotecia D.
Curvas fractales cuya D está comprendida entre 1 y 2

Las longitudes de las aproximaciones sucesivas de la curva de von Koch pueden medirse exactamente y el resultado es muy curioso: tiene exactamente la misma forma que la ley empírica de Richardson referente a la costa de Bretaña, esto es: L(η) ∝ η^1−D. Una diferencia importante es que esta vez D no es una magnitud que haya de ser estimada empíricamente, sino una constante matemática que, como se ve fácilmente, vale log 4/log 3 ~ 1,2618. Este comportamiento permitirá definir la dimensión de homotecia, nuevo avatar de la dimensión fractal. Examinaremos aquí también otras variantes de la curva de von Koch a fin de calcular sus dimensiones, comprendidas todas ellas entre 1 y 2.

El procedimiento parte de una propiedad elemental que caracteriza el concepto de dimensión euclídea en el caso de objetos geométricos sencillos que poseen una homotecia interna. Se sabe que si se transforma una recta por una homotecia de razón arbitraria, cuyo centro esté contenido en la propia recta, se encuentra la misma recta, y lo mismo sucede con un plano y con el espacio euclídeo entero. Del hecho de que una recta tenga dimensión euclídea E = 1, se sigue que, cualquiera que sea el entero K, el «todo» constituido por el segmento de recta 0 < x < X puede ser «adoquinado» exactamente (estando cada punto recubierto una vez y sólo una) por N = K «partes», que son segmentos («semiabiertos») de la forma (k − 1)X/K ≤ x < kX/K, donde k varía entre 1 y K. Cada parte se obtiene del total por medio de una homotecia de razón r(N) = 1/N. Análogamente, del hecho de que un plano tenga dimensión euclídea E = 2, se sigue que, cualquiera que sea K, el todo constituido por el rectángulo 0 ≤ x < X; 0 ≤ y < Y, puede adoquinarse exactamente con N = K² partes, a saber, los rectángulos

variando k y h entre 1 y K. Ahora, cada parte se deduce del todo mediante una homotecia de razón r(N) = 1/K = 1/N^1/2. Para un paralelepípedo rectángulo, un argumento parecido nos da r(N) = 1/N^1/3. En fin, ya se sabe que no hay ningún problema serio en definir espacios de dimensión euclídea D, con D > 3; en este caso se tiene que r(N) = 1/N^1/D. Así pues, en todos los casos clásicos, en que la dimensión euclídea es «evidentemente» un entero, se tiene:

Esta última igualdad es la que vamos a generalizar. Para ello, observemos que la expresión de la dimensión, en tanto que exponente de homotecia, sigue teniendo un significado formal para toda figura que —como la curva de von Koch— sin ser un segmento ni un cuadrado, cumple que el todo es descomponible en N partes, las cuales se pueden deducir de él por una homotecia de razón r (seguida de un desplazamiento o de una simetría). Esto demuestra que, por lo menos formalmente, el dominio de validez del concepto de dimensión de homotecia va más allá de los paralelepípedos y que, como novedad, el D así obtenido no tiene por qué ser entero. Por ejemplo, en el caso de la curva de von Koch, N = 4 y r = 1/3, con lo que D = log 4/log 3. Se puede también variar la construcción de von Koch modificando la forma de los promontorios y añadiendo bahías como por ejemplo en las Figuras 44 y 45. Se obtienen así, en cierto modo, las primas de dicha curva, de dimensiones iguales a log 5/log 4, log 6/log 4, log 7/log 4 y log 8/log 4 = 1,5. Después, la Figura 47 muestra una variante, interpretándola a renglón seguido de una nueva manera concreta.

Es fácil verificar que ninguna de nuestras curvas al estilo de von Koch tiene puntos dobles. Pero no tendría ya por qué ocurrir lo mismo si se extendiera la misma construcción con la esperanza de obtener un valor de D demasiado grande. Por ejemplo, la Figura 49 muestra qué ocurre en el caso r = 1/3, N = 9. Formalmente obtenemos D igual a 2, pero la curva límite correspondiente, que es una curva de Peano, tiene inevitablemente una infinidad de puntos dobles; se sigue de esto que, para dicha curva, el concepto de adoquinado cambia de significado, y que la definición de homotecia es, en estos casos, discutible.

Supongamos que una figura sea descomponible en N partes tales que, dos a dos, no tienen ningún punto común, pero que cada una sea deducible del total por una homotecia de razón r_n, seguida eventualmente de una rotación o una simetría. En el caso en que todas las r_n sean idénticas, sabemos que la dimensión de homotecia es D = log N/log (1/r). A fin de generalizar este concepto, consideremos g(d) = Σ^N_n=1, r_n^d como función de d; cuando d varía de 0 a ∞ esta función decrece continuamente desde n a 0, y pasa una vez y sólo una por el valor 1. Así pues, la ecuación g(d) = 1 tiene una única raíz positiva, que designaremos por D, y que generaliza la dimensión de homotecia.

D conserva un cierto sentido cuando las partes tienen puntos dobles en cantidad «suficientemente pequeña»; en otras palabras, en general hay que tratar la D formal con precaución; la falta de atención puede llevar a los peores absurdos, como se ve en la Figura 50.

Sentido físico de las dimensiones fractales, cuando uno se niega a pasar al límite. Cortaduras interna y externa

Para obtener la curva de von Koch, el mecanismo de adición de nuevos promontorios, cada vez menores, se extiende indefinidamente. Ello es indispensable para que se verifique la propiedad de homotecia interna, y para que, por consiguiente, una definición u otra de la dimensión fractal tenga sentido. Resulta que, en el caso de las costas, la suposición según la cual los promontorios se van añadiendo indefinidamente es razonable, aunque la homotecia interna no sea válida más que dentro de ciertos límites. En efecto, para escalas sumamente pequeñas, el concepto de costa ya no pertenece a la geografía. Hablando estrictamente, el detalle de la interfase entre el agua, el aire y la piedra pertenece a la física molecular; es pues necesario detenerse antes, y preguntarse qué es lo que ocurre cuando el paso al infinito está prohibido.

Es razonable suponer que la costa real está sometida a dos «cortaduras». Su «cortadura externa» Λ se mide en decenas o centenares de kilómetros; para una costa que no formara bucles, Λ podría ser la distancia entre los dos extremos; para una isla, Λ podría ser el diámetro del menor círculo que contenga toda la costa. La «cortadura interna», por su parte, se mide en centímetros.

Sin embargo, aún en este caso, el número D conserva el significado de una «dimensión física efectiva», bajo la forma en que se ha descrito este concepto en el Capítulo 1. Tanto intuitiva como pragmáticamente (desde el punto de vista de la simplicidad y de la naturaleza de los términos correctivos necesarios), una aproximación de alto grado a la curva original de von Koch se acerca más a una curva de dimensión log 4/log 3 que a una curva rectificable de dimensión 1. En suma, una costa es como un ovillo de hilo. Es razonable decir que, desde el punto de vista de la geografía (es decir, en la zona de las escalas comprendidas entre un metro y cien kilómetros), la dimensión de la costa es el D estimado por Richardson. Lo que no excluye que, desde el punto de vista de la física, tenga una dimensión distinta, que estará asociada al concepto de interfase entre agua, aire y arena, y que sería por ello insensible a las variadas influencias que dominan la geografía.

Resumiendo, el físico tiene razón al tratar el paso al límite matemático con prudencia. La dimensión fractal implica un paso de este tipo, y es por tanto motivo de sospecha. He perdido la cuenta de las veces que un físico o un ingeniero me lo han hecho notar. Es quizás a causa de esta desconfianza que el papel físico de la dimensión fractal no se ha descubierto antes de mis propios trabajos. Pero vemos que, en el caso que nos ocupa, la aplicación de lo infinitesimal a lo finito no ha de provocar ningún temor si se hace con prudencia.

LÁMINA 41. Longitudes aproximadas de las costas, según Lewis Fry Richardson

En el caso del círculo, que esta figura trata como si fuera una curva empírica, se ve claramente que la longitud aproximada L(η) varía como debe: tiende hacia un límite para η → 0. En todos los casos restantes, L(η) crece indefinidamente. Esta figura se ha tratado en coordenadas bilogarítmicas; si se denota la pendiente de cada gráfica por 1 − D, ésta nos da el método más directo de estimación de la dimensión fractal D.

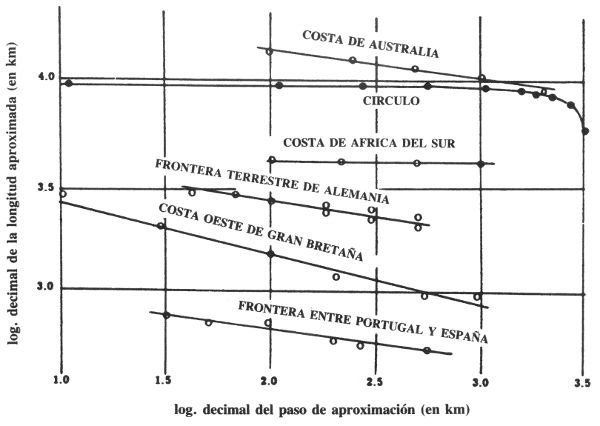
FIGURA 41

LÁMINAS 42 y 43. La curva de von koch y la isla quimérica en forma de copo de nieve

El ejemplo clásico de curva continua no rectificable y con homotecia interna lo constituye el tercio inferior del límite del presente diagrama. Éste se denomina «Curva de von Koch» y el interior de la curva se llama a menudo «copo de nieve», aunque yo prefiero la denominación «Isla de von Koch».

FIGURA 42

La construcción de la figura 42 parte de una isla en forma de triángulo equilátero. A continuación, en el tercio central de cada uno de los tres lados, se dispone un cabo en forma de △ con los lados iguales a un tercio. Se obtiene así un hexágono regular estrellado o Estrella de David, cuyo perímetro tiene una longitud de 12 × 1/3 = 4. Se hace lo mismo con cada uno de sus 12 lados, y así sucesivamente, obteniendo como resultado la figura 43a.

FIGURA 43a

Se constata fácilmente que la isla de von Koch se inscribe de forma natural en un hexágono regular convexo. De ahí un segundo método de construcción, en cierto modo inverso del descrito más arriba, que consiste en suprimir bahías de un hexágono. Cesàro ha combinado ambos métodos y la figura 43b muestra cómo se obtiene la curva, esto es, el contorno de la isla de von Koch, como límite de una superficie más y más deshilada.

FIGURA 43b

LÁMINAS 44 y 45. Método de von Koch generalizado

Cada una de las gráficas de más abajo nos proporciona la receta de construcción de una generalización de la curva de von Koch. En cada caso, r = 1 /4, con lo que la dimensión es una fracción de denominador log (1/r) = log 4. La construcción parte del intervalo [0,1], lo sustituye luego por uno de los «generadores» A, B, C, ó D, a continuación sustituye cada segmento del generador por una reducción a 1/4 del propio generador, y así sucesiva e indefinidamente. Es importante subrayar que ninguna de estas curvas tiene puntos dobles, contrariamente a lo que ocurre con la curva de Peano de la Figura 49.

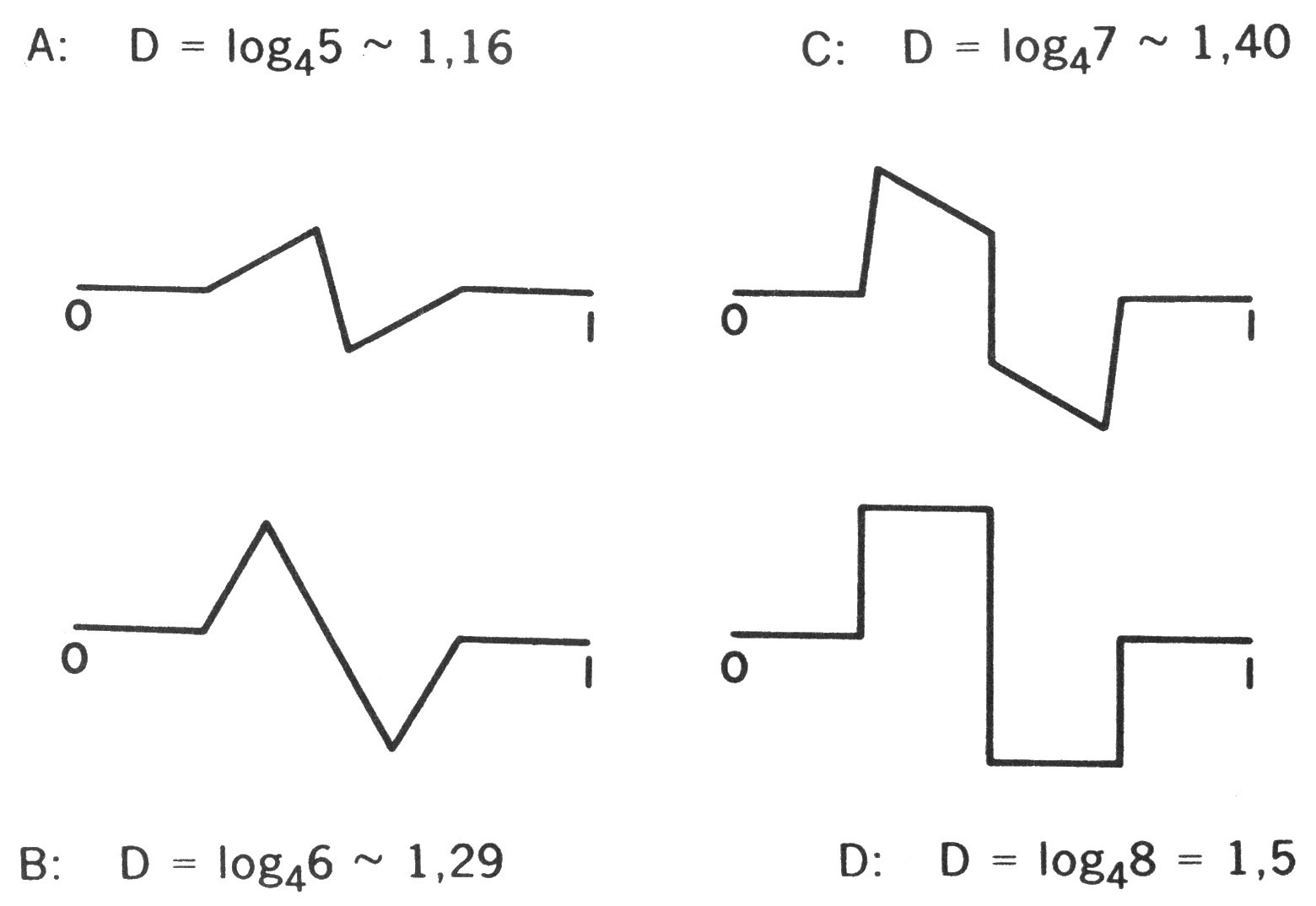
FIGURA 44

Cuatro iteraciones a partir de los generadores A ó D dan como resultado las aproximaciones a las curvas fractales que se muestran en la figura siguiente. La curva F tiene una dimensión excesiva comparada con la mayoría de las costas naturales. Por el contrario, la curva E tiene una dimensión demasiado pequeña.

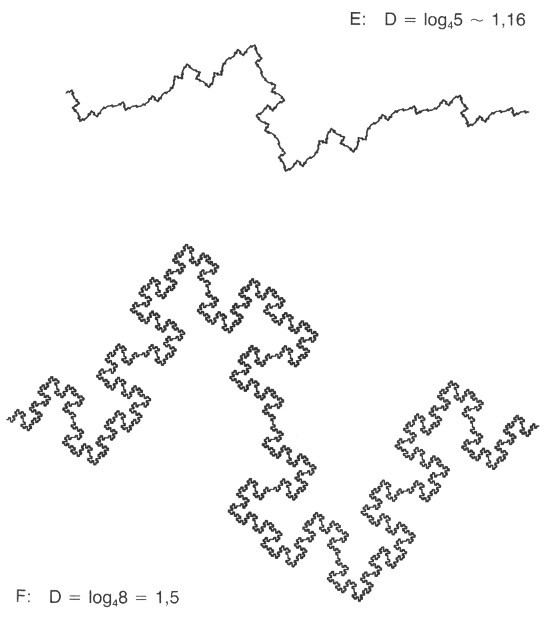
FIGURA 45

Cuando el diagrama de la figura 44 no tiene segmentos verticales, define una función y = f₀(x); este hecho, puede servir igualmente para la construcción siguiente.

f₁(x) se define como la función periódica, de período 1/4, igual, para 1 ≤ x < 1/4, a 3⁻¹ f₁(4x). Asimismo, f_n(x), de período 4⁻ⁿ, será igual para 0 ≤ x < 4⁻ⁿ, a 3⁻ⁿ f₀(4ⁿx). La serie Σf_n(x) obtenida así es convergente por doquier, y su suma es continua, pero no es derivable. Weierstrass estudió una construcción bastante parecida, y mucho más conocida, en la que las «partes» f_n(x) son sinusoides.

LÁMINA 47. Esquema arborescente del pulmón

FIGURA 47

Esta figura, una variante de la construcción de von Koch es interpretada como modelo de un corte de pulmón. De hecho, se trata de un modelo mediocre, pero suficiente para aclarar la relación existente entre, por una parte, las conexiones que permiten a este órgano establecer un contacto íntimo entre el aire y la sangre, y por otra, el concepto de objeto fractal.

Como indica el pequeño diagrama arriba a la izquierda, en la página 47, cada pulmón toma la forma de un triángulo isósceles, con el vértice ligeramente obtuso (ángulo de 90°+ε), y el contorno de la tráquea corresponde a un ángulo de abertura 2ε. En cada dirección sale un bronquio de ángulo 2ε, que divide el pulmón correspondiente en dos lóbulos, el superior y el inferior, ambos delimitados por triángulos isósceles semejantes al contorno inicial, con una razón de proporcionalidad 1/[2 cos(π/4 − ε/2)], esto es, algo menos de 0,707. Paralelamente, de cada segmento del contorno externo parte un triángulo de carne que divide el lóbulo correspondiente en dos sublóbulos. Se van añadiendo así, por orden, sub-sub-bronquios y sub-sub-triángulos de carne. Después de algunas iteraciones, el resultado es el que se observa en la figura central. Siguiendo indefinidamente con la misma construcción, se acabaría con la sección de un pulmón ideal, una curva de longitud infinita y de dimensión D algo menor que 2. Extrapolando a tres dimensiones, se tendría una superficie pulmonar de dimensión algo menor que 3.

Volviendo al plano, la identidad de los lóbulos superior e inferior es muy poco realista. También lo es el hecho de que el modelo prediga la misma área para las secciones del conjunto de los bronquios y del tejido. Además, los bronquios de verdad se bifurcan en sub-bronquios laterales. Estos defectos del modelo son todos ellos fáciles de corregir, gracias a la generalización de la homotecia interna descrita hacia el final del Capítulo 2 e ilustrada por la Figura 50.

En el límite ε = 0 y D = 2, la construcción sufre un cambio cualitativo; se obtiene la curva de Peano de la Figura 134, que es una variante de la de la Figura 49.

LÁMINA 49. La curva original de Peano

FIGURA 49

La denominación «curva de Peano» se aplica genéricamente a toda una familia de curvas patológicas que, desde 1890 hasta 1925, han jugado un papel decisivo en la elaboración del concepto de dimensión topológica, y que suministran un ejemplo maravilloso de las relaciones entre la dimensión topológica y la dimensión fractal. Para obtener la versión que se ilustra aquí, la curva originalmente debida a Peano se ha girado 45°, de modo que muestra un estrecho parentesco con la curva de von Koch. La primera aproximación es el intervalo de longitud 1. La segunda aproximación es el generador del diagrama A; incluye los tres tercios del intervalo de longitud 1, y añade seis intervalos de longitud 1 /3 que forman con el tercio central de la primera aproximación una especie de «ocho» en doble cuadrado. Para indicar cómo se recorre el generador el trazo se oscurece progresivamente y luego se aclara. El diagrama B muestra un cuadrado y el C muestra lo que ocurre si el generador se sitúa sobre cada lado del cuadrado. Todo lo que está «a la derecha» de las copias del generador (bordeando el cuadrado en el sentido de las agujas del reloj) aparece en negro. El diagrama D separa los puntos dobles del diagrama B, haciéndolo así más legible. Las aproximaciones tercera y cuarta (diagramas E y F) sustituyen los tercios centrales de cada segmento de la aproximación anterior por un ocho cuadrado, separando los puntos dobles como en el diagrama D.

En los estados finitos pero avanzados de la construcción, se ve aparecer una forma extraña que podemos llamar «isla de Peano». Su contorno es un cuadrado cuya superficie dobla a la del cuadrado B; las bahías penetran tan profunda y homogéneamente, que toda región termina por distribuirse a partes aproximadamente iguales entre el agua y tierra firme.

La curva de Peano establece una correspondencia continua entre el contorno del cuadrado inicial y el interior del contorno final, pero esta correspondencia no es exacta. La curva, en efecto, tiene un número infinito de puntos dobles, lo cual es inevitable —véase, en el Capítulo 14, la definición de dimensión topológica—. Subrayemos que estos puntos dobles no han podido ser indicados con claridad en el gráfico, dado que habrían hecho imposible seguir la continuidad de la curva; de hecho, por todos lados donde se ven dos puntos muy próximos, éstos se hallan, en realidad confundidos. Otra correspondencia entre una curva y el plano se establece a través del movimiento browniano llano (Figura 57), el cual puede ser considerado como una versión estocástica —yo la llamo «randonizada»— de la curva de Peano. Si se prescinde de contar repetidamente los puntos dobles, la curva de Peano revela tener hemotecia interna y una dimensión fractal igual a 2, conforme cubre el plano.

LÁMINA50. Trampas a evitar en el estudio de la homotecia interna generalizada

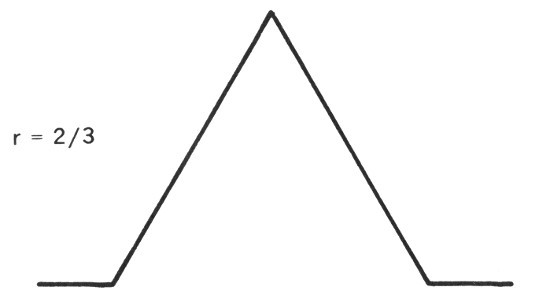
FIGURA 50

Otra manera de generalizar la curva de von Koch tiene como generador la línea quebrada dibujada aquí. La curva fractal que se obtiene así se puede recubrir con cuatro figuras, que se pueden deducir del total por homotecias de razones (1 − r)/2, r y (1 − r)/2, respectivamente, con 0 < r < 1. La dimensión formal se define entonces como el número D que satisface Σr_n^D = 1. Cuando r es suficientemente pequeño, incluido el caso clásico r_n = r = 1/3, esta dimensión formal se identifica con la de homotecia. Pero esta identificación tiene sus límites. En particular, es necesario que D < 2 en el plano; ahora bien, cuando r > r₂ = (1 + √6)/5 ~ 0,6898, la dimensión formal es superior a 2. La clave de la paradoja estriba en que la homotecia interna sólo tiene sentido estricto si no hay puntos dobles, cosa que no ocurre aquí más que si r permanece menor que un cierto valor crítico r_c, que acabamos de establecer que no puede superar r₂ = 0,6898. Más allá de r₂, una gran cantidad de puntos son contados muchísimas veces, y de ahí que la D formal supere la dimensión E = 2 del espacio envolvente. El caso r = 1, que daría D = ∞, ha de ser forzosamente excluido, puesto que, en este caso, la construcción de von Koch no converge hacia ningún límite.

Capítulo 2 ¿Cuánto mide la costa de Bretaña?

Capítulo 2
¿Cuánto mide la costa de Bretaña?