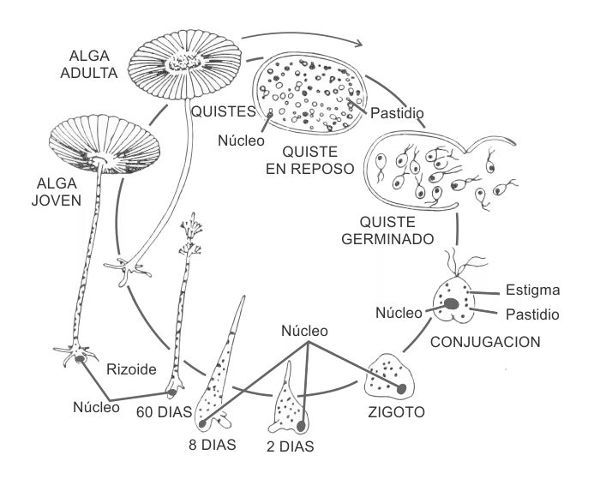
FIGURA 2.
Ciclo vital de Acetabularia acetabulum.
Cortesía de Brian Goodwin.
«Me miraron como si estuviera loco», recordó Stuart Kauffman. «Allí estaba, barajando mi paquete de tarjetas, y luego entregándoselas al programador». Eso fue en 1965, en la época en que había que alimentar el ordenador con una serie de tarjetas perforadas que contenían el programa y los datos. «La era del vapor». Para que el programa funcionara, las tarjetas tenían que estar en perfecto orden, todo el mundo lo sabía. Una tarjeta fuera de lugar y lo más probable era que la máquina produjera basura. «Y allí estaba yo, barajando mis tarjetas de datos, desordenándolas. No es de extrañar que me miraran con una sonrisa burlona».
Stu tenía entonces veinticuatro años, estudiaba segundo de medicina en la Universidad de California, San Francisco. Sin embargo, la incursión en el centro de cálculo de la facultad de Medicina no tenía nada que ver con sus estudios oficiales. Estaba allí para demostrar que tenía razón y que toda la comunidad biológica, desde Darwin en adelante, se equivocaba. «No era una empresa modesta», admitió Stu, mientras hablábamos en su desordenado despacho del departamento de bioquímica de la Universidad de Pennsylvania. «Pero estaba firmemente convencido de que yo tenía razón».
Conocí a Stu en un congreso científico sobre ritmos circadianos, en Berlín, hacía casi veinte años. El congreso había sido una mezcla de biología básica y extrañas —para mí— matemáticas, exactamente la clase de combinación intelectual con la que Stu y sus amigos disfrutaban. Stu siempre tiene que estar entusiasmado por alguna idea. «Es la persona con mayor índice boca-cerebro que conozco», me dijo una vez un colega y amigo íntimo suyo. «Y estamos hablando de una inteligencia privilegiada». Al parecer, la Fundación McArthur estuvo de acuerdo y le concedió una de sus prestigiosas becas para «genios». De modo que, cuando llamé a Stu a principios de 1990 y me dijo: «¿Por qué no vienes a Penn y te hablo de la complejidad? Es algo nuevo y va a ser muy importante», supe que tenía que ir. Iba a ser mi introducción a la complejidad como ciencia por derecho propio. Eso ocurrió en la primavera anterior al encuentro de Santa Fe sobre sociedades prehistóricas sudoccidentales.
A toda velocidad y con una característica mezcla de jerga y lúcidas metáforas, Stu explicó cómo una certeza interior lo había empujado a ese extravagante experimento informático en su época de estudiante de medicina, una certeza de que la explicación convencional de los orígenes del orden en el mundo de la naturaleza tenía que estar equivocada. Hay orden en todas partes, en las semejanzas morfogenéticas entre los grupos de organismos y en el modo notable en que los organismos individuales operan en sus respectivos medios, como si estuvieran cuidadosamente diseñados. El fenómeno había fascinado a los estudiosos desde los tiempos de Aristóteles. Y, a mediados del siglo XVIII, el sueco Carl von Linné agrupó los organismos conocidos según las semejanzas que presentaban en su Systema Naturae, una clasificación que los biólogos siguen utilizando hoy en día. La explicación convencional de todo ese orden es la selección natural, que los biólogos han considerado, a partir de Darwin, como la fuerza que hace encajar a los organismos en sus respectivos nichos. Las semejanzas entre grupos son el resultado de la descendencia común, «descendencia con modificación», como Darwin la describió.
«Se consideraba que la selección natural era la única fuente de ese orden, una fuerza omnipotente capaz de producir más o menos cualquier clase de forma biológica, dadas las circunstancias adecuadas», dijo Stu. «No me preguntes cómo, pero sabía que eso no podía ser así, que ahí afuera tenía que haber una gran cantidad de orden espontáneo». ¿Orden espontáneo? Eso huele a vitalismo, insinué, una noción antaño popular pero hoy desacreditada según la cual gran parte de las maravillas del mundo natural es consecuencia de un élan vital, o espíritu vital. Esta noción no explicaba tanto la naturaleza como la justificaba y, para la ciencia moderna, es anatema. «No me refiero a eso, por supuesto», respondió Stu. «Me refiero a que la autoorganización es una propiedad natural de los sistemas genéticos complejos. Ahí fuera hay “orden gratis”, una cristalización espontánea del orden a partir de sistemas complejos, sin necesidad de selección natural o de cualquier otra fuerza externa. Lo tenía claro en la facultad de medicina y lo sigo teniendo claro ahora».
Stu sigue siendo incapaz de dar plena cuenta de su vieja convicción de que el saber convencional tiene que estar equivocado. Algo que sin duda tiene que ver con su educación claramente no convencional. Había llegado a Dartmouth en el otoño de 1957 con la intención de convertirse en dramaturgo, no un dramaturgo corriente sino un Gran Dramaturgo. «Es inútil ser un escritor de teatro corriente». Tres semanas y dos obras mediocres más tarde y, animado por un amigo que había ido a Harvard, Stu decidió que sería un Gran Filósofo. «Los jóvenes se meten a estudiar filosofía porque están interesados por la ética, la mente, esa clase de cosas buenas», explicó.
Con un diploma en filosofía de Dartmouth (Phi Beta Kappa), Stu recibió una beca Marshall que lo llevó a la Universidad de Oxford en el otoño de 1961, donde estudió filosofía, psicología y fisiología en Magdalen College, uno de los cursos más prestigiosos en una de las facultades más prestigiosas de esa antigua universidad. «Fue una época maravillosa», declaró, colocando los brazos detrás de la nuca, resbalando en su crujiente silla y estirando las piernas, mientras lo inundaban los recuerdos. «Escalar los muros de la facultad por la noche y ese estilo de cosas». ¿Y lo de convertirse en un Gran Filósofo?, pregunté. «Pues llegué al siguiente silogismo: “Para llegar a ser un filósofo que valiera la pena tenías que ser tan listo como Immanuel Kant. Yo no soy tan listo como Immanuel Kant. Por lo tanto, decidí ser médico”. ¡Con ese tipo de razonamiento no es de extrañar que no fuera un Gran Filósofo!».
Aunque consideró que sólo tenía un nivel normal en filosofía, Stu descubrió su habilidad para inventar teorías que explicaran cualquier problema con el que se enfrentara en psicología, incluyendo algunos aspectos de las redes neuronales. Lo hacía tan bien que consideró el don como si se tratara de cierta facilidad de palabra y decidió dedicarse a algo más sólido. La facultad de medicina le proporcionaría la disciplina necesaria que deseaba adquirir. En primer lugar, sin embargo, tenía que cursar un año de estudios previos, un curso especial de Berkeley diseñado para obtener algunos conocimientos básicos de biología, incluyendo la embriología. Eso ocurrió en 1964, cuando Berkely ardía —literalmente— de radicalismo. «No participé mucho en las manifestaciones. Pero más tarde, durante el tercer año de medicina, firmé una declaración según la cual me negaba a servir en Vietnam. Poco después vi una flotilla entrando en la bahía, un portaaviones, varios acorazados y demás, y pensé: “Muchacho, van a hacer falta muchas firmas para parar esto”».
Los primeros años de la década de 1960 fueron también una época muy especial para la biología molecular, porque en los años anteriores dos investigadores franceses, François Jacob y Jacques Monod, habían realizado importantes avances en la comprensión de la regulación de la actividad de los genes. Habían descubierto la existencia de mecanismos de retroalimentación por medio de los cuales los genes se activaban o desactivaban, una especie de servosistema a nivel molecular análogo también al sistema conmutador binario de los ordenadores digitales. El trabajo no tardó en recibir el reconocimiento del comité Nobel. «Estaba muy entusiasmado por aprender esas cosas», dijo Stu. «Empezó a obsesionarme la embriología, en particular el modo en que las células embrionarias se diferencian, forman células musculares, células nerviosas, células del tejido conjuntivo, etcétera; el modo en que los cien mil genes de la dotación genética humana podían producir esa asombrosa combinación de tipos celulares diferentes, unos 250 en total. Todo iba encajando, las ideas de Jacob/Monod, incluso las redes con las que había estado trabajando en Oxford». La embriología, el modo en que una única célula fertilizada se multiplica, diferencia y combina para dar lugar a un organismo adulto, era y sigue siendo uno de los mayores desafíos de la biología. El joven Kauffman estaba listo para enfrentarse a él, equipado con la más exigua base biológica y con sólo un rudimentario dominio de las herramientas matemáticas que planeaba aplicar.
«Mi ignorancia fue mi fuerza», dijo con toda seriedad. «De haber tenido una formación biológica adecuada y conocimientos de matemáticas, habría sabido que lo que pretendía no iba a funcionar. No lo habría intentado». Stu llegó a la conclusión de que era casi imposible que la selección natural orquestara la actividad de los cien mil genes del genoma humano para generar una gama de alrededor de 250 tipos celulares diferentes. Eso representa 250 pautas diferentes de actividad génica. «¿Sabes cuántos estados potenciales de actividad hay en la combinación de cien mil genes?», preguntó sin esperar la respuesta. «1030.000. Es una cantidad muchísimo más grande que el número de átomos de hidrógeno del universo. Algunas personas sostienen que la selección natural conduce con éxito a través de las ciénagas de esos 1030 000 estados del sistema, para dar al final con los 250 deseados. Pero yo tenía una solución diferente, impensable y completamente contraintuitiva».
«Imagina que los genes están dispuestos como una red, en la que cada uno está activo o inactivo en función de las entradas que recibe de los otros genes», empezó Stu. Eso suena a una red de proceso en paralelo, dije. «Exacto. Pero imagina que los vínculos entre los genes están asignados de modo aleatorio. ¿Pensarías obtener un orden de todo eso?». Inexperto en esas cuestiones, supuse sin embargo que era improbable. Stu también lo habría considerado improbable de haber sabido, siendo estudiante de medicina, que varios grandes nombres de las matemáticas y la informática habían experimentado ya con sistemas similares y no habían encontrado nada interesante. «El resultado contraintuitivo es que se obtiene orden, y de la manera más notable».
Los sistemas de ese tipo se conocen con el nombre de redes booleanas aleatorias, en honor al inglés George Boole, inventor de un enfoque algebraico de la lógica matemática. La red procede a través de una serie de estados. En un momento dado, cada elemento de la red examina las señales que le llegan de las relaciones que tiene con otros elementos y se activa o desactiva, según sus reglas para reaccionar a ellas. A continuación, la red alcanza el siguiente estado, donde el proceso se repite otra vez. Y así sucesivamente. Bajo ciertas circunstancias una red puede recorrer todos los estados posibles antes de repetir cualquiera de ellos. Sin embargo, en la práctica, la red llega en algún punto a una serie de estados por los cuales gira repetidamente. Conocida con el nombre de ciclo límite, esta serie repetida de estados es, en realidad, un atractor en el sistema, como el remolino en el traicionero mar de la dinámica de los sistemas complejos. Una red puede concebirse como un sistema dinámico complejo, y es probable que tenga muchos atractores de ese estilo.
«Pasaba horas trabajando a mano en las redes», explicó Stu. «Mis cuadernos de farmacología están completamente llenos de ellas». Debido a que, incluso en redes pequeñas y poco conectadas, el número de estados posibles crece con rapidez al aumentar el número de elementos, las redes calculadas a mano pronto se hicieron inmanejables. Con más de ocho elementos, se hacía necesario un ordenador. «Conseguí que alguien me enseñara a programar y me preparé para la primera prueba, una red con cien elementos, con dos entradas cada uno, asignadas aleatoriamente. Por eso tenía que barajar las tarjetas de datos». Quien entró ese día de verano de 1965 en el centro de ordenadores era un joven con una intuición extraordinaria o un loco. La mayoría de los expertos se habrían inclinado por lo último, puesto que incluso esa modesta red tenía unos 1030 estados posibles, sólo 100 billones de veces la edad del universo, medida a razón de un estado por segundo. El ordenador funcionaba mucho más rápidamente que un estado por segundo; aun así, de haberse aventurado la red por el más insignificante de los caminos de su territorio de estados posibles antes de dar con un ciclo límite, el programa habría estado ejecutándose durante días y Stu se habría arruinado, puesto que él mismo pagaba el tiempo de ordenador.
«Había que ser muy ingenuo para hacer lo que hice», dijo Stu con una gran mueca. «Pero tuve suerte. El ordenador llegó a un ciclo límite tras pasar sólo por dieciséis estados, y el ciclo era de sólo cuatro estados. Me dije: “Dios mío, he encontrado algo profundo”. Y sigo pensándolo. Es la cristalización del orden a partir de sistemas masivamente desordenados. Es orden espontáneo».
Stu cursaba entonces el segundo año de carrera, con los estudios médicos bastante desatendidos mientras crecía en él la obsesión por las redes booleanas. Cuando no estaba computando redes, exploraba la bibliografía, gran parte de la cual le era extraña. Entonces, con una profunda conmoción, encontró un libro publicado en 1963 titulado Temporal Organization in Cells. Su autor, Brian Goodwin, había estudiado biología en la Universidad McGill, en Canadá, luego matemáticas en Oxford unos pocos años antes que Stu y se había doctorado en la Universidad de Edimburgo con C. H. Waddington, una de las principales figuras recientes de la biología británica. Waddington estaba firmemente convencido de que los organismos debían ser estudiados como globalidades y que el principal reto de la biología era comprender la génesis de la forma. Entusiasmado por este enfoque holístico, Brian lo integró en la biología molecular de Jacob y Monod y produjo una teoría sobre el modo en que la actividad génica junto con niveles oscilantes de sustancias bioquímicas podían contribuir a crear formas biológicas.
«Pensé, vaya, él lo ha encontrado primero», dijo Stu recordando su primera reacción ante el libro. «Luego pensé, un momento, no entiendo esto. ¿Qué es todo esto? Al final me dije: “Se ha equivocado. No sé por qué, pero estoy seguro de que se ha equivocado”». El libro era un intento de demostrar cómo los sistemas de control moleculares, como la retroalimentación, la represión, el control de la actividad enzimática —en otras palabras, la lógica local intrínseca de un sistema complejo—, daban lugar natural y espontáneamente a un comportamiento oscilatorio y a pautas globales. Semejante comportamiento es un componente importante de los sistemas vivos, como los ritmos circadianos y la actividad periódica de los sistemas hormonales y enzimáticos. El núcleo del libro —la generación del orden como un producto inevitable de la dinámica del sistema— estaba en profunda sintonía con la visión del mundo de Stu. Inmediatamente envió a Brian un ejemplar de los primeros resultados con redes booleanas, pero no establecieron ninguna correspondencia. «Stu no es un gran corresponsal, es incluso peor que yo», me dijo Brian. «Prefiere hablar; y, entonces, la experiencia es intensa. Unas pocas horas con Stu equivalen a semanas con cualquier otra persona».
Sabía lo que quería decir. Una conversación con Stu es como un combate entre una pistola de agua y una manguera de incendios: un flujo bastante unidireccional. Pero cada gota vale la pena. La conversación había llegado a un punto en que necesitaba un descanso, y Stu y yo nos dirigimos a un pequeño restaurante indio cerca del campus, la clase de lugar en que se puede escribir en la mesa. Le pregunté en tono especulativo si el auge y la caída de las sociedades complejas podría describirse también por medio de la ciencia de la complejidad. Una idea extraña, dije, pero he estado leyendo estudios sobre el auge y la caída de las civilizaciones a lo largo de la historia, y al espectador inexperto que era le había parecido que la repetición de la pauta «olía» a eso. «No he pensado nunca en ello», dijo Stu tras unos instantes de reflexión. «Pero no, no lo creo.» (Seis meses después había cambiado de opinión, y me llamó triunfante para decírmelo. En esa comida, sin embargo, estaba mucho más concentrado en las redes booleanas).
Admití que lo del orden espontáneo a partir de las redes booleanas era impresionante. ¿Pero no sería poco más que una analogía, una imagen seductora? «Es una especie de analogía, sin duda, pero es profunda. Mira». Stu empezó a describirme los innumerables experimentos que había hecho, que demostraban la emergencia de dos propiedades de naturaleza muy biológica. La primera se refería al número de tipos celulares que se encuentran en una gama de diferentes organismos de distinta complejidad y al modo en que pudieron haberse generado. La segunda se relacionaba con las limitadas posibilidades que tiene cualquier tipo celular de transformarse en otros tipos celulares.
«Llegué a la firme convicción de que los ciclos límite de mis redes booleanas eran equivalentes a diferentes tipos celulares», dijo. «Es obvio. Se trata sólo de un nuevo enfoque de mi búsqueda de orden. Pero entonces empecé a calcular cuántos ciclos límite obtenía en las redes con dos conexiones. El número resultó ser de modo aproximado la raíz cuadrada del número de elementos del sistema. Una red de 10 tiene unos 8 ciclos límite, 8 atractores si quieres;[1] una red de 1000 elementos tiene unos 30 atractores, y así sucesivamente. Una red con 100 000 elementos, aproximadamente el número de genes del genoma humano, tiene unos 370 atractores, lo cual se acerca bastante al número conocido de tipos celulares, 254». Al poco de empezar esa investigación, Stu se enfrascó de nuevo en la bibliografía, en busca de información sobre el número de tipos celulares en una gama dada de organismos, en relación con el número estimado de genes. Obtuvo información sobre bacterias, la levadura, algas, un hongo, medusas, gusanos anélidos y humanos, representativos de los diferentes grupos principales, o tipos, que se separaron unos de otros en el Cámbrico, hace 600 millones de años. El resultado fue claro: cuantos más genes poseía un organismo, más tipos celulares tenía. Todo encajaba bastante bien, no era exacto pero las divergencias no eran muy grandes y, por lo tanto, era biológicamente razonable. Sin embargo, igual de importante era el hecho de que el número de tipos celulares de cada organismo coincidía aproximadamente con la raíz cuadrada del número de genes. Las redes booleanas y los genomas seguían la regla de la raíz cuadrada.
«Por lo tanto, o bien se me convence de que 600 millones de años de evolución han perfilado de forma independiente los genomas de los diferentes tipos de organismos para que todos generen tipos celulares según la raíz cuadrada del número total de genes», dijo Stu, «o se tiene que admitir que mis redes booleanas son algo más que una analogía interesante, que hay algo fundamental en la dinámica de esta clase de sistema».
Stu me pidió que imaginara las redes como colecciones de bombillas, rojas si están fijas, azules cuando cambian. En las redes con dos conexiones por elemento, grandes zonas de luz permanecen estables, invariables para casi todos los atractores, salpicadas con manchas de cambio. Era una imagen gráfica de titilantes islas azules en un mar rojo. «Las consecuencias de este modelo son dos», explicó Stu. «Si se trata de un modelo razonable para la generación de tipos celulares, todos los tipos celulares deberían expresar una mayoría de genes idénticos, con sólo una pequeña fracción diferente». Esto, por lo que yo sabía, era correcto.
«Así es. La segunda consecuencia —y ésta es la segunda de las dos características biológicas de las redes— es que los atractores resisten la perturbación: las mutaciones en las islas no se propagan muy lejos. Pero, cuando cambian, sus opciones están limitadas por los atractores cercanos». Podía imaginar las titilantes islas comportándose de ese modo, y que su aislamiento en un mar congelado de color rojo restringiera su comportamiento frente a la perturbación. «Esto es otra vez lo que vemos en los sistemas vivos. Durante el desarrollo, los tipos celulares progresan por caminos muy limitados. Una vez que una célula ha emprendido un camino particular deja tras ella muchas otras opciones, y disminuye el número de tipos celulares diferentes en los que puede transformarse».
Entonces, pregunté, ¿la propiedad clave del sistema es que las reglas locales, el número de entradas que cada «gen» recibe y las reglas para responder a ellas, generan un orden global en el sistema? «Así es». ¿Una propiedad emergente? «Sí, es impredecible y contraintuitivo. Orden espontáneo. ¿No es hermoso?». Era hora de marcharse.
***
Si las redes booleanas aleatorias explican el modo en que podrían generarse los tipos celulares, ¿qué ocurre con el segundo componente principal de la embriología, el modo en que las células se combinan en un individuo maduro? «Ve a ver a Brian Goodwin», me urgió Stu. «Él es el poeta de la biología teórica». Los dos hombres se conocieron en 1967, en el Instituto de Tecnología de Massachusetts. Con anterioridad, ese mismo año, Stu había enviado sus resultados sobre redes booleanas a Warren McCulloch, un pionero en la teoría de redes. McCulloch había contestado enseguida con una característica hipérbole («Todo Cambridge se ha entusiasmado con su trabajo») e invitó a Stu y Elizabeth, su reciente esposa, a pasar tres meses en su grande y laberíntica casa de Cambridge. El MIT era el lugar donde había que estar, albergaba a todos los grandes nombres en el estudio de los sistemas de proceso en paralelo y a algunos de los investigadores punteros del campo de la biología teórica, incluyendo a Brian Goodwin durante una época.
Stu y Brian enseguida se dieron cuenta de que sus enfoques a la búsqueda de orden en biología no entraban en conflicto sino que eran complementarios, y entablaron una fuerte relación personal y profesional. Brian se estaba convirtiendo ya en una importante figura de la biología teórica y no tardó en destacar como inteligencia eminente. También es conocido por ocupar una posición extrema en el espectro intelectual.
«Poeta de la biología teórica. Mmm. Supongo que Stu cree que tengo cierta visión», manifestó Brian cuando nos encontramos en su despacho de la Universidad a Distancia, en Milton Keynes, a unos ochenta kilómetros al norte de Londres. Su gran estatura, las distinguidas canas y el buen aspecto mediterráneo encajan sin duda con la parte de poeta. «Lo que pasa es que mucha gente podría pensar que eso es peyorativo». Le pregunté por la dedicatoria que había escrito en el ejemplar de Stu de Temporal Organization in Cells. Decía: «No hay verdad más allá de la magia». ¿Qué quería decir? «En realidad, dos cosas. La primera es que, en ciencia, cuando descubres la verdad, resulta que posee una extraordinaria cualidad mágica. Ésa es la clave: al reconocer el orden profundo en la biología sientes que estás tocando algo fundamental. Pero también hay un sentido poético: la realidad es extraña. Mucha gente piensa que la realidad es prosaica. Yo no. En ciencia no justificamos las cosas. Nos acercamos al misterio». Suena romántico, insinué. «Si es una visión romántica de la ciencia, que lo sea. Sin ella, el mundo sería aburrido».
Me parecía que los osciladores químicos acoplados —el tipo de mecanismo que Brian había explorado en su libro y en el que todavía sigue interesado— estaban muy lejos de cualquier noción de misterio. «Te explicaré mi enfoque y lo verás». El problema fundamental de la biología es cómo se genera la forma, empezó Brian. «Mucho antes de Darwin, los estudiosos ya estaban fascinados por la forma biológica y por cómo ésta se relaciona con el mundo. Había dos enfoques muy diferentes: el enfoque angloamericano y el enfoque europeo continental, en especial el alemán».
El primero de ellos tenía sus raíces en la escuela de la teología natural, que se remonta al siglo XVIII. Se centraba en la función, en cómo funcionan los organismos. Pero su ideología dominante era que las maravillas del mundo proporcionaban la prueba de una Mano Divina. «Seguramente recuerdas el célebre pasaje al principio de la Natural Theology de Paley», continuó Brian. «La historia de alguien que encuentra un reloj en un brezal». Lo recordaba. Había comprado una edición de 1854 muchos años atrás —la primera se había publicado en 1802— y había releído varias veces los pasajes iniciales, todavía legibles a pesar de las manchas y la impresión defectuosa. «Supongamos que, al cruzar un brezal, mi pie tropieza con una piedra y me pregunto cómo había llegado esa piedra hasta ahí; seguramente podría responder que, por todo lo que sabía, había estado ahí desde siempre», empezaba. Y luego: «Pero supongamos que hubiera encontrado un reloj en el suelo y hubiera que averiguar cómo había llegado el reloj hasta ese lugar; difícilmente pensaría en la respuesta que había dado antes, que, por lo que sabía, podía haber estado siempre ahí».
Paley continúa explicando, en una larga analogía, que la existencia del reloj debe implicar un agente de diseño. «La diferencia, creemos, es inevitable; que el reloj debió de tener un fabricante; que debió de existir en algún momento, y en algún lugar, un artífice o artífices que lo creara con una finalidad cuya respuesta encontramos en la actualidad; que concibiera su construcción y diseñara su uso». El razonamiento se extiende entonces a la biología: «Las invenciones de la naturaleza superan las invenciones del arte, en complejidad, sutileza y curiosidad del mecanismo […]; sin embargo, en una multitud de casos, son no menos evidentemente mecánicas, no menos evidentemente invenciones, no menos evidentemente adecuadas a su fin, o su función, que las más perfectas producciones del ingenio humano». Y, pregunta Paley, ¿qué mejor ejemplo que el ojo, tan complejo, tan perfectamente adecuado a su papel?
«Ah, sí, el ojo», dijo Brian. «Incluso Darwin estaba preocupado por el ojo». En el Origen de las especies escribió: «Parece absurdo de todo punto —lo confieso espontáneamente— suponer que el ojo, con todos sus inimitables mecanismos para acomodar el foco a diferentes distancias, para admitir una cantidad variable de luz y para la corrección de las aberraciones esférica y cromática, pudo haberse formado por selección natural». No obstante, concluyó, puesto que «no hay imposibilidad lógica alguna —variando las condiciones de vida— en la adquisición por selección natural, de cualquier grado de perfección concebible», también el ojo es explicable por ese lento y gradual proceso de combinación.
Así, mientras Paley explicaba la exquisita morfología de los organismos en relación con su medio como una prueba del Designio Divino, Darwin la explicó como el resultado de la selección natural, la ciega adaptación de los organismos a las condiciones existentes en cada momento, los productos de la mutación aleatoria seleccionados de acuerdo con la supervivencia. «Ambas explicaciones se centran en la función: una es teológica, la otra científica. Pero creo que la segunda es casi tan errónea como la primera», dijo Brian. «Y sin embargo la noción de selección natural está hoy profundamente arraigada en nuestra cultura científica. Basta con acudir al celebrado libro de Richard Dawkins, El relojero ciego, para verlo». El título es un hermoso giro de la analogía de Paley de Dios el relojero, Dios el creador de la naturaleza. «Este libro se ha escrito con la convicción de que nuestra propia existencia, presentada alguna vez como el mayor de los misterios, ha dejado de serlo, porque el misterio está resuelto», empieza El relojero ciego. «Lo resolvieron Darwin y Wallace, aunque todavía continuaremos añadiendo notas a esta solución».
El libro es una ingeniosa y convincente exposición de la evolución por medio de la selección natural y no deja un lugar importante para otros mecanismos. «El argumento del punto de vista darwinista es que […] la selección natural lenta, gradual, acumulativa, es, en último término, la explicación a nuestra existencia», escribe Dawkins en el párrafo final. «Si existen versiones de la teoría de la evolución que nieguen el lento gradualismo, y el papel central de la selección natural, pueden ser ciertas en casos concretos. Pero no pueden constituir toda la verdad, porque niegan el verdadero centro de la teoría de la evolución, que le da el poder para disolver las improbabilidades astronómicas y explicar prodigios de un milagro aparente». Las redes booleanas aleatorias de Stuart Kauffman, vale la pena destacarlo, tienen el «poder para disolver las improbabilidades astronómicas» sin selección natural.
De modo que, pregunté a Brian, ¿estás buscando puntualizaciones a la teoría de Darwin? «Nada de eso. Necesitamos un libro nuevo».
La biología moderna ha perdido casi toda noción auténtica de «organismo», se lamentó Brian. «El organismo ha sido sustituido por una colección de partes: genes, moléculas y los componentes que se supone que forman los ojos, las extremidades o cualquier estructura en la que uno esté interesado». ¿Te refieres al enfoque reduccionista? «Exactamente». Pero el reduccionismo ha significado el triunfo de la biología moderna, al hacer la biología más parecida a la física, sugerí. Basta mirar lo que sabemos de la estructura de los genes, cómo se expresan, los increíbles detalles de la maquinaria metabólica que ahora se conocen. «Todo eso es cierto. No niego esos logros. Sólo insisto en que no dicen nada importante acerca de la forma biológica, de cómo se genera la forma». Stu me contó su analogía favorita: saber la estructura del H2O no ofrece ninguna pista de por qué el agua se va por un desagüe en un vórtice. «Necesitamos una noción de todo el organismo como una entidad fundamental en biología y luego comprender cómo eso genera partes que conforman su orden intrínseco», continuó. Eso suena un poco vago, sugerí. «Recuerda el congreso de Dahlem», contestó Brian, refiriéndose a un encuentro científico al que habíamos asistido los dos en Berlín una década atrás.
El congreso había sido sobre evolución y desarrollo y, en un momento dado, se produjo una enérgica batalla en torno a lo que hacía falta saber de verdad para comprender cómo se ensambla un organismo. Cáustico es mejor adjetivo que enérgico. De un lado, estaban los biólogos moleculares convencionales, que insistían en que todo quedaba claro cuando se conocía la secuencia de ADN de un organismo. «Las instrucciones de ensamblaje están escritas en los genes», era su posición. Del otro lado, estaba Brian y un pequeño grupo de biólogos moleculares heterodoxos, incluyendo a Gunther Stent, un destacado investigador de la Universidad de California, Berkeley. Stent era famoso —o, más bien, tenía mala fama— entre sus colegas por haber afirmado en un importante artículo de Science que la época dorada de la biología molecular había pasado, que ya no le quedaban desafíos intelectuales importantes. Otras vías del ámbito biológico, como el desarrollo embrionario, se enfrentarían a los problemas reales, había afirmado. «Los genes son sólo un principio», era el punto de vista Goodwin/Stent; «sin conocer la dinámica de las partes componentes no se va a ningún sitio». El debate no tuvo conclusión.
«Los biólogos moleculares descubrieron que la secuencia lineal de los nucleótidos en el ADN especifica de modo preciso la secuencia lineal de los aminoácidos en las proteínas», continuó Brian. «Nadie duda de su importancia. Pero cometieron el error de imaginar que, de modo similar, la secuencia lineal de los genes del genoma especifica la génesis de la forma en un embrión, de modo análogo a un programa de ordenador». Añadió enfáticamente: «No hay programa genético para el desarrollo, no hay programa que guíe el sistema a través de sus transiciones morfogenéticas». ¿No es eso afirmar que los genes son irrelevantes?, pregunté, pensando hasta dónde seguiría por esa línea de razonamiento. «No. Los genes establecen los valores de los parámetros». ¿Qué quiere decir eso? «Quiere decir que producen partes componentes del sistema, dentro de una gama de valores. Las transiciones morfológicas son entonces consecuencias del ciclo de la dinámica que genera geometría y la geometría que modifica la dinámica. Esto nos proporciona una visión que podría llamarse de “bufet libre” de la morfogénesis». Espera un momento, solicité. Vas más rápido que yo. ¿Es posible hacer todo esto un poco más tangible, algo que se pueda entender de modo intuitivo?
«Claro. Te enseñaré el modelo de Acetabularia».
Acetabularia acetabulum vive en las aguas poco profundas de las costas mediterráneas. Su ciclo de vida es regular y espectacular, empieza con la fusión de dos células «sexuales» que forman una sola célula, el zigoto. La célula única desarrolla rizoides y luego un tallo que llega a alcanzar los cinco centímetros de longitud. Este tallo produce anillos de «pelos» cerca de su extremo, el llamado verticilo. El verticilo acaba desplegándose al abrirse el extremo y formarse un disco, igual que el sombrero de un hongo.
«Mira esto», me dijo Brian mientras me enseñaba el verticilo en un dibujo de Acetabularia. «Es un misterio, o al menos lo era. No tiene ninguna función conocida, entonces ¿para qué está ahí? La explicación darwinista —la explicación funcionalista— sería que ha fracasado a la hora de encontrar su función o que una vez tuvo una que ahora es un simple vestigio». La verdad es muy diferente. Brian y varios colegas habían construido hacía poco un modelo matemático del desarrollo del organismo como forma de entender las transiciones morfogenéticas, los pasos principales que recorre el organismo en desarrollo. En esencia, el modelo incluye algunos aspectos de la regulación del calcio en la célula, los cambios del estado mecánico del citoplasma (elasticidad y viscosidad) y la respuesta de la pared celular. Ésos son los parámetros del sistema. «Biológicamente simple pero matemáticamente complejo», así describió Brian el modelo.
«Mira cómo se desarrolla la forma», dijo Brian mientras ejecutaba el modelo en un monitor. «Cuando empezamos a trabajar en esto esperábamos que serían posibles muchas pautas, que nos tomaría mucho tiempo encontrar los parámetros que simulaban la morfogénesis de Acetabularia». No fue así. Todo salió muy rápidamente, como si la forma de Acetabularia fuera una propiedad profunda del sistema, como un fantasma en una máquina molecular. Contemplé el modo en que el organismo pasaba por gran parte de su ciclo vital, mientras Brian explicaba el desarrollo de la dinámica del sistema.

FIGURA 2.
Ciclo vital de Acetabularia acetabulum.
Cortesía de Brian Goodwin.
«Algo que no habíamos entendido nunca es por qué y cómo el extremo inicialmente cónico se aplana antes de la formación del verticilo», dijo, siguiendo los cambios de la pantalla. «El modelo nos dio una explicación. El gradiente de calcio, con un máximo en el tallo, se vuelve inestable a medida que se produce el crecimiento, y da lugar a un anillo de elevada concentración de calcio y mayor tensión. La pared de este anillo se ablanda, debido a la combinación de la tensión citoplasmática y la elasticidad de la pared, de modo que la pared desarrolla una curvatura máxima en la región de este anillo y se aplana en la punta». Y así se forma el verticilo, dije viendo desarrollarse un anillo de cilios esquemáticos. «Sí». ¿Sólo como resultado de la dinámica del sistema? «Eso es. La razón por la cual todos los miembros de las dasicladáceas producen verticilos puede ser que ésa sea una forma natural que surge de los principios dinámicos contenidos en la organización de la célula. Algunas especies los utilizan, otras no, pero todas los generan».
Quedé sorprendido por el paralelismo con las redes booleanas de Stu Kauffman. ¿Las reglas locales generan orden global? «Sí. Es una propiedad emergente de los sistemas dinámicos. Concibo el desarrollo como un sistema dinámico. Volvamos al ojo».
Por diversas razones mecánicas, en Acetabularia y en las plantas, la generación de la forma está siempre acompañada de crecimiento, una expansión continua. Dado que no se encuentran tan restringidos mecánicamente, los embriones animales pueden generar complejidad de muchas más maneras, lo cual incluye la deformación externa o interna de capas de células, la migración celular y otros procesos. De resultas, los animales pueden producir una enorme complejidad interna, así como una intrincada morfología externa. A pesar de esas diferencias, los procesos fundamentales de la organización del desarrollo son los mismos que en Acetabularia, un baile de sistemas dinámicos.
Brevemente, Brian explicó los principales acontecimientos de la morfogénesis en el embrión animal, que implica procesos secuenciales de invaginación y pliegue de capas celulares, procesos que crean los cimientos de la estructura interna del organismo. «Podemos hacer modelos informáticos que simulan el proceso utilizando las mismas clases de parámetros que en el modelo Acetabularia», dijo Brian, mientras íbamos viendo imágenes de esas etapas clásicas del desarrollo. A continuación, describió los acontecimientos del desarrollo que establecen la forma del ojo, procesos de invaginación y pliegue de capas de células. «¿Ves cómo los acontecimientos morfogenéticos básicos de la formación del ojo son simples repeticiones de los movimientos básicos de los que hemos estado hablando en otros aspectos del desarrollo?». ¿Estás diciendo que, dados los procesos de desarrollo conocidos, hacer un ojo es fácil? «Sí». ¿Igual que es fácil hacer Acetabularia? «Eso es diciendo que hay un gran atractor en el espacio morfogenético que produce un sistema visual funcional».
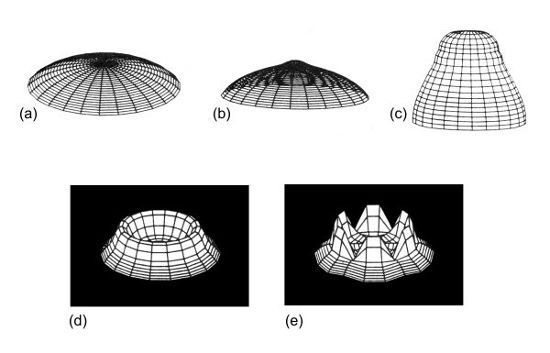
FIGURA 3.
Cinco etapas del desarrollo de los verticilos en el modelo informático de Acetabularia.
Cortesía de Brian Goodwin.
¿Los ojos han evolucionado independientemente, no sé cuántas veces, muchas, porque hay un atractor morfogenético que especifica esa clase de forma? «Más de cuarenta veces. Sí, eso creo. Los ojos son el producto de transformaciones espaciales de alta probabilidad de los tejidos en desarrollo. Esto es muy diferente de la posición neodarwinista, que afirma que los organismos generan estructuras altamente improbables, como el ojo, que persisten porque son útiles. La selección natural mantiene los organismos en esos estados improbables con programas genéticos que guían el organismo en desarrollo a través de la densa espesura de estados posibles hasta los que son consistentes con la supervivencia. Éste es más o menos el razonamiento neodarwinista».
Veía adónde apuntaba el razonamiento de Brian. Si hay un atractor morfogenético para el ojo, ¿es entonces probable lo mismo para otros órganos? «Sí». Y, en última instancia, ¿para un organismo? «Sí». ¿Quieres decir que las especies son atractores en un espacio de parámetros morfogenéticos? «Eso es lo que digo. Para un neodarwinista, todo punto de ese espacio es realizable como un organismo, siempre que las condiciones ambientales favorezcan su expresión. En otras palabras, cualquier clase de forma biológica es posible, dentro de ciertos límites mecánicos. Lo que digo es que eso no es correcto, que la dinámica organizativa de la morfogénesis define un número limitado de puntos en ese espacio, que la gama posible de las formas biológicas está restringida de un modo fundamental». Las especies como atractores en un sistema dinámico: una noción provocadora, bastante alejada del pensamiento biológico convencional. «Hay que tener en cuenta que lo que estoy diciendo es una conjetura plausible», admitió Brian. «Pero creo que es poderosa y que resultará ser más verdadera que falsa».
***
La posición de Brian —y también de Stu Kauffman— es la expresión más reciente de una tradición intelectual con raíces en la Ilustración del siglo XVIII. Conocida genéricamente como morfología racional —con una línea de distinguidos estudiosos desde Kant y Goethe, que incluye a Geoffroy Saint-Hilaire, el barón George Cuvier, William Bateson, Richard Owen, Hans Driesch, D’Arcy Wentworth Thompson, Waddington y otros—, su objetivo era la búsqueda de las «leyes de la forma» que explicaran las sorprendentes pautas de orden percibidas en la naturaleza. A pesar de cierta diversidad de enfoques, todos los morfologistas racionales albergaban una profunda convicción en la unidad del organismo individual y buscaron la fuente generadora del orden que percibían. Ésta es la segunda de las dos grandes escuelas interesadas en la forma biológica; la primera estaba formada por los funcionalistas, con la teología natural, Darwin y Dawkins.
«La nuestra es una ciencia de cualidades, no de cantidades, y es, por lo tanto, una ciencia goetheana», dijo Brian, al pasar de lo tangible a lo filosófico. «Goethe es aquí uno de mis héroes». En respuesta a la afirmación de que eso podía sonar un poco místico para algunos, Brian dijo: «Quizá. Pero nuestro enfoque considera la naturaleza como inteligible. Ciertamente, el principio creativo de la emergencia es un profundo misterio en muchos sentidos, y ésa es una propiedad de los sistemas dinámicos complejos. Pero, en última instancia, es inteligible. No se puede decir lo mismo del neodarwinismo». François Jacob comparó una vez la selección natural con un zapatero remendón, un táctico del momento, que iba juntando piezas para hacer frente a las circunstancias imperantes. Su objetivo era una descripción, no una crítica del concepto. «El problema de la forma queda así “reducido” efectivamente al problema de la adaptación funcional», dijo Brian. «Hace ininteligible la forma biológica».
Me pregunté si había un lugar para la selección natural en la visión del mundo de Brian. «No estoy negando la selección natural», dijo. «Estoy diciendo que no explica los orígenes de la forma biológica, el orden general que vemos ahí afuera». En una escala de uno a diez, dijo que puntuaría la importancia de la selección natural —en el contexto de la generación de la forma—, cerca del uno. «Y la posición de Stu es la misma. Pero no creo que esté dispuesto a decir que todo esto transforma el neodarwinismo. Lógicamente, lo que estoy diciendo lo transforma, pero él concede a la selección natural un papel más importante que yo».
***
«Cuando escribí por primera vez mis resultados sobre redes booleanas para una revista científica, apenas consideraba que la selección natural tuviera alguna importancia», me contó Stu. «Mira la cita al principio del artículo». Decía: «El mundo es efecto de la causa o del azar. En este último caso, sigue siendo un mundo a pesar de todo, es decir, una estructura regular y hermosa». La cita era del emperador Marco Aurelio. «Me gustó la cita porque yo estaba ahí, combinando redes al azar y, a pesar de eso, encontramos todo ese orden», explicó. «Conoces la frase de Einstein sobre “buscar los secretos del Viejo”. Bueno, pensé que el Viejo no se dedicaría a juguetear, que habría alguna lógica ahí afuera, y pensé que la había vislumbrado en las redes booleanas aleatorias. Sigue siendo hermoso. Y, no, no pensaba entonces que tuviera que preocuparme por la selección natural, pero ahora sí».
John Maynard Smith fue el responsable de que Stu diera su brazo a torcer en este aspecto. John es el más eminente biólogo evolucionista británico, un campeón del neodarwinismo, con una fuerte inclinación matemática. Con la apariencia del clásico profesor despistado, gafas y largo cabello blanco, John presenta la infrecuente combinación de penetrante inteligencia crítica y gran generosidad profesional. John y Brian fueron colegas en la facultad de ciencias biológicas de la Universidad de Sussex durante muchos años, y difícilmente cabría imaginar dos visiones del mundo más diferentes. John es también un apasionado jardinero y abre su jardín al público. Es una excursión sencilla y agradable visitar el jardín de John en Sussex por la mañana y el de Darwin en el cercano Kent por la tarde, con lo cual se satisfacen simultáneamente los intereses científicos y hortícolas.
A pesar de quedar impresionado por la emergencia de orden en las redes booleanas aleatorias de Stu Kauffman, John las consideró incompletas. «Hasta que no se meta la selección en esos modelos no tendrán nada que ver con la vida», me dijo John cuando lo visité en la Universidad de Sussex. «No son tan interesantes para un biólogo. Stu ya lo ha comprendido». El proceso de comprensión empezó cuando los dos hombres se encontraron por primera vez, en 1968, en un congreso de biología teórica celebrado en la Villa Serbelloni de la Fundación Rockefeller, a orillas del lago Como, en Italia. En esa ocasión, y cada vez que han vuelto a encontrarse a lo largo de los años, John intentaría convencer a Stu de la importancia de la selección natural en la conformación de los sistemas biológicos. Una vez, diez años atrás, caminaban los dos por South Downs, cerca de la Universidad de Sussex, cuando John dijo: «En gran medida, quienes han sostenido que la selección juega un papel importante en la evolución han sido caballeros rurales ingleses y quienes han sostenido que no, perdóname Stu, mayormente judíos urbanos».
Le pregunté a John qué había querido decir. «Caballeros rurales ingleses es un término demasiado restringido; europeos, quizás, y también mujeres», empezó. «Personas como Darwin y Wallace; eran gente de campo, y cultivaron una pasión por la historia natural. Pero como eran intelectuales se interesaron por el modo en que había surgido, por la increíble adaptación funcional que vemos. No se puede estudiar la naturaleza sin saber que ahí fuera hay extrañas adaptaciones, formas complicadas de vida que parecen hacer encajar un organismo en su medio ambiente. Así que el problema pasa a ser: ¿cómo se explica? La respuesta es la adaptación por medio de la selección natural». Entendía el razonamiento respecto a los caballeros rurales ingleses, pero ¿y los judíos urbanos? «Me refiero a los intelectuales urbanos, personas como Stu Kauffman y Steve Gould. Es la búsqueda de verdades universales. Parecen decir: si no hay verdades universales, ¿cómo hacer ciencia? También para ellos la selección parece estar ad hoc, sólo que la consideran adaptación oportunista. Para mí, así es como funciona la naturaleza».
Pregunté a Stu si realmente buscaba verdades universales. «Lo que busco es una teoría profunda del orden en la biología. Si se considera el mundo como lo hace John, nuestra única opción como biólogos es el análisis sistemático de máquinas en última instancia accidentales y de sus historias evolutivas en última instancia accidentales. Sé que hay algo más además de eso». Y la selección natural: ¿hizo un buen trabajo John al defender su importancia? «La teoría de la selección natural es brillante, no hay duda. Y sé que Brian no está de acuerdo conmigo, pero es una fuerza importante en la evolución: digamos que un cinco en nuestra escala del uno al diez. Pero hay cosas que Darwin no pudo saber. Si la nueva ciencia de la complejidad tiene éxito, logrará un matrimonio entre la autoorganización y la selección. Será una física de la biología».
Para los biólogos será difícil asimilar en su actual visión del mundo la noción de autoorganización. «Y hay más cosas», dijo Stu. «Está el límite del caos».