LÁMINAS C1, C3 y C16. Tres grandes artistas del pasado ilustran la naturaleza, y con ello llevan al lector a la puerta de los fractales.
Esta sección es un libro-dentro-del-libro y su objeto es que, si «ver es creer», ver en color puede producir una convicción más intensa aún, por muy torpes que fueran nuestros primeros esfuerzos con este medio. De ahí que los pies de figura de esta sección sean en cierto modo independientes del resto.
La Geometría Fractal de la Naturaleza mezcla las matemáticas y la ciencia necesarias para tratar ciertas clases amplias y generales de formas naturales. Aunque muchas de estas formas son bastante comunes, los autores del pasado rara vez hablan de los problemas que plantean. Las láminas C1, C3 y C16 son vivos ejemplos de los asuntos tratados por la geometría fractal.

FIGURA C1
Aquí crea Dios los círculos, las ondas y los fractales
FIGURA C1. LA PORTADA DE UNA BIBLE MORALISÉE. El periodo de la historia europea occidental centrado en 1200, aunque estancado en cuanto a ciencia y filosofía, registró una actividad exuberante en ingeniería. En una época que levantó las grandes catedrales góticas, ser maestro albañil era una vocación superior. Así, las Bibles Moralisées illustrées de esa época (Biblias con «historietas») a menudo representan al Señor sosteniendo compases de albañil (Friedman, 1974). La lámina C1 es la portada de una famosa Bible Moralisée, escrita entre 1220 y 1250, en el dialecto francés hablado en la Champagne oriental. Se encuentra ahora en la Biblioteca Nacional Austríaca de Viena (códice 2554), con cuya autorización se ha reproducido aquí. La leyenda reza:
Ici crie dex ciel et terre
Soleil et lune et toz elemenz
[Aquí crea Dios el cielo y la tierra
el sol y la luna y todos los elementos]
Percibimos tres clases de formas distintas en este mundo recién creado: círculos, ondas y unos «culebreos». Los estudios de los círculos y las ondas se han aprovechado de una colosal inversión de esfuerzo humano, y constituyen los mismísimos cimientos de la ciencia. En comparación con ellos, esos «culebreos» han permanecido prácticamente intactos. El objeto del presente libro es afrontar el reto de construir una geometría natural de ciertos «culebreos» que se llamarán «fractales». Uno de los rasgos más atractivos de esta lámina es que pide al científico que «tome la medida del universo». Aplicar compases de puntas a los círculos o a las ondas es una tarea que había resultado fácil desde mucho tiempo atrás. Pero ¿qué ocurre cuando aplicamos el compás a los culebreos de esta lámina… o a las costas de la Tierra? El resultado es inesperado; se discute en el capítulo 5, y en capítulos posteriores exploramos sus consecuencias, guiando de ese modo al lector por una senda que se podría decir que atraviesa la ciencia.

FIGURA C3
FIGURA C3. EL DILUVIO, DE LEONARDO DA VINCI. (De las Windsor Castle Collections. Reproducido por amabilidad de Su Majestad la Reina.) Uno de los muchos dibujos en los que Leonardo representó una corriente de agua por superposición de remolinos de muchos tamaños distintos. La ciencia no fue consciente de esta estructura de remolinos hasta que fue parcialmente formalizada por Lewis F. Richardson en los años veinte, con su imagen «escalante» de la naturaleza de la turbulencia. Sin embargo, esta imagen derivó enseguida hacia una búsqueda de fórmulas, perdiendo con ello todo sus tintes geométricos, y resultando también de una eficacia limitada. La teoría expuesta en este libro permite el regreso de la geometría al estudio de la turbulencia, y muestra que muchos otros ámbitos de la ciencia son geométricamente muy parecidos entre sí y pueden manejarse con técnicas afines.
EL CONCEPTO DE FRACTAL. Reuní algunas figuras geométricas cuya forma es muy irregular y fragmentada, y acuñé el término fractal para designarlas. Los fractales se caracterizan por la coexistencia de rasgos distintivos de todos los tamaños lineales imaginables, entre cero y un máximo, para el que pueden darse dos casos. Cuando el fractal está acotado, el tamaño máximo de los rasgos es del orden de magnitud del tamaño global del fractal. Cuando se dibuja una parte de un fractal no acotado en el interior de un cuadro de lado Ω, los rasgos del dibujo tienen un tamaño máximo del orden de Ω. En las láminas C5 a C15 se presentan ejemplos de fractales construidos matemáticamente. Los fractales protagonizan dos historias distintas, separadas en el tiempo por casi un siglo de diferencia, y entre estas dos épocas su papel cambió totalmente. En la primera etapa, algunos fractales (no los que ilustran esta sección) se diseñaron exprofeso para corroer los cimientos de la matemática predominante. Todo el mundo veía estos conjuntos como «monstruos». Mientras el resto de la matemática se consideraba un coto potencialmente prometedor para los físicos, a la caza de nuevos útiles, todos estaban de acuerdo en que, sin ningún miedo, se podía considerar esos monstruos totalmente irrelevantes en la descripción de la naturaleza. En cincuenta años no se creó casi ninguna variante de los mismos. La inversión de papeles comenzó cuando empecé a descubrir que, uno tras otro, esos monstruos podían servir como herramienta conceptual central para responder a alguna vieja pregunta que el hombre se había estado planteando acerca de la forma de su mundo.
EL PAPEL DE LOS GRÁFICOS. Los gráficos por ordenador tuvieron un papel central en la aceptación de la geometría fractal, aunque dicho papel sólo fuera marginal en su gestación. Esto es, dada la fascinación que actualmente ejercen los fractales sobre los practicantes del ordenador, uno se siente tentado de atribuir la aparición de la nueva geometría a la disponibilidad de esta nueva herramienta. En realidad, formulé la teoría de los fractales cuando los gráficos por ordenador estaban en mantillas. Sin embargo, dejé que su desarrollo se inclinara hacia temas que se prestaran a ilustraciones que ayudaran a la intuición.
COMPOSICIÓN PICTÓRICA CLÁSICA. Examínense ahora de nuevo las láminas C1 y C3. Aquí, como en casi cualquier otro cuadro «compuesto» clásicamente, es sorprendentemente fácil identificar al menos un «rasgo» para casi cada escala entre el tamaño total del cuadro y un corte interno por debajo del cual los detalles se hacen invisibles. Así pues, la propiedad escalante que caracteriza los fractales no sólo está presente en la naturaleza, sino también en algunas de las creaciones artísticas más cuidadas del hombre.

FIGURA C16
FIGURA C16. LA GRAN OLA, DE HOKUSAI. Katsushika Hokusai (1760-1849) fue un pintor y grabador de extraordinario talento y versatilidad, un gigante desde cualquier punto de vista. Los remolinos y espirales de toda clase le fascinaban, como lo demuestra uno de sus grabados que alcanzó tanta fama que bastará con una reproducción en tamaño reducido.
LÁMINA C5. Dragón fractal autocuadrado.
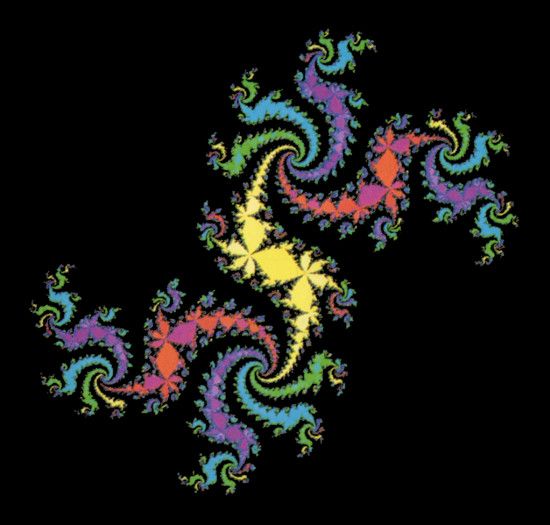
FIGURA C5
Por rimbombante que resulte este diseño, el fondo negro se debe considerar como un ejemplo de arte minimalista en grado extremo. En efecto, la fórmula
{z:limn→∞|fn(z)| = ∞, donde f(z) = λz(1 − z)},
es todo lo que hace falta para duplicar el fondo en cuestión con una precisión total y absoluta. Explicaré esta fórmula: una vez escogido el número complejo λ, que determina la «función generatriz» f(z), construimos f2(z) = f(f(z)), luego f3(z) = f(f2(z)), esto es f3(z) =f(f(f(z))), y así sucesiva e indefinidamente.
El número complejo λ que da lugar a esta lámina es ~ 1,64 + 0,96i. Está claro que no ha sido escogido porque sí. La forma del dragón es muy sensible al valor de λ, pero una teoría especial desarrollada por mí (esbozada en el capítulo 19) permite elegir λ de modo que uno obtenga el dragón que desea de entre muchas y muy variadas posibilidades.
LAS «PIEDRAS». En cuanto al diseño que resalta sobre el fondo negro, está formado por 25 clases de «piedras», definidas cada una por
{z:limn→∞|f25n(z)| = zg},
donde los 25 números complejos zg son raíces de la ecuación f25n(z) = z, y además satisfacen la ecuación |(d/dz)f25(z)| < 1.
Si se mira atentamente, se pueden ver 5 tonalidades distintas de rojo, 5 de azul, etc. Este esquema de coloreado se ha elegido así porque los 25 valores de zg se ordenan en 5 «géneros», formados a su vez cada uno por 5 «especies». Asignamos un color a cada género y una tonalidad o intensidad a cada especie. Así, por ejemplo, las 5 especies de oro se extienden a lo largo del cuerpo principal dorado del dragón, y se reúnen en los talles de avispa de este cuerpo.
UNA CARA ANTES OCULTA DE LA MATEMÁTICA CLÁSICA. La fórmula de f(z) es tan breve y parece tan carente de interés (porque procede de un capítulo elemental del cálculo), que poco se esperaba de ella. Así pues, ver una figura de esta clase en la pantalla del ordenador produjo sorpresa y también una fuerte conmoción estética.
El análisis matemático clásico (que es la forma más avanzada del cálculo) había gastado una broma a todos aquellos que o lo amaban o lo odiaban. Se nos han revelado ahora dos caras muy distintas del análisis. La que se nos había estado mostrando durante siglos, y que se había convertido en su orgullo (o su maldición), era irremisiblemente austera. Pero yo demuestro que el análisis tiene también una cara oculta que a menudo es sorprendentemente atractiva y alegre.
El respeto y la admiración por los grandes maestros del análisis austero hacen que uno se apresure a decir que la complicación extrema del perfil de este terciopelo negro no fue una sorpresa para el puñado de matemáticos (al que yo tuve la suerte de pertenecer) que estaban al tanto de los «antiguos» trabajos (la mayoría en torno a 1920) de Pierre Fatou y Gaston Julia. Pero la complicación de esas figuras había contribuido a aumentar la severidad del análisis, y nada hacía esperar que tantos espectadores pudieran percibir como bella esta complicación.
ALGORITMOS QUE CONTIENEN UN BUCLE. Los descubrimientos de Fatou y Julia confirman, en efecto, que con una herramienta muy simple (considéresela un cincel de escultor) se puede crear un artificio muy complejo, siempre y cuando la herramienta pueda aplicarse repetidamente. Aquí la herramienta es la función f(z) con la que se generan las funciones fn(z).
Por tanto, no tratamos aquí de una operación que se realiza una sola vez, y que se detiene cuando se ha acabado, sino de una operación que se realiza, luego se repite, etc. Esas funciones iteradas son ejemplos de rutinas o bucles, que a cada paso pueden iniciar una nueva tarea.
Los programas con bucles más simples son lineales, y eso significa que van añadiendo detalles que no son más que el eco de la forma global a una escala menor. Las figuras resultantes se denominan autosemejantes.
En este caso, por el contrario, los detalles se van deformando a medida que se van haciendo más pequeños, porque la función f(z) no es lineal. Como esta función es cuadrática, el contorno del fondo de terciopelo lo denominaremos autocuadrático en el capítulo 19.
LÁMINA C7. Parcheado fractal autoinverso.

FIGURA C7
Este colgante está parcheado con seis clases distintas de tela transparente. Se han cortado una multitud de discos abiertos (esto es, de interiores de círculos) de telas de 6 colores diferentes, y se han cosido sobre un forro transparente, aislados o superpuestos. La mayoría de estos discos están demasiado lejos o son demasiado pequeños para ser visibles.
Esta figura es una variante más intrincada de la que se discute en el capítulo 18. Su construcción empieza por escoger un generador, que en este caso es una colección de 4 círculos y 4 rectas, dispuestos del modo siguiente
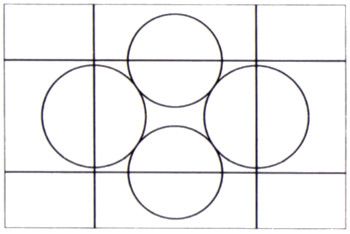
Por varias razones, expuestas en el capítulo 18, tiene mucho interés la figura L, que es la menor figura que permanece totalmente invariante si se realiza una transformación de simetría con respecto a una cualquiera de las rectas o una inversión con respecto a cualquiera de las circunferencias generatrices.
En teoría, la diferencia entre los conceptos de recta y circunferencia no es importante aquí. En efecto, si las rectas y circunferencias anteriores se someten a una inversión con respecto a un punto que no esté sobre ninguna de ellas, se obtienen 8 circunferencias. Por tanto, en vez de decir que L es «autoinversa y autosimétrica», basta con decir que es «autoinversa».
Pero el hecho de que en esta figura intervengan 4 simetrías respecto a rectas que forman un rectángulo tiene sus ventajas, y se incorporó para garantizar la periodicidad de este L. El primer periodo está limitado por nuestro rectángulo, y los otros se obtienen por traslaciones paralelas a los ejes.
El problema de determinar la estructura de L es antiguo y famoso, y yo le di la solución práctica que se ilustra aquí. Esta nueva solución muestra que L está formado por los puntos en que los parches de tela discoidales están en contacto con las circunferencias que los delimitan. Los puntos interiores de un disco nunca se cuentan como parte de L aunque estén en el contorno de otro disco distinto, tanto si es del mismo color como si no.
Pasemos ahora a explicar cómo se han escogido estos parches discoidales. Partiendo de la figura generatriz, se dibujan 6 circunferencias, que llamaremos Γ-circunferencias, ortogonales cada una de ellas a 3 de las 8 componentes de la figura generatriz. Hay muchas otras circunferencias ortogonales a 3 de las 8 componentes del generador, pero sólo necesitamos estas 6 como Γ-circunferencias.
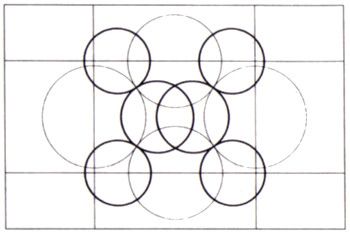
Cada Γ-circunferencia rodea un disco al que se asigna un color de tela determinado, y se emplea el mismo color para cada disco obtenido por transformación de un Γ-disco por inversión con respecto a las 4 circunferencias, o por simetría con respecto a las 4 rectas del generador. Los discos del «medallón» central se solapan a todos los demás, pero ninguno se solapa a cualquiera de sus inversos. Los discos de las esquinas, por el contrario, se solapan con algunos de sus inversos.
LÁMINA C9. Salida de un planeta sobre una colina Labelgraph (Recuerdo de una misión espacial que nunca existió).

FIGURA C9
Las láminas C9 a C15 quizá parezcan «realistas». Y algunas son, a su modo, obras de arte. Sin embargo, estas láminas no son fotografías y no pretendían ser artísticas. Además no son ejemplos de los falsos paisajes que pueden obtenerse por tratamiento de paisajes reales, del mismo modo que se sintetiza un producto químico por transformación de otros productos. Estas láminas son exactamente tan artificiales como las láminas C5 y C7. Son los equivalentes fractales de la síntesis «completa» de la hemoglobina a partir de los átomos que la componen, tiempo (muchísimo) y energía.
La lámina C9 combina la puesta en práctica de dos de mis teorías de las superficies de los planetas, presentadas por primera vez en Mandelbrot (1975w) sobre la base de las láminas 381 y 383, y estudiadas en los capítulos 27 y 28 de esta obra. Varias características de la presente lámina no consiguen ajustarse a la realidad, pero los capítulos en cuestión muestran cómo se pueden resolver algunos de estos defectos.
Un planeta en el que el agua se concentra en océanos y nieve (por ejemplo en los casquetes polares), mientras el cielo carece absolutamente de nubes, es —por no decir más— sólo una primera aproximación. El color se ha añadido después empleando las mejores técnicas disponibles actualmente, y la selección de colores es completamente ajena a mis teorías. Un primer algoritmo mostraba la altura mediante los mismos colores que en el The Times Atlas. Entonces nos pareció claro que una ligera mejora en el esquema de coloreado daría unos resultados considerablemente mejores, sin necesidad de recurrir a una gran cantidad de decisiones independientes.
Este arte no puede pretender ser tan minimalista como el de las láminas C5 y C7, ya que las definiciones de los dos planetas no se pueden reducir a una sola línea sin una artificialidad excesiva.
Una segunda razón por la que este arte no se puede llamar minimalista es que la realización del sombreado implica un gran ingenio; harían falta gruesos volúmenes para explicar cada detalle. Además, el algoritmo depende mucho de las herramientas disponibles, por lo que, para duplicar este trabajo, uno tendría que usar exactamente el mismo equipo informático.
Como una versión anterior de esta «salida de planeta» apareció en la sobrecubierta del Fractals de 1977, y algunas de las láminas de este último representaban también paisajes fractales, éstos han sido objeto de múltiples imitaciones. La baja calidad relativa de las mismas es una prueba más de la no minimalidad de este arte.
No obstante, los principales rasgos de ambos planetas pueden caracterizarse inequívocamente por un número muy pequeño de propiedades fundamentales de continuidad e invariancia, que exploraremos en los siguientes pies de figura.
DEDICATORIA. El nombre de Colina de Labelgraph es en homenaje a «Iblgraph», un paquete de programas gráficos un tanto caprichosos y a menudo muy maleducados que surgió del trabajo de Alex Hurwitz y Jack Wright de IBM en Los Ángeles. De 1974 a 1981 embelleció el T. J. Watson Research Center, respondía si se lo trataba con consideración, y (con su vivo sucesor, «yogui») hizo posible la ilustración de mis ensayos. R.I.P.
LÁMINA C11. Colinas gaussianas que nunca existieron.

FIGURA C11
El nombre de Carl Friedrich Gauss (1777-1855) aparece en casi todos los capítulos de la matemática y de la física, y eso le convierte en el primero (princeps) de los matemáticos (incluidos los físicos) de su tiempo. Pero el calificativo de gaussianas aplicado a estas colinas se debe a una distribución de probabilidad que se le atribuye indebidamente. Se trata de la distribución con gráfica «en forma de campana» u «ojiva de Galton». En las láminas C9 a C15, esta distribución es la que regula la diferencia de altura entre dos puntos dados cualesquiera del mapa, por lo menos después de realizar una transformación conveniente.
En su trabajo, muchos estudiosos recurren a la distribución gaussiana sin darse cuenta de que esta elección debe justificarse. Ya sea porque esta es la única distribución que conocen a fondo y que les merece confianza, o porque piensan que explica la distribución de cualquier magnitud aleatoria que se dé en la naturaleza, desde las alturas de los reclutas a los errores en las observaciones astronómicas.
En realidad, esta última creencia carece totalmente de fundamento. Este ensayo contiene muchos ejemplos que demuestran que el mundo está lleno de fenómenos enormemente no gaussianos. Por tanto, el recurso a la distribución gaussiana requiere otra justificación menos discutible. En mi opinión, las únicas justificaciones válidas se basan en el hecho de que la gaussiana es la única distribución que posees ciertas propiedades de invariancia por cambio de escala, y a pesar de ello conduce a relieves que varían con continuidad. La conclusión es que los relieves más simples posibles se rigen por una «función browniana», o al menos por una variante de la misma que yo llamé «función browniana fraccionaria».
El único parámetro que dejan indeterminado estos desiderata, y que por tanto se debe escoger por otras razones, se llama dimensión fractal del relieve, y se denota por D.
Cuando D alcanza su valor mínimo D = 2, el relieve es sumamente liso. A medida que D aumenta, el relieve se hace cada vez más «ondulado» y empieza a parecerse a las montañas altas de la Tierra. Al final se hace demasiado ondulado para ser parecido a las montañas, y acaba por casi llenar el espacio.
Una característica que define la función browniana es que cada corte vertical es una función browniana ordinaria, real de variable real.
Para cada paisaje, excepto el del planeta distante de la lámina C9, la altitud se calcula en función de las latitudes y longitudes dispuestas según una parrilla cuadrada. Luego se introduce una apariencia de redondez enrollando la base plana de este relieve alrededor de un cilindro cuyo eje va de izquierda a derecha. El ordenador está programado para simular la iluminación por un foco que está situado 60° a la izquierda.
Aunque parezca mentira, varios observadores, después de comentar brevemente que una caracterización del relieve que se base sólo en criterios de invariancia y continuidad es ingeniosa y eficiente, proceden a criticar largamente este enfoque del problema, pues sus criterios son demasiado abstractos y no se han deducido de «modelos» explícitos ni de mecanismos generadores, ni a priori ni a posteriori.
Tengo poco interés en replicar (torpemente) criticando las teorías concretas del relieve que constituyen la «corriente principal» por su incapacidad de presentar falsos paisajes que se aproximen tanto al realismo como los debidos a mis «teorías» abstractas. Creo que es mejor recordar que muchas de las más bellas teorías físicas empezaron con primorosas combinaciones de pistones, cuerdas y poleas, sólo para acabar (varias generaciones más tarde) en su esqueleto de principios de invariancia. Visto así, el trabajo que condujo a las presentes ilustraciones, y otros casos que se estudian en esta obra, parten de la línea de llegada. ¿Es esta una razón suficiente para ponerse triste?
LÁMINA C13. Colinas no gaussianas que nunca existieron.

FIGURA C13
Los pies de todos los paisajes gaussianos de esta obra, incluidos los del capítulo 28, se han allanado para formar un nivel de referencia fijado arbitrariamente. Este procedimiento se usó primero para generar islas. Y en los paisajes montañosos, originariamente pretendía ser una ayuda para que el ojo distinguiera entre superficies distintas.
Me explicaré un poco más. Cuando preparábamos el ensayo de 1975, no queríamos desperdiciar datos y representamos gráficamente todo lo que teníamos, pero el resultado fue penoso: a nuestros ojos les resultaba sorprendentemente difícil distinguir entre paisajes que sabíamos estaban caracterizados por valores de D significativamente distintos. Luego, el deseo de representar las costas de las islas junto con el relieve nos llevó a introducir una superficie plana de referencia en la misma imagen, y de repente las diferencias en las D se hicieron clarísimas. Deberíamos haber recordado que, para apreciar el movimiento, se necesita un patrón de reposo. Y lo mismo ocurre con la rugosidad.
Ahora nos encontramos con que, cuando se aplicaba el mismo procedimiento a los valles y también a los montes, tenía además un segundo efecto de lo más afortunado, aunque no fuera intencionado. Al crear los planos (que recuerdan lagos, montones de nieve o aluviones) se ocultan los fondos de los valles, lo que nos obliga a concentrarnos en las montañas altas, donde el modelo resulta mucho más potente de lo esperado. Si hubiéramos mirado demasiado pronto al relieve en su conjunto, nos habríamos llevado un fuerte desengaño, pues en los modelos gaussianos los fondos de los valles son tan «poco lisos» como las cimas de los montes, y en cambio los valles reales lo son mucho más. Por el momento, no me gusta ninguna de las explicaciones de esta diferencia.
Pero hay maneras de «arreglar» el modelo gaussiano de las montañas para dar mejor cuenta de los valles. El arreglo más simple supone que las únicas diferencias entre las distintas partes del relieve tienen que ver sólo con la escala vertical, siendo el valor de D el mismo en todas partes. Para justificar esta suposición, reduzcamos la escala vertical de las sierras gaussianas de la lámina C11. ¡Como por milagro se convierten en terreno ondulado! Y viceversa, consideremos cualquier superficie cuasi plana, como la de una pista de aterrizaje, y aumentemos sus asperezas. En primera aproximación, el resultado es muy a menudo parecido a las colinas gaussianas de la lámina C11, con una dimensión que depende de las circunstancias concretas. No hay razones para pensar que este resultado no es válido para los fondos de los valles. Por tanto, uno no puede dejar de preguntarse por las consecuencias de suponer que, si D es válida para las cimas de las montañas, también vale en primera aproximación para los fondos de los valles.
Una idea más concreta consiste en restringir la validez de la invariancia por cambio de escala a dominios pequeños, con la misma dimensión en todas partes, mientras la escala vertical aumenta con la altitud sobre el fondo del valle. Con este objeto en mente, en el grabado de la parte superior de esta lámina y en la colina Labelgraph de la lámina C9, las altitudes sobre el nivel del lago o sobre el fondo del valle se han elevado al cubo.
Cuando, por el contrario, la escala vertical se hace disminuir con la altitud sobre el fondo (elevándola a una potencia inferior a 1), se obtiene la meseta y el cañón de la parte inferior de esta lámina.
Aunque el truco pueda ser tosco, es sorprendentemente efectivo.
LÁMINA C15. Islas fractales que nunca existieron vistas desde el cénit.
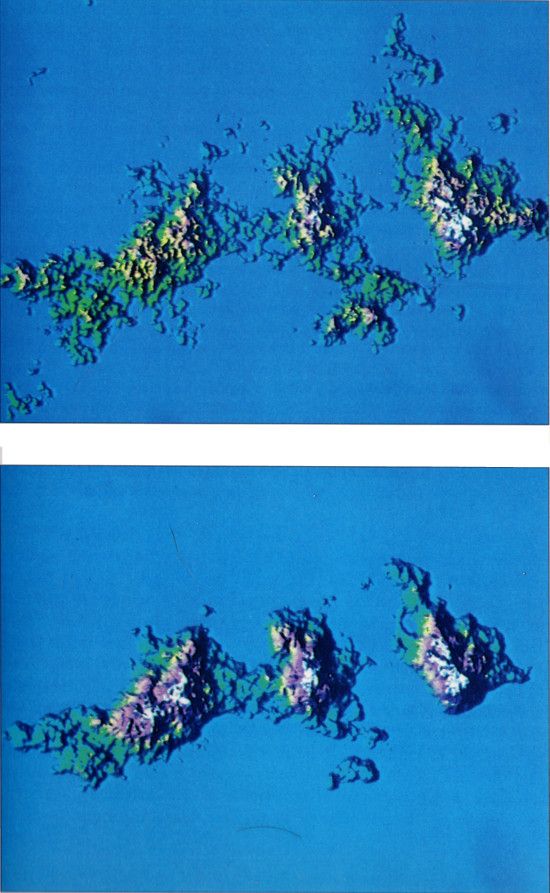
FIGURA C15
El algoritmo usado en la parte inferior de la lámina C9, y en las láminas C11 a C15, se basa en métodos numéricos de Fourier, y por tanto da una superficie lisa periódica, en tanto que por definición una superficie fractal es sumamente rugosa. Uno puede imaginar, sin embargo, que estamos inspeccionando nuestras montañas mediante una luz de longitud de onda igual a las celdas de la parrilla. Bajo esa luz, todos los detalles más finos resultan totalmente invisibles.
Para obtener islas centramos el relieve alrededor de un máximo y no representamos las alturas inferiores a cierto nivel de referencia que tomamos como 0.
El archipiélago de arriba corresponde a un relieve browniano ordinario. Es un mal modelo de Tierra, pues claramente es demasiado irregular en sus detalles. El ajuste es malo porque una dimensión fractal de superficie D = 5/2 y una dimensión de costa D = 3/2 son demasiado grandes.
En el archipiélago de abajo, la función browniana ordinaria se ha sustituido por una función browniana fraccionaria y de dimensión D = 2,200, y la costa tiene la dimensión razonable D = 1,200. Las crestas claramente visibles en la figura son totalmente compatibles con el hecho de que fuera generada por medio de un mecanismo isótropo.
El parecido con Hawai es mayor que el que nos merecíamos, pues no hay razones para pensar que el modelo tenga que ser válido para archipiélagos volcánicos.
La forma observada de las costas está muy influida por cuán apretadamente llenan el dibujo. Esta faceta de la forma no está totalmente determinada por D, pues las láminas C11 y C15 se refieren a una región próxima a un mínimo o a un máximo, y el nivel de referencia tiene un papel importantísimo.










