37
Variación de los precios y cambios de escala en economía

Desde que las páginas financieras de los periódicos vienen llenas de anuncios de supuestos «grafistas» que, mediante curvas de tendencias pasadas convenientemente arregladas, pretenden poder predecir el futuro a partir de su geometría, se puede decir, aunque sólo medio en broma, que la variación de los precios de las acciones y mercancías plantea un problema geométrico.

La contrarréplica fundamental, planteada por primera vez por Louis Bachelier en 1900, es que los gráficos no sirven para nada. El enunciado más fuerte es que las variaciones sucesivas de los precios son estadísticamente independientes. Un enunciado más débil es que cada precio sigue un proceso estocástico de «martingala», en el sentido de que el mercado es «perfecto»: todo su pasado ha sido completamente descartado. Un enunciado más débil aún es que las imperfecciones permanecen sólo mientras no superan los costes de transacción; tales mercados se denominan «eficientes». El concepto de eficiencia de Bachelier ha demostrado ser extraordinariamente preciso.

Otro enunciado de Bachelier más concreto es que, en primera aproximación, cualquier precio competitivo sigue un «movimiento browniano unidimensional» B(t). Vale la pena señalar el hecho de que un proceso tan fundamental en la física haya sido inventado por un matemático heterodoxo (véase capítulo 40). Es triste decirlo, pero cuando se dispuso de datos reales B(t) resultó representarlos muy mal. En el presente capítulo se presenta una descripción alternativa, que construí basándome en una hipótesis escalante (una de las primeras que se hizo en cualquier campo), la cual ha demostrado ser sorprendentemente precisa.

La discontinuidad de los precios

Mi argumento antibrowniano más simple se basa en una observación experimental tan directa y evidente que es sorprendente que sea tan fundamental. Pero los argumentos usados en capítulos anteriores para demostrar que D < 2 para las galaxias y D > 2 para la turbulencia son también sorprendentemente claros y directos. Esta sencilla observación consiste en que un fenómeno caracterizado por discontinuidades muy marcadas no puede explicarse mediante un proceso continuo. Sabemos que las funciones muestrales del movimiento browniano son continuas ▯ casi con toda seguridad y casi por doquier. ▮ Pero los precios en los mercados competitivos no tienen por qué serlo, y de hecho son notablemente discontinuos. La única razón para suponer la continuidad es que, a sabiendas o de forma inconsciente, muchas ciencias tienden a copiar los métodos que han resultado válidos y útiles en la física newtoniana. La continuidad sería una hipótesis razonable para diversas magnitudes y tasas «exógenas» que intervienen en la ciencia económica pero están definidas en términos físicos. Pero los precios son otra cosa: en mecánica no hay nada parecido, y ésta no sirve de guía al respecto.

El mecanismo típico de la formación de los precios implica tanto un conocimiento del presente como una previsión del futuro. Y aunque los determinantes físicos exógenos de un precio varíen de modo continuo, las previsiones cambian drásticamente en un abrir y cerrar de ojos. Cuando una señal física de energía y duración despreciables, «un plumazo», provoca un cambio brutal en las previsiones (y si ninguna institución inyecta inercia para complicar las cosas) un precio determinado de acuerdo con las previsiones puede dispararse, caer a cero o hacer cualquier cosa.

Falacias del comercio con filtros (Mandelbrot 1963b)

La idea de que un precio pueda ser discontinuo apenas tiene, aparentemente, valor predictivo por sí misma. Pero resultó fundamental para la muerte y sepultura del método de comercio con «filtros» de Alexander (1961). En principio, un filtro del p% es un instrumento que controla continuamente el precio, registra todos los máximos y mínimos locales, envía una señal de compra cuando el precio supera por primera vez un mínimo local en exactamente un p%, y envía una señal de venta cuando el precio desciende por primera vez por debajo de un máximo local exactamente el p%. Como el control continuo no es práctico, Alexander controlaba la sucesión de alzas y bajas diarias. Daba por supuesto que el registro de un precio se puede manejar como una función continua. El algoritmo busca los días en que el alza excede por primera vez la baja de un día anterior más un p%. Se asume que en algún momento del día d el precio era exactamente igual a dicha baja más el p%, y entonces el filtro había disparado una señal de compra. Y análogamente para las señales de compra. La conclusión empírica de Alexander es que las señales de compra y venta de un filtro dan mayor rendimiento que «comprar y retener».

En realidad, Mandelbrot (1963b, pág. 417) señala que las sesiones diarias de 24 horas en las que el filtro envía una señal de compra son muy probablemente días con una evolución al alza muy marcada. En muchos de estos días, en realidad, el precio sube por la noche o mientras el mercado está detenido por iniciativa de la Bolsa. Así, en los momentos en que el filtro de Alexander tuviese que emitir una señal de compra, ¡lo más probable es que estuviera desconectado! Emitirá una señal de compra en cuanto lo vuelvan a conectar, pero el precio de compra resultante será a menudo bastante más alto que el previsto por Alexander.

Otra posibilidad: muchos días la variación del precio se hace razonablemente continua por la acción deliberada de un especialista que realiza sus funciones de conectar compradores con vendedores y de «asegurar la continuidad del mercado» comprando o vendiendo valores de su propia cartera. Cuando el especialista no consigue asegurar la continuidad, tiene que presentar una explicación por escrito, y a menudo prefiere eliminar artificialmente la discontinuidad. Obviamente, las gangas se reservan para los amigos, mientras que el grueso de los clientes tiene que comprar a un precio más alto.

Tercera posibilidad: algunas variaciones diarias de precio están sujetas a límites, que pueden desplazarse tras varios días sin operación, impidiendo que se ejecuten las maniobras «stop limit».

Estudios teóricos y experimentales (que enseguida describiremos) me convencieron de que los sesgos anteriores eran significativos y que la ventaja aparente del mercado con filtros sobre el comprar y retener era falsa. Después de contrastarla, Alexander (1964) encontró correcta mi predicción de que el método de filtros no era mejor que «comprar y retener». Fama y Blume (1966) realizaron un examen «post mortem» completo, sustituyendo los índices de precios de Alexander por series de precios individuales; el método de los filtros está ahora enterrado para bien. Este episodio subraya el riesgo de error inherente en lo que llamo «la falacia de la continuidad de los precios».

Las «martingalas» ganadoras se parecen a los móviles perpetuos. Un mérito de la hipótesis del mercado eficiente de Bachelier es que hubiera predicho que los filtros no resultarían, pero también es un demérito del modelo de movimiento browniano de Bachelier que no pudiera explicar por qué parecía que los filtros daban buen resultado. Por tanto, corresponde a mis modelos concretos el mérito de permitir un análisis y el señalar los defectos de éste y otros caminos hacia la riqueza segura.

«Parches» estadísticos

El fracaso del movimiento browniano como modelo de la variación de precios tuvo como respuesta la invención de una plétora de «parches» ad hoc. Ante las pruebas estadísticas que rechazan la hipótesis browniana de un comportamiento gaussianos de los precios, el economista puede intentar una modificación tras otra hasta despistarlas.

Un parche corriente es la censura, hipócritamente etiquetada como «desestimación de los extremos estadísticos no representativos». Se distingue entre las variaciones de precio ordinarias, «pequeñas» y las grandes, que derrotan los filtros de Alexander. Las primeras son consideradas aleatorias y gaussianas, y se les dedican montañas de ingenio…, como si eso importara a alguien. Las otras se tratan aparte como «no estocásticas». Otro parche corriente es una mezcla de poblaciones aleatorias: si X no es gaussiana, a lo mejor es una mezcla de dos, tres, o más variables gaussianas. Un tercer parche es una transformación no lineal: cuando X es positiva y enormemente no gaussiana, a lo mejor log X es gaussiana; si X es simétrica y no gaussiana, a lo mejor arctg X pasa el test. Y otro procedimiento (que en mi opinión es un suicidio viniendo de un estadístico) sostiene que el precio sigue un movimiento browniano, pero los parámetros del movimiento varían sin control. Este último parche no es falsable, por lo que, según el filósofo Karl Popper, no puede tratarse de un modelo científico.

Un principio escalante en economía (Mandelbrot, 1963b)

Mi propio trabajo se sitúa en el extremo opuesto de los parches. Se aplica a diversos datos de la ciencia económica, pero donde mejor se expresa es en el contexto de los precios.

PRINCIPIO ESCALANTE DE LA VARIACIÓN DE LOS PRECIOS. Cuando X(t) es un precio, log X(t) tiene la propiedad de que su incremento a lo largo de un intervalo de tiempo arbitrario, log X(t + d) − log X(t), tiene una distribución independiente de d, aparte de un factor de escala.

Antes de explorar las consecuencias de este principio, repasemos una lista de sus propiedades.

Un principio científico debe hacer predicciones que se puedan contrastar con la experiencia. Éste lo hace, como veremos en un momento, y la concordancia es muy buena.

Es bello que los principios científicos puedan deducirse de otras consideraciones teóricas de su propio campo. El principio escalante de la variación de los precios se puede basar en la forma general (no necesariamente la estándar) del argumento probabilista del «límite central», pero éste todavía no se ha deducido de la economía estándar. Los únicos razonamientos «explicativos» (Mandelbrot, 1966b, 1971e) lo respaldan como consecuencia de la invariancia por cambio de escala en las variables físicas exógenas, pero estos argumentos están menos establecidos que el resultado que pretenden justificar.

Finalmente, aun cuando no se disponga de ninguna explicación real, es agradable que un principio científico no choque con supuestos anteriores. El presente principio escalante parece bastante inocente. La pregunta a la que responde nunca se había planteado antes, por lo que no podían haberse expresado opiniones contrarias. Todo lo que parece afirmar la invariancia por cambios de escala es que en un mercado competitivo ningún lapso de tiempo es más especial que otro. Afirma que los rasgos obviamente especiales del día y la semana (y del año en el caso de los productos agrícolas) se compensan. Como todos los «parches» habituales del movimiento browniano comportan escalas de tiempo privilegiadas, parece como si mi principio simplemente afirme que no hay «razones suficientes» para suponer que una cierta escala temporal es más privilegiada que otra.

El síndrome de la varianza infinita

No obstante, queremos que la realización práctica del principio escalante dé un resultado distinto del movimiento browniano. Para ello di un paso radical: suponer que log X(t + d) ~ log X(t) tiene varianza infinita. Antes de mis artículos, nadie dudaba en escribir «denotemos la varianza por V». La hipótesis subyacente de que V era finita ni tan sólo se mencionaba… y es correcto, pues la literatura científica se colapsa cuando uno hace constar todas las hipótesis con independencia de su fundada importancia. Mis razones para pensar en una varianza infinita se exponen más abajo en esta misma sección. No hace falta decir que el éxito de suponer V = ∞ me facilitó la consideración de curvas de longitud infinita y superficies de área infinita.

EL MAL COMPORTAMIENTO OBSERVADO EN LA VARIANZA DE LAS MUESTRAS DE LAS VARIACIONES DE PRECIOS. El nivel menos sofisticado de la descripción estadística lo constituyen los «valores típicos» que se usan para resumir los datos. Pero, en el caso de las variaciones de precios, los resúmenes habituales resultan ser engañosos y nada fiables. En efecto, el motivo por el que se usa la media de una muestra para medir la situación, y la media cuadrática de una muestra para medir la dispersión, es que se cree que éstas son características «estables» que al final convergen hacia los valores de la población. Pero la figura de Mandelbrot (1967b) demuestra que su comportamiento en el caso de los precios resulta extraordinariamente escurridizo:

LA HIPÓTESIS DE NO ESTACIONARIEDAD. Todas estas propiedades en conjunto, o incluso cualquiera de ellas por separado, sugieren a cualquiera que el proceso no es estacionario. Mi contrapropuesta preliminar es que el proceso es, de hecho, estacionario, pero que el desconocido segundo momento teórico es sumamente grande. En la hipótesis de un momento grande pero finito, los momentos muéstrales convergen de acuerdo con la ley de los grandes números, pero la convergencia es sumamente lenta y el valor límite importa muy poco en la práctica.

EL PRINCIPIO DE LA VARIANCIA INFINITA. Mi siguiente contrapropuesta es que la media cuadrática poblacional es infinita. La elección entre «muy grande» e «infinita» ya resultará familiar a quien haya llegado hasta aquí en este ensayo, pero quienes hayan empezado por aquí quizá tengan otra disposición de ánimo, y así ocurría con mis lectores de 1962. A cualquiera que tenga una formación corriente en estadística, una variancia infinita le asustará en el mejor de los casos y le parecerá estrafalaria en el peor. De hecho, «infinito» no difiere de «muy grande» en nada que se pueda detectar por medio de los momentos muéstrales. También, por supuesto, el hecho de que una variable X tenga variancia infinita no niega de ninguna manera que X sea finita con probabilidad 1. Así, por ejemplo, la variable de Cauchy de densidad 1/π(1 + x²) es casi con certeza finita, pero tiene variancia y esperanza infinitas. Así pues, la elección entre variables con variancia muy grande y variancia infinita no debería decidirse a priori, y tendría que depender sólo de qué es lo más conveniente. Yo acepto la variancia infinita porque hace posible conservar la invariancia por cambio de escala.

Modelo de Lévy estable (Mandelbrot, 1963b)

Mandelbrot (1963b) combina el principio escalante con la idea aceptable de que los cambios de precio sucesivos son independientes con esperanza nula, y además permite que la varianza de los cambios de precios sea infinita. Un breve razonamiento matemático conduce a la conjetura de que la variación del precio sigue una distribución estable según Lévy, que también aparece en los capítulos 32, 33 y 39.

Esta conjetura resulta ser de una validez muy general. Los primeros tests (Mandelbrot 1963b, 1967b) se ajustaban a los precios de muchos artículos, algunos tipos de interés y algunos precios de obligaciones del siglo XIX. Posteriormente, Fama (1963) estudió los precios recientes de las obligaciones, y Roll (1970) el de otros tipos de interés. Aquí tendremos que contentarnos con una única ilustración, la lámina 475.

El poder predictivo del modelo

El valor predictivo del principio escalante de la variación de precios reside en el siguiente descubrimiento. Se empieza con la distribución de variaciones diarias del precio sobre un periodo de cinco años de variabilidad regular. Se ve que, si esta distribución se extrapola a las variaciones mensuales del precio, su gráfica pasa por los datos de varias recesiones, depresiones, etc. Da cuenta de todos los eventos, por extremos que sean, de casi un siglo de la historia de una mercancía esencial y de lo más volátil.

En particular (lámina 475) el proceso que rige los cambios en el precio del algodón ha permanecido aproximadamente estacionario a lo largo del larguísimo periodo estudiado. Este sorprendente descubrimiento se expone mejor en dos etapas.

PRIMER TEST DE ESTACIONARIEDAD. La lámina 475 indica que, tanto la forma analítica del proceso de las variaciones del precio como el valor de D, permanecen constantes. No discutimos aquí los cambios principales en el valor del dinero, etc., sino que las tendencias globales son despreciables frente a las fluctuaciones que estamos considerando.

SEGUNDO TEST DE ESTACIONARIEDAD: CORRECCIÓN DE UN ERROR DE LA LÁMINA 475. El segundo test de estacionariedad se descubrió por pura casualidad. Las curvas (a⁺) y (b⁺) de la lámina —lo mismo que (a⁻) y (b⁻)— difieren en una traslación horizontal. Como la traslación en coordenadas bilogarítmicas corresponde a un cambio de escala en las coordenadas naturales, esta discrepancia llevó a Mandelbrot (1963b) a compartir la opinión de los economistas de que la distribución de la variación de precios había cambiado entre 1900 y 1950. Pensé que la forma de la distribución había permanecido idéntica, pero la escala había disminuido.

Sin embargo, esta concesión ha resultado ser superflua. Los datos en que se basan las curvas (a⁺) y (a⁻) no habían sido interpretados correctamente (Mandelbrot 1972b). Corregido el error, se tienen curvas casi idénticas a las (b⁺) y (b⁻).

No se puede negar que, a primera vista, los datos dan la impresión de ser sumamente no estacionarios, pero esto se debe a que las primeras impresiones están influidas por la creencia de que el proceso subyacente es gaussiano. Mi alternativa al proceso no estacionario y gaussiano es un proceso estable, estacionario, pero no gaussiano.

Conclusión

No sé de ninguna otra predicción en economía con un éxito comparable.

LÁMINA 475. Indicios originales de la invariancia por cambio de escala en economía.

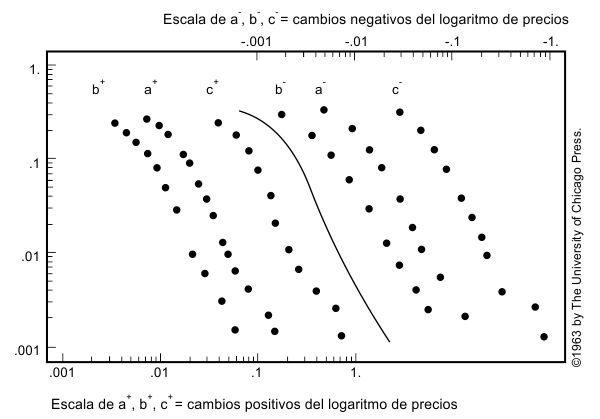
FIGURA 475

Tengo un cierto cariño a esta antigua lámina, reproducida de Mandelbrot (1963b) —como luego se lo tuve también a la lámina 383—. Combina gráficos bilogarítmicos de colas positivas y negativas correspondientes a cambios registrados en el precio del algodón, junto con la función de densidad acumulada de la distribución estable simétrica de exponente D = 1,7, que en realidad es un valor de D ligeramente sobreestimado. La ordenada da la frecuencia relativa de los casos en que el cambio de una de las magnitudes X definidas más adelante excede al cambio en la abscisa.

Si se copia la lámina en una transparencia y se la desplaza horizontalmente, se verá cómo la curva teórica se superpone a cualquier otra de las gráficas empíricas con ligeras diferencias respecto a la forma general. ¡Esto es precisamente lo que postula mi criterio escalante!

Las discrepancias se deben generalmente a una ligera asimetría en la distribución. Ésta es una observación importante que hace necesarias variantes sesgadas de la distribución estable.

Se han representado los siguientes conjuntos de datos, tratando por separado los valores positivos y negativos de X.

(a) X = log_eZ (t + 1 día) − log_eZ(t), siendo Z el precio de cierre diario en la lonja del algodón de Nueva York, 1900-1905 (datos suministrados por el Departamento de Agricultura de los EEUU).

(b) X = log_eZ (t + 1 día) − log_eZ(t), donde Z(t) es un índice de los precios diarios de cierre del algodón en varias lonjas de los EEUU, 1944-1958 (comunicado por Hendrik S. Houthakker).

(c) X = log_eZ (t + 1 mes) − log_eZ(t), siendo Z(t) el precio de cierre en el día 15 de cada mes en la lonja del algodón de Nueva York, 1880-1940 (comunicado por el Departamento de Agricultura de los EEUU).