35
Tremas generales y el control de la textura

De acuerdo con el método seguido en este ensayo, en los capítulos 31 y 32 se introdujeron los fractales por tremas mediante los ejemplos más simples, basados en segmentos, discos y bolas. Los resultados fueron gratificantes, pero el uso de tremas más generales produce una riqueza de resultados aún mayor.

Es cierto que El Hélou (1978) demuestra que la dimensión de un fractal por tremas queda determinada únicamente por la distribución de longitudes (áreas o volúmenes) de las tremas. Pero los días en que D era el único parámetro característico de un fractal acabaron en el capítulo 34, cuando introdujimos la subcolaridad y la lagunaridad. En el presente capítulo se muestra cómo estas características dependen de la forma trémica. Y, de nuevo, las exigencias concretas y la oferta geométrica caminan misteriosamente de la mano.

En lo que respecta a la subcolaridad, la forma de las tremas afecta al valor de D_crit y por tanto, para un valor dado de D, afecta al signo y la magnitud de D − D_crit.

En cuanto a la lagunaridad, las mejoras más simples respecto a capítulos anteriores se logran del modo siguiente. En el caso de fractales lineales por tremas (capítulo 31), los polvos de Lévy son los más lagunares, y cualquier grado menor de lagunaridad se puede conseguir del modo más simple y natural tomando como trema la unión de muchos intervalos. En el caso de fractales por tremas en el espacio obtenidas directamente (capítulo 33), lo más simple es tomar tremas que no sean bolas o discos. En el caso de fractales espaciales por tremas subordinados a un movimiento browniano, tanto ordinario como fraccionario (capítulo 32), lo más simple es tomar como subordinador un polvo fractal menos lagunar que el polvo de Lévy.

Desgraciadamente, el espacio se nos está acabando (este es de hecho el último capítulo que he escrito para esta obra), y los razonamientos relativos a los fractales por tremas requerirían mucha elaboración para adaptarlos al tono de este ensayo. Por tanto, el presente capítulo no pasa de ser un mero esbozo.

Generadores de tremas; isotropía

La expresión forma trémica empleada antes está relacionada con el concepto de generador de tremas. La expresión generador se ha usado ya en varios capítulos anteriores, por supuesto. Recordemos que los generadores de barras de las figuras de Cantor y de Koch. y los generadores de las tremas de las figuras de Sierpinski, determinan tanto la forma del fractal como su D. Aquí, por el contrario, el generador de tremas lo determina todo excepto D.

GENERADOR DE TREMAS NO ALEATORIO. Consiste en un conjunto abierto en el que se escoge un punto arbitrario como centro y de longitud (respectivamente, área o volumen) igual a 2 (respectivamente, π o 4π/3). Las tremas son réplicas a escala de este generador, y sus posiciones y tamaños son aleatorios, con la misma distribución que en los capítulos 31 y 33.

Por ejemplo, en el caso E = 1, el número de tremas con una longitud mayor que τ y centrados en un intervalo de longitud Δt sigue siendo una variable aleatoria de Poisson con valor esperado (E − D*)Δt/τ. El Hélou (1978) demuestra que la conocida fórmula D = máx(D*, 0) sigue siendo válida bajo algunas hipótesis poco restrictivas sobre la forma del generador de tremas. (La cuestión de si estas hipótesis restrictivas son intrínsecas o se deben al propio método de la demostración es algo que merece ser estudiado más a fondo).

GENERADOR ACOTADO. Como el objetivo filosófico de la construcción por tremas es crear estructuras globales a partir de una interacción local, es razonable mantener la hipótesis de que las tremas son locales, esto es, acotadas. Aunque las tremas no acotadas pueden llevar a sorpresas interesantes. En la lámina 285 se plasma un modelo por tremas más generalizado.

DEFINICIÓN DE LOS HUECOS. Los huecos no son ya reunión de tremas, sino reunión de componentes abiertas maximales de tremas.

ISOTROPÍA NO ALEATORIA. Para que el generador sea isótropo hace falta poder elegir el origen de modo que el generador sea el conjunto de puntos cuya distancia al origen caiga en algún conjunto del lado positivo de la recta real (normalmente es un conjunto de intervalos predeterminados). El caso isótropo es el más simple y el más investigado.

Sin embargo, la anisotropía no está excluida. Se ve, en particular, que un polvo fractal se puede hacer asimétrico con respecto al pasado y al futuro.

GENERADOR DE TREMAS ALEATORIO. Consiste en un conjunto, parcial o totalmente aleatorio, de longitud (área o volumen) igual a 1. Sería útil disponer de una revisión cuidadosa de la validez del teorema de El Hélou (1978) para este caso.

El nivel de azar mínimo consiste en tomar una muestra única de un proceso generador de conjuntos aleatorios, y hacer todas las tremas idénticas a la muestra (aparte de la posición y el tamaño). El siguiente nivel útil añade una rotación al azar, elegida independientemente para cada trema. O, con más generalidad, se pueden tomar como tremas muestras independientes de un proceso generador de conjuntos aleatorios. Los conjuntos muestra no tienen por qué tener todos el mismo volumen, ya que el volumen se fija mediante un ajuste de escala posterior, seguido de una rotación. Se puede pensar en rotaciones y muestras no independientes, pero por el momento no las he empleado.

ISOTROPÍA AL AZAR. En la primera de las alternativas anteriores la isotropía implica que la muestra sea invariante por rotación. En la segunda, la rotación de la muestra debe estar uniformemente distribuida. En la tercera, basta con que el proceso sea invariante por rotación.

ESTRATIFICACIÓN. Las definiciones anteriores permitirían construir tremas de longitud (o área o volumen) estratificada, esto es, restringida a valores de la forma r^k. Pero esto confundiría los distintos efectos de la estratificación y de las formas generales de las tremas.

Control de la subcolaridad mediante la Dcrit de fractales por tremas generales

En el capítulo 34 demostrábamos que es de esperar una estructura cirriforme si el fractal «casi» percola, esto es, si pertenece a una familia con una D_crit bien definida, y si su D es «sólo un poco» inferior a D_crit. En otras palabras, D y la intensidad de la estructura cirriforme se pueden ajustar simultáneamente si el modelo tiene como parámetros D y D_crit.

En un fractal por tremas los parámetros son el número real D y una función que determina el generador de tremas. Voy a demostrar que D_crit es una función de este último parámetro funcional: se puede hacer arbitrariamente próximo a E y, si E > 2, D_crit se puede hacer arbitrariamente próximo a 1.

UN CASO EN EL QUE D_crit ES ARBITRARIAMENTE PRÓXIMO A E. Basta con lomar como generador una aguja arbitrariamente delgada o una torta arbitrariamente plana de forma fijada pero con los ejes orientados isotópicamente (lámina 451). Para demostrar esta afirmación en el plano (E − 2) nótese que, dada una D < 2, los centros, tamaños y orientaciones de las tremas se pueden escoger con independencia del coeficiente de planitud del generador. Consideremos a continuación un cuadrado de lado L, y clasifiquemos las tremas en tres tipos: un tipo mediano con áreas mayores que πL²/10 y mayores que πη², un tipo superior y otro inferior. Cuando D es mucho mayor que la D_crit correspondiente a las tremas discoidales, y las tremas son discos ligeramente achatados, la situación es parecida a la del capítulo 33: las tremas de tipo mediano forman principalmente agujeros separados rodeados por un conjunto muy conexo. Pero si las tremas son muy achatadas, casi lineales, es casi seguro que cortarán nuestro cuadrado en pequeños polígonos desconectados entre sí. El efecto adicional de las tremas achatadas de tipo inferior sólo puede consistir en cortar aún más dichos polígonos. El efecto de las tremas de tipo superior puede ser eliminar nuestro cuadrado, cortarlo en pedazos o aislarlo. Cuando ocurre esto último, ya no puede percolar. En otras palabras, el achatado de las tremas puede hacer que D_crit sea mayor que cualquier D < 2 escogida previamente.

La generalización a E > 2 es trivial.

El mismo efecto se consigue para E ≥ 2, y se extiende también a E = 1, tomando como generador de tremas el dominio contenido entre una bola (o esfera) de radio mucho mayor que 1 y una bola (o esfera) convenientemente menor.

UN CASO EN QUE D_crit ES ARBITRARIAMENTE PRÓXIMO A 1. Un razonamiento heurístico sugiere que, cuando E ≥ 3, con tremas en forma casi de aguja, D_crit se puede hacer arbitrariamente próxima a 1.

Control de la lagunaridad mediante la L de fractales por tremas generales

En una sección del capítulo 34 se demuestra que, cuando las longitudes de las tremas están estratificadas, la lagunaridad se puede controlar. Hagamos ahora constar en acta (sin detallar demasiado) el hecho de que se puede conseguir el mismo objetivo con el generador de tremas. Nos centraremos en la medida de la lagunaridad mencionada en último lugar en el capítulo 34, en la que interviene la cota superior Ω.

De hecho, iremos un poco más allá, introduciendo una acotación doble y limitando la escala lineal de tremas al intervalo delimitado por ε > 0 y Λ < ∞.

Se ve fácilmente que un punto escogido al azar sigue teniendo una probabilidad (ε/Λ)^E−D de pertenecer al fractal por tremas truncado resultante. A continuación, asignemos masa a este conjunto con una densidad ε^E−D. Encontramos que el prefactor β = αΩ^E−D del capítulo 34 se convierte en Λ^E−D. Pasando al límite ε → 0, esta expresión sigue siendo válida para ε = 0. Y, por tanto, Ω = Λα^1/(E−D).

(Si Ω se define por medio de la definición variante, Ω = Λα^1/(E−D)(D/E)^1/(E−D)).

Nos resta aún evaluar α. Se encuentra que depende de la forma global del generador de tremas. Es mayor cuando el generador es un intervalo (disco o bola) y puede tomar valores arbitrariamente pequeños. El umbral Ω es pequeño en la misma medida.

Cuando la trema está contenida entre esferas concéntricas de radios α ≫ 1 y β ≫ 1, el resultado es muy simple: Ω ∝ 1/α.

Así pues, es posible hacer que 〈M(R)〉, y por ende la covarianza de la distribución de masa, pase de un modo arbitrariamente rápido a su comportamiento asintótico, en el sentido de que las densidades en dos puntos separados por una distancia mayor que Ω se hacen efectivamente independientes.

Es extraño que una disminución de la lagunaridad, debida a una disminución de α, tenga que conseguirse abriendo el generador. Más bien esperaríamos que un generador más abierto produjera un aumento en el tamaño de la región preasintótica. Este hecho confirma de nuevo que el comportamiento de 〈M(R)〉, y por tanto de la covarianza relativa de una distribución de masa, sólo nos da una visión parcial de la estructura de un conjunto. Los momentos de orden superior de M(R) contienen mucha más información adicional, pero no podemos extendernos más sobre el tema.

Control de la lagunaridad en polvos subordinados a trayectorias brownianas

Una vez controlada la lagunaridad de un polvo lineal, podemos aplicar el resultado en el espacio mediante el proceso de subordinación estudiado en el capítulo 32. Trabajando en el plano, y usando como subordinador una red browniana como la de la lámina 343, se puede conseguir un polvo tan parecido como se quiera a una red infinitamente ramificada. Partiendo de E = 2, tomemos como subordinando una red browniana fraccionaria con H > 1/2, cuyos huecos son menores que para H = 1/2. Si además la dimensión del subordinador cumple que D/H < E = 2, y su lagunaridad es baja, se puede conseguir que el subordinado parezca llenar el plano (tan aproximadamente como se quiera). Cuando E = 3 y H =1/3, el subordinando es una curva que llena el espacio. Y si D/H < E, y la lagunaridad del subordinador es baja, se puede hacer que el polvo subordinado llene el espacio con un grado de lagunaridad tan pequeño como se quiera, con independencia de D.

LÁMINA 451. Efecto del generador de tremas sobre la lagunaridad de un fractal por tremas.

FIGURA 451

Estas dos ilustraciones deberían dar una idea del efecto de la forma del generador de tremas sobre la lagunaridad. Ambos generadores tienen forma de diamante, pero uno es casi cuadrado y el otro es una aguja aguda. Contra el fondo blanco se pueden ver pequeños diamantes negros aislados.

En ambas construcciones se ha usado el mismo parámetro D y las mismas áreas para los diamantes mayor y menor. Se puede probar que las áreas de los residuos en blanco son iguales, aparte de fluctuaciones estadísticas. Sin embargo, resulta obvio a simple vista que uno de los residuos en blanco está muchísimo más disperso que el otro. Las medidas de lagunaridad que he introducido atribuyen un valor mucho menor de los coeficientes de lagunaridad al residuo más disperso

LÁMINA 453. Polvo fractal obtenido con tremas no esféricas: Proyección de un octante sobre un cielo esférico.

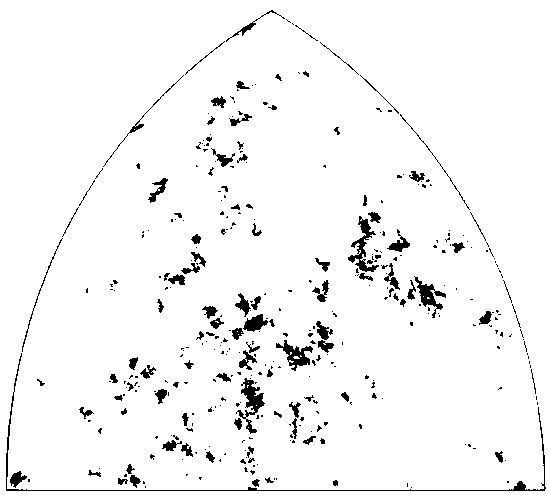
FIGURA 453

Por razones de lo más embarazoso, esta ilustración no sólo no es la que tenía que ir aquí, sino que, por el momento, no puedo dar las especificaciones precisas de esta lámina. En efecto, hacia enero de 1979 realizamos una gran cantidad de ilustraciones de fractales de dimensión D ~ 1,23 con grados de lagunaridad y subcolaridad variables y controlados. Pero el archivo que contenía el grueso de los resultados se ha extraviado (o quizá perdido), y los pocos ejemplares que han sobrevivido en otros archivos no llevan las etiquetas adecuadas. A falta de tiempo para reactivar el programa, sólo puedo mostrar lo que tengo a mano.

Hasta donde puedo recordar, el cálculo empieza con un patrón periódico, cuyo periodo es una cuadrícula cúbica de 600³. En otras palabras, el cálculo se realiza sobre una cuadrícula cúbica de 600³, cuyas caras opuestas se identifican, creando una especie de toro. La distribución de volúmenes de las tremas es truncada. Después de quitar las tremas, el origen se sitúa en un punto no borrado, que se elige, bien arbitrariamente, bien en una región de alta densidad.

Los puntos cercanos al origen no se representan, y los otros puntos se clasifican en capas definidas por R₁² < x² + y² + z² < R₂² correspondientes a distintas magnitudes de brillo. Cada capa se proyecta sobre un cielo esférico.

El objeto es procesar los datos disponibles a fin de extraer el máximo de información independiente. Para R₂ pequeños se puede proyectar el cielo entero, pero para R₂ mayores no se debe procesar más que una parte conveniente de un periodo del patrón periódico inicial. El valor de R₂ en la capa más externa es mayor cuando el mapa se limita a un solo octante del cielo, por ejemplo el dominio correspondiente a x > 0, y > 0, z > 0. En coordenadas esféricas se puede definir dicho octante como el correspondiente a latitudes positivas (hemisferio norte) y longitudes comprendidas entre −−45° y 45°. En la proyección de Hammer usada aquí, dicho octante es representado por la «ventana gótica ojival» del diagrama siguiente.

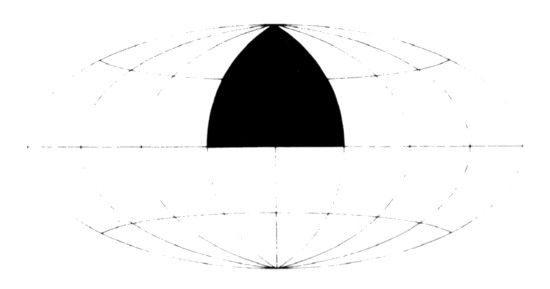
Cuando R₂ llega al valor 600, los datos de las proximidades de los tres vértices se hacen estadísticamente dependientes, y lo mejor es desechar los datos de los vértices inferiores. Así, los datos más allá de R₂ = 600, próximos a x = z = 0, y = 600, o próximos a y = z = 0, x = 600, se sacrifican para evitar la dependencia estadística inducida por la periodicidad. Por otra parte, para representar la región antipodal x < 0, y < 0, z < 0, esto es, las longitudes 0 del hemisferio sur tales que |θ − 180°l < 45°, no hace falta un nuevo cálculo, y el resultado puede parecer suficientemente distinto para considerar que contiene información adicional.

En un estadio final del proceso, cuya finalidad es eliminar las trazas de la red cúbica original, cada punto es desplazado según un vector cuyas coordenadas están uniformemente distribuidas en [0,1]. Desgraciadamente este proceso da lugar a zonas grises densas con intensidades diversas, que desfiguran el fractal subyacente: lo que vemos son versiones igualadas de zonas muy poco homogéneas.

En esta lámina, R₂ = 600 y R₁ = R₂/1,5, y por tanto las magnitudes caen en un intervalo estrecho de amplitud 2,51og₁₀(1,5)² ~ 0,88.

La figura 7 de Mandelbrot (1980b) muestra otro polvo fractal (también sin clasificar) obtenido con otra elección distinta de los f tremas.