Después de introducir el polvo de Lévy lineal como un fractal por tremas, mediante tremas aleatorios en forma de segmento (capítulo 31), nos hemos apartado del tema en el capítulo 32, donde generalizamos dicho polvo al plano y al espacio mediante el proceso de subordinación. En este capítulo y el siguiente generalizamos directamente las tremas aleatorias.

En este capítulo las tremas planas son discos, y las espaciales, bolas. La generalización nos lleva pues directamente a las formas de los cráteres de la Luna y de los meteoritos. Pero la aplicación más importante de las tremas espaciales es distinta y menos evidente. Si D es próxima a 1, el fractal por tremas es un polvo, y por tanto un candidato para sustituir las paradas del vuelo de Lévy en la modelización de los cúmulos de galaxias. La principal novedad con relación a los modelos basados en paseos aleatorios es que aquí las galaxias no están ordenadas sobre una trayectoria. De ahí que se gane algo en cuanto a la verosimilitud a priori, aunque también se pierda en lo que se refiere a las conveniencias del cálculo, y finalmente se salga ganando en la calidad del ajuste de los datos; las propiedades de covariancia predichas se aproximan aún más a la evidencia empírica. Y las tremas no esféricas del capítulo 35 mejorarán todavía más el ajuste a los datos.

Como preliminar a las tremas aleatorias y solapantes, reformularemos la construcción de la coagulación plana en una trama (capítulo 13 y 14) en términos de tremas virtuales. El primer paso de la cascada consiste en marcar N de los b² cuadrados y conservarlos como grumos. Se podría decir también que se eliminan b² − N tremas cuadradas. En el siguiente paso se quitan b²(b² − N) tremas cuadradas de segundo orden, de las que N(b² − N) son reales y los restantes (b² − N)² son «virtuales»: eliminan algo que había sido eliminado en el primer paso. Y así sucesivamente.

Si contamos todas las tremas, sean virtuales o auténticas, encontramos que el número de ellas con un área superior a s es proporcional a 1/s. El resultado correspondiente a la coagulación en el espacio tridimensional es que el número de tremas de volumen superior a v es proporcional a 1/v.

Análogamente, el grueso de este capítulo y del capítulo 35 se ocupa del caso en que el número de tremas independientes con centro en una celda de lados dx y dy, o dx, dy y dz, es una variable aleatoria de Poisson de valor esperado

〈Nr (área > a)〉 = (c/2a) dx dy,

〈Nr (volumen > v)〉 = (c/3v) dx dy dz,

Las propiedades fractales del conjunto residual son tan simples como en el caso lineal considerado en el capítulo 31. Si C < 1, dichas propiedades pueden obtenerse de las del caso lineal, y en los ensayos anteriores a éste se conjeturaba su validez para cualquier C, cosa que fue confirmada por El Hélou (1978).

Si C > E, el conjunto residual es casi seguramente vacío, y si C < E, es un fractal de dimensión D = E − C.

Por lo que respecta a la topología del fractal residual, se tiene a partir de principios generales que, si D < 1, entonces se trata de un polvo con D_T = 0. Por el contrario, si D > 1 los principios generales no bastan para determinar la topología del fractal, que dependerá de la forma de las tremas. Aparece aquí el problema de la percolación, aunque en otro contexto.

Empezaremos por un tema colateral que, además de servimos como aperitivo bidimensional, es divertido: la naturaleza geométrica de la parte de la Luna no cubierta por cráteres. En tanto que el griego κρατηρ significa tazón o recipiente para beber, casi todos los cráteres terrestres son de origen volcánico. Pero parece ser que los cráteres que se observan en la Luna, Marte, el satélite joviano Calisto, y otros planetas y sus satélites, se deben en su gran mayoría al impacto de meteoritos.

Cuanto mayor es el meteorito, mayor y más profundo es el cráter dejado por su impacto. Además, un gran cráter debido al impacto reciente de un meteorito pesado puede borrar del mapa varios cráteres menores, mientras que un cráter pequeño producido por el impacto reciente de un meteorito ligero puede «mellar» el borde de un cráter grande preexistente. Por lo que respecta a los tamaños, hay una evidencia empírica sólida de que, en el momento del impacto del meteorito, las áreas de los cráteres siguen una distribución hiperbólica: el número de cráteres con un área superior a s km² y cuyo centro está localizado en un cuadrado de 1 km de lado se puede expresar como C/s, siendo C una constante. La concordancia de esta ley con los datos está comentada en Marcus (1964), Arthur (1954), y Hartmann (1977).

Con objeto de simplificar los razonamientos (sin cambios en el resultado principal), aproximaremos la superficie lunar por un plano, y los cráteres lunares por tremas discoidales. Si la Luna fuera interceptando meteoritos eternamente, de un entorno estadísticamente invariante, resulta obvio que cualquier punto de su superficie sería cubierto una y otra vez por algún cráter. Sin embargo, podría ser que los cráteres fueran borrados del mapa con una cierta frecuencia, por lava volcánica por ejemplo, y en tal caso el conjunto no recubierto por cráteres en un momento dado sería no trivial. O podría ser también que el sistema solar evolucionara de modo que nuestra Luna sólo fuera bombardeada por meteoritos durante un período de tiempo finito. El parámetro C podría medir el tiempo transcurrido desde el último borrado de cráteres, o bien la duración total del bombardeo.

Con objeto de apreciar el efecto sobre la forma del fractal residual, tomemos siempre la misma semilla y variemos C. Mientras C aumenta de 0 a 2, la superficie de la Luna va quedando más y más saturada, y el resultado enunciado en la sección anterior indica que D disminuye hasta hacerse 0 para C > 2. Las láminas 429 a 432 ilustran el modo en que el fractal residual depende de D.

APPENZELL Y EMMENTHAL. Si C es muy pequeño, los aficionados al queso suizo compartirán conmigo la idea de que la figura que estamos tratando parece una loncha de queso casi totalmente tachonada de pequeños agujeros. Es como una extrapolación desenfrenada de la estructura del queso Appenzell. Si aumentamos C, la estructura acaba por parecer una extrapolación desenfrenada de una loncha de queso Emmenthal, con grandes agujeros solapados. (Así pues, la vieja poesía inglesa infantil según la cual la Luna estaría hecha de queso verde ha demostrado ser correcta, siempre y cuando se prescinda del color).

TOPOLOGÍA. Dimensiones críticas. Hemos calificado de «desenfrenadas» las dos extrapolaciones anteriores del queso porque el área de las «lonchas» fractales es nula. Mi conjetura al respecto es la siguiente: mientras C sea suficientemente pequeño el fractal residual será un σ-racimo, siendo cada racimo por contacto una malla de filamentos conexos, de dimensión topológica D_T = 1. Cuando D alcanza un cierto valor crítico, D_crit, el valor de D_T se hace 0 y la σ-malla colapsa en un polvo.

La siguiente dimensión crítica es D = 0. Si C ≥ 2, la superficie de la Luna está supersaturada, y cada punto es cubierto con casi toda seguridad por uno o más cráteres. Esto ocurriría, en particular, si la superficie de la Luna no se limpiara nunca de cráteres y recibiera el impacto de meteoritos por siempre jamás.

Cráteres no escalantes. Algunos planetas distintos de la Luna se caracterizan por una densidad de cráteres de la forma Ws^−γ con γ ≠ 1. El problema que plantean estos cráteres se trata en el apéndice de este capítulo.

En tanto que a las tremas de la Luna se les puede reconocer una existencia independiente como cráteres, las tremas esféricas con una distribución escalante aparecieron como la generalización natural del mismo método geométrico al espacio. Pensé que podían proporcionar un modelo alternativo al modelo de galaxias del capítulo 32. Por tanto, postulé la existencia de vacíos intergalácticos que resultan de la combinación de muchas tremas y pueden llegar a tener un tamaño enorme. Fue una sorpresa muy agradable que el modelo resultante concordara tan bien con los datos, cosa que hace necesario profundizar más en la teoría (capítulo 35) y en la experimentación.

COVARIANCIAS. Como los estadísticos y los físicos se fían tanto de las correlaciones y los espectros, la primera prueba a que se somete el fractal por tremas como modelo de los cúmulos de galaxias se basa en sus propiedades de correlación. La covariancia entre dos puntos del espacio es la misma que en mi modelo de paseo aleatorio, como debe ser, pues éste se ajustaba bien a los datos. Lo mismo vale, como debe ser, para la covariancia entre dos direcciones del cielo. Las covariancias entre tres y cuatro direcciones predichas por el modelo concuerdan mejor que las predichas por el modelo de paseo aleatorio, pero las mejoras son puramente técnicas y es mejor discutirlas en otra parte. Básicamente, una vez se tiene D, los distintos modelos dan la misma correlación.

Recordemos ahora que los fenómenos gaussianos, incluidos los fractales brownianos ordinarios y fraccionarios, están caracterizados completamente por las propiedades de covarianza. Si son escalantes, la D los caracteriza completamente. Dada la influencia de los fenómenos gaussianos en el modo de razonar de los estadísticos, uno podría estar tentado de detenerse en las covarianzas. Pero los polvos fractales no son fenómenos gaussianos, y no basta con la D para especificar muchos de sus detalles significativos.

DIMENSIONES CRÍTICAS. Más importante que la correlación es saber si los fractales por tremas tienen o no la topología correcta. Para comprobarlo, lo mejor es hacer como en la sección anterior, tomar una semilla fija y hacer que C varíe entre 0 y 3. Mientras C sea pequeña, D_T = 2, y nuestro fractal está formado por membranas ramificadas. Cuando D pasa de un cierto valor D_2crit, que se llama dimensión crítica superior, las membranas se descomponen en filamentos, con D_T = 1. Y cuando D disminuye más allá de otro valor D_crit, denominado dimensión crítica inferior, los filamentos se reducen a polvo, con D_T = 0. Como para modelizar los cúmulos de galaxias necesitamos un polvo, es importante comprobar que la D_crit es mayor que la D ~ 1,23 observada. Mis simulaciones en el ordenador han confirmado esta desigualdad.

PERCOLACIÓN. La esperanza de que el mundo no sea más complicado de lo necesario me inclina a pensar que D > D_crit es la condición necesaria y suficiente para que el fractal construido por tremas presente percolación, en el sentido descrito en el capítulo 13.

La distribución de masas de los meteoritos que chocan con la Tierra ha sido estudiada a fondo, por ejemplo en Hawkins (1964). Los meteoritos de tamaño mediano son pétreos, y 1 km³ de espacio contiene aproximadamente P(v) = 10^-25/v meteoritos de volumen superior a v km³.

Normalmente esta afirmación se expresa de un modo distinto, usando la siguiente mezcolanza de unidades. Cada año, la superficie terrestre recibe en promedio por km² 0,186/m meteoritos de masa superior a m gramos. Como su densidad media es de 3,4 g cm⁻³, esta relación se convierte en 5,4 × 10⁻¹⁷/v meteoritos de volumen superior a v km³. Como además la Tierra avanza aproximadamente 1 km en 10⁹ años (la inversa del orden de magnitud del perímetro de la órbita terrestre alrededor del Sol expresado en km), tenemos que mientras la Tierra avanza 1 km en el espacio cada km² terrestre se encuentra con 10⁻²⁵/v meteoritos de volumen superior a v km³ (aquí sólo hemos atendido a los órdenes de magnitud, de modo que el factor 5,4 lo hemos convertido en 10). Suponiendo que los meteoritos que chocan con la Tierra en su movimiento por el espacio sean una muestra representativa de la distribución espacial de meteoritos, obtenemos el resultado anunciado anteriormente.

Esta ley del 10⁻²⁵/v es formalmente idéntica a la ley del C/s de los cráteres lunares, aunque con una diferencia: mientras los cráteres pueden solaparse, los meteoritos no.

No obstante, es divertido ver qué ocurriría si P(r) = 10⁻²⁵/v fuese válido para cualquier valor de v, por pequeño que fuera, y si además —¡idea descabellada!— los meteoritos pudieran solaparse. Añadiendo la suposición inocua de que los meteoritos son esféricos, el conjunto de tremas puede ser estudiado directamente (sin necesidad de recurrir a los resultados de El Hélou, 1978).

Las secciones rectilíneas de los meteoritos con rectas trazadas al azar en el espacio son tremas rectilíneas, y se puede demostrar que el número de estas con centro en un intervalo de 1 km y de longitud mayor que u Km es C' 10⁻²⁵/u. (C' es un factor numérico cuyo orden de magnitud es 1 y no tiene mayor importancia en este contexto). Por tanto, según un resultado del capítulo 32, se tiene que la dimensión de las secciones rectilíneas del conjunto de tremas vale 1 − 10⁻²⁵. Si les sumamos 2 para pasar de las secciones rectilíneas a la figura total, obtenemos 3 − D = 10⁻²⁵.

Este resultado es una sandez, pues en particular implica que los meteoritos casi llenan el espacio, aun permitiendo que se solapen. No obstante, vale la pena echar una segunda mirada a esta codimensión 3 − D = 10⁻²⁵. Supongamos que, en primera aproximación, la relación 10⁻²⁵/v vale para todos los valores de v mayores que un corte positivo η > 0 y que no hay meteoritos de un tamaño menor. El razonamiento que hemos esbozado afirma que, si se pudiera pasar efectivamente al límite η → 0, el conjunto complementario de los meteoritos convergería a un fractal por tremas de dimensión D = 3 − 10⁻²⁵. Por suerte, este límite se alcanzaría tan lentamente que, en las escalas observables, el solapamiento de meteoritos no puede plantear ningún problema. Por desgracia, el valor de D no puede tener ninguna importancia práctica, sea cual sea.

Para lo que nos interesa ahora, expresaremos la distribución de cráteres de la Luna como Pr(A > a) = Fa^−γ, con γ = 1. Parece que para Marte vale el mismo y, pero en los satélites de Júpiter se encuentran otros valores de y distintos (Soderblom, 1980). Análogamente, para los meteoritos de pequeño volumen se tiene γ < 1. Los conjuntos residuales por tremas no son escalantes.

EL CASO γ > 1. En este primer caso no escalante, cualquier punto dado de la superficie del planeta, con independencia del valor de W, cae casi con toda certeza dentro de una infinidad de cráteres. La textura de la superficie está abrumadoramente dominada por los cráteres pequeños. El satélite joviano Calisto tiene esa estructura y se caracteriza, en efecto, por γ > 1. Cuando en los antecesores de este ensayo, antes de la misión Voyager, se discutía el caso γ > 1, éste no era más que una posibilidad teórica.

EL CASO γ < 1 CON LAS ÁREAS DE LOS CRÁTERES COTADAS. Denotemos por 1 esta cota. La probabilidad de que un punto no caiga en el interior de ningún cráter es positiva ▯ pues la integral ∫₀¹Pr(A>a) da converge ▮, pero disminuye al aumentar W. La superficie agujereada resultante nos recuerda una loncha de queso suizo (mejor aún que en el caso escalante). Cuanto mayor es el valor de γ, menor es el número de agujeros pequeños y más «macizo» es el queso resultante. Sin embargo, y con independencia del valor de y, la loncha tiene un área positiva, y es por tanto un conjunto (no autosemejante) de dimensión 2. Por otra parte, no me cabe la menor duda de que su dimensión topológica es 1, con lo que es un fractal.

En el espacio (meteoritos) las dimensiones de este fractal por tremas son D = 3 y D_T = 2.

LÁMINAS 429 y 430. Tremas redondas y más bien pequeñas, en blanco, y lonchas aleatorias de «queso suizo» (dimensiones D = 1,9900 y D = 1,9000).

FIGURA 429

Las tremas son discos circulares blancos. Sus centros están distribuidos al azar en el plano. El área del disco de rango p es K(2 − D)/ρ, donde la constante numérica se escoge convenientemente para reproducir el modelo de tremas descrito en el texto. En la lámina 429 se muestra una especie de Appenzell cuya parte en negro tiene una dimensión D = 1,9900, y en la lámina 430 una especie de Emmenthal con una parte en negro de dimensión D = 1,9000.

FIGURA 430

LÁMINAS 431 y 432. Tremas redondas más grandes, en negro, e hilos blancos ahorquillados al azar (dimensiones D = 1,7500 y D = 1,500).

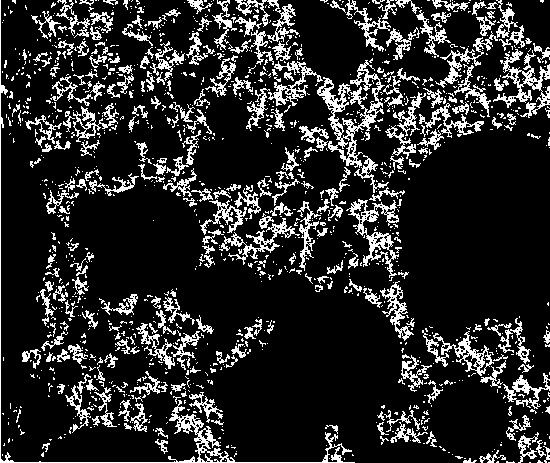
FIGURA 431

La construcción sigue el mismo método que en las láminas 429 y 430, aunque las tremas son mayores y se representan en negro. Así apenas queda nada por arrancar. Los valores de D son las dimensiones de los fractales residuales, en blanco

FIGURA 432

33 Cráteres circulares y esféricos: cráteres lunares y galaxias

33
Cráteres circulares y esféricos: cráteres lunares y galaxias