Este capítulo y el siguiente tratan principalmente de los cúmulos de galaxias, tema que ya ha sido considerado en los capítulos 9, 22 y 23. Las técnicas empleadas son una generalización al plano y al espacio de los polvos del capítulo anterior. En este capítulo nos ocuparemos en primer lugar de los polvos de Lévy espaciales. Siguiendo a Bochner, introduciremos estas fractales «tratando» el movimiento browniano por el método de la «subordinación». Bajo el polvo de Lévy se encuentra el vuelo de Lévy, una variante no estándar de paseo aleatorio. El capítulo empieza con un anticipo informal sobre los cúmulos asociados al paseo aleatorio. Luego se explica y justifica la subordinación, extendiéndola a un contexto no aleatorio. En la sección final se justifican las afirmaciones y conjeturas de la sección preliminar.

El objeto de mi modelo primitivo de los cúmulos de galaxias era presentar una distribución de masa con las siguientes propiedades: (a) la masa M(R) contenida en una esfera con centro en la distribución cumple que M(R) ∝ R^D, con D < 2; (b) la distribución cumple el principio cosmográfico condicional en su forma estadística.

PARADAS DEL VUELO DE RAYLEIGH. Consideremos ahora una construcción preliminar que no tiene las mismas dimensiones, ni topológica ni fractal, que los cúmulos de galaxias. Partiendo de un punto del espacio ∏(0), un cohete en vuelo de Rayleigh salta en una dirección isotrópicamente aleatoria. La duración de cada vuelo es Δt = 1 y la distancia U a la siguiente parada ∏(1) es una variable aleatoria gausiana con 〈[∏(1) − ∏(0)]²〉 = 1. A continuación, el cohete vuela hasta un ∏(2) tal que

son dos variables aleatorias vectoriales independientes y regidas por la misma distribución.

A fin de poder considerar que el viaje del cohete ha durado eternamente, le añadiremos las paradas anteriores ∏(−l), ∏(−2),… Para ello, y dado que el paseo aleatorio no cambia por inversión del tiempo, nos bastará con tomar dos trayectorias independientes a partir de ∏(0).

La trayectoria de nuestro cohete (incluyendo el «rastro» que deja al ir saltando) es un conjunto aleatorio. Y también lo es el conjunto de las paradas consideradas sin tener en cuenta el orden en el que son visitadas. Ambos conjuntos obedecen a la misma distribución si se examinan desde cualquiera de sus puntos ∏(t). Usando la expresión introducida en el capítulo 22, ambos conjuntos cumplen el principio cosmográfico condicional en su formulación estadística.

CARGA. Si a las paradas de un vuelo de Rayleigh les asignamos al azar unas masas estadísticamente independientes y con distribuciones idénticas, la estacionariedad condicional es extensiva a la masa.

LA DIMENSIÓN D = 2. Como es bien sabido, la distancia recorrida en K saltos es proporcional a √K. En consecuencia, una bola de radio R y centro ∏(t) contiene un número de paradas M(R) ∝ R². El exponente de esta fórmula concuerda con la idea de que la dimensión del conjunto de paradas ∏(t) es D = 2. Por otra parte, la densidad global es nula.

MOVIMIENTO BROWNIANO. Interpolando el vuelo de Rayleigh para un tiempo continuo, se obtiene una trayectoria browniana, que es (capítulo 25) una curva continua con D = 2. Así pues, el modelo del vuelo de Rayleigh es, en esencia, una curva fractal (D_T = 1 y D = 2) que cumple el principio cosmográfico condicional, pero no en su versión fuerte. Esta última conclusión es satisfactoria, pero los valores de D_T y D son inaceptables.

DENSIDAD GENERALIZADA. Si cargamos una trayectoria browniana entre los puntos ∏(t₀) y ∏(t) con la masa δ|t₀ − t|, la masa M(R) se convierte en el tiempo que el punto pasa en la bola de radio R multiplicado por la densidad generalizada uniforme δ.

EXPANSIÓN DEL UNIVERSO. En las discusiones estándar, la distribución inicial tiene una densidad uniforme δ. A medida que el universo se expande uniformemente, δ disminuye, manteniéndose uniforme la distribución. Por otra parte, es una creencia general que cualquier otra distribución cambia con la expansión. La trayectoria browniana con carga uniforme prueba de manera constructiva que tal conclusión es incorrecta: como antes, δ cambia con la expansión, pero permanece constante y uniforme.

Por tanto, las paradas del vuelo de Rayleigh son neutras en lo que res- pecta a la cuestión de si nuestro Universo está o no en expansión. Esta propiedad no se pierde si se hace disminuir D empleando un vuelo de Lévy, como consideramos a continuación.

PARADAS DEL VUELO DE LÉVY: DIMENSIONES NO ENTERAS < 2. Mi modelo de paseo aleatorio para la distribución de galaxias implementa cualquier dimensión fractal D < 2 empleando un polvo, esto es, un conjunto con la dimensión topológica correcta D_T = 0. Con este objeto, usaré un paseo aleatorio en el que el valor esperado 〈U²(t)〉 es infinito, pues U es una variable aleatoria hiperbólica, con un corte inferior en u = 1. Así pues, para u ≤ 1, Pr(U>u) = 1, mientras que para u > 1, Pr(U>u) ∝ u^−D, con 0 < D < 2.

Una de las principales consecuencias es que 〈M(R)〉 ∝ R^D para R ≫ 1. Ésta es la relación que queríamos obtener, y permite cualquier dimensión que puedan sugerir la observación o la teoría.

▯ APARTE SOBRE LA ESTABILIDAD DE LÉVY. Para t → ∞, la masa contenida en un intervalo de tiempo t (tomado a una escala conveniente) converge hacia una variable aleatoria independiente de t, investigada por primera vez por Paul Lévy, y de la que diremos que es «estable según Lévy» (capítulo 39). De ahí la expresión «vuelo de Lévy» propuesta para el proceso subyacente al modelo.

▯ Como 〈U²〉 = ∞ el teorema del límite central estándar no es válido y hay que reemplazarlo por un teorema del límite central especial. Esta sustitución tiene consecuencias notables. El teorema estándar es «universal», en el sentido de que el límite sólo depende de las cantidades 〈U〉 y 〈U²〉. El teorema no estándar no es universal. La distribución de M(R) depende explícitamente, a través de D, de la distribución de los saltos. ▮

En lo que resta de capítulo construiremos un polvo que es al vuelo de Lévy lo que el movimiento browniano al vuelo de Rayleigh. Una interpolación directa sería tediosamente técnica, pues habría de dar un significado a la distribución Pr(U>u) = u^−D hasta en la proximidad de u = 0, donde diverge. Por el contrario, hay ataques indirectos del problema que son a la vez sencillos y precisos, gracias al proceso de subordinación. Este proceso es interesante en sí mismo y tiene un gran número de generalizaciones obvias.

Introduciremos la subordinación por medio de un ejemplo. Para generar una dimensión D = 1 partiendo de la trayectoria browniana de dimensión D = 2, tenemos que intentar que D disminuya en 1. En el caso de las figuras euclídeas clásicas, esta disminución se consigue fácilmente. En el plano basta con tomar la intersección con una línea, en el espacio tridimensional basta con tomar la intersección con un plano, y en el espacio tetradimensional la intersección con un espacio de dimensión 3. Vimos también en el capítulo 23 que la misma regla es aplicable a las coagulaciones fractales aleatorias, y en el capítulo 25 que la función browniana real de variable real tiene dimensión 3/2, y que su conjunto de ceros, así como cualquier sección no ortogonal al eje t, tiene dimensión 1/2.

Por analogía formal, este método de disminuir D en 1 nos lleva a pensar que, si elegimos convenientemente la sección de una trayectoria browniana, obtendremos normalmente una dimensión 2 − 1 = 1. Esta sospecha ha sido efectivamente comprobada (Felle, 1971, pág. 348). Además, tendría que hacerse extensiva también a las secciones planas de una trayectoria en el espacio tridimensional, y a las secciones tridimensionales de una trayectoria en el espacio tetradimensional, en donde las coordenadas son x, y, z y humor.

Empezando con una trayectoria browniana en el espacio tetradimensional, consideremos aquellos puntos en los que humor = 0. Estos vértices «sin humor» se pueden ordenar según el orden de llegada del movimiento browniano de partida. Las distancias entre estas visitas son independientes e isótropas. En consecuencia, los vértices sin humor se pueden considerar paradas de un vuelo aleatorio cuyos pasos siguen unas reglas muy distintas de las del movimiento browniano. Este paseo se llamará movimiento o vuelo de Cauchy. Dados dos instantes de tiempo 0 y t, se encuentra que la densidad de probabilidad del vector que va de ∏(0) a ∏(t) es un múltiplo de

La sospecha formal de que D = 1 se encuentra confirmada en S. J. Taylor (1966, 1967). Una de las figuras de la lámina 298 es una ilustración del vuelo de Cauchy.

Meditemos por un momento acerca de la construcción anterior. Un movimiento browniano en el E-espacio, dependiente de una variable real, pasa por los puntos sin humor en los instantes de tiempo en que una de sus funciones coordenadas se anula. Pero recordemos que cada función coordenada es un movimiento browniano unidimensional. Aparte de que los ceros de esta función (capítulo 25) forman un conjunto de dimensión D = 1/2, como los intervalos entre cada dos ceros son independientes, se tiene que forman un polvo de Lévy. Resumiendo, el movimiento de Cauchy es la imagen de un polvo de Lévy lineal sobre un movimiento browniano. Recordemos que la decimación era el curioso método que empleaban los romanos para castigar a un grupo hostil, consistente en matar cada décimo componente. Así, el movimiento de Cauchy se obtiene como una variante fractal de la decimación. Ésta fue introducida por Bochner (1955), que la llamó subordinación (Feller, 1951, contiene comentarios dispersos no elementales sobre este concepto).

D_{trayectoria de Cauchy} = D_{trayectoria browniana} × D_{conjunto de ceros browniano}

Con objeto de comprender mejor la naturaleza de la subordinación fractal, la aplicaremos a algunas curvas fractales de Koch y de Peano. (Por raro que parezca, posiblemente sea aquí donde por primera vez se habla de subordinación en un contexto no aleatorio).

La idea es que uno puede modificar estas curvas manteniendo el mismo iniciador y sustituyendo el generador por una parte del original. Esto cambia el conjunto fractal límite original, que llamaremos subordinando, por un subconjunto subordinado del mismo. Primero describiremos algunos ejemplos y luego introduciremos la importante regla del producto de las dimensiones.

EJEMPLO CON D < 2. Tómese el generador formado por cuatro segmentos de la curva triádica de Koch, como se hace en la lámina 70. Si se eliminan los segmentos segundo y tercero se tiene el generador clásico del polvo triádico de Cantor. Por tanto, el polvo de Cantor es un subordinado de un tercio del copo de nieve. Se obtiene otro polvo subordinado distinto, no restringido a la recta, si se eliminan el primero y el tercero de los N = 4 lados del generador de Koch. En ambos casos la subordinación modifica la dimensión de log 4/log 3 a log 2/log 3. Si sólo se borra uno de los segmentos del generador, el polvo subordinado no está contenido en una recta, aunque su dimensión es log 3/log 3 = 1.

EJEMPLO CON D = 2. Tómese la segunda fase, formada por cuatro segmentos, de la curva de Peano-Cesàro de la lámina 234 y bórrense los segmentos segundo y tercero. El nuevo generador es ¡el propio intervalo [0,1]! Así pues, el segmento de recta es un subordinado (¡el más trivial!) de la curva de Peano-Cesàro. Si se borra cualquier otro par de segmentos componentes del generador se obtiene un polvo fractal con D = 1. Si se borra sólo uno de los segmentos se obtiene un conjunto de dimensión log 3/log 2.

Recuérdese que en los capítulos 6 y 7 decíamos que las curvas de Koch y de Peano se podían considerar trayectorias de «movimientos» con un parámetro de tiempo t que varía entre 0 y 1. Dicho tiempo se define de modo que, por poner un ejemplo, los cuatro elementos del generador del copo de nieve son recorridos durante los instantes cuya expresión en base cuatro empieza por 0,0; 0,1; 0,2 y 0,3. Siguiendo con el mismo ejemplo, el segundo cuarto del tercer cuarto es recorrido durante los instantes cuya expresión en base cuatro empieza por 0,21. Consideradas como movimientos, nuestras curvas de Koch o de Peano son «aplicaciones fractales» definidas en el intervalo [0,1]. En este contexto, el efecto de la primera decimación de los elementos del generador, citada en la sección anterior, es eliminar los valores de t cuya expresión en base 4 incluya las cifras 1 o 2 (o 0 y 3), de modo que t se reduzca a un cierto polvo de Cantor de [0,1].

Podemos, pues, describir esos conjuntos subordinados de las curvas de Koch o de Peano como imágenes fractales de un subconjunto fractal del tiempo. Dicho subconjunto es obviamente un polvo de Cantor y se llama subordinador. Su dimensión es log N/log N' = log 2/log 4 = 1/2. Y, en general, se obtiene la siguiente expresión, que no necesita de más explicaciones

Esto generaliza la relación que, como hemos visto, caracteriza el movimiento de Cauchy. Como ya sabemos, las sumas de dimensiones aparecen en el estudio de secciones e intersecciones. Acabamos de descubrir un «cálculo» precioso que asigna un significado a los productos de dimensiones y no sólo a las sumas.

Esta regla tiene excepciones, naturalmente, parecidas a las que encontrábamos para la regla de la suma de codimensiones en una intersección.

El primer subordinado usado por Bochner fue el polvo de Lévy lineal del capítulo 31, y su uso como subordinador por parte de los matemáticos puros está tan extendido que la escalera de Lévy correspondiente se conoce a menudo como función subordinadora estable. Para obtener conjuntos subordinados autosemejantes, se usa un subordinando autosemejante como, por ejemplo, un movimiento browniano estándar o fraccionario.

Nótese que, mientras la dimensión intrínseca del movimiento browniano es 2, la del movimiento browniano restringido a la recta es 1. Por tanto, habría que sustituir la regla de la sección anterior por

Y en general, la dimensión intrínseca de un movimiento browniano fraccionario es 1/H, pero

Por tanto, el mayor espacio que puede ser llenado hasta el tope por el conjunto subordinado corresponde a E = parte entera de 1/H.

EL MOVIMIENTO BROWNIANO COMO SUBORDINADO. El subordinando más importante es la trayectoria browniana. La imagen browniana de un polvo de Lévy de instantes de tiempo, con dimensión D/2 comprendida entre 0 y 1 es un polvo en el espacio con una dimensión D arbitraria comprendida entre 0 y 2. Merece el nombre de polvo espacial de Lévy.

En el supuesto de que tanto los huecos del polvo subordinador como los incrementos del subordinando sean estadísticamente independientes, los incrementos del proceso subordinado también lo serán. Y en el supuesto de que las longitudes de los huecos del subordinador cumplan Pr(W>w) = w^−D/2, y que durante un hueco de duración w el movimiento browniano se desplace una distancia del orden de u = √w, parece que los huecos del polvo espacial deban cumplir Pr(U>u) = Pr(W>u²) = u^−D. Y se puede demostrar que en efecto es así.

La fórmula Pr(U>u) = u^−D nos demuestra que el polvo subordinado es una implémentación del proceso contemplado al principio del capítulo.

DIMENSIONES. La dimensión del polvo es D. Si unimos por medio de segmentos rectilíneos las imágenes de los extremos de cada hueco se obtiene una trayectoria de Lévy, de dimensión max(1, D) —como en el estudio de los árboles del capítulo 16.

CORRELACIONES. Una trayectoria de Lévy introduce una ordenación total entre las galaxias que genera. Esto implica que cada galaxia sólo interacciona con sus vecinas inmediatas, y que la interacción entre cada par de vecinas es independiente de los otros pares. En este sentido, un vuelo de Lévy es equivalente a la sustitución injustificada de un problema irresoluble de N cuerpos por una combinación manejable de muchos problemas de dos cuerpos. El resultado podría haber sido terriblemente poco realista, pero no lo es. Mandelbrot (1975u; totalmente descrito en Peebles 1980, págs. 243-249) demuestra que el vuelo de Lévy da unas correlaciones a dos y tres puntos en la esfera celeste idénticas a las obtenidas en 1975 por P. J. E. Peebles y Groth por el método de ajuste de curvas; véase Peebles (1980).

LÁMINA 415. El «gazapo» informático como artista, Opus 2.

FIGURA 415

Esta lámina debe atribuirse en parte a una mala programación. El «gazapo» fue identificado y corregido enseguida (aunque esto ocurrió cuando el resultado ya se había registrado, naturalmente), y el resultado final fue la lámina 103.

El cambio producido por un solo gazapo en un lugar crítico había ido mucho más allá de lo que uno habría podido esperar.

Está claro que la lámina 103 ha sido diseñada con un orden muy estricto. Aquí, dicho orden está oculto, y no se manifiesta ningún otro tipo de orden.

El hecho de que, a primera vista, esta lámina pueda pasar por una obra de arte, quizá no sea casual. Mis ideas al respecto están esbozadas en Mandelbrot (1981) y pienso presentarlas con más detalle en un futuro no lejano.

LÁMINAS 416 y 417. Cúmulos del modelo primitivo de Mandelbrot. Dimensión D = 1,2600. El vuelo de Lévy y sus paradas.

FIGURA 416

Un vuelo de Lévy es una sucesión de saltos separados por paradas. En este capítulo sólo nos interesan estas últimas, pero los saltos son una parte necesaria de la construcción.

Por tanto, las figuras superiores (en negro sobre fondo blanco) de estas láminas contienen, como parte de la trayectoria del movimiento, los rastros dejados durante el vuelo real. La trayectoria en el espacio tridimensional se muestra por medio de sus proyecciones sobre dos planos perpendiculares. El original puede visualizarse manteniendo el libro semiabierto.

Pasemos ahora a las figuras inferiores (en blanco sobre fondo negro). Se borran los intervalos que representan los saltos y se toma el negativo fotográfico. Cada parada es una estrella, una galaxia o un agregado material más general.

Concretando más, los segmentos rectilíneos de las figuras superiores en negro sobre blanco tienen las características siguientes. Su dirección en el espacio es aleatoria e isótropa (esto es, paralela al vector que une el origen del espacio con un punto escogido al azar sobre una esfera). Los distintos segmentos son estadísticamente independientes y sus longitudes siguen la distribución de probabilidad Pr(U>u) = u^−D, excepto para u < 1, que es Pr(U>u) = 1. El valor D = 1,2600 es próximo al valor D ~ 1,23 que se ha encontrado para las galaxias reales.

FIGURA 417

La gran mayoría de los segmentos son demasiado cortos para ser visibles. De hecho, recubrimos el plano con una trama uniforme y marcamos las celdillas que contenían una o más paradas. Dicho de otro modo, cada punto representa todo un minicúmulo.

Además, y con independencia de D, los minicúmulos están a su vez agregados. Presentan unos niveles tan claros de jerarquización que es increíble que el modelo no tenga una jerarquía explícita y que todo sea fruto únicamente de la autosemejanza.

Precisando un poco más, todas las láminas de este grupo representan el principio de dos vuelos distintos, uno hacia adelante y otro hacia atrás, los cuales no son más que dos réplicas estadísticamente independientes del mismo proceso. Está claro que, si se desplaza el origen a alguna otra parada, las dos mitades siguen siendo independientes. Por tanto, todas las paradas tienen exactamente el mismo derecho a ser consideradas el Centro del Universo. Esta propiedad es la esencia del principio cosmográfico condicional que propongo en esta obra.

El método presentado aquí no pretende explicar cómo se han generado efectivamente las galaxias, pero deja claro que el principio cosmográfico condicional es compatible con una agregación ostensible a muchos niveles. Podría haber presentado una gran variedad de tales configuraciones.

LÁMINA 418. Subordinación no aleatoria: polvo fractal agregado, de dimensión D = 1, subordinado a una curva de Koch de dimensión D = 1,5.

FIGURA 418

Se puede modificar el método recurrente de la construcción de Koch para que rompa la recta sistemáticamente y nos dé un polvo con la misma dimensión D = 1, pero con una topología y un aspecto completamente distintos.

Imaginemos que una banda de goma, que inicialmente se extiende entre 0 y 1, se estira para darle la forma del generador de Koch de la lámina 76, que daba una curva fractal de dimensión 3/2. A continuación se fijan las esquinas con alfileres y se corta por la mitad cada uno de los 8 segmentos rectilíneos de la banda, quedando 16 trozos que se contraen hasta recuperar su longitud inicial 1/16. Los extremos libres de estos trozos se fijan también con alfileres y se vuelve a repetir el proceso con cada uno de ellos. El resultado es un polvo autosemejante jerárquicamente agragado con r = 1/16 y N = 16, y por tanto D = 1.

Esta construcción equivale a dejarnos marcar un lado del generador para eliminarlo en el estadio siguiente de la construcción de Koch. En el texto llamamos subordinación a este proceso. Los únicos puntos con los que nos quedamos son las posiciones de un movimiento de Koch correspondientes a los instantes de tiempo de un subconjunto de dimensión fractal log 16/log 64 = 4/6. Se tiene que (4/6) × (3/2) = 1, lo cual es un caso particular de la regla del producto de dimensiones que hemos comentado en el texto.

Nótese que todos los puntos de esta lámina están intrínsecamente ordenados por la curva de Koch de la que forma parte el generador. Además, se puede obtener fácilmente la distribución de frecuencias de las longitudes encogidas entre dos alfileres sucesivos. Aproximadamente, el número de longitudes ≥ u es proporcional a u^−D con D = 1. Las láminas 416 y 417 hacen uso de la misma distribución, aunque de un modo distinto.

LÁMINA 419. Disminución de D por subordinación. Cómo hacer que los cúmulos de Lévy estén más y más espaciados.

FIGURA 419

El grado de agregación de un polvo de Lévy plano depende de su dimensión. Este efecto se ilustra aquí por medio de una trayectoria browniana plana, con D + 2, y sucesivas subordinaciones lineales de Lévy, superpuestas cada una a la anterior. En todas las figuras, D_subordinador = 0,89, y por tanto los sucesivos polvos subordinados tienen dimensiones: 1,78 (= 2 × 0,89); 1,59; 1,41; 1,26; 1,12; 1 y 0,89. La escalera de Lévy que acompaña a casi cada polvo muestra la decimación del tiempo que dio lugar al mismo a partir del polvo de D = 1,78. Para la D próxima a 2 se percibe claramente un «espectro» del subordinando, que se va haciendo cada vez más tenue a medida que D disminuye (véase el capítulo 35). El aumento de la agregación no se debe a que todos los puntos se concentren en torno a unos pocos, sino a la desaparición de la mayoría de puntos, lo que da lugar a un número cada vez mayor de niveles jerárquicos aparentes.

LÁMINA 420. Viaje de aproximación hacia un polvo de Lévy con D = 1,2600.

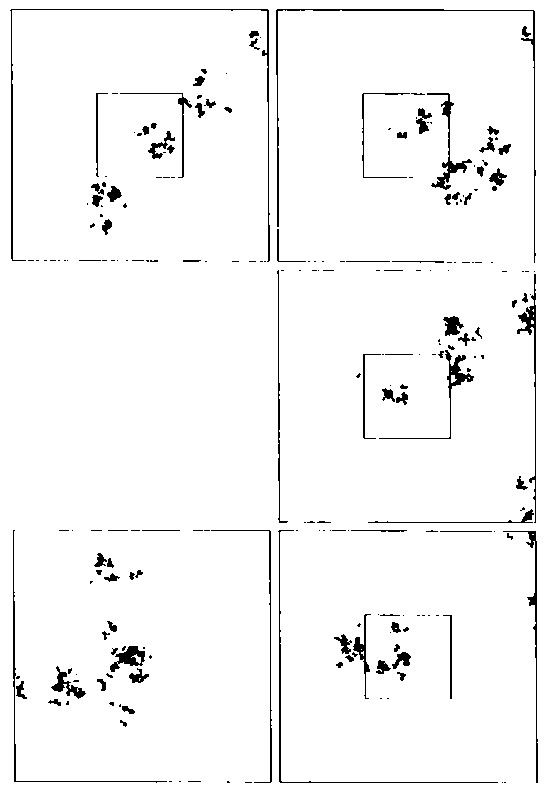
FIGURA 420

La primera figura, en la parte superior izquierda, representa un cúmulo de 12.500.000 posiciones de un movimiento de Lévy, visto desde la ventanilla cuadrada de una nave espacial lejana. Entre cada visita y la siguiente, en el sentido de las agujas del reloj, la distancia de la nave al centro del cúmulo y el campo de visión se dividen por b = 3. La estructura que se ve por la ventanilla cambia en cuanto a los detalles, pero en líneas generales es la misma. Esto era de esperar, pues el conjunto es autosemejante.

LÁMINA 421. Circunnavegación de cúmulos de Lévy de dimensión D = 1,3000.

FIGURA 421

La forma de los cúmulos generados como vértices de un vuelo de Lévy en el plano depende en gran manera de la muestra, en el sentido de que si uno simula varios cúmulos con la misma dimensión, es de esperar una gran variedad de formas.

Lo mismo vale para un pequeño cúmulo aislado de Lévy en el espacio visto desde distintos ángulos —sígase la «banda» de esta lámina en el sentido de las agujas del reloj empezando por arriba.

32 Subordinación: polvos de Lévy espaciales; galaxias ordenadas

32
Subordinación: polvos de Lévy espaciales; galaxias ordenadas