Este capítulo, cuyas ilustraciones principales son figuras completamente artificiales que imitan los mapas y las fotografías de islas y montañas, se propone demostrar que, en una primera aproximación, superficies fractales elegidas convenientemente y regidas por una especie de azar browniano permiten hacer modelos útiles de montañas como los Alpes. Así obtendremos, por fin, un modelo razonable de las formas naturales de las que hemos partido y que hasta ahora se nos habían estado escapando: las costas.

El punto de partida es la idea de que las superficies de las montañas son figuras escalantes. ¿Es nueva esta idea? ¡Ciertamente no! No se había formulado ni estudiado científicamente, pero es un tema literario recurrente. Como ejemplo añadido a la cita que abre el capítulo 2, en la pág. 88 de Scrambles Amongst the Alps in 1860-1869, de Edward Whymper, leemos: «Es interesante observar que… fragmentos de… roca… presentan a menudo las formas características de los peñascos de donde han sido arrancados… ¿Y por qué no habría de ser así si la masa de la montaña es más o menos homogénea? Las mismas causas que producen las formas pequeñas modelan las mayores; se trata de las mismas influencias, la misma helada y la misma lluvia son las que esculpen toda la masa y cada una de sus partes».

No hace falta tomarse al pie de la letra la explicación poética de Whymper para estar de acuerdo en que vale la pena examinar sus consecuencias. Así lo haré en este capítulo con el aparato matemático más manejable que se me ocurre: las superficies brownianas y las superficies brownianas fraccionarias.

Ya hasta en mis primeras simulaciones de montañas brownianas fraccionarias (láminas 104 y 105), «ver es creer». A medida que la calidad de los gráficos fue mejorando, también fue mejorando la intensidad de la «creencia». Pero al final se pusieron de manifiesto discrepancias entre el modelo y la experiencia, lo que obligó a cambiar de modelo, como se verá en el siguiente capítulo.

Atacamos el problema del relieve por medio de las secciones verticales. Como ya indiqué en el capítulo 4 y en la lámina 340, una de las fuentes inspiradoras de este ensayo fue la intuición, que ya señalé en Mandelbrot (1963e), de que un paseo aleatorio escalar podía ofrecer una primera aproximación de la sección vertical de una montaña. Así pues, empecé por buscar una superficie aleatoria cuyas secciones verticales fueran funciones brownianas reales de variable real. La caja de herramientas del constructor de modelos estadísticos no contenía ninguna superficie de esta clase, pero di con un candidato un tanto oscuro que adopté para el caso.

Se trata de la función browniana real definida en el plano, B(P), descrita en Lévy (1948). Para familiarizarse con ella sin invertir demasiado tiempo y aplicarla a un caso concreto, no hay nada mejor que un examen cuidadoso de la simulación mostrada en la lámina 374. El paisaje fractal imaginario tiene una dimensión D = 5/2, y es claramente más rugoso que la mayor parte del relieve terrestre.

Se trata de un primer modelo, que pide a gritos ser devuelto al taller. Pero ¿no es también un hermoso salto hacia adelante?

ATENCIÓN, NO CONFUNDIR CON LA SÁBANA BROWNIANA. Existe una proliferación interminable de variantes del movimiento browniano y la terminología es un tanto superficial. No hay que confundir la función browniana real definida en el plano con la sábana browniana. Esta última es un proceso completamente distinto, que se anula sobre los ejes y es fuertemente isótropo. Véase Adler (1981) y en especial las ilustraciones de las págs. 265 y 266.

Detengámonos aquí un momento e intentemos avanzar en el estudio de las costas, definiéndolas como conjunto de ceros: puntos situados al nivel del mar, que incluyen también los puntos de las costas insulares. La costa browniana de la lámina 371 fue el primer ejemplo que encontré de una curva que (a) no tiene autointersecciones, (b) carece prácticamente de puntos de autocontacto, (c) tiene una dimensión fractal claramente superior a 1, y (d) es isótropa. En la lámina 377 se presenta una variante más reciente.

Para ser más precisos, la dimensión es 3/2. Como este valor es mayor que la mayoría de los mostrados en la lámina 59, obtenidos por Richardson, resulta que la aplicabilidad de la costa browniana es sólo limitada. Recuerda el norte de Canadá, Indonesia, quizá el oeste de Escocia y el Egeo, y es aplicable a muchos otros ejemplos, pero ciertamente no a todos. A la vista de los datos de Richardson sería ingenuo esperar que una sola D tuviera validez universal.

Es una pena que no baste con el simple relieve browniano, de dimensión D = 5/2, ni con las costas brownianas, de dimensión D = 3/2, pues resultarían fácilmente explicables. En efecto, la función browniana es una aproximación excelente del relieve «poissoniano» creado por superposición de fallas rectilíneas independientes. Se rompe una meseta horizontal por una línea recta escogida al azar, y también se elige al azar el desnivel entre las dos partes del precipicio que se forma, tomando, por ejemplo, ± 1 con idéntica probabilidad, o según una distribución gaussiana. A continuación volvemos a empezar, y pasamos a la k-ésima etapa dividiendo por √k (de modo que cada precipicio tenga un desnivel despreciable en comparación con la suma acumulada de todos los demás).

El resultado obtenido por iteración indefinida generaliza el proceso de Poisson en el tiempo. Sin más detalles físicos o matemáticos, se ve fácilmente que el razonamiento capta al menos uno de los aspectos de la evolución tectónica.

Debido a la simplicidad del mecanismo, sería reconfortante pensar que en un cierto estado, especialmente «normal» y muy antiguo, todo el relieve terrestre fue browniano, con D = 5/2. Pero este tema debe posponerse para más adelante.

Lévy encontró que la función browniana real de varias variables tiene una propiedad que sorprende a primera vista y que tiene consecuencias prácticas muy directas. Enunciada sin gran precisión, esta propiedad establece que las distintas partes de un relieve browniano distan mucho de ser estadísticamente independientes. Así pues, en la inmersión de una función browniana real de una variable en una función browniana real de dos variables, tenemos que renunciar a un aspecto que hasta ahora había sido la virtud característica del azar browniano: la independencia de las partes.

Consideremos dos puntos situados respectivamente al este y al oeste de una sección meridiana del relieve. A lo largo del meridiano, el relieve es una función browniana real de una variable, y por lo tanto las «pendientes» en puntos distintos son independientes. Además, uno podría esperar que dicho meridiano hiciera de pantalla, de modo que el conocimiento del relieve en el lado este no influya para nada en la distribución del relieve en el del lado oeste. ▯ Si fuera así el relieve sería markoviano. ▮ De hecho, el lado oeste sí influye sobre el este, en el sentido de que el proceso generativo conlleva inevitablemente una fuerte dependencia global.

Esta dependencia implica que una superficie browniana es mucho más difícil de construir que una función browniana real de una variable. El proceso de desplazamiento aleatorio del punto medio del capítulo 25, que, como explicamos en los capítulos 26 y 27, no se puede generalizar a las funciones brownianas fraccionarias de una variable, tampoco se puede generalizar a las funciones brownianas ordinarias de dos variables. Esto es, no se puede proceder fijando de entrada la función sobre un retículo grueso y luego dar valores en cada celda con independencia de las otras celdas. Es también imposible construirla por capas: primero para x = 0, luego para x = ε sin tener en cuenta los valores para x < 0, luego para x = 2ε sin tener en cuenta los valores para x < ε, etc.

Dicho con más generalidad, todo algoritmo que prometa una fácil generalización por pasos de la función browniana de una variable al caso de un «tiempo multidimensional» lleva inevitablemente a una función sistemáticamente distinta de lo que se pretendía.

Como se dice en la última sección de este capítulo, las simulaciones en las que participé reformulan las definiciones teóricas intratables de modo que requieren una serie de aproximaciones sucesivas cuyos términos de error se conocen. Pero no puedo responder de quienes, estimulados por la lectura de mis ensayos anteriores, se han sumado a nuestro juego.

Tomemos ahora una esfera como base del relieve terrestre. Por suerte, la correspondiente función browniana real sobre la esfera, B₀(P), también fue investigada por mi mentor (véase Lévy, 1959). Es fácil de describir, divertida y puede que hasta sea importante. Pero, como veremos, tampoco es realista, pues también predice costas con D = 3/2, lo cual es un serio inconveniente.

Aunque la definición más simple de B₀(P) echa mano de elementos de la teoría del ruido, a cuyas definiciones tenemos que acudir incesantemente, éstos resultarán familiares a muchos lectores. Se dispone una capa de ruido blanco gaussiano sobre una esfera y B₀(P) es la integral de este ruido blanco sobre la semiesfera de centro P.

Si nos movemos en distancias angulares que no superen los 60°, B₀(P) se parece mucho a una función browniana de dos variables. Pero considerada globalmente, el parecido se desvanece.

Así, por ejemplo, B₀(P) tiene la sorprendente propiedad de que, si P y P' son puntos antipodales de la esfera, la suma B₀(P) + B₀(P') es independiente de P y P'. En efecto, dicha suma es simplemente la integral sobre toda la esfera del ruido blanco empleado en la construcción de B₀(P).

Por tanto, una gran montaña en P se corresponde con una gran fosa en su punto antipodal P'. Una tal distribución tendría un centro de gravedad distinto del de la superficie de base, y difícilmente podría estar en equilibrio estable. Pero no hay por qué preocuparse: el modelo se salva de la inestabilidad estática —y por tanto de ser rechazado a las primeras de cambio— gracias a la teoría de la isostasia. Según esta teoría, la corteza sólida terrestre es muy delgada en los lugares más profundos del océano y muy gruesa bajo las montañas más altas, de modo que una esfera concéntrica con la Tierra y trazada ligeramente por debajo del punto más profundo del océano prácticamente biseca la corteza. Una vez se ha aceptado que la cresta visible de una montaña debe considerarse siempre en conjunción con su invisible raíz bajo la esfera de referencia, la constancia de B₀(P) + B₀(P') no deja de ser una sorpresa, pero ya no implica un gran desequilibrio estático.

¿Cómo concuerda la variante anterior del relieve browniano con los datos observados? Si nos basamos en los continentes y los océanos actuales, D no es correcta, y por tanto la concordancia es pobre.

Por otra parte, la tectónica de placas (la teoría de la deriva y fragmentación de los continentes) sugiere hacer la prueba con la Tierra primitiva, tal como era hace 200 millones de años. Al ser menos firmes los datos, no es tan seguro que el test vaya a fallar. Según Wegener (y sus ideas han acabado siendo aceptadas; véase, por ejemplo, Wilson 1972) hubo un tiempo en que los continentes estaban unidos en una Pangea y los mares formaban un superocéano, la Pantalasia.

Como Pangea, el relieve de la lámina 379 es una mancha de tierra mellada aquí y allá por grandes sinuosidades. Pero esta apariencia es engañosa. Tiende a resaltar demasiado los detalles a muy gran escala debido a la combinación de la geometría esférica con el hecho de que en la esfera las reglas brownianas de dependencia producen una correlación grande para ángulos inferiores a los 60° y una gran correlación negativa entre puntos antipodales. Una mirada más atenta y centrada en aspectos menos globales nos da la impresión de una concordancia más pobre: para ángulos inferiores a los 30° (por ejemplo), una costa browniana sobre la esfera no se distingue de una costa browniana plana. Todos los defectos de esta última vuelven a resurgir.

Un copo fractal en el que la altitud sea la misma función que la Pangea anterior, con una escala cuyo orden de magnitud sea la mitad del radio, parece una de las lunas irregulares de los planetas exteriores. En contraste con las láminas 25 y 26, no va acompañada de chorros ni restos, por tanto D sólo es una medida de la irregularidad y no de la fragmentación.

El problema de los dos modelos brownianos anteriores del relieve terrestre es que D = 3/2 es demasiado para las costas. Como consecuencia, nuestra búsqueda de un modelo más general toma un giro inesperado. En los capítulos 5 y 6 señalábamos que D > 1 y empezábamos a buscar maneras de hacer que D se hiciera mayor que 1. Ahora tenemos que encoger D por debajo de 3/2. Para conseguir costas menos sinuosas necesitamos un relieve menos escarpado y unas secciones verticales menos sinuosas.

Por suerte el capítulo anterior nos ha preparado el camino. Para obtener un modelo de las secciones verticales he sustituido la función browniana real de variable real por su variante fraccionaria. Existen efectivamente funciones estocásticas B_H(P) reales y de dos variables. La D de sus superficies es 3 − H (Adler, 1989) y la de sus curvas de nivel y secciones verticales es 2 − H.

Por tanto, modelizar y simular cualquier dimensión indicada por los datos empíricos ya no representa ninguna dificultad.

DETERMINACIÓN DE D. Se puede esperar, a partir de los datos de Richardson (capítulo 5), que las dimensiones «típicas» de las costas estén alrededor de 1,2, y las del relieve alrededor de 2,2. Podemos, pues, recorrer un largo trecho con H = 0,8 (valor que justifica la lámina 375). Sin embargo, determinadas zonas concretas de la Tierra pueden requerir de otros valores. Valores de D ~ 2,05 servirían para explicar relieves dominados por componentes de variación muy lenta. Si esta componente es una gran pendiente, el relieve es una meseta inclinada y accidentada, y la costa sólo difiere de una recta por la presencia de pequeñas irregularidades. Cerca de una cumbre el relieve es un cono accidentado y la costa un óvalo moderadamente irregular.

Los relieves con una D próxima a 3 son también potencialmente útiles, aunque difícilmente ilustrables. Basta con observar, en la lámina 371, que la costa correspondiente a una D próxima a 3 recuerda una llanura aluvial inundada. Por tanto, todos los valores de H encontrarán su lugar en la caja de herramientas del diseñador de modelos estadísticos.

Los principios cosmográficos del capítulo 21 se pueden reformular en términos propios del relieve. El principio cosmográfico fuerte combina los conceptos probabilísticos de estacionariedad e isotropía. Por tanto, se puede decir que el relieve z(x,y) sobre una Tierra plana es fuertemente cosmográfico si las reglas que generan dicho relieve son las mismas en cualquier sistema de referencia cuyo origen de coordenadas (x₀, y₀, z₀) satisfaga z₀ = 0 y el eje z sea vertical. En particular, dichas reglas tienen que ser invariantes al intercambiar x₀ por y₀ y bajo rotaciones del plano horizontal. Ni mi relieve browniano sobre una Tierra plana, ni su versión fraccionaria, cumplen este principio.

Pero sí cumplen una versión «condicional» en la que el origen tiene que satisfacer z₀ = B(x₀, y₀), de modo que esté sobre la superficie terrestre.

Se han hecho varios intentos de ajustar el relieve a un proceso estacionario. Se recubre el plano z = 0 con una cuadrícula regular y se toman las alturas en las distintas celdas de la cuadrícula como variables aleatorias independientes. Tales modelos no pueden explicar ninguna de las leyes de cambio de escala examinadas en este capítulo.

El relieve browniano sobre una Tierra esférica satisface el principio cosmográfico en su versión fuerte, que es la más útil para tratar con grandes áreas de la Tierra. La versión condicional es forzosamente válida y es preferible cuando uno trata con efectos locales.

El horizonte de un observador situado a una distancia finita sobre la superficie terrestre lo constituyen los puntos no ocultos de mayor altura aparente, en cualquier dirección que se mire.

Si el relieve es una perturbación sobre una Tierra esférica, el horizonte estará obviamente a una distancia finita del observador.

Si el relieve es una perturbación browniana o una perturbación browniana fraccionaria sobre un plano horizontal, la existencia del horizonte no es evidente: tras cada montaña y a una cierta distancia puede haber otra más alta, y así sucesiva e indefinidamente. De hecho, una montaña situada a una distancia R del observador tiene una altura relativa del orden de R^H, de modo que la tangente de su ángulo aparente sobre el plano horizontal es aproximadamente R^H−1 que tiende a 0 para R → ∞. Así pues, el horizonte está también definido.

Para hacernos una idea más clara, dividamos la distancia del observador al horizonte por su valor medio. En una Tierra plana esta función es estadísticamente independiente de la altura del observador. En una Tierra esférica, por el contrario, el horizonte tiende a hacerse circular a medida que el observador asciende. Además, el horizonte de una Tierra plana está por encima de un plano que pasa por el observador, independiente de la altura del mismo. En cambio, el horizonte de una Tierra esférica cae por debajo de dicho plano si el observador está a suficiente altura. Resumiendo, las propiedades observadas del horizonte confirman que la Tierra es esférica. La conclusión contraria habría sido un desastre.

Como de costumbre, uno se pregunta por qué unos modelos escogidos por su simplicidad resultan ser tan atractivamente aplicables. Tengo algunas ideas al respecto, aunque no puedo pretender que sean convincentes (capítulo 42).

▯ En primer lugar, se puede construir B_H(P), igual que se hizo con B(P), mediante superposición de fallas rectilíneas (Mandelbrot, 1975f). Sin embargo, el perfil de las fallas ya no debe ser un precipicio nítido, sino que su pendiente tiene que aumentar a medida que uno se va acercando a la falla. Por desgracia, el perfil apropiado es artificioso, de manera que ésta no es una buena aproximación al problema.

▯ Parece preferible empezar con un modelo browniano y luego intentar disminuir la dimensión como hacíamos en el capítulo 27 con los ríos. Un alisado exclusivamente local transforma una superficie de área infinita en otra de área finita. Y además no afecta en nada a los rasgos a mayor escala. Por tanto, el alisado local convierte un objeto con una misma dimensión bien definida a todas las escalas en otro que presenta una dimensión efectiva global de 5/2 y una dimensión efectiva local de 2.

▯ Más generalmente, K alisados distintos con distintas escalas fundamentales producen K + 1 zonas con dimensiones distintas, unidas por zonas de transición. Sin embargo, el objeto considerado globalmente puede acabar siendo indistinguible de una fractal de dimensión intermedia. En otras palabras, una superposición de fenómenos con escalas bien definidas puede imitar la invariancia por cambio de escala.

▯ Por otra parte, a menudo y de modo espontáneo, un fenómeno escalante se divide mentalmente en una jerarquía en la que cada nivel tiene una escala definida. Así, por ejemplo, los cúmulos de galaxias del capítulo 9 no tienen por qué ser reales, como se verá en los capítulos 32 a 35. Por tanto, no hay que empeñarse en seguir al pie de la letra la recomendación de Descartes y empezar a subdividir cada dificultad. Aunque nuestra mente descomponga espontáneamente las configuraciones geomorfológicas en una superposición de rasgos con escalas claramente separadas, dichos rasgos no tienen por qué ser reales.

▯ Por suerte, el relieve terrestre tiene un corte superior finito, pues su superficie de base es esférica. Por tanto, para mayor seguridad se puede suponer que las distintas transformaciones producidas a lo largo de la historia geológica implican sólo escalas inferiores al orden de magnitud de los continentes. La suposición realista de que H cambia de un lugar a otro deja abierta la posibilidad de que la intensidad relativa de dichas transformaciones varíe. ▮

Como se dijo en el capítulo 1, acuñé el término fractal a partir del latín fractus, que describe el aspecto de una piedra rota: irregular y fragmentada. La etimología no es razón suficiente para que la superficie real de una piedra sea fractal, pero es muy probable que no sea una superficie estándar, y si es escalante debería ser un fractal.

El argumento en favor del carácter escalante se basa en que una piedra está formada por granos cohesionados en dominios organizados jerárquicamente. La cohesión entre los dominios grandes es menor que la cohesión de sus componentes más pequeños. La energía generada cuando se golpea una piedra se disiparía más fácilmente si se separaran sólo pedazos grandes, pero nada implica que tal separación sea geométricamente posible. Por tanto, lo más probable es que la ruptura combine porciones correspondientes a dominios de distintos niveles jerárquicos.

La ciencia que trata de la fricción y el desgaste se llama tribología, del griego τριβω = frotar. La evidencia aportada por Sayles y Thomas, 1978 (corrigiendo un análisis defectuoso; véase Berry y Hanndy, 1978), respalda la creencia de que las superficies brownianas fraccionarias nos proporcionan buenas representaciones en primera aproximación de las pistas de aterrizaje y de muchas superficies rugosas naturales. Los valores empíricos de D (deducidos de una gráfica de 7 − 2D de Sayles y Thomas, figura 1) están entre 2 y 3.

Ahora que mi «principio» del carácter escalante del relieve ha sido corroborado de varias maneras, examinemos un corolario. Como se demuestra en el capítulo 38, podemos esperar que cualquier cantidad asociada al relieve siga una distribución de probabilidad hiperbólica («ley de Zipf», «ley de Pareto»). Y, en efecto, así ocurre en muchas ocasiones. De hecho, mi estudio de las costas (capítulo 5), que sugería que el relieve es escalante, había sido precedido por Mandelbrot (1962n), donde se encontraba que las distribuciones de petróleo y otros recursos naturales eran hiperbólicas. Este hallazgo está en desacuerdo con la idea dominante de que tales cantidades siguen una distribución logarítmica normal. La diferencia es sumamente importante, pues las reservas serían mucho mayores si la distribución fuera hiperbólica en vez de logarítmica normal. Mis conclusiones no despertaron mucha atención en 1962, pero volveré a intentarlo.

Se vuelve a tratar de los minerales en el capítulo 39, en la entrada sobre «fractales no lagunares».

Simplificaciones: superficies periódicas y superficies por desplazamiento del punto medio

Como mis relieves brownianos, o brownianos fraccionarios, se basan en algoritmos complicados, necesitamos aproximaciones y simplificaciones. Así, en las láminas 378, 381 y 383 se usa una aproximación poissoniana de nuestro proceso gaussiano. En las láminas 374 a 377, y C5 a C13, se cambia una función no periódica de x e y por una función periódica calculada por métodos rápidos de Fourier y «recortada» luego para que una parte central no quede afectada por la periodicidad.

Además, usé el método del desplazamiento del punto medio, como en el capítulo 26, para generar superficies fractales, que denoto por B*_H(x, y). El modo más fácil de construir dichas superficies consiste en tomar como iniciador un triángulo equilátero J. Prescribiendo los valores de B*_H(x, y) en los vértices de J, el primer paso interpola por separado esta función sobre los tres puntos medios de los lados de J, siguiendo el mismo proceso que para las funciones coordenadas de B*_H(t). El segundo paso interpola en los 9 puntos medios de segundo orden, y así sucesivamente.

Seguro que el resultado es más realista que cualquier superficie no fractal o que la mayoría de superficies fractales no aleatorias. Pero ¿es estacionario? ΔB*_H − B*_H(x, y) − B*_H(x + Δx, y + Δy) debería depender sólo de la distancia entre los puntos (x, y) y (x + Δx, y + Δy). De hecho, este ΔB*_H depende explícitamente de x, y, Δx y Δy. Por tanto, B*_H no es estacionario, ni tan siquiera en el caso H = 1/2.

También he examinado y comparado una docena de simplificaciones que sí son estacionarias y espero publicar algún día el resultado de dicha comparación.

LÁMINAS 374 y 375. Paisajes lacustres brownianos, ordinario y fraccionario (dimensiones comprendidas entre D ~ 2,1 y D = 5/2, en el sentido de las agujas del reloj).

FIGURA 374a

FIGURA 374b

La figura 375a es un ejemplo de relieve browniano fraccionario de dimensión bastante próxima a 2, y es mi modelo de paisaje terrestre. Las otras figuras extrapolan el mismo modelo a valores de D mayores, acabando en la figura 374a con un relieve browniano ordinario sobre el plano. Este tiene la característica específica de que todas sus secciones verticales son funciones brownianas ordinarias de una variable real, como las de la lámina 340. Un relieve browniano es un mal modelo de Tierra, pues es demasiado irregular en los detalles. La mala calidad del modelo se cuantifica por el hecho de que tanto la dimensión de su superficie, D = 5 / 2, como la de sus costas, D = 3/2, son demasiado grandes.

FIGURA 375a

FIGURA 375b

En cada paisaje la altura se calcula según las latitudes y longitudes de una cuadrícula. Se ha programado el ordenador para que simule una iluminación procedente de una fuente situada 60° a la izquierda, mientras que el observador está situado 25° sobre el nivel de la base. Para más detalles, véanse los pies de figura de las ilustraciones en color.

LÁMINAS 376 y 377. Costas brownianas y «cadenas» de islas.

FIGURA 376

La primera intención de estas láminas era subrayar un efecto muy importante descubierto recientemente. Cuando la D del relieve llega a 2,5 y supera este valor, hay una tendencia cada vez mayor a que el océano se descomponga en «mares» separados. Estos mares están comunicados entre sí, pero cada uno tiene una individualidad bien marcada. Por otra parte, las islas parecen formar «cadenas». El mismo efecto es visible (aunque no tan claramente) en las crestas que se forman en todos los «paisajes»: láminas 374, 375 y 383.

Esta falta de isotropía en las muestras es plenamente compatible con el hecho de que el mecanismo que las genera sea isótropo.

Estas láminas son equivalentes (aparte de la semilla) a las secciones planas de los copos de las láminas 25 y 26 (que se explican al final del capítulo 29). Aquí, como en las láminas 25 y 26, empleamos una versión recortada de un periodo de una variante periódica del proceso que nos interesa. Esto disminuye la dependencia en D de la forma global. Las formas globales de las costas brownianas verdaderas difieren más de lo que muestran estas láminas.

En los capítulos 34 y 35 se comenta un efecto relacionado con estas cadenas.

FIGURA 377

LÁMINA 378. Curvas de nivel de paisajes brownianos fraccionarios.

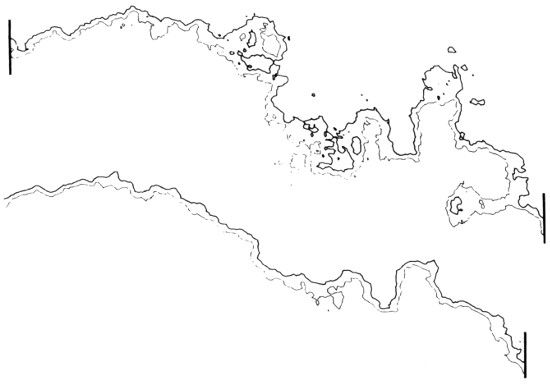
FIGURA 378

Las dos figuras de esta lámina combinan dos o tres curvas de nivel (las líneas gruesas son las costas) de funciones brownianas fraccionarias. Las figuras corresponden a dimensiones distintas, pero se han realizado con el mismo programa y la misma semilla: para la figura superior D ~ 1,333, y para la inferior D ~ 1,6667. A primera vista ambas dimensiones son creíbles por lo que respecta a la geografía, pero una está en la banda superior y la otra en la inferior.

Estas curvas parecen mucho menos «escabrosas» que sus análogas de la lámina 377 con la misma D. La causa es que en las láminas anteriores cada sección presenta un máximo muy marcado, y no hay una pendiente sistemática. Aquí, por el contrario, vemos la ladera de una gran montaña con una pendiente global muy marcada. En su aspecto «genérico» esta lámina se parece a una versión ampliada de un trozo pequeño, especialmente escabroso, de la lámina 377.

Comparando estas diferentes curvas de nivel nos vamos dando cuenta del amplio margen intermedio entre la irregularidad y la fragmentación, incluso para una D fija.

LÁMINAS 379 y C9 (superior). Pangea browniana (dimensión de la costa D = 3/2).

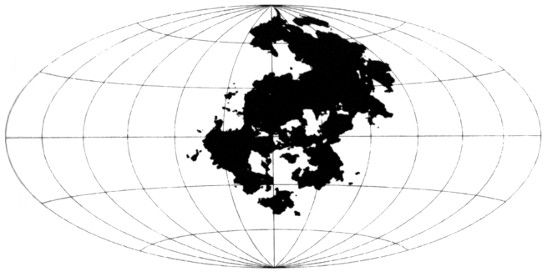
FIGURA 379

El «planeta distante» de la lámina C9 representa una Pangea fractal imaginaria vista desde lejos en el espacio. El relieve se generó simulando con un ordenador (y por lo que yo sé, por primera vez) una superficie aleatoria debida a Paul Lévy: una función browniana real (la altura) de los puntos de la esfera (la latitud y la longitud). El nivel del mar se ajustó de modo que tres cuartas partes del área total estuvieran cubiertas por las aguas. La costa se obtuvo por interpolación.

Esta lámina muestra un mapa de Hammer de la misma Pangea, la proyección preferida por los estudiosos de la teoría de Wegener de la deriva de los continentes.

¿Hasta qué punto este modelo de Pangea se parece al «real»? No es de esperar que los detalles locales concretos sean correctos, sino sólo el grado de ondulación, tanto local como global. El parecido es imperfecto, como era de esperar. En efecto, la costa de este modelo de Pangea tiene D = 3/2, mientras que los grabados imaginarios de los libros de geología atribuyen a la Pangea real la misma D que se observa en los continentes actuales, D ~ 1,2. Si nuevos datos resultaran compatibles con D = 3/2, se podría explicar la geometría de la Pangea mediante hipótesis tectónicas bastante elementales.

FRACTALES EN UN ESPACIO NO EUCLÍDEO. En la geometría no euclídea de Riemann, la esfera interpreta el papel del plano. Así, las geometrías no euclídeas están a mitad de camino: estudian figuras euclídeas en un sustrato no euclídeo. El grueso de este ensayo también está a mitad de camino, al estudiar figuras no euclídeas en un sustrato euclídeo. En la Pangea que hemos considerado aquí confluyen ambas generalizaciones: es un ejemplo de figura no euclídea en un sustrato no euclídeo

LÁMINA 381. Los primeros ejemplos que se conocen de costas brownianas (ordinarias y fraccionarias).

FIGURA 381

Mi pretensión de que las funciones brownianas fraccionarias convenientemente elegidas sirven como modelos razonables del relieve terrestre se basó originariamente en estos cuatro modelos de costas. Al igual que la lámina 379, son un saldo sentimental de mi ensayo en francés de 1975, excepto porque las zonas en negro estaban rellenadas allí con más cuidado, con lo que representaban mejor los detalles del original.

Cuando D es próxima a 1 (figura superior) la costa es demasiado recta para ser realista.

Por otra parte, la costa correspondiente a D = 1,3000 (segunda figura empezando por arriba) nos recuerda mucho un atlas real. Encontramos una reminiscencia inequívoca de África (en la isla grande de la izquierda), de Sudamérica (también en la isla de la izquierda, aunque en imagen especular) y de Groenlandia (isla grande de la derecha si giramos la parte superior de la página, de las doce a las nueve). Finalmente, si giramos la página hasta las tres, ambas islas parecen una Nueva Zelanda desnutrida con una isla Bounty doble.

Cuando D aumenta hasta 3/2 (tercera figura) este juego del atlas resulta más difícil de jugar.

Cuando D aumenta acercándose más a 2 (figura inferior) el juego geográfico se hace aún más difícil, o por lo menos más especializado (¿Minnesota? ¿Finlandia?). Y al final se hace imposible.

Otras semillas dan el mismo resultado. Aunque los mismos tests basados en gráficos más afinados abogan por D ~ 1,2000

LÁMINA 383. Los primeros ejemplos que se conocen de islas brownianas fraccionarias (dimensión D = 2,3000).

FIGURA 383

El hecho de incluir esta lámina puede que se deba a un ataque de sentimentalismo, pues no dice nada que no se haya expresado mejor en otras láminas. Pero estas vistas de una isla con un nivel del mar variable fueron presentadas en Mandelbrot (1975w) y en mi ensayo de 1975, y me gustan. Formaban parte de una secuencia completa de islas brownianas fraccionarias con distintos valores de D y niveles del mar variables. Fue la primera vez que se dibujaban islas como estas. (En 1976 realizamos una película de esta isla concreta emergiendo del mar; en 1981 la película parece ya de un primitivismo ridículo, aunque pudiera tener valor museístico).

En muchas ocasiones me pongo a pensar en qué viaje he visto efectivamente la vista de la figura inferior, con sus pequeñas islas dispersas como semillas en el extremo de una península estrecha.

La ilustración original era una fotografía de un tubo de rayos catódicos al que le faltaba nitidez; por tanto los datos han tenido que volverse a procesar. Aquí (a diferencia de las láminas 374 y 375, y de la C9 a la C15) no hace falta simular una iluminación determinada. Por suerte o por desgracia, el mismo proceso gráfico antiguo crea la impresión de que el mar brilla en la profundidad del horizonte.

El lector observará que, en comparación con los paisajes más recientes, esta lámina presenta una dimensión sorprendentemente grande. Ello es debido a que las técnicas gráficas primitivas no eran capaces de representar los pequeños detalles, por lo que la dimensión de los paisajes primitivos parecía menor que la D introducida en los programas que los generaban. Para compensar, aumentábamos la D por encima de la gama que nos sugerían los datos. Al mejorar los gráficos, no obstante, el sesgo se hacía notorio y resultaba contraproducente. En la actualidad hemos llegado a un punto en que las dimensiones sugeridas por los datos de Richardson dan unos paisajes perfectamente aceptables.

28 Relieve y costas

28
Relieve y costas