Pasar a los fractales brownianos fraccionarios constituye uno de los principales puntos decisivos de este ensayo. Hasta ahora nos hemos limitado a fractales cuya construcción requiere una trama temporal y/o espacial, con las consiguientes restricciones sobre sus propiedades de invariancia, esto es, sobre las posibles traslaciones y semejanzas que aplican dicha fractal sobre sí misma.

Tales restricciones contradicen la segunda de las razones aducidas en el capítulo 22 para aleatorizar las fractales. Además, en muchos casos de interés no tienen ninguna realidad física. Por contra, en los capítulos 27 a 35 pasaremos a estudiar fractales cuyas invariancias por traslación y semejanza no están sometidas a ninguna restricción.

En este capítulo se estudia un movimiento browniano generalizado, que denotaremos B_H(t), y que en Mandelbrot y Van Ness (1968) se denomina movimiento browniano fraccionario (abreviado, mbf). Su motivación son las descargas fluviales anuales, aunque también citamos las redes escalantes y los ruidos escalantes («1/f»). En los capítulos 28 a 30 se estudian las superficies construidas por procedimientos análogos.

Una primera característica común a los capítulos 27 a 30 es que únicamente tratan de procesos gaussianos. Para los estadísticos, el ser gaussiano es algo extraordinariamente especial, pero yo hace tiempo que he dejado de compartir esta opinión. (Véanse mis comentarios al respecto en el capítulo 22). Sin embargo, los procesos gaussianos siguen siendo un hito importante, y requieren ser estudiados con mucho cuidado antes de ir más allá.

Los capítulos 27 a 30 tienen también en común otra característica que no se presenta en ningún otro lugar de este ensayo.

Las construcciones de todos los demás capítulos, sean o no aleatorias, proceden iterativamente, añadiendo cada vez más detalles a las figuras menos detalladas obtenidas en los pasos anteriores del proceso constructivo. Las propiedades de los fractales resultantes se obtienen a partir de las reglas de dicho proceso iterativo.

Ahora, por el contrario, establecemos de entrada qué propiedades son deseables, y sólo después buscamos unas reglas de construcción que satisfagan nuestros deseos. Desgraciadamente, si bien las propiedades deseables son fáciles de enunciar y en apariencia simples, las reglas para realizarlas no son iterativas, y de hecho son bastante incómodas.

Si esto es así ¿por qué habríamos de insistir en tales propiedades? La respuesta es que entre ellas están la autosemejanza y la carencia de pliegues (es decir, la estacionariedad), propiedades que son inmanentes al mismísimo corazón de la ciencia y también a la teoría de fractales.

El coste relativo del enfoque «axiomático» de este capítulo se hace especialmente evidente cuando el resultado se compara con un fractal obtenido por iteración. Por ejemplo, cualquiera que investigue un caso concreto que requiera una curva fractal plana de dimensión D comprendida entre 1 y 2 puede dudar entre un proceso de desplazamiento del punto medio, como en el capítulo 26, y un proceso como el que describiremos en este capítulo. El primero tiene pliegues, lo cual es un inconveniente que no presenta el segundo. Y, en la mayoría de casos, la sucesión de pasos discretos que hace tan atractivo el proceso iterativo se traduce en estratos que no tienen ningún significado ni son deseables.

La afirmación del capítulo 1 de que muchas estructuras no uniformes que se dan en la naturaleza han llamado la atención del hombre desde muy antiguo es, en muchos casos, difícil de documentar con precisión. Pero la Biblia nos ofrece dos excepciones fantásticas:

«… se hendieron todas las fuentes del gran abismo y se abrieron las compuertas del cielo. Y hubo aguacero sobre la tierra cuarenta días y cuarenta noches». (Génesis, 7: 11-12)

«He aquí que llegan siete años de grande abundancia en toda la tierra de o. Después de ellos vendrán siete años de hambre.» (Génesis, 41: 29-30.)

Se hace difícil no tomar el relato de Noé como una parábola acerca de la desigualdad de las precipitaciones en el Oriente Medio y el relato de José como una parábola sobre la tendencia que presentan los años secos y los años húmedos a agruparse en periodos de sequía y periodos lluviosos. En mis lecciones sobre Nuevas formas de azar en las ciencias (no publicadas pero esbozadas parcialmente en Mandelbrot y Wallis, 1968, y Mandelbrot, 1973 f), apliqué a estos relatos los nombres de efecto Noé y efecto José. Como se puede confirmar con datos controlables, los «siete y siete» bíblicos son una simplificación poética de la realidad, y (aunque no es tan obvio) cualquier apariencia de periodicidad en el comportamiento real del Nilo es ilusoria. Por otra parte, es un hecho bien comprobado que los caudales y las crecidas anuales sucesivas del Nilo y de muchos otros ríos son extraordinariamente persistentes.

Esta persistencia resulta tan fascinante para muchos estudiosos como vital para quienes se dedican a proyectar embalses. Durante mucho tiempo, no obstante, estuvo fuera del alcance de las posibilidades de medida, y por tanto de las posibilidades de análisis. Como en todos los campos en los que se empieza a introducir la estadística, la hidrología empezó suponiendo que los caudales sucesivos de cada río eran independientes y con distribuciones gaussianas idénticas; lo que también se conoce como ruido blanco gaussiano. Tradicionalmente, el segundo paso consiste en suponer una dependencia markoviana. Sin embargo, ambos modelos son poco realistas. Mandelbrot (1965h) significó un avance importante basado en resultados empíricos de Hurst (1951, 1955). (La historia de Hurst se cuenta en el capítulo 40).

Denotemos por X*(t) la descarga acumulada de un río entre el principio del año 0 y el final del año t. Ajustémosla restando la descarga media muestral entre los años 0 y d, y definamos R(d) como la diferencia entre el máximo y el mínimo de la X*(t) ajustada cuando t varía entre 0 y d. En realidad, R(d) es la capacidad que debería tener un embalse para asegurar un funcionamiento ideal durante los d años en cuestión. Un embalse tiene un funcionamiento ideal si al final acaba tan lleno como al principio, sin vaciarse ni desbordarse nunca, y mantiene un flujo de salida uniforme. Dicho ideal es obviamente inalcanzable, pero R(d) es la base de un método para proyectar embalses, debido a Rippl, que iba a seguirse en la Gran Presa de Asuán. Hurst se dio cuenta de que R(d) podía ser útil en la investigación del comportamiento real de los registros de caudal fluvial. Por razones de conveniencia, dividió R(d) por un factor de escala S(d) y examinó la dependencia en d del cociente R(d)/S(d).

Si se supone que las descargas anuales se comportan como un ruido gaussiano blanco, el factor S no es importante y un conocido teorema prueba que la descarga acumulada X*(t) es aproximadamente una función browniana B(t), real y de variable real.

Por tanto, R(d) es proporcional a la raíz de la media cuadrática de X*(d) que es ∝ √d. Este razonamiento nos lleva a R/S ∝ √d (Feller, 1951). El mismo resultado vale si las descargas anuales son dependientes pero markovianas ▯ con varianza finita ▮, o si la dependencia toma una cualquiera de las formas descritas en los textos elementales de probabilidad y estadística.

Sin embargo, la evidencia empírica llevó a Hurst a la conclusión claramente distinta y totalmente inesperada de que R/S ∝ d^H, con H casi siempre superior a 1/2. Las avenidas anuales del Nilo, lejos de ser independientes, presentan H = 0,9. Para los ríos San Lorenzo, Colorado y Loira, H está entre 0,9 y 1/2. El Rhin es un río excepcional, sin leyenda de José ni fenómeno de Hurst, y para él H = 1/2 dentro del margen de error experimental. En Mandelbrot y Wallis (1969b) se recogen diversos datos observacionales.

Propongo llamar ruido de Hurst a un ruido o fluctuación X(t) tal que R/S ∝ d^H. En Mandelbrot (1975w) se demuestra que se debe cumplir 0 ≤ H ≤ 1.

H. A. Thomas Jr. me pidió que explicara las razones del fenómeno de Hurst y propuse la conjetura de que sería un síntoma de la invariancia por cambio de escala. Para definir de modo intuitivo un ruido escalante, recordemos que cualquier fluctuación natural se puede procesar para hacerla audible, como indica la misma palabra ruido. Grabémosla y escuchémosla en un altavoz que funcione bien entre, pongamos, 40 Hz y 14.000 Hz. Hagamos pasar la cinta con distintas velocidades, más rápido y más lento de lo normal. En general, uno esperaría encontrar grandes variaciones. Un violín, por ejemplo, deja de sonar como un violín. Y si un canto de ballena se reproduce lo bastante deprisa, pasa de ser inaudible a poderse oír. Hay una clase especial de sonidos, sin embargo, que se comporta de forma muy distinta. Al cambiar la velocidad de la cinta basta con ajustar convenientemente el volumen para que el sonido emitido por el altavoz «suene igual» que antes. Propongo que estos sonidos o ruidos se denominen escalantes.

El ruido blanco gaussiano así transformado proporciona siempre el mismo zumbido soso, y por tanto es escalante. Pero se puede disponer de otros ruidos escalantes para la realización de modelos.

En el capítulo 21 se define la delta variancia de una función aleatoria como la variancia del incremento de la función durante el incremento de tiempo Δt. La delta variancia de la función browniana ordinaria es |Δt| (capítulo 25). Para explicar la relación R(d)/S(d) ∝ d^H de Hurst, con H arbitrario, Mandelbrot (1965h) observa que bastaría con que el proceso acumulativo X* fuera gaussiano con una delta esperada nula y con una delta variancia igual a |Δt|^2H. Estas condiciones determinan un único proceso estocástico gaussiano escalante. Y, como el exponente 2H es fraccionario, este proceso único merece el nombre de función browniana fraccionaria real de variable real. Para más detalles e ilustraciones véase Mandelbrot y Van Ness (1968) y Mandelbrot y Wallis (1968, 1969abc).

Pasando de la B_H(t) real de variable real a la función B_H(t) de una variable real en el plano, una definición alternativa es la siguiente: entre las curvas de dimensión D = 1/H parametrizadas con el tiempo, la trayectoria B_H(t) es la única cuyos incrementos son gaussianos, estacionarios bajo cualquier traslación (y por tanto «sin pliegues») y escalantes para cualquier factor r > 0.

El valor H = 1/2, esto es, D = 2, da el movimiento browniano ordinario, que como ya sabemos es un proceso sin persistencia (incrementos independientes). Los otros mbf pertenecen a una de las dos clases siguientes, muy distintas entre sí. Los valores 1/2 < H < 1 corresponden a mbf persistentes, cuyas trayectorias son curvas de dimensión D = 1/H, comprendida entre 1 y 2. Los valores 0 < H < 1/2 corresponden a mbf antipersistentes.

Después de haber concretado una delta varianza conveniente, nos falta ahora realizarla efectivamente. Si se parte del movimiento browniano, hay que añadirle la persistencia. Un método estándar consiste en integrar, pero esto añade más persistencia de la necesaria. Por suerte hay un modo de atenuar parte de los efectos no deseados de la integración. Para 0 < H < 1/2 se puede hacer lo mismo con la derivada. La idea se esconde en uno de los rincones clásicos, aunque oscuros, de la matemática. Hay reminiscencias en Leibniz (capítulo 41) y fue desarrollada por Riemann, Liouville y H. Weyl.

Recuérdese del cálculo ordinario que, si m es un entero positivo, la función x^1/2 se transforma en x^{1/2 − m} después de m derivaciones seguidas, y en x^{1/2 + m} tras m integraciones seguidas (con la adición en cada caso de un factor constante). El algoritmo de Riemann-Liouville-Weyl generaliza esta transformación a valores no enteros de m. La integrodiferenciación fraccionaria de orden 1/D − 1/2, aplicada al movimiento browniano, nos da un mbf. De este modo, la típica fórmula browniana, desplazamiento ∝ √tiempo, es sustituida por la generalización desplazamiento ∝ (tiempo)^1/D, con 1/D ≠ 1/2. ¡Hemos logrado nuestro objetivo!

Las fórmulas pertinentes se pueden encontrar en Mandelbrot y Van Ness (1968); en Mandelbrot y Wallis (1969c) y Mandelbrot (1972f) se describen aproximaciones (honestas).

▯ Hay sin embargo una complicación más, y un peligro potencial. En el algoritmo de Riemann-Liouville-Weyl interviene una convolución, y resulta tentador llevarla a cabo mediante transformadas de Fourier rápidas (tFr). Esta técnica da una función periódica, es decir, una función preparada de modo que no tenga una tendencia sistemática. En las investigaciones de series temporales estándar, la eliminación de las tendencias carece de efectos importantes, pues la dependencia se limita al corto plazo. En el caso del mbf, por contra, sí es importante la eliminación de la tendencia, cuya importancia aumenta con |H − 1/2| y puede ser altamente significativa. Este efecto se ilustra en el capítulo siguiente, en un contexto más amplio, con la comparación de distintas figuras de montañas. Las láminas 374 y 375, obtenidas por tFr, no presentan ninguna tendencia global, y recuerdan cimas montañosas, mientras que la lámina 378, obtenida sin emplear tales atajos, presenta una clara tendencia global.

▯ Teniendo en cuenta la economía que comportan las tFr, a menudo su uso es conveniente a pesar de todo, pero entonces hay que tomar un periodo mucho más largo que el tamaño de la muestra deseado y admitir un desgaste que aumenta cuando H → 1. ▮

En el caso H > 1/2, la propiedad más notable de la función B_H(t) es que la persistencia de sus incrementos toma una forma muy especial: dura siempre. Por tanto, la relación entre el mbf y el fenómeno de Hurst sugiere que la persistencia encontrada en los registros de descarga fluvial no se limita a lapsos de tiempo cortos (como la duración en el cargo de los ministros del faraón), sino que se alarga durante siglos (algunos húmedos y otros secos), quizá incluso milenios. El parámetro H mide la intensidad de la persistencia.

La persistencia se manifiesta muy claramente en las gráficas de los incrementos de B_H(t) y del caudal fluvial anual modelizados por dichos incrementos. Casi todas las muestras, con independencia de su duración, parecen un «ruido estocástico» superpuesto a un fondo que realiza varios ciclos. Dichos ciclos, no obstante, no son periódicos, esto es, no se pueden extrapolar a muestras de mayor duración. Además, se observa a menudo una tendencia subyacente que no se mantiene necesariamente en la extrapolación.

El interés de estas observaciones aumenta porque a menudo se observa un comportamiento parecido en la economía, donde los estudiosos suelen descomponer cualquier conjunto de datos en una tendencia, unos cuantos ciclos y un ruido.

La descomposición pretende hacer más inteligible el mecanismo subyacente, pero el ejemplo del mbf demuestra que tanto la tendencia como los ciclos pueden deberse al ruido, que no significa nada.

▯ INTERPOLACIÓN. Si se conoce una B(t) browniana ordinaria en los instantes t₁, t₂, …, no necesariamente equidistantes, los valores esperados de B(t) entre cada par de instantes se obtienen por interpolación lineal. En particular, la interpolación en [t_j, t_j+1] depende solamente de los valores de B en los instantes t_j y t_j+1. Por contra, en todos los casos en que H ≠ 1/2, la interpolación de B_H(t) es no lineal, y depende de todos los t_m y todos los B_H(t_m). A medida que t_m − t_j aumenta, la influencia de t_m disminuye, aunque lentamente. Por tanto, se puede decir que la interpolación de B_H es global. Las curvas por desplazamiento aleatorio del punto medio del capítulo 26 se comportan de un modo muy distinto, pues sus interpolaciones son lineales a lo largo de ciertos intervalos de tiempo. Éste es el aspecto crucial de la diferencia entre ambos procesos. ▮

La persistencia de los incrementos es sinónima de una gráfica de B_H(t) menos irregular a cualquier escala que la gráfica de la B(t) browniana ordinaria. Esto se manifiesta en que su dimensión es 2 − H. La dimensión del conjunto de ceros, por su parte, es 1 − H.

Cuando pasamos a una B_H(t) con valores en el plano, buscamos movimientos cuya dirección tienda a persistir en cualquier escala. La persistencia implica una tendencia de una intensidad apropiada, pero no la obligación de evitar las autointersecciones. Como en este ensayo también queremos mantener la autosemejanza, supondremos que las funciones coordenadas X_H(t) e Y_H(t) son dos funciones brownianas fraccionarias del tiempo, con valores en la recta, estocásticamente independientes y con el mismo parámetro H. De este modo se obtiene una trayectoria browniana fraccionaria en el plano dependiente de una variable real (lámina 362).

Su dimensión fractal es D = 1/H que como mínimo es 1/1 = 1, como corresponde a una curva, y como máximo 1/(1/2) = 2. Este último resultado sugiere que la trayectoria de B_H(t) llena el plano menos «densamente» que la trayectoria browniana ordinaria. Para confirmar esta sugerencia, examinaremos por separado las trayectorias limitadas y no limitadas.

El efecto de H sobre las trayectorias limitadas es notable. Para H > 1/2, igual que para H = 1/2, una trayectoria browniana limitada es una red fractal con una infinidad de huecos. Poderosas consideraciones heurísticas sugieren que las áreas de dichos huecos satisfacen Pr(U>u) ∝ u^−D/E = u^i/2H.

También he investigado empíricamente los contornos de las trayectorias limitadas, para distintos valores de D, por si encontraba desviaciones respecto al valor 4/3 que, según se muestra en la lámina 342, se obtiene para el caso browniano. ¡No pude encontrar ninguna desviación clara!

Por otra parte, el parámetro H afecta cualitativamente el comportamiento de las trayectorias sin límites. Para una trayectoria que parte de 0 en el instante 0, el número esperado de regresos a una pequeña caja en torno a 0 (infinito en el caso browniano) es finito para H > 1/2. ▯ La razón es que la integral ∫₁^∞t^−2H dt, obtenida en la penúltima sección del capítulo 25, es divergente para H = 1/2 y convergente para H > 1/2. ▮ Si se superpone un número finito de redes fractales sobre un cuadro, éste resulta recubierto de un modo menos lagunar, pero es casi seguro que no se alcanza un recubrimiento denso. El número de redes superpuestas es pequeño para H próximo a 1 y crece sin límite para H = 1/2.

Los movimientos brownianos fraccionarios con 0 < H < 1/2 dan funciones y trayectorias antipersistentes. La antipersistencia consiste en la tendencia a regresar constantemente al lugar de procedencia, y por tanto a difundirse más lentamente que sus homólogos brownianos.

La fórmula D = 1/H sólo vale si E > 1/H. Si E < 1/H (en particular en el caso del plano, en que E = 2) la dimensión fractal alcanza su valor máximo posible D = E. Recordemos que la dimensión máxima posible de una trayectoria browniana es D = 2, y que éste sólo se puede realizar si E ≥ 2. Si se la comprime en la recta real, con E = 1, la trayectoria browniana tiene que adaptarse a D = 1. Si H = 1/3, la trayectoria del mbf apenas llena el espacio tridimensional ordinario.

Volviendo al plano, E = 2, el análisis dimensional demuestra que la trayectoria ilimitada y con H < 1/2 pasa, casi con toda seguridad, una infinidad de veces por cualquier punto dado. Así pues, y en contra de lo que ocurre con B(t), que no responde a lo que se esperaría de su D = 2 y sólo llena el plano densa pero no completamente, cualquier pequeño exceso de 1/H respecto a 2 nos da un relleno completo. Para demostrar que B_H(t) regresa, casi con toda seguridad, una infinidad de veces al punto de partida, recordemos (capítulo 25) que la dimensión del conjunto de instantes de regreso es 1 − 2H, que es un valor positivo para H < 1/2. Así pues, la intersección de una trayectoria browniana fraccionaria ilimitada de H < 1/2 con un cuadrado de lado 1 tiene área unidad.

Una trayectoria limitada es una red con huecos, pero tiene un área positiva (¡una reminiscencia del capítulo 15!).

Como otras veces, el móvil inicial de la introducción de B_H procede de la experiencia personal de este geómetra acerca de qué trucos gráficos y qué trucos matemáticos es probable que den buenos resultados. Ante este posible reproche, tengo preparado un contraargumento: es preferible un modelo que carezca de una motivación seria, pero que se ajuste bien a los datos, a un modelo aparentemente bien motivado que se ajuste mal. Los científicos buscan insaciablemente ambas cosas. Por desgracia, las «explicaciones» actuales son, en mi opinión, artificiosas y poco convincentes.

Para entender por qué las descargas anuales sucesivas de un río son interdependientes, se empieza considerando el agua que aportan, de un año al siguiente, los embalses naturales. Sin embargo, el almacenamiento natural sólo produce una suavización de los registros a corto plazo y, como mucho, sólo puede dar lugar a una persistencia a corto plazo. Desde el punto de vista de la influencia a largo plazo, la gráfica de la descarga acumulada continúa teniendo una dimensión «efectiva» (en el sentido del capítulo 3) igual a 3/2.

Para ir más lejos, muchos autores están más dispuestos que yo a invocar toda una jerarquía de procesos, cada uno de los cuales funciona en su propia escala. En el caso más simple las contribuciones son aditivas. La primera componente considera los embalses naturales, la segunda los cambios microclimáticos, la tercera los cambios climáticos, y así sucesivamente.

Desafortunadamente, una persistencia de alcance infinito precisa de una infinidad de componentes, y el modelo acaba dependiendo de una infinidad de parámetros. Sigue siendo necesario explicar por qué la suma de diversas contribuciones es escalante.

En determinado punto de la discusión, una función (la correlación) se expresa como una serie infinita de exponenciales. He perdido horas y más horas haciendo hincapié en que la demostración de que esta suma es hiperbólica no es más fácil que explicar por qué es hiperbólica la curva original, y argumentando que una invocación de las posibles causas sólo puede tener un valor mágico (no científico) siempre que siga siendo vacía. Qué alegría me dio, pues, descubrir que había estado trabajando codo con codo con James Clerk Maxwell (véase la entrada «Invariancia por cambio de escala: panaceas antiguas que perduran», del capítulo 41).

No hace falta decir que el ingeniero hidrólogo práctico puede imponer a cada proceso una cota superior finita cuyo orden de magnitud sea el del horizonte del proyecto de ingeniería más largo.

DEFINICIÓN FORMAL. Se dice que un ruido X(t) es escalante si el propio X, su integral o su derivada (de orden superior al primero si hace falta) es autoafín. Esto es, si X(t) es estadísticamente idéntica a su transformada por una contracción temporal seguida del correspondiente cambio de intensidad. Así pues, debe existir un exponente α > 0 tal que, para cada h > 0, X(t) es estadísticamente idéntica a h^+αX(ht). Más generalmente, y en especial para valores de t discretos, se dice que X(t) es asintóticamente escalante si existe una función de variación lenta L(h) tal que h^−αL⁻¹(h)X(ht) tiene límite cuando h → ∞.

Esta definición requiere que se comparen todas las propiedades matemáticas de X(t) y de h^−αX(ht). Por tanto, en las ciencias empíricas nunca puede demostrarse el carácter escalante, y en la mayoría de casos, la propiedad de invariancia por cambio de escala se infiere de un único test que sólo considera una faceta de la semejanza, como por ejemplo la distribución de longitudes de los huecos (capítulo 8) o el R/S de Hurst.

▯ El test de invariancia por cambio de escala más extendido se basa en espectros. Un ruido es espectral mente escalante si su densidad espectral para la frecuencia f es de la forma 1/f^β, siendo β un exponente positivo. Si β es lo bastante próximo a 1 para que pueda tomarse abreviadamente 1/f en vez de 1/f^β, se dice que se trata de un «ruido 1/f». ▮

Muchos ruidos escalantes tienen implicaciones notables en sus campos respectivos y su naturaleza ubicua es una realidad genérica destacable.

LÁMINA 362. Trayectorias brownianas fraccionarias (dimensiones D ~ 1,1111 y D ~ 1,4285).

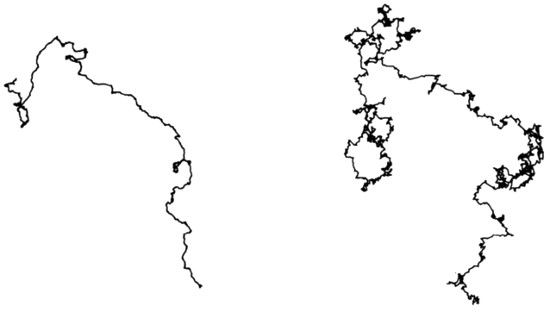
FIGURA 362

La figura de la izquierda constituye un ejemplo de curva fractal estadísticamente autosemejante con D = 1/0,9000 ~ 1,111. Sus funciones coordenadas son funciones brownianas fraccionarias independientes con exponente H = 0,9000, que explican el efecto José del Nilo. El hecho de que H sea próximo a 1 no basta para eliminar las autointersecciones, pero las reduce bastante al hacer que la «tendencia» de la curva persista en cualquier dirección que haya tomado. Si se piensa en las curvas complicadas como superposición de convoluciones de tamaños grande, medio y pequeño, se puede decir que, en caso de persistencia grande y dimensión próxima a 1, las convoluciones pequeñas apenas si son visibles.

La figura de la derecha se ha elaborado con el mismo programa de ordenador y D ~ 1/0,7000 ~ 1,4285. El generador pseudoaleatorio no se ha cambiado, con lo que la forma global es parecida. Pero el aumento de D hace que crezca la importancia de las pequeñas convoluciones y también, aunque algo menos, la de las medianas. Detalles que antes no eran visibles ahora lo son.

27 Caudales fluviales, ruidos y redes escalantes

27
Caudales fluviales, ruidos y redes escalantes