El lugar de este capítulo en este ensayo responde a un compromiso. Le correspondería estar en la parte siguiente, pero parte de él es un requisito previo al capítulo 26.

Como vimos en el capítulo 2, Jean Perrin tuvo la brillante idea de comparar el movimiento browniano con las curvas continuas y no diferenciables. Con ello, hacia 1920, inspiró en el joven Norbert Wiener la definición y el estudio de una realización matemática conocida como proceso de Wiener. Mucho después se supo que el mismo proceso había sido considerado en detalle, aunque sin rigor, por Bachelier (1900, capítulos 37 y 39).

Extrañamente, pues es extraordinariamente importante en otros campos, el movimiento browniano no encuentra nuevas aplicaciones en este ensayo. Algunas veces nos ayuda a bosquejar un problema, pero aun así el siguiente estadio de la investigación lo sustituye por otro proceso distinto. Es sorprendente, sin embargo, lo lejos que se puede llegar en muchos casos mediante simples modificaciones del movimiento browniano, siempre y cuando dichas modificaciones sean escalantes.

Por esta y otras razones, los otros fractales aleatorios no acaban de captarse por completo sin una comprensión completa de las propiedades concretas de este prototipo. Sin embargo, los miles de páginas dedicados al tema o bien desdeñan o bien pasan por alto los aspectos que se tratan en este capítulo. Si al lector se le hace duro seguir adelante, puede —como siempre— saltarse la sección o pasar al capítulo siguiente.

Desgraciadamente, la expresión movimiento browniano es ambigua. Para empezar, puede significar la gráfica de B(t) como función de t. Si B(t) es la ordenada de un punto del plano, la gráfica es una curva plana como la de la lámina 340. Si B(t) es un punto del espacio E-dimensional, la gráfica es una curva en un espacio (E + l)-dimensional (donde la coordenada t se añade a las E coordenadas de B). En muchos casos, sin embargo, sólo nos interesa la curva en el espacio E-dimensional que constituye la trayectoria del movimiento. Cuando la trayectoria se curva en instantes uniformemente separados, la función se puede deducir de la trayectoria y viceversa. Sin embargo, en un movimiento browniano continuo ambos aspectos no son equivalentes, por lo que emplear el mismo término para designarlos a ambos puede llevar a confusión.

Cuando haya peligro de ambigüedad, hablaré defunción browniana o trayectoria browniana. La misma ambigüedad se presenta para las curvas de Koch, pero aquí es más patente a causa del término «movimiento».

En los capítulos 28 al 30, además, las funciones brownianas son de varias variables. Así, por ejemplo, uno de los modelos de relieve terrestre del capítulo 28 supone que la altura es una función browniana de la latitud y la longitud. Por tanto, a menudo hará falta precisar más la terminología. Cuando sea necesario hablaremos de funciones y trayectorias brownianas de la recta en la recta, de la recta en el espacio, del espacio en la recta, de la recta en el espacio E-dimensional, etc.

«CAMPOS» BROWNIANOS. «Campo aleatorio» es una expresión que está en boga (ver, por ejemplo, Adler, 1981) para referirse a una «función aleatoria de varias variables». No hay ninguna justificación para dicha expresión y habría que prohibirla antes de que arraigue. Según parece, es una mala traducción del ruso, ▯ como automodelo (cuya difusión pude detener a tiempo), que era una mala traducción del término ruso que significa autosemejante. ▮

La trayectoria browniana plana, construida como una curva aleatoria de Peano con N = 2

Las trayectorias brownianas arrojan nueva luz sobre las curvas de Peano, y son una variante aleatorizada de las mismas. Este método de construcción no fue identificado como tal por un grupo de estudiosos consultados por mí al azar, ni se cita como tal en muchos libros sobre el tema, también consultados al azar. Sea como fuere, los matemáticos esquivan este método porque su ingrediente fundamental (una jerarquía de estratos con detalles cada vez más finos, controlada por una escala de tiempos diádica) no es intrínseco al resultado de la construcción. Por ello, según los matemáticos, este método es artificial, aunque por eso mismo encaja perfectamente en este ensayo.

El procedimiento parte de una curva de Peano cualquiera con N = 2 y r = 1/√2. El truco consiste en relajar varías ligaduras en pasos sucesivos.

Los fractales intermedios, los «híbridos de Peano y Brown», son dignos de estudio por derecho propio, y los dejaremos para mejor ocasión.

DESPLAZAMIENTO TRANSVERSAL DEL PUNTO MEDIO. En las láminas 96 a 100, el estadio (k + 1)-ésimo transforma el k-ésimo terágono desplazando transversalmente el punto medio de cada lado en |ΔM| = (√2)^−k−1, a la izquierda o a la derecha de acuerdo a unas reglas específicas, por ejemplo la paridad de k.

Denotemos ahora por ΔP, Δ₁P y Δ₂P los desplazamientos de una curva de Peano durante un lapso de tiempo Δt − t^−k y sus dos mitades Δt₁ y Δt₂. Tenemos la identidad pitagórica:

DIRECCIÓN DE DESPLAZAMIENTO ISÓTROPA. En una primera modificación de las reglas de cualquier curva de Peano, aleatorizamos las direcciones de desplazamiento. Una manera consiste en ir a la izquierda o a la derecha con igual probabilidad, con lo que se obtiene un «zigzag aleatorio». Otra manera distinta consiste en tomar un punto al azar (con densidad uniforme) sobre un círculo graduado en grados y leer el ángulo correspondiente. Este procedimiento define los desplazamientos como isótropos.

Ambas formas de aleatorización preservan la identidad pitagórica: los desplazamientos isótropos sobre subintervalos diádicos de un intervalo diádico son ortogonales.

LONGITUD DE DESPLAZAMIENTO ALEATORIA. Nuestra segunda modificación de las reglas de construcción no aleatorias consiste en hacer aleatoria la longitud de los desplazamientos. A partir de ahora 2^−k−1 no será el cuadrado de un |ΔM| no aleatorio, sino la medía cuadrática de un |ΔM| aleatorio. Los desplazamientos ΔP^* resultantes cumplirán:

INICIADOR ALEATORIO. El paso siguiente consiste en hacer que el propio iniciador sea aleatorio con una longitud cuadrática media igual a 1. Se sigue entonces necesariamente que 〈|ΔP^*|²〉 = 2^−k−1 con lo que tenemos la identidad pitagórica media

Dicho de otro modo, los lados ortogonales en sentido geométrico han sido sustituidos por lados que los probabilistas llaman ortogonales en sentido estadístico o no correlacionados.

INCREMENTOS GAUSSIANOS. La curva de Peano aleatorizada se convierte en una trayectoria browniana B(t) cuando los desplazamientos de los puntos medios siguen una distribución gaussiana. ▯ En el plano, el cuadrado del módulo de esta variable sigue una distribución exponencial. Por tanto, una construcción directa elige U uniformemente en [0, 1] y toma |ΔM| = [−2 log_eU]^1/2. ▮

GENERALIZACIÓN AL ESPACIO. La construcción final sigue teniendo sentido para E > 2.

LA DIMENSIÓN D = 2. La identidad pitagórica media es una definición generalizada de la dimensión de semejanza. Se ajusta a la trayectoria browniana porque su dimensión de Hausdorff-Besicovitch también es igual a 2. Su conveniencia caso de que el desplazamiento del punto medio no sea gaussiano está aún por estudiar.

PUNTOS MÚLTIPLES. Aun en el caso de que la aleatorización se detenga después de la primera etapa descrita en la sección anterior, se produce una destrucción absoluta del orden exquisito que, a corto y largo plazo, hacía que las curvas de Peano no presentaran autointersecciones. Los terágonos aleatorizados se cortan a sí mismos al cabo de unos cuantos pasos, y es casi seguro que la trayectoria límite se autointerseca constantemente.

HUECOS BROWNIANOS. Es bien sabido que, si se extrapola una trayectoria browniana para todos los valores de t entre −∞ y +∞, entonces cubre el plano de un modo denso. Volveremos a obtener esta propiedad en esta sección. Sin embargo, la trayectoria trazada durante un lapso de tiempo unidad tiene su propia geometría, que es de lo más peculiar. (No recuerdo haber visto una descripción de la misma en ninguna parte).

Para compensar, aparentemente, el hecho de que algunos puntos son visitados varias veces para t ∈ [0, 1], B(t) deja de pasar por otros puntos. Los puntos no visitados forman un conjunto abierto dividido en una parte exterior que contiene el punto del infinito y una infinidad de huecos brownianos disjuntos. El conjunto exterior y cada hueco están rodeados por curvas fractales que forman parte de la trayectoria browniana. Se trata, pues, de una red fractal. Tenemos ejemplos de la misma en las láminas 342 y 343.

▯ En el capítulo 14 se describen redes de dimensión D, en las cuales el número de huecos de área U mayor que u es Nr(U>u) ∝ u^−D/E. En un contexto aleatorio con D = E = 2, una generalización formal de esa ley es P(u) = Pr(U>u) ∝ u⁻¹. Sin embargo, esto no puede ser así, por cuanto ∫₀^εPr(U>u)du debe ser convergente. Mi conjetura es, por tanto, que Pr(U>u) ∝ u⁻¹L(u), siendo L(u) una función de variación lenta que decrece lo bastante rápido para que la integral anterior sea convergente. Debido a la necesidad de esta L(u) no constante, la dimensión D = 2 no se puede conseguir en una red autosemejante, igual que, como se demostraba en el capítulo 15, no se puede conseguir D = 2 en una curva simple autosemejante. ▮

EL ÁREA DE LA RED BROWNIANA ES NULA. A pesar del valor D = 2 de su dimensión, una red browniana tiene área nula. Y lo mismo tiene que valer para los híbridos de Peano-Brown.

LA TRAYECTORIA SIN LÍMITES ES DENSA EN EL PLANO. Esta propiedad se debe al hecho, que demostraremos en una sección posterior en la que nos ocuparemos del conjunto de los ceros, de que la trayectoria sin límites «vuelve» con una frecuencia infinita sobre cualquier dominio plano dado D, como un disco, por ejemplo. Tomando D arbitrariamente pequeño y con centro en cualquier punto P, vemos que la trayectoria sin límites llega una infinidad de veces arbitrariamente cerca de cualquier punto del plano.

Sin embargo, como también veremos al estudiar los conjuntos de ceros, la probabilidad de que una trayectoria concreta pase exactamente por un punto dado es nula. Por tanto, es casi seguro que un punto dado no es visitado por la trayectoria browniana sin límites.

La parte de la trayectoria sin límites contenida en un dominio D se puede aproximar mentalmente por una infinidad numerable de redes limitadas independientes, distribuidas apropiadamente sobre D. El resultado nos recuerda una infinidad numerable de puntos distribuidos aleatoria e independientemente sobre [0, 1]. Como es bien sabido, el conjunto resultante es denso por doquier, pero su longitud es nula.

El cambio de escala por √t es una característica de muchos aspectos del movimiento browniano. Por ejemplo, la distancia recorrida en un tiempo t, medida en línea recta, es un múltiplo aleatorio de √t. Asimismo, el tiempo total de permanencia en un círculo de radio R alrededor de B(0) = 0 es un múltiplo aleatorio de R².

Ponderando los diferentes tramos de una trayectoria browniana con unas «masas» proporcionales al tiempo invertido en recorrerlas, se encuentra que, en el plano o en el espacio (E ≥ 2), la masa total contenida en un círculo de radio R es M(R) ∝ R².

Formalmente, esta relación es precisamente la misma que en el caso de la curva de Koch estudiado en el capítulo 6 y en el del polvo de Cantor del capítulo 8. Es forzosamente la misma que en los casos clásicos de un intervalo, un disco o una esfera homogéneos.

La trayectoria browniana «no tiene pliegues», sus incrementos son estacionarios

Al aleatorizar la curva de Peano se obtienen de propina más propiedades de las que se pretendían inicialmente. Fijémonos, de entrada, en que las curvas de Koch y de Peano no aleatorias presentan unos «pliegues» constantes en los instantes de tiempo de la forma N^−k. Por ejemplo, si dividimos en cuartos una tercera parte del contorno del copo de nieve, el ángulo formado por los cuartos 1 y 2 es distinto del formado por los cuartos 2 y 3. En consecuencia, es imposible confundir la mitad izquierda con la mitad central.

La trayectoria browniana, por el contrario, «no tiene pliegues». Dado un intervalo correspondiente a un lapso de tiempo t, no podemos adivinar cuál es la posición de dicho laso en el eje temporal. Los probabilistas dicen que la trayectoria browniana tiene «incrementos estacionarios».

Esta propiedad es notable, pues (a) es la base de una definición alternativa, independiente de la trama, que describimos más adelante en este mismo capítulo, y (b) las formas aleatorizadas análogas de las curvas y superficies fractales simples no presentan una propiedad similar.

Un corolario de la ausencia de pliegues es una forma fuerte de autosemejanza estadística. Hagamos B(0) = 0 y tomemos dos números positivos h y h'. En un capítulo de la teoría de la probabilidad llamado teoría de la convergencia débil se demuestra que las funciones h^−1/2B(ht) y h'^−1/2B(h't) son estadísticamente idénticas. También, tomando t < ∞ y h < 1, y variando t entre 0 y T, se tiene que h^−1/2B(ht) equivale a una porción de B(t) cambiado de escala. El hecho de que dicha porción sea estadísticamente idéntica al todo es una forma de autosemejanza.

La autosemejanza aplicada a los conjuntos aleatorios es menos restrictiva que el concepto introducido en el capítulo 5, pues no hace falta que las partes sean precisamente semejantes al todo. Basta con que las partes y el todo reducido por la semejanza tengan distribuciones idénticas.

Nótese que las curvas de Koch requieren razones de semejanza de la forma r = b^−k, siendo la base b un entero positivo. En cambio, en el caso de la trayectoria browniana vale cualquier r. Ésta es una característica importante.

En el estudio de las funciones brownianas reviste especial importancia el estudio de los conjuntos antiimagen de un valor dado, o conjuntos en los que las funciones coordenadas X(t) e Y(t) toman valores constantes. Así, por ejemplo, se define el conjunto de ceros por aquellos instantes t en los que X(t) = 0.

Dichos conjuntos antiimagen son autosemejantes, y el hecho evidente de que son sumamente ralos se manifiesta en su dimensión fractal D = 1/2. Constituyen un caso especial de los polvos de Lévy, que estudiaremos en el capítulo 32.

Las longitudes de los huecos de un conjunto de ceros browniano satisfacen Pr(U>u) = u^−D, con D = 1/2. Esta relación juega un papel análogo a la ley Nr(U>u) = u^−D que ya conocemos, válida para los huecos de Cantor. No obstante, aquí Pr sustituye a Nr, y los escalones desaparecen debido a la aleatorización.

Por contra, las gráficas de X(t), Y(t) y de la función vectorial B(t) no son autosemejantes, sino sólo autoafines. Esto es, la curva comprendida entre t = 0 y t = 4 puede ser descompuesta en M = 4 porciones obtenidas contrayendo la(s) coordenada(s) espacial(es) en una proporción r = 1/2, y la coordenada temporal en proporción distinta r² = 1/M. Por tanto, la dimensión de semejanza no está definida para ninguna de las gráficas X(t), Y(t) o B(t).

Es más, en los espacios afínes no se pueden comparar las longitudes sobre el eje t con las distancias sobre los ejes X o Y. Por tanto, no podemos definir discos y, en consecuencia, la fórmula M(R) ∝ R^D no tiene una análoga que pudiera servir para definir D en el caso de las funciones brownianas.

Por otro lado, si es extensible a ellas la dimensión de Hausdorff-Besicovitch. Este ejemplo concuerda con lo que afirmábamos en los capítulos 5 y 6 de que la dimensión de Hausdorff-Besicovitch nos ofrece el modo más general de caracterizar el contenido intuitivo de la dimensión fractal (¡y también el más pesado!). Para X(t) el valor de D es 3/4, y para B(t) es 2.

▯ BOSQUEJO DE DEMOSTRACIÓN. Durante un lapso de tiempo Δt, max X(t) − min X(t) es del orden de √Δt. Si recubrimos el trozo de gráfica correspondiente con cuadrados de lado Δt, necesitaremos del orden de 1/√Δt cuadrados. Por tanto, para recubrir toda la gráfica entre t = 0 y t = 1 harán falta del orden de (Δt)^−3/2 cuadrados. Comparando este número con (Δt)^−D (capítulo 5), tenemos heurísticamente que D = 3/2. ▮

El conjunto de ceros de la función browniana real de una variable real es una sección horizontal de una función browniana X(t). Aplicando otra vez una regla enunciada en el capítulo 23, esperamos que la dimensión del conjunto de ceros sea 3/2 − 1 = 1/2, cosa que ya sabemos. Otras aplicaciones de esta regla son de un valor heurístico extraordinario, como veremos a continuación. Sin embargo, hay excepciones a esta regla, y en especial en el caso de fractales no isótropos. Así, la intersección de una aplicación browniana de la recta en una recta vertical se reduce a un solo punto.

De modo análogo, la intersección de una recta con una trayectoria browniana plana debería ser 2 − 1 = 1, y así sucede en efecto.

Dicho en forma más general, y exceptuando algunas configuraciones especiales, la regla estándar es: las codimensiones E − D se suman en las intersecciones. Por tanto, la codimensión de la intersección de k trayectorias brownianas planas es k · 0 = 0. En particular, se espera que las autointersecciones de una trayectoria browniana formen un conjunto de dimensión 2, y así ocurre. (Sin embargo, y al igual que sucede con la propia trayectoria browniana, los puntos múltiples no llenan el plano).

La regla de adición de las codimensiones se puede emplear para razonar que (como ya dijimos más arriba) es casi seguro que el movimiento browniano no regresa al punto de partida B(0) = 0, pero es casi seguro que vuelve una infinidad de veces al entorno de 0. Para dar mayor generalidad a estos argumentos y poder utilizarlos sin modificaciones en el capítulo 27, denotaremos por H la dimensión del conjunto de ceros browniano.

Los instantes en que B(t) regresa a 0 son aquellos en que, simultáneamente X(t) = 0 e Y(t) = 0. Pertenecen por tanto a la intersección de los conjuntos de ceros de X(t) e Y(t), los cuales son independientes entre sí. La codimensión de la intersección es 1 − 2H, con H = 1/2, con lo que su dimensión es D = 0. De donde se sigue una clara indicación (¡la demostración completa es más complicada!) de que es casi seguro que B(t) nunca regresa a B(0) = 0.

Consideremos, por otra parte, el conjunto de instantes en que B(t) regresa a un cuadrado de lado 2ε, centrado en 0 y paralelo a los ejes. Esto es aproximadamente la intersección de los conjuntos en que t está a una distancia ε^1/H de un punto del conjunto de ceros de X(t), o de Y(t). Para cada uno de estos conjuntos, la masa en el lapso de tiempo [0, t] es ∝ ε^1/Ht^1−H, y la probabilidad de que el instante t esté contenido en este lapso es ∝ ε^1/Ht^−H. Por tanto, la probabilidad de que t esté contenido en la intersección de estos conjuntos es ∝ ε^2/Ht^−2H. Como H = 1/2, tenemos ∫^∞t^2H dt = ∞; de donde, gracias a un teorema de Borel y Cantelli, se llega a que el número de regresos al cuadrado centrado en 0 es casi seguramente infinito. Aunque se podría decir también «apenas» infinito. Como consecuencia de ello, los huecos de una red browniana con límites se van llenando lentamente y con una desgana manifiesta.

El movimiento browniano se puede generar también por medio de un paseo aleatorio sobre una celosía. Citamos aquí esta posibilidad, pero varias complicaciones nos obligan a posponer su discusión al capítulo 36.

Decimos que un punto P(t) = (X(t), Y(t)) de R² lleva a cabo un paseo aleatorio sobre una celosía si, en sucesivos instantes de tiempo separados por un intervalo Δt, se mueve por pasos de longitud |ΔP| fija según direcciones escogidas al azar siguiendo una celosía dada.

Si la red está formada por los puntos del plano de coordenadas enteras, las cantidades (x + y)/√2 y (x − y)/√2 cambian en ± 1 a cada paso, y se dice que cada una de ellas realiza un paseo aleatorio sobre la recta. Tenemos un ejemplo en la lámina 340. A gran escala, esto es, para Δt pequeño y |ΔP| = √Δt, el paseo aleatorio es indistinguible del movimiento browniano.

Las definiciones anteriores del movimiento browniano parten, bien de una trama temporal, bien de una celosía espacio temporal, aunque estos «accesorios» no aparecen en el resultado final. De hecho, es posible caracterizar éste último sin recurrir a ellos.

La caracterización directa de Bachelier (1900) postula que, sobre una sucesión arbitraria de incrementos de tiempo Δt iguales, los vectores desplazamiento ΔB(t) son independientes, isótropos y aleatorios, obedeciendo a una distribución gaussiana de probabilidad con

Por tanto la raíz de la media cuadrática de ΔB es √|Δt|. Esta definición es independiente del sistema de coordenadas, pues la proyección de ΔB(t) sobre cualquier eje es una variable aleatoria escalar gaussiana, de media nula y varianza 1/2|Δt|.

La definición que prefieren los matemáticos va más allá y prescinde de la división del tiempo en intervalos iguales. Impone la isotropía de los movimientos entre dos instantes cualesquiera t y t₀ > t, la independencia del movimiento futuro con respecto a las posiciones ocupadas en el pasado y, finalmente, que el vector que va de B(t) a B(t₀), dividido por √|t₀ − t|, tenga una densidad de probabilidad gaussiana reducida, para cualesquiera t y t₀.

El movimiento de una partícula coloidal en un río que fluye uniformemente o el de un electrón en un alambre conductor puede representarse por B(t) + δt. La trayectoria de esta función es indistinguible de la de B(t) cuando t < 1/δ², y de la de δt cuando t > 1/δ². Así pues, la dimensión de la trayectoria pasa de D = 2 a D = 1 para t_c ∝ 1/δ² y r_c ∝ 1/δ.

▯ En la terminología de los fenómenos críticos, δ es la distancia a un punto crítico, y los exponentes de las fórmulas de t_c y r_c son los exponentes críticos. ▮

▯ La aleatorización de las curvas de Peano por medio del desplazamiento del punto medio aprovecha unas circunstancias especiales. Las construcciones análogas para curvas de Peano con N > 2 son mucho más complicadas. Se consigue también un paralelismo más cercano con el cambio de escala no aleatorio si el desplazamiento del punto medio sigue una distribución gaussiana cuya desviación cuadrática media es 1/2 |ΔB|, cosa que implica que r₁ y r₂ son gaussianas, independientes y satisfacen la relación más común (r₁² + r₂² − 1) = 0. El proceso resultante es muy interesante aunque, obviamente, no es el movimiento browniano. No carece de pliegues. ▮

Terminaremos esta discusión mencionando una nueva versión fractal de la presentación de la mecánica cuántica. Feynman y Hibbs (1965) señalan que la trayectoria típica de una partícula cuántica es continua y no diferenciable, y para muchos autores hay semejanzas entre el movimiento browniano y el de una partícula cuántica (véase, por ejemplo, Nelson, 1966, y las referencias que allí se dan). Inspirados en este paralelismo y mis primeros ensayos, Abbot y Wise (1980) demuestran que la trayectoria observada de una partícula en mecánica cuántica es una curva fractal con D = 2. La analogía es interesante, por lo menos desde el punto de vista pedagógico.

LÁMINA 340. Una muestra de paseo aleatorio que aproxima una función browniana real de variable real (dimensión D = 3/2) y su conjunto de ceros (dimensión D = 1/2).

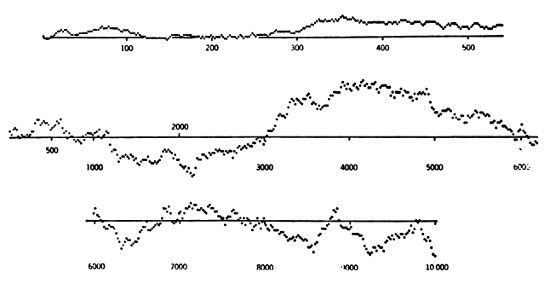
FIGURA 340

El juego de azar más duradero (¡y el menos complicado!) empezó hacia 1700, cuando la teoría de la probabilidad estaba dominada por la familia Bernouilli. Cuando una moneda permanentemente bien equilibrada cae de cara, Carlos gana un centavo, y cuando sale cruz, lo gana Cristóbal. (Se les suele llamar Pedro y Pablo, pero así nunca recuerdo quién apuesta cara y quién cruz).

Hace algún tiempo, William Feller estudió este juego y representó las ganancias acumuladas de Carlos en la figura superior de esta lámina, que pertenece a Feller (1950). (Reproducida de An Introduction to Probability Theory and Its Applications. Volume I, de William Feller, por amabilidad de los editores, J. Wiley y Sons, copyright 1950).

Las figuras central e inferior representan las ganancias acumuladas de Carlos durante un juego más largo, usando los datos a intervalos de 200 tiradas.

Cuando se representan conjuntos de datos cada vez más largos en papel gráfico cada vez más fino, se obtiene asintóticamente una muestra de los valores de una función browniana real de variable real.

Feller ha confesado en una conferencia que estas figuras son «atípicas», y fueron seleccionadas frente a otras que parecían demasiado disparatadas para ser creíbles. Sea como fuere, la contemplación continuada de estas figuras tuvo un papel decisivo en la elaboración de dos teorías incorporadas en este ensayo.

LA GRÁFICA GLOBAL. Mandelbrot (1963e) observa que la forma global de la gráfica recuerda la silueta de una montaña o de una sección vertical del relieve terrestre. Después de varias generalizaciones, esta observación condujo a los sucesivos modelos que se describen en el capítulo 28.

CONJUNTO DE CEROS DE LA GRÁFICA. El conjunto de ceros de la gráfica es el conjunto de instantes en los que las fortunas de Carlos y Cristóbal vuelven a sus valores iniciales. Por construcción, los intervalos de tiempo entre ceros son mutuamente independientes. Sin embargo, es obvio que las posiciones de los ceros no son independientes, ni muchísimo menos. Se presentan muy claramente agrupados. Así, por ejemplo, si se examina la segunda curva con el mismo detalle que la primera, casi cada cero es sustituido por toda una nube de puntos. Al tratar con el movimiento browniano, dichas nubes de puntos admiten una organización jerárquica de infinitos grados.

Cuando me pidieron que colaborara en la realización de un modelo de la distribución de errores telefónicos, tuve la suerte de recordar el diagrama de Feller. Aunque se sabía que los errores se agrupaban en ráfagas (esta era la esencia del problema práctico que se planteaba), sugerí que los intervalos entre errores podían ser independientes. Un estudio empírico detallado confirmó esta conjetura y condujo a los modelos comentados en los capítulos 8 y 31.

▯ El conjunto de ceros browniano constituye el polvo de Lévy más sencillo, a saber, un polvo de Cantor aleatorio de dimensión D = 1/2. Cualquier otra D entre 0 y 1 se puede obtener de modo análogo con los ceros de otras funciones estocásticas. Con este modelo es posible definir la dimensión fractal de una línea telefónica. Las dimensiones reales dependen de las características concretas del proceso físico subyacente. ▮

LÁMINAS 342 y 343. Envolturas / islas brownianas; movimiento browniano autoevitante.

BUCLE BROWNIANO. Llamo así a una trayectoria recorrida en un tiempo finito Δt por un movimiento browniano plano que regresa al punto de partida. Se trata de una curva de Peano aleatoria cuyo iniciador tiene longitud nula.

FIGURA 342

FIGURA 342. Envoltura de una trayectoria browniana sin bucles.

FIGURA 343

FIGURA 343. ENVOLTURA BROWNIANA. Al estar acotado (casi con toda certeza), un bucle browniano divide el plano en dos partes: una exterior a la que se puede llegar desde un punto distante sin atravesar el bucle, y otra interior, para la que propongo los nombres de envoltura browniana o isla browniana.

COMENTARIO. No sé de ninguna investigación acerca de la envoltura browniana, pero creo que merece mucha atención. En los ejemplos de la derecha se han empleado 200.000 pasos brownianos, y cada uno se ha dibujado en una pantalla de (1.200)².

Por construcción, las envolturas brownianas correspondientes a Δt distintos son estadísticamente idénticas, aparte de la escala. Y hay buenas razones para creer que los detalles más finos del contorno de la envoltura son asintóticamente autosemejantes. La frontera no puede ser estrictamente escalante, ya que un lazo no puede descomponerse en piezas que tengan la misma estructura, pero cuanto menores son las piezas más aproximadamente escalantes son.

MOVIMIENTO BROWNIANO AUTOEVITANTE. Por razones que se expondrán en el capítulo 36, cuando estudiemos el paseo aleatorio autoevitante propongo llamar movimiento browniano autoevitante, al contorno de la envoltura browniana.

La dimensión del movimiento browniano autoevitante. Después de haber interpretado que ciertas relaciones conocidas (que citaremos en el capítulo 36) implican que el paseo aleatorio autoevitante tiene dimensión 4/3, mi conjetura es que lo mismo vale para el movimiento browniano autoevitante.

Una comprobación empírica de esta conjetura nos proporciona también una ocasión magnífica para comprobar la relación longitud-área del capítulo 12. Se recubre la lámina con cuadrículas cada vez más finas y se cuenta el número de cuadrados de lado G intersecados por (a) la envoltura, para obtener la G-área, y (b) el contorno, para obtener la G-longitud. La gráfica de la G-longitud en función de la G-área en papel bilogarítmico resulta ser notablemente recta, con una pendiente prácticamente igual a D/2 = (4/3)/2 = 2/3.

Vale la pena señalar el parecido entre las curvas de las láminas 343 y 328, y sus dimensiones.

NOTA. Las zonas grises de la lámina 343 representan los dominios abiertos máximos que no son visitados por B(t). Se pueden interpretar también como tremas de contorno fractal, con lo que el bucle es una red en el sentido del capítulo 14.

▯ Se puede plantear la pregunta de si el bucle es un tamiz o una alfombra por lo que respecta a su orden de ramificación. Yo conjeturé que se trataba de lo segundo, en el sentido de que las redes brownianas satisfacen la propiedad de Whyburn (descrita en la pág. 193). Esta conjetura ha sido confirmada por Kakutani y Tongling (no publicado). Se sigue de ello que la trayectoria browniana es una curva universal en el sentido de la definición de la página 206. ▮

25 Movimiento browniano y fractales brownianos

25
Movimiento browniano y fractales brownianos