El capítulo anterior describe la forma de aleatorizar la coagulación sin tocar la trama espacial subyacente de base b. En una coagulación aleatoria, el «material» que se encuentra en una celda de la red en el paso k-ésimo permanece en ella por siempre jamás, en tanto que su distribución se hace cada vez menos uniforme. El proceso es muy simple, pues la evolución de cada celda es independiente de lo que ocurra en las demás. Sin embargo, hay que dejar que el azar y las propiedades del espacio determinen la topología de los fractales resultantes.

En este capítulo se muestra cómo se pueden imponer condiciones al proceso de coagulación para que la fractal resultante tenga unas determinadas propiedades de conexión. Así, por ejemplo, si se pretende modelar una costa o el curso de un río, se necesita una curva «autoevitante». En otro campo totalmente diferente, el de la ciencia de polímeros, encontramos otro ejemplo: una molécula sumamente larga flotando en un buen disolvente se mueve erráticamente pero, como es obvio, le está prohibido ocupar la misma porción de espacio más de una vez.

En los métodos iterativos que garantizan que el conjunto resultante del proceso de coagulación será conexo y autoevitante, el iniciador sigue siendo un dominio plano, pongamos un cuadrado, y el generador también es un conjunto de dominios más pequeños contenidos en el iniciador. En el capítulo 23 la única condición sobre dichos dominios era que no se solaparan, aunque estaban permitidos los vértices o lados comunes. En este capítulo, por el contrario, se impone la existencia de vértices o lados comunes.

El caso de vértices comunes, que examinaremos en primer lugar, es el de las «cadenas aleatorias» que nos dan una generalización directa de ciertas curvas de Koch y de Peano.

El caso de lados comunes da una familia de fractales mucho más atractiva e interesante, que fue introducida en Mandelbrot (1978r, 1979c). Algunas de ellas son «curvas simples» autoevitantes y sin ramificaciones, otras son bucles y otras árboles. El proceso de construcción se puede generalizar a superficies. Propongo para estas figuras el nombre de garabatos.

La razón principal para preferirlos a las cadenas aleatorias es que su menor versatilidad parece reflejar una propiedad fundamental del espacio.

Los garabatos lineales son modelos toscos de polímeros lineales y de cursos fluviales, mientras que los garabatos que forman bucles son modelos de costas, y los garabatos ramificados de árboles fluviales.

Se puede considerar que los dominios en blanco de la lámina 71 forman una cadena de triángulos unidos por los vértices. En la siguiente etapa de la construcción, cada triángulo es sustituido por una subcadena contenida totalmente en su interior, de lo que resulta una cadena de triángulos menores unidos por un solo punto. Esta sucesión de cadenas encajadas converge hacia la curva de Koch. (El procedimiento recuerda las cadenas de Poincaré del capítulo 18).

De este mismo modo se pueden construir muchas otras curvas de Koch, como, por ejemplo, el tamiz de Sierpinski de la lámina 204, cuya cadena es la figura que se obtiene eliminando las tremas triangulares centrales.

Este método de construcción se puede aleatorizar fácilmente, por ejemplo sustituyendo cada triángulo, bien por dos triángulos con r = 1/√3, como en la lámina 71, bien por tres triángulos con r = 1/3.

La curva «garabato» más simple es una curva fractal aleatoria diseñada en Mandelbrot (1978r, 1979c) y estudiada también por Peyrière (1978, 1979, 1981). Es un modelo de curso fluvial trazado según unas figuras bien conocidas en geografía y en geología, que muestran los sucesivos estadios de un río que va excavando su valle, definiendo su curso con una precisión creciente.

Antes del k-ésimo estadio de excavación, el río fluye por un valle «pregarabato» formado por celdas de una red triangular regular de lado 2^−k. Naturalmente, ninguna celda de la red puede ser visitada dos veces, y cada celda del valle debe estar en contacto con dos vecinos a través de un lado común, mientras que el tercer lado está «bloqueado».

El k-ésimo estadio de la excavación sustituye este pregarabato por otro más detallado dibujado sobre una celosía interpolada de lado 2^−k−1. Está claro que el pregarabato de orden (k + 1) incorpora necesariamente la mitad de cada lado compartido entre dos celdas de orden k. Y se cumple también un enunciado inverso más fuerte, a saber: la posición de las mitades compartidas (no bloqueadas) determina sin ambigüedad el pregarabato de orden (k + 1).

GARABATOS SIMÉTRICAMENTE ALEATORIOS. Tómese al azar el medio lado a bloquear, con la misma probabilidad para ambas alternativas posibles. El número de enlaces de orden (k + 1) contenidos en un enlace de orden k es 1, con probabilidad 1/4, o 3 con probabilidad 3/4. El número medio es, pues, 2,5.

A cada paso el valle se hace cada vez más congosto, convergiendo asintóticamente hacia una curva fractal. Naturalmente conjeturé que la dimensión del límite sería D = log 2,5/log 2 = 1,3219. La demostración (bastante delicada) se encuentra en Peyrière (1978).

GARABATOS ASIMÉTRICAMENTE ALEATORIOS. Divídase cada lado en dos mitades y sea p ≠ 1/2 la probabilidad de que el subvalle cruce la «mitad de la izquierda». Esta puede definirse en relación a un observador orientado río abajo o a uno situado en el centro del triángulo a subdividir. En el primer caso, D = log[3 − p² − (1 − p)²]/log 2, y varía entre 1 y log 2,5/ log 2. En el segundo caso, D = log[3 − 2p(1 − p)]/log2, variando entre log 2,5/log 2 y log 3/log 2. En conjunto se pueden alcanzar todos los valores de D comprendidos entre 1 y log 3/log 2.

Usando otras celosías interpoladas se obtienen garabatos alternativos. La generalización es inmediata siempre y cuando el conocimiento de los segmentos por los que un pregarabato de orden (k + 1) cruza los lados comunes a las celdas de orden k baste para identificar el pregarabato de orden (k + 1). Un ejemplo lo tenemos en una celosía rectangular, en la que el cociente entre el lado largo y el corto es √b, y la interpolación se hace sustituyendo cada celda por otras b semejantes a ella, dispuestas transversalmente.

Pero este no es el caso de las celosías triangulares, cuyas celdas se subdividen por interpolación en b² ≥ 9 triángulos, ni el de las celosías cuadradas, cuyas celdas se subdividen en b² ≥ 4 cuadrados. En ambos casos la interpolación de los pregarabatos precisa de pasos adicionales.

Si b = 3, en el caso de los triángulos, o b = 2, en el de los cuadrados, basta con un paso extra muy natural. En efecto, considérense los cuatro «rayos» irradiados desde el centro del cuadrado que lo dividen en cuatro cuadrados menores, o los seis rayos que sirven para dividir el triángulo en nueve triángulos menores. Tan pronto se bloquea uno de estos rayos, el subvalle queda completamente determinado. En mi definición de los garabatos, el rayo bloqueado se escoge al azar, con idénticas probabilidades para todas las alternativas. Se tiene que D ~ 1,3347 para los triángulos que se dividen en 9, y que D ~ 1,2886 para los cuadrados que se dividen en 4. Si recordamos que los garabatos más simples dan D ~ 1,3219, observamos que la D de un garabato es casi universal: próxima a 4/3.

Si se divide un triángulo o un cuadrado en b² partes, con b > 3 para el triángulo o b > 2 para el cuadrado, hacen falta más especificaciones para determinar el subvalle, con lo que la construcción tiene una componente arbitraria creciente. En el espíritu de la discusión de la sección siguiente, acaban por perderse los méritos de la construcción por garabato.

Detengámonos ahora para recordar que, si se obtiene una curva fractal por el método de las cadenas de Cesàro o por el método original de Koch, el error cometido al truncar el proceso se reparte a lo largo de la curva de un modo muy heterogéneo. El hecho de que algunos puntos se alcancen con una precisión infinita al cabo de un número finito de estadios puede resultar ventajoso. Le sirvió a Koch, por ejemplo, en su búsqueda de la curva más simple que carece de tangente en todos sus puntos. Pero el significado esencial del concepto de curva queda muchísimo más claro cuando ésta se presenta como límite de una banda de anchura uniforme. Mis curvas garabato satisfacen este desiderátum.

Otro elemento de comparación tiene que ver con el número de decisiones arbitrarias que debe tomar el «diseñador» en cada paso. El enfoque de fractales a lo Koch es muy potente, tanto si son aleatorios como si no (en particular, se consigue cualquier D que se quiera con una simple curva), pero implica un gran número de elecciones concretas por parte del diseñador, que no tienen una motivación independiente. La base b es especialmente no intrínseca.

Después de haber padecido la aridez de los modelos euclídeos de las formas rugosas que se dan en la naturaleza, el que las fractales nos liberaran de esta incuestionable inconveniencia fue un motivo de alegría. Pero en el estado actual de la teoría tenemos que superar la euforia inicial y arreglamos con menos decisiones arbitrarias.

A la luz de este comentario, el hecho de que la construcción por garabatos esté mucho más condicionada por la geometría del plano (en el sentido de ser menos versátil que la construcción por cadenas) resulta ser una virtud.

En particular, hay que tener presente que la dimensión de los garabatos es D ~ 4/3. El hecho de que este valor se encuentre también en el capítulo 25 (lámina 343) y en el capítulo 36, no puede ser fruto de una coincidencia, y puede llevarnos finalmente a la comprensión de aspectos fundamentales de la estructura geométrica del plano.

Volvamos a la construcción del curso de un río. Una vez sustituido el intervalo triangular de un valle por un subvalle formado por 1 o 3 subtriángulos, imaginemos que los 3 o 1 subtriángulos restantes desaguan en el nuevo subvalle. El patrón de drenaje queda totalmente determinado. Los puntos por los que los afluentes cruzan las divisorias entre triángulos son escogidos por el mismo procedimiento empleado para el río principal. La construcción resultante converge hacia un árbol que llena un triángulo al azar, como se ve en la figura.

Es interesante, y quizá incluso significativo, que un modelo tan tosco como mis garabatos lineales bastara para explicar —aunque sólo sea aproximadamente— las dimensiones observadas de los ríos.

Y también da la dimensión del modelo más corriente de polímero lineal altamente diluido, el paseo aleatorio autoevitante sobre una celosía (PAAE, capítulo 36).

La razón por la cual las ligaduras derivadas de la geometría del plano son muchísimo más fáciles de manejar en el caso de los garabatos que en el PAAE tiene que ver obviamente con el hecho de que los garabatos se construyen por interpolación.

Se definen en un cubo que se subdivide en b³ subcubos. He encontrado procedimientos apropiados de «bloqueo» que determinan unívocamente una especie de edredón de espesor constante pero decreciente. Por desgracia, el algoritmo es demasiado largo para reproducirlo aquí.

LÁMINA 325. Costa aleatoria de Koch (dimensión D = 1,6131).

FIGURA 325

En muchos casos se puede obtener una curva de Koch con una D prescrita y sin puntos de autocontacto mediante diversos procedimientos, manteniendo la misma trama global y el mismo iniciador. Supongamos además que por lo menos dos generadores distintos encajan en el mismo esquema global. En tal caso es fácil aleatorizar la construcción escogiendo al azar entre dichos generadores. Se puede, por ejemplo, alternar los dos generadores siguientes

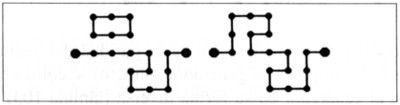
El resultado es el que se muestra sobre estas líneas.

La forma global de una isla de Koch aleatoria construida de este modo depende mucho de la figura inicial. En particular, todas las simetrías de la misma se mantienen visibles a lo largo de todo el proceso. Por esta razón, y otras apuntadas en el capítulo 24, la barajadura aleatoria de las partes de una curva de Koch es un método de alcance limitado.

LÁMINA 326. Curva aleatoria de Peano (dimensión D = 2).

FIGURA 326

El siguiente generador, aplicado al iniciador [0,1], proporciona una manera de barrer un triángulo

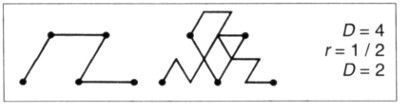
La posición del generador depende de la paridad del segmento del terágono. Sobre los lados impares, el generador (directo) se coloca a la derecha. Y sobre los pares, el generador en su forma inversa (lámina 103) se coloca a la izquierda. El método de aleatorización seguido aquí consiste en escoger al azar estos puntos focales. En este ejemplo, la distribución es simétrica con respecto al punto medio. Cada subtriángulo se subdivide luego en cuatro, independientemente de sus vecinos e indefinidamente.

Para facilitar el seguimiento del terágono, cada intervalo se sustituye por dos, añadiendo como punto extremo el centro de dicho intervalo.

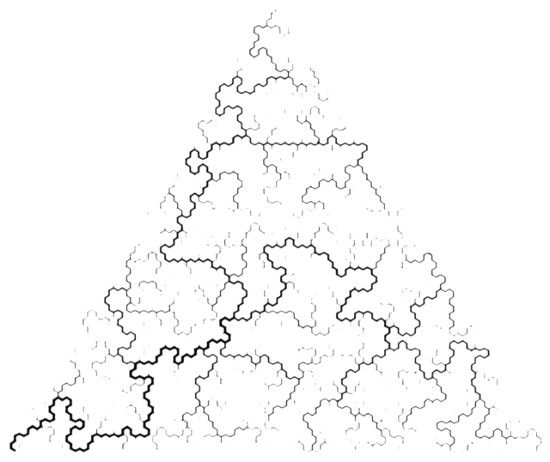
LÁMINA 327. Triángulo y curva garabato.

FIGURA 327

Aquí se ilustra el garabato más simple mediante una superposición de varios diagramas. El orden de dichas figuras es el indicado por las distintas tonalidades de gris, de la más clara a la más oscura. La ilustración empieza con el triángulo gris claro y acaba con una curva en negro. La escala de las etapas 6 a 10 es mayor que la de las etapas 0 a 5. En el texto se describen los distintos pasos sucesivos.

LÁMINA 328. Una costa garabato hexagonal.

FIGURA 328

Esta lámina enlaza seis garabatos formando un circuito autoevitante. La dimensión es muy próxima a D = 4/3. Este valor también se da en gran número de casos autoevitantes, por ejemplo en la frontera del casco browniano de la lámina 343, cuyo parecido con un garabato hexagonal es particularmente digno de mención.

24 Cadenas aleatorias y garabatos

24
Cadenas aleatorias y garabatos