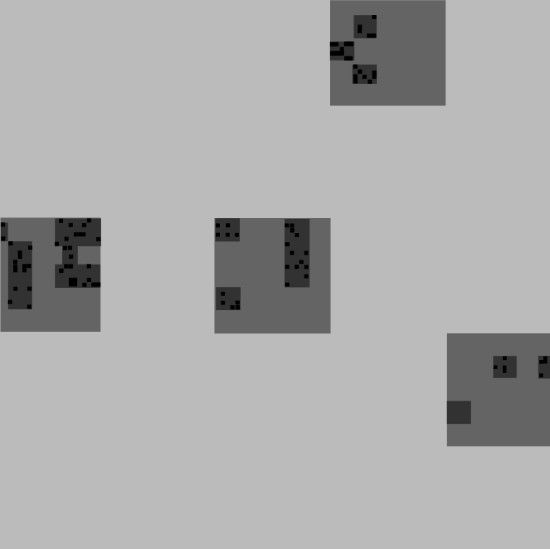23
Coagulaciones aleatorias: racimos de contacto y percolación fractal

Este grupo de capítulos demuestra que diversos dispositivos de una simplicidad casi ridícula conducen a fractales efectivamente aleatorios. En el capítulo 23 se aleatoriza la coagulación, con un procedimiento empleado para esbozar un modelo de ruido inspirado en el polvo de Cantor (capítulo 8), un modelo de las galaxias basado en un polvo de Cantor espacial (capítulo 9), uno de intermitencia turbulenta (capítulo 10), etc. La intención principal del capítulo 24 es introducir mis garabatos, una nueva forma aleatorizada de curva de Koch. El capítulo 25 se ocupa del movimiento browniano y el 26 define otros fractales por «desplazamiento aleatorio del punto medio».

El calificativo «estratificado» del título de este grupo de capítulos expresa que, en todos los casos considerados, tratamos con fractales construidos por superposición de estratos (en latín, strata), cada uno con detalles más finos que el anterior. En muchos casos los estratos son jerárquicos. Sin decirlo, los capítulos anteriores tratan exclusivamente de fractales estratificados. Pero en capítulos posteriores se establece que los fractales aleatorios no tienen por qué ser necesariamente estratificados.

Los fractales de este capítulo implican una cuadrícula o celosía, formada por segmentos, cuadrados o cubos, divididos cada uno de ellos en b^E subsegmentos, subcuadrados o subcubos; b es la base de la celosía.

Polvos lineales aleatorizados

El polvo aleatorio más simple sobre una recta, que puede mejorar el modelo cantoriano de los errores visto en el capítulo 8, empieza como la forma más simple de coagulación cantoriana: con una red de segmentos de base b y un número entero N < b. Pero, en vez de partir de un generador determinado, se parte de una lista de posibles generadores cantorianos, esto es, de todas las distintas alineaciones de N cajas llenas y b − N cajas vacías. Cada vez se toma al azar uno de estos generadores, con probabilidades iguales.

Cualquier punto P del grumo se define por una sucesión de segmentos de «pregrumo» encajados, de longitudes R_k = b^−k. Si la masa total inicial es 1, cada precoágulo contiene la misma masa R_k^D. La masa contenida en el segmento de longitud 2R_k, centrado en P, es R_k^D multiplicado por una variable aleatoria con valores entre 1 y 2, e independiente de k.

Nótese que los valores de D están limitados a los de la sucesión log (b − 1)/log b, log (b − 2)/log b, … Dicha restricción acostumbra a ser un inconveniente. Y lo que es más grave, la definición anterior de coagulación es difícil de implementar en un ordenador y de manejar analíticamente. Como la principal virtud de la coagulación reside en su simplicidad, preferiremos una definición alternativa que vamos a presentar a continuación. Para distinguir la definición de esta sección la denominaremos constreñida. (En Mandelbrot, 1974f, se la denomina microcanónica).

Polvos lineales por coagulación aleatoria

Se puede obtener una definición mejor de coagulación, tal como se presenta en Mandelbrot (1974f), donde recibe el nombre de canónica, tomando una sucesión de elecciones binarias aleatorias, reguladas por un simple lanzamiento de moneda. Después de lanzar varias veces la moneda, el primer paso de una cascada decide la suerte que correrá cada uno de los b subintervalos. Cuando sale cara, cosa que tiene una probabilidad p < 1, el subintervalo «sobrevive» como parte de un pregrumo: en caso contrario, es eliminado. Después de cada iteración, se eliminan los puntos aislados que quedan entre dos subintervalos eliminados de cualquier longitud. Se trata sólo de un problema menor, pero sus homólogos en el plano o en el espacio (rectas aisladas, etc.) darían lugar a falsas conexiones en el conjunto resultante. El número esperado de subintervalos supervivientes es 〈N〉 = pb = p/r. Luego el proceso se vuelve a repetir con cada subintervalo, independientemente de los demás.

FORMALISMO DEL PROCESO DE NACIMIENTO. Si llamamos «hijos» a los subintervalos y «familia» a toda la cascada, tenemos que la distribución del número de hijos se rige por el conocido proceso de nacimiento y muerte (Harris, 1963).

El resultado fundamental es la existencia de un valor crítico de 〈N〉. Este hecho fue descubierto por Irénée Bienaymé en 1845 (véase Heyde y Seneta, 1977) y merece llamarse Efecto Bienaymé.

El valor 〈N〉 = 1 es crítico en el sentido de que el número N(m) de la descendencia presente en la m-ésima generación se rige por la alternativa siguiente. Si 〈N〉 ≤ 1, es casi seguro que, a la larga, la familia acaba por extinguirse, en el sentido de que la cascada acaba dando un conjunto vacío. Si, por el contrario, 〈N〉 > 1, la línea familiar de cada grumo tiene una probabilidad no nula de prolongarse durante un número infinito de generaciones. En este caso, la coagulación aleatoria da un polvo aleatorio en la recta.

SIGNIFICADO DE LA DIMENSIÓN DE SEMEJANZA. Como el cociente log N(m)/log (1/r) es ahora aleatorio, el concepto de dimensión de semejanza requiere pensar un poco más sobre el tema. La relación casi segura,

lim_m→∞log N(m)/log (1/r^m) = log 〈N〉/log (1/r),

sugiere una dimensión de semejanza generalizada

D^* = log 〈N〉/log (1/r) = E − log p/log r.

Con esta D^* la condición de existencia de un conjunto final no vacío, 〈N〉 > 1, se expresa en una forma muy razonable: D^* > 0. Cuando D^* > 0, se tiene D = D^*. Una aplicación formal de esta fórmula para 〈N〉 < 1 nos daría D ≤ 0, pero de hecho la dimensión del conjunto vacío es siempre D = 0.

Coágulos encajados con D decreciente

Vamos a construir una serie de coágulos aleatorios de dimensiones D decrecientes, encajados cada uno en el anterior.

Hay un paso preliminar independiente de D: a cada remolino de cualquier orden se le asigna un número aleatorio U comprendido entre 0 y 1. Sabemos ya (capítulo 21) que todos estos números en su conjunto equivalen a un solo número que mide la contribución del azar. A continuación se escoge la D y se introduce en la última fórmula escrita para obtener un umbral de probabilidad, p. Finalmente, la coagulación se basa en el siguiente «proceso de decimación fractal». Siempre que U > p, el remolino es «eliminado» y se convierte en suero, y la misma suerte corren todos sus subremolinos. Y siempre que U ≤ p, el remolino sobrevive, y sigue participando del proceso de coagulación.

Este método permite seguir todas las características del coágulo, el suero y todos los demás conjuntos interesantes en función de una dimensión que varía continuamente. Basta con mantener fijos todos los números aleatorios U, mientras p disminuye de 1 a 0 y D disminuye de 3 a 0.

Dados los coágulos Q₁ y Q₂, correspondientes a las probabilidades P₁ y P₂ < P₁, con dimensiones D₁ y D₂ < D₁, la transformación de Q₁ en Q₂ ⊂ Q₁ puede llamarse «decimación fractal relativa» de probabilidad relativa P₂/P₁ y dimensión relativa D₂ − D₁. Para llevar a cabo directamente una decimación relativa, se buscan los remolinos de lado 1/b pertenecientes a Q₁ y se los deja sobrevivir con la nueva probabilidad P₂/P₁. A renglón seguido se procede de modo análogo con los remolinos supervivientes de lado 1/b², etc. Si por decimaciones sucesivas obtenemos una sucesión Q₁, Q₂, …, Q_g, las probabilidades relativas se multiplican y las dimensiones relativas se suman… hasta que el valor de la suma es menor que cero, y Q es el conjunto vacío.

Coagulación de Hoyle para las galaxias

La coagulación constreñida tiene un homólogo espacial que puede servir como realización del modelo de coagulación de Hoyle para la distribución de galaxias, láminas 313 y 314.

La disipación turbulenta de Novikov-Stewart implica un proceso de coagulación

La coagulación espacial aleatoria se plantea también, sin saberlo, en un modelo muy primitivo de la intermitencia de la turbulencia. Novikov y Stewart (1964) suponen que la distribución espacial de la disipación es generada por una cascada: cada estadio toma el precoágulo del estadio anterior y lo coagula un poco más, en N pedazos más pequeños, con una razón r. Véanse las láminas 315 a 318.

Se trata de un modelo muy tosco, más aún que el de Berger y Mandelbrot (1963) para ciertos ruidos excedentes (capítulos 8 y 31). Despertó poca atención y poca adhesión, y por tanto no fue continuado ni desarrollado. Pero el desdén con que fue recibido no está justificado. Mis investigaciones revelan que muchas características de modelos más refinados, pero más complicados, están ya presentes en el proceso de coagulación.

QUESO. Aunque no deba tomarse literalmente la imagen sugerida por el término coagulación, ni por el término complementario suero, podría ser que la formación del queso auténtico fuera consecuencia de una inestabilidad bioquímica, del mismo modo que se supone que la coagulación de Novikov y Stewart es fruto de una inestabilidad hidrodinámica. Sin embargo, no tengo datos para asegurar que los quesos comestibles son también quesos fractales.

Consecuencias del hecho de que los coágulos aleatorios sean figuras «intermedias»

Sabemos que las figuras espaciales estándar con D < 3 (puntos, líneas y superficies) tienen un volumen nulo. Lo mismo vale para los coágulos aleatorios.

El área de los precoágulos presenta también un comportamiento simple. Si D > 2, tiende a infinito. Si D < 2, tiende a cero. Y si D = 2, la coagulación deja dicha área prácticamente constante.

De modo análogo, cuando m → ∞,la longitud acumulada de las aristas de los precoágulos tiende a infinito cuando D > 1 y a cero cuando D < 1.

Estas propiedades relativas a las áreas y volúmenes confirman que las coagulaciones con una dimensión fractal tal que 2 < D < 3 están a medio camino entre una superficie ordinaria y un volumen.

▯ DEMOSTRACIONES. Son de lo más simple si la coagulación está constreñida. El volumen del m-ésimo pregrumo es L³r^3mN^m = L³(r^3−D)^m, el cual → 0 con la escala interna η = r^m. Por lo que respecta al área, el caso D < 2 se resuelve determinando una cota superior. El área del precoágulo de orden m-ésimo es como máximo igual a la suma de las áreas de los remolinos que lo forman, pues esta última incluye también las caras de subremolinos que se neutralizan por ser comunes a coágulos adyacentes. Como el área de cada remolino de orden m-ésimo es 6L²r^2m, el área total es como máximo 6L²r^mN^m = 6L²(r^2−D)^m. Cuando D < 2, esta cota superior tiende a 0 para m → ∞ que demuestra lo que pretendíamos. En el caso D > 2, obtenemos una cota inferior si observamos que la superficie de la unión de los remolinos de m-ésimo orden contenidos en el precoágulo de orden m-ésimo contiene al menos un cuadrado de lado r^m y área r^2m que está contenido en el pregrumo de orden (m − 1)-ésimo y no puede ser borrado. Por tanto, el área total es mayor o igual que L²r^2mN^m−1 =(L²/N)(r^2−D)^m que → ∞ con m. Finalmente, para D = 2 ambas cotas son finitas y positivas. ▮

Las D de las secciones fractales: regla de la suma de las codimensiones

Pasamos a estudiar un tema que hemos citado ya en capítulos anteriores y que ahora estamos preparados para abordar explícita y plenamente en un caso especial.

Recordemos, para empezar, una propiedad estándar de la geometría euclídea plana: si la dimensión D de una figura satisface D ≥ 1, y su intersección con una línea es no vacía, entonces el valor «típico» de su dimensión es D − 1. Así, por ejemplo, una sección lineal no vacía de un cuadrado (D = 2) es un segmento, de dimensión 1 = D − 1. Y la intersección de una línea con otra línea (D = 1) es un punto, de dimensión 0 = 1 − 1, excepto en el caso de que ambas líneas coincidan.

Y, en general, las reglas geométricas estándar relativas al comportamiento de la dimensión para las intersecciones se resumen del modo siguiente: si la suma de las codimensiones C = D − E es menor que E, dicha suma es la codimensión típica de la intersección; en caso contrario, la intersección es típicamente vacía. (Animamos al lector a que compruebe este enunciado para distintas configuraciones de rectas y planos en el espacio).

Es una suerte que esta regla valga también para las dimensiones fractales. Gracias a ello, muchos razonamientos relativos a los fractales son más simples de lo que se podría esperar de entrada. Pero hay que tener presentes las numerosas excepciones. En particular, vimos en el capítulo 14 que, si cortamos un fractal no aleatorio F por una recta o un plano con una orientación convenientemente escogida, la dimensión de dicha sección no siempre es deducible de la dimensión de F. Pero, en este aspecto, los fractales aleatorios son más simples.

Las D de las secciones de las coagulaciones aleatorias

Para demostrar la regla fundamental en el caso de coágulos fractales, consideremos las trazas (cuadrados y segmentos) que dejan los remolinos y subremolinos de la cascada de grumos en una cara o una arista del remolino inicial de lado L. Cada paso de la cascada sustituye un trozo de pregrumo por un número de piezas que se determina por un proceso de nacimiento y muerte. Designemos por N₁(m) el número de la descendencia de la m-ésima generación alineada sobre una arista del remolino inicial. Según resultados clásicos, de los que ya hemos hecho uso a lo largo de este capítulo, se tiene que N₁(m) se rige por la siguiente alternativa. Cuando 〈N₁〉 = Nr² ≤ 1, esto es, D ≤ 2, es casi seguro que la familia acaba a la larga por extinguirse, con lo que la arista acaba vaciándose, y por tanto su dimensión es cero. En cambio, cuando 〈N₁〉 > 1, esto es, D > 2, la línea de descendencia de cada remolino tiene una probabilidad no nula de prolongarse durante un número infinito de generaciones. Y la dimensión de semejanza es D − 2, debido a la relación casi segura

lim_m→∞log N₁ (m)/log (1/r^m) = log 〈N₁〉 log(1/r) = D − 2.

Las trazas bidimensionales de los remolinos obedecen al mismo argumento, si cambiamos N₁ por un N₂ aleatorio tal que 〈N₂〉 = Nr. Si 〈N₂〉 ≤ 1, esto es, D ≤ 1, todas las caras de los remolinos acaban por desaparecer a la larga. Si 〈N₂〉 > 1, esto es, D > 1, la dimensión de semejanza es D−1, debido a la relación casi segura

lim_m→∞log N₂ (m)/log (1/r^m) = log 〈N₂〉 log(1/r) = D − 1.

La coagulación constreñida conduce a idénticas conclusiones. Una confirmación adicional de que, por lo que respecta a las intersecciones, la dimensión fractal se comporta igual que la euclídea la tenemos en el hecho de que la intersección de varios fractales coagulados de dimensiones respectivas D_m, y soportados por la misma trama, satisface E − D = ∑ (E − D_m).

La topología de los coágulos: racimos

Aún a riesgo de ponerme pesado, reiteraré que las desigualdades básicas D < 2 para las galaxias (capítulo 9)y D > 2 para la turbulencia (capítulo 10) no son topológicas, sino fractales.

En una coagulación no aleatoria, con E ≥ 2 (capítulos 13 y 14), el diseñador controla también la topología. Entre los coágulos planos conexos tenemos las alfombras de Sierpinski (D > D_T = 1), y entre los coágulos espaciales conexos tenemos las esponjas (D > D_T = 1) y las espumas (D > D_T = 2). Otros coágulos son los σ-racimos o los polvos. Así, para E = 3 y D > 2, que es el caso que interesa en el estudio de la turbulencia, una cascada no aleatoria puede dar D_T = 0 (polvo), D_T = 1 (curvas o σ-curvas) o D_T = 2 (superficies o σ-superficies). Si E = 3 y D < 2, que es el caso interesante en astronomía, D_T puede ser 0 o 1.

Por contra, una cascada de coagulación aleatoria equivale a una mezcla estadística de generadores que casi con toda seguridad impone una cierta topología determinada (final del capítulo 21). Por su propia tosquedad, la coagulación es tan simple que es esencial examinar sus predicciones. El conocimiento actual al respecto es una mezcla de verdades probadas e inferencias a partir de evidencias circunstanciales.

DIMENSIONES CRÍTICAS. La D_T del coágulo cambia bruscamente cuando D cruza ciertos umbrales críticos, que denotaremos por D_crit, D_2crit, …, D_(E−1)crit. En otras palabras, casi nunca se encuentran mezclas de coágulos formadas por porciones con distintos valores de D_T.

El umbral más importante es D_crit. Es al mismo tiempo una cota superior de los valores de D para los que el coágulo es casi con toda seguridad un polvo, y una cota inferior de los valores de D para los que el coágulo se descompone casi con toda seguridad en una colección infinita de pedazos disjuntos, siendo cada uno de éstos un conjunto conexo. Por las razones expuestas en el capítulo 13, dichos pedazos se denominan racimos de contacto.

El siguiente umbral, D_2crit, separa los valores de D para los que el coágulo es una σ-curva de aquellos para los que es una σ-superficie, etc. Cuando la topología del suero empieza a ser también interesante, pueden aparecer nuevos umbrales críticos.

LA DIMENSIÓN DE LOS RACIMOS. Cuando D > D_crit, los racimos de contacto tienen una dimensión fractal D_c < D. Y a medida que D decrece desde E hasta D_crit, D_c disminuye desde E hasta D_cmin > 1, y luego cae repentinamente a 0.

DISTRIBUCIONES DE LOS TAMAÑOS. Las Pr(Λ>λ), Pr(A>a), etc. se obtienen por sustitución de Nr por Pr en las fórmulas del capítulo 13.

COTAS PARA D_crit y D_2crit. Obviamente D_crit ≥ 1 y D_2crit ≥ 2. Y en la sección siguiente se prueba que D_crit tiene una cota superior menor que E, lo que demuestra que las definiciones anteriores no están vacías de contenido.

Además, y con independencia de b, valen cotas inferiores más finas. Se puede demostrar que una condición suficiente para que D_T = 0 es D < 1/2(E + 1). De donde, D_crit > 1/2(E + 1) > 1. Y una condición suficiente para que D_T sea 0 ó 1 es D < E/2 + 1. De donde, D_2crit > E/2 + 1 > 2.

Para E = 3 tenemos que D < 1/2(E + 1) = 2, condición satisfecha (sobradamente) por el valor D = 1 de Fournier-Hoyle, y por el valor empírico D ~ 1,23 de las galaxias. Así pues, un coágulo aleatorio con cualquiera de estas dimensiones es un polvo, tal como queremos.

La condición D < E/2 + 1 da D < 2,5 para E = 3. Este valor umbral resulta ser también la dimensión estimada del soporte de la intermitencia turbulenta. La experiencia nos enseña que las condiciones suficientes obtenidas sin afinar demasiado rara vez son óptimas. Así pues, podríamos concluir que el modelo de coagulación para el soporte de la turbulencia es menos que hojaldrado.

DEDUCCIÓN DE COTAS INFERIORES. Se basan en el hecho, señalado en el capítulo 13, de que los racimos por contacto de la coagulación se forman cuando el contenido de las celdas vecinas forma grumos. Consideremos por tanto la intersección del coágulo con un plano perpendicular a un eje, con una coordenada de la forma αb^−β, siendo α y β enteros. Ya sabemos que, si D > 1, esta intersección tiene una probabilidad positiva de ser no vacía. Sin embargo, la formación de grumos implica un solapamiento entre las contribuciones parciales a dicha intersección de lados opuestos de un lado de longitud b^−β. Si la intersección es no vacía, estas contribuciones son estadísticamente independientes, con lo que su solapamiento tiene la dimensión formal D^* = E − 1 − 2(E − D) = 2D − E − 1.

Cuando D^* < 0, es decir, cuando D < 1/2(E + 1), las contribuciones no se solapan. De lo que se sigue que el coágulo no puede contener ninguna curva continua que cruce nuestro plano, y D_T < 1.

Cuando D^* < 1, esto es, cuando D < E/2 + 1, el solapamiento, si lo hay, no puede contener ninguna curva. De ahí que el coágulo no pueda contener ninguna superficie continua que cruce nuestro plano, y D_T < 2.

Cuando D^* < F, con F > 1, es decir, cuando D < 1/2(E + 1 + F), el mismo argumento sirve para excluir la posibilidad de una hipersuperficie de dimensión D_T = F.

Aceptados estos resultados, el resto de la demostración de las desigualdades anteriores es inmediato: cuando el coágulo contiene una curva (o una superficie), cualquier punto P de la misma está contenido en una caja de lado b^−β, que es intersecada por la curva (o superficie) en algún punto (o curva). Se descubre que, casi con toda seguridad, tal punto (o curva) no existe cuando D < 1/2(E + 1) (o D < E/2 +1).

Racimos fractales percolantes

Para seguir con esta discusión topológica es mejor emplear el vocabulario propio de la percolación. Según la definición del capítulo 13, se dice que una figura trazada en el interior de un cuadrado o un cubo percola si contiene una curva conexa que una dos lados opuestos del cuadrado o dos caras opuestas del cubo. La percolación se plantea normalmente en el contexto de Bernouilli discutido en los capítulos 13 y 14. Pero surge también el mismo problema en el contexto de los fractales aleatorios. Aquí lo plantearemos para coágulos aleatorios.

El hecho fundamental es que, si una figura es un σ-racimo, percola si lo hace uno de sus racimos por contacto. Cuando los racimos por contacto son fractales y sus longitudes siguen una distribución hiperbólica sin escalas preferidas, la probabilidad de percolación es independiente del lado del cuadrado, y no degenera a 0 ni a 1. En la percolación de Bernouilli, el «cuando» de la frase anterior se satisface para el estrecho margen p = p_crit En la percolación a través de un coágulo fractal, el margen se amplía hasta D > D_crit Y esta es una diferencia considerable. Sin embargo, la comprensión de la percolación de Bernouilli sirve para entender mejor la percolación de los coágulos, y viceversa.

UNA COTA SUPERIOR DE LA D_crit. Razonaré ahora que, si b ≥ 3, D_crit cumple que b^Dcrit > b^E + 1/2b^E−1. Concretando más, cuando N es fijo (coagulación constreñida), esta condición hace que la percolación sea casi segura. En la coagulación sin ligaduras, esta condición asegura que la probabilidad de que no haya percolación es positiva, aunque pequeña.

Consideremos en primer lugar el caso de un N no aleatorio. La condición más restrictiva b^E − N ≥ 1/2b^E−1 − 1 implica que no hay ninguna posibilidad de que cualquier cara que separe dos celdas del pregrumo no sobreviva. Aun en el peor de los casos, suponiendo que todos los subremolinos que perecen se alinearan sobre dicha cara, su número es tan pequeño que es seguro (no casi, sino absolutamente) que ningún camino llegará a desconectarse. Si se impone la condición más débil b^E − N ≥ 1/2b^E−1, el mismo resultado ya no es absolutamente seguro, sino casi seguro. La coagulación resultante estará formada por hojas que envuelven huecos separados entre sí y llenos de suero. Dos puntos del suero sólo pueden conectarse si están en el mismo hueco. La topología es, con casi toda seguridad, la de una alfombra de Sierpinski, o la de una espuma (capítulo 14).

Si se aplica la misma condición a la coagulación sin ligaduras, la no percolación ya no es un suceso imposible, sino improbable.

Examinemos ahora ejemplos numéricos con E = 2. Cuando b = 3, la más débil y útil de las condiciones anteriores nos da N > 7,5, que tiene sólo una solución N = 8 (¡el valor correspondiente a la alfombra de Sierpinski!). A medida que b → ∞, la cota superior anterior a la D_crit se va acercando cada vez más a 2.

COTA INFERIOR PARA D_crit. Cuando b >> 1, D_crit > E + log_bp_crit, donde p_crit es la probabilidad crítica de la percolación de Bernouilli. Esta cota se basa en que el primer paso de una coagulación fractal aleatoria equivale a embaldosar un suelo de Bernouilli con unas baldosas cuya probabilidad de ser conductoras es b^D−E. Si esta probabilidad es menor que p_crit la probabilidad de que el suelo sea conductor es pequeña. Y si lo es, es probable que se deba a una sola hilera de baldosas conductoras. El segundo paso de la coagulación fractal aleatoria construye un suelo de Bernouilli sobre cada baldosa conductora del primer paso, con la misma probabilidad b^D−E. Y es muy probable que este paso destruya el camino percolante.

Cuando b → ∞ la nueva cota tiende a E, y en su dominio de validez (b > 1) supera la cota 1/2(E + 1). Por tanto, D_crit → E.

LÁMINAS 313 y 314. Realización del modelo de Hoyle (dimensión D = 1) por coagulación aleatoria en una parrilla.

En el modelo de Hoyle (capítulo 9) una nube de gas de muy baja densidad colapsa varias veces para formar cúmulos de galaxias, galaxias y así sucesivamente. La descripción de Hoyle es, sin embargo, demasiado esquemática, y para su realización geométrica efectiva hay que añadir algunas suposiciones concretas. En estas láminas se presenta una proyección plana de la realización más simple.

FIGURA 313

FIGURA 313. Un cubo iniciador de lado l se subdivide en 5³ = 125 subcubos de lados 5^−l los cuales se subdividen a su vez y así sucesivamente hasta 125^k subcubos de k-ésimo orden, de lado 5^−k cada uno de ellos. En el k-ésimo estadio de la cascada, la materia contenida en un subcubo de (k − l)-ésimo orden se concentra en 5 subcubos de orden k-ésimo, que llamaremos k-pregrumo. La coagulación de Hoyle reduce siempre la dimensión de D = 3 a D = 1.

En esta lámina se representan superpuestos los tres primeros estadios, y se emplean tonos de gris cada vez más oscuros para indicar densidades crecientes del gas. Comparada con Hoyle (1975, pág. 286) esta lámina puede parecer un tanto tosca. Pero se ha dibujado cuidadosamente a escala porque los temas relacionados con la dimensión requieren una gran precisión.

Como presentamos una proyección plana de una coagulación, no es raro que dos cubos se proyecten sobre el mismo cuadrado. En el límite, no obstante, las proyecciones de dos puntos casi nunca coinciden. El polvo es tan poco denso que el espacio es prácticamente transparente.

FIGURA 314

FIGURA 314. Aquí se representa sólo el cuarto estadio de la coagulación (con una semilla distinta). No queda ningún rastro de la parrilla subyacente, lo que es una suerte porque en la naturaleza tampoco hay evidencias de una tal parrilla (capítulo 27). En este ejemplo, la parte superior del remolino, que queda cortado por el borde de la página, está vacía.

Control de la lagunaridad. El concepto de lagunaridad, que se presenta en el capítulo 34, se puede aplicar directamente a la coagulación aleatoria sobre la recta y la coagulación de Hoyle. Si el valor N = 5 de Hoyle se sustituye por el valor «real» de Fournier de N = 10²² (figura 139), la lagunaridad de la coagulación aleatoria obtenida resulta muy pequeña.

LÁMINAS 315 a 318. Coagulaciones aleatorias de Novikov-Stewart en una parrilla plana (dimensiones comprendidas entre D = 1,5936 y D = 1,9973) seguidas de percolación.

FIGURA 315

FIGURA 316

FIGURA 317

FIGURA 318

La cascada de Novikow-Stewart nos sugiere una idea general de cómo la disipación turbulenta se concentra en un volumen relativamente pequeño. La idea básica es muy parecida a la cascada de Hoyle que se ilustra en las dos láminas anteriores, aunque los valores de la dimensión fractal D son muy distintos. Para las galaxias D ~ 1, mientras que para la turbulencia D > 2, con D entre 2,5 y 2,6, es una buena conjetura. Estas láminas ilustran varios valores distintos de la dimensión, con objeto de dar una mejor idea genérica del proceso de coagulación. En los cincos casos tomamos r = 1/5 y

N = 5×24,

N = 5×22,

N = 5×19,

N = 5×16 y

N = 5×13,

respectivamente. Por tanto, los valores de las dimensiones son

D = 1 + log 24 / log 25 = 2,9973;

D = 2,9426;

D = 2,8505;

D = 2,7227 y

D = 2,5936

El suero se representa en gris y el coágulo en blanco y negro. La parte blanca es un racimo de contacto precolante, a saber, las partes conexas que tocan tanto la parte superior como la inferior del gráfico. La parte negra reúne los racimos de contacto restantes.

Dado que en la turbulencia se tiene D > 2, estos coágulos son esencialmente opacos y (al contrario que los de Hoyle) estas láminas representan sus secciones planas, cuyas dimensiones son

D = 1,9973;

D = 1,9426;

D = 1,8505;

D = 1,7227 y

D = 1,5936

La esquina inferior derecha de la lámina ilustra el caso D ~ 1,9973, que carece de detalles interesantes. El resto de la lámina ilustra el caso D ~ 1,9426.

El programa generador y la semilla son los mismos en los cinco casos, y se puede advertir la desaparición progresiva de los grises. Se empezó amontonando al azar los 25 subrremolinos de cada remolino. Luego, para valores enteros sucesivos de 5^D − N, se «agrisaron» los primeros 25 − N subrremolinos del montón.

Para las dos dimensiones menores no hay percolación. Con N = 19 hay un poco de negro y mucho blanco. Unas pocas semillas ya dan percolación para N = 18. Pero los estadios representados en esta ilustración son demasiado bajos para permitir una estimación fiable de D_crit