Este capítulo pretende familiarizar al lector con una teoría que evolucionó independientemente de los fractales, pero que está siendo invadida por éstos. Su nombre más corriente es «teoría de los atractores extraños y de la evolución caótica (o estocástica)», aunque, como espero, a lo largo del presente capítulo se harán evidentes las razones por las que sugiero el nuevo nombre que le he dado en el título.

Su relación con los fractales bastaría para justificar que dicha teoría sea mencionada en este ensayo, pero pienso que hay razones para dedicarle todo un capítulo. Una de ellas, de tipo práctico, es que no hace falta un tratamiento demasiado específico, ya que varios de los temas principales se pueden presentar como una simple reinterpretación de los resultados de los capítulos 18 y 19.

En segundo lugar, diversas propiedades de la geometría fractal de la naturaleza se clarifican al contrastarlas con la teoría de los atractores fractales. En efecto, mi trabajo se ocupa principalmente de figuras en el espacio real que se pueden ver, por lo menos al microscopio, mientras que la teoría de los atractores se ocupa en última instancia de la evolución temporal de puntos pertenecientes a un espacio representativo, invisible y abstracto.

Este contraste resulta especialmente sorprendente en el contexto de la turbulencia: la intermitencia turbulenta fue el primer gran problema que abordé (en 1964) haciendo uso de formas primitivas de las técnicas frac- tales, y (de modo completamente independiente) la teoría de los atractores extraños ño despegó en serio hasta el estudio de la turbulencia por Ruelle y Takens (1971). Por el momento ambos enfoques no se han encontrado, pero es inevitable que lo hagan pronto.

Los interesados en la sociología de la ciencia encontrarán apetecible el hecho de que, mientras mis estudios de casos que conectaban monstruos matemáticos con formas físicas reales encontraron cierta resistencia, las figuras monstruosas de los atractores abstractos fueron aceptadas con ecuanimidad.

Una tercera razón para mencionar los atractores fractales viene sugerida por el hecho de que las evoluciones correspondientes parecen «caóticas» o «estocásticas». Como se verá en los capítulos 21 y 22, muchos estudiosos cuestionan la inclusión de lo aleatorio en la ciencia; con los atractores fractales nace la esperanza de que dicho uso quede justificado.

Por fin, aquellos que hayan aceptado desde hace muchos capítulos (o uno o dos ensayos) mi pretensión de que muchas facetas de la naturaleza sólo pueden describirse con la ayuda de ciertos conjuntos que anteriormente tenían fama de patológicos quizá estén impacientes por pasar del «cómo» al «por qué». Los artículos de divulgación han demostrado en muchos casos que no es difícil endulzar los aspectos geométricos de los capítulos anteriores y hacerlos más fácilmente digeribles. Sin embargo, una de las cosas que quisiera transmitir al lector es un cierto gusto por los fractales, por muy amargo que pueda resultar en primera instancia para los científicos ya formados. Además, como explico en el capítulo 42, pienso que las seudoexplicaciones endulzadas nunca son convincentes. Por tanto, la explicación se ha bajado de nivel, excepto en aquellos casos en que, como en el capítulo 11, una explicación convincente era asequible. Además, sospecho que aparecerán muchas explicaciones auténticamente nuevas cuando los atractores fractales se conviertan en el fundamento de la geometría fractal de las formas naturales visibles.

Como las transformaciones que tienen atractores son no lineales, es probable que los fractales visibles no sean autosemejantes. Esto es perfecto: mi empleo de homólogos fractales de la recta para tratar fenómenos regidos por ecuaciones no lineales resultaba paradójico. Los fractales escalantes que explican bien un fenómeno natural serían aproximaciones locales de fractales no lineales.

Este capítulo se centra en una observación debida a Poincaré que permaneció largo tiempo olvidada: las «órbitas» de los sistemas dinámicos no lineales pueden ser «atraídas» por conjuntos extraños que identifico con fractales no lineales.

Examinemos en primer lugar el atractor más simple: un punto. La «órbita» seguida por el movimiento de una bolita en un embudo empieza con un balanceo que depende de la posición y velocidad iniciales, pero a la larga converge hacia el vértice del embudo; si la bola es mayor que la abertura del embudo, acabará por detenerse en el fondo. El vértice es, pues, un punto de equilibrio estable, o punto fijo estable, de la bola. En lo que es una bella terminología descriptiva alternativa (que hay que guardarse de interpretar en términos antropocéntricos), el fondo del embudo se denomina punto atractor.

Un sistema físico puede tener también un círculo (o una elipse) como atractor estable. Por ejemplo, se cree (y se desea fervientemente, aunque nadie vivirá lo bastante como para que ello sea motivo de preocupación) que el sistema solar es estable, en el sentido de que, si algo perturbara la órbita de la Tierra, ésta sería en última instancia «atraída» de nuevo hacia su trayectoria actual.

En general, un sistema dinámico se suele definir del modo siguiente: su estado en el instante t es un punto σ(t) de la recta, del plano o de un «espacio de fases» euclídeo de muchas dimensiones, R^E, y su evolución entre los instantes t y t + Δt viene determinada por reglas que no dependen explícitamente del valor de t. Cualquier punto del espacio de fases puede tomarse como estado inicial σ(0) en t = 0, y de él parte una órbita σ(t) para todos los t > 0.

La diferencia principal entre tales sistemas estriba en la distribución geométrica de σ(t) para valores de t grandes. Se dice que un sistema dinámico tiene un atractor si existe un subconjunto propio A del espacio de fases R^E, tal que para casi todos los puntos iniciales σ(0) y para t grande, σ(t) está próximo a algún punto de A.

Por otra parte, una bola puede estar suspendida en equilibrio inestable sobre la punta de un lápiz. Cuando la posición inicial está cerca de este punto de equilibrio, parece como si la bola fuera impulsada hacia fuera, antes de alcanzar el equilibrio estable en algún otro lugar.

El conjunto de todos los estados de equilibrio inestable, junto con sus puntos límite, se llama repulsor.

Muchas veces los atractores y repulsores intercambian sus papeles, invirtiendo las ecuaciones. En el caso gravitatorio basta con invertir el sentido de la gravedad. Considérese, por ejemplo, una lámina horizontal con una depresión en ambos sentidos. Si tenemos una bola en la cara superior de la hoja y la gravedad tira hacia abajo, denotemos por A la depresión atractora y por R la repulsora. Si a continuación se pone la bola en la cara inferior de la hoja y se invierte el sentido de la gravedad, A y R intercambian sus papeles. Este tipo de intercambios jugará un papel importante en este capítulo.

La mayor parte de los libros de texto de mecánica se ocupan de sistemas dinámicos cuyos atractores son puntos, figuras cuasicirculares u otras figuras euclídeas. Pero estas son excepciones raras. El comportamiento de la mayoría de sistemas dinámicos es mucho más complejo: sus atractores o repulsores tienden a ser fractales. En las secciones que siguen se describen ejemplos en los que el tiempo varía de forma discreta, con Δt = 1.

UN POLVO ATRACTOR. LA α DE FEIGENBAUM. El ejemplo más simple se obtiene con transformaciones cuadráticas (capítulo 19). Como preludio, considérese una vez más otra representación del polvo de Cantor C con N = 2 y r < 1/2, extendido sobre [−r/(1 − r), r/(1 − r)]. Este C es el límite de los C_n definidos como conjuntos de puntos de la forma ± r ± r² ± … ± rⁿ. Al pasar de n a n + 1, cada punto de C_n se bifurca en 2, y C es el resultado de una infinidad de bifurcaciones.

Interpretando a P. Grassberger, el atractor A_λ de x → λx (1 − x) para λ real es análogo a C_n, pero con dos razones de semejanza distintas, una de las cuales es la 1/α ~ 0,3995… de Feigenbaum (1981). Después de una infinidad de bifurcaciones, este atractor es un polvo fractal A con D ~ 0,538.

«CAOS». Ningún punto de A es visitado dos veces en un intervalo de tiempo finito. Muchos autores llaman «caótica» a la evolución sobre atractores fractales.

▯ ARBOLES AUTOAFINES. Si se yuxtaponen los A_λ en el plano (x, λ), se obtiene un árbol. Como δ ~ 4,6692 ≠ α, este árbol es asintóticamente autoafín con residuo. ▮

COMENTARIO. Lo ideal sería que la teoría se concentrara en sistemas dinámicos intrínsecamente interesantes y realistas (aunque simples), cuyos atractores sean fractales bien comprendidos. La literatura sobre atractores extraños —aunque sumamente importante— dista mucho de satisfacer este ideal: normalmente sus fractales no se comprenden del todo, pocos son intrínsecamente convincentes y la mayoría no son soluciones a problemas bien motivados.

Esto me llevó a idear «sistemas dinámicos» apropiados, o lo que es lo mismo, a plantear nuevas preguntas para obtener viejas y gratas respuestas. Esto es, me inventé problemas cuyas soluciones fueran fractales bien conocidas. Y aunque en cierto modo sea sorprendente, dichos sistemas son de interés.

En el capítulo 18 se describen los conjuntos L de las cadenas de Poincaré como los menores conjuntos autoinversos y conjuntos límite. Esta última propiedad se puede reformular como sigue: dado un punto inicial arbitrario P₀, para cada punto de L hay una sucesión de inversiones tal que las imágenes de P₀ convergen hacia dicho punto. Supongamos ahora que dicha sucesión de inversiones es elegida por un proceso independiente de la posición actual y las posiciones pasadas de P. Bajo unas condiciones muy poco restrictivas, se puede esperar, y de hecho se demuestra, que las sucesiones resultantes de puntos P sean atraídas por L. De este modo, la enorme literatura relativa a los grupos generados por inversiones se puede interpretar en términos de sistemas dinámicos.

Mi búsqueda de nuevos sistemas con atractores fractales interesantes me llevó a considerar sistemas conocidos con atractores estándar en el sentido geométrico, que tenían, sin embargo, repulsores interesantes. Es posible invertir los papeles de estos dos conjuntos, haciendo que el tiempo transcurra hacia atrás, siempre y cuando el sistema dinámico en consideración tenga inverso (es decir, que las órbitas no se crucen ni confluyan) de modo que el conocimiento de σ(t) determine σ(t') para t' < t. Sin embargo, los sistemas concretos en los que queremos invertir el tiempo son distintos. Sus órbitas son como los ríos: la trayectoria está unívocamente determinada en sentido descendente, pero en sentido ascendente cada bifurcación implica una decisión especial.

Probemos a invertir, por ejemplo, la transformación f(x) en V que nos da el polvo de Cantor en el capítulo 19. Para x > 1,5 hay definidas dos imágenes inversas, y se podría estar de acuerdo en transformar todos los x > 1,5 en x = 1 /2. Análogamente, x → λx(1 − x) tiene dos inversas posibles. En ambos casos, la inversión de la transformación implica elegir entre dos funciones. En otros ejemplos el número de alternativas es aún mayor. De nuevo, queremos que la elección se realice mediante un proceso aparte. Estas ideas apuntan a los sistemas dinámicos generalizados, que introduciremos y describiremos en la sección siguiente.

Supondremos que una de las coordenadas del estado σ(t) —a la que llamaremos índice determinante y denotaremos por σ^†(t)— evoluciona independientemente del estado de las E − 1 coordenadas restantes —que denotaremos por σ^*(t)— mientras que la transformación de σ^*(t) en σ^*(t + 1) depende a la vez de σ^*(t) y de σ^†(t). En los ejemplos que yo he estudiado preferentemente, la transformación σ^†(t) → σ^†(t + 1) se elige entre un conjunto finito de G posibilidades distintas J_g, que se pueden seleccionar de acuerdo con el valor de una cierta función g(t) = γ[σ^†(t)], a valores enteros. Así pues, estudié la dinámica en el espacio producto del espacio σ^* por un conjunto indicial finito.

De hecho, en los ejemplos que han motivado esta generalización la sucesión g(t) o es aleatoria o se comporta como tal. Aunque este ensayo no aborda el azar hasta el próximo capítulo, dudo que ésta sea una dificultad insoslayable. Más serio es el hecho de que los sistemas dinámicos sean el mismísimo modelo del comportamiento plenamente determinista, ¡por lo que constituyen un terreno prohibido para el azar! No obstante, los efectos de éste pueden ser introducidos sin necesidad de postularlo efectivamente, tomando para g(t) el valor de un proceso suficientemente ergódico. Se puede tomar, por ejemplo, un número irracional β y hacer que g(t) sea la parte entera de σ^†(t) = β^†σ^†(0). Los detalles necesarios son en principio simples pero sofisticados, y no los especificaremos aquí.

Los estudiosos de los atractores extraños sugieren el siguiente argumento doble: (A) Dado que los sistemas dinámicos con atractores estándar no sirven para explicar la turbulencia, quizá ésta se pueda explicar por medio de atractores topológicamente «extraños». (Recordemos mi razonamiento del capítulo 11, de que si una ecuación diferencial tiene singularidades no estándar, uno debería probar con las singularidades fractales.) (B) Los atractores de sistemas ridiculamente simples, tales como z → λz(1 − z) para λ real y z en [0,1], son extraños y en muchos aspectos característicos de sistemas más complejos y más realistas. Por tanto, no puede caber la menor duda de que los atractores topológicamente extraños son la regla.

TODOS LOS ATRACTORES «EXTRAÑOS» CONOCIDOS SON FRACTALES. Se ha evaluado la D de muchos atractores «extraños», y en todos los casos D > D_T. Por tanto, estos atractores son conjuntos fractales. Para muchos fractales que son atractores extraños, la D no es una medida de la irregularidad, sino que mide el apilamiento de un conjunto de curvas o superficies diferenciables —o lo que vendría a ser una variante de la fragmentación (capítulo 13).

S. Smale introdujo un famoso atractor, conocido como solenoide. Lo hizo en dos etapas. La definición original era puramente topológica, y dejaba la D sin definir, pero en una revisión se introdujo una definición métrica (Smale 1977, pág. 57). Para esta revisión, se evaluó la D (Mandelbrot 1978b), que se introdujo así en el estudio de los atractores extraños. En el caso del atractor de Saltzman-Lorenz con v =40, σ = 16 y b = 4, M. G. Velarde y Ya. G. Sinai obtuvieron independientemente el valor D = 2,06 (comunicación oral). Esta D es superior a 2, aunque no mucho, y esto significa que este atractor no es una superficie estándar, pero no se aleja mucho de ellas. Morf y Fujisaka (1980) confirman mi D para el atractor de Smale y la D del atractor de Saltzman-Lorenz. Para la transformación de Hénon, con a = 1,4 y b = 0,3, encuentran D = 1,26. Se están preparando otros artículos sobre el mismo efecto.

A LA INVERSA. La pregunta de si todos los atractores fractales son o no extraños es una cuestión semántica. Un número cada vez mayor de autores está de acuerdo conmigo en que para la mayoría de fines, un atractor es extraño si es fractal. Ésta es una actitud saludable, si «extraño» se toma como sinónimo de «monstruoso», «patológico» y otros epítetos que en algún momento se aplicaron a los fractales.

Pero a veces «extraño» se toma en un sentido técnico, ▯ tan excluyente que el atractor de Saltzman-Lorenz no es «extraño», sino «extraño- extraño». ▮ A la luz de esto, en la «extrañeza» de un atractor intervienen propiedades topológicas no estándar, «superpuestas» a propiedades fractales no estándar. Una curva cerrada sin puntos dobles no es «extraña» en este sentido, por muy arrugada que esté; de ahí que muchos atractores fractales estudiados por mí no sean extraños.

Con esta definición de extraño, el razonamiento de la sección anterior deja de ser convincente. Pero vuelve a serlo otra vez si la extrañeza deja de ser un concepto topologico para convertirse en un concepto fractal. Así pues, yo creo que los que definen «extraño» como «fractal» merecen ganar. Y como están efectivamente, ganando, no vale la pena conservar un término cuya motivación desapareció cuando demostré que los fractales no son más extraños que las costas o las montañas. En cualquier caso, no puedo ocultar una cierta antipatía personal hacia el calificativo «extraño».

LÁMINAS 282 y 283. Atracción hacia fractales.

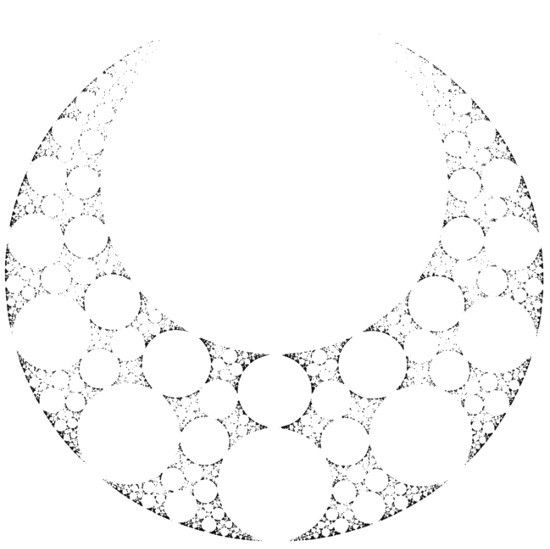
FIGURA 282

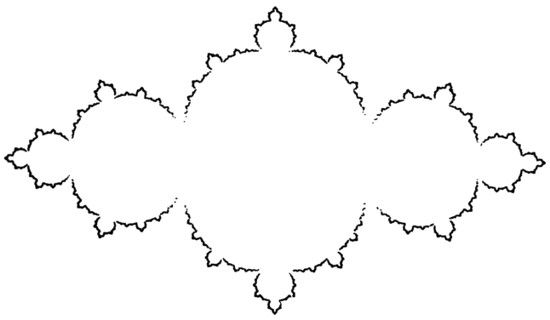
FIGURA 283

Estas dos figuras ilustran órbitas largas de posiciones sucesivas de dos sistemas dinámicos descomponibles. El Peto del Faraón de la figura 283 es autoinverso (capítulo 18), y es generado por 4 inversiones escogidas de modo que el conjunto límite L sea una colección de circunferencias. El Dragón de San Marco de la figura 282 es autocuadrático (capítulo 19) y es generado por las dos inversas de x → 3x(1 − x).

El índice determinante se escoge entre 4 posibilidades, respectivamente 2, y se emplea un algoritmo pseudoaleatorio que se repite 64.000 veces. Las primeras posiciones no se han representado.

Las regiones próximas a las cúspides y a las autointersecciones se rellenan muy lentamente.

20 Atractores fractales y evoluciones fractales («caótica»)

20
Atractores fractales y evoluciones fractales («caótica»)