En este capítulo se abordan dos familias muy simples de transformaciones y se investigan ciertos conjuntos fractales invariantes bajo dichas transformaciones, las cuales pueden servir como generadores de los mismos.

En primer lugar, una transformación quebrada de la recta real servirá para profundizar nuestra comprensión del polvo de Cantor. Quizá estas observaciones hubieran podido incluirse en el capítulo 8, pero aquí se apreciará mejor su valor.

En particular, nos servirán para apreciar el efecto de las transformaciones cuadráticas, tanto reales como complejas, de la forma x → f^*(x) = x₂ − μ, donde x y μ son números reales, o z → f^*(z) = z₂ − μ, donde z = x + iy y μ. son números complejos.

El caso elemental μ = 0 es geométricamente trivial, pero otros valores de μ llevan asociada una riqueza fractal extraordinaria, que en buena parte fue revelada por vez primera en Mandelbrot (1980n).

Las figuras invariantes en cuestión se obtienen como subproducto del estudio de la iteración, esto es, de la aplicación repetida de una de las transformaciones anteriores. Denotaremos por x₀ o por z₀ los valores iniciales, mientras que x_k o z_k denotarán las imágenes respectivas después de k iteraciones de la transformación f^*.

En líneas generales, se puede decir que la iteración se estudió en tres estadios. El primero, que se ocupaba del caso complejo, estuvo dominado por Pierre Fatou (1878-1929) y por Gaston Julia (1893-1978). Sus publicaciones son obras maestras del análisis complejo clásico, muy admiradas entre los matemáticos, aunque demasiado difíciles para tomarlas aquí como punto de partida. En mi trabajo, del que este capítulo sólo es un esbozo muy conciso, se hacen intuitivos algunos de sus hallazgos fundamentales, combinando análisis, física y representación gráfica. Se pone así de manifiesto una gran cantidad de hechos nuevos.

El consiguiente resurgir de este campo de investigación hace que las propiedades de iteración sean esenciales para la teoría de los fractales. El hecho de que los resultados de Fatou-Julia no progresaran por sí solos hasta convertirse en el origen de esta teoría nos sugiere que incluso el análisis clásico necesita de la intuición para avanzar, y que los ordenadores pueden ser útiles para este fin.

El estadio intermedio incluye los estudios de P. J. Myrberg sobre la iteración de aplicaciones cuadráticas reales (sobre R), por ejemplo Myrberg (1962), Stein y Ulam (1964), y Brolin (1965).

El estadio actual ignora en gran medida el pasado, y se concentra en las aplicaciones de [0,1] en sí mismo, como se estudia en Gurel y Rossler (1979), Helleman (1980), Collet y Eckman (1980), Feigenbaum (1981), y Hofstadter (1981). La última sección de este capítulo se ocupa del exponente 5 de Grossmann y Thomas (1977) y Feigenbaum (1978): se demuestra que la existencia de 5 se sigue de una propiedad más evidente (fractal) de la iteración en el plano complejo.

Ya sabemos desde el capítulo 8 que el polvo triádico de Cantor C es invariante bajo transformaciones de semejanza con razones de proporcionalidad de la forma 3 Esta autosemejanza es una propiedad vital, aunque no basta para especificar C. En cambio, C está determinado completamente como el mayor conjunto acotado invariante bajo la siguiente transformación no lineal en «V invertida»:

Concretando más, si aplicamos repetidas veces esta transformación del eje real en sí mismo, con x₀ extendido sobre el eje x, los valores finales se reducen a x = ∞ más el polvo de Cantor C. Los puntos fijos x = 0 y x = 3/4 pertenecen a C.

ESBOZO DE UNA DEMOSTRACIÓN DE LA INVARIANCIA DE C. Como para x < 0, f(x) = 3x, las iteraciones de todos los puntos x₀ < 0 convergen directamente a −∞, esto es, sin dejar de cumplirse x_n < 0. Para los puntos x₀ > 1, dicha convergencia directa va precedida por un paso preliminar, pues x_k < 0 para todo k ≥ 1. Para los puntos del hueco 1/3 < x < 2/3 hacen falta 2 pasos preliminares, puesto que x₁ > 0, pero x_k < 0 para todo k ≥ 2. Los puntos de los huecos 1 9 < x < 2/9 o 7/9 < x < 8/9 necesitan de 3 pasos preliminares. Y en general, si un intervalo está acotado por un hueco que tiende a −∞ después de k iteraciones, el tercio central (abierto) de dicho inter- vaio tenderá directamente a −∞ después de la (k + 1)-ésima iteración. Pero resulta que, de todos los puntos de C, ninguno converge hacia −∞.

Para extender estos resultados al polvo de Cantor generalizado con N = 2 y r comprendido entre 0 y 1/2, basta con introducir el r escogido en la fórmula f(x) = {1/2 − |x − 1/2|}/r. Si se quiere obtener cualquier otro tipo de polvo de Cantor, el grafo de f(x) tiene que ser una curva en zigzag apropiada.

Sin embargo, no se dispone de un método comparable para el polvo de Cantor extrapolado a todo el eje real. Éste es un caso especial de una propiedad muy general: normalmente una f(x) no lineal comporta en sí misma una cota superior finita Ω; mientras que, como ya sabemos, todas las transformaciones lineales (semejanzas y afinidades) se caracterizan porque Ω = ∞, y (en caso de que haga falta) un Ω finito se tiene que imponer artificialmente.

Ya sabemos por el capítulo 7 que C es un conjunto muy «delgado», pero el comportamiento de las iteraciones de f(x) nos proporcionará una mejor comprensión de las distinciones entre sus puntos.

Cualquiera podría estar tentado, a primera vista, de pensar que C se reduce a los extremos de los huecos abiertos. Pero la realidad es muy otra, pues C contiene, por definición, todos los límites de sucesiones de puntos extremos de los huecos.

Este hecho no pasa por intuitivo. No me habría extrañado que nuestro maltrecho conocido Hans Hahn hubiera incluido estos puntos límite en su lista de conceptos, cuya existencia sólo se puede imponer por medio de la fría lógica. Pero la presente discusión constituye una prueba intuitiva de que estos puntos límite tienen unas personalidades muy marcadas y diversas.

Así, por ejemplo, el punto x = 3/4, que es invariante según f(x), no cae en el tercio central ni en la frontera de ningún intervalo. Algunas de las imágenes iteradas de los puntos de la forma x = (1/4)/3^k converge a x = 3/4. Además, hay una infinidad de ciclos límite, cada uno de ellos formado por un número finito de puntos. Y C contiene también puntos cuyas imágenes lo recorren indefinidamente.

La función generatriz en V invertida usada en las secciones anteriores se eligió para obtener un resultado ya conocido, pero da al polvo de Cantor una apariencia artificial. A continuación la sustituiremos por

cuya riqueza inesperada ya fue observada por Fatou (1906). Si se cambia el origen y la escala de las x, y se escribe μ = λ²/4 − λ/2, esta función se puede escribir como

Dichas funciones recibirán el nombre de generador cuadrático. Elevar al cuadrado es, naturalmente, una operación algebraica, aunque aquí se le da una interpretación geométrica, y llamaremos conjuntos autocuadráticos a aquellos que son invariantes bajo una transformación cuadrática. La más simple es la que transforma el punto de abscisa x en el punto de abscisa x². En tal caso los puntos autocuadráticos de la recta se reducen a x = 0, x = ∞ y x = 1. Y aunque el añadido del término −μ pueda parecer totalmente inocuo, introduce de hecho unas posibilidades completamente inesperadas, que pasamos a considerar a continuación.

Como la transformación en V invertida nos ha dado como resultado un producto bien conocido, el polvo de Cantor, nos facilitará muchísimo la introducción de un descubrimiento extraordinario, aunque de difusión siempre restringida, de Pierre Fatou. Fatou (1906) supone que λ es real y que λ > 4, y estudia el mayor conjunto acotado de R invariante según f(x). Éste es un pariente próximo del polvo de Cantor al que llamo polvo de Fatou real. No precisa de mayor explicación y se encuentra ilustrado en la lámina 274.

En el plano complejo, el mayor conjunto autocuadrático acotado para los valores de λ, anteriores sigue siendo el polvo de Fatou real.

La curva autocuadrática más simple se tiene para μ = 0, y se trata de la circunferencia |z| = 1. La transformación z → f(z) convierte una cinta que envuelve una vez la circunferencia en una cinta que da dos vueltas a la misma, dejando fijo el «empalme» en z = 1. El máximo dominio acotado y autocuadrático correspondiente es el disco |z| ≤ 1.

Sin embargo, si se introduce un μ ≠ 0 real (láminas 265 y 266), y luego un μ complejo (láminas 271 y 272), se abren las cajas de Pandora de las posibilidades, las curvas fraciales de Julia, tan gratas a la vista como al intelecto.

EL SEPARADOR S. La topología del mayor conjunto acotado autocuadrático depende del lugar que ocupa μ con respecto a una curva ramificada S, descubierta por mí, a la que llamo separador. Es la frontera conexa de la figura en negro de la parte inferior de la lámina 268; se trata de una «lemniscata límite», a saber, el límite para n → ∞ de las curvas algebraicas denominadas lemniscatas, definidas por |f^*_n(0)| = R para un cierto R grande. En la lámina 269 se explica más en detalle la estructura de S.

LOS ÁTOMOS. El dominio abierto interior de S se descompone en una infinidad de componentes conexas para las que propongo el nombre de átomos. Las fronteras de dos átomos dados, o bien son disjuntas o bien sólo tienen un punto en común, que llamaremos «enlace», perteneciente a S.

DIMENSIÓN TOPOLÓGICA. Si μ cae fuera de S, el mayor conjunto acotado autocuadrático es un polvo (de Fatou). Si μ pertenece a S o es un enlace, el conjunto máximo correspondiente es un dominio limitado por una curva autocuadrática. Hay algún μ de S que da lugar a una curva en forma de árbol.

FRACTALES AUTOCUADRÁTICAS. Se dice que estos polvos y curvas son fractales cuando μ ≠ 0, según ha demostrado plenamente Dennis Sullivan en algunos casos, y no me cabe la menor duda de que se podrá probar para todos los demás.

La forma de una curva o un polvo autocuadráticos varía continuamente con μ, por lo que D es necesariamente una función continua de μ.

RAMIFICACIÓN. Si λ pertenece a uno de los discos abiertos de la parte superior de la lámina 269, la curva autocuadrática es un arco simple cerrado (un circuito sin ramificaciones), como en las láminas 265 y 266.

Si λ cae sobre las circunferencias |λ| = 1 o |λ − 2| = 1, o en la región abierta y conexa que las rodea, la curva autocuadrática correspondiente es una red ramificada, con tremas rodeadas por circuitos fractales, como los dragones de la lámina 272.

Si λ cae en las importantísimas moléculas isla, que, como pronto se demostrará, son regiones de no confluencia a 1, la curva autocuadrática es un σ-lazo o un σ-dragón, como el de la parte inferior de la lámina 271. La σ no introduce ningún nuevo lazo.

Un análisis más completo de la dependencia en el parámetro es más fácil si éste es μ. Un μ-átomo puede tener forma de corazón, en cuyo caso es la «semilla» donde se enlaza una infinidad de átomos ovales, ya sea directamente, ya sea por átomos intermedios. Los átomos mutuamente enlazados, junto con los enlaces, forman una «molécula». La cúspide de una semilla nunca es un enlace.

Cada átomo tiene asociado un número entero w, su «periodo». Si μ pertenece a un átomo de periodo w, las imágenes iteradas f_n^*(z)convergen a ∞ o a un ciclo límite estable formado por w puntos. En un átomo de período w, |f_w^*'(z_μ)| < 1, siendo z_μ un punto cualquiera del ciclo límite correspondiente a μ. Sobre la frontera del átomo, |f_w^*'(z_μ)| = 1, siendo f_w^*'(z_μ) = 1 la característica de una cúspide o una «raíz». Cada átomo contiene un punto que llamamos «núcleo», que cumple f_w^*'(z_μ) = 0 y f_w^*(0) = 0.

Los núcleos en el eje real fueron introducidos por Myrberg (véase Myrberg, 1962) y redescubiertos en Metropolis, Stein y Stein (1973). Las transformaciones correspondientes se suelen llamar «superestables» (Collet y Eckman, 1980).

Considerada una ecuación algebraica en μ, la igualdad f_w^*(0) = 0 es de orden 2^w−1. Por tanto, podría haber como máximo 2^w−1 átomos de período w, pero de hecho hay menos, excepto en el caso w = 1. Para w = 2, f₂^*(0) = 0 tiene 2 raíces, pero una de ellas ya es el núcleo de un átomo «antiguo» de periodo 1. En general, todas las raíces de f_m^*(0) = 0 lo son también de f^*_km(0) = 0, donde k es un entero mayor que 1. Nótese además que cada punto racional de la frontera de un átomo de periodo w, definido por la condición f_w^*'(z_μ) = exp(2πim/n), donde m/n es una fracción irreducible menor que 1, lleva implícito un «enlace receptor» listo para conectarse a un átomo de periodo nw. Como consecuencia de ello, algunos nuevos átomos se conectan a enlaces receptores ya existentes. Pero esto no agota todas las posibilidades de nuevos átomos, y a los restantes no les queda otra alternativa que sembrar nuevas moléculas. El número de moléculas es, pues, infinito.

Si μ varía continuamente en una molécula, cada vez que se atraviesa un enlace yendo hacia afuera aparece una bifurcación: w se multiplica por n. Por ejemplo, al aumentar μ tomando valores reales se tiene el doblamiento de período de Myrberg. La inversa de la bifurcación, que se estudia en Mandelbrot (1980n) y se llama confluencia, se detiene al llegar al período de la semilla de la molécula. La molécula continente es la región de confluencia para c = 1 y cada molécula isla es la región de confluencia para c > 1. La forma del dragón o del subdragón correspondiente viene determinada por los valores de f_w^*' (z_μ) y de w/c.

Mi conjetura ▯ basándome en un argumento de «renormalización» ▮ es que cuanto más alejados están de la semilla de su molécula, los átomos tienden cada vez más a tener una forma idéntica.

Como corolario se tiene que la frontera de cada molécula es localmente autosemejante. Y como a pequeñas escalas no es lisa, se trata de una curva fractal.

Esta autosemejanza fractal generaliza un efecto relativo a la bifurcación de Myrberg, descubierto por Grossmann y Thomas y por Feigenbaum. Las anchuras de las intersecciones de retoños cada vez menores con el eje real λ o μ convergen a una sucesión geométrica decreciente de razón 8=4,66920… (Collet y Eckman, 1980). En su forma original, la existencia de δ parece un resultado analítico técnico. Ahora se ha demostrado que es un aspecto de una propiedad más general de los fractales escalantes.

LÁMINA 265. Curvas fractales autocuadráticas con X real.

FIGURA 265

Las figuras de las láminas 265 a 274 se presentan aquí por primera vez, a excepción de algunas reproducidas de Mandelbrot (1980n).

La figura de la izquierda representa los dominios acotados autocuadráticos máximos para λ = 1; 1,5; 2,0; 2,5 y 3,0. La figura central en negro corresponde a todos los valores de λ comprendidos entre 0 y 1.

λ = 1: VENERA.

λ = 3: CURVA DRAGÓN DE SAN MARCO. Tenemos aquí una extrapolación fantástica del perfil de la basílica de Venecia, completada con su reflejo sobre una «Piazza» inundada; la bauticé dragón de San Marco.

La figura de la derecha corresponde a λ = 3,3260680. Es la λ nuclear (según la definición de la pág. 263) que corresponde a w = 2. La figura autocuadrática correspondiente se ha girado 90° para que quepa en la página.

LÁMINA 266. Compuesto de curvas autocuadráticas con λ real.

FIGURA 266

Esta «escultura» cubierta se construyó en la memoria de un ordenador, mediante un proceso que consiste básicamente en ir recortando poco a poco, a partir de un cubo inicial, todos los puntos cuyas imágenes iteradas por z → λz(1 − z) converjan hacia ∞. El parámetro λ es un número real que varía entre 1 y 4. El eje λ está orientado verticalmente a lo largo de un lado de la escultura, mientras que x e y forman el número complejo z = x + iy.

Cada sección horizontal es una figura acotada autocuadrática maximal de parámetro λ.

En el caso del valor especial λ = 2, el contorno de la sección correspondiente es una circunferencia: el «ceñidor» de la cortina.

Para todos los demás valores de λ, el contorno de la figura autocuadrática es una curva fractal, incluidas las que ya vimos en la lámina 265. Se perciben unos «pliegues» sorprendentes cuya posición varía con λ; por debajo del ceñidor forman entrantes y por encima salientes.

Tienen especial interés las manchas de la pared que sostiene la cortina. Posiblemente esta escultura no pueda hacer justicia a la complicación de la parte superior de la cortina.

(A) Para cada valor de λ, la cortina contiene un árbol fractal (que hace de «espina dorsal») formado por las antiimágenes iteradas del intervalo [0,1] del eje x. Para todos los valores pequeños y algunos grandes de λ < 3, las ramas de dicho árbol están totalmente «cubiertas de carne». Sin embargo, para otros valores grandes de λ la carne no existe. Aquí, las ramas a lo largo de x = 1 /2 o de y = 0 son visibles, pero el resto se pierde irremediablemente en el proceso gráfico.

(B) Algunas bandas horizontales de la pared que queda por detrás de la cortina están completamente cubiertas de pequeños «montículos» o «arrugas», aunque aquí sólo se pueden ver unas pocas de las mayores. Estas bandas y montículos tienen que ver con las «moléculas isla» (láminas 268 y 269) intersecadas por el eje real.

Las observaciones (A) y (B) generalizan la teoría de Myrberg-Feigenbaum.

LÁMINAS 268, 269 y 270. Los separadores de z → λz(1 − z) y de z → z₂ − μ.

FIGURA 268

FIGURA 268. MAPA μ. Los μ de la región cerrada en negro (limitada por una curva fractal) son aquellos para los que las imágenes iteradas de z₀ = 0 por la transformación z → z₂ − μ no convergen hacia ∞. La gran cúspide corresponde a μ = −l /4, y el punto del extremo derecho es μ = 2.

FIGURA 269

PARTE SUPERIOR DE LA FIGURA 269. mapa λ. Los λ de la región cerrada en negro, junto con los del disco vacío, cumplen Reλ > 1 y son tales que las imágenes iteradas de z₀= 1/2 por z → λz(1 − z) no convergen hacia ∞. El mapa λ completo es simétrico con respecto a la línea Reλ = 1.

El disco |λ − 2| ≤ 1, y el disco |λ| ≤ 1 excepto λ = 0. Los λ en estos dominios son tales que las imágenes iteradas de z₀ = 1/2 convergen a un punto límite acotado.

LA CORONA Y LOS RETOÑOS. El mapa λ fuera de los discos vacíos forma una «corona», que se descompone en «retoños» cuyas «raíces» son los «enlaces receptores» definidos como los puntos de la forma λ = exp(2πim/n) o λ = 2 − exp(2πim/n), donde m/n es una fracción irreducible menor que 1.

FIGURA 270

FIGURA 270. Ésta es una parte de la inversión del mapa λ, con respecto a λ = 1. Si en el mapa λ se examinan los retoños cuyas raíces son de la forma λ = exp(2πi/n), uno se queda con la impresión de que los «puntos correspondientes» están sobre circunferencias. Esta figura nos lo confirma. Otras inversiones nos confirman que otras figuras que parecen círculos lo son realmente.

MOLÉCULAS ISLA. Muchas de las «manchas» de los alrededores del mapa son verdaderas «moléculas isla», lo que es señalado por primeva en Mandelbrot (1980n). Tienen la misma forma que el mapa μ entero, aparte de una distorsión no lineal.

SEPARADOR, ESPINAS Y ÁRBOLES. Los contornos de los dominios en negro de los mapas λ o μ son curvas conexas que yo mismo descubrí y denominé separador S. El conjunto interior a S se compone de átomos abiertos (véase el texto). Si el periodo del átomo es w, definamos su espina como la curva sobre la que f_w^*'(z_μ) es real.

Las espinas que están sobre el eje real se conocen en la teoría de las aplicaciones de [0,1] sobre sí mismo, y se sabe que su adherencia es [−2,4],

Descubrí también que, en general, la adherencia de las espinas de los otros átomos se descompone en una colección de árboles, cada uno de ellos plantado en un enlace receptor. La lista de órdenes de ramificación en los distintos puntos de uno de dichos árboles es l para los puntos de ramificación, más los órdenes de bifurcación que nos llevan a la raíz del árbol. Además, si el árbol está plantado en un átomo isla, hay que añadir los órdenes de bifurcación que llevan de |λ − 2| ≤ 1 o |λ| ≤ 1 hasta dicho átomo.

PARTE INFERIOR IZQUIERDA DE LA FIGURA 269. Éste es un mapa λ detallado en la proximidad de λ = 2 − exp(−2πi/3). El conjunto interior a S es el límite de dominios de la forma |f_n(l/2)| < R, cuyos contornos son unas curvas algebraicas llamadas lemniscatas. Aquí se muestran unos cuantos de estos dominios superpuestos. Para valores grandes de n dichos dominios parecen inconexos, como ocurre también con el mapa λ, pero de hecho están conectados por fuera de la cuadrícula empleada en el cálculo.

PARTE INFERIOR DERECHA DE LA FIGURA 269. Éste es un mapa λ detallado cerca de λ = 2 − exp(−2πi/100). Este árbol de cien ramificaciones comparte unos rasgos sorprendentes con el mapa z de la lámina 272.

LÁMINAS 271 y 272. Dragones autocuadráticos; aproximación al límite de «Peano».

Todas las curvas autocuadráticas tienen su encanto particular. Y para mí, las más atractivas son los «dragones» que se muestran en estas láminas y en la C5.

LA MUDA DEL DRAGÓN. ¡Ver un dragón en el proceso de autotransformación cuadrática tiene que ser un espectáculo fascinante! Una «muda» monstruosa despega las pieles de los innumerables pliegues de la espalda y el vientre del dragón. Luego las estira hasta doblar su longitud, ¡que por supuesto se mantiene infinita! A continuación vuelve a plegar cada piel alrededor de la espalda y del vientre. Y por fin vuelve a pegar todos los pliegues en sus nuevas posiciones.

HERÁLDICA FRACTAL. No hay que confundir el dragón autocuadrático con el autosemejante de Harter y Heightway (láminas 99 y 100). El lector podría entretenerse en detallar las semejanzas y las múltiples diferencias.

BIFURCACIONES SUCESIVAS. Los mejores dragones autocuadráticos se obtienen cuando λ cae en un retoño de la lámina 269 correspondiente a θ/2π = m/n, para valores pequeños de los enteros m y n. Si el orden de bifurcación es n, el número de cabezas o colas (o como se quiera llamar a estos dominios) del dragón que parten de cada punto de articulación es n. Una segunda bifurcación de orden m'/n' descompone cada uno de estos dominios en n' «enlaces salchicha», y los hace adelgazar aún más.

Cuando λ cae en el interior de un retoño, lejos de la raíz, se obtienen dragones robustos, ni obesos ni delgados. Si λ cae cerca de uno de los dos subretoños que corresponden a un orden de bifurcación de 4 a 10, se obtienen dragones con una torsión, a la izquierda uno y a la derecha el otro.

FIGURA 271-1

PARTE DERECHA DE LA FIGURA 271-1 . «DRAGÓN FAMÉLICO». Un dragón que sufre una infinidad de bifurcaciones pierde toda la carne y se convierte en una curva ramificada esquelética.

La dimensión topológica del conjunto que no es atraído hacia ∞ es 0 para los polvos de Fatou, 1 para los dragones hambrientos y 2 para el resto de dragones.

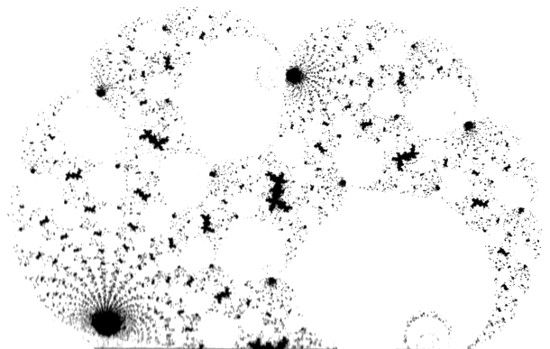
FIGURA 271-2

FIGURA 271-2. σ-DRAGÓN. Esta figura es conexa; su λ cae en la «gran isla» que hay junto a la costa de la parte inferior derecha de la lámina 269.

FIGURA 272

FIGURA 272. EL LÍMITE SINGULAR λ= 1. DRAGONES DE PEANO. Supongamos que λ cae en una isla unida a la costa por el enlace de θ = 2π/n. Cuando n → ∞, θ → 0, con lo que λ tiende a 1. El dragón correspondiente debe tender pues a la forma de venera basal en la cortina de la lámina 266. Pero existe una diferencia cualitativa entre n = ∞ y n grande pero finito.

Cuando n → ∞, el número de brazos del dragón aumenta, la piel se repliega y la dimensión de ésta aumenta. En realidad, toda la figura intenta converger a un «dragón ermitaño» que llene hasta rebosar la concha de una venera de λ = 1, es decir, que tienda a la dimensión D = 2. ¿Una curva de Peano autocuadrática? Sí, pero ya sabemos (capítulo 7) que las curvas de Peano no son tales: en cuanto alcanza D = 2, nuestra curva dragón muere como curva para convertirse en un dominio plano.

LÁMINA 274. Polvos de Fatou reales autocuadráticos en [0,1].

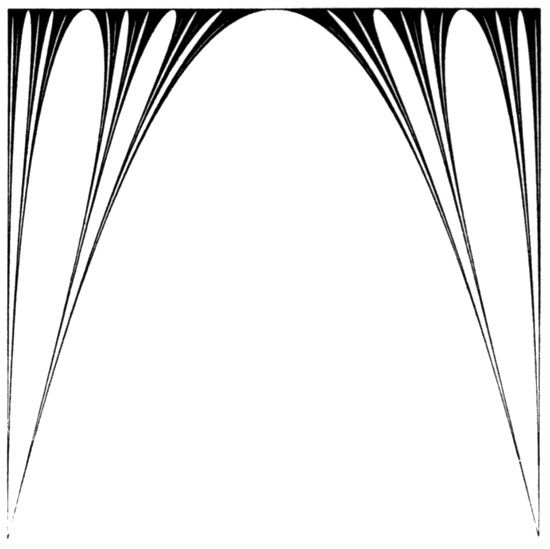
FIGURA 274

Fatou (1906) es una obra maestra de un antiguo género literario: el Comptes Rendus Notes de la Academia de Ciencias de París. En muchos casos el objetivo es revelar poco, pero dejando constancia de que el autor ha pensado en todo.

Entre otras maravillosas observaciones muy bien comprendidas después de largo tiempo dedicado al estudio del tema, Fatou señala lo siguiente. Cuando λ es real y mayor que 4 o menor que −2, el mayor conjunto acotado invariante por la transformación x → f(x) = λx(1 − x) es un polvo contenido en [0,1]. Esta lámina ilustra la forma de dicho polvo para λ > 4. A lo largo de la coordenada vertical, −4/λ varía desde −1 hasta 0. Los intervalos en negro señalan los extremos de las tremas de órdenes comprendidos entre 1 y 5. Los extremos x₁ y x₂ de la trema central son las soluciones de la ecuación λx(1 − x) = 1; y están sobre una parábola. Las tremas de segundo orden acaban en los puntos x_1,1, x_1,2, x_2,1 y x_2,2 tales que λx_m,n(1 − x_m,n) = x_m.

La notable relación entre los polvos de Cantor y una de las funciones más elementales merece ser conocida fuera de los círculos de especialistas.

19 Los polvos de Cantor y de Fatou; dragones autocuadráticos

19
Los polvos de Cantor y de Fatou; dragones autocuadráticos