El grueso de este ensayo está dedicado a fractales que, o bien son totalmente invariantes por transformaciones de semejanza, o son por lo menos «casi» autosemejantes. A consecuencia de ello, el lector puede haberse formado la idea de que el concepto de fractal está casado con la autosemejanza. Esto no es así, ni muchísimo menos, pero la geometría fractal debe empezar tratando los homólogos fractales de las rectas… o, por así llamarlos, de los «fractales lineales».

En los capítulos 18 y 19 se avanza un paso más. Se esbozan las propiedades de los fractales que son, respectivamente, conjuntos mínimos invariantes por inversión geométrica y fronteras de los conjuntos acotados máximos invariantes bajo ciertas transformaciones cuadráticas.

Ambas familias difieren de los fractales autosemejantes en aspectos fundamentales. Unas transformaciones lineales adecuadas dejan invariantes los fractales escalantes, pero para generarlas hay que dar primero un generador y unas reglas de construcción. Por otra parte, el hecho de que un fractal sea «generado» por una transformación no lineal basta a veces para determinar, y por tanto generar, su forma. Más aún, muchos fractales no lineales son acotados, esto es, llevan ya incorporado un corte superior n < ∞. Aquellos que encuentren objetable Ω = ∞, deberían sentirse encantados con su desaparición.

Los primeras fractales autoinversos fueron introducidos hacia la década de 1880 por Poincaré y Félix Klein, no mucho después de que Weierstrass descubriera una función continua y no diferenciable, aproximadamente hacia la misma época en que aparecieron los conjuntos de Cantor, y bastante antes que las curvas de Peano y de Koch y toda su estirpe escalante. Lo irónico del caso es que los fractales escalantes encontraron un nicho duradero como material para contraejemplos famosos y juegos matemáticos, mientras que los fractales autoinversos se convirtieron en un tema especial de las funciones automórficas. Esta teoría fue abandonada durante cierto tiempo y luego resurgió en forma muy abstracta. Una de las razones de que los fractales autoinversos casi cayeran en el olvido es que su forma no ha sido explorada hasta este capítulo, en el que se presenta un nuevo método de construcción efectiva.

La última sección del capítulo aborda un problema de física, cuyo protagonista resulta ser un fractal autoinverso.

Como se verá, muchos fractales no lineales «parecen orgánicos», y de ahí este aparte relacionado con la biología. Como las formas en biología son a menudo muy complejas, podría parecer que los programas que codifican dichas formas son a su vez muy largos. Cuando la complicación parece no tener objeto alguno (como suele ser el caso en criaturas simples), resulta paradójico que los programas generadores no estén simplificados, dejando lugar para instrucciones útiles.

Sin embargo, las complicaciones en cuestión tienen a menudo una estructura muy repetitiva. Recordemos que al final del capítulo 6 decíamos que una curva de Koch no debe considerarse ni irregular ni complicada, por cuanto las reglas que rigen su construcción son sistemáticas y simples. La clave está en que dichas reglas se apliquen una y otra vez, en períodos sucesivos. En el capítulo 17 se generaliza esta idea a la precodificación de la estructura del pulmón.

En los capítulos 18 y 19 vamos mucho más allá y nos encontramos con algunos fractales generados mediante reglas no lineales que nos recuerdan ciertos insectos o cefalópodos, y con otras que nos recuerdan ciertas plantas. La paradoja queda así destruida, dejando pendiente una tarea increíblemente ardua de aplicación práctica.

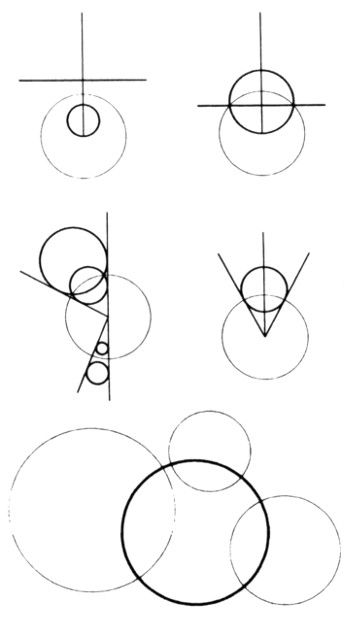
La figura más simple de la geometría euclídea, después de la recta, es la circunferencia. La propiedad de ser una circunferencia se conserva por las transformaciones de semejanza y también por las de inversión. Como muchos estudiosos no han oído hablar de la inversión desde sus últimos años en el instituto, vale la pena dedicar algún tiempo a resumir sus propiedades fundamentales. Dada una circunferencia C de centro O y radio R, la inversión con respecto a C transforma un punto P en otro P’ tal que P y P’ están en una misma semirrecta con origen en O, y las distancias |OP| y |OP’| cumplen |OP||OP’|= R². Las imágenes por inversión de las circunferencias que pasan por O son líneas rectas que no pasan por O, y viceversa (véase más abajo). Las circunferencias que no pasan por O se transforman en circunferencias (tercera figura inferior). Las circunferencias ortogonales a C son invariantes por inversión con respecto a C (cuarta figura).

Consideremos ahora tres circunferencias a la vez, C₁, C₂ y C₃. Normalmente, por ejemplo en el caso en que los discos abiertos limitados por las C_m no se solapan, existe una circunferencia r ortogonal a todas las C_m (arriba). Si esta r existe, es simultáneamente autoinversa con respecto a todas las C_m.

Los resultados sencillos anteriores son casi todo lo que la geometría estándar nos puede decir acerca de los conjuntos autoinversos. Otros conjuntos autoinversos son fractales, y la mayoría son cualquier cosa menos sencillos.

EL GENERADOR. CONJUNTOS AUTOINVERSOS. Como de costumbre, partiremos de un generador, que ahora estará formado por un cierto número M de circunferencias C_m. Las transformaciones consistentes en una sucesión de inversiones con respecto a estas circunferencias constituyen lo que los algebristas llaman el grupo generado por dichas inversiones; llamémosle G. La expresión formal para designar un «conjunto autoinverso» es «conjunto invariante bajo las transformaciones del grupo G».

SEMILLAS Y CLANES. Tómese un conjunto cualquiera S (al que llamaremos semilla) y añádansele sus imágenes por todas las transformaciones de G. El resultado, al que aquí llamaremos clan de S, es autoinverso. A veces, sin embargo, es un conjunto trivial. Por ejemplo, si S es el plano completo R^* (el plano R más el punto del infinito), el clan de S es idéntico a R^* = S.

GRUPOS DE INVERSIÓN CAÓTICOS. Además, dado un grupo G generado por un cierto número de inversiones, podría darse el caso de que el clan de cualquier S recubriera el plano. En tal caso, el único conjunto autoinverso es todo el plano. Por razones que se comprenderán en el capítulo 20, propongo llamar caóticos a tales grupos. Los grupos no caóticos son debidos a Poincaré, aunque se denominan kleinianos: Poincaré había atribuido a L. Fuchs cierto trabajo de Klein y éste protestó, por lo que Poincaré le prometió dar el nombre de Klein a su siguiente gran descubrimiento, ¡y así lo hizo!

Limitándonos aquí a los grupos no caóticos, estudiamos primero tres fractales autoinversos distinguidos por Poincaré, luego un cuarto conjunto cuya historia es un tanto incierta y por fin otro cuya importancia descubrí yo.

Pocos admiradores de Maurits Escher saben que su célebre inspiración de dibujante procede a menudo directamente de matemáticos y físicos «desconocidos» (Coxeter, 1979). En muchos casos Escher no ha hecho más que adornar teselaciones autoinversas conocidas por Poincaré y extensamente ilustradas en Fricke y Klein (1897).

Estos conjuntos, que denotaremos por J, se obtienen reuniendo los clanes de las circunferencias C_m.

▯ Si se supone que G es no caótico, el complementario de la reunión de los clanes de los C_m es una colección de polígonos circulares que llamaremos «baldosas abiertas». Una baldosa abierta (o su adherencia) se puede transformar en otra baldosa abierta (o cerrada) por una sucesión de inversiones de G. En otras palabras, el clan de cualquier baldosa cerrada es R^*. Y lo que es más importante, el clan de cualquier baldosa abierta es el complementario de J. Y J es, por así decirlo, la «línea de yeso» de estas baldosas. R^* es autoinverso, y J y su complementario lo son también, y comportan un «embaldosado hiperbólico» o «teselación» de R^*. (Esta palabra viene del latín tessera = cuadrado, que a su vez procede del griego τεσσαρεs = cuatro, aunque nuestras baldosas pueden tener cualquier número de lados mayor que 2). En los grabados de Escher cada baldosa es un dibujo imaginario. ▮

El conjunto autoinverso más interesante es el menor de todos. Se denomina conjunto límite y lo denotaremos por L, porque es también el conjunto de puntos límite de las imágenes iteradas de cualquier punto inicial por transformaciones del grupo G. Está contenido en el clan de cualquier semilla S. Para precisar más una cuestión técnica: es el conjunto de los puntos límite que no pueden alcanzarse también por un número finito de inversiones. O intuitivamente, es la región en la que se concentran los descendientes infinitesimales.

Puede ser que L se reduzca a un punto o a un círculo, pero en general es un conjunto fractal irregular y/o fragmentado.

▯ En una teselación L aparece como el «conjunto de las baldosas infinitesimales». En relación a las partes finitas de la teselación juega un papel análogo al de las puntas de las ramas (capítulo 16) con respecto a las ramas. Aunque aquí la situación es más simple: al igual que L, la teselación J es también autoinversa sin residuo. ▮

Diremos que un conjunto es apoloniano cuando consista en una infinidad de circunferencias junto con sus puntos límite. En este caso su condición de fractal se debe sólo a su fragmentación. Este caso se comprendió ya (aunque de una manera un tanto difusa) en los inicios históricos del tema.

Primero construiremos un ejemplo básico y luego demostraremos que es autoinverso. Apolonio de Pérgamo fue un gran matemático de la escuela de Alejandría hacia el año 200 a. C., seguidor de Euclides, que descubrió un algoritmo para trazar las cinco circunferencias tangentes a otras tres dadas. Cuando éstas son mutuamente tangentes, el número de circunferencias apolonianas se reduce a dos. Como enseguida veremos, no se pierde generalidad suponiendo que dos de las tres circunferencias dadas son exteriores y están contenidas en la tercera, a la manera siguiente:

Estas tres circunferencias definen dos triángulos circulares con ángulos de 0°, y las dos circunferencias apolonianas son las circunferencias máximas inscritas en ellos:

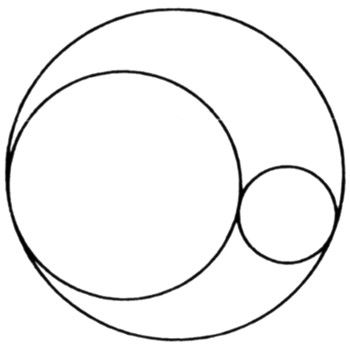
El resultado de la construcción apoloniana son cinco circunferencias, tres dadas y dos apolonianas, que a su vez definen seis triángulos circulares. A continuación repetimos la operación, trazando la circunferencia inscrita máxima para cada triángulo. La iteración indefinida de este procedimiento es lo que se conoce como relleno apoloniano. El conjunto consistente en la colección infinita de circunferencias y puntos límite constituye el conjunto que yo denomino red apoloniana. Y una porción de la misma contenida en un triángulo circular, como en la figura de la derecha, constituye lo que llamaré tamiz apoloniano.

Si se cambia una de las circunferencias apolonianas de la primera generación por cualquier otra de las circunferencias interiores dadas, el conjunto límite no varía. ▯ Si se cambia dicha circunferencia por la circunferencia exterior, la construcción empieza con tres circunferencias tangentes exteriores y una de las circunferencias apolonianas de la primera generación es la menor circunferencia circunscrita a las tres dadas. Aparte de este paso atípico, la construcción sigue como en el caso anterior, cosa que demuestra que, como decíamos, no se pierde generalidad ▮.

RELLENO DE LEIBNIZ. El relleno apoloniano recuerda una construcción que yo denomino relleno de Leibniz de una circunferencia, pues Leibniz lo describió en una carta a de Brosses: «Imaginemos una circunferencia, inscribamos en ella tres circunferencias congruentes entre sí y de radio máximo; procedamos del mismo modo con el interior de cada una de estas circunferencias, e imaginemos que el proceso sigue indefinidamente…»

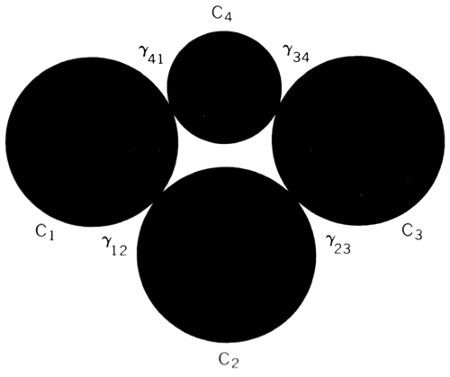
Volvamos ahora al principio de la construcción de la red apoloniana: tres circunferencias tangentes entre sí. Añadámosle una cualquiera de las circunferencias apolonianas correspondientes y llamemos circunferencias Γ a las 4 circunferencias escogidas. Las representamos en trazo grueso.

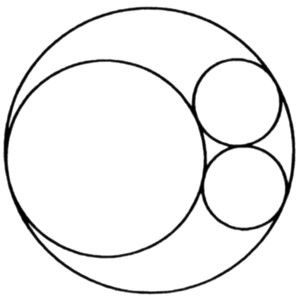
Con estas circunferencias Γ se pueden formar 4 combinaciones de tres elementos, que llamaremos tripletes. Cada uno de éstos determina una circunferencia simultáneamente ortogonal a las 3 que lo forman. Tomaremos ahora como generador estas nuevas circunferencias, que designaremos C₁, C₂, C₃ y C₄, (el diagrama siguiente las representa en trazo fino). Designaremos por Γ_ijk la Γ circunferencia ortogonal a C_i, C_j y C_k.

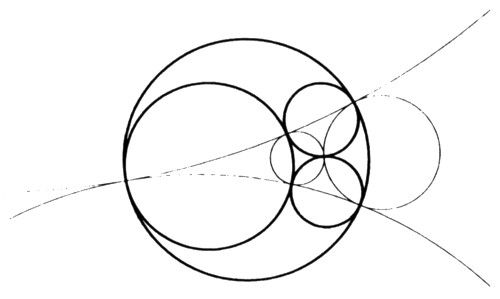
Esta notación tan pesada se ve por fin recompensada: como se puede ver fácilmente, el menor conjunto (cerrado) autoinverso con respecto a las cuatro circunferencias C_m es la red apoloniana construida a partir de las cuatro circunferencias Γ. Curiosamente, esta observación no se encuentra explícitamente formulada en la literatura, aunque seguramente es bastante conocida.

Un examen más cuidadoso muestra que cada circunferencia de la red se transforma en una de las circunferencias Γ por la acción de una única sucesión de inversiones con respecto a las circunferencias C. Por tanto, las circunferencias de la red apoloniana se pueden clasificar en cuatro clanes, y la descendencia de Γ_ijk se denotará por GΓ_ijk.

El tamiz apoloniano y el de Sierpinski de la lámina 204 tienen un rasgo común importante: el complementario de un tamiz de Sierpinski es una reunión de triángulos, o un σ-triángulo, y el complementario de una red o tamiz apoloniano es una reunión de discos, o un σ-disco.

Pero ya sabemos que el tamiz de Sierpinski admite una construcción alternativa por el método de Koch, cuyas aproximaciones finitas son terágonos (líneas quebradas) sin autocontactos, y los puntos dobles no aparecen hasta que se pasa al límite. En consecuencia, el tamiz de Sierpinski se puede dibujar sin levantar el lápiz del papel, pasando dos veces por algunos puntos, pero sin repasar ningún trozo finito de línea.

O usando una metáfora, ¡el tamiz de Sierpinski se puede tejer con un solo trozo de hilo!

Los triángulos circulares del relleno apoloniano no son semejantes entre sí, por lo que la cascada apoloniana no es autosemejante y la red apoloniana no es un conjunto escalante. Hay que recurrir pues a la definición de D de Hausdorff Besicovitch (como exponente que interviene en la definición de la medida), que se puede aplicar a cualquier conjunto, aunque su determinación resulte ser sorprendentemente difícil. Por el momento (Boyd, 1973a,b) lo más que podemos decir es que

si bien los últimos experimentos numéricos de Boyd (no publicados aún) dan D ~ 1,3058.

En cualquier caso, como D es una fracción y D_T = 1, el tamiz o red apoloniana es una curva fractal. En el contexto que nos ocupa, D nos da una medida de la fragmentación. Si «eliminamos», por ejemplo, los discos de radio menor que ε, los intersticios que quedan tienen un perímetro proporcional a ε^1−D y una superficie proporcional a ε^2−D

Las inversiones con respecto a configuraciones no tan especiales de las circunferencias generatrices C_m dan otras fractales autoinversas no tan simples como la red apoloniana. Una construcción práctica mía, que presentaré dentro de un momento, nos da una caracterización conveniente de L en la mayoría de casos, y constituye un gran avance respecto al método anterior, debido a Poincaré y Klein, que es intrincado y converge lentamente.

Sin embargo, como el método antiguo conserva su interés, lo vamos a ver aplicado a un caso especial. Supongamos que los C_m forman una configuración, que podemos llamar cadena de Poincaré, consistente en M círculos C_m numerados cíclicamente, de modo que C_m es tangente a C_m−1 y a C_m+1 (módulo M) y no corta ningún otro círculo de la cadena. En este caso L es una curva que divide el plano en dos partes, una interior y otra exterior. (En homenaje a Camille Jordán, que fue el primero en percatarse de que no es obvio que el plano pueda ser así dividido por un solo circuito, tales circuitos se llaman curvas de Jordán).

Si todos los C_m son ortogonales al mismo círculo Γ, L coincide idénticamente con Γ. Este caso, que se denomina fuchsiano, no se considera en este capítulo.

Método de poincaré para la construcción de L. Describiremos exhaustivamente la construcción de L, según el método habitual y según mi método alternativo, para la siguiente cadena especial con M = 4:

Para determinar L, Poincaré, además de Fricke y Klein (1897), sustituyen la cadena original por cadenas formadas por un número cada vez mayor de eslabones cada vez más pequeños. En el primer paso se sustituye cada eslabón C_i por los inversos respecto a C₁ de los restantes eslabones C_m, con lo que se crean M(M − 1) = 12 eslabones más pequeños. Estos pueden verse en la columna de al lado, sobreimpresos en un negativo fotográfico (gris) de los eslabones originales. A partir de ahí, cada etapa consiste en tomar la cadena inicial correspondiente e invertirla respecto de cada uno de los C_m originales. Aquí se muestran varios de estos pasos, en negro, superpuestos al paso anterior correspondiente, en blanco sobre fondo gris. Al final, la cadena se hace cada vez más fina y tiende a L, que es un hilo.

Por desgracia, después de un número bastante grande de pasos, algunos eslabones siguen teniendo un tamaño considerable, e incluso cadenas aproximadas bastante avanzadas dan una idea bastante mala de L. La lámina 257 sirve para ejemplificar esta horrenda dificultad.

En mi construcción de L interviene un nuevo concepto fractal de osculación que generaliza una faceta obvia del caso apoloniano.

OSCULACIÓN ESTÁNDAR. Este concepto está relacionado con el de curvatura. En primer orden, una curva estándar cerca de un punto regular P es aproximada por la recta tangente. En segundo orden es aproximada por la circunferencia osculatriz, esto es, la que tiene la misma tangente y la misma curvatura.

Un parámetro conveniente, u, para distinguir las distintas circunferencias tangentes a una curva en P es la inversa de la distancia (arbitrariamente orientada) de P al centro de dicha circunferencia. Si u₀ es el parámetro correspondiente a la circunferencia osculatriz y u < u₀, entonces una pequeña parte de la curva centrada en P queda totalmente a un lado de la circunferencia tangente, mientras que si u > u₀ queda totalmente al otro lado.

Este u₀ es lo que los físicos llaman valor crítico y los matemáticos cortadura. Y |u₀| define la «curvatura» local.

OSCULACIÓN FRACTAL GLOBAL. En el caso de la red apoloniana, carece de sentido definir la osculación por medio de la curvatura. Sin embargo, es obvio que en cada punto de la red donde se produce la tangencia de dos circunferencias de relleno, éstas «abarcan» el resto de L. Resulta, pues, tentador llamarlas osculatrices a ambas.

Para generalizar este concepto a conjuntos L no apolonianos, tomemos un punto en que L tenga tangente y empecemos con la definición de la osculación ordinaria basada en el comportamiento crítico (= cortadura). La novedad ahora es que, al variar u de −∞ a +∞ en vez de tener un único u₀ crítico tenemos dos, u' y u'' > u' definidos del modo siguiente: para todo u < u', L queda completamente a un lado de la circunferencia, mientras que para u < u'', queda completamente al otro lado, y para u' < u < u'' hay partes de L a ambos lados de la circunferencia. Sugiero denominar fractalmente osculatrices a las circunferencias de parámetros u' y u''.

Cada circunferencia delimita dos discos abiertos (uno de los cuales contiene el centro y el otro el punto del infinito). Los discos abiertos limitados por las circunferencias osculatrices y que no contienen L se llamarán discos osculadores.

Puede darse el caso de que una o las dos circunferencias osculatrices degeneren en un punto.

LOCAL FRENTE A GLOBAL. Volviendo a la osculación estándar, observamos que se trata de un concepto local, pues su definición no depende de la forma de la curva lejos de P. Dicho de otro modo, la curva, la tangente y la circunferencia osculatriz pueden cortarse en otros puntos además de P. Por contra, la definición anterior de osculación fractal es global, aunque esta distinción no es crucial. La osculación fractal se podría redefinir localmente, con el correspondiente desdoblamiento de la «curvatura» en 2 números. Sin embargo, en la aplicación que nos ocupa, la osculación local y la global coinciden.

TRIÁNGULOS OSCULADORES. ▯ La osculación fractal global tiene un análogo en un contexto que nos es familiar. Para definir el interior de nuestro viejo amigo el copo de nieve de Koch como un sigma-triángulo (σ-triángulo), basta con que los lados de los triángulos que se van colocando en cada nuevo paso de la lámina 70 se prolonguen tanto como sea posible sin intersecar la curva copo de nieve. ▮

La clave de mi nuevo método de construcción de L, que nos ahorra los inconvenientes citados en la pág. 248, reside en los discos y los σ-discos osculadores. Este método se ilustra aquí por vez primera (¡aunque fue anticipado en 1980, en The 1981 Springer Mathematical Calendar!). La clave está en tomar las inversas, no de las circunferencias C_m sino de algunas de las Γ_ijk que (como se establece en la definición de la página 171) son ortogonales a los tripletes C_i, C_j y C_k. De nuevo, supondremos que las Γ_ijk no se reducen a una única Γ.

RESTRICCIÓN A M = 4. La suposición M = 4 nos garantiza que, para cada triplete i, j, k, uno de los dos discos abiertos limitados por Γ_ijk —a saber, su interior o su exterior— no contiene ninguno de los puntos γ_mn definidos en la página 248. Denotaremos por Δ_ijk este disco sin puntos.

Mi construcción de L se basa en las siguientes observaciones: todo Δ_ijk sin puntos oscula L, y lo mismo ocurre con sus inversos de órdenes sucesivos con respecto a las circunferencias C_m, y los clanes construidos tomando como semillas los Δ_ijk recubren todo el plano excepto la curva L.

En la lámina 255 se parte de la misma cadena de Poincaré que en la página 248, dibujada a una escala mayor. Como suele ocurrir en la mayoría de casos, en el primer paso ya se perfila L con bastante precisión. En pasos posteriores, la producción de nuevos detalles es muy «eficiente», y después de unos pocos pasos más se puede interpolar mentalmente la forma de la curva L sin el peligro de error que se da en el método de Poincaré.

CADENAS DE CINCO O MÁS ESLABONES. Si el número original de eslabones de una cadena de Poincaré es M > 4, mi nuevo método de construcción de L precisa de una acción adicional, que empieza por clasificar las circunferencias Γ en 2 montones. Los dos discos abiertos limitados por las circunferencias Γ de una de las clases contienen al menos un punto γ_mn; en consecuencia, Δ_ijk no está definido. Esas circunferencias Γ cortan la curva L en vez de oscularla, pero no son necesarias para su construcción.

Las restantes circunferencias Γ_ijk definen discos osculadores Δ_ijk que se pueden distinguir en dos clases. Si se reúnen los clanes de los Δ_ijk de la primera clase, se representa el interior de L, y si se hace lo mismo con los clanes de los Δ_ijk de la segunda clase, se obtiene el exterior.

Lo mismo vale para muchos otros casos (aunque no para todos) en los que las C_m no forman una cadena de Poincaré.

CADENAS SOLAPANTES Y/O DESMONTADAS. Cuando C_m y C_n se cortan en dos puntos γ'_mn y γ''_mn, el conjunto de los dos sustituye a γ. Y cuando C_m y C_n son disjuntas, es sustituido por los dos puntos mutuamente inversos γ'_mn y γ''_mn. El criterio para identificar los Δ_ijk es difícil de enunciar, aunque la idea de fondo es la misma.

FRACTALES AUTOINVERSAS RAMIFICADAS. L puede presentar a la vez propiedades típicas de un circuito sinuoso (una curva de Jordan) y de una red apoloniana, obteniéndose una curva fractalmente ramificada del tipo de las estudiadas en el capítulo 14, aunque generalmente de una apariencia más barroca, como en la lámina C7.

En esta sección se esboza el papel que tienen los rellenos apolonianos y la dimensión fractal en la descripción de una clase de «cristales líquidos». Al hacerlo, echaremos una ojeada a una de los campos más activos de la física, la teoría de los puntos críticos, de los cuales tenemos un ejemplo en el «punto» del diagrama presión-temperatura que describe las condiciones físicas bajo las cuales pueden coexistir en equilibrio las tres fases (sólida, líquida y gaseosa) de un sistema físico. Las características analíticas de un sistema en el entorno de un punto crítico son escalantes, y por tanto regidas por leyes potenciales, más concretamente por exponentes críticos (capítulo 36). Muchos de ellos resultan ser dimensiones fractales, y aquí nos encontramos con el primer ejemplo.

Como los cristales líquidos no son un campo demasiado conocido, los describiremos parafraseando a Bragg (1934). Estas bellas y misteriosas sustancias son líquidas en cuanto a movilidad y cristalinas en cuanto a comportamiento óptico. Sus moléculas tienen una estructura relativamente complicada, son largas y forman cadenas. Ciertas fases de un cristal líquido se llaman esmécticas, del griego σμηγμα que significa jabón, porque constituyen un modelo de sistema orgánico de aspecto jabonoso. Un cristal líquido esméctico está formado por moléculas que se ordenan paralelamente una junto a otra como las espigas en un sembrado, de modo que el espesor de una capa viene dado por la longitud de dichas moléculas. Las capas u hojas resultantes son muy flexibles y fuertes, y si se las dobla tienden a enderezarse de nuevo. A bajas temperaturas se apilan de un modo regular, como las hojas de un libro, formando un cristal sólido. Pero cuando aumenta la temperatura las hojas pueden deslizarse fácilmente unas respecto a otras. Cada capa constituye un líquido bidimensional.

Tiene especial interés la estructura de cónicas focales. Dado un bloque de cristal líquido, lo descomponemos en dos conjuntos de pirámides, la mitad de los cuales se asienta en una de dos caras opuestas del bloque, con los vértices en la otra. Dentro de cada pirámide, las capas de cristal líquido se pliegan formando conos muy puntiagudos. Todos ellos tienen el mismo vértice y son aproximadamente rectos. A consecuencia de ello, sus bases son discos limitados por circunferencias. El radio mínimo e es el espesor de la capa de cristal líquido. En el interior de un dominio espacial, como una pirámide cuadrangular, los discos que forman las bases de los conos están distribuidos sobre la base de la pirámide. Para obtener una distribución de equilibrio se empieza inscribiendo en la base un disco de radio máximo. A continuación se inscriben discos con el radio máximo posible en cada uno de los cuatro rincones restantes, y así sucesivamente. Si fuera posible iterar esta operación indefinidamente, obtendríamos exactamente un relleno apoloniano.

Las propiedades físicas de este modelo de jabón dependen de la superficie y el perímetro de la suma de los intersticios. Todo ello tiene que ver con la dimensión fractal D de una especie de «negativo» fotográfico, el tamiz que no es penetrado por las moléculas de jabón. Para más detalles sobre la física del problema, véase Bidaux, Boceara, Sarma, Sèze, de Gennes y Parodi (1973).

LÁMINA 255. Un fractal autoinverso (construcción de Mandelbrot)

FIGURA 255

Esta lámina ilustra la discusión anterior del apartado σ-discos que osculan L.

FIGURA SUPERIOR. En las cadenas de Poincaré con M = 4, por lo menos uno de los discos Δ_ijk no es acotado, llamémosle Δ₁₂₃, y se solapa con el disco Δ₃₄₁. (Aquí Δ₃₄₁ tampoco es acotado, pero no tiene por qué ser siempre así). La reunión de Δ₁₂₃ y Δ₃₄₁, en gris, nos da una primera aproximación del exterior de L. Es una situación análoga a la aproximación del exterior de la K de Koch por el hexágono regular convexo de la lámina 71.

Los discos Δ₂₃₄ y Δ₄₁₂ se cortan y su reunión, en negro, nos da una primera aproximación del interior de K. Es una situación parecida a la aproximación del interior de K por los dos triángulos que forman la estrella regular de seis puntas de la lámina 71.

FIGURA CENTRAL. Una segunda aproximación del exterior de L se obtiene añadiendo a Δ₁₂₃ y Δ₃₄₁ sus inversos con respecto a C₄ y C₂, respectivamente. El resultado, en gris, es análogo a la segunda aproximación del exterior de K en la lámina 71.

La segunda aproximación correspondiente al interior de L se obtiene añadiendo a Δ₂₃₄ y Δ₄₁₂ sus inversos con respecto a C₁ y C₃, respectivamente. El resultado, en negro, es análogo a la segunda aproximación del interior de K en la lámina 71.

FIGURA INFERIOR. El exterior de L, en gris, es la reunión de los clanes de Δ₁₂₃ y Δ₃₄₁, y su interior, en negro, es la reunión de los clanes de Δ₂₃₄ y Δ₄₁₂. La estructura fina del interior de L se ve en la parte inferior de la lámina 257, donde se parte de otra cadena de Poincaré distinta. Juntos, los dominios abiertos en negro y en gris recubren todo el plano menos L.

LÁMINA 256. Fractal autohomográfico, cerca del límite de Peano

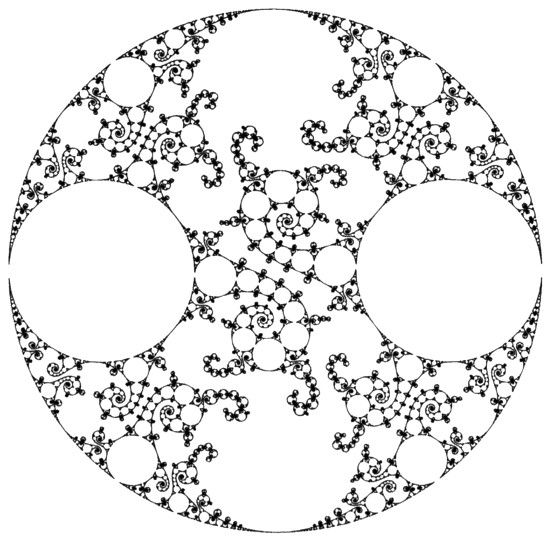
FIGURA 256

Para el matemático, el principal interés de los grupos generados por inversiones reside en su relación con ciertos grupos de homografías. Una homografía (también llamada transformación bilineal o de Möbius) transforma el plano complejo según z → (az + b)/(cz + d), donde ad − bc = 1. La homografía más general se puede descomponer en producto de una inversión, una simetría axial (que es una inversión degenerada) y una rotación. Por esta razón, en ausencia de rotaciones, el estudio de las homografías aprovecha muchas cosas del estudio de los grupos generados por inversiones. Aunque, claro está, la introducción de las rotaciones enriquece más el tema.

He aquí un ejemplo de conjunto límite L para un grupo de homografías. Lo ideó David Mumford en el curso de unas investigaciones inspiradas por los nuevos resultados presentados en este capítulo, quien ha tenido la amabilidad de permitir su publicación aquí. Esta figura casi barre un dominio plano y presenta extraordinarias analogías y diferencias con la figura de la lámina 176.

Bajo condiciones muy generales T. Akaza, A. F. Beardon, R. Bowen, S. J. Patterson y D. Sullivan han demostrado que el conjunto límite de un grupo de homografías es un fractal. Véase Sullivan (1979).

LÁMINA 257. Un célebre fractal autoinverso corregido (construcción de Mandelbrot)

FIGURA 257

La figura superior izquierda es una reproducción de la figura 156 de Fricke y Klein (1897), que pretende (en mi terminología) representar el fractal autoinverso generado por las cinco circunferencias que delimitan el dominio central en negro. Esta figura ha sido ampliamente reproducida.

El contorno de la figura negra de la parte superior derecha muestra la verdadera forma de dicho fractal, según mi construcción basada en los σ-discos osculadores. Como se ve, la discrepancia es horrorosa. Fricke ya sabía que L contenía círculos, y dio a su delineante las instrucciones pertinentes, pero por lo demás Fricke no tenía idea de qué clase de figura irregular era de esperar.

El verdadero L contiene el contorno L^* de la figura dibujada en la parte inferior izquierda empleando mi algoritmo. Este L^* es el fractal autoinverso que corresponde a las cuatro circunferencias generatrices que forman una cadena de Poincaré. Es claro que las imágenes de L^* por otras inversiones están también contenidas en L. En Mandelbrot (1982i) se comenta esta lámina.

18 Fractales autoinversos, redes apolonianas y jabón

18
Fractales autoinversos, redes apolonianas y jabón