En el presente capítulo se estudian los «árboles» de tubos gruesos empalmados que forman los pulmones, los sistemas vasculares, los árboles de la botánica, las redes fluviales y otros sistemas por el estilo.

Dichos objetos naturales son sumamente familiares y, de hecho, ningún otro sistema natural sirve mejor para ilustrar la idea de una figura que tenga un gran número de escalas lineales distintas. Por desgracia, los árboles son menos simples de lo que parece. No se abordaron antes debido a la dificultad con que nos tropezamos en el capítulo anterior: los árboles no pueden ser autosemejantes. Todo lo más que uno puede esperar es que las puntas de las ramas sí formen un conjunto autosemejante, como se supondrá a lo largo de este capítulo. Además de la dimensión fractal D de las puntas, en los árboles interviene un segundo parámetro, Δ, al que llamaremos exponente diametral. Cuando el árbol es autosemejante aparte de un residuo, como ocurría en el capítulo 16, Δ coincide con la D de las puntas. En caso contrario, Δ y D son características independientes, y tratamos con lo que los biólogos llaman «alometría». Nos encontraremos con ejemplos tanto de Δ = D como de Δ < D.

En sus Libros de apuntes, nota n.° 394, Leonardo da Vinci afirma que «La suma de los grosores de todas las ramas de un árbol a una cierta altura es igual al grosor del tronco común (que tienen por debajo)». La expresión formal de esta afirmación es que, antes y después de cada bifurcación, los diámetros de las ramas de un árbol, d, d₁ y d₂, satisfacen la relación

siendo el exponente Δ = 2. La consecuencia de esto es la siguiente: si se tiene en cuenta el grosor de las ramas, los árboles de la botánica no son autosemejantes ni su corteza llena el espacio. En efecto, para que haya autosemejanza se tiene que cumplir Δ = D, y la condición de que casi se llene el espacio implica que D se acerque a E =3.

Dicho de otro modo, siempre que la relación anterior se satisfaga, Δ es un nuevo parámetro a tener en cuenta junto con D. Lo llamaremos exponente diametral. Mucha gente lo ha considerado, a menudo sin conocimiento mutuo, como prueban las referencias de Thompson (1917 - 1942 - 1961). En este capítulo se demuestra que, para los bronquios, Δ ~ 3; para las arterias, Δ ~ 2; los árboles de la botánica están cerca del Δ = 2 de Leonardo, y para el ancho de los ríos se tiene Δ = 2. En este capítulo se investigan también algunas de las consecuencias físicas, fisiológicas y geométricas del valor de Δ.

▯ PARADIMENSIÓN. En mi Fractals de 1977 se decía que Δ es una paradimensión, pero ya no soy partidario de usar este término. Unas veces Δ es una dimensión y otras no, cosa que encontramos también en el exponente de Besicovitch y Taylor (1954; véase el capítulo 39). ▮

Como primer ejemplo, la subdivisión que presentan los tubos de aire del pulmón es, a efectos prácticos, autosemejante, con Δ = D, y D ~ E =3.

La forma interna del pulmón no se conoce demasiado bien. Por ello sería instructivo presentar aquí una fotografía real (se tienen ejemplos en Weibel, 1963, y Comroe, 1966). Sin embargo, la política de este ensayo es limitarse a las simulaciones (quizá sea ésta la única ocasión en que haya que lamentarlo). Por tanto, tendremos que conformarnos con una breve descripción verbal. Si reemplazamos el aire del pulmón con plástico no vulcanizado y eliminamos el tejido pulmonar, nos queda un árbol muy densamente ramificado que llena el contorno del pulmón con una compacidad, uniformidad e impenetrabilidad a la vista que no se da en los árboles de la botánica. Entre las dos primeras ramificaciones, que caen fuera de nuestro campo de interés, y las tres últimas, que acaban en los alvéolos (de los que hablamos en el capítulo 12), se producen 15 bifurcaciones sucesivas con una regularidad sorprendente.

De los datos de Weibel (1963) resulta que los segmentos de tubo son semejantes entre sí en primera aproximación, y que Δ ~ 3. El flujo de aire es una cantidad determinada y constante que se divide entre las ramas de cada bifurcación, y como el flujo de aire es igual al área de la sección transversal del tubo multiplicada por la velocidad del aire, vemos que esta velocidad varía según d^{Δ− 2}: el aire se ralentiza a medida que llega a los bronquios más internos.

Es importante que ∆ valga precisamente 3. Una primera interpretación se basa en un argumento de Murray (1927), presentado en Thompson (1942, pág. 954, o 1961, pág. 129). «La superficie creciente de las ramas implica enseguida un aumento del rozamiento, y una corriente de fluido más lenta, con lo que la capacidad de dichas ramas es mayor de lo que pudiera parecer a primera vista». Se trata de una cuestión de resistencia más que de capacidad; y en términos generales la respuesta es que la razón de la resistencia a la sección recta debe ser la misma en cualquier lugar del sistema, antes y después de cada bifurcación, a fin de que su resistencia total sea la menor posible; la sección recta total de las ramas, pues, tendrá que ser mayor que la del tronco, para compensar la resistencia creciente. Un resultado aproximado, conocido por los estudiantes de hidrodinámica [para un tratamiento moderno, véase Hersfield y Cummings, 1967, y Wilsons, 1967], es que la resistencia es mínima, y la condición se optimiza cuando la razón de ramificación es 2^1/3 ~ 1,26 en todas partes.

Así pues, Δ = 3 es el mejor valor que se podría esperar, ya sea por un proyecto orientado a unos objetivos o por una selección evolutiva. Naturalmente, el criterio de optimización de Murray es puramente local, y el proyectista nunca puede estar del todo seguro de que partes localmente óptimas vayan a encajar unas con otras.

Mi razonamiento fractal alternativo en favor de Δ = 3 es muy distinto: invoca el efecto de condicionantes geométricos involuntarios sobre el crecimiento del pulmón prenatal y sobre la forma completamente desarrollada de sus tubos. Una ventaja obvia es que la razón de ramificación 2^1/Δ ~ 2^1/3 no tiene por qué estar codificada genéticamente (como debería ser en la interpretación de Murray).

El dato fundamental es que el crecimiento del pulmón prenatal comienza con un brote, que evoluciona hasta formar un tubo, el cual forma a su vez dos brotes, y cada uno de ellos repite el proceso anterior. Además, este proceso de crecimiento es autosemejante (¡el tronco hace aquí de residuo!) Para justificar la autosemejanza, no hace falta pensar que es lo óptimo, nos basta con que sea lo más simple: el programa regulador del proceso de crecimiento es más corto si cada paso es una repetición del anterior a una escala menor, o a la misma escala después de que el estadio anterior haya crecido. Si esto es así, el resultado del crecimiento está completamente determinado por la razón grosor/longitud de las ramas y por el exponente diametral. Hace falta también una regla que indique cuándo debe detenerse el crecimiento.

Ahora bien, dependiendo del valor de Δ (y suponiendo fija la razón grosor/longitud) el crecimiento según estas reglas llega a uno de los tres resultados siguientes: (a) después de un número finito de pasos, las ramas agotan el espacio disponible para el crecimiento; (b) las ramas nunca llegan a llenar más que una parte del espacio accesible, o (c) resulta que el espacio disponible es precisamente el que necesitan. Si se quiere que el límite sea un árbol que llena un dominio espacial no hace falta incorporar instrucciones especiales al programa de crecimiento, pues la competencia por el espacio deja poco lugar para la indeterminación. En las láminas 234 y 235 se muestra una reducción bidimensional del proceso. Se comprueba que, a medida que la razón grosor/longitud tiende a 0, la razón de ramificación que recubre el plano aumenta hasta 2^1/2, dando Δ = E = 2. Análogamente, la razón de ramificación que llena el espacio correspondiente a ramas infinitamente delgadas es 2^1/3, que nos da Δ = E = 3.

Como Δ = 3 corresponde al límite de tubos infinitamente finos, este caso es, de hecho, irrealizable. Y es una pena, pues un árbol formado por bifurcaciones infinitamente delgadas tiene una «piel» que llena un dominio en el espacio. Esta última propiedad podría habernos sugerido una interpretación teleológica que rivalizaría con la de Murray: sería la forma óptima en el sentido de que tendría la mayor superficie posible, cosa que favorecería los intercambios químicos entre el aire y la sangre.

Pero los tubos reales no son infinitamente finos, y lo más que se puede conseguir es unos valores de Δ y de D ligeramente inferiores a 3, en perfecto acuerdo con la evidencia empírica. Esto implica el mismo grado de imperfección en todos los puntos de ramificación, pero esta propiedad se obtiene como una simple consecuencia adicional de la autosemejanza con residuo, y no hace falta introducirla como objetivo previo.

DIMENSIÓN. La reunión de todas las ramas da un conjunto estándar, siendo E tanto su dimensión fractal como la topológica. Si la corteza de cada rama es lisa, la corteza total tiene dimensión Δ.

Como de costumbre, la interpolación a bronquios cada vez más finos se interrumpe en un corte inferior. Éste es gradual a partir de la decimoquinta bifurcación, y encuentro que es un diseño geométrico excelente.

Una observación fundamental es que, en tanto que la bifurcación autosemejante acabaría por llenar todo el espacio accesible, ésta va más lentamente, de modo que las primeras 15 etapas de bifurcación del pulmón sólo llenan una pequeña parte del volumen pulmonar total. Para llenar el espacio restante en unas pocas etapas, los tubos tienen que ser claramente más anchos de lo que se deduciría de una interpolación autosemejante. En efecto, el resultado de Weibel (1963, págs. 123-124) puede interpretarse como un indicio de que, en los estadios posteriores al decimoquinto, el grosor de los tubos deja de disminuir (Δ ya no está definida), y las longitudes de los tubos son mayores de lo que sugiere la semejanza, siendo 2 el multiplicador final. Como la lámina 235 sugiere que las ramas autosemejantes entran aproximadamente hasta la mitad del espacio vacío disponible más cercano, un multiplicador igual a 2 parece de lo más razonable, y sugiere que buena parte del programa de diseño del pulmón viene impuesto por propiedades espaciales y no requiere de una codificación separada.

Volvamos ahora al punto culminante del capítulo 15, donde proclamo que los monstruos fractales de Lebesque-Osgood son el constituyente esencial de nuestra carne. Si partimos de que un dominio ramificado A (el sistema arterial) ocupa un volumen de aproximadamente el 3% del volumen de otro dominio B (el cuerpo), pero que se supone que llega a estar infinitamente cerca de cualquier punto de B, concluyo que el grosor de las ramas de B debe disminuir más deprisa que en los árboles autosemejantes. Ahora que ya sabemos que la tasa de adelgazamiento se puede medir por Δ, podemos preguntamos si las arterias tienen una Δ definida.

Esto no sólo es cierto en un amplio subdominio de las entre 8 y 30 bifurcaciones que uno encuentra entre el corazón y los capilares, sino que hace ya casi un siglo que se conoce este hecho. En efecto, Thoma (1901) y Groat (1948) resumieron sus resultados experimentales diciendo que Δ = 2,7. Su estimación fue notablemente confirmada por Suwa y Takahashi (1971).

Después de jugar con objetos que llamamos árboles en sentido figurado, volvamos a los árboles que estudian los botánicos. Los valores «normales» que sugiere el análisis son D = 3 y Δ = 2. No se puede decir, sin embargo, que sean demasiado universales: dada la asombrosa diversidad de las formas botánicas, las desviaciones específicas pueden resultar más interesantes que la «norma». Una consecuencia de Δ = 2 es que, en comparación con las ramas casi autosemejantes que dan forma al pulmón, las de las plantas están muy espaciadas. No se puede ver a través de un pulmón y sí a través de un árbol sin hojas.

La causa subyacente al hecho de que Δ y D tomen respectivamente los valores enteros de las dimensiones de las superficies y los cuerpos sólidos es, según palabras de D’Arcy Thompson, que «un árbol está gobernado por las reglas físicas sencillas que determinan los cambios relativos del área y el volumen». O en los términos más concretos de Hallé, Oldeman y Tomlinson (1978): «El problema del intercambio de energía en los árboles se puede simplificar considerando el árbol como un sistema en el que [el área] mayor posible debe ser irrigada con la mínima inversión de volumen, garantizando al mismo tiempo la evacuación de la energía absorbida». Como los volúmenes y las áreas no son conmensurables en el marco de la geometría euclídea, el problema geométrico de la arquitectura de los árboles es intrínsecamente fractal, Cuando D y/o Δ dejan de ser enteros, el carácter fractal del problema se hace más manifiesto aún.

EL VALOR D = 3. El lector ya sabe que la realización de una hoja de área máxima consiste en una superficie que llene un dominio espacial, como ocurre con esos matojos cuyas hojas o agujas llegan tan cerca como se quiera de cualquier punto contenido en cierto contorno (aparte, quizá, de una parte central muerta que pasamos por alto). Una diferencia 3 − D muy pequeña basta para permitir la entrada de aire y luz solar.

MAGNOLIAS. Sin embargo, pueden aparecer varios condicionantes adicionales que impidan la viabilidad de D = 3. La única alternativa estándar es una superficie estándar de dimensión D = 2, por ejemplo la superficie de una «magnolia» esférica con una parte central sin hojas y entrelazada de ramas. Ésta es la razón por la cual Horn (1971), que se limita a la geometría estándar, contempla las dos posibilidades, D = 3 y D = 2. Sin embargo, D = 2 no ofrece ventajas claras; de hecho, para terminar en una magnolia esférica, las ramas deben ajustarse a unas leyes muy especiales.

Por otra parte, los fractales amplían muchísimo la libertad de diseño del «arquitecto de árboles». En primer lugar, las superficies varias veces festoneadas de muchos árboles grandes pueden representarse por medio de fractales escalantes de dimensión D comprendida entre 2 y 3, y este valor de D puede servir para caracterizarlas. Nos vienen también a la mente el brécol y la coliflor, aunque plantean un problema distinto, sobre el que enseguida volveremos. Y se puede pensar en plantas trepadoras de dimensión inferior a 2 (y conjeturar que los bonsais de «armoniosidad» bien lograda son también fractales de D < 3).

EL VALOR Δ = 2. La cita inicial de Leonardo da Vinci no vale para los pulmones (Δ = 3) ni para las arterias (Δ = 2,7). Pero la anatomía de las plantas es distinta de la humana. El valor A=2 se basa en la imagen mental de los árboles como haces de vasos no ramificados de diámetro fijo que enlazan las raíces con las hojas y ocupan una parte proporcional de la sección recta de cada rama. Según Zimmermann, los trabajadores japoneses llaman a esta representación «modelo de cañería».

MEDIDA DE Δ. La evidencia empírica resulta ser asombrosamente escasa e indirecta. Murray (1927, citado en Thompson, 1917) encuentra por vía empírica que el peso de la rama es proporcional a (diámetro de la rama)^w, con M ~ 2,5, pero en mi opinión su M es mayor que eso. Afirma que M = Δ, pero según mis propios análisis tendría que ser M = 2 + Δ/D. Para D = 3, el valor de Leonardo, A = 2 correspondería a M ~ 2,66, mientras que M ~ 2,5 daría Δ = 1,5. Recientemente, el prof. McMahon tuvo la amabilidad de pasarme los datos referentes a tres «árboles de McMahon» empleados en el artículo de McMahon y Kronauer (1976) y los he analizado. Escribiendo x por d₁/d e y por d₂/d, buscaríamos un valor de Δ tal que X = x^Δ e Y = y^Δ cayeran sobre la línea X + Y = 1. Desgraciadamente, el error experimental es muy grande para cada Δ y la estimación del valor de este parámetro resulta poco fiable. De nuevo, no queda descartado el valor Δ = 2, pero se sugiere un valor ligeramente inferior. Por el momento, la conclusión segura es que Δ = 2 es una aproximación razonable, aunque la arquitectura del árbol se inclina ligeramente por el lado conservador, con unas ramas hijas más delgadas de lo que sería necesario.

COROLARIOS DE D = 3 Y Δ = 2. Un primer corolario es que el área de las hojas soportadas por una rama es proporcional tanto al volumen de la rama como al área de su sección recta. Esta inferencia es empíricamente correcta y se debe a Huber (1928).

Otro corolario es que el cociente (altura del árbol)³/(diámetro del tronco) es constante para cada especie y es igual al cociente (escala lineal del volumen de drenaje de una rama)³/(diámetro de la rama)². Se podría esperar también que dicho cociente varíe relativamente poco de unas especies a otras. Nótese que la fuerza del viento sobre un árbol desnudo, o sobre un árbol con hojas, es aproximadamente proporcional al área de las ramas, o de las ramas y las hojas, respectivamente. Y también es proporcional, en este modelo, al cubo de la altura. La resistencia del tronco, por su parte, es proporcional al (diámetro)². Esto sugiere que la proporcionalidad de ambas cantidades es un factor de seguridad.

En un árbol tipo magnolia con Δ = 2 y D = 2, el cociente (altura)²/(diámetro del tronco)² es constante. Y, en general, la razón (altura)^D/(diámetro del tronco)^Δ es constante.

DIGRESIÓN SOBRE LOS HUESOS DE LAS PIERNAS. La relación entre la altura y el diámetro característica de los árboles con D = 3 y Δ = 2 vale también para los esqueletos de los animales, siendo d el diámetro de los huesos que soportan más peso.

Mientras los árboles pulmonar y vascular tienen un soporte externo, la mayoría de plantas se sostienen por sí mismas. Greenhill (citado en Thompson, 1961) introduce en este lugar el concepto de semejanza elástica, en oposición a la geométrica. La idea de la semejanza elástica estática consiste en que un árbol tiene que limitar su altura global a una fracción fija de la altura crítica de combadura de un cilindro uniforme con el mismo diámetro basal que soporta su propio peso. Esta condición da precisamente los mismos resultados que los fractales con D = 3 y Δ = 2. Por tanto, un árbol según el «modelo de cañería» con hojas que llenan un dominio espacial no se combará.

McMahon y Kronauer (1976) continúan la idea de Greenhill introduciendo la semejanza elástica dinámica, y recuperan el mismo resultado.

En algunas plantas el tallo, además de sostener el peso y transportar la savia, también sirve para almacenar nutrientes. En tal caso, y aun cuando el sistema vascular siga el «modelo de cañería», el valor Δ = 2 no tiene por qué ser necesariamente bueno.

Un ejemplo en el que las puntas de las ramas forman una «magnolia» no estándar con D < 3 y Δ = D lo podemos ver en la lámina 233 (se trata de una proyección plana que muestra D − 1 y A − 1). Se observa que la forma geométrica de coliflor presenta oclusiones… exactamente igual que las coliflores de verdad. ¿Se trata de una simple coincidencia? No hace falta sobrecargar el mensaje genético con características predeterminadas por la geometría.

Cuando discutíamos acerca de la geometría del cerebro en el capítulo 12, no teníamos en cuenta la red de axones que interconectan las distintas partes. En el caso del cerebelo, los axones conectan la superficie con el exterior y nos encontramos con una superficie de materia gris que envuelve un árbol de materia blanca. Revisé los argumentos del capítulo 12 para incorporar este árbol y encontré que los términos correctivos resultantes en la relación área-volumen permitían un mejor ajuste a los datos empíricos. Pero esto es algo demasiado extenso para explicarlo aquí.

RAMIFICACIÓN DE LAS NEURONAS. Las células de Purkinje del cerebelo de los mamíferos son prácticamente planas, y sus dendritas forman un laberinto que recubre un dominio plano. Al pasar de los mamíferos a la paloma, el lagarto, la rana y el pez, la eficacia de este recubrimiento disminuye (Llinas, 1969). Sería bonito que esto correspondiera a una disminución de D, pero la idea de que las neuronas son fractales no pasa de ser una conjetura.

LA LEY DE RALL. Rall (1959) observa que los árboles neuronales que conservan la cantidad d^Δ con Δ = 1,5 son eléctricamente equivalentes a cilindros, y por tanto especialmente dignos de estudio. Para más detalles véase Jack et al. (1975).

Pasemos ahora a los ríos. A pesar de su importancia conceptual, mi modelo «estilo Peano» del capítulo 7 no pasa de ser una primera aproximación. Una consecuencia es que la anchura de los ríos es nula, cuando sabemos que en realidad no es así.

Una cuestión empírica importante es saber si en todas las bifurcaciones de los ríos el exponente diametral Δ es el mismo. Y si éste está efectivamente definido, la cuestión siguiente es saber si 2 − Δ = 0 o mayor que 0. No sé de ninguna comprobación directa, pero la descarga de un río, Q, se conserva en las bifurcaciones, y por tanto podría hacer el papel de d^Δ. Maddock (véase Leopold, 1962) encuentra que d ~ Q^1/2, con lo que Δ = 2. Además, la profundidad de un río es proporcional a Q^0,4, y la velocidad es proporcional a Q^0,1. Sumando debidamente los exponentes, 0,5 + 0,4 + 0,1 = 1.

En los años treinta, G. Lacey observó que Δ = 2 vale también para los canales de regadío estabilizados de la India, que plantean un problema hidráulico bien definido. Es de esperar, pues, que exista una explicación basada en la mecánica de fluidos con un papel análogo al que tenía la de Murray para el pulmón.

Δ = 2 tiene una consecuencia interesante. Si se representan los ríos de un mapa por medio de cintas que tengan una anchura relativa correcta, es imposible adivinar la escala del mapa a partir de la forma del árbol fluvial. (También es imposible en el caso de los meandros, pero esta es otra historia).

Aquellos que crean que Leonardo ya lo sabía todo interpretarán el Δ = 2 que sigue a la cita que abre este capítulo como: «Todos los ramales de una corriente de agua en un estadio cualquiera de su curso, y suponiendo que todos ellos tengan la misma velocidad, son iguales al cuerpo de la corriente principal».

LÁMINA 233. Modelos fractales planos de inflorescencias

FIGURA 233

Escojamos una magnolia de entre las de la lámina 221, con θ < π, y sustituyamos cada barra por un triángulo isósceles que lo tenga como lado, siendo 1/2 θ y π − θ los ángulos en los extremos de dicha barra. Como θ es el menor valor para el que el árbol no presenta autosolapamiento, los tallos triangulares engrosados tampoco se solaparán y rellenarán el «interior» de la magnolia. Para mayor claridad, se ha recortado ligeramente uno de los Jados de todos los triángulos que forman una de las figuras.

Nótese que las ramas se hacen más y más finas a medida que D se acerca a 1 o 2, esto es, a medida que la D de la figura espacial se acerca a 2 o 3. ¿Corresponden realmente los valores de D observados a las ramas más gruesas posibles?

LÁMINAS 234 Y 235. Bronquios iterativos que recubren un dominio plano

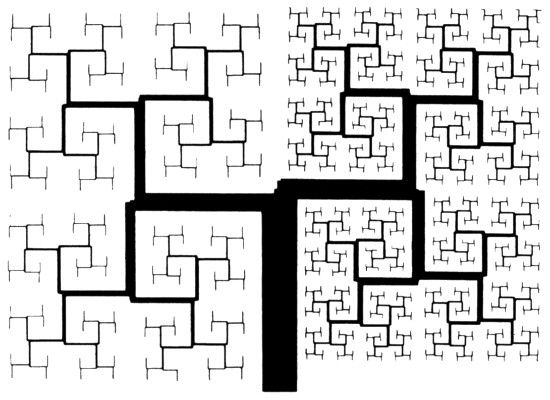
FIGURA 234

FIGURA 234. En la iteración de Koch, cada segmento rectilíneo de una aproximación finita se rompe al final en pedacitos más cortos. En muchas aplicaciones es útil generalizar este procedimiento dejando que algunos segmentos sean «estériles», de manera que no sufran modificaciones en estadios posteriores.

Aquí hemos usado este procedimiento para hacer crecer un «árbol». Se empieza con un tronco cuyos lados son estériles y que tiene un «brote» fértil. Este genera dos «ramas» en las que, como antes, sólo hay dos «brotes» fértiles en los extremos. Y así sucesiva e indefinidamente. El crecimiento es asimétrico para asegurarnos de que el árbol cubre una región plana aproximadamente rectangular, sin huecos ni solapamientos. Sin embargo, el autocontacto asintótico es inevitable, y cualquier punto de la corteza puede ser obtenido también como el límite de la punta de alguna rama.

Los «subárboles» que se obtendrían partiendo de las dos ramas principales son semejantes al árbol entero, con dos razones de semejanza, r₁ y r₂. Pero el árbol no es autosemejante, porque además de los dos subárboles tiene el tronco. Por otra parte, el conjunto límite de las puntas de las ramas es autosemejante. De los pies de figura de las láminas 85-86, la dimensión de semejanza es la D que satisface la ecuación r₁^D + r₂^D = 1. En la figura superior de la lámina 235, las puntas casi llenan el plano y 2 − D es pequeño. En la figura inferior, en cambio, D es muy inferior a 2.

Incidentalmente, si la razón diámetro/longitud está fijada de antemano, la codimensión 3 − D de una figura espacial es menor que la codimensión 2 − D de su reducción plana.

FIGURA 235

FIGURA 235. Esta figura compuesta se ha obtenido de una construcción de Koch en árbol en la que el generador cambia a cada paso, de modo que la razón anchura/longitud vaya disminuyendo hasta anularse. En la parte izquierda de la figura, dicha razón disminuye más aprisa que en la parte derecha. La consecuencia de ello es que las puntas de las ramas ya no forman un conjunto autosemejante. Sin embargo, se obtiene D = 2 para las puntas. Es una nueva manera de conseguir el mismo objetivo que en el capítulo 15.

17 Los árboles y el exponente diametral

17
Los árboles y el exponente diametral