En este capítulo estudiaremos árboles fractales filiformes y otras fractales cuasiescalantes, esto es, escalantes salvo un residuo fractalmente despreciable. Se observa que dichas fractales son no uniformes, en el sentido de que D y/o D_T toman valores distintos para distintas partes de tales conjuntos. Por contra, si echamos una mirada atrás, vemos que todas las fractales consideradas hasta ahora son uniformes.

INTERVALOS ESTÁNDAR. El intervalo semiabierto ]0,1], que contiene el extremo derecho pero no el izquierdo, es escalante, pues es la unión de N = 2 réplicas reducidas de sí mismo, ]0,1/2] y ]1/2,1 ]. Por el contrario, el intervalo abierto ]0,1[ no es escalante, ya que además de las N = 2 réplicas reducidas de sí mismo, ]0,1/2[ y ]1/2,1[, contiene también el punto medio x = 1/2. Propongo para este punto el nombre de residuo escalante. Para el cálculo de D, y a otros muchos efectos, no tiene ninguna importancia. Un físico diría que es de un orden de magnitud menor que el del todo y las partes.

A partir del ejemplo anterior uno está tentado de considerar todos los términos residuales como complicaciones rebuscadas que no afectan en nada el resultado del cambio de escala, pero en ejemplos análogos en los que intervienen fractales, que calificaré de no uniformes, el residuo puede ser sorprendentemente significativo. Un fractal no uniforme es la suma (o la diferencia) de varias partes con dimensiones fractales y topológicas distintas. Ninguna de dichas partes se puede despreciar del todo, aunque lo pueda ser tanto en el sentido fractal como en el topológico. Estos dos puntos de vista chocan a menudo, y sus efectos son importantes e interesantes.

POLVOS DE CANTOR Y PUNTOS AISLADOS. ▯ Construyase un polvo de Cantor dividiendo [0,1] en b = 4 partes y guardando [0,1/4] y [3/4,1], La construcción alternativa consistente en borrar ]1/4,1/2[ y ]1/2,3/4[ da el mismo polvo más el punto residual 1/2. Este residuo aislado no es fractal, pues tanto D como D_T valen 0.

▯ En la generalización al espacio R^E, el polvo de Cantor satisface D_T = 0 y D > 0, en tanto que para el residuo no fractal se tiene D_T = D = E − 1. Podría muy bien suceder que el residuo dominara al polvo en sentido topológico y/o en sentido fractal. ▮

En la lámina 221 se muestran ejemplos de magnolias con tallos infinitamente delgados. No pueden tener vida, y su calidad como modelos de plantas se mejora sustancialmente en el capítulo 17. Sin embargo, los esqueletos arbóreos tienen bastante interés en muchos capítulos de la matemática. Según el topólogo son idénticos, pues para él cualquier árbol consiste en una infinidad de hilos elásticos, y nuestros árboles se pueden deformar los unos en los otros por estiramiento o por contracción. Sin embargo, intuitivamente estos árboles son distintos, y también lo son como fractales.

LAS PUNTAS DE LAS RAMAS. Un árbol es la suma de dos partes, las ramas propiamente dichas y las puntas de las ramas, cuyas dimensiones se entremezclan de un modo muy interesante. La parte más fácil de estudiar es el conjunto de las puntas. Es un polvo fractal parecido a muchos otros que ya conocemos bien. Es un escalante con N = 2 y un valor de r comprendido entre 1/√2 y 0. Por tanto, D vale entre 2 y 0, aunque los valores de D de los árboles representados varían sólo entre 1 y 2. El ángulo que forman las dos ramas que concurren en cada horcadura es siempre θ, y su valor puede variar en un intervalo bastante amplio sin que ello afecte a r ni a D. Por tanto, se puede tener una gran variedad de árboles con la misma D.

Si 1 < D < 2, el árbol se interseca a sí mismo para ε < θ_crit Así pues, la condición de que no haya autointersección limita la elección de θ. Para los árboles de la lámina 155, θ = θ_crit, pero en primer lugar razonaremos como si tuvieran θ = θ_crit + ε.

ÁRBOLES. A primera vista cada árbol como un todo parece autosemejante, pues cada rama con sus vástagos es una versión a escala reducida del todo. Sin embargo, la unión de las dos ramas que parten de la horcadura principal no da el árbol entero a menos que le añadamos un residuo. Intuitivamente, éste no es despreciable ni mucho menos. De hecho uno tiende a dar más importancia á los troncos y las ramas de los árboles que a las puntas de las ramas. Intuitivamente, las ramas «dominan» sobre las puntas.

Con independencia del valor de D, las puntas de las ramas de un árbol autoevitante forman un polvo, con D_T = 0, mientras que las ramas forman una curva, con D_T = 1, tanto si las puntas se consideran incluidas en las ramas como si no. Topológicamente, pues, las ramas dominan. ▯ En efecto, para desconectar un punto P de su entorno hay que borrar 1 (si P es una punta de rama), 2 (si P está en el interior de una rama) o 3 puntos (si P es una horcadura). ▮

Veamos ahora el punto de vista fractal. La dimensión de las puntas de las ramas es D, y la de cada rama es 1. Como conjunto no es escalante, pero su dimensión fractal, definida por la fórmula de Hausdorff-Besicovitch, no puede ser menor que D ni que 1, y resulta ser el mayor de ambos. Consideremos las dos posibilidades por separado.

ARBOLES FRACTALES. Si D > 1, la dimensión del árbol fractal completo también es D. Aun cuando las ramas predominen tanto intuitiva como topológicamente, ¡son insignificantes en sentido fractal! Como D > D_T el árbol es un conjunto fractal en el que D mide la abundancia de la ramificación. Nos encontramos, pues, con otra faceta de la dimensión fractal añadida a su papel de medida de la irregularidad y la fragmentación. Cuando en el capítulo 17 pasemos a los árboles no filiformes, nos encontraremos con que una superficie lisa que tenga un número suficiente de «granos» puntiagudos localizados puede convertirse en «algo más» que una superficie estándar.

ARBOLES SUBFRACTALES. Si 0 < D < 1, por el contrario, la medida lineal total (la longitud acumulada) del árbol es finita y positiva, con lo que su dimensión es necesariamente 1. Por tanto D = D_T, y el árbol no es fractal.

De hecho, si tomamos las unidades de modo que la longitud del tronco sea 1 − 2r, las ramas (consideradas como intervalos abiertos) se pueden disponer llenando los huecos de un polvo de Cantor lineal C contenido en [0,1], con el mismo N = 2 y la misma r que las puntas de las ramas. Análogamente, las puntas de las ramas se pueden disponer sobre C. Vemos que las imágenes de los puntos del árbol agotan completamente el intervalo [0,1]. Los únicos puntos del árbol que quedan excluidos en esta representación son las horcaduras, pero éstas forman un residuo numerable.

Recordemos el comentario de la lámina 121, en el sentido de que la curva Escalera del Diablo es peculiar sin ser fractal. Si la importancia de tales figuras aumenta, habrá que buscarles un nombre apropiado. Por el momento nos bastará con subfractales.

Como último comentario, sustituyamos las ramas rectilíneas por curvas fractales de dimensión D^* > 1. Si D < D^* las ramas dominan en lo que respecta a las propiedades fractales del árbol, y el árbol es un fractal de dimensión D^*. Pero si D > D^*, el árbol es un fractal de dimensión D.

Estamos ya preparados para una nueva definición. Diremos que un fractal F es uniforme si la intersección de F con cualquier disco (o bola) con centro en F tiene los mismos valores para D_T y para D > D_T.

Nos damos cuenta de que las curvas de Koch, los polvos de Cantor, las curvas ramificadas, etc., son fractales uniformes. Pero los esqueletos de los árboles fractales de la sección anterior con D > 1 son fractales no uniformes.

De hecho, se puede decir que los árboles son sólo parcialmente fractales: su intersección con un disco suficientemente pequeño con centro en un punto de una rama no es un fractal, sino que está formada por un intervalo o unos pocos.

Hasta aquí, hemos utilizado la lámina 221 para ilustrar árboles fractales apenas autoevitantes. En realidad, las puntas de esos árboles confluyen asintóticamente. A consecuencia de ello, el conjunto de las puntas de rama deja de ser un polvo con D_T = 0 para convertirse en una curva con D_T = 1, sin que cambie por ello su dimensión fractal. Propongo que a esta nueva clase de curvas fractales se las llame bóvedas fractales generalizadas. Nótese que la longitud de su sombra vertical aumenta con D.

Como la luz es de vital importancia para los árboles, es de esperar que las ramas que terminan en los pliegues de una bóveda fractal generalizada acaben por marchitarse. Un diseñador de árboles puede, bien dejar que algunas ramas crezcan y luego se marchiten por falta de luz solar, bien hacer un programa más complicado en el que estas ramas dejen de crecer. Yo me inclinaría por el programa más sencillo.

Cuando D < 1, la fusión de un polvo para dar una curva es inconcebible. Cuando se intenta llegar al autocontacto disminuyendo el ángulo de abertura θ, esto no se consigue hasta que θ = 0 y el árbol colapsa dando un intervalo. Si, como alternativa, se mantiene la sombra vertical del árbol constante e igual a 1, y se intenta llegar al autocontacto alargando las ramas, nunca se llega al resultado buscado: el árbol tiende a un polvo de Cantor lineal C, con semirrectas arrancando de cada punto del mismo.

Los árboles fractales construidos en las secciones anteriores no agotan todas las posibilidades. Recordemos, por ejemplo, la construcción de la página 203. Tomemos alternativamente como generador de Koch una cruz con ramas de longitudes r_s (superior), r_i (inferior) y r_l (laterales), de modo que r_s² + r_i² + 2r_l² < 1. Cada rama del árbol fractal resultante, por corta que sea, está llena de subramas. Si se excluye el punto raíz, el árbol es un escalante estará término residual.

Feynman (1979) cuenta que los árboles fractales le permitieron visualizar y modelizar los «haces» que se forman en los choques frontales de partículas a muy altas energías. Los informes del CERN de G. Veneziano profundizan en el estudio de esta idea.

LÁMINA 221. Magnolias y bóvedas fractales

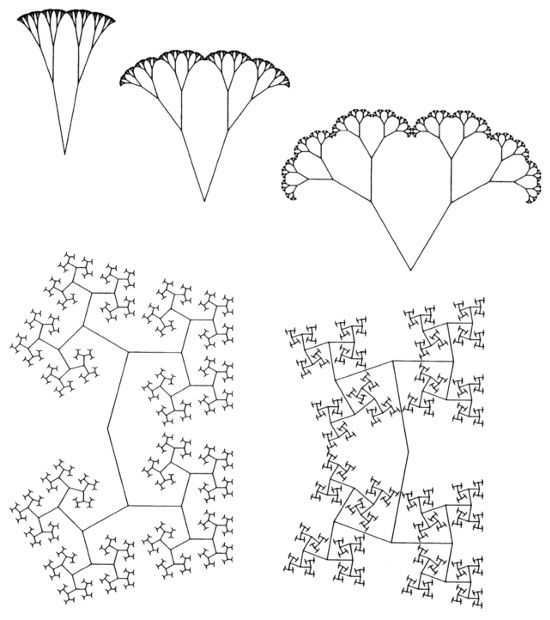
FIGURA 221

Los troncos y las ramas de los árboles de esta lámina son infinitamente delgados. El ángulo θ entre cada par de ramas es siempre el mismo. Las D varían entre 1 y 2 y, para cada D, θ toma el mínimo valor compatible con la condición de ser autoevitante.

Para D apenas superior a 1 (arriba a la izquierda), el resultado parece un pincel, después se va pareciendo más a una escoba. A medida que D aumenta, las ramas se abren y el perfil de la bóveda se extiende en pliegues ocultos a la luz solar. Nos recuerdan las flores de algunas variedades de la especie Brassica olerácea: la coliflor (B. o. botrytis) y el brécol (B. o. itálica). ¿Podría ser importante que parte de las diferencias geométricas entre la coliflor y el brécol fueran cuantificables por una dimensión fractal?

A un francés, el árbol con una D mayor (abajo a la izquierda) le evocaría las fortificaciones de Vauban. Los valores D = 2 y θ = π dan un árbol que llena un dominio plano. Para poder tomar θ > π (abajo a la derecha) hay que volver a disminuir la D, sustituyendo el parecido con una sombrilla por formas retorcidas dignas de las clásicas esculturas danzantes de la India.

En una de las figuras más famosas de On Growth and Form (Thompson, 1917) se presentan los cráneos de distintas especies de peces enlazados por una sucesión de transformaciones continuas y suaves, con un fondo euclídeo. Las transformaciones que convierten cada uno de estos árboles en el siguiente comparten una inspiración similar, pero el fondo es muy distinto.

16 Arboles, residuos escalantes y fractales no uniformes

16
Arboles, residuos escalantes y fractales no uniformes