En el capítulo 6 tratábamos las curvas planas de Koch que satisfacen D < 2 y carecen de puntos dobles, por lo que se las puede denominar autoevitantes o sin ramificaciones. A su vez, el capítulo 7 trataba de las curvas de Peano en las que, al pasar al límite, se llega inevitablemente a un conjunto denso por doquier de puntos dobles. En este capítulo abordaremos el paso siguiente y estudiaremos ejemplos de figuras autosemejantes con un grado de ramificación arbitrario: curvas planas con 1 < D < 2, curvas en el espacio con 1 < D < 3 y superficies con 2 < D < 3. Una curva ramificada autosemejante tiene una infinidad de puntos dobles.

La matemática de este capítulo es antigua (aunque sólo sea conocida por unos pocos especialistas), pero su aplicación a la descripción de la naturaleza es totalmente nueva.

Propongo la expresión tamiz de Sierpinski para referirnos a la figura de la lámina 141. En la lámina 143 se muestra una generalización tridimensional.

Hahn (1956) comenta lo siguiente: «Se dice que un punto de una curva es un punto de ramificación cuando la frontera de un entorno arbitrariamente pequeño corta la curva en más de dos puntos… La intuición parece indicar la imposibilidad de que una curva esté formada exclusivamente de… puntos de ramificación. Esta convicción intuitiva fue refutada por la curva de Sierpinski…, cuyos puntos son todos de ramificación».

De nuevo la opinión de Hahn carece por completo de originalidad, y su poco habitual «parece indicar» es una frase prudentemente elegida.

Tomo prestado de la ingeniería mi primer contraejemplo. (Como ya razoné antes de referirme a los ordenadores al final del capítulo 12, no tiene nada de ilógico que incluyamos los sistemas de la ingeniería de estructuras en esta obra que se ocupa de la naturaleza.)

Sostengo que (bastante antes de von Koch, Peano y Sierpinski) la torre que Gustave Eiffel construyó en París incorpora la idea de curva fractal llena de puntos de ramificación.

En una primera aproximación, la torre Eiffel está formada por cuatro estructuras en forma de A. Cuenta la leyenda que Eiffel escogió la A para expresar el Amor por su obra. Las cuatro Aes coinciden en el vértice y cada dos Aes vecinas tienen un lado común. A su vez, el conjunto está rematado por una torre recta.

Sin embargo, ni las Aes ni la torre están construidas con vigas macizas, sino con unos entramados colosales. Un entramado es una configuración de elementos interconectados, y no puede ser deformada sin deformar al menos uno de dichos elementos. Un entramado puede ser muchísimo más ligero que una viga cilíndrica que tenga la misma resistencia. Y Eiffel sabía que un entramado cuyos «elementos» son a su vez entramados es más ligero todavía.

El hecho, divulgado por Buckminster Fuller, de que la clave de la resistencia reside en los puntos de ramificación era algo conocido ya por los sofisticados diseñadores de las catedrales góticas. Cuanto más lejos se vaya en la aplicación de este principio más nos acercaremos al ideal de Sierpinski. Dyson (1966, pág. 646) presenta una extrapolación infinita del diseño de la torre Eiffel con la que un ex alumno de Sierpinski pretende introducir unas estructuras interplanetarias a la vez fuertes y de poco peso.

Volvamos a la naturaleza o, para ser más exactos, a una imagen de la naturaleza que se usa en física estadística. Yo creo que el estudio de la percolación en redes reclama figuras de la familia del tamiz de Sierpinski. En el capítulo 13, al empezar a tratar de este tema, afirmábamos que los racimos de percolación son fractales. Ahora digo además que la estructura ramificada del tamiz de Sierpinski es un modelo prometedor para la estructura de la espina dorsal de dichos racimos.

Los físicos juzgarán este modelo principalmente en función de que en seguida respondió a las expectativas: Gefen, Aharony, Mandelbrot y Kirkpatrick (1981) demuestran que el modelo permite realizar exactamente cálculos habituales en este terreno. Los detalles son, sin embargo, demasiado técnicos para presentarlos aquí, y las razones que originalmente motivaron mi afirmación siguen teniendo interés. Todo empezó con un cierto parecido que percibí entre el tamiz y la espina dorsal de un racimo, como se muestra en esta figura:

La característica más notable reside en las tremas que quedan vacías al eliminar los enlaces colgantes (cuando se reduce el racimo a su espina dorsal) y los racimos totalmente contenidos en el racimo de interés. En segundo lugar, en el capítulo 13 se demuestra que la forma en que el tamiz de Sierpinski es autosemejante es una propiedad muy deseable para un modelo geométrico de los racimos de percolación. Finalmente, ¡la dimensión cuadra con un grado de precisión que difícilmente puede ser casual! S. Kirkpatrick estima que D ~ 1,6 en el plano, sorprendentemente próxima a la D del tamiz de Sierpinski. Y en el espacio D ~ 2,00, sorprendentemente próxima a la de la red fractal oblicua de la lámina 205. Además, en Gefen, Aharony, Mandelbrot y Kirkpatrick (1981) se señala que la igualdad entre la D de la espina dorsal y la del tamiz generalizada se mantiene en R⁴. Más adelante se presenta una razón más en favor del modelo de tamiz, como una última aplicación de la ramificación.

Pasemos ahora de las redes triangulares a las ortogonales. Permiten una gran variedad de diseños, dando curvas en el plano o en el espacio, o superficies en el espacio. Y las curvas que resultan, a pesar de tener un parecido superficial con el tamiz de Sierpinski, son muy distintas en lo que se refiere al aspecto fundamental de la ramificación, sobre el que volveremos después de definirlas.

La generalización inmediata al plano del método cantoriano de borrar el tercio central se inicia con un cuadrado y viene descrito en el pie de la figura 205. El fractal que se obtiene al iterar indefinidamente el proceso es conocido familiarmente como alfombra triádica de Sierpinski. Su dimensión es D =log 8/log 3 = 1,8927.

Dado un entero b > 3, tomamos como de costumbre r = 1/b, y obtenemos una alfombra con «un gran medallón central», si se toma como iniciador un cuadrado, como trema un cuadrado de lado 1 − 2r concéntrico con el anterior, y como generador un anillo delgado de 4(b − 1) cuadrados de lado r. La dimensión es D = log [4(b − 1)]/log b. Dado un entero impar b > 3, se obtiene una alfombra con «un pequeño medallón central», si se toma como trema un cuadrado de lado r concéntrico con el iniciador y como generador un anillo grueso de b³ − 1 cuadrados menores. La dimensión es D = log (b³ − 1)/log b. Así pues, con una alfombra centrada se puede alcanzar cualquier D arbitraria comprendida entre 1 y 2.

Para b ≥ 2 se pueden definir alfombras descentradas. Así, por ejemplo, con b = 2 y N = 3 se puede colocar una trema consistente en un subcuadrado situado en la parte superior derecha. El conjunto límite correspondiente resulta ser un tamiz de Sierpinski formado por el triángulo rectángulo isósceles de la mitad inferior izquierda del iniciador.

La generalización espacial inmediata de la alfombra triádica consiste en tomar como trema el cubito veintisieteavo central, dejando como residuo una cascara de 26 cubitos. El fractal resultante tendría que llamarse espuma fractal triádica, y su dimensión es D = log 26/log 3 = 2,9656.

En este caso cada trema está totalmente contenida en el interior de una envoltura ininterrumpida que, a su vez, se escinde en una infinidad de capas, infinitamente delgadas e infinitamente densas. Para unir dos puntos pertenecientes a dos tremas distintas hay que cruzar una infinidad de capas. Me hace pensar en la «espuma espaciotemporal» que, según J. A. Wheeler y S. W. Hawking, caracteriza la estructura íntima de la materia, aunque no domino el tema lo bastante para exponerlo aquí.

Karl Menger toma una trema distinta, en forma de cruz con dos salientes, uno por delante y otro por detrás. El generador consiste en n = 20 cubitos de lado 1/3 conectados entre sí. Doce de ellos forman «barras» o cuerdas, y los ocho restantes son nudos o empalmes. El límite (lámina 207) tiene una D = log 20/log 3 = 2,7268. Lo llamo esponja porque tanto la coagulación como el suero son conjuntos conexos. Se podría pensar en una corriente de agua que fluyera entre dos puntos cualesquiera del suero.

Para obtener una mezcla de cuerdas y membranas, hay que tomar como trema una cruz triádica con una punta saliente hacia delante. Si se va cambiando cada vez la dirección de este saliente, se acaba por obtener una serie de membranas pinchadas. Quizá valga la pena apuntar aquí que pensé en todas esas formas antes de leer a Menger, cuando estaba buscando modelos de intermitencia turbulenta.

Dada una base no triádica b > 3, se obtienen esponjas de Menger generalizadas con tremas formadas por la reunión de tres prismas cuadrados cuyos tres ejes coinciden con los del cubo unidad, de altura 1, y con las aristas básales paralelas a las del cubo. Cuanto más largo es el lado de las bases de dichos prismas, más «ligera» es la esponja resultante. Para E = 3, dicho lado vale 1 − 2/b, y el generador resultante consiste en 12b − 16 cubitos de lado r = 1/b. Así pues, la dimensión es D = log(12b − 16)/log b. De modo análogo, se puede obtener una esponja «gruesa», aunque sólo con b impar, con prismas cuadrados de base de lado 1/b. Si E = 3, el generador que queda consiste en b³ − 3b + 2 cubitos de lado 1/b. En este caso, D = log(b³ − 3b + 2)/log b.

Las espumas fractales se generalizan de modo análogo. Para E = 3, las espumas de «pared gruesa» dan D = log(b³ − 1)/log b, y las espumas de «pared delgada» dan D = log(6b² − 12b + 8)/log b. Para agujeros grandes y D próxima a 2, la espuma se parece a un queso Emmenthal ultraligero, mientras que para agujeros pequeños y D próxima a 3 se parece a un Appenzell.

Las tremas de las esponjas están conectadas entre sí, pero las de las alfombras y espumas están separadas como los huecos de un polvo de Cantor (capítulo 8). La distribución de sus escalas lineales satisface

donde F es una constante. Ya estudiamos a fondo esta ley para el caso del polvo de Cantor y las islas y racimos del capítulo 13.

Las celosías de la geometría estándar están formadas por líneas paralelas que limitan cuadrados, triángulos u otras figuras regulares iguales. El mismo término se puede aplicar a los fractales regulares en los que dos puntos cualesquiera pueden enlazarse al menos por dos caminos que no tienen ningún otro punto común. Si el grafo no es regular, como en el caso aleatorio, cambiaré el término celosía por malla.

Sin embargo, un examen más detenido de las celosías fractales y las estándar pone de manifiesto diferencias importantes. La primera de ellas es que las celosías estándar son invariantes por traslación pero no por cambio de escala, mientras que para las celosías fractales vale lo contrario. Una segunda diferencia es que si se contrae cualquier celosía estándar converge hacia el plano entero. Además, algunas celosías planas estándar pueden interpolarse añadiendo nuevas líneas equidistantes y paralelas a cada par de líneas ya existentes. Este proceso puede repetirse indefinidamente y el límite es otra vez todo el plano. Análogamente, cuando una celosía estándar en el espacio puede ser interpolada, el límite es también todo el espacio. Así pues, el límite no es una celosía. En el contexto fractal, por el contrario, el límite de una celosía fractal aproximada es una celosía fractal.

El término celosía fractal ramificada puede aplicarse también a las espumas fractales.

UNA REGLA BÁSICA. En muchos estudios de fractales es importante conocer las dimensiones de las secciones lineales y planas. El hecho básico (empleado ya en el capítulo 10 para demostrar que en la turbulencia D > 2) se refiere a la intersección de una figura fractal plana con un intervalo «independiente del fractal». Se tiene que, si la sección es no vacía, es «casi seguro» que la dimensión es D − 1.

EXCEPCIONES. Por desgracia es muy difícil ilustrar este resultado en el caso de fractales no aleatorias con ejes de simetría. Los intervalos que uno tendería a considerar paralelos a dichos ejes (es obvio que se trata de intervalos atípleos) y casi todas las intersecciones pertenecen al conjunto excepcional en que la regla general falla.

Tómense, por ejemplo, la alfombra de Sierpinski, la esponja triádica de Menger y la espuma triádica. La dimensión casi segura, D − 1 , de las secciones de estas figuras a intervalos son respectivamente:

Por otra parte, sea x la abscisa de un intervalo paralelo al eje y de la alfombra de Sierpinski. Si la expresión de x en base 3 acaba en una sucesión ininterrumpida de ceros o doses, las secciones son a su vez intervalos, con lo que D = 1, que es más de lo esperado. Por el contrario, si x acaba en una sucesión ininterrumpida de unos, las secciones son polvos de Cantor, con lo que D = log 2/log 3, que es demasiado poco. Y si x acaba en una sucesión periódica de longitud M formada por pM unos y (1 − p)M ceros o doses, la dimensión de la sección es p(log 2/log 3) + (1 − p). El valor que esperaríamos para D se obtiene para p ~ 0,29. ▯ Lo mismo pasa si la sucesión de cifras es aleatoria. ▮ Aquí aparecen, pues, tres dimensiones, la máxima, la mínima y la media.

En lo que respecta al tamiz de Sierpinski, la D casi segura es log(3/2)/log 2, pero los valores de D que se obtienen con los cortes «naturales» varían entre 0 y 1. Por ejemplo, un intervalo corto que corte casi perpendicularmente uno de los lados del tamiz por su punto medio sólo lo cortará en ese punto, con lo que D = 0.

En parte, la variabilidad de estas secciones especiales es atribuible a la regularidad de las figuras originales. Pero por otra parte es inevitable: el concepto de sección más económica (y no necesariamente por un segmento de recta) está en la base de los conceptos de dimensión topológica y de orden de ramificación, que pasamos a considerar a continuación.

Como ya se ha dicho, en este ensayo curva es sinónimo de «figura conexa de dimensión topológica D_T = 1». De hecho, esta frase no acaba de satisfacer a los matemáticos, y una definición más precisa es algo bastante delicado. Afortunadamente, en el capítulo 6 nos bastaba con dar alguna razón por la cual cualquier curva de Koch que tenga [0,1] por iniciador merezca ser llamada curva, como el propio [0,1], que es conexo pero se hace disconexo si le quitamos un punto cualquiera distinto de 0 o 1. El contorno de un copo de nieve es como un círculo, conexo, pero se convierte en disconexo si le quitamos un par cualquiera de puntos.

Ahora nos hará falta una definición algo más rebuscada de la dimensión topológica. Es una definición recurrente. El conjunto vacío tiene D_T = −1. Para cualquier otro conjunto S, el valor de D_T es una unidad mayor que la menor D_T de cualquier subconjunto de S que al ser eliminado lo convierta en disconexo. Así, los conjuntos finitos y los polvos de Cantor fienen D_T = 1 − 1 = 0, pues no hay que quitarles nada (el conjunto vacío) para hacerlos disconexos. Y los siguientes conjuntos se hacen disconexos quitándoles una parte con D_T = 0: el círculo, [0,1], el contorno de un copo de nieve, el tamiz de Sierpinski, la alfombra de Sierpinski, las esponjas de Menger. (En los tres últimos casos basta con evitar las intersecciones especiales que dan lugar a segmentos enteros.) Por tanto, todos estos conjuntos tienen D_T = 1.

Una demostración alternativa de que D_T = 1 para el tamiz, las alfombras y las esponjas que tienen D < 2, se basa en que D_T es un entero menor o igual que D. Ahora bien, como D < 2, D_T sólo puede ser 1 o 0. Pero los conjuntos en cuestión son conexos y, por tanto, D_T no puede ser menor que 1. La única posibilidad es D_T = 1.

La dimensión topológica y los conceptos asociados de polvo, curva y superficie nos proporcionan sólo un primer nivel de clasificación. En efecto, dos conjuntos finitos que contengan respectivamente M' y M'' puntos tienen la misma D_T = 0, pero topológicamente son distintos. Y un polvo de Cantor es distinto de cualquier polvo finito.

Veamos ahora cómo una distinción parecida, basada en el número de puntos de un conjunto ▯ su cardinal ▮ puede aplicarse a las curvas, dando lugar al concepto topológico de orden de ramificación, definido por Paul Urysohn y Karl Menger a principios de los años veinte. Este concepto no es citado en muchos textos matemáticos, aparte de los de sus pioneros, pero está resultando cada vez más indispensable en la física, con lo que se va haciendo cada vez más conocido tras haber sido domesticado. Demuestra que las razones para estudiar primero un tamiz y después una alfombra son más profundas que las meramente estéticas o la búsqueda de la completitud.

El orden de ramificación considera la parte de S con el menor número de puntos que hay que sacar para convertir S en disconexo. Y considera por separado el entorno de cada punto de S.

EL CÍRCULO. Empecemos tomando para S una figura de la geometría estándar: una circunferencia de radio 1. Si P es un punto de dicha circunferencia, una circunferencia B con centro en P corta S en R = 2 puntos, excepto si el radio de B es mayor que 2, en cuyo caso R = 0. El círculo delimitado por B es lo que se llama un entorno de P. Así, cualquier punto P tiene entornos arbitrariamente pequeños cuyas fronteras cortan S en R = 2 puntos. Esto es todo lo más que se puede conseguir: si B es la frontera de un entorno genérico de P, no necesariamente circular, pero «no demasiado grande», R es por lo menos 2. La expresión «no demasiado grande» del enunciado anterior es una complicación, pero por desgracia es inevitable. Se dice que el orden de ramificación del círculo es R = 2. Notemos que es el mismo para todos los puntos del círculo.

EL TAMIZ. A continuación, tomemos para S un tamiz de Sierpinski, construido por el procedimiento de las tremas. Ahora R ya no vale lo mismo para todos los P. Demostraremos, siguiendo a Sierpinski, que, excepto para los vértices del iniciador, R puede valer 3 = R_mín o 4 = R_máx.

El valor R = 4 se obtiene para los vértices de cualquier aproximación finita a S por medio de triángulos. Un vértice de una aproximación de orden h ≥ k es el vértice común P de dos triángulos de lado 2^−k. Como antes, una circunferencia de radio 2^−k con h > k corta a S en 4 puntos y delimita un entorno arbitrariamente pequeño de P. Y si B delimita un entorno «suficientemente pequeño» de P (en el nuevo sentido de que los vértices del iniciador caigan fuera de B) se puede demostrar que corta S en 4 puntos por lo menos.

El valor R = 3 se obtiene para los puntos de S procedentes del límite de una sucesión infinita de triángulos, cada uno contenido en su predecesor y con vértices distintos de los de este último. Los círculos circunscritos a estos triángulos cortan S en 3 puntos y definen entornos de P arbitrariamente pequeños. Se tiene también que, si B delimita un entorno de P «suficientemente pequeño» (como antes, los vértices del iniciador deben quedar fuera de B), se puede demostrar que B corta S en 3 puntos por lo menos.

LAS ALFOMBRAS. Si S es una alfombra de Sierpinski, el resultado es radicalmente distinto. La frontera de cualquier entorno suficientemente pequeño corta S en una infinidad no numerable de puntos, independientemente de los parámetros N, r o D.

COMENTARIO. En esta dicotomía finito o infinito, el tamiz se comporta como las curvas estándar, mientras que la alfombra no es diferente del plano.

HOMOGENEIDAD, UNICIDAD. Denotando por R_mín y R_máx los valores mínimo y máximo que toma R en los puntos de S, Urysohn demuestra que R_máx > 2R_mín − 2. Se dice que la ramificación es homogénea cuando se tiene R_máx = R_mín; este es el caso cuando R ≡ 2, como en las curvas simples cerradas, y cuando R ≡ ∞.

Para otras celosías con R_máx = 2R_mín − 2, propongo el término cuasihomogéneas. Un ejemplo sencillo y famoso, el tamiz de Sierpinski, es autosemejante. Los otros ejemplos no aleatorios forman parte de una colección construida por Urysohn (1927), y no son autosemejantes. Así pues, sólo se conoce un caso en que concurran las condiciones de cuasihomogeneidad y autosemejanza, el tamiz de Sierpinski. ¿Se podría confirmar rigurosamente esta unicidad aparente?

CELOSÍAS ESTÁNDAR. En estos casos el orden de ramificación varía entre un mínimo de 2 para los puntos que no son verdees de la celosía y un máximo finito y variable para los vérfices: 4 (celosías cuadradas), 6 (celosías triangulares y cúbicas) o 3 (celosías hexagonales). Sin embargo, si reducimos la escala de cualquier celosía estándar, ésta pasa de curva a dominio plano, y su ramificación se hace R = ∞.

Este último hecho queda más claro cambiando lo infinitamente pequeño por lo infinitamente grande. Si dejamos fijo el tamaño de las celdas de la celosía, observamos qué para aislar una parte cada vez mayor de la misma hay que cortar un número cada vez mayor de puntos.

DEFINICIÓN FORMAL. ▯ Véase Menger (1932) y Blumenthal y Menger (1970, pág. 442). ▮

Hagamos frente ahora a una pregunta ya repetida. Sea cual sea el interés que puedan tener las figuras de Sierpinski y Menger para los matemáticos, ¿no es evidente que podrían no tener ningún interés para el estudioso de la naturaleza? La respuesta es tan conocida —¡para nosotros!— como la propia pregunta. El orden de ramificación ya es importante en el «mundo real» de las aproximaciones finitas que se obtienen cuando el proceso de interpolación que tiende a un fractal se detiene en un cierto corte inferior, ε.

En efecto, dado un tamiz de Sierpinski aproximado, formado por triángulos rellenos de lado £, un dominio cuya escala lineal sea superior a ε se puede aislar del resto sacando 3 o 4 puntos, cada uno de los cuales pertenece a las fronteras de dos huecos vecinos. Este número (3 o 4) no cambia si se refina la aproximación. Por esta razón, todos los tamices aproximados presentan, desde el punto de vista de la ramificación, un comportamiento semejante al de las curvas.

Por el contrario, todas las alfombras tienen la propiedad de que las fronteras de dos agujeros cualesquiera son disjuntas. Para desconectar una aproximación finita de esa figura, en la que no se denen en cuenta los agujeros de diámetro menor que ε, hay que sacar segmentos enteros. El número de éstos aumenta cuando ε → 0. Whyburn (1958) demuestra que todas las curvas fractales que tienen esta propiedad son topológicamente idénticas ▯ homeomorfas ▮ y se caracterizan por no tener ninguna parte que pueda aislarse del resto quitando un único punto.

Debido a los comentarios precedentes, no es ninguna sorpresa que la finitud de la ramificación tenga consecuencias claras cuando se invoca la geometría fractal para cuanfificar la diferencia entre una cierta curva fractal y sus dos límites en geometría estándar, a saber, la recta y el plano. En general, no basta con conocer la dimensión fractal. Por ejemplo, en Gefen, Mandelbrot y Aharony (1980) se estudian los fenómenos críticos para modelos de Ising en una red fractal y se encuentra que la propiedad más importante ▯ si la temperatura crítica es 0 o positiva ▮ depende de la finitud de R.

Estamos ahora ya en condiciones de dar una explicación que habíamos postergado. La razón por la cual la espina dorsal de un racimo en la percolación de Bernouilli crítica parece modelarse mejor con un tamiz que con una alfombra se basa en el siguiente resultado de Kirkpatrick (1973). Aun en el caso de redes muy grandes, se puede cortar una espina dorsal crítica eliminando un pequeño número de enlaces, esencialmente constante, del orden de 2. Aun teniendo en cuenta los posibles márgenes de error, parece que este resultado indica muy claramente que R < ∞.

Hay dos variantes del copo de nieve de Koch en las que se consigue la ramificación empleando ramas sin lazos. La primera es una curva plana que se obtiene con un cuadrado como iniciador y con el generador

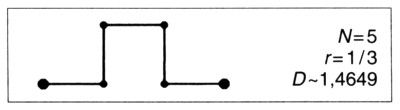
La figura resultante, que mostramos a continuación de estas líneas, es completamente distinta del copo de nieve.

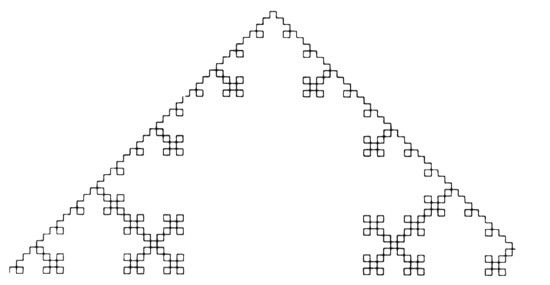
El ejemplo siguiente es una superficie de volumen cero, área infinita y dimensión log 6/log 2 = 2,58497. El iniciador es un tetraedro regular. Sobre el cuarto central de cada cara (= el triángulo que tiene por vértices los puntos medios de los lados) se monta un tetraedro semejante al anterior con razón 1/2. Se repite el proceso con cada cara del 24-edro regular cóncavo resultante, y así sucesiva e indefinidamente. A partir del segundo estadio los tetraedros añadidos presentan líneas de autocontacto, sin intersecarse entre sí. Al final acaban recubriendo todo el iniciador. Llamaremos pirámide de Koch a cada cuarto de esta figura.

Una pirámide de Koch es una figura maravillosa, aparentemente simple, pero que presenta un sinfín de cámaras ocultas que desafían la imaginación.

Vista desde arriba, es un tetraedro con un triángulo equilátero por base cuyas otras tres caras son triángulos rectángulos isósceles unidos por los vértices correspondientes a los ángulos rectos. Si se colocan tres pirámides de Koch sobre los lados de un tetraedro regular, se obtiene una caja cúbica.

Levantemos ahora esa pirámide del suelo del desierto. Desde una cierta distancia, vemos que su base se subdivide en cuatro triángulos equiláteros iguales, pero en vez del triángulo central encontramos la entrada a una «cámara de primer orden», en forma de tetraedro regular cuyo cuarto vértice coincide con la cúspide de la pirámide. Si a continuación nos aproximamos un poco para apreciar mejor los detalles, nos encontramos con que los triángulos regulares que forman los cuartos periféricos de la base y las paredes de la cámara de primer orden tampoco son lisos. Cada uno se abre a una cámara tetraédrica de segundo orden, cuyas caras presentan a su vez una cámara de tercer orden en su parte central. Y así van apareciendo generaciones sucesivas de cámaras cada vez más pequeñas.

La suma de los volúmenes de todas las cámaras es precisamente el volumen de la pirámide de Koch. Por otro lado, si consideramos las cámaras con sus bases pero sin las otras tres caras, entonces no se solapan. Si la pirámide tuviera que ser excavada en un terraplén, los excavadores deberían vaciar todo el volumen, dejando sólo la cascara. La curva del plano de la base sobre la que se apoyaría esta superficie, así como las «paredes» de las cámaras, serían tamices de Sierpinski.

Lieb y Lebowitz (1972) hacen una aportación inconsciente a la geometría fractal, rellenando R^E con bolas cuyos radios son de la forma ρ_k = ρ₀r^k, con r < 1; el número de bolas de radio ρ_k por unidad de volumen es de la forma n_k = n₀ν^k, siendo ν un entero de la forma ν = (1 − r)r^−E, que nos da una restricción fuerte sobre r. Así pues, el exponente de la distribución de los tamaños de los huecos es

Se empieza tomando esferas grandes de radio ρ, y centros en los vértices de una celosía de lado 2ρ₁. Fuera de estas esferas hay bastantes vértices de una celosía de radio 2ρ₂ para tomarlos como centros de una segunda generación de esferas, y así sucesivamente. El proceso de construcción establece las siguientes cotas superiores para r:

En el relleno de R3 con bolas no solapantes se puede proceder más rápidamente. Por ejemplo, en la línea el máximo de r es 1/3, ¡el valor que corresponde a un polvo triádico de Cantor! La existencia de polvos de Cantor con r > 1/3 prueba que el relleno unidimensional puede dejar residuos de una dimensión arbitrariamente pequeña. Sin embargo, un relleno más apretado implica una estructura más rica.

El orden de ramificación R, junto con las dimensiones D_T y D, no bastan para caracterizar del todo un fractal. El concepto adicional de lagunaridad, introducido por mí, es de especial importancia. Los huecos de un fractal muy lagunar son muy grandes, y viceversa. Las definiciones básicas podrían haberse presentado aquí, pero es mejor dejarlas para el capítulo 34.

LÁMINA 204. Puntra de fecha de Sierpinski (dimensión de la frontera D ~ 1,5849)

En Sierpinski (1915) el iniciador es [0,1] y el generador y el segundo terágono son

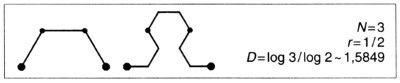
Los siguientes estadios de la construcción son

La costa de la porción superior de la figura 204 (por encima del mayor triángulo relleno de negro) nos da el aspecto de un estadio avanzado de la construcción.

AUTOCONTACTOS. Los estadios de orden finito de la construcción no presentan puntos de autocontacto, igual que en el capítulo 6, pero la curva límite tiene una infinidad de ellos.

PUNTAS DE FLECHA EMBALDOSANTES. La punta de flecha de la lámina 141 (puesta de lado se convierte en un pez tropical) se define como el sector de la curva de Sierpinski comprendido entre dos pasos sucesivos por un punto de autocontacto, por ejemplo, el punto medio del intervalo [0,1]. Las puntas de flecha embaldosan el plano, y las baldosas contiguas se engarzan por una especie de velero extrapolado hasta la pesadilla. (Mezclando las metáforas, las aletas de un pez encajan exactamente con las de otros dos peces.) Además, uniendo cuatro baldosas vecinas convenientemente escogidas se obtiene otra baldosa dos veces mayor.

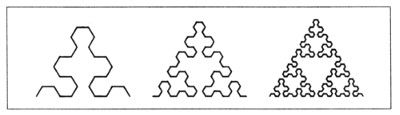
LAS TREMAS DEL TAMIZ DE SIERPINSKI. Llamo «tamiz» a la curva de Sierpinski porque hay una construcción alternativa, basada en extraer «tremas». Éste es un método que se utiliza continuamente en los capítulos 8, 31 y 35. El tamiz de Sierpinski se obtiene con el iniciador, el generador y los dos estadios sucesivos que se muestran a continuación:

Este generador de tremas contiene el generador poligonal presentado más arriba como subconjunto propio.

LA CUENCA. Me encontré por primera vez con la curva «punta de flecha» sin tener conocimiento del trabajo de Sierpinski, cuando estudiaba cierta cuenca en Mandelbrot (1975m).

FIGURA 204

LÁMINA 205. Una telaraña fractal oblicua (dimensión D = 2)

FIGURA 205

Esta telaraña se obtiene por un proceso iterativo, con N = 4 y r = 1/2, tomando un tetraedro cerrado como iniciador y un conjunto de tetraedros como generador.

Su dimensión es D = 2. Proyectémoslo según la dirección de un segmento que una los puntos medios de dos lados opuestos. El tetraedro iniciador se proyecta sobre un cuadrado, al que llamaremos inicial. Cada tetraedro de la segunda generación se proyecta sobre un subcuadrado, que cubre 1/4 del cuadrado inicial, etc. De este modo, la telaraña se proyecta sobre todo el cuadrado inicial. Las fronteras de los subcuadrados se solapan.

LÁMINA 207. La alfombra de Sierpinski (dimensión D ~ 1,8928) y la esponja de Menger (dimensión D ~ 2,7268)

LA ALFOMBRA DE SIERPINSKI. En Sierpinski (1916), el iniciador es un cuadrado macizo, mientras que el generador y los dos pasos siguientes son

N = 8, r = 1/3, D ~ 1,8928

El área de esta alfombra es nula, en tanto que el perímetro total de los agujeros es infinito.

FIGURA 207. LA ESPONJA DE MENGER. El mecanismo de construcción resulta obvio. Proseguido indefinidamente deja como residuo lo que se llama una esponja de Menger. Lamento haberlo atribuido equivocadamente a Sierpinski en ensayos anteriores (reproducido de Studies in Geometry, de Leonard M Blumenthal y Karl Menger, con la autorización de la editorial W. H. Freeman & Co., copyright 1970). Las intersecciones de la esponja con las diagonales y las medianas del cubo inicial son conjuntos triádicos de Cantor.

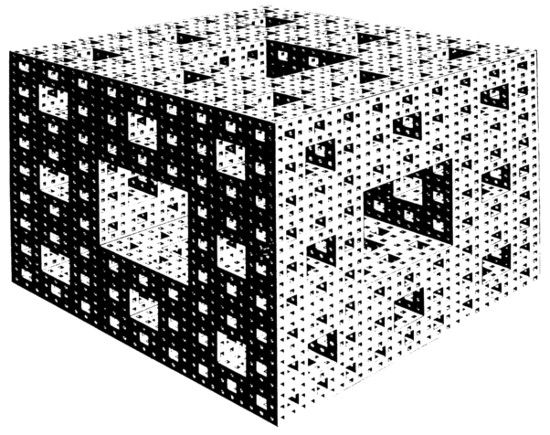
FIGURA 207

ISLAS FUSIONADAS. La alfombra, así como el tamiz de la figura 205, se pueden obtener también por otra generalización de la iteración de Koch en la que se permite el autosolapamiento, aunque las partes solapadas se cuentan sólo una vez.

Para obtener un tamiz el iniciador es un triángulo equilátero y el generador es el de la izquierda. Para obtener una alfombra, el iniciador es un cuadrado y el generador el de la derecha.

Nos encontramos de nuevo con dos fenómenos que ya aparecieron en el capítulo 13: la costa de cada isla es rectificable, con lo que su dimensión es 1, y la dimensión del tamiz o de la alfombra expresa el grado de fragmentación de la tierra firme en islas en vez de la irregularidad de las costas de éstas.

Sin embargo, el resultado es algo distinto. En el capítulo 13 el mar es conexo, cosa que parece una interpretación topológica correcta del espacio abierto náutico. También es abierto en el sentido topológico de no contener su frontera. La novedad introducida por esta construcción es la posibilidad de que las islas de Koch se «fusionen» asintóticamente en una superisla maciza: no hay continente y las costas se enlazan formando una celosía.

▯ Topológicamente hablando, la alfombra de Sierpinski es una curva plana universal y la esponja de Menger es una curva espacial universal. Esto es, (véase Blumenthal y Menger, 1970, págs. 433 y 501) estas figuras son respectivamente la curva plana más complicada y la curva más complicada en un espacio de dimensión superior. ▮

LÁMINA 208. Los salones del Palacio del Copo de Nieve (dimensión D ~ 1,8687)

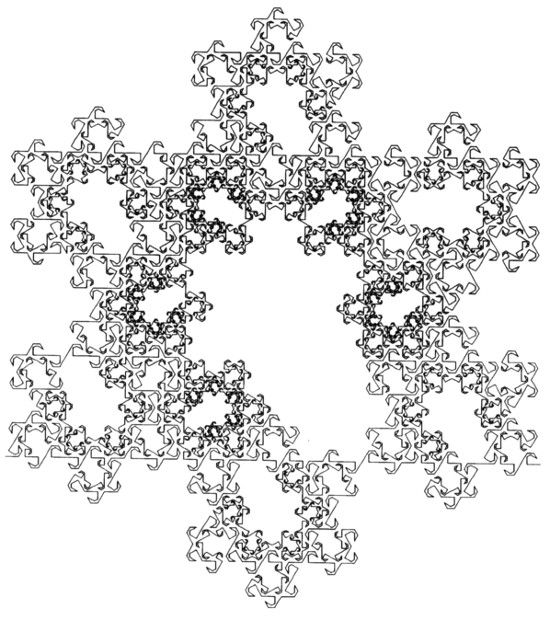
FIGURA 208

En un país y una época muy lejanas, el Gran Señor y su séquito asentaron su poder en los espléndidos salones del Palacio del Copo de Nieve. Se produjo un cisma, seguido de una guerra que llegó a un punto muerto, hasta que los Ancianos trazaron una línea que dividía los salones entre ambos bandos, el Norte y el Sur.

ENIGMAS DEL LABERINTO. ¿Quién controla el Gran Salón y cómo se llega a él desde el exterior? ¿Por qué algunos salones no están orientados hacia ninguno de los puntos cardinales? Para pistas, véase el Árbol de los Monos de la lámina 57.

14 La ramificación y las redes fractales

14
La ramificación y las redes fractales