Este capítulo está dedicado a las σ-curvas fractales, esto es, a fractales que se descomponen en una infinidad de fragmentos disjuntos, cada uno de los cuales es una curva conexa. Los casos concretos a considerar abarcan desde las costas de las islas de un archipiélago hasta un problema importante de la física, la percolación. El material de algunas de las primeras secciones está tomado del Fractals de 1977, y el grueso del resto del capítulo es nuevo.
Para empezar, volvamos a la cuestión de cuánto mide la costa de Bretaña y preguntémonos cuántas islas hay alrededor de la costa de Bretaña. Con toda seguridad su número es muy grande y también está mal determinado. A medida que vayamos incluyendo pequeños islotes en la lista de islas, ésta se alargará más y más, y el número total de islas resultará ser prácticamente infinito.
Como el relieve terrestre está finamente «arrugado», no cabe duda de que el área total de una isla, al igual que la longitud de una costa, es geográficamente infinita. Pero a los dominios delimitados por las costas les corresponden «áreas planas» bien definidas. Y una característica geográfica importante es el modo en que una cierta área plana total se reparte entre las diversas islas. Se podría incluso aducir que esta relación «área-número» contribuye más a la forma geográfica que las formas de las costas individuales. Así, por ejemplo, se hace difícil pensar en las costas del mar Egeo sin considerar también las de las islas griegas. El tema merece, pues, un estudio cuantitativo, y en este capítulo haremos uno basado en una generalización de las curvas de Koch.
Luego se estudian también otras figuras fragmentadas obtenidas por generalización de los procesos generadores de fractales ya conocidos, bien sea por el método de Koch o el de coagulación. Las figuras resultantes se denominan aquí racimos de contacto y se demuestra que tienen la misma relación diámetro-número que las islas.
Tienen especial interés los racimos de contacto que llenan el plano, y en particular los generados por ciertas curvas de Peano cuyos terágonos no se cortan a sí mismos, pero cuyos puntos de autocontacto están cuidadosamente controlados. ¡La epopeya de la doma de los monstruos de Peano se enriquece así con una nueva escena!
Y finalmente, aunque no por ello es menos importante, veremos también en este capítulo la primera parte del estudio de la geometría de la percolación, fenómeno físico de gran importancia que también estudiaremos en el capítulo 14.
Generalización de la ley empírica de Korčak
Hagamos una lista de todas las islas de una región por orden decreciente de tamaños y sea Nr (A > a) el número de ellas de tamaño mayor que a ▯ notación análoga a Pr (A > a) de la teoría de la probabilidad. ▮ Aquí a será un posible valor del área plana de una isla y A denota la variable «área plana».
Se encuentra la sorprendente relación siguiente:
Nr (A > a) = F'a−B
donde F' y S son dos constantes positivas que llamaremos prefactor y exponente. Casi habría que atribuir esta ley a Korčak (1938) (el nombre se pronuncia Kor’chak), si no fuera porque sostiene que B = 112, afirmación que me pareció increíble y que los datos probaron infundada. En realidad, B varía de una región a otra y es siempre > 1/2. Permítaseme ahora mostrar que la ley generalizada de más arriba es el equivalente de la distribución que se obtiene en el capítulo 8 para las longitudes de los huecos de un polvo de Cantor.
Continentes e islas de Koch y sus diversas dimensiones
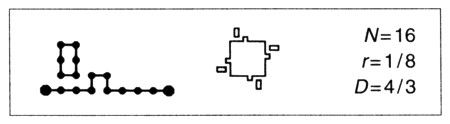
Con objeto de producir un equivalente de Koch de los huecos de Cantor, tomaré un generador formado por varias porciones inconexas. Y para asegurarme de que el fractal límite se pueda seguir interpretando en términos de costas, una de estas porciones del generador será una línea quebrada conexa de NC < N enlaces, uniendo los extremos del intervalo [0,1]. Esta parte la llamaré generador de la costa, pues determina la transformación de una costa inicialmente recta en otra fractal. Los demás N – NC enlaces forman un circuito cerrado que «siembra» nuevas islas y que llamaremos generador de islas. He aquí un ejemplo:

En estadios posteriores, la subisla siempre se mantiene a la izquierda del generador de la costa (yendo de 0 a 1) y del generador de islas (recorrido en el sentido de las agujas del reloj).
Una primera novedad es que en la fractal límite aparecen ahora dos dimensiones distintas. Juntando todas las costas de las islas se tiene D = log N/log(1/r), pero para la costa de cada isla por separado resulta DC = log NC/log(1/r), con las desigualdades
1 < DC < D.
Al no ser conexa, la costa total no es una curva, sino una suma (∑, sigma) infinita de circuitos. Propongo que se la llame sigma-circuito o, abreviadamente, σ-circuito.
Nótese que para modelizar la relación observada entre D y DC en las islas reales harían falta otras hipótesis adicionales, a menos que se pudieran deducir de una teoría, como en el capítulo 29.
La relación diámetro-número
La demostración de la validez de la ley de Korčak para las islas de la sección anterior es muy simple cuando el generador sólo tiene una isla y los terágonos son autoevitantes. (Recuérdese que los terágonos son las líneas quebradas que aproximan la curva.) En tal caso, el primer paso de la iteración produce una isla. Sea λ0 su «diámetro», definido como √a. El segundo paso crea N islas de diámetro λ0, Y en el estadio m-ésimo se crean Nm islas de diámetro λ = rmλ0. Globalmente, cuando se multiplica λ por r, Nr (Λ > λ) queda multiplicado por N. Por tanto, la distribución de Λ (para los valores de λ de la forma rλ0) tiene la forma
Nr(Λ > λ) = Fλ−D,
¡en la que el exponente decisivo es la dimensión fractal de la costa! Y como corolario
Nr(A > a) = F'a−B, con B = D/2
con lo que hemos obtenido la ley de Korčak. Para otros valores de λ o de a, se tiene una gráfica escalonada como las que obtuvimos para las longitudes de los huecos de Cantor en el capítulo 8.
Este resultado es independiente de NC y de DC, y vale también cuando el generador tiene dos o más islas. Vemos también que la B empírica correspondiente a toda la Tierra es del orden de 0,6, muy próxima a la mitad de la D medida a partir de las longitudes de las costas.
Generalización a E > 2
En la misma construcción generalizada al espacio, sigue cumpliéndose que el diámetro E dimensional, definido como volumen 1/E, se ajusta a una expresión hiperbólica de la forma Nr (volumen1/E > λ) = Fλ−D donde el exponente crucial también es D.
El exponente D gobierna también el caso especial de los polvos de Cantor para E = 1, pero en ese caso surge una diferencia importante: la longitud fuera de los huecos de Cantor es nula, mientras que el área exterior a las islas de Koch puede ser, como generalmente ocurre, positiva. Volveremos sobre el tema en el capítulo 15.
La dimensión fractal puede ser solamente una medida de fragmentación
En la construcción anterior también puede darse el siguiente generador
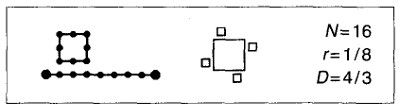
La D global no varía, pero la DC de la costa toma el mínimo valor posible, DC = 1. En este modelo, las costas de las islas son rectificables. En tal caso la D global no mide la irregularidad, sino sólo la fragmentación. En vez de medir el grado de ondulación de las curvas individuales, la D mide la relación número-área de la familia infinita de islas rectangulares.
Sigue siendo cierto que, si se mide la longitud con una regla de longitud ε, el resultado tiende a infinito para ε → 0, pero ahora por un nuevo motivo. Con dicha regla sólo pueden considerarse islas de diámetro mayor o igual que ε. Pero el número de tales islas aumenta al tender ε a 0, y la longitud medida se comporta como ε1−D, exactamente igual que en ausencia de islas.
En el caso general, con DC > 1, este valor mide sólo la irregularidad, mientras que la D cuantifica la irregularidad y la fragmentación en conjunto.
UN FRACTAL FRAGMENTADO PUEDE TENER TANGENTE EN TODOS SUS PUNTOS. Redondeando las esquinas de las islas se puede hacer que cada costa tenga una tangente en cada punto, sin alterar las áreas, y con ellas la D global. Así pues, las propiedades de ser una curva fractal y de no tener tangentes no son equivalentes.
La infinidad de islas
UNA DIVERGENCIA INOCUA. Cuando a → 0, Nr (A > a) = Fa−B tiende a infinito. Por tanto, la ley de Korčak concuerda con nuestro comentario inicial de que el número de islas es prácticamente infinito.
ÁREA RELATIVA DE LA ISLA MAYOR. Este último hecho es matemáticamente aceptable por cuanto el área acumulada de las islas muy pequeñas es finita y despreciable. ▯ La contribución al área total de todas las islas de área menor que ε se comporta como la integral de a(BaB−1) = Ba−B entre 0 y −. Como B < 1, esta integral converge y su valor, B(1 − B)−1ε1−B, tiende a 0 con ε. ▮
En consecuencia, la contribución relativa de la mayor de las islas al área total acumulada tiende a un límite positivo finito a medida que aumenta el número de islas consideradas. No es asintóticamente despreciable.
LONGITUD RELATIVA DE LA COSTA MAS LARGA. Por otro lado, si suponemos que DC = 1, los perímetros de las costas siguen una distribución hiperbólica de exponente D > 1. De ahí que la contribución de las islas más pequeñas al perímetro acumulado de las costas sea infinita y que, a medida que avanza la construcción y aumenta el número de islas, el perímetro de la isla mayor se vaya haciendo relativamente despreciable.
CONJUNTOS RELATIVAMENTE DESPRECIABLES. En general, la desigualdad DC < D expresa que la curva obtenida sólo con el generador de costas es despreciable en relación a la costa total. Del mismo modo, una recta (D = 1) es despreciable con respecto al plano (D = 2). Igual que un punto del plano elegido al azar casi nunca cae sobre el eje X, un punto elegido a] azar sobre la costa de un archipiélago formado alrededor de una isla principal casi nunca cae sobre la costa de dicha isla principal.
Búsqueda del continente infinito
En un universo escalante la distinción entre islas y continente no puede basarse en la tradición ni en el «tamaño relativo». El único enfoque razonable consiste en definir el continente como una isla especial de diámetro infinito. Demostraré ahora que las construcciones presentadas al comienzo del capítulo prácticamente nunca generan un continente. ▯ Para quienes conocen la teoría de la probabilidad: la probabilidad de que se genere un continente es nula. ▮
En una búsqueda razonable de un continente ya no podemos elegir el iniciador y el generador por separado. A partir de ahora el mismo generador debe servir para la interpolación y para la extrapolación. El proceso se desarrolla por estadios sucesivos, y cada uno de éstos se descompone en varios pasos. Se parece muchísimo a la extrapolación del polvo de Cantor que vimos en el capítulo 8, pero merece una descripción más completa y detallada.
El primer paso consiste en aumentar el generador escogido en un factor 1/r. En el segundo se «marca» uno de los enlaces de dicho generador aumentado. El tercero lo desplaza hasta hacer coincidir el enlace marcado con [0,1]. Y el cuarto y último interpola los restantes enlaces del generador aumentado.
Este proceso se repite indefinidamente, y la sucesión de posiciones de los enlaces «marcados» determina el avance y resultado del mismo. Dicha sucesión puede tomar distintas formas.
En la primera de ellas hace falta que el generador de la costa contenga un número positivo NC − 2 de enlaces «no extremos», definidos por la condición de pertenecer al generador de la costa y no acabar ni en 0 ni en 1. Si se hace la marca consistentemente en un enlace no extremo, cada etapa de la extrapolación amplía el trozo de costa original hasta incorporarlo, a la larga, en una costa fractal de extensión infinita en ambos sentidos. Esto demuestra que es efectivamente posible obtener una costa continental por este método de construcción.
En la segunda forma, se marca siempre un enlace extremo del generador de la costa, eligiendo ambas posibilidades un número infinito de veces. Nuestro pedazo de costa se irá ampliando también indefinidamente. Pero si siempre marcamos el mismo enlace, esta ampliación sólo se producirá en un sentido.
Tercera posibilidad, márquese siempre un enlace del generador de islas. En tal caso, la isla mayor antes de extrapolar aparece junto a la costa de otra isla mayor después de una extrapolación, y esta segunda isla quedará junto a otra mayor después del siguiente estadio, y así sucesivamente, con lo que nunca se llega a obtener el continente.
El comentario siguiente requiere un poco de «sentido común probabilístico» al que cualquier lector tendría que estar acostumbrado. Supongamos que las «marcas» se hacen según los resultados de las tiradas de un dado de N caras. Resulta obvio que, para que la extrapolación genere un continente, es necesario que, a partir de un cierto estadio finito (el k-ésimo), todas las marcas caigan en uno de los NC − 2 enlaces no extremos del generador de la costa. Llamémosles enlaces «favorables». Para poder decir que hemos llegado al continente después de k pasos, tenemos que saber que a partir de entonces todas las tiradas del dado, sin excepción, van a ser favorables. Tanta suerte no es imposible, pero su probabilidad es nula.
Combinación de isla, lago y árbol
Al ser las islas de Koch mutuamente autosemejantes, su diámetro se puede definir como la distancia en línea recta entre dos puntos dados cualesquiera, preferiblemente escogidos sobre la costa. Observamos también que la deducción de la relación diámetro-número utiliza la hipótesis de que el generador contiene un generador de costas. Pero, de hecho, la condición de que los enlaces restantes del generador formen islas o que sean autoevitantes, no se usan nunca en dicha deducción. Así pues, la relación
Nr (Λ > λ) = Fλ−D
tiene una validez muy general. ▯ Se puede incluso relajar la condición de que los terágonos iniciados por dos intervalos no se corten. ▮ Mostraremos ahora algunos ejemplos en los que la configuración de los N − NC enlaces iniciales puede afectar la topología del fractal resultante.
COMBINACIÓN DE ISLAS Y LAGOS. Prescindamos de la condición de que el generador de islas caiga a la izquierda al ir en el sentido de las agujas del reloj. Si cae a la derecha, formará lagos en vez de islas. Alternativamente, se pueden tener a la vez lagos e islas en el mismo generador. En cualquier caso, el fractal final es un σ-circuito cuyos circuitos componentes están encajados unos en otros. Considérese, por ejemplo, el siguiente generador
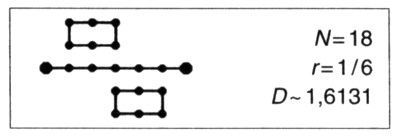
Si se inicia con un cuadrado, este generador da lugar al siguiente terágono avanzado
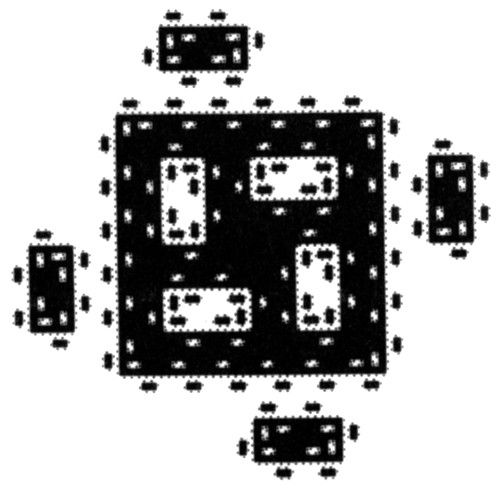
EL ESCURRIDIZO CONTINENTE. En el diagrama superior, la longitud del lado del iniciador introduce un corte superior no intrínseco. Un enfoque más consistente sería extrapolar como en el caso de islas sin lagos. Y también es prácticamente seguro que nunca se llegará a tener un continente, y que este encajarse de las islas en lagos, encajados a su vez en islas, continuará indefinidamente.
RELACIÓN ÁREA-NÚMERO. Para definir el área de una isla (o un lago) se puede tomar el área total, o el área de la tierra (o el agua) encerrada por su costa. Ambos valores difieren en un factor numérico fijo, con lo que dicha elección afectará al prefactor F' y no al exponente D/2 de la relación Nr (A > a).
COMBINACIÓN DE ARCOS Y ÁRBOLES. Supongamos ahora que los NNC enlaces forman una línea quebrada o un árbol. En cada caso el fractal se descompone en un número infinito de pedazos inconexos, siendo cada uno de ellos una curva. Esta σ-curva ya no es un σ-circuito, sino un σ-árbol o un σ-arco.
El concepto de racimo de contacto
El generador puede también combinar circuitos, ramas y otras distintas configuraciones topológicas. En tal caso, las partes conexas de los fractales límite nos recuerdan los racimos de la teoría de la percolación (como veremos más adelante en este mismo capítulo) y de muchos otros campos de la física. El uso del término racimo resulta sumamente desafortunado para nuestras intenciones, debido al distinto significado que le hemos dado en el estudio de los polvos (capítulo 9). Necesitamos una expresión más específica, como por ejemplo «racimo de contacto». Por suerte, el término σ-racimo no es ambiguo.
(Obsérvese que racimo de contacto tiene una definición matemática natural y única, cosa que no ocurre con el concepto de agregación en un polvo, que es difuso e intuitivo y al que, como mucho, se le puede dar una definición mejor mediante reglas estadísticas discutibles).
RACIMOS DE CONTACTO QUE LLENAN EL PLANO. Cuando D alcanza su valor máximo, los argumentos de la sección anterior siguen siendo válidos, pero son necesarios algunos comentarios adicionales. Cada racimo individual dende a un límite, que puede ser una recta, pero que en la mayoría de casos es una curva fractal. Por otro lado, el conjunto de todos los racimos forma una σ-curva cuyas hebras llenan el plano de forma cada vez más tupida. El límite de esta σ-curva se comporta como en el capítulo 7: deja de ser una σ-curva para convertirse en un dominio del plano.
EL ESCURRIDIZO RACIMO INFINITO. El presente planteamiento no implica ningún racimo realmente infinito. Es fácil disponer la topología del generador de modo que sea prácticamente seguro que cualquier dominio acotado esté rodeado por un racimo de contacto. Éste, a su vez, estará rodeado casi con seguridad por otro mayor, etc. No hay una cota superior para el tamaño de los racimos. En general, cuando un racimo parece infinito porque se extiende sobre un área muy grande, es casi seguro que la consideración de un área mayor pondrá de manifiesto que en realidad es finito.
Relación masa-número y relación ponderada diámetro-número. Los exponentes D − DC y D / DC
Reformulemos ahora la función Nr(Λ > λ) de dos nuevas maneras: primero sustituyendo el diámetro λ, del racimo por su masa μ y luego asignando un peso mayor a los racimos de contacto mayores.
Aquí la masa de un racimo no es otra cosa que el número de enlaces de longitud b−k que lo forman (¡en un racimo que forma lazos no se cuentan los enlaces interiores!). Lo que hacemos en realidad es (capítulos 6 y 12) crear una salchicha de Minkowski modificada (lámina 59), tomando un cuadrado de lado b−k centrado en cada vértice y añadiendo medio cuadrado a cada extremo.
La masa de cada racimo de diámetro Λ será el área de esa salchicha modificada, de modo que M ∝ (Λ / bk)D(bk)2 = ΛD / (bk)D−2 como D < 2, M → 0 para k → ∞. La masa de todos los racimos de contacto en conjunto es ∝ (bk)D−2, y si D < 2 también → 0. Y la masa relativa de cualquier racimo de contacto individual es ∝ (bk)Dc−D, que tiende a 0 con una velocidad que aumenta con D − DC.
RELACIÓN MASA-NÚMERO. Es claro que
Nr(M > μ) ∝ (bk)−D+2D/Dμ−D/Dc
DISTRIBUCIÓN DE DIÁMETROS PONDERADA CON LA MASA. Nótese que Nr(Λ > λ) cuenta el número de líneas anteriores a la línea λ en una lista que empieza en el racimo de contacto más largo, sigue con el más largo de los restantes, etc. Pero dentro de un momento tendremos que atribuir a cada racimo de contacto un número de líneas igual a su masa. Se ve fácilmente que la relación resultante es
Nrp(Λ > λ) ∝ k−D+DC.
El exponente másico Q = 2DC − D
Denotemos por F una fractal de dimensión D construida por iteración a partir de un iniciador [0, Λ] y supongamos que su masa es ΛD. Si F es un polvo de Cantor, en el capítulo 8 se demuestra que la masa contenida en un disco de radio R < Λ centrado en 0 es M(R) ∝ RD. ▯ La cantidad log[M(R)RD] es una función periódica de log b(Λ/R), pero dejaremos de lado estas complicaciones porque desaparecerán cuando modifiquemos el fractal de modo que todas las r > 0 sean razones de autosemejanza admisibles. ▮
Sabemos ya que la relación M(R) ∝ RD vale también para la curva de Koch del capítulo 6. Esta fórmula es extensible también a las islas y racimos recurrentes de este capítulo, cambiando D por DC. En todos los casos, la masa contenida en un disco de radio R centrado en 0 tiene la forma
M(R, Λ) = RDC ø(R/Λ),
siendo ø una función que depende de la forma de F. En particular,
M(R, Λ) ∝ RDC para R << Λ, y
M(R, Λ) ∝ ΛDC para R >> Λ.
Consideremos ahora la media ponderada de M(R), que denotaremos por <M(R)>, correspondiente al caso en que Λ varía según una distribución hiperbólica del tipo Nrp(Λ > λ) ∝ λ−D+DC. Sabemos que 1 ≤ DC ≤ D ≤ 2, y si excluimos la combinación DC = 1 y D = 2, 0 < D − DC < DC. Se tiene que
<M(R)> ∝ RQ con Q = 2DC − D > 0.
Si el disco está centrado en un punto de F distinto del 0, el factor de proporcionalidad cambia pero el exponente se mantiene, y también se mantiene si se calcula la media para todas las posibles posiciones del centro sobre F, y si se cambia [0,1] por otro iniciador. ▯ Normalmente, un arco de tamaño aleatorio A también tiene una forma aleatoria. Pero las fórmulas anteriores para M(R, Λ) valen para <M(R, Λ)> promediado sobre todas las formas, y el resultado final es el mismo. ▮
OBSERVACIÓN. La deducción anterior no dice nada de la topología de los racimos. Estos pueden ser circuitos, intervalos, árboles, o cualquier otra cosa.
CONCLUSIÓN. La fórmula <M(R)> ∝ RQ prueba que cuando Λ sigue una distribución hiperbólica, y por tanto muy dispersa, uno de los papeles esenciales de la dimensión es traspasado a un exponente distinto de D. El más natural es 2DC − D, pero distintas funciones de peso dan otros valores de Q.
ADVERTENCIA: NO TODOS LOS EXPONENTES MÁSICOS SON DIMENSIONES. La cantidad compuesta Q es importante y, al tratarse de un exponente másico, resulta tentador, calificarlo (inmerecidamente) de dimensión. Si se mezclan muchos racimos de la misma DC, pero distinta Λ, DC no cambia, puesto que la DC no es una propiedad de una población de conjuntos, sino de cada uno de ellos en particular. Tanto D como DC, son dimensiones fractales, pero Q no lo es.
En general, las relaciones de la forma <M(R)> ∝ RQ se dan en muchos campos de la física, pero dicha fórmula no es por sí misma una garantía de que Q tenga que ser una dimensión fractal. Y decir que Q es una dimensión efectiva, como proponen algunos autores, es un gesto vacío, pues Q no posee ninguna de las otras propiedades que caracterizan a D (por ejemplo, las sumas y productos de las D tienen un significado que no tiene homólogo en el caso de Q). Además, este gesto vacío ha resultado ser una fuente potencial de confusión.
Racimos de coagulación no grumosos
Pasamos ahora a describir otras dos maneras de generar racimos de contacto. Una se basa en la coagulación y es aplicable cuando D < 2, mientras que la otra se basa en las curvas de Peano y es aplicable cuando D = 2. El lector interesado en la percolación puede saltarse esta sección y la siguiente.
Sustituyamos primero la construcción de Koch por la generalización natural al plano de la coagulación de Cantor. A modo de ilustración, considérense los siguientes cinco generadores, con el correspondiente segundo estadio dibujado inmediatamente debajo de cada uno.
En todos estos casos, el fractal límite tiene área nula y carece de puntos interiores. Su topología puede ser muy diversa, según sea el generador.
Con el generador A, tenemos que en cada estadio k la precoagulación es conexa y el fractal límite es una curva. Se trata de un ejemplo del importante tamiz de Sierpinski, que estudiamos en el capítulo 14.
Con el generador F, la precoagulación se descompone en porciones inconexas cuya escala lineal máxima disminuye sin cesar para k → ∞. El fractal límite es un polvo, semejante al modelo de Fournier del capítulo 9.
Los generadores B, C y E son más interesantes: en estos casos, la precoagulación se descompone en pedazos que llamaremos pre-racimos. Se podría decir que cada estadio transforma los «viejos» prerracimos haciéndolos más delgados y ondulados, y a la vez hace aparecer «nuevos» prerracimos. Sin embargo, debido a una elección deliberada de los generadores, cada prerracimo recién aparecido está totalmente contenido en una sola celda elemental de la red que dominaba antes de su aparición. En contraste con los «racimos grumosos» de la sección siguiente, éstos se llamarán «no grumosos». Se obtiene que la dimensión de los racimos de contacto límite es de la forma log Nc/log b, siendo Nc un entero menor o igual que el número de celdas de la mayor componente del generador.
Este máximo se alcanza en los casos de los generadores B y C, para los que los racimos de contacto son, respectivamente, segmentos con DC = 1 y árboles fractales con DC = log 7/log 4. Pero el fractal generado por el generador E no alcanza dicho valor máximo: en este caso los prerracimos en forma de F se siguen descomponiendo en partes, y en el límite acaba por estar formado por segmentos rectilíneos conDC = 1.
Sustituyendo la pseudosalchicha de Minkowski por el conjunto de celdas de lado b−k que intersecan el racimo de contacto, la relación diámetro-número y los otros resultados de la sección anterior siguen siendo válidos en estos casos.
Racimos de coagulación grumosos
Ahora, el generador de coagulación plano toma una de las formas siguientes (junto a cada generador figura el segundo estadio de la construcción correspondiente):

Ambos casos presentan una «grumosidad» en masa, en el sentido de que cada prerracimo recién nacido recibe aportaciones procedentes de varias celdas menores de la red dominante en el estadio anterior a su nacimiento.
En el contexto de las construcciones de Koch se da una situación semejante cuando se permite que los terágonos tengan autocontactos, cosa que motiva la fusión de pequeños terágonoracimos. En cualquier caso, el análisis es laborioso y no podemos detenernos en él. Pero la relación Nr(Λ > λ) sigue siendo válida para λ pequeños.
▯ Sin embargo, si uno intenta estimar D a partir de esta relación y no excluye los λ grandes, la estimación presenta un sesgo sistemático hacia valores menores que el verdadero. ▮
Nos encontramos también con novedades en lo que respecta a la cantidad bD ya no tiene por qué ser un entero inmediatamente deducible del generador, sino que puede ser una fracción. Ello se debe a que en cada racimo de contacto se combinan: (a) un núfnero entero de versiones de sí mismo reducidas en la razón l/b, y (b) muchas versiones reducidas debido a la grumosidad, en las que intervienen razones de semejanza menores de la forma rm = b−k(m). Si se expresa la ecuación que determina la dimensión ΣrmD = 1 (véase pág. 85) en función de x = b−D, se obtiene otra de la forma Σamxm = 1. El cociente 1/x sólo toma valores enteros en casos excepcionales.
Monstruos de Peano enmarañados, domesticados
La coagulación no permite crear familias de racimos que llenen el plano (D = 2), pero encontré un camino alternafivo basado en unas curvas de Peano distintas de las que vimos domesticar en el capítulo 7. Como el lector recordará, las curvas de Peano con terágonos autoevitantes dan lugar a árboles fluviales y cuencas. Sin embargo, otros terágonos de Peano (los de la lámina 93 sin redondear las esquinas, por ejemplo) no son más que simples trozos de red. A medida que la iteración avanza, las celdillas abiertas separadas por tales curvas «convergen» hacia un polvo denso por doquier, es decir, los puntos tales que ni x ni y son múltiplos de b−k.
Entre estos extremos tenemos una nueva e interesante clase de curvas de Peano. Un ejemplo de generador, junto con el segundo estadio de la iteración, es el siguiente

Esta clase de curvas de Peano está lista ya para ser domesticada. Observamos que el «nudo» de cada punto de autocontacto «aparta» un prerracimo abierto, que a su vez presentará ramificaciones y autocontactos, verá cómo partes de sí mismo son «arrancadas» por futuros nudos y por último se adelgazará hasta convertirse en una curva muy ramificada que definirá un racimo de contacto. El diámetro Λ de un racimo, definido como en las secciones anteriores, está determinado desde el instante de su nacimiento y es aproximadamente igual al lado del cuadrado que «sembró» dicho racimo. Su distribución es regida por la ya conocida relación Nr(Λ > λ) ∝ λ−2.
Nótese de paso que, así como los racimos de contacto de Koch son el límite de curvas construidas iterativamente, estos racimos son el límite (en un sentido peculiar) de las componentes abiertas del complemento de una curva.
Racimos de percolación de Bernouilli
Sea cual sea el método seguido para generar racimos de contacto fractales con D = E y DC < D, éstos nos proporcionan un modelo geométrico que se echaba en falta en un problema físico muy importante: las redes de percolación de Bernouilli. El problema fue planteado e investigado por vez primera por J. M. Hammersley, sin asociar el nombre de Bernouilli a este contexto, pero la percolación fractal que estudiaremos en el capítulo 23 nos obliga a emplear aquí la expresión completa. (Smythe y Wiermann, 1975, la adoptan independientemente.)
BIBLIOGRAFÍA. Tenemos estudios de la percolación de Bernouilli en Shante y Kirkpatrick (1971), Domb y Green (1972), en especial un capítulo de J. W. Essam, Kirkpatrick (1973), deGennes (1976), Stauffer (1979) y Essam (1980).
DEFINICIONES. En la percolación intervienen conceptos probabilísticos, y para ser plenamente consistentes no debería discutirse en este momento. Pero una falta ocasional de consistencia tiene a veces su recompensa. El problema de percolación más simple con E = 2 es la percolación de enlaces en una red cuadrada. Para ilustrarla en términos domésticos, imaginemos que construimos una gran red cuadrada con barritas de vinilo y de cobre, aislante y conductor, respectivamente. Se obtiene una red de Bernouilli si se elige al azar cada barrita, independientemente de las demás, siendo p la probabilidad de elegir una barrita conductora. Los conjuntos maximales de barritas de cobre (o de vinilo) conectadas entre sí forman lo que llamamos los racimos de cobre (o de vinilo). Si en la red tenemos por lo menos una hilera ininterrumpida de barritas de cobre, la corriente puede atravesarlo, y se dice que la red percola (del latín colare = fluir y per = a través). Las barritas en contacto eléctrico ininterrumpido con los lados extremos de la red forman un «racimo percolante», y las barritas realmente activas de la conducción forman su «espina dorsal».
La generalización a otras redes y a E > 2 es inmediata.
PROBABILIDAD CRÍTICA. El descubrimiento más notable de Hammersley consiste en el papel especial que juega una cierta probabilidad umbral: la probabilidad crítica pcrit. Esta cantidad aparece cuando el tamaño de la red de Bernouilli (medida en número de barritas) tiende a infinito. Se encuentra que para p > pcrit la probabilidad de que haya un racimo percolante aumenta con el tamaño de la red y tiende a 1. Por el contrario, cuando p < pcrit la probabilidad de percolación tiende a 0.
Dado que, en la percolación de enlaces en redes cuadradas, o bien el cobre o bien el vinilo deben percolar, tenemos que pcrit = 1/2.
ESCALANTES ANALÍTICOS. El estudio de la percolación se dedicó durante mucho tiempo a la búsqueda de expresiones analíticas que relacionaran las cantidades estándar de la física. Se vio que todas esas cantidades eran escalantes, en el sentido de que las relaciones entre ellas venían dadas por potencias. Para p ≠ pcrit, el carácter escalante se extiende hasta un corte superior ξ que depende de p − pcrit. Cuando p → pcrit el corte tiende a ∞. Los físicos postulan (véase Stauffer, 1979, pág. 21) que <M(R, Λ)> sigue la regla obtenida en la página 179.
La geometría fractal de los racimos
LA FORMA DE LOS RACIMOS. Supongamos que p = pcrit y que el tamaño de cada barrita disminuye mientras el tamaño total de la red permanece constante. Los racimos se hacen cada vez más delgados («todo piel, sin carne»), presentan cada vez más convoluciones, ramificaciones y rodeos («ramificados y fibrosos»). Más concretamente (Leath, 1976) el número de barritas externas al racimo y que están en contacto con una barrita del mismo es aproximadamente proporcional al número de barritas del racimo.
HIPÓTESIS DE QUE LOS RACIMOS SON FRACTALES. De un modo natural se plantea la conjetura de que el carácter escalante de las propiedades analíticas se extiende también a la geometría de los racimos. Pero esta idea no podía realizarse en el marco de la geometría estándar, pues los racimos no son rectilíneos. La geometría fractal fue ideada para responder a dificultades de este upo, con lo que conjeturé que los racimos se pueden representar por curvas con D = 2 y 1 < DC < D. Esta conjetura fue aceptada y ha dado sus frutos. La ampliaremos en el capítulo 36.
▯ Para ser precisos, se toman los fractales escalantes para representar los racimos que no son truncados por los bordes de la red original. Ello excluye el racimo percolante. (¡El término racimo tiene un don especial para generar confusión!) Para entender la dificultad, comencemos con una red muy grande, tomemos uno de los racimos y un cuadrado menor parcialmente cubierto por dicho racimo. Por definición, la intersección del racimo y el cuadrado contiene un racimo percolante menor, pero contiene además un «residuo» conectado con dicho racimo percolante menor por unos enlaces que caen fuera del cuadrado. Nótese que dejar de tener en cuenta este residuo hace que la estimación de DC sea menor de lo que realmente vale. ▮
MODELOS FRACTALES NO ALEATORIOS EXPLÍCITOS AUNQUE MUY GROSEROS. La pretensión de que cualquier fenómeno natural es fractal debe ir acompañada de la descripción de un conjunto fractal concreto, que sirva de modelo en primera aproximación, o por lo menos de representación mental. Mi modelo de costa al estilo de Koch y el modelo de Fournier para los cúmulos de galaxias han demostrado que las representaciones no aleatorias pueden ser de mucha utilidad. Por ello espero que los racimos de contacto construidos por iteración (como los presentados en este capítulo) proporcionen modelos fractales útiles para fenómenos naturales mal conocidos que usualmente se modelizan por medio de racimos de Bernouilli.
Ahora bien, los racimos de Bernouilli en sí se conocen perfectamente (por lo menos en principio); modelizarlos mediante fractales recurrentes es, pues, una tarea distinta. Los racimos de contacto de Koch que estudié no sirven, debido a la disimetría entre el vinilo y el cobre, incluso cuando tenemos el mismo número de barras de ambas clases. Examinemos a continuación los racimos formados con curvas de Peano anudadas. Tomemos un terágono avanzado y cubramos las celdas de la izquierda de la curva con cobre y el resto con vinilo. El resultado tiene que ver con una forma de percolación referida a las celdas de la red (o a sus centros). El problema es ahora simétrico, pero distinto del problema de Bernouilli, pues las configuraciones del cobre o del vinilo no son las mismas que cuando hay independencia. Por ejemplo, en el caso de Bernouilli, 9 celdas que formen un supercuadrado pueden ser todas de cobre o todas de vinilo, y no pueden serlo en el caso de la curva de Peano anudada. (Por otra parte, ambos modelos permiten que grupos de 4 celdas formen supercuadrados con cualquiera de las configuraciones posibles.) Esta diferencia tiene consecuencias importantes: por ejemplo, ni el cobre ni el vinilo percolan en el problema de Bernouilli para los nudos con p = 1/2, y ambos lo hacen en cambio en el caso de los racimos de Peano anudados, cosa que implica que 1/2 es una probabilidad crítica.
La lista de variantes de percolación de enlaces de Bernouilli ya es larga y sería fácil alargarla aún más. Yo mismo he examinado ya muchas variantes de racimos de contacto fractales construidos por iteración. La comparación detallada de ambas listas es, por desgracia, complicada y no me detendré en ello.
Démonos pues por satisfechos con la conclusión un tanto vaga de que, según parece, los elementos fractales esenciales del problema de percolación de Bernouilli quedan bien ilustrados por los σ-racimos no aleatorios que llenan el espacio definidos en este capítulo. La principal debilidad de este modelo es que, aparte de lo dicho, es completamente indeterminado, y puede acomodarse a cualquier grado de irregularidad y fragmentación observado. Por lo que a la topología se refiere, véase el capítulo 14.
MODELO DE RACIMOS CRÍTICOS. Consideremos ahora los racimos críticos, esto es, aquellos para los que p = pcrit. Para representarlos, se extrapola un σ-racimo recurrente según la manera indicada en secciones anteriores. Luego se trunca deteniendo la interpolación cuando el corte inferior llegue al tamaño de las celdas de la red original.
MODELOS DE RACIMOS NO CRÍTICOS. Para extender esta representación geométrica a los racimos no críticos, es decir, a aquellos para los que p ≠ pcrit, buscamos fractales con un corte inferior positivo y un corte superior finito. Por razones analíticas, la extensión del mayor racimo de cobre tiene que ser del orden de ξ cuando p < pcrit, e infinita cuando p > pcrit. Ambos resultados se pueden realizar fácilmente. Así, por ejemplo, se puede partir del mismo generador que en el subapartado anterior y, en vez de extrapolarlo de forma natural, se lo inicia con alguna de las figuras siguientes
RACIMOS SUBCRÍTICOS. El iniciador de la izquierda, preparado para p < pcrit, está formado por cuadrados de lado 1/2ξ. Colocaremos el generador elegido hacia dentro sobre el lado izquierdo del iniciador y hacia fuera sobre el derecho. Cada cuadrado del iniciador se transformará en un racimo atípico de longitud ξ rodeado de muchos racimos típicos de longitud menor que ξ.
RACIMOS SUPERCRÍTICOS. El iniciador de la derecha, preparado para p > pcrit, está formado por las líneas de la red cuadrada original cuyas coordenadas x o y son números pares. De cada nodo de coordenadas pares salen cuatro enlaces, y el generador escogido se coloca siempre a la izquierda. En el caso especial en que el generador de costas no tenga lazos ni enlaces colgantes, la figura resultante es una variante no aleatorizada y sistematizada de un modelo tosco de racimos basado únicamente en «nodos y enlaces».
Nótese que la representación geométrica fractal deduce los racimos no críticos a partir de los críticos, mientras que los físicos prefieren considerar los racimos críticos como límite de los no críticos para ξ → ∞.
La DC de los racimos de Bernouilli críticos
El valor de DC se puede deducir inmediatamente, ya sea a partir del exponente D/DC = E/DC de la fórmula Nr(M > μ), o del exponente Q = 2DC − D = 2DC − E de la fórmula de <M(R)>. Usando las letras griegas τ, δ y η con el significado habitual en este contexto, encontramos que E/DC = τ − 1 y 2DC − E =2 − η. Por tanto,
DC = E(τ − 1) = E/(1 + δ+1), y
DC = 1 + (E − η)/2.
Debido a las relaciones entre τ, δ y η establecidas por los físicos, ambas fórmulas para DC son equivalentes. Y a la inversa, su equivalencia no reside sólo en la física, puesto que se sigue de la geometría.
Harrison, Bishop y Quinn (1978), Kirkpatrick (1978) y Stauffer (1979) obtienen independientemente la misma DC. Parten de las propiedades de los racimos con p > pcrit con lo que su resultado viene expresado en función de los diferentes exponentes críticos (β, γ, ν y σ). Y sus deducciones no presuponen explícitamente una representación fractal subyacente. Un ejemplo de los peligros inherentes a este planteamiento del problema, de los que ya hemos hablado, lo tenemos en el hecho de que Stanley (1977) se confundiera al avanzar que Q y DC son dos dimensiones igualmente legítimas.
Para E = 2, el valor numérico es DC = 1,89, que es compatible con la evidencia empírica obtenida mediante un procedimiento conocido en otras formas. Tomamos una r, que no tiene por qué ser de la forma 1/b (con b entero). Tomamos luego un gran remolino, que será simplemente una red cuadrada o cúbica de lado igual a 1. Lo enlosamos luego con subremolinos de lado r, contamos el número N de cuadrados o de cubos que intersecan el racimo y calculamos log N/log(1/r). Repetimos luego el mismo proceso para cada subremolino no vacío de lado r, formando subsubremolinos de lado r2, y continuamos mientras sea posible. Los resultados más significativos se obtienen para r próximo a 1. Algunas simulaciones primitivas dieron la estimación sesgada D+ ~ 1,77 (Mandelbrot 1978h, Halley y Mai 1979), pero simulaciones de más alcance (Stauffer 1980) confirmaron el valor D.
▯ La D+ experimental sesgada es muy próxima a Q, cosa que parecía confirmar los argumentos teóricos de Stanley, Birgenau, Reynolds y Nicoll (1976) y de Mandelbrot (1978h), que estaban equivocados al pretender que la dimensión es Q. S. Kirkpatrick me hizo ver el error. Otra estimación incorrecta distinta y anterior a las citadas se encuentra en Leath (1976). ▮
Los cipreses de Okefenokee
Cuando se observa desde un avión un bosque no «cuidado» sistemáticamente, ios linderos recuerdan la costa de una isla. El contorno de cada macizo de árboles es sumamente accidentado o festoneado, y cada macizo grande lleva un rastro de macizos satélites de área variable. Mi sospecha de que estas formas podrían obedecer las leyes de Richardson y/o de Korčak ha sido efectivamente confirmada por un estudio no publicado de la marisma de Okefenokee (Kelly 1951) hecho por H. M. Hastings, R. Monticciolo y D. Vunkannon. El patrón parcheado que genera el ciprés es grande, con D ~ 1,6; en cambio, el producido por los árboles de hoja grande es mucho menos pronunciado, con D próxima a 1. Mis informantes señalan la presencia de una variedad de escalas impresionante, basándose tanto en la inspección personal como en el examen de mapas de vegetación. Hay un corte inferior de unos 40 acres, debido probablemente a la fotografía aérea.