LÁMINA 168. Log(perímetro) en función del log(área) para nubes (⚬) y zonas lluviosas (•). De Lovejoy 1982
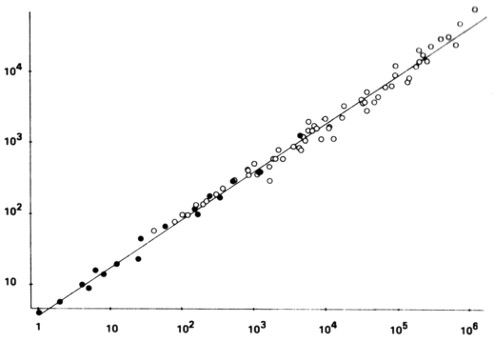
FIGURA 168
Los capítulos 12 y 13 extienden las propiedades de la dimensión fractal a numerosos casos menores de importancia variable y dificultad creciente. El capítulo 14 demuestra que la geometría fractal necesita de conceptos que van más allá de la simple dimensión fractal.
El presente capítulo describe, y aplica a ciertos casos concretos, los equivalentes fractales (desarrollados por mí) de ciertos resultados comunes de la geometría euclídea. Se pueden considerar análogos a las relaciones fractales de la forma M(R) ∝ RD obtenidos en los capítulos 6, 8 y 9.
Análisis dimensional estándar
Del hecho de que la longitud de la circunferencia de radio R valga 2πR y que el área del círculo correspondiente sea πR2, se sigue que
(longitud) = 2π1/2(área)1/2.
Para los cuadrados, la relación correspondiente es
(longitud) = 4 (área)1/2
Y, en general, en cada familia de figuras planas corrientes, geométricamente semejantes y de tamaños distintos, la razón (longitud)/(área)1/2 es una constante determinada por la forma común de todas ellas.
En el espacio (E = 3), la longitud, el (área)1/2 y el (volumen)1/3 dan evaluaciones alternativas del tamaño lineal de la figura, y la razón entre dos cualesquiera de ellas es un parámetro de forma, independiente de las unidades de medida.
La equivalencia de distintas medidas del tamaño lineal es útil en muchas aplicaciones. Y su generalización a sus magnitudes tiempo y masa es la base de una técnica muy potente que los físicos conocen como «análisis dimensional». (Una exposición recomendable de sus características fundamentales se encuentra en Birkhoff, 1960.)
Resultados dimensionales paradójicos
No obstante, esta equivalencia entre distintos tamaños lineales resulta insidiosamente escurridiza en un número de casos cada vez mayor. Por ejemplo, para el cerebro de los mamíferos se tiene
(volumen)1/3 ∝ (área)1/D,
con D ~ 3, muy superior al valor 2 que se presumía. En el caso de las cuencas de drenaje fluvial, Hack (1957) mide la longitud a lo largo del río principal y encuentra
(área)1/2 ∝ (longitud)1/D
con D definitivamente superior al valor previsto. Los autores primitivos interpretaban que este resultado implicaba que las cuencas fluviales no eran autosemejantes, siendo más alargadas las mayores y más rechonchas las menores. Por desgracia esta interpretación contradice la evidencia.
En este capítulo describo mi explicación de estos y otros resultados de un modo más convincente. Mi instrumento de trabajo será una nueva relación, fractal, entre la longitud, el área y el volumen.
Relación fractal longitud-área
Para precisar más el argumento, consideremos un conjunto de islas geométricamente semejantes con costas fractales de dimensión D > 1. En este contexto, la razón estándar (longitud)/(área)1/2 es infinita, pero yo propongo que tiene un equivalente fractal útil. Llamaremos G-longitud a la longitud de la costa obtenida con una regla de longitud G, y G-área a la superficie de la isla medida en unidades de G2. Sabiendo que la dependencia de la G-longitud respecto a G es no estándar, pero que la de la G-área sí lo es, definimos la razón generalizada
(G-longitud)1/D/(G-área)1/2
Lo que yo digo es que esta razón vale lo mismo para todas nuestras islas geométricamente semejantes.
En consecuencia hay dos maneras distintas de evaluar el tamaño lineal de cada isla en unidades de G: la expresión estándar (G-área)1/2 y también la no estándar (G-longitud)1/D.
Lo nuevo de todo esto es que, si sustituimos la regla de longitud G por otra de longitud G', la nueva razón entre los dos tamaños lineales alternativos es
(G'-longitud)1/D/(G'-área)1/2,
que difiere de la anterior en un factor (G'/G)(1/D)−1.
La razón entre tamaños lineales varía de un conjunto de figuras mutuamente semejantes a otra, tanto si son fractales como si no lo son. Por tanto, cuantifica un aspecto de la forma de las figuras.
Nótese que la relación longitud-área se puede usar para estimar la dimensión fractal de una curva que delimita un dominio estándar.
DEMOSTRACIÓN DE LA RELACIÓN. El primer paso consiste en medir la longitud de cada costa con el patrón intrínseco (definido a partir del área)
G* = (G-área)1/2/1000.
Si aproximamos las costas de cada una de nuestras islas por polígonos de lado G*, todos los polígonos obtenidos serán también semejantes entre sí, y sus longitudes serán proporcionales a los tamaños lineales estándar (G-área)1/2.
Sustituyamos ahora G por la regla prescrita G. Ya sabemos, por el capítulo 6, que la longitud cambia en la proporción (G/G*)1/D. En consecuencia,
(G-longitud) ∝ (G-área)1/2 (G/G*)1−D
(G-área)1/2 − G1−D1000D−1 =
(G-área)D/2 − G1−D1000D−1.
Por fin, elevando cada miembro a la potencia 1/D, se obtiene la relación que se pretendía demostrar. (Dem. 12.2)
¿Cuánto serpentea el Missouri?
Los argumentos anteriores arrojan también cierta luz sobre las longitudes medidas de los ríos. Con objeto de definir una longitud para el río principal de una cuenca de drenaje fluvial, aproximamos el curso del río por una línea ondulada autosemejante de dimensión D > 1 que va de un punto, que llamaremos nacimiento a otro que llamaremos desembocadura. Si todos los ríos, así como todas las cuencas, son semejantes entre sí, el argumento fractal sobre la relación longitud-área predice que
la (G-longitud del río)1/D es proporcional a
la (G-área de la cuenca)1/2.
Además, por razones de geometría estándar se tiene que
la (G-área de la cuenca)1/2 es proporcional a
la distancia recta del nacimiento a la desembocadura.
Combinando ambos resultados, llegamos a que
la (G-longitud del río)1/D es proporcional a
la distancia recta del nacimiento a la desembocadura.
Y lo más notable, como ya hemos mencionado, es que Hack (1957) encuentra empíricamente que la razón
(G-longitud del río)/(G-área de la cuenca)0,6
es en efecto común a todos los ríos. Esta estimación indirecta de D/2 = 0,6 nos da D = 1,2, que nos recuerda los valores deducidos a partir de las longitudes de las costas. Si se mide el grado de irregularidad por la D, ¡resulta que el grado de irregularidad de los serpenteos locales de las riberas y el de las curvas enormemente globales son idénticos!
Sin embargo, para cuencas de área > 104 km2 y ríos consecuentemente largos, J. E. Mueller observa que el valor de D disminuye hasta 1. Estos dos valores distintos de D hacen pensar que, si se trazan mapas de todas las cuencas sobre hojas de papel del mismo tamaño, los mapas de los ríos cortos y los de los ríos largos tienen el mismo aspecto, pero los de los ríos sumamente largos se parecen más a rectas. Pudiera ser que la autosemejanza no estándar se acabara en un corte superior n del orden de 100 km.
LONGITUD ACUMULADA DE UN ÁRBOL FLUVIAL. El argumento precedente sugiere también que la longitud acumulada de todos los ríos de una cuenca de drenaje tendría que ser proporcional al área de dicha cuenca. Me han comunicado que esta predicción es correcta, pero no tengo ninguna referencia.
DE VUELTA A LA GEOMETRÍA. Para los ríos y cuencas de la curva del «barrido del copo de nieve» de las láminas 102 y 103 teníamos D ~ 1,2618, algo superior al valor observado. La dimensión correspondiente para las láminas 70 y 71 es D ~ 1,1291, ligeramente inferior.
Las curvas de Peano de las láminas 93 y 96, con D = 1, están muy fuera de lugar.
Nótese que la igualdad de las dimensiones de los ríos y sus cuencas no es una necesidad lógica, sino sólo un rasgo de ciertos modelos recurrentes concretos. Por contra, una red fluvial relacionada con la curva punta de flecha (lámina 204) y descrita en Mandelbrot (1975m) tiene ríos de dimensión D = 1, que es demasiado pequeña, y cuencas de dimensión D ~ 1,5849, que es demasiado grande.
Geometría de la lluvia y de las nubes
En las páginas 15, 25, 26 y 138 se habla de la posibilidad de usar fractales para hacer modelos de las nubes. Lovejoy (1982) ha venido a confirmar esta expectativa, mediante la gráfica fractal área-perímetro de la lámina 168. En meteorología hay muy pocas gráficas que reúnan todos los datos disponibles en una gama de tamaños tan enorme, y son casi tan rectas como ésta.
Dichos datos combinan observaciones por radar de zonas lluviosas del Atlántico tropical (con tasas de lluvia por encima de los 0,2 mm/hora), con observaciones infrarrojas desde satélites geoestacionarios de zonas nubladas sobre el océano Indico (zonas en las que la temperatura de la cima de la nube está por debajo de −10 °C). Las áreas de las zonas varían entre 1 y 1.000.000 Km2. La dimensión del perímetro, ajustado hasta seis cifras significativas por lo menos, es 4/3. Dejo al doctor Lovejoy el placer de aportar una explicación física.
La mayor de las nubes se extendía desde el África Central hasta el sur de la India, que corresponde a una distancia muy superior al grosor de la atmósfera, al cual se asimila demasiado a menudo la cota superior L de la turbulencia atmosférica. La cita de Richardson de la pág. 149 podría resultar profética.
La relación área-volumen. Condensación por microgotas.
La deducción de la relación longitud-área se generaliza fácilmente a dominios espaciales limitados por superficies fractales, llegándose a la relación
(G-área)1/D ∝ (G-volumen)1/3
Para ilustrar esta relación, considérese la condensación de un vapor. Es un fenómeno físico muy corriente, y sin embargo la teoría que lo explica es reciente. Según Fisher (1967), la siguiente representación geométrica fue presentada, al parecer independientemente, por J. Frenkel, W. Band y A. Bijl, a finales de los años treinta. Un gas está constituido por moléculas aisladas muy separadas entre sí, aparte de unos pocos condensados que se mantienen con más o menos firmeza por las fuerzas atractivas. Los condensados de distintos tamaños coexisten en mutuo equilibrio estadístico, asociándose y disociándose, pero la probabilidad de que haya condensados de buen tamaño, más parecidos a «gotitas» de líquido, es pequeña. Un condensado bastante grande (que no sea demasiado «alargado», como un pedazo de alga, por ejemplo), tiene un área bastante bien definida. La superficie de un condensado le proporciona su estabilidad. Si se hace descender la temperatura, a los condensados les resulta ventajoso combinarse formando gotitas, y a las gotitas les conviene amalgamarse, reduciendo con ello el área total y disminuyendo por tanto la energía total. En condiciones favorables las gotitas crecen rápidamente, y la presencia de una gotita microscópica indica que se ha producido la condensación.
Basándose en esta representación, M. E. Fisher propone que el área y el volumen de una gotita que se condensa guardan una relación equivalente a área1/D ∝ volumen1/3. Fisher calcula D por medios analíticos sin preocuparse de su significado geométrico, pero ahora resulta inevitable la conjetura de que las superficies de las gotitas son fractales de dimensión D.
Los pliegues del cerebro de los mamíferos
Para ilustrar la relación área-volumen en el caso límite importante en que D = 3, y al mismo tiempo reforzar el exorcismo de las figuras de Peano presentado en el capítulo 7, interpretaremos un famoso problema de anatomía comparada por medio de superficies que casi llenan el espacio.
El volumen del cerebro de los mamíferos oscila entre los 0,3 y los 3000 ml, siendo el córtex de los animales pequeños relativa o completamente liso, mientras que el de los grandes tiende a presentar convoluciones, con independencia de la situación del animal en la escala evolutiva. Los zoólogos razonan que la proporción entre materia blanca (formada por los axones neuronales) y materia gris (donde terminan las neuronas) es aproximadamente la misma para todos los mamíferos, y que para mantener esta proporción un córtex cerebral grande tiene necesariamente que plegarse. La certeza de que el grado de plegamiento tiene un origen puramente geométrico libera al hombre de sentirse amenazado por el delfín o la ballena: son mayores que nosotros, pero no por ello están más arriba en la escala evolutiva.
El estudio cuantitativo de dicho plegamiento cae fuera del dominio de la geometría estándar, pero encaja muy bien en el de la geometría fractal. El volumen de materia gris es aproximadamente igual a su grosor multiplicado por el área de la membrana superficial del cerebro, llamada «pía». Si este grosor E fuera el mismo para todas las especies, el área de la pía sería proporcional al volumen de la materia gris y también al de la materia blanca, y por tanto al volumen total. En consecuencia, a partir de la relación área-volumen tendríamos D = 3, con lo que la pía sería una superficie que, módulo E, llenaría el espacio.
La relación área-volumen empírica más ajustada es A ∝ VD/3, con D/3 ∝ 0,91 a 0,93 (Jerison, comunicación oral, basada en los datos de Elias y Schwartz, Brodman, y otros). La interpretación más inmediata es que la pía sólo llena el espacio parcialmente, con una D comprendida entre 2,73 y 2,79. Al resumir este tema en el capítulo 17, esbozaremos un argumento más sofisticado.
Membranas alveolares y celulares
¿Tendrá algún biólogo la amabilidad de levantarse y proclamar que la sección precedente no aporta ningún resultado nuevo ni ninguna opinión inesperada? Me encanta que me formulen esta objeción, porque refuerza los argumentos que presenté al principio del capítulo 7. A pesar de que un biólogo echaría a correr ante una superficie de Peano tal y como la presentan los matemáticos, puedo afirmar que la idea de fondo es bien conocida para las mentes teóricas avanzadas en este campo.
Así pues, la mayor novedad de la sección anterior son las superficies con D < 3, que (como vimos) son necesarias para un buen ajuste. Sigamos con su nueva aplicación a la biología, con un esbozo de cómo desenmarañar la estructura detallada de varias membranas vivas.
Para empezar, resumiremos en un párrafo la sección 4.3.7 de Weibel (1979). Las estimaciones del área alveolar del pulmón humano son contradictorias: según la microscopía óptica es de 80 m2, mientras que según la microscopía electrónica, es de 140 m2. ¿Es importante esta discrepancia? La estructura fina no juega ningún papel en el intercambio de gases, pues es suavizada por un revestimiento líquido (que da un área funcional aún menor), pero es importante en el intercambio de sustancias disueltas. Las mediciones (estimuladas por mi artículo Coast of Britain) indican que, en primera aproximación y para una amplia gama de escalas, la dimensión fractal de la membrana es D = 2,17.
Paumgartner y Weibel (1979) estudian las membranas sub-celulares de las células hepáticas. Como en el caso anterior, el marcado desacuerdo que había entre distintas estimaciones del área por unidad de volumen se desvanece si se postula que D = 2,09 para la membrana mitocondrial extema (que envuelve la célula y sólo se aparta ligeramente de la suavidad característica de las membranas con una razón área/volumen mínima). Por otra parte, se tiene D = 2,53 para las membranas mitocondriales internas y D = 1,72 para el retículo endoplasmático.
Señalemos también que la estructura del hueso nasal de muchos animales presenta una complicación extraordinaria, de modo que la «piel que recubre dicho hueso tiene un área muy grande en un volumen pequeño. En el ciervo y el zorro ártico quizá desempeñe una función olfativa, pero el objeto de una forma análoga en el camello es economizar agua (Schmidt-Nielsen 1981).
Geometría de los ordenadores modulares
Para ilustrar mejor aún la relación área-volumen, abordaremos una faceta de los ordenadores. Aunque éstos no sean sistemas naturales, esto no tiene por qué ser un obstáculo. Este caso y otros permitirán comprobar que los métodos fractales sirven para analizar cualquier sistema, tanto natural como artificial, que se componga de «partes» articuladas en forma autosemejante y tales que las propiedades de las partes sean menos relevantes que las reglas de articulación.
Los circuitos de los ordenadores complejos se subdividen siempre en gran número de módulos. Cada uno de ellos consta de una gran cantidad C de componentes y está conectado con su entorno por un gran número T de terminales. Con un pequeño porcentaje de error, se tiene que T1/D ∝ C1/E. Dentro de un momento justificaré esta manera de escribir el exponente. En IBM la regla anterior se atribuye a E. Rent (véase Landman y Russo, 1971).
Los primeros datos sugerían D/E = 2/3, resultado que Keyes (1981) extrapola a grandes «circuitos» del sistema nervioso (como el nervio óptico y el corpus callosum). Sin embargo, la razón D/E aumenta con el rendimiento del circuito. El rendimiento, a su vez, refleja el grado de paralelismo presente en el diseño. En particular, en los diseños con características extremas se llega a valores extremos de D. En un registro de desplazamiento, los módulos forman una cadena y T = 2 independientemente de C, con lo que D = 0. En caso de paralelismo integral, cada componente precisa de su propio terminal y por tanto, T = C, con lo que D = E.
Para explicar D/E = 2/3, R. W. Keyes observó que, normalmente, las componentes están dispuestas en el interior del volumen de los módulos, mientras que las conexiones se distribuyen por su superficie. Para probar que esta observación implica la regla de Rent, basta con suponer que todas las componentes tienen aproximadamente el mismo volumen V y la misma superficie σ. Como C es igual al volumen total del módulo dividido por V, C1/3 es aproximadamente proporcional a su radio. Por otro lado, T es la superficie total del módulo dividida por σ, con lo que T1/2 es aproximadamente proporcional también al radio. La regla de Rent no es más que otra expresión de la equivalencia de dos medidas del radio de una figura espacial estándar. E = 3 es la dimensión euclídea del circuito y D = 2 es la dimensión de una superficie común.
Nótese que el concepto de módulo es ambiguo y casi indefinido, aunque la regla de Rent es compatible con esta característica, siempre que los submódulos de cualquier módulo estén interconectados por sus superficies.
Los casos extremos mencionados más arriba tienen una interpretación igualmente sencilla. En una estructura lineal estándar, E = 1 y la frontera se reduce a dos puntos, con lo cual D = 0. Y en una estructura plana estándar, E = 2 y D = 1.
Sin embargo, cuando la razón E/D no es ni 3/2 ni 2/1, la geometría euclídea no nos permite interpretar C o T como expresiones del volumen o la superficie, respectivamente. Sin embargo, tales interpretaciones sí son posibles y resultan útiles en geometría fractal. En un circuito espacial que está en contacto con el exterior a través de su propia superficie, E = 3 y D toma un valor comprendido entre 2 y 3. En un circuito plano que esté en contacto con el exterior a través de la curva que lo delimita, E = 2 y D toma un valor entre 1 y 2. El caso de paralelismo integral, D = E, corresponde a contomos de Peano. Por otra parte, si el contomo se utiliza de modo incompleto, el «contomo efectivo» puede ser cualquier superficie con una D entre 0 y E.
LÁMINA 168. Log(perímetro) en función del log(área) para nubes (⚬) y zonas lluviosas (•). De Lovejoy 1982

FIGURA 168