El principal objetivo de este capítulo es que el lector se familiarice sin demasiado esfuerzo con otro objeto matemático que ordinariamente se considera patológico, el polvo de Cantor C. Éste y otros polvos parecidos que describiremos tienen dimensiones fractales comprendidas entre 0 y 1.

Al estar formados por puntos sobre una recta son fáciles de estudiar. Además, ayudan a introducir de la forma más simple varios conceptos centrales referentes a las fractales que, al haber sido tan poco utilizados en el pasado, no han recibido nombres específicos. Primero se da un significado técnico a la palabra polvo, sinónimo informal de conjunto de dimensión topológica D_T = 0, al igual que «curva» y «superficie» denotan conjuntos de dimensión topológica D_T = 1 y D_T = 2. Otras voces nuevas serán coágulo, hueco y trema, y las explicaremos más adelante.

Para un profano, ruido es un sonido demasiado fuerte, sin un ritmo agradable o pauta, o que interfiere con otros sonidos más deseables.

▯ Partridge (1958) afirma que el término noise (ruido) «se deriva del latín nausea (relacionado con nautes = marinero); el enlace semántico habría que buscarlo en el ruido que hacía el pasaje de un barco antiguo gimiendo y vomitando durante el mal tiempo». (El Oxford English Dictionary no está tan seguro de ello) ▮.

Por lo que respecta al significado del término en la física contemporánea, no es tan pintoresco ni tampoco tan preciso: es un sinónimo de fluctuación al azar o de error, independientemente de cuál sea su origen y cómo se manifieste. En este capítulo se introduce C mediante el caso de un ruido esotérico pero simple.

Un canal de transmisión es un sistema físico que conduce la electricidad. Ahora bien, la corriente eléctrica es susceptible de ruido espontáneo. La calidad de la transmisión depende de la probabilidad de error debida a la distorsión, que depende a su vez de las intensidades relativas de la señal y el ruido.

Este capítulo se ocupa de canales que transmiten datos informáticos y utilizan señales muy intensas. Es importante el hecho de que la señal sea discreta, pues la distribución de errores reduce la distribución de ruido, por así decirlo, a su esqueleto. La función de ruido puede tomar diversos valores, mientras que el error es descrito por una función que sólo puede tomar dos valores. Podría ser, por ejemplo, la función del indicador, que es 0 cuando no hay error en el instante t, y 1 cuando sí lo hay.

Los físicos son maestros en lo que concierne a la estructura de los ruidos que predominan en el caso de señales débiles, el ruido térmico, por ejemplo. Sin embargo, en el problema que acabamos de describir, la señal es tan fuerte que los ruidos clásicos son despreciables.

Los ruidos excedentes no despreciables son fascinantes y difíciles de tratar, pues se sabe muy poco de ellos. En este capítulo estudiaremos un ruido excedente que, hacia 1962, tuvo importancia práctica para la electrotecnia, por lo que se indicó un cierto esfuerzo a investigar el problema. Mi contribución a estas investigaciones fue la primera situación concreta en la que experimenté la necesidad de usar los fractales. Por aquel entonces nadie podía imaginar ni remotamente que un estudio minucioso de ese modesto problema de ingeniería fuera a llevarnos tan lejos.

Sometamos los errores a un análisis cada vez más refinado. Un ligero examen muestra la presencia de períodos en los que no se da ningún error. Llamemos «huecos de orden 0» a estos periodos de remisión, si su duración es superior a una hora. Por contra, cualquier intervalo de tiempo flanqueado por huecos de orden 0 queda singularizado como una «ráfaga de errores de orden 0». Un análisis tres veces más fino revela que la ráfaga original es a su vez «intermitente», esto es, que hay unos huecos más cortos «de orden 1», de unos 20 minutos de duración o más, que separan ráfagas, también más cortas, «de orden 1». Del mismo modo, cada una de éstas contiene varios huecos «de orden 2», de unos 400 segundos de duración, intercalados entre ráfagas «de orden 2», y así sucesivamente, de modo que cada estadio está formado por huecos y ráfagas tres veces más cortos que el anterior. La lámina 117 presenta una ilustración aproximada de todo el proceso. (Aunque de momento no hay que hacer demasiado caso al pie de figura).

La descripción anterior nos sugiere una propiedad de las posiciones relativas de las ráfagas de orden k contenidas en una ráfaga de orden k − 1. Parece que la distribución de probabilidad de dichas posiciones relativas no tenga que depender de k. Esta invariancia es un ejemplo claro de autosemejanza, y la dimensión fractal no puede andar lejos, pero no nos precipitemos. Los diversos casos que se tratan en este ensayo pretenden, entre otras cosas, sacar temas nuevos o clarificar otros ya conocidos. Con esta idea, parece más apropiado prescindir del orden histórico e introducir un tema nuevo a partir de una variante no aleatoria del modelo estocástico de Berger y Mandelbrot para los errores (capítulo 31).

En la sección anterior se ha construido el conjunto de errores a partir de una línea recta, el eje de tiempos, a la que se van arrancando huecos sin errores cada vez más cortos. Aunque este procedimiento pueda ser poco habitual en las ciencias de la naturaleza, la matemática pura lo ha utilizado ya, por lo menos desde Georg Cantor (Hawkins, 1970, en especial pág. 58).

En Cantor (1883) el iniciador es el intervalo cerrado [0,1]. El adjetivo «cerrado» y los corchetes indican que los extremos están incluidos; esta notación se usó ya en el capítulo 6, pero hasta ahora no ha sido necesario explicitarla. El primer estadio de la construcción consiste en dividir [0,1] en tres partes y extraer el tercio central abierto, denotado por ]1/3, 2/3[. El adjetivo «abierto» y los corchetes invertidos indican que se excluyen los extremos. A continuación se quitan los tercios centrales abiertos de cada uno de los N = 2 tercios restantes, y así sucesivamente.

El conjunto C resultante se llama, bien diádico, por el hecho de que N = 2, bien triádico o ternario, por el hecho de que [0,1] se subdivide en tres partes.

En general, el número de partes se llama base y se denota por b. Así la razón entre cada N-ésimo del conjunto y el todo es r = 1/b. C se llama también discontinuo de Cantor, y yo sugeriré la denominación polvo fractal de Cantor. Como cada punto del eje de tiempos señala un «suceso», C es una sucesión fractal de sucesos.

El procedimiento de Cantor es una cascada, por usar un término que Lewis Richardson aplicó a la turbulencia, y que ya tomamos prestado en el capítulo 6 para referirnos a las costas y a la curva de Koch. Un «material» uniformemente distribuido sobre un iniciador |0,1] es sometido a un remolino centrifugador que lo manda a los tercios de los extremos.

El tercio central arrancado de [0,1] para formar un hueco se denomina en lo sucesivo generador de tremas. En esta sección se acuña este neologismo a partir de TREMA, que significa agujero y está en cierto modo emparentada con el latín termes=termita. Acaso sea la palabra griega más corta a la que todavía no se le ha dado un significado científico importante.

En el presente contexto, las tremas y los huecos coinciden, pero no será así en otras situaciones que encontraremos más adelante, por lo que son necesarios dos términos distintos.

Al vaciarse una «trema de primer orden», el material total se conserva y se redistribuye uniformemente sobre los tercios extremos, que llamaremos pregrumos. Luego vienen dos remolinos centrífugos y repiten la misma operación con los dos intervalos [0,1/3] y [2/3,1]. El proceso continúa como una cascada de Richardson y, en el límite, converge hacia un conjunto que llamaremos coágulo. Si la duración de cada estadio es proporcional al tamaño de los remolinos, el proceso total tiene una duración finita.

Paralelamente, propongo el término suero para denotar el espacio que no está ocupado por el coágulo.

Sugiero también que esas palabras se usen con un sentido físico, además de matemático. Así, el proceso de coagulación denotará una cascada de inestabilidades que produzca una contracción, y el coágulo será el volumen en el que se concentra una característica física como resultado de dicho proceso.

Obsérvense las asociaciones libres siguientes: coágulo → queso → leche → Vía Láctea → Galaxia (γαlα=leche) → galaxias. Acuñé el término curdling (coágulo) cuando trabajaba con galaxias, y las connotaciones etimológicas de «curdling galáctico» no me pasaron desapercibidas.

Como preludio de la extrapolación de C, recordemos un aspecto histórico. Cuando Cantor introdujo el conjunto C apenas se apartó de su tema original, el estudio de las series trigonométricas. Como dichas series se ocupan de las funciones periódicas, la única extrapolación posible es la repetición indefinida. Recordemos ahora las expresiones corte interior y exterior, que se explican por sí mismas, y que en el capítulo 6 se tomaron prestadas de la teoría de la turbulencia. Son los tamaños ε y Ω de los rasgos menor y mayor, respectivamente, presentes en el conjunto. Se puede decir que Cantor se limitó al caso Ω = 1. En el k-ésimo estadio de la iteración se tiene que ε = 3^−k, pero, para C, ε = 0. Para obtener cualquier otro Ω < ∞ (por ejemplo 2π, como correspondería a una serie de Fourier) se dilata el polvo de Cantor periódico en un factor Ω.

Sin embargo, la autosemejanza, que es una característica muy apreciada en este ensayo, se pierde con la repetición. Aunque se puede recuperar fácilmente si el iniciador se usa sólo en la extrapolación y ésta sigue una cascada inversa o ascendente. El primer estadio dilata C en un factor 1/r = 3, situándolo en [0, 3]. El resultado es el propio C y una réplica de sí mismo separada de C por una nueva trema de longitud 1. En el segundo estadio, el resultado del primero se dilata también en un factor 3 y queda situado en la posición [0, 9]. El resultado es C, más tres réplicas de sí mismo, separadas por dos tremas de longitud 1 y una de longitud 3. La cascada ascendente continúa, dilatando C en factores sucesivos de la forma 3^k.

Si se prefiere, se pueden realizar alternativamente dos estadios de interpolación y uno de extrapolación. De este modo, cada serie de tres pasos multiplica el corte exterior Ω por 3 y el interior ε por 9.

▯ En este polvo extrapolado, el eje negativo está vacío, es una trema infinita. El concepto subyacente se comentará más adelante, en el capítulo 13, cuando ataquemos el problema del continente (infinito) y el racimo infinito. ▮

El conjunto que resulta de estas extrapolación e interpolación infinitas es autosemejante y

Con otras reglas de coagulación distintas se pueden obtener otras D; de hecho, cualquier valor entre 0 y 1 es alcanzable. Si la trema del primer estadio tiene longitud 1 − 2r, con 0 < r < 1/2, entonces la dimensión es log 2/log(1/r).

Se puede tener una mayor variedad dejando que N = 2. Para los conjuntos con N = 3 y r = 1/5, obtenemos

Aunque tengan la misma D, los dos últimos conjuntos tienen «aspectos» muy distintos. Volveremos sobre esta apreciación en el capítulo 34, y reflexionando sobre ella llegaremos al concepto de lagunaridad.

Nótese también que hay por lo menos un polvo de Cantor para cada D < 1. Además, de Nr < 1 se sigue que N < 1/r, con lo que D nunca es mayor que 1.

Mientras la D de un conjunto de Cantor puede variar entre 0 y 1, desde el punto de vista topológico todos los conjuntos de Cantor tienen dimensión D_T = 0, pues, por definición, cada punto está separado de los demás, sin que haya que sacar nada para separarlo del resto. Mirado así, ¡no hay ninguna diferencia entre C y los conjuntos finitos de puntos! El hecho de que en este último caso D_T = 0 es algo ya sabido en la geometría estándar, y se usa en el capítulo 6 para razonar que la curva K de Koch tiene dimensión topológica 1. Pero para los conjuntos totalmente inconexos, D_T = 0.

A falta de un equivalente coloquial de «curva» y «superficie» (que son conjuntos conexos con D_T = 1 y D_T = 2), propongo llamar polvos a los conjuntos con D_T = 0.

Considérese un polvo de Cantor, sea u un valor posible de la longitud de un hueco, y denótese por U la variable aleatoria longitud y por Nr (U>u) el número de huecos o tremas cuya longitud U sea mayor que u. ▯ Esta notación es un derivado de la notación Pr (U>u), propia de la teoría de la probabilidad. ▮ Se encuentra que hay un factor constante F tal que la gráfica de la función Nr (U>u) corta constantemente la gráfica de Fu^−D. Y vuelve a aparecer la dimensión. Si tomamos como coordenadas log u y log Nr, los escalones son uniformes.

Como en el caso de una costa, uno puede obtener una imagen aproximada de la secuencia de errores si la coagulación de Cantor se detiene al llegar a intervalos de ε = 3^−k. Podría tomarse como e el tiempo necesario para transmitir un símbolo. Hay que usar también la extrapolación periódica de Cantor con un Ω grande pero finito.

El número de errores entre los instantes 0 y R, que denotamos por M(R), registra el tiempo contando sólo aquellos instantes que tienen algo que merezca la pena. Es un ejemplo de tiempo fractal.

Si la muestra empieza en t = 0 (es el único caso que consideraremos aquí), la M(R) se obtiene como en el caso de la curva de Koch. Siempre y cuando R sea menor que n, el número de errores se dobla cada vez que R se triplica. En consecuencia, M(R) ∝ R^D.

Esta expresión es parecida a la fórmula conocida de la masa de un disco o una bola de radio R en un espacio euclídeo de dimensión D. Es también idéntica a la fórmula obtenida en el capítulo 6 para la curva de Koch.

Tenemos como corolario que el número medio de enores por unidad de longitud varía aproximadamente como R^D−1 para R comprendido entre los cortes inferior y superior. Si Ω es finito, el número medio de errores por unidad de longitud disminuye hasta el valor final Ω^D−1, que se alcanza para R = Ω. A partir de ahí la densidad permanece más o menos constante. Si Ω es infinito, el número medio de errores disminuye hasta hacerse nulo. Finalmente, los datos empíricos sugieren que Ω es finito y muy grande, pero no permiten determinar su valor con ninguna precisión. Si las cosas son así, el número medio de errores tiene un límite inferior no nulo, que, al estar tan mal determinado, en la práctica carece de utilidad.

▯ Los elementos más destacados de C, a saber, los extremos de las tremas, no llenan todo C; de hecho sólo son una pequeña parte del mismo. En el capítulo 19 comentaremos la importancia Física de los otros puntos. ▮

Al lector que haya llegado hasta aquí y/o haya oído el eco de la creciente literatura sobre las Escaleras del Diablo (pie de la lámina 121) le parecerá difícil creer que, cuando empecé con este tema en 1962, todo el mundo estaba de acuerdo en que los polvos de Cantor eran por lo menos tan monstruosos como las curvas de Koch y Peano.

Cualquier físico con amor propio «desconectaba» automáticamente con la simple mención de Cantor, fácilmente echaba a correr ante cualquiera que pretendiera que C tenía algún interés científico, y afirmaba vehementemente que tales pretensiones se habían presentado ya, habían sido sometidas a prueba y habían resultado defectuosas. Sólo recibí aliento de las sugerencias de S. Ulam, tentadoras a pesar de que ni fueron aceptadas ni progresaron, relativas al posible papel de los conjuntos de Cantor en el equilibrio gravitatorio de los agregados estelares (véase Ulam, 1974).

¡Para publicar algo sobre polvos de Cantor tuve que eliminar cualquier mención a Cantor!

Pero aquí hemos llegado a C por las propias peculiaridades de la naturaleza. En el capítulo 19 se describe un segundo significado físico de C, completamente distinto del presente. Lo cual debe significar que la verdadera naturaleza del polvo de Cantor es muy distinta.

Es innegable que en la mayoría de casos C es sólo un modelo muy tosco que precisa de muchas mejoras. Sostengo, no obstante, que son precisamente las mismas propiedades que hacen patológicos los discontinuos de Cantor las que son indispensables en un modelo de la intermitencia, y hay que conservarlas al buscar alternativas más realistas a C.

LÁMINAS 117 y 118. Barra y pastel triádicos de Cantor (dimensión de la sección horizontal D = log 2/log 3 = 0,6309). Anillos de Saturno. Cortinas de Cantor

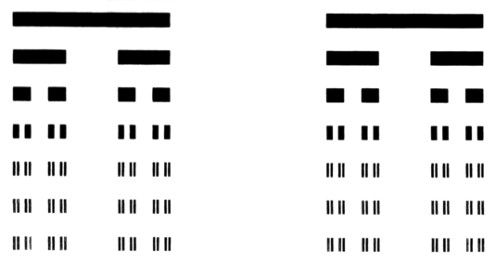
FIGURA 117

El iniciador del polvo de Cantor es [0,1] y su generador es

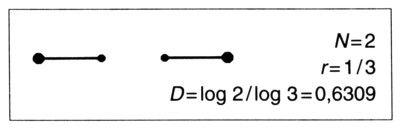
LÁMINA. 117. El polvo de Cantor es extraordinariamente difícil de ilustrar, pues, de tan fino y disperso, resulta invisible. Para ayudar a la intuición a hacerse una idea de su forma, lo hacemos más grueso hasta convertirlo en lo que se podría llamar una barra de Cantor.

▯ En palabras técnicas, la figura representa el producto cartesiano de un polvo de Cantor de longitud 1 por un intervalo de longitud 0,03. ▮

COAGULO. La construcción de la barra de Cantor es el resultado del proceso que llamo de coagulación. Empieza con una barra cilíndrica (cuya proyección es un rectángulo con anchura/longitud=0,03). Lo mejor es considerar que su densidad es muy baja. La materia del tercio central se «cuaja» en los dos tercios de ambos extremos, de manera que la posición de éstos no cambia. Luego, la materia del tercio central de cada tercio extremo coagula en sus tercios extremos, y así indefinidamente hasta que sólo queda una infinidad de lingotes infinitamente delgados con una densidad infinitamente grande. Estos lingotes se distribuyen sobre la recta de una manera muy concreta, inducida por el propio proceso generador. En esta ilustración, la coagulación se detiene cuando tanto la imprenta como nuestro ojo claudican; la última línea y la penúltima son indistinguibles: cada una de las partes últimas parece más un lingote gris que un par de lingotes negros y paralelos.

PASTEL DE CANTOR. Cuando la coagulación empieza con una torta, mucho menos gruesa que ancha, y la masa cuaja en tortitas más delgadas (rezumando un relleno apropiado), se obtiene un Napoleón infinitamente extrapolado, que podríamos llamar pastel de Cantor.

ANILLOS DE SATURNO. Al principio se pensaba que Saturno estaba rodeado por un solo anillo. Pero luego se descubrió un corte, después dos, y ahora el Voyager I ha identificado un número muy grande de cortes, la mayoría de ellos muy finos. El Voyager ha descubierto también que son diáfanos y dejan pasar la luz del Sol… como corresponde a un conjunto que hemos calificado de «fino y disperso».

Así pues, la estructura de los anillos (véase Stone y Minen, 1981, y en especial la ilustración de la sobrecubierta) sugiere una colección de círculos próximos, cuyos radios corresponden a la distancia de un cierto origen a los puntos de un polvo de Cantor. ▯ La expresión técnica es «producto cartesiano de un polvo de Cantor por un círculo». En realidad, una imagen más realista sería quizá la dada por el producto cartesiano de un círculo por un polvo de medida positiva, como los que se estudian en el capítulo 15. ▮ Inserción de última hora: Avron y Simón (1981), introducen independientemente la misma idea, relacionándola con la ecuación de Hill; su Nota 6 contiene muchas otras referencias interesantes.

ESPECTROS. Harter 1979-1981 describe algunos espectros de moléculas orgánicas cuyo parecido con un polvo de Cantor es asombroso.

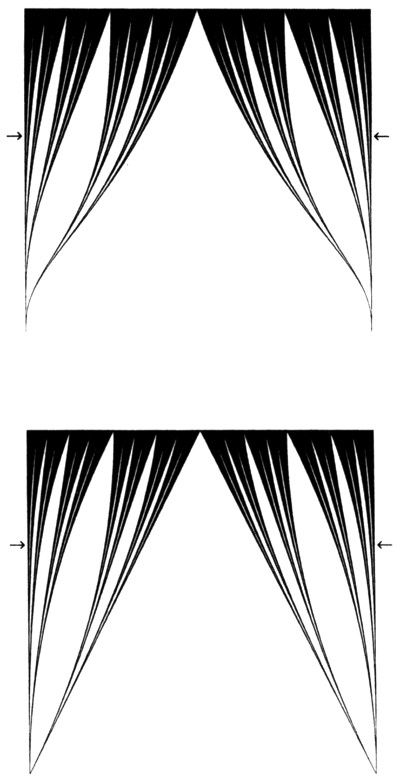
FIGURA 118

LÁMINA 118. Aquí se aclara la forma del polvo de Cantor colocándolo entre otros polvos generalizados con N = 2 y r variable. La coordenada vertical corresponde a r (figura inferior), que varía entre 0 y 1/2, o D (figura superior), que varía entre 0 y 1. La parte superior de ambas cortinas de teatro está rematada por el intervalo [0,1]. Los cortes horizontales son polvos de Cantor. Las flechas señalan el caso r = 1/3 y D = 0,6309.

UNA FAMOSA PARADOJA GRIEGA. Los filósofos griegos creían que, para ser indefinidamente divisible, un cuerpo tenía que ser continuo. Sin duda no sabían de los polvos de Cantor.

LÁMINA 121. Función de Cantor o escalera del diablo (dimensión D = 1, las abscisas de los ascendentes tienen dimensión D ~ 0,6309). Movimiento de Cantor

FIGURA 121

La función de Cantor describe la distribución de masa sobre la barra de Cantor de la lámina 117. Su gráfica es denominada escalera del diablo por muchos autores, pues es verdaderamente estrambótica. Tómense iguales a 1 la longitud y la masa de la barra, y para cada valor R de la abscisa defínase M(R) como la masa comprendida entre 0 y R. Como los huecos no tienen masa, M(R) permanece constante sobre un conjunto de intervalos que tienen una longitud total igual a la de la barra. No obstante, como el martilleo no afecta a la masa total de la barra, M(R) tiene que apañárselas para encontrar alguna parle en la que crecer desde (0,0) hasta (1,1). Los incrementos se producen en una infinidad de saltos infinitamente pequeños y muy agrupados, que corresponden a los lingotitos. Hille y Tamarkin (1929) describen con detalle las propiedades singulares de esta función.

APLICACIONES REGULARIZADORAS. La escalera del diablo lleva a cabo la proeza de aplicar la drástica falta de uniformidad de la barra de Cantor en algo uniforme y homogéneo. A partir de dos intervalos distintos, de la misma longitud sobre la escala vertical, la función inversa de la escalera de Cantor da dos conjuntos de lingotes que contienen la misma masa (aun cuando, normalmente, sus aspectos son muy distintos).

Como la ciencia se siente cómoda en la uniformidad, suele ocurrir que esas transformaciones regularizadoras hacen que la irregularidad fractal sea accesible al análisis.

HOMOGENEIDAD FRACTAL. Por conveniencia, diremos que la distribución de masa de la barra de Cantor es fractalmente homogénea.

MOVIMIENTO DE CANTOR. Como en el caso de la curva de Koch, que hemos interpretado como un movimiento de Koch, o en el del movimiento de Peano, a veces es útil interpretar la ordenada M(R) como un tiempo. En tal caso, la función inversa R(M) da la posición de un movimiento de Cantor en el instante M. Tal movimiento es discontinuo. En los capítulos 31 y 32 se describen generalizaciones lineales y espaciales aleatorias del mismo.

DIMENSIÓN FRACTAL. La suma de las alturas de los escalones, así como la de sus longitudes, es 1, con lo que esta curva tiene una longitud bien definida e igual a 2. Una curva de longitud finita se dice que es rectificable, y su dimensión es D = 1. Con este ejemplo se demuestra que la dimensión D = 1 es compatible con la existencia de una infinidad de irregularidades, siempre y cuando estén lo bastante dispersas.

▯ Uno se sentiría tentado de decir que esta curva es un fractal, pero para ello habría que definir los fractales de forma menos rigurosa y en base a otros conceptos aparte de la D. ▮

FUNCIONES SINGULARES. La escalera de Cantor es una función no decreciente, no constante y singular, en el sentido de que es continua pero no diferenciable. Su derivada es nula casi por doquier y su variación se produce en un conjunto de longitud —es decir, medida lineal— nula.

Cualquier Función no decreciente se puede expresar como suma de una función singular, una función formada por saltos discretos, y una función diferenciable. Las dos últimas componentes son clásicas en matemáticas y su uso en física está muy extendido. Por el contrario, en física se considera que la componente singular es patológica y carece de aplicaciones prácticas. Una de las tesis centrales de este ensayo es que tal opinión carece de sentido.

ESCALERAS DEL DIABLO EN FÍSICA ESTADÍSTICA. La publicación de esta lámina en mi ensayo de 1977 atrajo la atención de los físicos sobre la escalera del diablo y estimuló una literatura bastante extensa. Cada vez es más frecuente encontrarse con diagramas semejantes a las «cortinas» de la lámina 118, o la cortina de Fatou de la lámina 265. Véase Aubry (1981). Importantes trabajos anteriores (Azbel, 1964, Hofstadter, 1976), aparentemente aislados, se comprenden conjuntamente a la luz de estos nuevos avances.

8 Sucesos fractales y polvos de Cantor

8
Sucesos fractales y polvos de Cantor