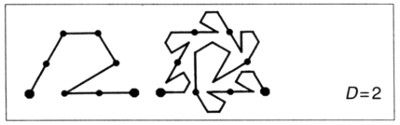
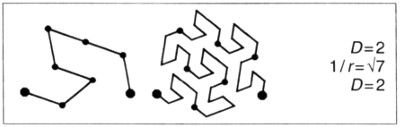
Acabamos de ver, al tratar de las curvas de Koch generalizadas que no se cortan a sí mismas, que hay razones de peso para detenerse un poco antes de D = 2. Cuando llegamos a D = 2 se produce un cambio cualitativo profundo.

Supondremos que los terágonos no se cortan a sí mismos, aun cuando puedan presentar puntos de autocontacto. Uno de los síntomas que se presentan cuando D llega a D = 2 es que los puntos de autocontacto son asintóticamente inevitables. El síntoma principal es que es inevitable que la curva límite llene un «dominio» del plano, esto es, un conjunto que contiene discos (círculos rellenos).

Esta doble conclusión no se debe a una falta de imaginación, corregible, por parte de los matemáticos, sino que es consecuencia de un principio fundamental que tuvo un papel central en la crisis de la matemática entre 1875 y 1925.

Los límites correspondientes, de los que se dan ejemplos en las próximas láminas, se llaman curvas de Peano, pues la primera de ellas se encuentra en Peano (1890). Se las llama también curvas que cubren el plano. En su caso, la definición formal de la dimensión como [log N/log (1/r)] = 2 está justificada, pero por razones decepcionantes. Desde el punto de vista del matemático, una curva de Peano no es más que una manera rara de considerar un dominio plano, que es un conjunto al que todas las definiciones clásicas asignan la dimensión 2. Es decir, que la expresión curva que recubre el plano no debería emplearse si se pretende hablar con precisión.

Por suerte, la mayoría de «curvas» de Peano, incluso las que se obtienen por una construcción iterativa de Koch, están parametrizadas de un modo natural por un escalar t, al que podemos llamar «tiempo». En tal caso, y sin ningún temor a los guardianes del rigor, podemos usar las expresiones: movimientos de Peano, movimientos que recubren el plano, movimientos de barrido por baldosas, o barridos por baldosas (hablaremos de los embaldosados más adelante en este mismo capítulo). Y así lo haremos cuando nos parezca conveniente, aunque los ensayos no tienen por qué presentar una consistencia absoluta bajo ningún concepto.

«¡Todo se ha trastornado! Es difícil expresar en palabras el efecto que el resultado de [Giuseppe] Peano tuvo sobre el mundo matemático. Parecía como si todo se hubiera venido abajo, como si los conceptos matemáticos fundamentales hubieran perdido su significado» (Vilenkin 1965). «Posiblemente [el movimiento de Peano] no pueda ser captado por la intuición; y sólo se puede entender por medio del análisis lógico» (Hahn 1956). «Algunos objetos matemáticos, como la curva de Peano, son totalmente antiintuitivos…, extravagantes» (Dieudonné, 1975).

Yo creo que las citas anteriores sólo prueban que ningún matemático ha examinado nunca con detenimiento una buena gráfica de Peano. Un observador despiadado podría decir que estas citas demuestran falta de imaginación geométrica.

Por el contrario, yo afirmo que, después de observar atentamente los terágonos de Peano, dejando vagar la mente, resulta muy difícil no asociarlos con diversos aspectos de la naturaleza. Este capítulo aborda las curvas «autoevitantes», es decir, aquéllas cuyos terágonos evitan los puntos de autocontacto. En el capítulo 13 se estudiarán los terágonos que presentan un autocontacto moderado. Los terágonos que recubren un retículo (una cuadrícula, por ejemplo) deben pasar por un tratamiento previo para eliminar los puntos de autocontacto.

Al examinar distintos terágonos de Peano, vi en cada caso un conjunto de árboles (o de conjuntos de árboles) que presentaban una variedad inagotable de interpretaciones concretas. Éstas son especialmente evidentes en la curva de Peano que llamo «barrido del copo de nieve», y que presento en la lámina 103. Es fácil imaginar dicha figura como un conjunto de arbustos plantados uno junto a otro sobre el tercio inferior de un copo de nieve de Koch, que trepan por una pared. O también, el perfil remarcado en negro puede evocarnos un conjunto de riachuelos que serpentean y acaban desembocando en un río que sigue la parte inferior del copo de nieve. Esta segunda interpretación sugiere enseguida que las curvas que separan los ríos entre sí forman las cuencas fluviales. Por supuesto, las etiquetas río y cuenca son intercambiables.

Esta nueva analogía con los ríos y cuencas es tan clara a posteriori que conjura cualquier pensamiento de que la curva de Peano es necesariamente patológica. De hecho, si un árbol formado con ríos de anchura nula tiene que drenar completamente una superficie, debe llegar necesariamente a todas partes. Alguien que siga la ribera total de los ríos realiza un movimiento que recubre el plano. ¡Preguntad a cualquier niño y os lo confirmará!

Con la ayuda intuitiva que nos proporciona la lámina 102, resulta difícil no ver redes conjugadas análogas en cualquier otro terágono de Peano. Hasta una isla tosca como la de la lámina 93 empieza a adquirir sentido intuitivo. Los delgados dedos de agua que la penetran no se pueden contemplar ya como una marina, por exagerada que sea, sino como ríos que se ramifican.

La ciencia que trata de los ríos debería llamarse potamología (término acuñado por Maurice Pardé, a partir de πoταμos (= río) y λoγos). Pero la costumbre ha incluido el estudio de los ríos en la ciencia del agua, la hidrología, de la que echaremos mano muchas veces a lo largo de este ensayo.

Los puntos múltiples son inevitables en los árboles, y por lo tanto también en los movimientos de Peano

Muchas propiedades matemáticas de las curvas de Peano se hacen evidentes también de repente. Para explicar los puntos dobles, supongamos que uno empieza en un punto de la orilla de un río de un árbol fluvial de Peano y se mueve río arriba o río abajo, dando un rodeo alrededor de cada rama (moviéndose cada vez más rápido a medida que disminuye el grosor de las ramas). No cabe duda de que a la larga uno acaba encontrándose en la orilla opuesta del punto de partida. Pero, como el río límite es infinitamente estrecho, uno regresa de hecho al punto de partida. Así pues, en una curva de Peano los puntos dobles son inevitables, no sólo desde el punto de vista lógico, sino también desde el intuitivo. Más aún, forman un conjunto denso.

También es inevitable que algunos puntos sean visitados más de dos veces, pues en los puntos de confluencia de ríos coinciden por lo menos tres puntos de la ribera. Si todos los puntos de confluencia corresponden sólo a pares de ríos, la multiplicidad mayor que se da es tres. Por otra parle, si se acepta que pueda haber puntos de multiplicidad superior uno se puede arreglar perfectamente bien sin puntos triples.

Todas las afirmaciones de los párrafos anteriores han sido demostradas, pero, como las demostraciones son delicadas y dieron lugar a controversias, las propiedades mismas parecen «técnicas». Aunque en realidad lo cierto es lo contrario. ¿Quién sería capaz de seguir discutiendo que mi propio enfoque intuitivo es preferible al puramente lógico?

Los ríos de la curva de Peano no son formas estándar, sino curvas fractales. Esto es una suerte, especialmente para su aplicación en modelado, puesto que todas las razones aducidas en el capítulo 5 a favor de que las curvas geográficas no son rectificables son aplicables también a las riberas de los ríos. De hecho, muchos de los datos de Richardson incluyen fronteras que discurren a lo largo de ríos. Los ríos también aparecen en la cita de Steinhaus (1954). En cuanto a las cuencas de drenaje fluvial, se pueden rodear por curvas cerradas semejantes a las costas de las islas, formadas por partes de la cuenca. Cada cuenca está formada por la yuxtaposición de cuencas parciales y está surcada por los propios ríos, pero las curvas que recubren porciones del plano y están delimitadas por curvas fractales presentan toda la estructura que nos hace falta para esta descripción.

Tómese la curva de Peano original (lámina 93) y escríbase t en la base de numeración N = 9. Se tendrá una expresión de la forma 0, τ₁, τ₂,… Los tiempos cuyo primer «dígito» sea el mismo estarán en el mismo noveno del cuadrado inicial; de éstos, los que tengan el mismo segundo dígito estarán en el mismo 9²-avo, etc. Así pues, el embaldosado de [0,1] en novenos se traduce en un embaldosado del cuadrado, y los novenos de las baldosas lineales se traducen en los correspondientes novenos de las baldosas planas. Y la propiedad del intervalo [0,1] de estar perembaldosado (pág. 74), esto es, de ser recurrente e indefinidamente subdivisible en baldosas semejantes a [0,1] y más pequeñas, se traduce al cuadrado. Otros movimientos de Peano alternativos, como los de Cesàro, Pólya y otros, aplican esta propiedad del intervalo en diversos perembaldosados del triángulo.

En general, la mayoría de movimientos de Peano generan perembaldosados del plano. En el caso más simple hay una base N y se empieza con un perembaldosado lineal consistente en divisiones sucesivas en N-avos. Sin embargo, el barrido del copo de nieve de las láminas 102-103 precisa una división irregular del intervalo [0,1] recorrido por t en cuatro subintervalos de longitud 1/9, otros cuatro de longitud 1/9√3, uno de longitud 1/9, dos de 1/9√3 y dos de 1/9.

Las relaciones donde la longitud y el área intercambian su papel son típicas del movimiento de Peano, especialmente cuando éste es isométrico, esto es, cuando un intervalo de tiempo [t₁,t₂] se aplica sobre un área igual a la longitud |t₁ − t₂|. (La mayoría de movimientos de Peano son isométricos y perembaldosantes, pero se trata de propiedades distintas). Si llamamos intervalo de Peano plano a la imagen del intervalo de tiempo [t₁,t₂], tendremos que, en vez de medir distancias por medio del tiempo, podremos hacerlo mediante el área. Nos encontramos, sin embargo, con una complicación crucial, pues los puntos que están uno frente a otro en riberas opuestas de un río coinciden en el espacio y son visitados varias veces.

La definición de la «distancia de Peano» debe tener en cuenta el orden de las visitas. Si denotamos por t'₁, y t'₂ los instantes de los primeros pasos por los puntos P₁ y P₂, y por t''₁, y t''₂ los de las últimas visitas, definiremos el intervalo de Peano por la izquierda L{P₁, P₂} como la aplicación de [t'₁, t'₂] y el intervalo de Peano por la derecha R{P₁, P₂}, como la aplicación de [t''₁, t''₂]. Las longitudes de dichos intervalos permiten definir la distancia por la izquierda y la distancia por la derecha como |L{P₁, P₂}| = |[t'₁, t'₂]| y |R{P₁, P₂}| = |[t''₁, t''₂]|. Estas distancias son aditivas, en el sentido de que si tres puntos P₁, P₂ y P₃ están ordenados por la izquierda, según el orden de los primeros tiempos de paso, se tiene

Otras definiciones alternativas de distancia distinguen entre los puntos del río y de la cuenca. Denótese por t' y t'' los instantes de las visitas primera y última a P. P es un punto del río si los límites de la imagen de [t', t''] son P y la cuenca. Las visitas sucesivas de P están una frente a otra en algún río. P es un punto de la cuenca si la imagen de [t', t''] está delimitada por P y el río.

Además, si hemos representado una curva de Peano como la playa común a mi árbol lluvial y su correspondiente cuenca, entre los caminos que enlazan P₁ con P₂ sobre los ríos (o, alternativamente, sobre las cuencas) hay un camino mínimo común. Parece razonable usar este camino para medir la distancia entre P₁ y P₂. Salvo en casos excepcionales, la dimensión D de los ríos y las cuencas tiene un valor comprendido estrictamente entre 1 y 2, por lo que ese camino mínimo no se puede medir con la longitud ni con el área, sino que en los casos típicos tiene una medida de Hausdorff no trivial con dimensión D.

MÁS. Nuevas e importantes consideraciones sobre los movimientos de Peano se encontrarán en los pies de figura que vienen a continuación.

LÁMINA 93. Una construcción cuadrangular de Koch con dimensión D = 2: la curva de Peano original, un barrido del cuadrado.

FIGURA 93

La curva de Peano de esta lámina es la original. El algoritmo increíblemente conciso de Giuseppe Peano fue plasmado gráficamente en Moore (1900) —a quien atribuyo injustificadamente el mérito en mi Fractals de 1977—. Esta lámina gira 45° la curva de Peano, convirtiéndola en una curva de Koch en el sentido más estricto; el generador se coloca siempre del mismo modo sobre los lados del terágono obtenido en el estadio anterior.

El iniciador es el cuadrado unidad (que en la figura aparece en negro) y el generador es

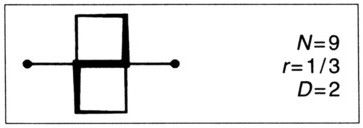
Como el generador tiene puntos de autocontacto, las islas de Koch finitas que resultan son conjuntos de cuadrados negros que semejan un sector de un tablero de ajedrez infinito. El n-ésimo terágono de Koch es una cuadrícula de lado η = 3ⁿ que llena un cuadrado de área 2. Dicho llenado es más ajustado a medida que k → ∞. Basta con un ejemplo (que en la lámina está junto al cuadrado negro de partida) para que el lector se haga idea de un dibujo tan soso.

En las tres ilustraciones de la parte superior de la página 93 se evita la ambigüedad de los puntos dobles recortando las esquinas de modo que el área total sea la misma.

A la misma escala, el cuarto estadio de esta secuencia sólo permitiría ver un cuadrado gris al 50%, pero un dibujo mayor de un cuarto de la costa se puede seguir sin perderse (aunque uno corra el riesgo de marearse). Nos muestra gráficamente qué se quiere decir cuando se afirma que la curva de Koch límite llena el plano.

Habría estado bien poder definir una isla límite, como en el caso de las islas de Koch del capítulo 6, pero en este caso resulta imposible. Es casi seguro que un punto elegido al azar pasa continuamente de estar en tierra firme a estar en el mar. Los terágonos avanzados están tan profunda y uniformemente penetrados por golfos y ríos que un cuadrado de lado x, tal que η << x << 1, se compone de agua y tierra firme prácticamente al 50%.

INTERPRETACIÓN. La curva límite de Peano establece una aplicación continua entre la recta y el plano. El hecho de que los autocontactos sean matemáticamente inevitables es algo clásico, pero el hecho de que esto tenga interés en la modelización de la naturaleza es una innovación de esta obra.

ORDEN DE LARGO ALCANCE. Alguien que no conociera la cascada descendente que hemos seguido para construir nuestras curvas de Peano finitas se quedaría perplejo ante el extraordinario orden de largo alcance que presentan y que les permite evitar las autointersecciones y también los autocontactos. El menor desliz haría que tanto las unas como los otros fueran altamente probables.

▯ Y la relajación total de la disciplina haría que la repetición indefinida de las autointersecciones fuera casi segura, pues un movimiento de Peano totalmente indisciplinado es el movimiento browniano, que hemos mencionado en el capítulo 2 y que estudiaremos en el capítulo 25.

▯ TEOREMA DE LIOUVILLE Y ERGODICIDAD. En mecánica se representa el estado de un sistema complejo por medio de un punto en un «espacio de fases». Al evolucionar de acuerdo con las ecuaciones del movimiento, cada dominio de este espacio se comporta de modo que su medida (hipervolumen) permanece constante (teorema de Liouville), pero su forma cambia, dispersándose y llenando todo el espacio que le es accesible con una uniformidad cada vez mayor. Ambas características se dan en el comportamiento del dominio pintado en negro de la construcción de Peano que hemos presentado aquí. Resulta pues interesante profundizar un poco más, observando que en muchos sistemas «dinámicos» simplificados en los que se puede realizar un estudio detallado, cada dominio se dispersa transformándose en una banda cada vez más larga y delgada. Sería interesante ver si, por el contrario, la dispersión de otros sistemas funciona según árboles como los de Peano. ▮

LÁMINAS 96 y 97. Construcciones cuadrangulares de Koch de dimensión D = 2: barridos triangulares de Cesàro y Polya, y otras variantes.

El generador más simple que se puede imaginar está formado por N = 2 segmentos iguales formando un ángulo θ tal que 90° ≤ θ ≤ 180°. El caso límite θ = 180° genera un segmento rectilíneo; el caso θ = 120° (ilustrado al pie de la lámina 71) da lugar (entre otras) a la curva triádica de Koch. El caso límite θ = 90° es

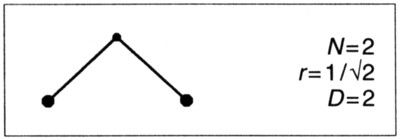
Este generador da lugar a una extraordinaria variedad de curvas de Peano, según cuáles sean el iniciador y la regla de colocación del generador sobre los lados del terágono precedente. En las láminas 96 a 100 se examinan unos cuantos ejemplos.

▯ Además, en el capítulo 25 se obtiene el movimiento browniano aleatorizando la clase de todas las curvas de Peano con estas mismas N y r. ▮

BARRIDO TRIANGULAR DE PÓLYA. El iniciador es [0,1], el generador el mismo de más arriba, y se va disponiendo alternativamente a derecha y a izquierda del terágono. La primera posición se va alternando también. Los primeros estadios de la construcción son los siguientes

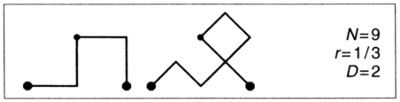
Los terágonos son fragmentos de una cuadrícula contenida en el interior de un triángulo rectángulo isósceles de lado [0,1]. La curva límite barre dicho triángulo.

FIGURA 96

LÁMINA 96. BARRIDO DE POLYA DE UN TRIÁNGULO RECTÁNGULO NO ISÓSCELES. El generador se ha cambiado por dos segmentos desiguales y ortogonales. Se deja como ejercicio para el lector adivinar el procedimiento seguido para evitar los puntos de autocontacto.

BARRIDO TRIANGULAR DE CESÀRO. El iniciador es [0,1], el generador es el mismo de antes y los dos primeros pasos de la construcción son los siguientes (para mayor claridad, el dibujo se ha hecho con θ = 85° en vez de θ = 90°).

Como resulta patente, en todos los pasos impares el generador se coloca a la derecha, con lo que el terágono resultante es un enrejado de líneas paralelas a las diagonales del generador. En los estadios pares de la construcción, el generador se coloca a la izquierda, y el terágono resultante es una cuadrícula paralela a los lados del iniciador. Asintóticamente esta curva llena el triángulo rectángulo isósceles de hipotenusa [0,1].

FIGURA 97

LÁMINA 97. Esta lámina representa un barrido cuadrangular obtenido por yuxtaposición de los barridos de Cesàro iniciados con [0,1] y [1,0]. (Para mayor claridad, hemos tomado otra vez θ = 85° en vez de 90°.)

AUTOSOLAPAMIENTO. Cada intervalo de las cuadrículas recubiertas por los terágonos de Cesare es repasado dos veces. Además de tener puntos de autocontacto, esta construcción presenta autosolapamiento.

«EFICACIA» DEL LLENADO DEL PLANO, UNA PROPIEDAD EXTREMAL DE LA DISTANCIA DE PEANO-CESÀRO. La curva de Peano de la lámina 93 aplica [0,1] en el cuadrado de diagonal [0,1] y área 1/2. La curva de Pólya recubre la misma área. Pero la curva de Cesàro barre un triángulo rectángulo isósceles de hipotenusa [0,1] y área 1/4. Para recubrir el mismo cuadrado, Cesàro debe unir las aplicaciones de [1,0] y [0,1]. Por tanto, la curva de Cesàro es la menos «eficaz» de las dos. De hecho, es la menos eficaz de las curvas de Peano sin autointersecciones que se pueden trazar sobre una cuadrícula. Esto la dota de una virtud compensadora: la distancia de Peano por la izquierda o por la derecha (véase la fig. 91) entre dos puntos P₁ y P₂ es mayor o igual que el cuadrado de la distancia euclídea:

|L(P₁, P₂)| ≥ |P₁P₂|²

|R(P₁, P₂)| ≥ |P₁P₂|²

En otras curvas de Peano la diferencia entre las distancias de Peano y euclídea puede tomar un signo u otro.

EL PROBLEMA DE KAKUTANI-GOMORY. Escogiendo M puntos P_m del cuadrado [0,1]², Kakutani (comunicación oral) estudia la expresión inf(∑|P_mP_m+1|²), donde el ínfimo se toma con respecto a todas las cadenas que unen la sucesión de los P_m. Demuestra que inf ≤ 8, pero conjetura que esta cota superior no es la óptima. Y así es, R. E. Gomory (comunicación oral) obtiene una cota mejor: inf ≤ 4. En su demostración usa la curva de Peano-Cesàro y procede del modo siguiente;

(A) Añádanse las cuatro esquinas del cuadrado si no se encuentran ya entre los P_m;

(B) ordénense los M puntos P_m según las primeras visitas en la cadena de las cuatro curvas de Peano-Cesàro dibujadas en el interior del cuadrado (construidas tomando los lados como iniciadores);

(D) nótese también que no hay disminución si sustituimos cada sumando |P_mP_m+1|² por |L(Z_mZ_m+1)|;

(E) nótese por fin que ∑|L(Z_mZ_m+1)| = 4. Si se hubieran usado otras curvas de Peano, los pasos (B) y (D) de la demostración no habrían sido válidos.

LÁMINAS 99 y 100. Un barrido cuadrangular y el barrido del dragón.

Aquí el generador es el mismo que en las láminas 96 y 97, pero unos cuantos cambios aparentemente simples en las reglas de construcción tienen consecuencias importantes.

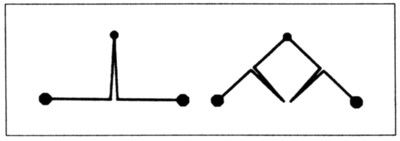
UN ÚLTIMO BARRIDO CUADRANGULAR DE PEANO. El iniciador es [0,1], y los estadios segundo, cuarto y sexto de la iteración son ahora

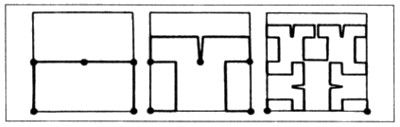
EFICACIA, UNA PROPIEDAD EXTREMAL. Esta curva llena un dominio de área 1, en tanto que las curvas de las láminas 96-97 y la curva dragón de más abajo sólo cubren áreas de 1/2 o 1/4. Si los terágonos se adaptan a una cuadrícula ortogonal, el área barrida no puede ser mayor que I. Este valor máximo se alcanza siempre que los terágonos sean autoevitantes. Dicho de otro modo, la ausencia de autocontactos tiene una importancia mayor que la meramente estética, y una curva con puntos de autocontacto en la que éstos se evitan mediante recortes, como en la lámina 93, no es equivalente a una curva de Koch autoevitante.

Si se toman los terágonos impares de este barrido cuadrangular y se unen los puntos medios de los lados consecutivos, de modo que se eviten los puntos de autocontacto, se obtiene una curva de Peano ideada por Hilbert.

LÁMINA 100. UNA CURVA QUE BARRE UN TRAPECIO RECTÁNGULO. Se cambia el generador por otro formado por dos segmentos desiguales y perpendiculares. El procedimiento para evitar los autocontactos es el mismo que en la lámina anterior.

EL DRAGÓN DE HARTER-HEIGHTWAY. (Véase Gardner, 1967, Davis y Knuth, 1970.) El iniciador es aquí [0,1] y el generador es el mismo de antes, pero se va alternando entre la derecha y la izquierda del teragono. La única diferencia con el barrido triangular de Pólya es que la primera posición siempre cae a la derecha del teragono en todos los pasos de la iteración. Los primeros estadios son los siguientes

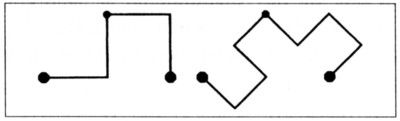
Las consecuencias de este cambio son espectaculares, y un estadio avanzado de la iteración presenta este aspecto

En esta ilustración la curva en sí resulta indistinguible y lo que vemos es el contorno, que llamamos curva dragón. Por tanto, la curva de Peano merece el nombre de barrido del dragón. Al igual que todas las curvas de Koch iniciadas con [0,1], el dragón es autosemejante. Además, se aprecia una segmentación tal que los segmentos, semejantes entre sí pero no al conjunto del dragón, están enlazados por cinturas de avispa.

DRAGONES SIAMESES. En Fractals (1977) se señalaba que, con las mismas reglas de construcción del dragón, un iniciador más natural es [0,1] seguido de [1,0], y la forma barrida resultante recibía el nombre de dragones siameses. Esta forma tiene varias representaciones (Knuth, 1980). Presenta el siguiente aspecto (uno de los dragones está en negro y el otro en gris).

RÍO DE LOS DRAGONES SIAMESES. Si se borran las corrientes próximas a la fuente (en aras de una mayor legibilidad), el árbol lluvial de los dragones siameses presenta este aspecto.

Los dragones siameses se pueden embaldosar mediante replicas reducidas de sí mismos, tal como muestra la figura.

LA PIEL DE LOS DRAGONES SIAMESES. Se trata de una curva de Koch con el generador

Las longitudes de los segmentos corto y largo son, respectivamente, r₁ = 1/2√2 y r₂ = 1/√2 = r₁³, con lo que la función generatriz de la dimensión es (1/√2)^D + 2(1/2√2)^D = 1, y la cantidad 2^D/2 es una raíz de x³ − x² − 2 = 0.

DRAGONES ALTERNADOS. (Davis y Knuth, 1970) Tómese una sucesión infinita cualquiera x₁, x₂, … en la que cada x_k puede tomar los valores 0 y 1, y úsese el valor de x_k, para determinar la primera posición del generador en el k-ésimo estadio de la iteración, de modo que para x_k = 1 el primer generador se orienta hacia la derecha, mientras que para x_k = 0 se orienta hacia la izquierda. Cada sucesión genera un dragón alternado distinto.

LÁMINAS 102 y 103. Los barridos en copo de nieve: Nuevas curvas y árboles de Peano (dimensiones del río y la cuenca D ~ 1,2618)

Estas láminas ilustran una familia de curvas de Peano de mi invención. Rellenan el copo de nieve original de Koch (lámina 73), con lo que se relacionan dos monstruos clásicos que datan de 1900.

Una virtud más importante es que basta con una mirada para documentar uno de los temas principales del presente ensayo: las curvas de Peano no son, ni mucho menos, monstruos matemáticos sin una interpretación concreta. Si no tienen autocontactos, presentan una serie de árboles conjugados fácilmente visibles e interpretables. En una primera aproximación, son buenos modelos de los ríos, las cuencas fluviales, los árboles de la botánica y los sistemas vasculares humanos.

De rebote, obtenemos una manera de embaldosar el copo de nieve con copos desiguales.

GENERADOR DE SIETE SEGMENTOS. Sea [0,1] el iniciador, y sean el generador y el segundo estadio de la construcción

Concretando más, denotemos por S el generador de arriba, al que llamaremos directo, y definamos el generador inverso F como la imagen especular de S según la vertical x = 1/2. En cualquier estadio de la construcción del barrido del copo de nieve se puede escoger libremente el generador F o el S. Por tanto, cada sucesión infinita de F y S da un barrido distinto del copo de nieve.

REDONDEO DE LOS TERÁGONOS. Las líneas quebradas suelen parecer toscas, pero se puede dar a los terágonos del barrido del copo de nieve una apariencia más «natural» e isótropa si se redondea cada segmento sustituyéndolo por un sexto de circunferencia.

LÁMINA 73. Ya en la lámina 73, y con la idea de tener un sombreado de fondo ondulante, hemos presentado un terágono avanzado de un barrido de copo de nieve de siete segmentos, redondeado y rellenado. Mirándolo de nuevo, evoca una corriente de líquido pasando junto a un contorno fractal, y los remolinos entre dos corrientes paralelas con velocidades distintas.

GENERADOR DE TRECE SEGMENTOS. Modifiquemos ahora el anterior generador de 7 segmentos sustituyendo la quinta pata por una réplica del total a tamaño reducido. Dicha réplica se puede colocar tanto en posición S como F. En este último caso, el generador y el segundo estadio de la iteración presentan el siguiente aspecto

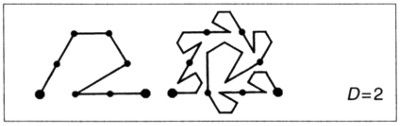
FIGURA 102

LÁMINA 102. Este terágono avanzado, como frontera entre dos dominios fantásticamente entrelazados, vale más que cualquier número de palabras para explicar qué significa llenar un dominio plano,

FIGURA 103

LÁMINA 103. Redondéese el anterior generador de 13 segmentos y hágase lo propio con la curva del copo de nieve. El resultado, al cabo de unos pocos pasos en la construcción, es el que se muestra en la figura 103.

DIMENSIONES DE LOS RÍOS. En la curva original de Peano, cada río por separado tiene longitud finita y, por lo tanto, su dimensión es 1. Aquí cada río tiene dimensión log 4/log 3. Para alcanzar la dimensión D = 2 hay que tomar todos los ríos a la vez.

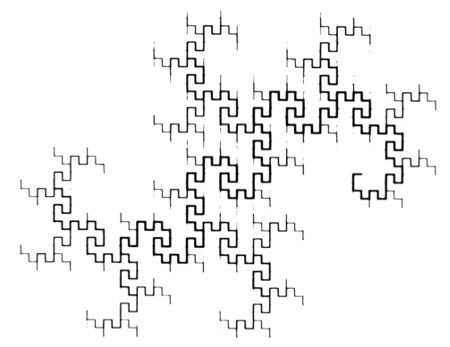
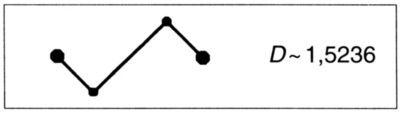
LÁMINAS 104 y 105. La curva de Peano-Gosper. Sus árboles y sus parientes de Koch (dimensiones del río y la cuenca D ~ 1, 1291)

VOLVAMOS A LA LÁMINA 74. Las líneas quebradas delgadas de esta lámina, que no hemos comentado en su momento, representan los primeros estadios (del primero al cuarto) de una curva debida a Gosper (Gardner 1976). Se trata de la primera curva de Peano autoevitante construida por el método de Koch sin otros aditamentos.

El iniciador es [0,1] y el generador es

Si hacemos girar el generador en sentido contrario al de las agujas del reloj hasta situar el primer tramo en posición horizontal, se ve que tiene la forma de un retículo triangular, con 7 de los 3 × 7 enlaces ocupados. Esta característica hace extensiva a los retículos triangulares una propiedad que hemos discutido para los cuadrangulares las figuras 99 y 100.

Una vez visto cómo esta curva de Peano llena la curva de Koch de la lámina 74, se puede explicar la idea del grosor variable de las líneas de la lámina 74: representa el quinto estadio de la construcción de la curva de Gosper.

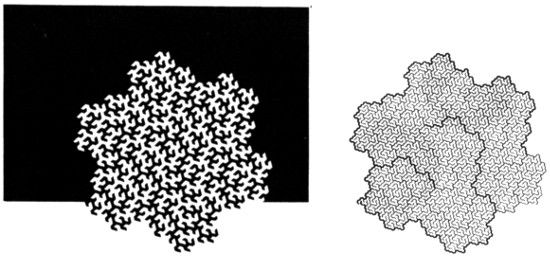
FIGURA 104

FIGURA 104, IZQUIERDA. Representa el cuarto terágono de la curva de Gosper como frontera de las zonas blanca y negra.

FIGURA 104, DERECHA, CUENCAS Y ÁRBOLES FLUVIALES. Se han dibujado los ríos y las cuencas siguiendo las líneas medias de los «dedos» blancos y negros de la figura de la izquierda.

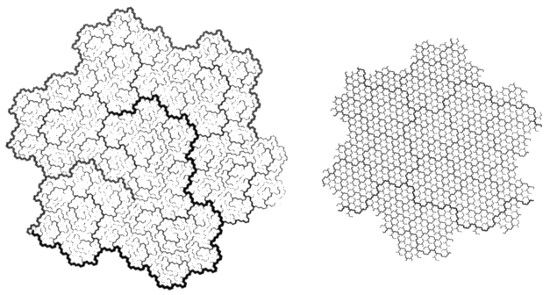
FIGURA 105

PARTE IZQUIERDA DE LA FIGURA 105. Partiendo de las cuencas y árboles fluviales de la derecha de la figura 104, se han dibujado de nuevo las líneas de acuerdo con su importancia relativa en el esquema de Horton-Strahler (Leopold, 1962). En este ejemplo se ha dado a los enlaces que forman los ríos y las cuencas una anchura proporcional a sus longitudes en línea recta. Los ríos van en negro y las cuencas en gris.

DIMENSIONES. Cada curva de Peano determina la D de su propia frontera. En las láminas 93 y 96 se trataba simplemente de un cuadrado. En otras láminas posteriores ha sido la piel de un dragón, y luego una curva en copo de nieve. En este caso se trata de un fractal con D ~ 1,1291.

FRANCIA. Cualquiera que en sus tiempos de escolar haya echado una mirada a un mapa que represente los ríos Loira y Garona no se sentirá demasiado lejos de casa.

PARTE DERECHA DE LA FIGURA 105. ÁRBOL FLUVIAL CONSTRUIDO DIRECTAMENTE POR UNA CASCADA DE KOCH. Cuando el mismo generador ya tiene forma de árbol, genera un árbol. Tómese, por ejemplo, el generador

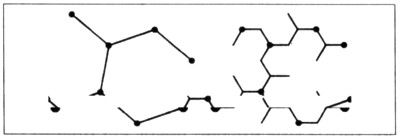
Se obtiene una manera alternativa de drenar la curva de Koch de la lámina 74. (Se han recortado las ramas últimas y más cercanas a las «fuentes»).

LÁMINAS 107 y 108. Árboles fractales que llenan el plano, copo deforme y cuarteto.

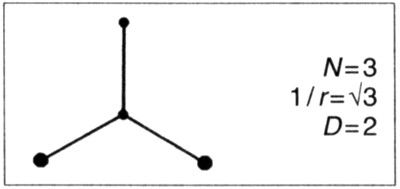
Los árboles «fluviales» que llenan un dominio plano deducidos a partir de algunas curvas de Peano se pueden obtener también por iteración directa. La clave consiste en tomar el propio generador en forma de árbol. Tenemos un ejemplo trivial en el caso del generador formado por cuatro patas dispuestas en forma de signo +. De este modo se obtiene el árbol fluvial de la curva de Peano Cesàro (lámina 97).

COPO DEFORME. Tenemos un ejemplo mejor lomando el iniciador [0,1] y el generador siguiente

Empezamos por notar que cada río en particular es generado por desplazamiento del punto medio, como en la lámina 71. Por lo tanto, cada río asintótico tiene dimensión D = log 2/log√3 = log 4/log 3. Esto es, el valor ya conocido de la dimensión del copo de nieve. Pero ahora no se trata de un copo de nieve, pues la colocación de los generadores sucesivos sigue una regla distinta.

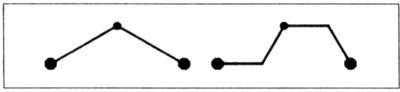
Con objeto de dejar lugar para los ríos, hay que alternar el generador a derecha e izquierda. Con ello, la simetría del copo de nieve queda contrahecha, y por ello llamamos copo deforme al dominio drenado por estos ríos.

Consideremos ahora el árbol fluvial. Sus terágonos no se autosolapan, pero irremediablemente presentan autocontactos. Este rasgo de la variante asintótica es inevitable y también perfectamente aceptable, pues expresa a la perfección el hecho de que varios ríos puedan nacer del mismo punto. Sin embargo, veremos más adelante cómo los terágonos de los ríos pueden evitar los autocontactos. Debido a estos autocontactos, el teragono de los ríos que estamos considerando es un pedazo de papel ilegible con una cuadrícula hexagonal, limitado por un fractal aproximado.

FIGURA 107

LÁMINA 107. El aspecto general del árbol fluvial resulta más aparente si se borran todos los segmentos de río que están en contacto con una fuente y se marca el río principal con un trazo más grueso. El área drenada por este árbol es √3/2 ~ 0,8660.

BARRIDO DEL COPO DEFORME. Dibújese ahora una curva de Peano con un iniciador en forma de ▲ y un generador en forma de Z con los tres trazos iguales y formando un ángulo de 60°. Se trata del caso extremo, para M = 3, de la familia de generadores usados en las láminas 74 y 75, pero es muy distinto de todos los demás casos. Esta estudiado en Davis y Knuth (1970).

Se puede comprobar que el árbol fluvial correspondiente a esta curva no es otro que el que acabamos de dibujar directamente. Los lados del iniciador tienen longitud I y la curva de Peano correspondiente barre un área igual a √3/6 ~ 0,2886 (¡vaya ineficacia!).

CUARTETO. A continuación consideraremos otra curva de Koch y tres curvas que la llenan: una es una curva de Peano y las otras dos, árboles. Dichas curvas, diseñadas por mí, ilustran otro tema de interés. Tómese el iniciador [0,1] y el generador siguiente

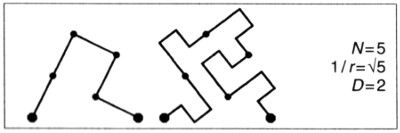
La frontera de estas curvas converge a una curva de Koch de dimensión D = log 3/log√5 = 1,3652. En el centro de la lámina 76 se pueden ver terágonos avanzados de esta curva de Peano y su frontera. Las llamo el cuarteto. Cada «jugador», y la mesa entre ellos, están perembaldosados.

El interior del cuarteto es drenado, por supuesto, por su propio árbol fluvial intrínseco, aunque se pueden obtener formas de encadenado completamente distintas con cualquiera de los generadores siguientes

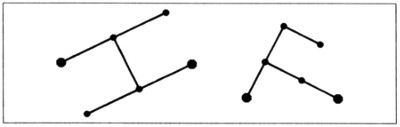
El generador de la izquierda da lugar a terágonos con autocontactos, como en el primer ejemplo de este pie de figura, y el área drenada es 1/2. El generador de la derecha produce terágonos sin autocontactos y el área drenada es 1. En la figura 108 se muestra un terágono avanzado.

FIGURA 108

7 Domando las curvas monstruosas de Peano

7
Domando las curvas monstruosas de Peano