Para entender completamente mi interpretación de la D de Richardson como dimensión fractal, pasaremos de los fenómenos naturales, que no podemos controlar, a las construcciones geométricas, que podemos modificar a placer.

Hasta aquí hemos insistido en que la geometría de una costa es complicada, pero su estructura presenta también un alto grado de orden.

Aunque los mapas dibujados a distintas escalas difieran en sus detalles concretos, comparten las mismas características genéricas. Es bastante cierto que, aparte de la escala, los pequeños y grandes detalles de las costas son geométricamente idénticos.

Podría pensarse que esas formas han sido creadas por una especie de fuego de artificio, en que cada estadio creara detalles más finos que los de los estadios anteriores. Pero el trabajo ya citado de Lewis Richardson sobre la turbulencia sugiere un término más apropiado para este mecanismo generador: el de cascada.

Cuando cada trozo de una cierta figura es geométricamente semejante al todo, se dice que tanto la figura como la cascada que la produce son autosemejantes. En este capítulo investigamos la autosemejanza mediante figuras muy regulares.

Los contrastes más extremos respecto a las figuras autosemejantes los proporcionan las curvas que o bien (a) tienen una sola escala, como el círculo, o bien (b) tienen dos escalas claramente distintas, como un círculo «festoneado». De estas formas puede decirse que son escalonadas.

Para asegurarse de que una curva presentará una infinidad de escalas, lo mejor es introducirlas deliberadamente y por separado. Un triángulo equilátero de lado 1 tiene una sola escala, los de lado 1/3 tienen una escala menor, y los de lado (1/3)^k, una escala cada vez menor. Amontonando estos triángulos uno encima de otro, como en la lámina 70, se obtiene una forma que combina todas las escalas inferiores a 1.

En efecto, suponemos que un pedazo de costa dibujado a escala 1:1.000.000 es un segmento de recta de longitud 1, que llamaremos iniciador. A continuación suponemos que el detalle que se hace visible en un mapa a escala 3:1.000.000 consiste en sustituir el tercio central del segmento por un promontorio triangular. Lo que resulta como aproximación es una línea quebrada formada por cuatro segmentos iguales, que llamaremos generador. Suponemos luego que el nuevo detalle que aparece a escala 9:1.000.000 resulta de sustituir cada uno de los cuatro segmentos del generador por generadores de tamaño reducido en un tercio, formando subpromontorios.

De este modo, rompemos cada segmento, sustituyendo el iniciador por una curva cada vez más quebrada. Como estas curvas serán omnipresentes en este ensayo, permítaseme acuñar para designarlas el término terágono, del griego τεραs, que significa «monstruo, criatura extraña», y γωυτα, que significa «esquina, ángulo». Con gran acierto, el sistema métrico usa el prefijo tera para indicar el factor 10¹².

Si este mismo proceso en cascada se continúa indefinidamente, nuestros terágonos convergerán a un límite que fue considerado por primera vez por von Koch (1904), lámina 73, al que llamaremos curva triádica de Koch y denotaremos por K.

El área de esta curva es nula, como se deduce de la lámina 71. Pero, por otra parte, cada paso de la construcción incrementa su longitud en un factor 4/3, con lo que la curva límite tiene una longitud infinita. Además, es continua y no tiene tangente en ningún punto (como la gráfica de una función continua sin derivada).

Como modelo de costa, K sólo es una aproximación sugerente, pero no por ser demasiado irregular, sino porque, comparada con una costa, presenta una irregularidad demasiado sistemática. En los capítulos 24 y 28 la «relajamos» un tanto para hacer que se ajuste mejor.

Según la hemos introducido en la sección anterior, parece como si la curva de Koch fuera la cosa más intuitiva que se pueda dar en geometría. Pero la actitud convencional hacia ella es completamente distinta. ¡Tal es así que casi todos los matemáticos están de acuerdo en calificar K de monstruosa! Para concretar más, vayamos a La crisis de la intuición (Hahn, 1956), obra a la que volveremos más veces. Leemos que

«la naturaleza [de una curva no rectificable o de una curva sin tangentes] escapa completamente a la intuición; después de unas pocas repeticiones del proceso de segmentación, la figura que va resultando es tan complicada que la intuición a duras penas puede captarla, y nos abandona totalmente en lo que respecta a la curva que se obtiene pasando al límite. Sólo el pensamiento, o el análisis lógico, pueden seguir la evolución de ese extraño objeto hasta su forma final. Así pues, si en este caso hubiéramos confiado en la intuición, hubiéramos caído en un error, pues parece ser que la intuición nos lleva forzosamente a concluir que no puede haber curvas que no tengan tangente en ningún punto. Este primer ejemplo del fracaso de la intuición tiene que ver con los conceptos fundamentales de la diferenciación».

Lo mejor que uno puede decir de estas palabras es que se detienen justo antes de llegar a una famosa proclama de Charles Hermite, en una carta de 20 de mayo de 1893 a T. Stieltjes, en la que declaraba que «abandonaba con espanto y horror esta lamentable plaga de funciones sin derivadas». (Hermite y Stieltjes, 1905, II, pág. 318.) A uno le gustaría creer que los grandes hombres son perfectos y que Hermite estaba ironizando, pero la Notice de Lebesgue de 1922 (Lebesgue, 1972,1) sugiere lo contrario. Lebesgue había escrito un artículo sobre superficies sin planos tangentes, «pañuelos totalmente arrugados», y quería que la Académie des Sciences se lo publicara, pero «Hermite se opuso implacablemente a su inclusión en los Comptes Rendas; esto ocurría hacia la época de la carta a Stieltjes…».

Recordemos que Perrin y Steinhaus pensaban de modo distinto, pero el único matemático que razonaba como ellos, basándose sólo en la intuición (Steinhaus razona basándose en la realidad) es Paul Lévy (Lévy, 1970): «Siempre [me ha] sorprendido oir que la intuición geométrica lleva inevitablemente a pensar que todas las funciones continuas son diferenciables. Desde mi primer encuentro con el concepto de derivada, la experiencia me ha demostrado que lo cierto es todo lo contrario».

Sin embargo, estas voces no se han hecho oír. Casi todos los libros, y también casi todos los museos de la ciencia, proclaman que las curvas no diferenciables son contrarias a la intuición, «monstruosas», «patológicas» y hasta «psicopáticas».

Una curva de Koch es un modelo de costa tosco pero evocador. Como primer test cuantitativo, investiguemos la longitud L(ε) del terágono triádico de Koch de lado ε. Dicha longitud se puede medir exactamente, obteniéndose un resultado extraordinariamente satisfactorio:

Esta fórmula exacta es idéntica a la ley empírica de Richardson para la costa de Bretaña. Para la curva triádica de Koch,

Claro que la constante D de Koch no es empírica sino matemática. Y así las razones para decir que D es una dimensión son más convincentes en el caso de la curva de Koch que en el de las costas.

Además, la medida de Hausdorff aproximada de dimensión D (concepto que hemos introducido en el capítulo anterior) vale ε^D multiplicado por el número de segmentos de longitud ε, con lo que da ε^Dε^−D = 1. Esto es un buen indicio de que la dimensión de Hausdorff es D. Pero, por desgracia, la definición de Hausdoríf es difícil de manejar rigurosamente. Es más, aun en el caso de que hubiera sido fácilmente manejable, la generalización del concepto de dimensión más allá de los números enteros es una idea tan trascendental que son de agradecer todas las motivaciones que nos lleven a ella.

En el caso de figuras autosemejantes, se tiene fácilmente una motivación adicional en el concepto de dimensión de semejanza. A menudo se oye decir que los matemáticos usan la dimensión de semejanza para estimar la dimensión de Hausdorff, y en el grueso de este ensayo sólo se dan casos en los que dicha estimación da el resultado correcto. En tales contextos no hay peligro en tomar como sinónimos la dimensión de semejanza y la dimensión fractal. ▯ Tenemos en ello una contrapartida al uso sinónimo de dimensión topológica y dimensión «intuitiva». ▮

A modo de preludio motivador examinemos las figuras autosemejantes estándar: los segmentos de recta, los rectángulos en el plano, etc.; véase la lámina 72. Como la dimensión euclídea de la recta es 1, tenemos que para cada «base» entera b, el intervalo 0 ≤ x < X se puede «enlosar» (de modo que cada punto sólo sea recubierto una vez) con N = b «partes». Éstas son los intervalos (k − l) X/b ≤ x < kX/b, yendo k de 1 a b. Cada parte se obtiene a partir del todo con una razón de semejanza r(N) = 1/b = 1/N.

Análogamente, como la dimensión euclídea del plano es 2, tenemos que, dado cualquier b, el «todo» constituido por un rectángulo 0 ≤ x < X, 0 ≤ y < Y puede ser «enlosado» con exactamente N = b² partes. Éstas son los rectángulos definidos por las desigualdades (k − 1) X/b ≤ x < kX/b y (h − 1) Y/b ≤ y < hY/b, donde k y h van de 1 a b. Ahora cada parte guarda con el todo una relación de semejanza de razón r(N) = 1/b = 1/N^1/2.

Y no hay ningún problema en definir espacios de dimensión euclídea E > 3. (La dimensión euclídea —o cartesiana— la denotamos por E). Todos los paralelepípedos D-dimensionales definidos para D ≤ E satisfacen

Pasemos ahora a examinar figuras no estándar. Para que el exponente de autosemejanza tenga significado formal, sólo se tiene que cumplir que la figura sea autosemejante, esto es, que se pueda descomponer en N partes relacionadas con el todo por una transformación de semejanza de razón r (seguida quizá de un desplazamiento y una simetría). La D así obtenida cumple siempre

En el ejemplo de la curva triádica de Koch, N = 4 y r = 1/3, con lo que D = log 4/log 3, que coincide con la dimensión de Hausdorff.

Hasta ahora hemos dicho, sin preocuparnos demasiado por ello, que la K de Koch era una curva. Ahora debemos volver sobre este concepto. Intuitivamente, un arco es un conjunto conexo que se convierte en inconexo si se le quita cualquier punto. Y una curva cerrada es un conjunto conexo que se convierte en dos arcos cuando le quitamos dos puntos cualesquiera. Por esto mismo, la K de Koch es una curva.

El matemático dice que todas las figuras con una de estas propiedades, por ejemplo K, [0,1] o un círculo, tienen dimensión topológica D_T = 1. ¡He aquí, pues, otra clase de dimensión a tener en cuenta! Como discípulos de Guillermo de Ockham, todos los científicos saben que «no hay que multiplicar los entes sin necesidad». Hay que confesar, por lo tanto, que nuestro continuo ir y venir entre las distintas y casi equivalentes formas de dimensión fractal es cuestión de conveniencia. Sin embargo, la coexistencia de una dimensión fractal y otra topológica es una cuestión de necesidad. Aconsejo a los lectores que se saltaron la definición de fractal del capítulo 3 que la lean ahora con atención, y a todos que lean la entrada del capítulo 41 dedicada a la «dimensión».

Y así es en efecto: las limitaciones actúan sobre los científicos tanto como sobre el Troilus y la Cressida de Shakespeare. Para llegar a la curva de Koch, la cascada de promontorios cada vez más pequeños se extrapola hasta el infinito, pero en la naturaleza las cascadas o se detienen o cambian de carácter. Aunque puede ser que haya un sinfín de promontorios, la idea de que sean autosemejantes sólo puede ser válida entre ciertos límites. Por debajo del límite inferior, el concepto de costa deja de pertenecer a la geografía.

Es pues razonable considerar que una costa real conlleva dos escalas de corte. El corte superior Ω podría ser el diámetro del menor círculo que contuviera una isla, o un continente quizá, y el corte inferior ε podría ser los 20 metros que decíamos en el capítulo 5. Aunque resulta difícil precisar valores numéricos concretos, la necesidad de los cortes está fuera de toda duda.

Sin embargo, una vez se prescinde de los detalles demasiado grandes y demasiado pequeños, D sigue teniendo el valor de una dimensión efectiva en el sentido que mencionábamos en el capítulo 3. En términos estrictos, el triángulo, la estrella de David y los terágonos infinitos de Koch tienen dimensión 1. Pero, tanto intuitivamente como por razones pragmáticas de simplicidad y naturalidad de los términos correctivos necesarios, es razonable considerar que un terágono de Koch avanzado está más cerca de una curva de dimensión log 4/log 3 que de una curva de dimensión 1.

En lo que respecta a una costa, no es improbable que tenga varias dimensiones distintas (recuérdense las bolas de hilo del capítulo 3). La dimensión geográfica es la D de Richardson, pero en la gama de magnitudes que interesan a la física podría tener otra dimensión distinta (asociada al concepto de interfase entre aire, agua y arena).

Volvamos ahora a los principios básicos de la construcción de la curva triádica de Koch. Se empieza con dos figuras, un iniciador y un generador. Este último es una línea quebrada orientada formada por N lados iguales de longitud r. Cada paso de la construcción empieza con una línea quebrada y consiste en sustituir cada segmento rectilíneo por una copia del generador, reducida y desplazada de modo que sus extremos coincidan con los de dicho segmento. En todos los casos se tiene D = log N/log(1/r).

Se puede cambiar fácilmente esta construcción modificando convenientemente el generador; combinando promontorios y bahías, por ejemplo, como se muestra en las láminas que siguen. De este modo se obtienen terágonos de Koch que convergen a curvas de dimensión comprendida entre 1 y 2.

Todas estas curvas de Koch se «autoevitan», no se cortan a sí mismas. Esto permite que las figuras totales se puedan dividir sin ambigüedad en partes disjuntas, y esta propiedad influye en la definición de D. Sin embargo, una construcción de Koch a partir de un generador que no haya sido elegido cuidadosamente corre el riesgo de conducir a una curva con puntos de contacto que se corte a sí misma, o incluso que se autosolape. Si la D deseada es pequeña, es fácil evitar los puntos dobles eligiendo cuidadosamente el generador. Aunque esta tarea resulta cada vez más difícil a medida que D aumenta, es posible siempre que D < 2.

Sin embargo, cualquier construcción de Koch que pretenda llegar a una dimensión D > 2 acaba inevitablemente en curvas que recubren el plano una infinidad de veces. El caso D = 2 merece discusión aparte y lo trataremos en el capítulo 7.

En algunos casos conviene sustituir la expresión curva de Koch por otra terminología más precisa y pedante. La figura inferior de la lámina 72 es, en términos técnicos, la imagen de Koch de un intervalo lineal, y se le puede llamar arco de Koch. De este modo, el contorno de la lámina 73 está formado por tres arcos de Koch. A menudo resulta útil extrapolar un arco dando lugar a una semilínea de Koch: dicha extrapolación consiste en aumentar el arco original tomando como foco el extremo izquierdo y como razón de semejanza, primero 1/r = 3, después 3², etc. Cada paso sucesivo de la extrapolación contiene el anterior, y la curva límite contiene todos los estadios intermedios finitos.

Generalizaremos ahora para las dimensiones fractales un resultado común en el caso de dimensiones euclídeas. En el caso de objetos físicos ideales de densidad uniforme ρ, el peso M(R) de una barra de longitud 2R, un disco de longitud R o una bola de radio R es proporcional a ρR^E. Para E = 1, 2 y 3, las constantes de proporcionalidad respectiva son 2, 2π y 4π/3.

La relación M(R) ∝ R^D también es válida para los fractales autosemejantes.

En el caso triádico de Koch, la demostración es muy simple cuando se toma como origen el extremo de una semilínea. Si un círculo de radio R₀ = 3^−k (con k ≥ 0) contiene una masa M(R₀), el círculo de radio R = R₀/3 contiene una masa M(R) = M(R₀)/4. Tenemos, por lo tanto, que

En consecuencia, el cociente M(R)/R^D es independiente de R, y puede emplearse para definir una «densidad» ρ.

Imaginemos un punto recorriendo una semilínea de Koch que emplee tiempos iguales en recorrer arcos de la misma medida. Si invertimos la función que da el tiempo en función de la posición, obtenemos la posición en función del tiempo, es decir, una ley de movimiento. Con velocidad infinita, por supuesto.

La curva de Koch nos recuerda los mapas reales, pero presenta defectos importantes que uno encuentra casi invariablemente en todos los modelos primarios de los ejemplos de este ensayo. Sus parles son idénticas entre sí y la razón de autosemejanza r pertenece a un espectro muy estricto de valores de la forma b^k, siendo b un entero, a saber, 1/3, (1/3)², etc. Así, una curva de Koch sólo es un modelo muy primitivo de costa.

He ideado diversas maneras de evitar ambos defectos, aunque todas ellas conllevan complicaciones probabilísticas que es mejor dejar para cuando se hayan asentado muchas otras ideas relacionadas con los fractales no aleatorios. No obstante, los lectores curiosos que dominen las probabilidades pueden echar una mirada rápida a los modelos basados en mis «curvas garabato» (capítulo 24) y, más importante aún, a las curvas de nivel de las superficies brownianas fraccionarias (capítulo 28).

En toda esta parte del libro se sigue el mismo método de exposición. Se comentan numerosas estructuras de la naturaleza contrastándolas con fractales regulares, que sirven de modelo preliminar, mientras que los modelos aleatorios que preconizo se dejan para capítulos posteriores.

RECORDATORIO. En todos los casos en que D se conoce con exactitud no es un entero y se da en forma decimal para facilitar las comparaciones, precisando hasta la cuarta cifra decimal. Este número de decimales se ha elegido para dejar bien patente que D no es ni un valor empírico (en la actualidad los datos empíricos se conocen con 2 cifras decimales como máximo) ni un valor geométrico incompletamente determinado (actualmente éstos se conocen bien sea con 1 o 2 decimales, o con 6 decimales o más).

Las curvas de Koch presentan una nueva e interesante combinación de complejidad y simplicidad. A primera vista son muchísimo más complejas que las curvas euclídeas comunes. Sin embargo, la teoría de los algoritmos matemáticos de Kolmogorov y Chaitin sugiere lo contrario, que una curva de Koch no es significativamente más complicada que un círculo. Esta teoría parte de una colección de «letras» u «operaciones atómicas» y considera que la longitud del algoritmo más corto conocido para reproducir la función deseada es una cota superior objetiva que permite evaluar la complejidad de dicha función.

Aplicando estas ideas a las curvas, tomemos los «trazos» rectilíneos como letras o átomos del proceso gráfico. En este alfabeto, para dibujar un polígono regular hacen falta un número finito de trazos, y cada uno de estos es descrito por un número finito de líneas de instrucción. Se trata por tanto de una tarea de complejidad finita. Por el contrario, un círculo precisa de «una infinidad de trazos infinitamente cortos», con lo que aparentemente es una curva de complejidad infinita. Sin embargo, una construcción recurrente del círculo sólo precisa de un número finito de instrucciones y es, por tanto, una tarca de complejidad finita. Cada paso parte, por ejemplo, de un polígono de 2^m lados (m>2), y consiste en sustituir cada trazo de longitud 2sen(π/2^m) por dos trazos de longitud 2sen(π/2^m+1). En la construcción de una curva de Koch se sigue el mismo procedimiento, aunque las operaciones son más simples, pues la longitud de cada trazo simplemente se multiplica por r, y las posiciones relativas de los trazos sustituidos son siempre las mismas. De ahí que sea sorprendentemente cierto que, si se mide la complejidad por la longitud del mejor algoritmo actual expresado en este alfabeto particular, una curva de Koch es efectivamente más simple que un círculo.

No hay que tomar demasiado en serio esta clasificación peculiar de las curvas en razón de su simplicidad relativa. Nótese que si el alfabeto se basara en la regla y el compás, el círculo adquiriría la condición de «atómico» y se llegaría a la conclusión opuesta a la subrayada más arriba. Sin embargo, siempre que se use un alfabeto razonable, las curvas de Koch, aparte de tener una complejidad finita, son más simples que muchas curvas euclídeas.

Siendo como soy un aficionado a las cuestiones etimológicas, no puedo dejar esta discusión sin manifestar que me molesta sobremanera llamar «irregulares» a las curvas de Koch. Este término está relacionado con regla, y es satisfactorio mientras uno no se salga de la siguiente acepción de regla: instrumento que sirve para trazar líneas rectas; pues las curvas de Koch no son rectas, ni mucho menos. Pero si uno piensa en la acepción ordenanza, esto es, un conjunto de leyes detalladas que hay que seguir sin rechistar, declaro silenciosamente que nada hay más «regular» que una curva de Koch.

LÁMINA 70. Isla triádica de Koch o copo de nieve K. Construcción original de Helge von Koch (dimensión de la costa D = log 4/log 3 ~ 1,2618)

FIGURA 70

La construcción empieza por un «iniciador», a saber, una ▲ (triángulo equilátero) en negro de lado unidad. A continuación, sobre el tercio central de cada lado, se adosa una península en forma de ▲ con lados de longitud 1/3. Este segundo paso acaba en una estrella de seis puntas o de David. Se repite luego el mismo proceso de adición de penínsulas sobre los lados de la estrella, y así sucesiva e indefinidamente.

Cada adición desplaza los puntos del tercio central de cada intervalo perpendicularmente al mismo. Los vértices del iniciador triangular no se mueven de su sitio. Los otros 9 vértices de la estrella de David alcanzan sus posiciones definitivas al cabo de un número finito de pasos. Hay también puntos que no dejan de desplazarse, pero la amplitud de sus movimientos es decreciente y a la larga tienden a unas posiciones límite que definen la costa.

La propia isla es el límite de una sucesión de dominios acotados por polígonos, de modo que cada uno de ellos contiene el dominio acotado por el polígono anterior en la sucesión. La lámina 73 presenta un negativo de la fotografía de dicho límite.

Nótese que esta lámina, así como muchas otras de este libro, representa islas y lagos en vez de costas y que, generalmente, se representan «áreas rellenas» y no sus contornos. Este método aprovecha al máximo las posibilidades de la alta resolución de nuestro sistema de gráficos.

POR QUÉ NO SE PUEDE DEFINIR AQUÍ UNA TANGENTE. Tómese como punto fijo uno de los vértices del ▲ original y dibújese una cuerda que una dicho vértice con un punto de la costa límite. Si hacemos converger este punto hacia el vértice, manteniéndonos siempre a la izquierda del mismo, la cuerda oscila dentro de un ángulo de 30° y no da muestras de tender a un límite que se pueda llamar tangente por la izquierda. Tampoco se puede definir una tangente por la derecha. Los puntos en los que no hay tangente porque las cuerdas de la derecha y las de la izquierda oscilan dentro de ángulos bien definidos se llaman hiperbólicos. Los puntos de K que se alcanzan asintóticamente tampoco tienen tangente, aunque por otras razones.

LÁMINA 71. Isla triádica de Koch o copo de nieve K. Construcción alternativa de Ernesto Cesàro (dimensión de la costa D = log 4/log 3 ~ 1,2618)

FIGURA 71

En Cesàro (1905) se da una construcción alternativa de la isla de Koch. Se trata de un trabajo tan maravilloso que me hace olvidar lo que me costó encontrar el original (y la rabia que me dio encontrarlo después reimpreso en Cesàro, 1964). He aquí una traducción libre de unas cuantas líneas extáticas: «La inagotable inmersión de esta figura en sí misma nos da una idea de lo que Tennyson describe en alguna parte como el infinito interno, que es, al fin y al cabo, el único que podemos concebir en la naturaleza. Esta semejanza entre el todo y sus partes, aún las infinitesimales, nos hace considerar la curva triádica de Koch como algo realmente maravilloso. Si tuviera vida, sería imposible exterminarla sin destruirla completamente, pues renacería y volvería a renacer desde las profundidades de sus triángulos, igual que la vida en el universo».

El iniciador de Cesàro es un hexágono regular de lado 3/3. El océano circundante está en gris. Incesantemente van surgiendo bahías en forma de ▲, obteniéndose la isla de Koch como límite de estas aproximaciones decrecientes.

En esta lámina se han presentado en paralelo ambos métodos de construcción, de modo que la costa de Koch queda comprendida entre dos terágonos, uno interno y otro externo, que se van aproximando cada vez más. Se podría pensar en un proceso en cascada que empieza con tres cercos sucesivos: la tierra firme (en negro), la marisma (en blanco) y el agua (en gris). En cada estadio de la cascada, pedazos de marisma son transferidos tanto a la tierra firme como al agua. En el límite, la marisma se agota, pasando de «superficie» a curva.

INTERPRETACIÓN POR EL MÉTODO DE DESPLAZAMIENTO DEL PUNTO MEDIO. En este método el generador y el segundo paso son los siguientes (el ángulo es de 120°)

Si se aplica al exterior del k-ésimo terágono interno, se obtiene el k-ésimo terágono externo, y si se aplica al k-ésimo terágono externo resulta el (k + 1)-ésimo terágono interno. Esta regla de construcción es la aplicada en las láminas 96 y 97, y en el capítulo 25.

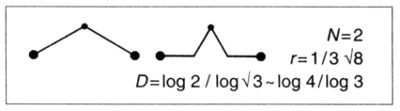
LÁMINA 72. Dos tipos de autosemejanza: la estándar y la fractal

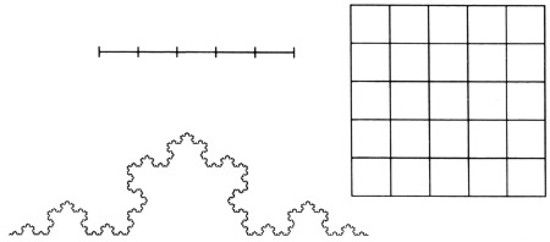
FIGURA 72

Las figuras superiores nos recuerdan cómo, dado un número entero (b = 5, en este caso), se puede dividir un segmento de longitud unidad en N = b subintervalos de longitud r = 1/b. Análogamente, un cuadrado unidad se puede dividir en N/b² cuadrados de lado r = 1/b. En ambos casos, log N/log (1/r) es la dimensión de semejanza de la forma considerada (este es un concepto al que la geometría escolar no da gran importancia, pues su valor se reduce al de la dimensión euclídea).

La figura inferior es una curva triádica de Koch, la tercera parte de una costa de Koch. Se la puede descomponer también en partes de tamaño reducido, con N = 4 y r = 1/3. La dimensión de semejanza resultante D = log N/log (1/r) tiene un valor no entero (vale aproximadamente 1,2618), y no tiene contrapartida en la geometría estándar.

Hausdorff demostró que esta D tiene aplicación matemática, y que es idéntica a la dimensión fractal o de Hausdorff. Yo sostengo que D también es de vital importancia en las ciencias de la naturaleza.

LÁMINA 73. Lago triádico de Koch

(dimensión de la costa D = log 4/log 3 ~ 1,2618)

FIGURA 73

Aquí se representa un negativo fotográfico de la construcción presentada en las láminas 70 y 71, iterada muchas veces, con lo que se obtiene un lago en vez de una isla.

La forma peculiar de las «ondas» grises que llenan el lago no es accidental, y se explica en las láminas 102 y 103.

La costa de esta lámina no es autosemejante, puesto que una curva cerrada no se puede descomponer en reunión de otras curvas cerradas. ▯ No obstante, en el capítulo 13 se aplica el concepto de autosemejanza a una colección infinita de islas. ▮

LÁMINAS 74 y 75. Isla y lago de Koch alternativos

(dimensión de la costa D = log 9/log 7 ~ 1,1291)

Esta variante de la isla de Koch se debe a W. Gosper (Gardner 1976): el iniciador es un hexágono regular y el generador es

LÁMINA 74. En esta lámina se representan diversos estadios de la construcción de la «isla de Gosper» mediante una línea «envolvente» gruesa. La línea fina correspondiente al «relleno» se explicará en la lámina 104.

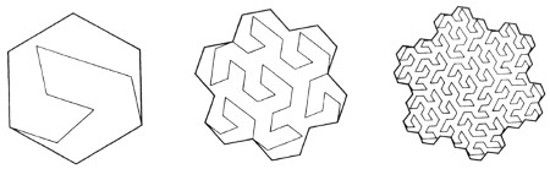
FIGURA 74

LÁMINA 75. Representa un estadio avanzado de la construcción de la «envolvente». El «relleno» de grosor variable se explicará también en la lámina 104. Nótese como, en contra de lo que sucede con el original de Koch, este generador es simétrico respecto a su punto medio. Combina penínsulas y bahías, de modo que el área de la isla permanece constante durante toda la construcción. Lo mismo vale para todas las curvas de Koch desde aquí hasta la figura 86.

FIGURA 75

EMBALDOSADO. Se puede recubrir el plano mediante islas de Gosper. Esta propiedad se denomina embaldosado.

PEREMBALDOSADO. Esta isla es además autosemejante, como pone de manifiesto el sombreado de espesor variable. Así pues, cada isla se divide en siete «regiones» relacionadas con el todo por una semejanza de razón r = 1/√7. Denotaré esta propiedad con el neologismo perembaldosado, acuñado a partir del prefijo latino per-, con una acepción como la que tiene en «perfumar»=«penetrar completamente con vapores».

En general, los embaldosados no se pueden descomponer en otros embaldosados iguales semejantes al conjunto. Por ejemplo, suele resultar bastante irritante que no se pueda construir un hexágono mayor yuxtaponiendo varios hexágonos. El copo de Gosper deforma el hexágono justo lo suficiente para que se lo pueda subdividir exactamente en 7 partes. Otros embaldosados fractales permiten subdivisiones en distinto número de partes.

FRANCIA. Un perfil geográfico inusualmente regular y que se describe a menudo como el Hexágono, a saber el perfil de Francia, se parece menos a un hexágono que a la figura de la figura 75 (a pesar de que aquí Bretaña salga un tanto desnutrida).

▯ RAZÓN POR LA QUE NO SE PUEDEN TRAZAR TANGENTES EN NINGÚN PUNTO DE ESTAS COSTAS. Fíjese un punto cualquiera alcanzado por la costa después de un número finito de iteraciones y únase con una cuerda dicho punto a otro punto móvil de la costa límite. Cuando se hace tender el punto móvil hacia el fijo a lo largo de la costa límite, ya sea en el sentido de las agujas del reloj o en el contrario, la dirección de la cuerda oscila indefinidamente alrededor del punto fijo. Un punto tal se llama toxodrómico. ▮

LÁMINA 76. Isla y lago de Koch alternativos

(dimensiones de la costa entre 1 y D = log 3/5 ~ 1,3652)

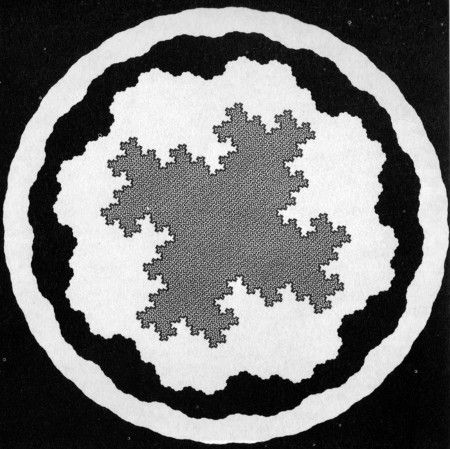
FIGURA 76

En esta sucesión de curvas fractales el iniciador es un polígono regular de M lados, y el generador es tal que N = 3 y el ángulo formado por cada dos lados sucesivos es θ = 2π/M. En las láminas 74 y 75 consideré el caso concreto M = 6 (que no se repite aquí), y el valor M = 3 se discute en la lámina 107. Esta lámina presenta terágonos avanzados para los valores M = 4, 8, 16, 32, en forma de sucesión encajada de lagos e islas. Por ejemplo. M = 4 corresponde al generador

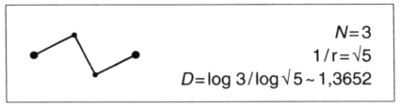
El sombreado de la isla central (M = 4) se explica en las láminas 107 y 108. Si se prolongaran estas figuras hasta M = ∞ tenderían a la forma circular. Si nos movemos hacia el interior, las figuras se van «arrugando», y este fenómeno se hace más pronunciado cuanto más nos acercamos al centro. El siguiente grado de arrugado nos llevaría a M = 3, pero la curva correspondiente ya no evitaría cortarse a sí misma. Nos la volveremos a encontrar en las láminas 107 y 108.

UNA DIMENSIÓN CRÍTICA. Cuando el iniciador es [0,1], el ángulo θ puede tomar cualquier valor entre 60° y 180°. Hay un valor crítico θ_crit para el cual la «costa» no presenta autointersecciones si, y sólo si, θ > θ_crit. La D_crit correspondiente es una dimensión crítica para la autointersección. El valor de θ_crit, es próximo a los 60°.

GENERALIZACIÓN. Las construcciones de las láminas 74 a 86 se generalizan fácilmente del modo siguiente. Llamemos directos (D) a los generadores que se han mostrado, y definamos como inversos (I) las imágenes especulares de los anteriores con respecto a la recta y = 0. Cada paso de la construcción debe emplear siempre el mismo generador, ya sea D o I, pero en estadios distintos se pueden seleccionar generadores distintos. Estas láminas y muchas de las que siguen usan sólo generadores D, pero otras sucesiones infinitas de D e I dan variantes inmediatas.

▯ Si se alternan D e I, los puntos que eran toxodrómicos se convierten en hiperbólicos, como en la curva de Koch. ▮

LÁMINA 78. Una isla de Koch cuadrangular

(dimensión de la costa D = 3/2 = 1,5000)

FIGURA 78

Las láminas comprendidas entre la 76 y la 83 muestran varias construcciones de Koch iniciadas a partir de un cuadrado (de ahí el término cuadrangular). Una ventaja es que se puede experimentar con estas construcciones usando sistemas gráficos poco sofisticados. ▯ Otra ventaja reside en que las curvas fractales cuadrangulares nos llevan directamente a la curva original de Peano, descrita en la lámina 93. ▮

LÁMINA 78. El iniciador es un cuadrado y el generador es

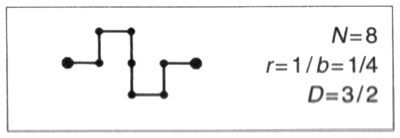
Como en las láminas 74 a 76, el área total de la isla permanece constante durante toda la iteración. La lámina 78 muestra dos estadios a una escala pequeña, y el siguiente a una escala mayor.

En el último estadio, más aumentado aún, se observan como unas barbas muy finas y apenas visibles, pero buena parte de este detalle no sería perceptible con un sistema gráfico de calidad inferior.

Ni los terágonos ni la curva límite se solapan, se cortan o tienen puntos de autocontacto. Lo mismo se cumple hasta la lámina 83.

▯ No hay que olvidar que lo que es fractal en las láminas que van de la 78 a la 83 es la costa; la tierra firme y el mar son formas convencionales de área positiva y finita, en la lámina 206 se presenta un caso en que sólo el «mar» tiene un área bien definida, y está constituido por la reunión de tremas de forma simple, mientras la tierra firme no tiene ningún punto interior. ▮

EMBALDOSADO Y PEREMBALDOSADO. Esta isla se puede descomponer en 16 islas semejantes al total con una razón r = 1/4. Cada una de éstas es la isla de Koch que se obtendría a partir de cualquiera de los 16 cuadrados que forman el primer estadio de la construcción.

▯ Los capítulos 25 y 29 muestran que D = 3/2 es también la dimensión de varias funciones brownianas. Así pues, este valor se obtiene fácilmente con curvas y superficies aleatorias. ▮

LÁMINA 80. Una isla de Koch cuadrangular

(dimensión de la costa D = log 18/log 6 ~ 1,6131)

FIGURA 80

El iniciador vuelve a ser un cuadrado y el generador es

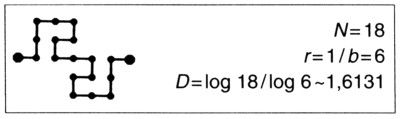
Un hecho notable es que la forma de las islas de Koch cuadrangulares de esta colección de ilustraciones depende en gran medida de D. Sin embargo, el que tenga más o menos el mismo perfil global se debe a que el iniciador es un cuadrado. Si el iniciador es un polígono regular de M lados (M>4) la forma global parece menos rugosa, y lo parece cada vez menos a medida que M aumenta. Una verdadera relación entre la forma global y el valor de D no aparecerá hasta el capítulo 28, donde trataremos de las costas aleatorias, en las que generador e iniciador efectivamente se determinan a la vez.

▯ MAXIMALIDAD. Otro hecho que contribuye a la semejanza del perfil global es que las curvas de Koch cuadrangulares de las láminas 76 a 83 presentan una interesante propiedad de maximalidad. Considérense todos los generadores de Koch que dan lugar a curvas que no se cortan a sí mismas y que se pueden trazar sobre una cuadrícula formada por rectas paralelas o perpendiculares a [0,1], y que, además, se aplican a un iniciador que sea parte de esta cuadrícula. Llamaremos maximales a aquellos generadores que den un valor máximo de N, y también por tanto de D. Se tiene que, cuando b es par, N_max = b²/2, y cuando b es impar, N_max = (b² + 1)/2.

▯ Cuando el valor de b aumenta, también aumenta el valor del N maximal, y también el número de los diversos polígonos maximales. Por tanto, la curva de Koch límite depende cada vez más del generador original. También parece cada vez más artificial, por cuanto el deseo de conseguir una dimensión máxima sin puntos de contacto impone un grado de disciplina que aumenta con D. Este llega al paroxismo en el capítulo siguiente, con el límite de Peano D = 2.

▯ LAGUNARIDAD. Las curvas fractales con la misma D pero con N y r distintas pueden presentar diferencias cualitativas. En el capítulo 34 se discute el parámetro adicional necesario, además de D, para describir tales diferencias. ▮

LÁMINA 82 y 83. Islas de Koch cuadrangulares

(dimensiones de la costa D = 5/3 ~ 1,6667 y D = log 98/log 14 ~ 1,7373)

Aquí se presenta la misma construcción con los siguientes generadores. En la figura 83,

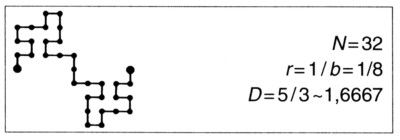
y en la figura 82,

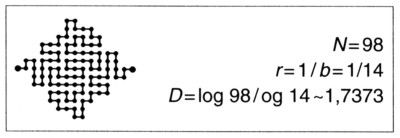
Los arrecifes y los canales de estas marinas de pesadilla se hacen cada vez, más estrechos a medida que uno avanza hacia los extremos de las penínsulas o hacia el fondo de los golfos. La anchura de dichos accidentes tiende también a disminuir al aumentar la dimensión fractal, y los «talles de avispa» aparecen hacia D ~ 5/3.

FIGURA 82

FIGURA 83

▯ DIGRESIÓN SOBRE LA DISPERSIÓN TURBULENTA. Encuentro un parecido extraordinario entre la sucesión de fractales aproximadas de la figura 83 y los estadios sucesivos de la dispersión turbulenta de la tinta en agua. La dispersión real es menos sistemática, por supuesto, pero esto se puede conseguir invocando el azar.

▯ Casi se puede ver una cascada de Richardson en funcionamiento. Una pizca de energía difunde una gota cuadrada de tinta. Luego el remolino inicial se rompe en remolinos de una escala menor, que tienen efectos más locales. La energía inicial cae hacia escalas típicas cada vez menores, y eventualmente acaba contribuyendo sólo a difuminar ligeramente el perfil de la gota de tinta final, exactamente como en este diagrama de Corrsin (1959b).

▯ La conclusión de que una cascada de Kichardson conduce a una figura delimitada por un fractal es ineludible, pero la conclusión de que D = 5/3 es dudosa, Este valor corresponde a las secciones planas de superficies espaciales con D = 8/3, valor que se da a menudo en turbulencia. En el caso de isosuperficies de escalares (que se estudian en el capítulo 30), D = 8/3 se puede deducir de la teoria de Kolmogorov. No obstante, no hay que confiar demasiado en las analogías numerológicas.

▯ En realidad, es probable que el valor de D dependa de la energía inicial del fluido y del tamaño del recipiente en el que tiene lugar la dispersión. Con una energía inicial pequeña, una gota en forma de disco se arrugaría poco, dando lugar a una curva de dimensión D próxima a 1 (lámina 76). Una energía inicial grande en un recipiente pequeño podría dar lugar a una dispersión más completa, con secciones planas que nos recordarían más a la figura 82 (D ~ 1,7373), o incluso de dimensión D = 2 (capítulo 8). Véase Mandelbrot 1976c.

▯ Si esta última conclusión es válida, el paso siguiente sería investligar la relación entre D y la energía inicial, y buscar el menor valor de la energía para el cual D = 2 en el plano, es decir, D = 3 en el espacio. Cuando estudiemos el caso límite D − 2 (capítulo 7), veremos que difiere cualitativamente de D < 2, pues, en el primer caso, dos partículas de tinta que inicialmente están alejadas tienden asintóticamente a tocarse. Así pues, no me sorprendería nada descubrir que la expresión «dispersión turbulenta» se esté empleando para designar dos fenómenos marcadamente distintos.

▯ POSDATA. Mucho después de que esta lámina hubiera aparecido publicada por vez primera en el Fractals de 1977. Paul Dimotakis fotografió secciones tenues de un chorro turbulento dispersándose en un medio laminar. El parecido con esta lámina es de lo más satisfactorio. ▮

LÁMINA 85 y 86. Curvas de Koch generalizadas y autosemejanza con partes distintas (D = 1,4490. D ~ 1,8797, D ~ 1 + ε)

FIGURA 85

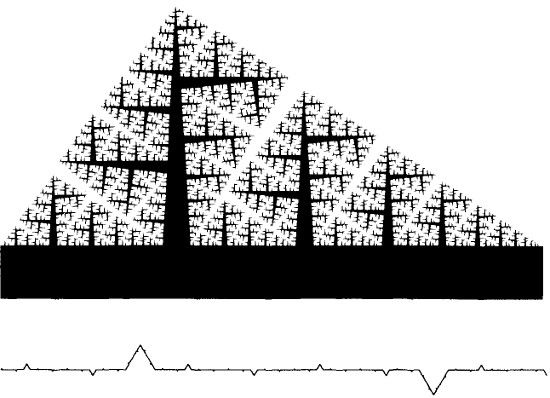
FIGURA 86

Estas láminas se han construido con el mismo método de Koch, aunque las longitudes de los lados de los generadores toman valores r_m distintos. Hasta ahora hemos supuesto que las N «partes» en que se descomponía nuestro «todo» tenían la misma razón de semejanza r. Usando r_m distintas la curva de Koch resulta menos inexorablemente regular. Así pues, la figura 85 presenta una curva de Koch más variada.

Obsérvese que, en esta serie de láminas, la construcción continúa hasta alcanzar detalles de un tamaño predeterminado. Cuando r_m = r, esto se consigue después de un número predeterminado de pasos, pero en el caso presente este número es variable.

La tarea siguiente consiste en extender el concepto de dimensión de semejanza a esta generalización de la iteración de Koch. Para encontrar alguna pista, consideremos una forma euclídea ordinaria pavimentada con partes que guarden unas proporciones r_m con el todo. Si D = 1, las r_m satisfarán ∑r_m = 1 y, en general, para las formas euclídeas se cumplirá que ∑r_m^D = 1. Además, las fractales que se pueden descomponer en partes iguales cumplen la condición ya conocida Nr^D = 1, que se puede escribir también como ∑r_m^D = 1. Estos precedentes nos sugieren definir la función generatriz de la dimensión, a saber G(D) = ∑r_m^D = 1, y definir D como la única raíz real de G(D) = 1. Quedaría por ver si esta D coincide siempre con la dimensión de Hausdorff-Besicovitch, cosa que se da en todos los casos que conozco.

EJEMPLOS. La dimensión de la figura 85 es mayor que el log 4/log 3 de la curva de Koch original. La figura superior de la figura 86 tiene una D ligeramente inferior a 2. Cuando D → 2, la costa de esta figura tiende a la curva de Peano-Pólya, que es una variante de las curvas de Peano que estudiamos en el capítulo siguiente. El parecido entre esta figura y una hilera de árboles no es accidental, como veremos en el capítulo 17. Finalmente, la D de la figura inferior de la figura 86 es ligeramente superior a 1.

6 Los copos de nieve y otras curvas de Koch

6
Los copos de nieve y otras curvas de Koch