Para empezar con un primer tipo de fractales, a saber, las curvas de dimensión fractal mayor que 1, considérese un tramo de costa. Es evidente que, por lo menos, mide tanto como la distancia en línea recta entre sus extremos. Ahora bien, una costa típica es irregular y sinuosa, y sin duda es mucho más larga que dicha recta.

Hay varias maneras de evaluar su longitud con mayor precisión, y en este capítulo se analizan algunas de ellas. El resultado es de lo más curioso: la longitud de una costa es un concepto esquivo, que se nos escapa entre los dedos cuando pretendemos asirlo. Todos los métodos de medida llevan a la conclusión de que la longitud de una costa típica es muy grande, tan indeterminada que es mejor considerarla infinita. En consecuencia, si se quiere comparar la «extensión» de distintas costas, la longitud es un concepto inadecuado.

En este capítulo se busca una alternativa mejor y, al hacerlo, resulta imposible no introducir diversos conceptos fractales de dimensión, medida y curva.

MÉTODO A: Se toma un compás de puntas con una abertura ε, que llamaremos longitud patrón, y se traslada a lo largo de la costa, empezando cada paso donde termina el anterior. El número de pasos multiplicado por ε es una longitud aproximada L(ε). Hemos aprendido que, si se repite la operación disminuyendo la abertura del compás, L(ε) tiende rápidamente a un valor bien definido llamado longitud verdadera. Pero no es eso lo que ocurre en realidad. En los casos típicos, el valor L(ε) observado crece indefinidamente.

La causa de esto es obvia: Si una bahía o una península observable en un mapa a escala 1/100.000 se contempla en un mapa a escala 1/10.000, se hacen visibles las subbahías y las subpenínsulas. En un mapa a escala 1/1000 aparecerán sub-subbahías y sub-subpenínsulas, y así sucesivamente. Todos estos accidentes contribuyen a aumentar la longitud medida.

Nuestro procedimiento parte del hecho de que una costa es demasiado irregular para ser medida directamente, leyendo en un catálogo de longitudes de curvas geométricas sencillas. Por tanto, el método A sustituye la costa por una línea quebrada de segmentos rectilíneos, una curva que sabemos manejar.

MÉTODO B: Esta «suavización» puede conseguirse también por otros métodos. Imaginemos un hombre andando a lo largo de la costa por el camino más corto sin alejarse del agua más de una distancia prescrita ε. Imaginemos que repite este paseo varias veces, reduciendo cada vez esta distancia patrón, hasta que ε se reduce a, pongamos por caso, 50 cm. El hombre es demasiado grande y torpe para afinar más. Se podría argüir que una precisión mayor (a) no tiene interés directo a escala humana y (b) varía tanto con la estación y las mareas que carece de significado. Trataremos más adelante del argumento (a), pero mientras podemos neutralizar el argumento (b) restringiéndonos a la observación de una costa rocosa, durante la bajamar y sin oleaje. En principio el hombre puede seguir esa curva con la máxima precisión amaestrando primero un ratón, luego una hormiga, etc. Y nos volvemos a encontrar con que, a medida que nuestro paseante se ajusta más y más a la costa, la distancia a cubrir aumenta sin límite.

MÉTODO C: El método B introduce una asimetría entre agua y tierra. Para evitarla. Cantor sugiere contemplar la costa con una cámara desenfocada que convierta cada punto en una mancha circular de radio ε. Dicho de otro modo. Cantor considera todos los puntos de tierra y agua que distan de la costa menos de ε. Estos puntos forman una especie de salchicha o cinta de anchura 2ε, como la que se muestra en la lámina 58 en un contexto distinto. Midamos el área de esta cinta y dividámosla por 2ε. Si la costa fuera recta, la cinta sería rectangular y el cociente nos daría su longitud. En el caso de una costa real obtenemos una estimación de la longitud L(ε) que aumenta indefinidamente al disminuir ε.

MÉTODO D: Imagínese un mapa dibujado al estilo puntillista, mediante manchitas circulares de radio ε. En vez de usar círculos con centro en la costa como en el método C, pondremos como condición que el número de manchitas que recubren la costa sea el menor posible. Tendremos que cerca de los cabos la mayor parte de cada manchita estará sobre la tierra, mientras que en los golfos estará en el mar.

El área de dicho mapa dividida por 2ε nos da una estimación de la longitud que, como las anteriores, también «se comporta mal».

Resumiendo lo dicho en la sección anterior, básicamente encontramos siempre el mismo resultado. A medida que ε se va haciendo más y más pequeño, las longitudes aproximadas crecen continua e indefinidamente.

Con objeto de captar el significado de este resultado, realicemos las mismas medidas para una curva euclídea corriente. Para un segmento de recta, las medidas aproximadas dan prácticamente el mismo resultado, y este define su longitud. Para un círculo, las medidas aproximadas crecen al disminuir ε, pero convergen rápidamente hacia cierto límite. Las curvas que admiten una longitud así definida se dicen rectificables.

Y al considerar los resultados de medir una costa domesticada por el hombre, como puede ser la costa actual de Chelsea, nos encontramos con un contraste más interesante aún. Como la mano del hombre no ha alterado los rasgos a gran escala, las medidas obtenidas con un patrón muy grande crecen de nuevo al disminuir ε.

Sin embargo, hay una gama intermedia de valores de ε, entre los 20 metros y los 20 centímetros (sin fijar demasiado estrictamente estos límites) en que L(ε) varía poco. Cuando ε disminuye por debajo de los 20 centímetros, las medidas se ven afectadas por la irregularidad de las piedras y L(ε) vuelve a aumentar. Así pues, no cabe duda de que, si trazamos la gráfica de L(ε) en función de ε, encontraremos una porción prácticamente plana entre ε = 20 metros y ε = 20 centímetros, que no se observaba antes de que la costa fuera domesticada.

Es obvio que las medidas tomadas en esta zona son de gran importancia práctica. Como la separación entre las diversas disciplinas científicas depende generalmente de la división convencional del trabajo entre los científicos, se podría restringir la geografía a los accidentes fuera del alcance de la mano del hombre (escalas superiores a los 20 metros, por ejemplo). Esta restricción daría un valor bien definido de la longitud geográfica. El guardacostas podría decidir tomar el mismo ε para costas no domesticadas, con lo que las enciclopedias y almanaques podrían adoptar la L(ε) correspondiente.

Resulta difícil imaginar, sin embargo, que todas las agencias de un mismo gobierno adopten el mismo ε, y es del todo inconcebible que lo adopten todos los países. Por ejemplo, las longitudes de las fronteras comunes entre España y Portugal, o entre Bélgica y Holanda, según datos de las enciclopedias de estos países vecinos, difieren en un 20% (Richardson, 1961). Dicha discrepancia tiene que deberse en buena parte a la elección de distintos valores de ε. Un descubrimiento empírico que discutiremos pronto demuestra que basta que los ε difieran en un factor de 2, y no debe sorprendernos que un país pequeño (Portugal) mida sus fronteras con mas precisión que su gran vecino.

La segunda razón, y la más importante, que nos decide contra la elección de un ε arbitrario es de tipo filosófico y científico. La naturaleza tiene una existencia independiente del hombre, y quienquiera que dé demasiado peso a unos ε y L(ε) determinados estará supeditando el estudio de la naturaleza al dominio del hombre, sea a través de la magnitud de su patrón típico o de su altamente variable capacidad tecnológica. Si alguna vez la investigación científica se interesa por las costas, la incertidumbre de sus longitudes no se puede eliminar por decreto. Sea como sea, el concepto de longitud geográfica no es tan inofensivo como pueda parecer a primera vista. No es completamente «objetivo». El observador interviene inevitablemente en su definición.

No cabe duda de que la idea de que las longitudes de las costas no son rectificables es algo aceptado por mucha gente, y yo mismo no recuerdo haber pensado nunca lo contrario. Pero mi búsqueda de enunciados escritos de este efecto prácticamente ha sido un fracaso. Además de la cita de Perrin del capítulo 2, tenemos la observación de Steinhaus (1954) de que «la ribera izquierda del Vístula, medida con precisión creciente, daría resultados diez, cien y hasta mil veces mayores que la longitud que figura en los mapas… [Una] afirmación muy próxima a la realidad sería decir que la mayoría de arcos que se encuentran en la naturaleza no son rectificables. Este enunciado va contra la creencia corriente de que los arcos no rectificables son un invento de los matemáticos y que los arcos naturales son rectificables; lo cierto, sin embargo, es lo contrario». Pero ni Perrin ni Steinhaus profundizaron en esta idea.

Aquí encaja una historia que me contó C. Fadiman. Su amigo Edward Kasner pidió a unos jovenzuelos «que adivinaran la longitud de la costa este de los Estados Unidos. Después de dejarles un tiempo “prudencial”… les hizo notar que el resultado aumentaría una barbaridad si se tenía en cuenta el perímetro de cada cala y cada golfo, el de cada proyección y curva de cada uno de éstos, la distancia entre cada dos partículas de materia de la costa, cada molécula, átomo, etc. Evidentemente la longitud de la costa es tan grande como uno quiera. Los niños lo entendieron a la primera; pero Kasner tuvo más problemas con la gente mayor». Aunque es una bella historia, es irrelevante aquí: Kasner no pretendía destacar un aspecto de la naturaleza que mereciera ser estudiado con más detenimiento.

Por lo tanto, Mandelbrot (1967) y este ensayo son, en efecto, los primeros trabajos sobre el tema.

«El vasto campo para los nuevos descubrimientos… es siempre el residuo sin clasificar. Alrededor de los hechos acreditados y ordenados de cada ciencia siempre flota algo como una nube de polvo de observaciones excepcionales, sucesos minúsculos, irregulares e infrecuentes, que siempre resulta más fácil ignorar que tener en cuenta. El ideal de todas las ciencias es el de un sistema de verdad completo y cerrado… Los fenómenos inclasificables en el sistema son absurdos, paradójicos, y hay que declararlos falsos… se los niega u olvida con plena conciencia científica… Para renovar una ciencia hay que interesarse por los fenómenos irregulares. Y una vez se ha renovado la ciencia, sus nuevas fórmulas a menudo expresan más la excepción que lo que se suponía que era la regla».

Este ensayo, que pretende efectivamente renovar la geometría de la naturaleza, se basa en muchos rompecabezas tan inclasificables que sólo se publican cuando los censores se duermen. En la siguiente sección comentamos un primer ejemplo.

Richardson (1961) estudió empíricamente la variación de la longitud aproximada L(ε) obtenida por el método A. El azar (o el destino) hizo que esta referencia cayera en mis manos. Le presté atención porque (capítulo 40) sabía que Lewis Fry Richardson era un gran científico, muy original y a la vez excéntrico. Como veremos en el capítulo 10, le debemos algunas de las ideas más profundas y permanentes acerca de la naturaleza de la turbulencia, sobre todo la idea de que la turbulencia trae aparejada una cascada autosemejante. Se ocupó también de otros problemas difíciles, como la naturaleza de los conflictos armados entre estados. Sus experimentos fueron de una simplicidad clásica, pero no dudaba en usar conceptos refinados cuando los creía necesarios.

Los gráficos reproducidos en la lámina 59, hallados entre sus papeles después de su muerte, fueron publicados en un Anuario prácticamente confidencial (y totalmente inadecuado para el tema). Todos ellos llevan a la conclusión de que hay dos constantes, que llamaremos F y D, tales que, para aproximar una costa con una línea quebrada hacen falta unos Fε^−D segmentos de longitud ε, con lo que su longitud total es

Parece ser que el exponente D depende de la costa considerada, y que distintas partes de la misma costa, consideradas por separado, dan valores distintos de D. Para Richardson, la D en cuestión no era más que un simple exponente, sin mayor trascendencia. Parece, sin embargo, que su valor es independiente del método elegido para estimar la longitud de la costa. Así pues, parece justificado dedicarle mayor atención.

Después de desenterrado el trabajo de Richardson, propuse (Mandelbrot 1967s) que, a pesar de que el exponente D no fuera un entero, podía y debía interpretarse como una dimensión, en el sentido de dimensión fractal. En efecto, me di cuenta de que los métodos citados para medir L(ε) se correspondían con generalizaciones no estándar de la definición de dimensión, que ya se usaban en matemática pura. La definición de longitud basada en recubrir la costa con el menor número posible de manchas de radio ε es usada en Pontrjagin y Schnirelman (1932) para definir la dimensión de recubrimiento. La definición de longitud basada en recubrir la costa con una cinta de anchura 2ε lleva a la práctica una idea de Cantor y Minkowski (Lámina 58), y la dimensión correspondiente se debe a Bouligand. Sin embargo, estos dos ejemplos sólo dan una idea de las muchas dimensiones que se dan en diversos capítulos especializados de la matemática (la mayoría de ellas sólo son conocidas por unos pocos especialistas). En el capítulo 39 volveremos sobre algunas de ellas.

¿Por qué emplean los matemáticos esta plétora de definiciones distintas? Porque en determinados casos toman valores distintos. Por suerte, sin embargo, esos casos no se dan en este ensayo, y la lista de posibles dimensiones alternativas se puede reducir a dos que no he citado aún. La más antigua y mejor conocida se debe a Hausdorff y sirve para definir la dimensión fractal; volveremos sobre ella en un momento. La más simple es la dimensión de semejanza que, si bien es menos general, en muchos casos es más que suficiente, y la estudiaremos en el capítulo siguiente.

Quede claro que no me propongo dar una demostración matemática de que la D de Richardson es una dimensión. En ninguna ciencia natural es concebible una demostración de esta clase. El propósito sólo es convencer al lector de que la idea de longitud plantea un problema conceptual y de que la D proporciona una respuesta conveniente y razonable. Ahora que ya hemos introducido la dimensión fractal en el estudio de las costas, aunque habrá que afrontar todavía problemas concretos, pienso que ya no podemos volver al estadio en el que aceptábamos ingenuamente sin más que D = 1. Quien siga pensando que D = 1 tendrá que dar sus razones.

El paso siguiente en la explicación de la forma de las costas y en la deducción del valor de D a partir de consideraciones más básicas se aplaza hasta el capítulo 28. Baste aquí decir que en primera aproximación D = 3/2. Aunque este valor es con mucho demasiado grande para describir la realidad, nos bastará para establecer que es natural, apropiado y esperable que la dimensión de una costa exceda el valor euclídeo estándar D = 1.

Si aceptamos que la longitud de varias costas naturales es realmente infinita y que la longitud basada en un valor antropocéntrico de ε sólo da una idea parcial de la realidad, ¿cómo podemos comparar entre sí distintas costas? Dado que infinito es igual a cuatro veces infinito, cada costa es cuatro veces más larga que cada uno de sus cuartos, pero esta conclusión no nos sirve de gran cosa. Necesitamos una manera mejor de expresar la idea lógica de que la curva entera debe «medir» cuatro veces más que cada uno de sus cuartos.

Félix Hausdorff dio una solución de lo más ingenioso para resolver este problema. Se inspira en el hecho de que el perímetro de un polígono se calcula sumando sin más las longitudes de sus lados, sin transformarlas de ninguna manera. Se podría decir (el porqué se verá enseguida) que estas longitudes están elevadas a la potencia D = 1, que es la dimensión euclídea de la recta. Análogamente, el área encerrada en el interior de un polígono se calcula embaldosándolo con cuadrados y sumando los lados de los cuadrados elevados a la potencia D = 2, la dimensión euclídea del plano. Además, si se usa la potencia «equivocada» el resultado no nos da ninguna información concreta: el área del contorno de un polígono es cero y la longitud de su interior es infinita.

Procedamos de un modo análogo con las aproximaciones poligonales a una costa dada, formadas por pequeños segmentos de longitud ε. Si elevamos sus longitudes a la potencia D, obtenemos una cantidad que podríamos llamar «medida aproximada de dimensión D». Como, según Richardson, el número de lados es N = Fε^−D, tenemos que dicha medida aproximada toma el valor Fε^Dε^−D = F.

Así pues, la medida aproximada de dimensión D es independiente de ε. Con datos reales, encontraríamos simplemente que esta medida aproximada varía poco con ε.

Además, el hecho de que la longitud del interior de un cuadrado sea infinita tiene una generalización simple: la medida aproximada de una costa evaluada en una dimensión d menor que D tiende a ∞ cuando ε → 0. De manera análoga, así como el área y el volumen de una línea recta son nulos, cuando d toma un valor mayor que D, la medida aproximada correspondiente tiende a 0 cuando ε → 0. La medida aproximada sólo se comporta bien cuando d = D.

Por construcción, la dimensión de Hausdorff conserva el papel de la dimensión ordinaria como exponente en la definición de una medida.

Pero en otros aspectos D es verdaderamente muy rara: ¡es una fracción! Y en particular es mayor que 1, que es la dimensión intuitiva de las curvas y que, como se puede demostrar rigurosamente, es su dimensión topológica D_T.

Propongo que las curvas cuya dimensión fractal sea mayor que su dimensión topológica 1 se llamen curvas fractales. Y este capítulo se puede resumir diciendo que, en las escalas que interesan al geógrafo, las costas se pueden representar por curvas fractales. Las costas son figuras fractales.

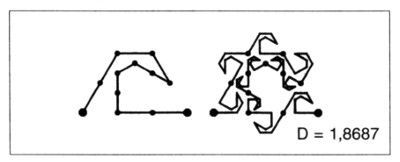
LÁMINA 57. El árbol de los monos

FIGURA 57

Aquí, esta lámina pequeña y accesoria no es más que un dibujo decorativo, que sirve para llenar un hueco.

Sin embargo, cuando el lector acabe el capítulo 14, este dibujo le proporcionará una pista para descifrar la «arquitectura» de la lámina 208. Una pista más discreta la tiene en el siguiente generador.

LÁMINA 58. Un ejemplo de salchicha de Minkowski

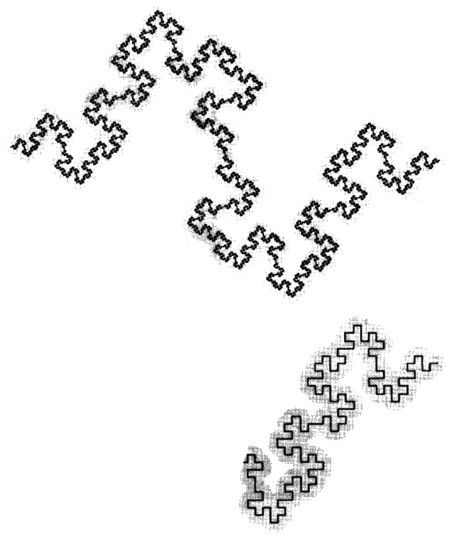
FIGURA 58

Cuando un matemático quiere «domesticar» una curva desmadradamente irregular, un procedimiento normal consiste en elegir un radio ε y dibujar un disco de este radio alrededor de cada punto. Este procedimiento, que data por lo menos de la época de Hermann Minkowski y quizá de la de Georg Cantor, es burdo pero muy eficiente. (Parece ser que el término salchicha, según un rumor incomprobable, es una reminiscencia de una aplicación de este procedimiento a las curvas brownianas por Norbert Wiener).

En esta ilustración, dicho método de suavización no se aplica a una costa real sino a una curva teórica que construiremos más adelante (Lámina 76) mediante la adición continuada de detalles cada vez más pequeños. Comparando el pedazo de salchicha de la derecha con el extremo derecho de la salchicha de encima, se observa que la construcción de la curva pasa por un estadio crítico cuando aparecen los detalles de tamaño menor que ε. Los estadios posteriores de la construcción dejan la salchicha prácticamente inalterada.

LÁMINA 59. Los datos experimentales de Richardson referentes a la tasa de aumento de la longitud de las costas

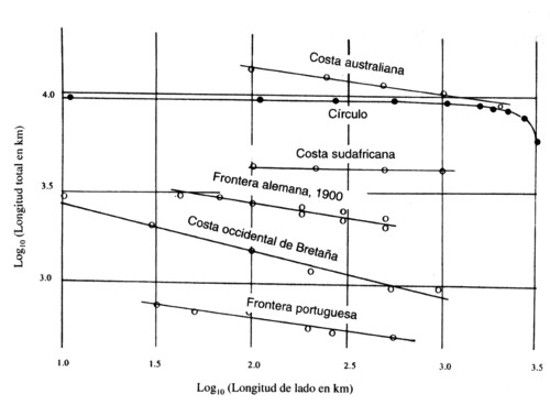
FIGURA 59

Esta figura reproduce las medidas experimentales de la longitud de varias curvas, usando polígonos equiláteros de lado ε cada vez más corto. Como era de esperar, las medidas cada vez más precisas realizadas sobre un círculo se estabilizan muy rápidamente cerca de un valor bien determinado.

En el caso de las costas, por el contrario, las longitudes aproximadas no se estabilizan en absoluto. A medida que la longitud patrón ε tiende a cero, las longitudes aproximadas, representadas en papel bilogarítmico, se ordenan según una recta de pendiente negativa. Y lo mismo ocurre con las fronteras entre países. El registro de Richardson en los archivos pone de manifiesto diferencias notables en las longitudes de las fronteras comunes entre España y Portugal (987 frente a 1.214 Km), y entre Holanda y Bélgica (380 frente a 449 Km). Con una pendiente de −0,25, la diferencia del 20% entre estos datos se puede explicar suponiendo que los ε respectivos difieren en un factor 2, cosa que no es inverosímil.

Richardson no dio ninguna interpretación teórica a las pendientes de sus líneas. En este ensayo, por el contrario, se interpreta que las costas son curvas aproximadamente fractales, y la pendiente de cada línea da una estimación de 1 − D, siendo D la dimensión fractal.

5 ¿Cuánto mide la costa de Bretaña?

5
¿Cuánto mide la costa de Bretaña?