«Toda belleza es relativa… No hemos de… creer que las orillas del mar sean realmente deformes por no tener la forma de un baluarte regular; que las montañas hayan perdido la forma porque no son exactamente como pirámides o conos; ni que las estrellas estén situadas desmañadamente por no estar a una distancia uniforme. Estas irregularidades no son naturales, sino sólo por lo que respecta a nuestro gusto; ni resultan incómodas para los verdaderos usos de la vida y de los designios de la vida del hombre en la tierra». Esta opinión de Richard Bentley, sabio inglés del siglo XVII (repetida en las frases del comienzo de este ensayo), muestra que la idea de reunir las formas de las costas, las montañas y el cielo para contrastarlas con lo euclídeo viene de antiguo.
Del puño y letra de Jean Perrin
A continuación sintonizamos una voz más próxima en el tiempo y también en el oficio. Para dar más detalles acerca del carácter irregular o fragmentado de las costas, el movimiento browniano y otras estructuras naturales que trataremos en el presente ensayo, permítaseme presentar, en una traducción más o menos libre, unos extractos de Perrin (1906). El trabajo posterior de Jean Perrin sobre el movimiento browniano le valió el premio Nobel y espoleó el desarrollo de la teoría de la probabilidad. Aquí, sin embargo, cito de un manifiesto filosófico anterior que, aunque fue parafraseado posteriormente en el prólogo de Perrin (1913), pasó desapercibido hasta que apareció citado en la primera versión (francesa) de este ensayo. Aunque me enteré de su existencia demasiado tarde como para que tuviera un efecto importante sobre mi trabajo, me estimuló en un momento en que me hacía falta, y es de una elocuencia sin par:
«Como sabe todo el mundo, antes de dar una definición rigurosa de continuidad, todo buen maestro demuestra a los principiantes que, de hecho, poseen ya la idea subyacente a este concepto. Traza una curva bien definida y, sosteniendo una regla, dice: “Como ven, en cada punto hay una tangente”. O también, al introducir el concepto de velocidad instantánea de un móvil en un punto de su trayectoria, dice: “Vean cómo la velocidad media entre dos puntos próximos no varía apreciablemente al acercar infinitamente dichos puntos”. Y muchos, sabedores de que para ciertos movimientos corrientes estas afirmaciones parecen ser bastante ciertas, no se dan cuenta de que encierran un número considerable de dificultades.
»Los matemáticos, sin embargo, son muy conscientes de lo pueril de tratar de demostrar, con dibujos solamente, que toda función continua tiene derivada. Aunque las funciones diferenciables son las más simples y las más fáciles de manejar, son una excepción. Hablando en términos geométricos, lo normal son las curvas sin tangente, mientras que las curvas regulares, como el círculo, son casos interesantes pero muy particulares.
»A primera vista, la consideración del caso general parece un mero ejercicio intelectual, ingenioso pero artificial, el deseo de una precisión absoluta llevado a un extremo ridículo. Quienes oyen hablar de curvas sin tangente, o de funciones sin derivadas, piensan a menudo que cosas tan complicadas ni se dan en la naturaleza, ni nos son sugeridas por ella.
»Sin embargo, lo cierto es lo contrario, y la lógica de los matemáticos les ha mantenido más cerca de la realidad que las representaciones prácticas que usan los físicos. Ilustraré esta afirmación considerando algunos datos experimentales sin ninguna idea preconcebida.
»Consideremos, por ejemplo, un copo blanco de los que se obtienen al echar sal al agua jabonosa. De lejos, su contorno puede parecer claramente definido, pero a medida que lo examinamos más y más cerca, esa claridad desaparece. El ojo no ve ya una tangente en cada punto. Una línea que pudiera a primera vista tener esta propiedad resulta, después de un examen más minucioso, ser perpendicular u oblicua al contorno. Y si tomamos una lupa o un microscopio, la incertidumbre se mantiene, pues cada vez que incrementamos el aumento aparecen nuevas irregularidades, y nunca llegamos a tener una imagen clara y nítida, como en el caso, por ejemplo, de una bola de acero. Así pues, si se acepta que este último caso ilustra la forma clásica de la continuidad, el copo anterior podría lógicamente ilustrar el concepto más general de función continua sin derivada».
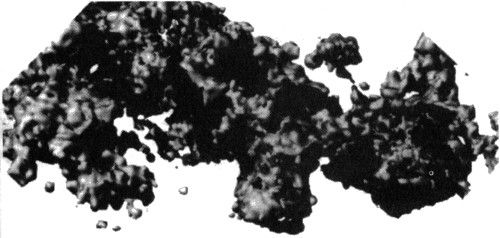
Conviene interrumpir aquí la cita para prestar atención a las siguientes figuras 25 y 26. Las láminas en blanco y negro se encuentran al final del capítulo en que han sido citadas por primera vez y el número es el de la página correspondiente.[2] Las láminas en color forman un capítulo aparte y sus pies son bastante independientes del resto del libro.

FIGURA 25 y 26. Copos fractales artificiales

Y sigue la cita:
«Hay que tener en cuenta que la incertidumbre en la posición de la tangente en un punto no tiene nada que ver con la incertidumbre que uno observa en un mapa de Bretaña. Aunque se obtendría un resultado distinto según la escala del mapa, siempre habría una tangente, pues un mapa es un diagrama convencional. Por el contrario, tanto nuestro copo como la costa presentan la característica esencial de que sospechamos, sin verlo absolutamente claro, que en cada escala aparecen detalles que prohiben del todo determinar una tangente.
»Sin abandonar el reino de la realidad experimental, observemos con un microscopio una partícula suspendida en un fluido agitándose por el movimiento browniano [véase la lámina 29 de este ensayo]. Se observa cómo la dirección de la línea recta que une las posiciones de la partícula en dos instantes de tiempo muy próximos cambia de manera absolutamente irregular al disminuir el intervalo de tiempo entre ambos instantes. Para un observador imparcial la conclusión sería que no está tratando con una curva sobre la que se puedan trazar tangentes, sino con una función sin derivada.
»No hay que olvidar que, a pesar de que una observación cada vez más fina de cualquier objeto nos llevaría normalmente al descubrimiento de una estructura muy irregular, a menudo resulta ventajoso aproximar sus propiedades por medio de funciones continuas. Aunque la madera pueda tener una porosidad indefinida, resulta útil considerar que una viga que ha sido serrada y pulida tiene un área finita. Es decir, a ciertas escalas y según para qué métodos de investigación, muchos fenómenos pueden representarse por funciones regulares y continuas, de manera parecida a como se puede envolver una esponja con papel de aluminio sin seguir exactamente el contorno complicado de la misma.
»Si, yendo algo más lejos…, atribuimos a la materia la estructura infinitamente granular que plantea la teoría atómica, la posibilidad de aplicar a la realidad el concepto matemático riguroso de continuidad sufrirá un serio revés.
»Consideremos, por ejemplo, la definición de la densidad del aire en un punto y en un instante dados. Nos representamos una esfera de volumen v con centro en ese punto. Si la masa del aire contenido es m, el cociente m/v es la densidad media en el interior de esa esfera, y llamamos densidad verdadera a un cierto valor límite de dicho cociente. Esta definición implica, sin embargo, que, en el momento considerado, la densidad media es prácticamente constante para todas las esferas de un tamaño inferior a un volumen dado. Aunque esa densidad media pueda variar considerablemente entre una esfera de 1000 metros cúbicos y otra de 1 centímetro cúbico, uno espera que varíe sólo en una millonésima al comparar 1 centímetro cúbico con una milésima de milímetro cúbico.
»Supongamos que el volumen decrece continuamente. En vez de ser cada vez menos importantes, resulta que estas fluctuaciones son cada vez mayores. A escalas en las que es importante el movimiento browniano, el efecto de las fluctuaciones puede ser de una parte en un millar, y llegan a ser de 1 parte de cada 5 cuando el radio de la esfera hipotética alcanza la centésima de micra.
»Siguiendo un poco más, nuestra esférula llega al tamaño de una molécula. En un gas, lo más probable es que se encuentre en el espacio intermolecular, con lo que la densidad media será nula. En el punto en cuestión, la densidad verdadera será nula también. Pero aproximadamente una de cada mil veces nuestro punto estará en una molécula, y entonces la densidad media será mil veces mayor que el valor que solemos tomar como densidad verdadera del gas.
»Sigamos disminuyendo el tamaño de nuestra esférula. Excepto en casos excepcionales, pronto llegará a estar vacía debido al vacío interatómico; con lo que la densidad verdadera es nula casi por doquier, excepto en un número infinito de puntos aislados, en los que tiene un valor infinito.
»Otras propiedades tales como la velocidad, la presión o la temperatura son susceptibles de consideraciones análogas. Descubrimos que se hacen cada vez más irregulares a medida que incrementamos el aumento de nuestra imagen necesariamente imperfecta del universo. En el espacio intermaterial, la función que representa cualquier propiedad física formará un continuo con un número infinito de puntos singulares.
»Una materia infinitamente discontinua, un éter continuo sembrado de minúsculas estrellas, también aparece en el universo cósmico. Y se puede llegar también a la misma conclusión que más arriba, imaginando esferas cada vez mayores que abarquen sucesivamente planetas, sistemas solares, estrellas, nebulosas,…
»Permítasenos pues una hipótesis que, aun siendo arbitraria, no es lógicamente inconsistente. Podrían darse casos en los que usar una función no diferenciable fuera más simple que usar una que sí lo fuera. Cuando esto ocurra, se habrá probado el valor práctico del estudio matemático de los continuos irregulares».
Luego, en el comienzo de otra sección, subraya:
«Pero, por el momento, esta hipótesis no es más que un ensueño».
De cómo una «Galería de los Monstruos» se convierte en Museo de la Ciencia
Una parte de este ensueño, la que se refiere al movimiento browniano, se hizo realidad en tiempos del propio Perrin. La reflexión de Perrin captó casualmente la atención de Norbert Wiener (Wiener, 1956, págs. 38-39, o 1964, págs. 2-3), quien, con gran «sorpresa y placer», se animó a definir y estudiar con rigor un primer modelo no diferenciable del movimiento browniano.
Este modelo sigue vigente, si bien los físicos arguyen que su no diferenciabilidad procede de una idealización excesiva, a saber, considerar despreciable la inercia. Con ello los físicos vuelven la espalda a un aspecto del modelo de Wiener que es de la máxima importancia para la presente obra. Las otras aplicaciones de las matemáticas a la física previstas por Perrin ni tan sólo fueron intentadas hasta esta obra. La familia de conjuntos a que aludía Perrin (las curvas de Weierstrass, los polvos de Cantor y otros por el estilo) siguieron formando parte de la «matemática pura».
Algunos autores, por ejemplo Vilenkin (1965), llaman a esta familia «Museo de Arte Matemático», sin sospechar siquiera (estoy convencido) cuan acertado iba a resultar este nombre. Cité ya en el capítulo 1 que otros autores (empezando por Henri Poincaré) dijeron que era una «Galería de los Monstruos», parafraseando el Treatise of Algebra de John Wallis (1685), donde se dice que la cuarta dimensión es «un monstruo en la naturaleza, menos posible que una quimera o un centauro».
Uno de los objetivos del presente ensayo es mostrar, insistiendo una y otra vez sobre diversos «casos» concretos, que esa misma «Galería» se puede visitar en calidad de Museo de la Ciencia.
Los matemáticos son dignos de elogio por haber inventado el primero de estos conjuntos hace ya mucho, pero al mismo tiempo son los culpables de habernos disuadido de hacer uso de ellos.
LÁMINA 29. Los dibujos clásicos del movimiento browniano según Jean Perrin
En un texto inspirador citado en el capítulo 2, Jean Perrin hace un comentario sobre la forma de los «copos blancos que se obtienen echando sal en agua jabonosa». El objeto de estas figuras es ilustrar las observaciones de Perrin.
Hay que apresurarse a señalar que no se trata de fotografías ni de reconstrucciones por ordenador de ningún objeto real, ya sea éste un copo de jabón, una nube de lluvia o volcánica, un pequeño asteroide o un pedazo de cobre nativo. Tampoco pretenden ser el resultado de una teoría que simule los distintos aspectos —químicos, físicoquímicos e hidrodinámicos— de la formación real de copos.
A fortiori, no pretenden estar directamente relacionados con ningún principio científico. Son formas producidas en un ordenador con el fin de ilustrar, de la manera más sencilla posible, ciertas características geométricas que parecen estar presentes en la descripción de Perrin, y que propongo modelizar mediante el concepto de fractal.
Estos copos existen únicamente en la memoria de un ordenador. Nunca se realizaron modelos tridimensionales de los mismos, y el sombreado es obra también del diseño por ordenador.
Los detalles de la construcción de estos copos se dan en el capítulo 30. Las diferencias apreciables entre ellos dependen del parámetro D, cuyo valor se indica al lado de cada figura. Se llama dimensión fractal, se define en el capítulo 3 y tiene un papel fundamental en el presente ensayo. El hecho de que las tres figuras tengan la misma forma global se debe a un sesgo asociado al método de aproximación. Este efecto se comentará en los pies de las láminas 376 y 377.
Una versión anterior tenía un extraño parecido con una presunta fotografía del monstruo del lago Ness. ¿Podría ser fortuita esta convergencia de forma?
La descripción del movimiento browniano por Perrin (1909) es la siguiente:
«En una masa de fluido en equilibrio, como por ejemplo el agua de un vaso, todas las partes están aparentemente en reposo. Si introducimos en ella un objeto más denso, cae. Es cierto que cuanto menor es el objeto más lenta es la caída; pero cualquier objeto visible siempre acaba en el fondo de la vasija y por ningún motivo tiende a ascender de nuevo. Sin embargo, sería difícil observar durante mucho rato una preparación de partículas muy finas en un líquido sin observar un movimiento perfectamente irregular. Se mueven, se detienen, vuelven a arrancar, suben, bajan, vuelven a subir, sin tender al reposo en lo más mínimo».
Esta lámina, la única del libro que representa un fenómeno natural, está tomada de Les atomes de Perrin. Vemos cuatro trazas distintas de partículas coloidales con un radio de 0,53 micras, observadas al microscopio. Cada dos posiciones sucesivas están separadas por un intervalo de 30 segundos, y los segmentos de recta que los unen no tienen ningún significado físico (la cuadrícula tiene un lado de 3,2 micras).
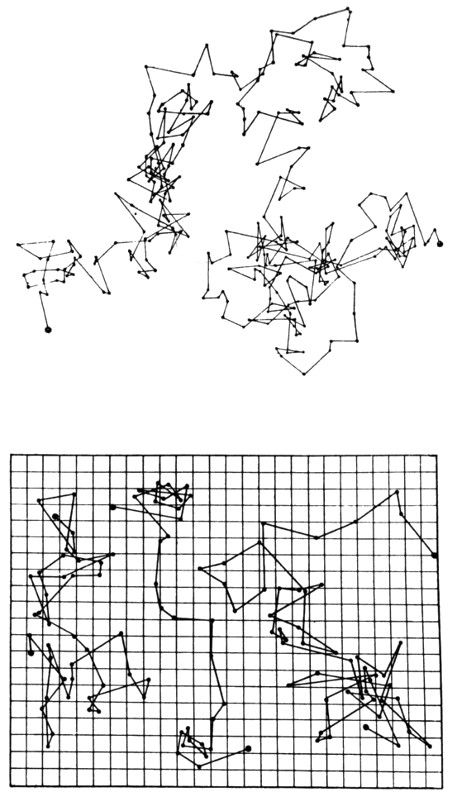
FIGURA 29
Volviendo a nuestra traducción libre de Perrin,
«Uno podría sentirse tentado a definir una “velocidad media de agitación” siguiendo una partícula concreta con tanta precisión como le fuera posible. Pero esas evaluaciones son enormemente erróneas. Tanto el módulo como la dirección de la velocidad media aparente varían a lo loco. Esta lámina sólo da una ligera idea de lo enrevesado de la trayectoria real. En efecto, si se marcaran las posiciones de la partícula a intervalos de tiempo 100 veces menores, cada segmento rectilíneo sería sustituido por una poligonal tan compleja como el presente gráfico, aunque más pequeña. Se comprende fácilmente, pues, que el concepto de tangente no tenga sentido en tales curvas».
Este ensayo comparte las inquietudes de Perrin, pero aborda la irregularidad desde un ángulo distinto. Nos fijaremos (capítulo 25) en que al examinar el movimiento browniano bajo aumentos crecientes, su longitud crece indefinidamente.
Además, la traza del movimiento browniano acaba por llenar casi por completo el plano. ¿No resulta pues tentador concluir que, en cierto sentido aún no definido, este tipo peculiar de curvas tiene la misma dimensión que el plano? Y en efecto, así es. Uno de los principales objetivos de este ensayo es mostrar que el vago concepto de dimensión presenta distintos aspectos. La traza del movimiento browniano es, desde el punto de vista topológico, una curva, y por tanto tiene dimensión 1. Sin embargo, como barre la práctica totalidad del plano, tiene dimensión dos en sentido fractal. De acuerdo con la terminología que se introduce en este ensayo, la discrepancia entre estos dos valores determinará que el movimiento browniano sea un fractal.