Jornadas de Courchevel: adelanto de las actas de próxima aparición
En el tiempo transcurrido entre la entrega de este libro al editor y su publicación, y luego en el breve periodo que tardó en agotarse la primera edición, la geometría fractal no permaneció inactiva: siguió avanzando con una velocidad creciente en los dominios en los que ya había sido aceptada y entró en unos cuantos ámbitos nuevos.
En particular, en julio de 1982 organicé un encuentro de una semana de duración sobre fractales, en Courchevel (Francia), y muchos nuevos avances se presentaron allí por primera vez. El principal objetivo de esta actualización es resumir estos resultados y otros íntimamente relacionados con ellos. Algunas referencias suplementarias (marcadas con un asterisco) llaman la atención sobre otros trabajos presentados en ese encuentro.
Más generalmente, cada vez resulta más difícil creer que, hace sólo unos pocos años, la geometría fractal de la naturaleza se reducía casi exclusivamente a mi trabajo y al de colaboradores próximos. Sin embargo, lo más que puedo hacer es llamar la atención sobre algunos nuevos autores, por medio de referencias suplementarias adicionales.
Los temas se han dispuesto más o menos en el mismo orden que en el cuerpo principal del libro.
La definición de «fractal»
Este tema tan soso es por desgracia inevitable, pero gracias a Dios nos ocupará poco espacio.
Con gran disgusto mío, el término «dimensión de Hausdorff» ha empezado a aplicarse indiscriminadamente a cualquiera de las dimensiones enumeradas en el capítulo 39 y a nuevas variantes de éstas. Lo mismo ocurre con la «dimensión de Minkowski», expresión usada una vez en la página 164 de los Objets Fractals de 1975 para denotar la dimensión de Bouligand. Según parece, ciertos artículos escritos en idiomas extranjeros, cuyos autores y temas dejan de ser temidos como consecuencia de mi trabajo, adquieren prestigio, y se les atribuye por tanto todo un conjunto de hazañas… o delitos.
Otros autores se pasan por el otro extremo: dan excesiva importancia a los métodos usados más a menudo para estimar D en la práctica como la dimensión de semejanza, tal como se usaba en las págs. 187 y 308, el exponente de la relación masa-radio o un exponente espectral) y los elevan al rango de definición de «la» dimensión fractal.
Es una pena que la mayoría de estas reacciones al Fractals de 1977 se manifestaran un poco demasiado tarde. Me habrían animado a volver en este libro al enfoque genial tomado en los Objets fractals de 1975: dejar el término «fractal», sin una definición rebuscada, emplear «dimensión fractal» como expresión genérica aplicable a todas las variantes del capítulo 39, y en cada caso concreto usar la definición más apropiada.
Turbulencia fractal homogénea
Mi principal conjetura sobre la turbulencia es el tema del capítulo 11: la turbulencia en el espacio real es un fenómeno soportado por un conjunto fractal de dimensión D ∼ 2,5 a 2,6.
Continúan los trabajos numéricos en apoyo de esta conjetura, como lo atestigua Chorin (1982a, b).
Además de ello, Hentschel y Procaccia (1982) han propuesto recientemente un enfoque totalmente diferente, que maneja el alargamiento y plegamiento de los vórtices del capítulo 10 con los métodos desarrollados para tratar con los polímeros del capítulo 36, y sugiere una relación entre la dimensión de la turbulencia y la de los polímeros.
Fracturas metálicas y fractales (B. B. M., Passoja y Paullay, 1983)
Como se señaló en el capítulo 1, los neologismos requieren un cierto cuidado y habría que evitar los conflictos entre significados. Una revisión casual sugirió que, si es muy poco probable que las superficies de fractura de los vidrios sean fractales, muchas superficies de fractura de piedras o metales sí lo son. Este indicio informal sugirió que fractal y fractura no estarían en conflicto.
Mandelbrot, Passoja y Paullay (1983) refuerzan esta impresión informal mediante muchas pruebas experimentales con probetas de tracción de acero 1040, 1095 y Cor-99 y con probetas de resistencia de acero Maraging. Se comprueba el carácter fractal y se estima el valor de la dimensión D usando métodos como los usados en los capítulos 5 y 28 para el relieve. El éxito de estos métodos es notable, pues las superficies de las fracturas son claramente no gaussianas y completamente distintas del relieve.
Recuérdese que los capítulos 5 y 28 procedían a través de las costas de las islas y las secciones verticales. Desgraciadamente, las fracturas no presentan islas de manera natural, y es raro encontrar una dirección que satisfaga la definición de vertical (como la dirección según la cual la altura es una función univaluada de la posición en el plano horizontal).
No obstante, podemos definir una vertical informal por la condición de que la altura sea univaluada para «la mayoría» de puntos. Hacemos luego un análisis espectral de las alturas a lo largo de secciones horizontales rectilíneas y representamos log(energía espectral para frecuencias superiores a f) en función de log f.
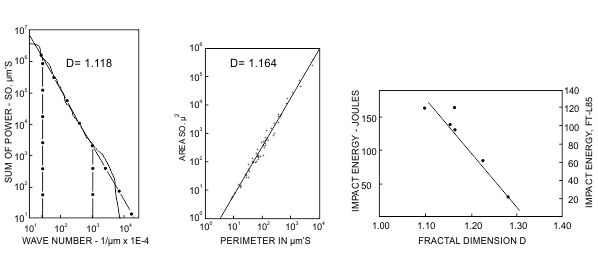
Además, resulta útil crear «islas rebanada» cortando la muestra según planos casi horizontales (primero se niquela la muestra con un depósito químico de níquel y se monta en una montura de epoxy por impregnación al vacío). A continuación usamos un patrón fijo para medir el área y el perímetro de cada isla sobre una imagen digitalizada, y representamos gráficamente el logaritmo como se sugiere en el capítulo 12, para comprobar la validez del análisis de la dimensión fractal.
Como muestran los dos ejemplos de la página 597, muchísimas superficies de fractura siguen el modelo fractal admirablemente bien: ambos diagramas son muy aproximadamente rectos y sus pendientes dan esencialmente los mismos valores de D. Además, si se someten al mismo procedimiento distintas muestras del mismo metal se obtiene la misma D. Esto contrasta con las estimaciones tradicionales de la rugosidad, que son difícilmente repetibles.
Repitiendo un comentario de la página 163 relativo a la lámina 168, en metalurgia hay muy pocos gráficos que afecten a todos los datos disponibles y a una gama muy amplia de tamaños, y que sean tan directos como los nuestros.
Los datos son tan buenos que podemos proceder sin más a una comparación más fina. Observamos que |D(espectral) − D(islas)| es sistemáticamente del orden de unas pocas centésimas. Una primera causa posible es un sesgo en la estimación. Por ejemplo, el espectro de altas frecuencias está sobrecargado por el ruido de la medición, y por tanto debe ignorarse. Además, tratamos los «lagos» y las «islas cercanas a la costa» de modo más fácil: contamos los unos y despreciamos las otras por no estar bien definidas.
Pero la discrepancia podría ser real. En realidad, la cuasi identidad de los valores de D sugería que los materiales que estábamos estudiando eran muchísimo más isótropos de lo esperado. Y para muestras que tenían que ser isótropas por el modo en que habían sido preparadas, D(espectral) y D(islas) eran en efecto claramente distintas.
Una explicación alternativa de los distintos valores de D es que la fractura podría ser isótropa pero no autosemejante, con una D que varie con la escala (capítulo 13). Al dar distinto peso a escalas distintas, nuestros dos métodos reflejarían la variación de la D. Y, en efecto, para algunos metales examinados, las islas rebanada o los diagramas espectrales mostraban dos zonas distintas claramente rectas, y para otros metales los diagramas eran más complejos aún.
Para relacionar D con otras características del metal, tomamos probetas de resiliencia de Charpy de acero Maraging de grado 300 y tratadas térmicamente a distintas temperaturas. El diagrama resultante, presentado también al final de la página siguiente, muestra también una relación inequívoca entre la energía de impacto y el valor de D.
Una vez comprobados los hechos, vale la pena reflexionar sobre las posibles causas. Según nuestra opinión, en la fractura interviene una forma atípica de percolación. Recordemos que, al romper en dos una muestra, los huecos que inevitablemente hay alrededor de las inclusiones aumentan de tamaño y se agregan formando hojas que dividen la muestra en varias partes. Si el crecimiento de un hueco fuera independiente de su posición, la percolación sería como en el capítulo 13. En consecuencia, la dimensión de la fractura tomaría algún valor universal independiente del material. En realidad, tan pronto el crecimiento de un hueco local hace que se una a otros formando pequeñas hojas locales, aumentan las tensiones sobre los ligamentos soporte y el hueco crece a un ritmo que depende de su posición. No cabe duda de que esta variabilidad depende de la estructura, y por tanto la D no tiene por qué ser universal.
Formas de las zonas lluviosas y de las nubes (Lovejoy, 1981, Lovejoy y B. B. M., 1983)
La notable relación área-perímetro de Lovejoy (lámina 168) es un incentivo para hacer lo mismo que en el capítulo 28 para el relieve terrestre; a saber, generar mapas fractales de nubes o de zonas lluviosas que ni el ojo ni la medida pudieran distinguir de los mapas meteorológicos.

Un ingrediente vital en el caso de las zonas lluviosas nos lo proporciona el descubrimiento de Lovejoy (1981) de que las discontinuidades en las precipitaciones siguen precisamente la misma distribución de probabilidad hiperbólica que las discontinuidades en los precios de las mercancías según Mandelbrot (1963b, véase el capítulo 37).
Lovejoy y Mandelbrot (1983) se basan en este descubrimiento. Se demuestra que las discontinuidades distribuidas hiperbólicamente concuerdan con la bien sabida observación de que las discontinuidades en las precipitaciones se producen según «frentes» aproximadamente rectilíneos. Para mantener la invariancia por cambio de escala, se introduce una lista conveniente de exponentes, que recuerdan los de la teoría de fenómenos críticos, y más aún los exponentes de turbulencia introducidos por Mandelbrot (1976o). El resultado es sumamente provechoso.
Cambios de escala, fractales y terremotos (Kagan, Knopoff y Andrews)
Recordemos lo que decíamos en el capítulo 28, que el relieve terrestre es un fractal escalante que se puede generar por superposición de «fallas» en bruto. Si uno cree esto, estará preparado para oír que los terremotos, que son cambios dinámicos del relieve, son autosemejantes, esto es, que ninguna escala concreta tiene un papel privilegiado en sus patrones de magnitud-distancia-tiempo, y que su geometría es fractal. Éstos son en verdad los principales mensajes que retiene un estudiante de fractales si lee (como aprovecho aquí para aconsejarle) a Kagan y Knopoff (1978, 1980, 1981) y a Andrews (1980-1981).
Es aleccionador comprobar que Omori descubrió la invariancia por cambio de escala en los terremotos hace ya casi cien años, y sin embargo el grueso del trabajo estadístico sobre terremotos siguió basándose en el postulado de que los sucesos eran poissonianos. Otra vez, poco bien se puede esperar (como argumento en el capítulo 42) cuando una ciencia cede a las presiones sociales que priman la modelización y la teorización mientras desdeñan la «mera» descripción sin «teoría».
Interfases fractales en las pilas de litio (A. Le Méhauté et al.)
Una pila eléctrica tiene que almacenar electricidad en grandes cantidades y descargarla rápidamente. Si todo lo demás es fijo, la capacidad de almacenaje depende del volumen, pero la velocidad de descarga depende de la superficie. Esta propiedad no es desconocida para el estudioso de los fractales (capítulos 12 y 15) y convenció a Alan Le Méhauté de que el compromiso entre capacidad y descarga plantea un problema fractal.
Como una pila cuyas secciones planas sean terágonos de Peano (p. e., lámina 104) no se puede realizar en la práctica, Le Méhauté et al. (1982) estudian teóricamente diseños verosímiles y también examinan pilas reales. La efectividad de la geometría fractal es muy sorprendente.
Racimos de percolación críticos
PERCOLACIÓN EN REDES: EXAMEN DEL MODELO DEL CAPÍTULO 13. El modelo fractal concreto de racimos por contacto en la percolación de Bernouilli, propuesto en el capítulo 13, pide a voces una comprobación experimental. Cosa que ya se ha hecho por fin.
Kapitulnik, Aharony, Deutscher y Stauffer (1983) estudian el número de nudos de un racimo que se encuentran a una distancia menor que R de un origen dado, y recuperan la D ∼ 1,9 correcta. Además, recuperan ξ a partir de la transición entre el dominio fractal y el dominio de homogeneidad.
PERCOLACIÓN EN CAPAS DELGADAS DE ORO Y PLOMO. La percolación de Bernouilli es, por supuesto, un proceso matemático. Hammersley la introdujo con la esperanza de que sirviera para ilustrar y aclarar muchos fenómenos naturales. La aplicabilidad de la geometría fractal de la percolación de Bernouilli fue comprobada con oro no de ley por Voss, Laibowitz y Alessandrini (1982), y con plomo noble por Kapitulnik y Deutscher (1982). Por ejemplo, los que estudiaban el Au preparaban capas delgadas a temperatura ambiente mediante evaporación por haz de electrones sobre ventanas de Si3N4 amorfo de 30 nm de grueso sobre una oblea de Si.
El grosor de la muestra se hacía variar para producir simultáneamente toda una gama de muestras, de las aislantes a las conductoras. Las predicciones del capítulo 13 se satisfacen puntualmente.
Modelos fractales de baja lagunaridad de algunos espacios formales en física (Gefen, Mair, B. B. M. y Aharoni, 1983)
En mecánica estadística es útil postular espacios de dimensión fraccionaria. Para los matemáticos estos espacios son muy desconcertantes, pues su construcción no está en ninguna parte, y tampoco se ha demostrado su existencia ni su unicidad. Sin embargo, se obtienen resultados físicos útiles suponiendo que dichos espacios existen y poseen algunas propiedades importantes y deseables: son invariantes por traslación, y las integrales y relaciones de recurrencia de tumo se pueden obtener por prolongación analítica formal de los resultados para espacios euclídeos.
Estos espacios dejan perplejo al estudioso de los fractales. De una parte, existen muchos espacios alternativos fractalmente interpolados, con lo que la interpolación habría sido indeterminada. De otra, los fractales que Gefen, Mandelbrot y Aharoni (1980) aplican a la física no son invariantes por traslación. En lo que se refiere a esto, los fractales podrían parecer inferiores a los espacios fraccionarios postulados.
Una crítica similar levantada por mi primer modelo de la distribución de galaxias sugirió una respuesta. Aunque es imposible que un fractal sea exactamente invariante por traslación, los capítulos 34 y 35 demuestran que se puede llegar tan cerca como se quiera de esta propiedad dando a la lagunaridad un valor suficientemente bajo.
A la luz de esto, Gefen, Meir, Mandelbrot y Aharoni (1983) consideran una cierta sucesión de alfombras de Sierpinski (capitulo 14) cuyas lagunaridades tienden a 0. Se calculan ciertas propiedades físicas y se demuestra que sus límites para lagunaridad nula son idénticos a los de las propiedades correspondientes de los espacios fraccionarios postulados.
El tamiz de Sierpinski: juguete de los físicos
A los físicos les gustan tanto los modelos manejables que cualquier construcción que prometa cálculos sin necesidad de recurrir a aproximaciones atraerá la atención de muchos.
La más importante de entre las figuras ramificadas examinadas en el capítulo 14 es la alfombra de Sierpinski, pero es difícil trabajar con ella.
En cambio, el tamiz de Sierpinski es fácil de manipular. Lo usan de manera divertida y provechosa Stephen (1981), Rammal y Toulouse (1982, 1983) y Alexander y Orbach (1982).
▯ Contra mi costumbre, acuñé la expresión «gasket» (junta) sin un equivalente francés. Los autores de un diccionario matemático no sabían que yo tenía en mente la parte que impide las fugas en los motores, y un diccionario corriente les condujo a barcos y cuerdas, y por tanto a hádeme (badema) o garcette (garceta). ¡Como la palabra no correspondía, se redefinió para ser aplicada al complemento de lo que yo había querido decir! Yo prefiero tamis (tamiz). ▮
Autómatas celulares y fractales
Preparé el ejemplo de la pág. 460 para mostrar que el orden global puede ser el resultado de fuerzas que actúan solamente entre vecinos. Alguien pronto indicó que este ejemplo implica un «autómata celular» según John von Neumann (Burks 1970). Ullam había demostrado (Burks 1970) que el resultado de tales autómatas puede ser muy enrevesado y parecer aleatorio. Willson (1982), Wolfram (1983) y Vichniac (1983) observan que este resultado puede, de hecho, ser fractal.
Iteración de z → z2 − μ en el plano complejo: nuevos resultados y demostraciones
Mandelbrot (1983p) contiene muchas ilustraciones para las que faltó espacio en el capítulo 19, e informa de nuevas observaciones.
Dos observaciones importantes del capítulo 19 se han confirmado ya matemáticamente.
Douady y Hubbard (1982), y Douady (1983), demuestran que el conjunto cerrado M es en efecto conexo. Su método consiste en aplicar el exterior de M en el de un círculo.
Ruelle (1982) demuestra que la dimensión de Hausdorff de un dragón de Julia es una función analítica del parámetro μ.
Las aplicaciones cuadráticas en los cuaterniones
En el capítulo 19 se establecía que las propiedades de la aplicación z → z2 − μ para z reales se entienden mejor como casos especiales de sus propiedades para z y μ complejos, y que la iteración para valores de z complejos produce unos gráficos apasionantes e inesperados. Era natural, pues, buscar nuevas ideas y nueva belleza en una nueva generalización de z. Norton sugirió que el siguiente escalón natural son los cuaterniones de Hamilton. Introducidos en 1847, los cuaterniones son un concepto conocido en matemáticas y física, si bien se han mantenido siempre en un papel marginal. En el contexto de la iteración, no obstante, los cuaterniones han resultado sumamente provechosos tanto en el aspecto matemático como en el aspecto estético, como pronto se verá detalladamente en próximos artículos de Norton y yo mismo.
Una objeción que se hace a menudo contra los cuaterniones es que, mientras los números complejos sumergen un espacio con E = 1 en otro con E = 2, que puede ser representado, los cuaterniones implican un salto a un espacio con E = 4, que no puede representarse. Otra objeción es que el producto de cuaterniones no es conmutativo: en particular, las aplicaciones z → λz(1 − z), z → z2 − μ, z → μz2 − 1, y z → μαz2μ1−α son distintas si z es un cauternión.
Para ilustrar las interconexiones topológicas de los repulsores fractales de la aplicación cuadrática en los cuaterniones, Norton (1982) desarrolla nuevas técnicas infográficas. Los conjuntos de todos los cuaterniones cuyas iteraciones no acaban en el infinito se examinaron por medio de sus secciones tridimensionales. Sus secciones según planos complejos son, a su vez, los dragones fractales del capítulo 19.
La no conmutatividad del producto de cuaterniones ha resultado ser una ventaja fascinante y totalmente inesperada. Para explicarlo, considérese la lámina C6. Pregunta: los dominios amarillo oscuro, en su totalidad o en parte, ¿están interconectados en el espacio de cuaterniones? Respuesta: en general, cada forma de escribir z → z2 − μ o z → λz(1 − z) (antes de pasar al espacio de los cuaterniones) induce unos enlaces totalmente distintos entre los dominios amarillo oscuro. De ahí que haga falta más información para concretar las interconexiones topológicas.
Como ejemplo que no induce a confusión, examínese la lámina 604, que es una adaptación de Norton (1982) e ilustra un caso simple con un ciclo cuaternario. Cada segmento principal del dragón obtenido por sección compleja está sumergido en un segmento principal de la figura espacial. En este caso, las secciones espaciales principales son cuasiinvariantes por rotación, y están rodeadas por multitud de cinturones poco ajustados que conectan las secciones secundarias. La lámina II muestra un fractal espacial distinto obtenido más o menos del mismo modo. Stein (1983) reproduce más ilustraciones.
Universalidad y caos: z → λ(z − 1/z) y otras transformaciones
Un contemporáneo de Fatou y Julia, S. Lattés, escogió una razón de cuarto orden entre polinomios cuyas iteraciones son «caóticas» en todo el plano, esto es, no atraídas por ningún conjunto más pequeño. Este ejemplo nos incita a buscar comportamientos caóticos en transformaciones de órdenes inferiores. Un segundo tema a tratar en esta sección son las clases de universalidad de las formas de las islas en los λ-mapas.
***
λ-MAPA DE z → λ(z − 1/z). En el caso especial λ = 1/2, y = −iz sigue la ley y − 1/2(y + 1/y), que se obtiene de la aplicación del método de Newton en la búsqueda de las raíces de z2 − 1. Nótese que podemos escribir z = cotgθ, con lo que 1/2(z − 1/z) se convierte en (cos2θ − sin2θ)/2cosθsinθ = cotg2θ. Así pues, z → 1/2(z − 1/z) sólo es un modo curioso de escribir θ → 2θ. Para estudiar otros valores de λ se dibujó un mapa análogo al de las láminas 268 y 269, parte del cual se muestra en la lámina X.
Observamos una forma muy interesante de «universalidad»: las «moléculas isla» de la lámina X tienen precisamente la misma forma que en el caso de la transformación cuadrática. Así pues, las láminas X y 188-189 se construyen con los mismos «bloques elementales». En el disco abierto |λ| > 1, la iteración de z → λ(z − 1/z) tiende a infinito excepto para un polvo de puntos z. En el disco blanco |λ + i/2| < 1/2, la iteración tiene dos puntos límite. Cuando λ cae en una de las «puntas» de la «corona» negra, hay un ciclo límite de tamaño superior a 2, aunque no mucho mayor. En cuanto a los valores de λ del interior de la corona del λ-mapa, dan lugar a movimiento caótico.
▯ Al realizar el cálculo se usaron las hipótesis simplificadoras siguientes. A) Cuando λ conduce a un ciclo muy grande, pertenece a un átomo tan pequeño que no vale la pena buscarlo. B) Todos los ciclos convenientemente pequeños caen «cerca» de z = 0. Así pues, una órbita que se «aleje» de z = 0 será presumiblemente caótica. La aproximación no tiene una justificación concreta, pero el λ-mapa que genera está formado por partes que nos resultan familiares, por lo que el método parece razonable. ▮
CONJUNTOS DE JULIA DE λ(z − 1/z). Cuando |λ| > 1, el infinito es un punto atractor, y el conjunto de Julia es, como en el capítulo 19, la frontera del conjunto de los puntos z que no convergen hacia infinito. Un ejemplo de conjunto de Julia definido como la frontera de las cuencas de atracción de λ(z − 1/z) se encuentra dibujada en la lámina VIII, frente al prólogo.
CLASES DE «UNIVERSALIDAD» DE UN λ-MAPA. En muchos otros λ-mapas, uno se encuentra las mismas «moléculas isla» que para z2 − μ, excepto por el hecho de que determinados condicionantes específicos pueden dar lugar a un «continente» atípico.
Además, los λ-mapas de z → zm − λ también se dividen en un continente y unas islas. Sin embargo, cada m induce una forma muy característica de los átomos y de las moléculas isla.
Cuando el comportamiento local de z → f(z) es el mismo cerca de todos los z críticos donde f(z) = 0, la forma de las islas está localmente determinada. Cuando f(z) se comporta de modo distinto cerca de distintos z críticos, en el λ-mapa interviene más de un tipo «universal» de bloque elemental. Buscamos una «tabla de Mendeleyev» para este problema.