Capítulo 3

Pensar el determinismo

El determinismo parece robarnos nuestras oportunidades, sellar nuestros destinos en una red global de cadenas causales que se remontan indefectiblemente al pasado. Todos nosotros pasamos buena parte de nuestro tiempo pensando cómo podrían irnos las cosas hoy o el año que viene, o cómo podrían habernos ido si hubiera pasado esto o lo otro. En otras palabras, parecemos presuponer que nuestro mundo no es determinista.

MUNDOS POSIBLES

En nuestras deliberaciones distinguimos sin problemas entre cosas que podrían haber ocurrido y cosas que no podrían haber ocurrido, cosas que no ocurrirán en ningún caso y cosas que podrían ocurrir perfectamente, si así lo queremos. Tal como dicen los filósofos, con frecuencia imaginamos mundos posibles.

En el Mundo A, los disparos de Oswald no hicieron blanco en Kennedy sino en LBJ, lo que introdujo millones de cambios en la historia subsiguiente.

Y usamos estos productos de nuestra imaginación para guiar nuestras elecciones, aunque sólo un filósofo utilizaría fórmulas como las siguientes para expresarlo:

Por muy familiar que nos resulte este ejercicio de imaginación, a menudo nos juega malas pasadas cuando tratamos de pensar rigurosamente el determinismo vía causalidad. En el presente capítulo sostendré que el determinismo es enteramente compatible con las presuposiciones que gobiernan nuestra manera de pensar acerca de lo que es posible. La aparente incompatibilidad es, lisa y llanamente, una ilusión cognitiva. Tal conflicto no existe. Tanto en nuestras reflexiones cotidianas sobre lo que vamos a hacer a continuación como en nuestro pensamiento científico más riguroso en relación con las causas de los fenómenos, empleamos conceptos de necesidad, posibilidad y causalidad que son estrictamente neutrales respecto a la cuestión de si la verdad está del lado del determinismo o del indeterminismo. Si estoy en lo cierto, más de un eminente filósofo está equivocado, por lo que cabe esperar bastante artillería pesada (aunque no será más que un rumor en la distancia, porque no pienso presentarles batalla en este libro). Christopher Taylor me ha ayudado mucho a clarificar mi pensamiento en relación con este tema y me ha mostrado el modo de lanzar una campaña más profunda y radical en apoyo de mis tesis iniciales, y el artículo que hemos escrito en colaboración (Taylor y Dennett, 2001) aporta mayores detalles técnicos de los necesarios aquí. Voy a presentar una versión más asequible del argumento, y subrayaré las ideas principales para que los no-filósofos puedan al menos ver dónde están los puntos en disputa y cómo proponemos resolverlos, y dejaré a un lado casi todas las fórmulas lógicas. Los filósofos pueden consultar la versión completa, por supuesto, para ver si hemos atado realmente los cabos sueltos y cubierto las lagunas que pasamos por alto en esta exposición. Y como lo que sigue se debe en gran medida a Taylor, habrá un cambio temporal de los pronombres de autor al «nosotros».

Nuestra tarea consiste, pues, en clarificar los conceptos cotidianos de posibilidad, necesidad y causalidad que forman parte de nuestras reflexiones, proyectos, preocupaciones y fantasías, y que nos ayudan a enfrentarnos al mundo y a sus desafíos. Podemos hacernos la tarea más fácil si restringimos nuestras reflexiones sobre los mundos posibles a los universos democriteanos de Quine. Es conocido el escepticismo de Quine hacia cualquier intento de hablar seriamente sobre la posibilidad y la necesidad —el tema de la lógica modal—, y sus universos democriteanos están diseñados para proporcionar la base de operaciones más manejable y ordenada posible para explorar estas cuestiones. Como se recordará del capítulo 2, el Vasto número de universos democriteanos consiste en una colección de puntos-átomos cuyas travectorias a través del espacio y el tiempo vienen dadas por sus coordenadas tetradimensionales (x, y, z, t). Una completa descripción de estado del mundo en un tiempo t es simplemente el catálogo exhaustivo de las direcciones ocupadas (x, y, z) en t. Llamamos al conjunto de todos los mundos lógicamente posibles la Biblioteca de Demócrito, y podemos llamar al subconjunto que contiene sólo los mundos físicamente posibles Φ (phi). Por supuesto, no conocemos aún todas sus leyes físicas, y no podemos saber con certeza si son deterministas o indeterministas, pero podemos pretender que los conocemos. (Ahora que disponemos del mundo Vida de Conway, siempre podemos contrastar nuestras intuiciones dentro del mundo Vida de Conway, donde sí conocemos perfectamente las leyes físicas y del que sabemos que es determinista).

Dado un mundo posible, tenemos muchas maneras de realizar aserciones sobre él. Tal como vimos en el caso del mundo simplificado de Vida, lo más natural será saltar por encima del nivel atómico y describir el mundo en términos de pedazos más grandes. Del mismo modo que podemos seguir los pasos de un planeador particular desde su nacimiento hasta su muerte sobre el plano de Vida, podemos seguir el rastro también de las trayectorias en el espacio y el tiempo de «hipersólidos compactos» (objetos tetradimensionales) como las estrellas, los planetas, los seres vivos y demás parafernalia cotidiana (objetos familiares que aparecen en la vida humana). Una famosa imagen de Platón dice que debemos cortar la naturaleza siguiendo sus propias articulaciones, y las articulaciones por las que nosotros comenzamos —literalmente, donde una cosa termina y comienza la siguiente— son aquellos rasgos que resultan lo bastante prominentes y estables para nosotros como para que podamos identificarlos (y seguirles la pista, y volverlos a reconocer) como objetos macroscópicos. Tal como vimos en el mundo Vida, la «física» subyacente (la regla de transición entre estados) dicta qué configuraciones son lo bastante resistentes a lo largo del tiempo como para constituir regularidades macroscópicas (no microscópicas), las cuales sirven de punto de apoyo para nuestra imaginación a la hora de pensar en causas y posibilidades. Podemos describir tales configuraciones de tamaño medio por el método familiar de los predicados informales aplicables a dichas entidades, tales como (en orden de menos a más dudosos) «tiene una longitud de un metro», «es rojo», «es humano», «cree que la nieve es blanca». Estos predicados informales plantean una infinidad de problemas relacionados con la vaguedad, la subjetividad y la intencionalidad, y son estos problemas —los problemas que surgen cuando saltamos del nivel básico de los átomos y el espacio a categorías ontológicas superiores— los que alimentaron el escepticismo de Quine acerca de la posibilidad de hablar con sentido sobre la posibilidad y la necesidad. Pensamos que si hacemos explícito este paso y si concentramos todos los puntos oscuros en el desplazamiento del nivel físico atómico al nivel cotidiano, podemos mantener dichos problemas aislados y evitar que pongan en peligro nuestro planteamiento básico. Si procedemos, pues, con cautela y suponemos que podemos apoyarnos tentativamente en los predicados informales, no nos creará muchos problemas de conciencia formar proposiciones como

(1) Hay algo que es humano

y determinar si son aplicables a diferentes mundos posibles. No hay seres humanos en ningún mundo Vida, puesto que los seres humanos son seres tridimensionales, pero en algunos de ellos podría haber entidades bidimensionales prodigiosamente parecidas a los seres humanos. Llevando la cuestión a un terreno más cercano: ¿cabría considerar que hay algo humano en un mundo posible donde las criaturas bípedas parlantes, tecnológicas y culturales tuvieran plumas en lugar de pelo en la cabeza y descendieran de las avestruces? ¿O tal vez consideraríamos que tal criatura es una persona no humana? ¿Es «humano» una categoría biológica o, tal como sugiere la palabra «humanidades», una categoría sociocultural y política? Es posible que haya opiniones divergentes respecto a la interpretación del predicado informal «humano». A menudo encontraremos términos fronterizos sobre los que nos resultará difícil llegar a veredictos incontestables.

Merecen una atención especial los predicados de identificación de la forma «es Sócrates». «Es Sócrates», cabe suponer, es aplicable a cualquier entidad de cualquier mundo posible que comparta suficientes rasgos con el conocido habitante de nuestro mundo como para que estemos dispuestos a considerarlo la misma persona. En nuestro mundo, por supuesto, «es Sócrates» se aplica a una única entidad; en otros mundos, puede ser que no haya tal ser, o que haya uno, o incluso cabe concebir que haya dos o más seres a quienes el predicado se aplique con la misma validez. Igual que sucede con otros predicados informales, los predicados de identificación adolecen de vaguedad y subjetividad, pero es posible aislar y manejar estas fastidiosas cuestiones cuando se plantean en casos particulares^[1].

Ahora ya estamos en condiciones de definir los conceptos fundamentales que precisamos —necesidad, posibilidad y causalidad— en términos de mundos posibles. Una proposición del tipo

(2) Necesariamente, Sócrates es mortal

puede traducirse como

(3) En todo mundo (¿físicamente?) posible t, la proposición «Si algo es Sócrates, entonces es mortal*» es verdadera.

En otras palabras, cuando nos ponemos a examinar todas las posibilidades que somos capaces de contemplar, descubrimos que no hay ni un solo mundo posible en el que haya un Sócrates inmortal. Eso es lo que significa decir que Sócrates es necesariamente mortal. En este caso «es Sócrates» y «es mortal» son predicados informales del tipo que acabamos de ver. Sin duda, decidir si la proposición es verdadera plantea muchos problemas, que proceden en gran medida del carácter inevitablemente ambiguo de los predicados: ¿es un candidato a Sócrates que sea mortal pero que pueda volar como Superman menos merecedor del predicado «es Sócrates» que un candidato a Sócrates incapaz de elevarse del suelo pero que milagrosamente no se vea afectado por su copa de cicuta? ¿Quién puede resolver la cuestión? Es más, todavía no hemos decidido si el conjunto de mundos posibles entre los que podría estar /debería ser la Biblioteca de Demócrito al completo (todos los mundos), o Φ (los mundos físicamente posibles), o incluso algún conjunto X más restringido. La lógica sola no puede resolver esta cuestión, pero el lenguaje lógico sí nos ayuda a poner de relieve tales cuestiones y señalar con mayor precisión el tipo de vaguedad al que nos enfrentamos.

Ahora podemos definir la posibilidad. Lo posible es todo aquello que no es necesariamente falso, de modo que

(4)Es posible que Sócrates hubiera tenido el pelo rojo

significa

(5)Existe (al menos un) mundo posible t en el que la proposición «Hay algo que es Sócrates y que tiene el pelo rojo» es verdadera.

Una vez más, debemos decidir si estamos hablando de posibilidad física o lógica. Tal hipótesis es físicamente posible si existe un mundo dentro del conjunto O donde hay un Sócrates pelirrojo. En caso contrario, queda descartado desde el punto de vista físico, por más comunes que sean los Sócrates pelirrojos en los mundos lógicamente posibles pero físicamente imposibles.

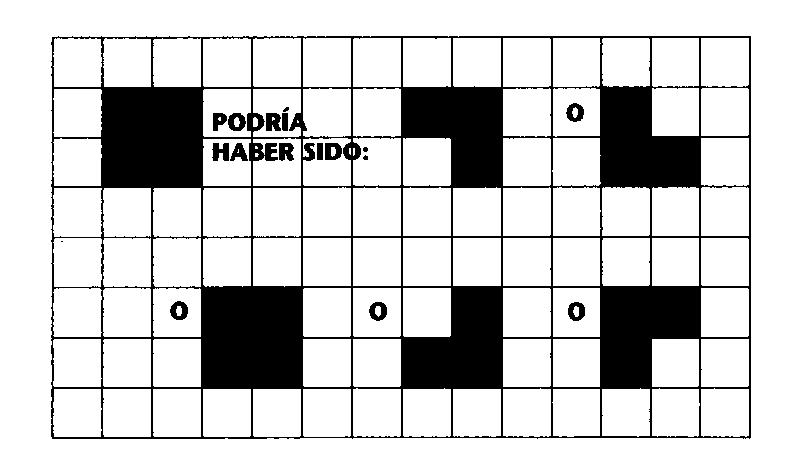
Ahora ya estamos en condiciones de clarificar la definición del determinismo ofrecida al comienzo del capítulo 2: en cada momento dado hay exactamente un único futuro físicamente posible. Decir que el determinismo es verdadero es decir que nuestro mundo forma parte de un subconjunto de mundos que poseen la interesante propiedad siguiente: no hay dos mundos que comiencen exactamente igual (si comienzan siendo iguales, siguen siendo iguales para siempre: no son mundos diferentes en ningún sentido), y siempre que dos mundos compartan cualquiera de sus descripciones de estado, compartirán también todas las descripciones de estado posteriores a esta. El mundo Vida ilustra claramente esta idea. Sólo es determinista en una dirección; en general no se puede extrapolar el instante previo, mientras que siempre se puede extrapolar el instante siguiente. Por ejemplo, un plano Vida que contenga una naturaleza muerta cuadrada de cuatro píxels en el tiempo t (véase la figura 3.1) tiene un pasado ambiguo. El próximo estado (y el siguiente, y el siguiente) es exactamente el mismo —a menos que irrumpa algo—, pero el estado previo podría haber sido cualquiera de estos cinco (o una cantidad indefinida de configuraciones con píxels que se apagan a mayor distancia).

FIGURA 3.1. Naturaleza muerta y lo que podría haber sido.

En consecuencia, si el determinismo —así definido— es verdadero, podemos concluir que incluso aunque muchos pasados, diferentes pudieran haber llevado exactamente al estado presente, nuestro futuro está «fijado» por nuestro estado presente. Desde esta perspectiva, el determinismo parece ser exactamente lo opuesto a nuestro punto de vista corriente, según el cual el pasado está «fijado» y el futuro está «abierto». Podríamos definir una versión más fuerte (y no estándar) del determinismo que excluya tal ambigüedad en el pasado, y descarte lo que llamo hechos históricos inertes, es decir, hechos sobre el pasado que, por lo que respecta a nuestras leyes de la física, podrían haber sido de una manera o de otra sin dejar ningún efecto subsiguiente. La capacidad de los cosmólogos de «rebobinar la película» y calcular de este modo los hechos relativos a los primeros momentos posteriores al Big Bang muestra que, en relación con ciertas propiedades, podemos leer el pasado a partir del presente con sorprendente precisión y alcance, pero esto no sirve en absoluto para demostrar que no haya hechos históricos inertes. El hecho de que parte del oro que tengo en los dientes perteneciera una vez a Julio César —o su negación, el hecho de que no le perteneció jamás— es un ejemplo plausible de un hecho histórico inerte. No hay duda de que es prácticamente inerte. Como se da el caso de que no mantenemos ningún registro de la cadena de propietarios de los fragmentos de oro del mismo modo que lo hacemos, por ejemplo, con las pinturas de Rembrandt, es prácticamente inimaginable que ninguna investigación del estado presente de la distribución de átomos del mundo pudiera permitir descubrir cuál de esas dos proposiciones es la verdadera, aunque seguramente una de ellas lo es.

Y cuando miramos hacia el futuro, resulta casi imposible decir cuándo un hecho histórico inerte hasta el momento vendrá a «marcar una diferencia» en lo que pase a continuación. Supongamos que el determinismo es verdadero y que conocemos a la perfección las leyes de la física, tal como las conoce el demonio de Laplace. Sin embargo, a menos que tengamos un conocimiento perfecto y completo de una descripción de estado del universo, no seremos capaces de decir cuál es el mundo en el que vivimos dentro del Vasto número de universos posibles con diferencias microscópicas que forman parte del conjunto O. Es precisamente porque nuestro conocimiento es inevitablemente incompleto por lo que es un recurso tan bueno pensar en términos de mundos posibles.

Una de las aplicaciones más útiles del modelo de los mundos posibles consiste en usarlo para la interpretación de proposiciones hipotéticas, como

(6)Si Greenspan hubiera llorado en el Congreso, el mercado se habría desplomado

y

(7)Si le hubiéramos puesto la zancadilla a Arthur, habría caído.

Siguiendo a David Lewis (1973), vemos que la proposición (7) es (aproximadamente) verdadera, y que si y sólo si en cualquier mundo aproximadamente parecido al nuestro se cumpliera el antecedente, lo mismo sucedería con el consecuente. En otras palabras,

(8)Tomemos el conjunto X de mundos parecidos a nuestro mundo presente: en todos los mundos de este conjunto se verifica que si le ponemos la zancadilla a Arthur, también se verifica que Arthur cae.

A veces, cuando hacemos afirmaciones hipotéticas de este tipo, tenemos tendencia a comprobarlas por el procedimiento de imaginar unas cuantas variaciones. («Veamos: supongamos que Arthur llevara una camisa roja, ¿le hubiera impedido eso caer? Supongamos que la radio estuviera apagada, supongamos que la calefacción estuviera encendida, supongamos que llevara rodilleras… No, hubiera caído igualmente. Supongamos que la habitación estuviera llena de bolsas de aire hinchadas o que el edificio entero estuviera en caída libre a gravedad cero; eso hubiera impedido que cayera… Pero eso es demasiado distinto de nuestro mundo como para que pueda valer»). Y en experimentos controlados, no nos limitamos sólo a imaginar, sino que investigamos realmente estas variaciones. Alteramos metódicamente las condiciones y vemos cuáles son los cambios que se verifican. Tal como veremos, esto no es un procedimiento tan evidente como podría parecer a primera vista.

Con independencia de si realizamos algún experimento práctico o mental, la presunción que hay detrás de la aserción hipotética es que hay un conjunto de mundos X parecidos al nuestro donde se cumple esta regularidad. Y, en general, podemos expresar la interpretación de un hecho hipotético como (6) o (7) del siguiente modo:

(9)En el conjunto de mundos X, A = C,

donde A es el antecedente y C el consecuente.

Pero ¿cuán parecidos a nuestro mundo deben ser los mundos del conjunto X? No siempre es fácil en estos casos escoger un valor óptimo para X, pero podemos seguir las siguientes directrices:

En proposiciones como (6) y (7), X debería:

contener mundos en los que A se cumple, no-A se cumple, C se cumple, y no-C se cumple,

contener mundos parecidos al mundo presente en todo lo demás (en la medida en que lo permita la cláusula precedente).

De modo que para analizar (7), debemos escoger un conjunto X que contenga mundos en los cuales le ponemos la zancadilla a Arthur, mundos en los cuales nos abstenemos de hacerlo, mundos en los que Arthur cae, y mundos en los que sigue de pie. (Nótese que para reunir estos mundos empleamos nuestras ontologías de nivel superior. No graduamos el parecido de los mundos calculando cuántos vóxels están llenos de hierro o de oro; para determinar qué mundos queremos incluir usamos los predicados informales, a pesar de la imprecisión y la vaguedad que comportan. Tal como veremos, se da el caso que muchos de los dilemas que surgen a propósito de la causalidad y la posibilidad dependen de cómo escojamos definir X, el conjunto de referencia de mundos posibles vecinos).

CAUSALIDAD

Por último, ¿qué pasa con la causalidad? Algunos filósofos esperan descubrir algún día una descripción «verdadera» de la causalidad, pero dada la naturaleza informal, vaga y a menudo contradictoria del término, pensamos que un objetivo más realista sería desarrollar un análogo (o análogos) formal que nos ayudara a pensar más claramente en el mundo. Nuestras intuiciones previas sobre la causalidad nos servirán de guía, pero deberíamos desconfiar siempre de que alguien pretenda hacer pasar un argumento informal por una «prueba» capaz de validar o desacreditar doctrinas particulares sobre la causalidad^[2]. Cuando decimos

(10) La zancadilla que Bill le puso a Arthur hizo que este cayera

hay una serie de factores que parecen venir en apoyo de nuestra aserción. En un orden aproximado de importancia, la lista sería la siguiente:

Necesidad causal: nuestro asentimiento a la proposición (10) depende de nuestra convicción de que si Bill no le hubiera puesto la zancadilla a Arthur, este no hubiera caído. Aplicando la interpretación de las hipótesis que acabamos de proponer, escogemos como conjunto X una colección de mundos parecidos al nuestro que incluye mundos en los que (i) Bill le pone la zancadilla a Arthur; mundos en los que (ii) Bill no le pone la zancadilla; mundos en los que (iii) Arthur cae; y mundos en los que (iv) Arthur no cae. Y nos aseguramos de que en todos los mundos del conjunto X donde Arthur cae, Bill le puso la zancadilla.

Para comprender mejor estas condiciones, veamos cómo encajan en algunos casos de prueba, algunos de los cuales están tomados de Lewis (2000). Primero consideremos el caso de un tirador experto que apunta hacia una víctima situada a cierta distancia. Supongamos que un examen del historial del tirador muestra que la probabilidad de que acierte en este caso es de 0,1; por si alguien piensa que puede marcar alguna diferencia, podemos imaginar que el resultado viene determinado en parte también por los eventos cuánticos irreduciblemente azarosos que puedan producirse en el aire que los separa, o en el cerebro del tirador. Supongamos que en el caso presente la bala da efectivamente en la víctima y la mata. En tal caso no dudamos en afirmar que las acciones del tirador fueron la causa de la muerte de la víctima, a pesar de su insuficiencia causal. De acuerdo con eso, parece que, al menos en casos de este tipo, la gente valora la necesidad por encima de la suficiencia al hacer juicios causales.

Sin embargo, la suficiencia sigue conservando cierta relevancia. Supongamos que tanto el rey como el alcalde están interesados en el destino de cierto joven disidente; se da el caso de que ambos dictan órdenes de exilio contra él; el disidente va al exilio. Este es un caso típico de sobredeterminación. Sea A1 «el rey dicta una orden de exilio», y A2 «el alcalde dicta una orden de exilio», y C «el disidente va al exilio». Dentro de este escenario, ni A1 ni A2 son individualmente necesarios para C: por ejemplo, si el rey no hubiera dictado ninguna orden, el disidente hubiera ido al exilio por orden del alcalde, y viceversa. Sin embargo, la suficiencia viene al rescate y nos permite escoger entre los dos. En este caso A2 no logra pasar la prueba: resulta fácil imaginar un universo donde el alcalde dicta su decreto y, sin embargo, el disidente logra sustraerse a él (sólo hay que cambiar la orden del rey por su perdón). La orden del rey, en cambio, es verdaderamente efectiva, por más pequeños cambios que introduzcamos en el universo (incluidos cambios en las órdenes del alcalde), la orden del rey tiene como resultado el exilio del disidente. De acuerdo con esto, podemos decir que A1 es la «causa real» (si sentimos la necesidad de satisfacer nuestro impulso en este sentido).

Por último, consideremos el caso de Billy y Susie. Ambos niños están jugando a tirar piedras a una botella de cristal, y se da el caso de que la piedra de Susie va un poco más rápida, llega antes a la botella y la rompe. La piedra de Billy llega exactamente al sitio donde estaba antes la botella, pero al hacerlo un momento más tarde no encuentra sino cascos rotos por el aire. Si debemos escoger entre A1 («Susie lanza la piedra S») y A2 («Billy lanza la piedra B»), votamos por A, como causa de C («La botella se rompe»), a pesar del hecho de que ninguna de las proposiciones es necesaria (si Susie no hubiera lanzado su piedra, la botella se habría roto igualmente por la acción de Billy, y viceversa) y ambas son suficientes (el tiro de Billy es suficiente para producir la ruptura de la botella, haga lo que haga su compañera de juegos, y lo mismo sucede en el caso de Susie). ¿Por qué? La noción general de la prioridad temporal (introducida antes en relación con la posibilidad de distinguir la causa del efecto) nos parece una condición determinante en este caso. Igual como sucede en las disputas de prioridad en el campo de la ciencia, el arte y el deporte, parecemos conceder un reconocimiento especial al que aporta una innovación primero, y como la piedra S llegó a las inmediaciones de la botella antes que la piedra B, le damos el crédito a Susie. Por otro lado, está claro que, aunque la botella se habría roto igualmente sin el lanzamiento de Susie, el suceso de la ruptura hubiera sido significativamente diferente, al ocurrir en un momento posterior y con una piedra diferente que lanzaría cascos rotos en direcciones diferentes. (Nótese que este problema surge precisamente porque hemos dado el salto a la ontología cotidiana de botellas y rupturas, y sus fastidiosas condiciones de identidad. El problema aquí es lo que debe valer como el «mismo efecto», no cualquier incertidumbre subyacente en relación con lo ocurrido).

Podemos diseñar el conjunto X para que refleje este hecho (de acuerdo con las directrices): deberá contener mundos en los que (1) la botella no se rompe o (2) se rompe de un modo muy parecido a como se rompe en la realidad. Entonces, para todo mundo de X, se verifica que

C = A1

siempre que la botella se rompe en X, encontramos que Susie ha lanzado primero su piedra. Por otro lado,

C=*A2

puede ser perfectamente falso en X; X puede contener ciertamente mundos en los que la botella se rompe pero Bill no llega a tirar su piedra. En resumen, si escogemos bien el conjunto X, A1 es «más necesario» que A2. La vaguedad de X, aunque a veces resulte fastidiosa, puede servir también para superar algunos puntos muertos.

Eso no significa que los puntos muertos se puedan superar siempre. Debemos contemplar con ecuanimidad la posibilidad de que a veces las circunstancias impidan señalar una única «causa real» para un evento, por más que la busquemos. Un caso paradigmático es el clásico dilema de las escuelas de derecho:

Todo el mundo en los puestos adelantados de la Legión Extranjera francesa odia a Fred y quiere verlo muerto. Durante la noche previa a una expedición de Fred por el desierto, Tom le envenena el agua de la cantimplora. Luego Dick, sin conocer la intervención de Tom, vierte el agua (envenenada) y la sustituye por arena. Finalmente, viene Harry y agujerea la cantimplora, de modo que esta se va vaciando de «agua». Más tarde, Fred se levanta y se pone en marcha, provisto de su cantimplora. No descubrirá que su cantimplora está casi vacía hasta que sea demasiado tarde, pero además encontrará que lo que queda en ella es arena, no agua, ni siquiera agua envenenada. Como consecuencia, Fred muere de sed. ¿Quién fue el causante de su muerte^[3]?

Muchos sentirán la tentación de insistir en que debe haber una respuesta para esta pregunta, y para otras parecidas. Ciertamente podemos ponemos de acuerdo para legislar una respuesta si sentimos la necesidad de hacerlo, y algunas propuestas legislativas serán sin duda más atractivas, más intuitivas, que otras, pero no queda claro que haya ningún hecho —relativo a cómo es el mundo, o a cuál es el auténtico sentido de nuestras palabras, o incluso a cuál debería ser el sentido de nuestras palabras— que pueda resolver la cuestión.

EL TIRO AL HOYO DE AUSTIN

Ahora que tenemos una mejor comprensión de los mundos posibles, podemos exponer tres grandes confusiones relativas a la posibilidad y la causalidad que han oscurecido siempre la búsqueda de una teoría sobre la libertad. En primer lugar, está el miedo a que el determinismo limite nuestras posibilidades. Podemos comprender el aparente crédito que merece esta idea si consideramos el famoso ejemplo propuesto hace muchos años por John Austin:

Consideremos el caso de que fallo un golpe muy corto y me enfado conmigo mismo porque podría haberlo embocado. Eso no significa que debería haberlo embocado si lo hubiera intentado: lo intenté, y fallé. Tampoco significa que debería haberlo embocado si las condiciones hubieran sido distintas de las que fueron: por supuesto que podrían haberlo sido, pero estoy hablando de las condiciones exactamente tal como se dieron, y afirmo que podría haberlo embocado. Ahí está el problema. «¿Puedo embocarlo esta vez?» tampoco significa que vaya a embocarlo esta vez si lo intento o si cualquier otra cosa; pues puede ser que lo intente y falle, y sin embargo eso no me convencería de que no podría haberlo hecho; los experimentos posteriores no harán sino confirmar mi creencia de que podría haberlo hecho aquella vez, aunque no lo hiciera (Austin, 1961, pág. 166).

Austin no embocó su golpe. ¿Acaso lo hubiera conseguido, si el determinismo fuera verdadero? Una interpretación del caso en términos de mundos posibles pone al descubierto el paso en falso del razonamiento de Austin. Primero, supongamos que el determinismo es verdadero y que Austin falla; sea H la proposición «Austin emboca el golpe». Debemos escoger ahora el conjunto X de mundos posibles relevantes que debemos sondear para ver si podría haberlo conseguido. Supongamos que escogemos como X el conjunto de mundos físicamente posibles que son idénticos al mundo presente en algún tiempo to previo al golpe. Como el determinismo afirma que en cada momento hay exactamente un solo futuro físicamente posible, dicho conjunto de mundos tiene un solo miembro, el mundo presente, el mundo donde Austin falla. De modo que, si escogemos el conjunto X siguiendo este criterio, el resultado que obtenemos es que H no es cierto para ningún mundo de X. Así pues, de acuerdo con esta interpretación, no era posible que Austin embocara el golpe.

Por supuesto, este método para escoger X (llamémoslo el método estrecho) es sólo uno de los muchos posibles. Supongamos que admitiéramos también mundos que contuvieran diferencias microscópicas respecto al mundo presente en to podría muy bien ser que ahora hubiéramos incluido mundos en los que Austin emboca el golpe, aunque sean deterministas. Este es, después de todo, el resultado al que han llegado los recientes trabajos en relación con el caos: muchos fenómenos de interés para nosotros pueden cambiar radicalmente con sólo pequeñas alteraciones en las condiciones iniciales. De modo que la cuestión es: cuando la gente mantiene que hay acontecimientos posibles, ¿están pensando realmente en términos del método estrecho o no?

Supongamos que Austin es del todo incompetente como jugador, y que su compañero en el partido de parejas de hoy se inclina por negar que hubiera podido embocar el golpe. Si dejamos que X abarque demasiado, corremos el riesgo de incluir mundos en los que Austin, gracias a años de caras lecciones de golf, termina por convertirse en un jugador de campeonato que emboca el golpe con facilidad. Pero cabe presumir que Austin no se refiere a eso. Austin parece suscribir el método estrecho para la elección de X cuando insiste en que está «hablando de las condiciones exactamente tal como se dieron». Y, sin embargo, en la proposición posterior parece echarse atrás de tal suscripción al observar que «los experimentos posteriores no harán sino confirmar mi creencia de que podría haberlo hecho aquella vez, aunque no lo hiciera». ¿Qué clase de experimentos ulteriores podrían confirmar la creencia de Austin de que podría haberlo hecho? ¿Experimentos en el green? ¿Podría verse apuntalada su creencia si embocara diez réplicas casi idénticas de aquel golpe corto? Si esta es la clase de experimento en que está pensando, entonces no está tan interesado como pretende en las condiciones tal como se dieron. Para verlo más claro, supongamos que los «experimentos ulteriores» de Austin consisten en sacar una caja de cerillas y encender diez seguidas. «Ahí tienes —dice—, podría haber metido ese golpe en concreto». Nosotros tendríamos toda la razón en objetar que dichos experimentos no guardaban la menor relación con su afirmación. Embocar diez tiros cortos tampoco guardaría relación con su afirmación, interpretada en sentido estrecho, en cuanto afirmación respecto a las condiciones «exactamente tal como se dieron». Nosotros sugerimos que Austin haría mejor en considerar que «Austin emboca el golpe» es posible si, en situaciones muy parecidas a la situación en cuestión, Austin emboca el golpe. Pensamos que esto es lo que quería decir en realidad, y que haría bien en conceptualizar de este modo su golpe. Esta es la manera familiar, razonable y útil de conducir los «experimentos ulteriores» siempre que estemos interesados en comprender las causas que intervienen en un fenómeno que nos interesa. Variamos levemente (y a menudo metódicamente) las condiciones iniciales para ver qué cambia y qué permanece inalterado. Esta es la forma de reunir información útil del mundo para guiar nuestras campañas ulteriores de evitación y progreso.

Curiosamente, esa idea misma es la que propuso, al menos indirectamente, G. E. Moore en la obra que Austin estaba criticando en el pasaje citado. Los ejemplos de Moore eran muy sencillos: los gatos pueden trepar a los árboles y los perros no, y un barco de vapor que viaja ahora a 25 nudos puede, naturalmente, hacerlo también a 20 nudos (pero no, por supuesto, en las circunstancias precisas en que se encuentra ahora, con el motor en «avante a toda máquina»). El sentido del término «poder» invocado en estas afirmaciones nada problemáticas, el sentido que Honoré (1964) llamó «poder (general)» en un artículo importante pero ignorado, es tal que nos exige que prestemos atención no a las «condiciones exactamente tal como se dieron», sino a variaciones menores respecto a aquellas condiciones.

Así pues, las consideraciones de Austin sobre posibilidades resultan equívocas. En realidad, el método estrecho para escoger X no tiene la importancia que él y muchos otros imaginan. De ello se sigue que la verdad o la falsedad del determinismo no debe afectar a nuestra creencia de que ciertos eventos no realizados eran sin embargo «posibles», en un sentido importante y cotidiano de la palabra. Podemos reforzar esta idea si realizamos una visita a un dominio limitado en el que sabemos con certeza que reina el determinismo: el reino de los programas informáticos de ajedrez.

UNA MARATÓN DE AJEDREZ PARA ORDENADORES

Los ordenadores son un excelente ejemplo de los ideales deterministas de Laplace y Demócrito. Es de sobra conocido que se puede hacer que un ordenador ejecute algunos billones de pasos, para luego volverlo a situar al estado (digital) exacto en el que estaba antes, y ver cómo ejecuta exactamente los mismos billones de pasos otra vez, y otra, y otra. El mundo subatómico en el que viven los ordenadores podrá ser o no determinista, y por lo tanto también las partes subatómicas de las que están hechos estos, pero los ordenadores en sí han sido brillantemente diseñados para ser deterministas frente al ruido microscópico e incluso al azar cuántico, ya que el hecho de ser digitales en lugar de analógicos les permite absorber estas fluctuaciones. La idea fundamental que hay detrás de digitalizar para producir determinismo es que el propio diseño nos permite crear hechos históricos inertes. Al clasificar forzosamente todos los eventos relevantes en dos categorías —alto o bajo; ENCENDIDO o APAGADO; 0 o 1— se garantiza que las diferencias mínimas (entre diferentes voltajes, diferentes matices de ENCENDIDO, diferentes sombras de 0) sean brutalmente descartadas. No se permite que nada oscile en ellos, y los hechos relativos a variaciones históricas que no suponen diferencia alguna para la serie subsiguiente de estados por los que pasa el ordenador se desvanecen sin dejar rastro.

CONRAD: ¿Los ordenadores son deterministas? ¿Se puede hacer que repitan exactamente el mismo billón de pasos una y otra vez? ¡Y qué más! Si es así, ¿por qué se cuelga tantas veces mi portátil? ¿Por qué mi procesador de texto se bloquea el martes cuando estaba haciendo la misma cosa que funcionó perfectamente el lunes?

Lo que pasa es que no estaba haciendo la misma cosa. Si se colgó no es porque sea indeterminista, sino porque el martes no estaba exactamente en el mismo estado que el lunes. Su portátil tiene que haber hecho algo en el intervalo que puso alguna «marca» oculta o activó alguna parte del procesador de textos que nunca antes había activado, y que ha cambiado un bit en alguna parte que quedó guardado en la nueva posición al apagarse el ordenador, y ahora el programa ha tropezado con aquel pequeño cambio y se ha colgado. Y si de algún modo consigue volver a ponerlo una segunda vez exactamente en el mismo estado que el martes por la mañana, volverá a colgarse.

CONRAD: ¿Y qué pasa con el «generador de números aleatorios»? Yo creía que mi ordenador llevaba incorporado un dispositivo para generar azar siempre que fuera preciso.

Todos los ordenadores actuales vienen equipados con un generador de números aleatorios interno que puede ser consultado siempre que sea necesario por cualquier programa activo. La secuencia de números que genera no es realmente aleatoria, sino sólo pseudoaleatoria: es «matemáticamente comprimible» en el sentido de que se trata de una secuencia infinitamente larga de números que puede ser recogida en un mecanismo de especificaciones finitas que se encarga de irlos mostrando. Cada vez que usted activa el generador de números aleatorios —cada vez que reinicia el ordenador, por ejemplo— este ofrece exactamente la misma secuencia de dígitos, aunque se trata de una secuencia que en apariencia no sigue ningún patrón, como si hubiera sido generada por fluctuaciones genuinamente aleatorias (es más bien como una larga cinta de vídeo en la que hay grabada la historia de miles de jugadas a la ruleta. La cinta regresa siempre al «principio» cuando se reinicia el ordenador). A veces esto puede ser un problema; los programas informáticos que recurren al azar en varios puntos de «elección» tenderán a ofrecer exactamente la misma secuencia de estados si son ejecutados una y otra vez desde el arranque del ordenador, y si queremos comprobar si un programa tiene fallos acabaremos probando siempre la misma «muestra azarosa» de estados, a menos que tomemos medidas (bastante sencillas) para obligar al programa a buscar en otro lado, de vez en cuando, dentro de su flujo de dígitos para encontrar su nuevo número «aleatorio».

Supongamos que instalamos dos programas de ajedrez diferentes en nuestro ordenador y que los conectamos a través de un pequeño programa supervisor que los obliga a jugar el uno contra el otro, partida tras partida, en una serie potencialmente infinita. ¿Jugarán la misma partida, una y otra vez, hasta que apaguemos el ordenador? Podríamos hacer que fuera así, pero entonces no aprenderíamos nada interesante sobre los dos programas, A y B. Supongamos que A gana a B en esta repetitiva partida. No podríamos deducir de esto que A es en general un programa mejor que B, o que A ganaría a B en una partida distinta, y la repetición exacta de la misma partida no nos permitiría aprender nada sobre las fuerzas y las debilidades respectivas de los dos programas. Sería mucho más informativo organizar un torneo para que A y B jugaran una sucesión de partidas distintas. No es muy difícil de conseguir. Si cualquiera de los dos programas consulta su generador de números aleatorios en sus cálculos (si, por ejemplo, «lanza una moneda» periódicamente para escapar a los casos en los que no encuentra ninguna razón para hacer una cosa en lugar de otra en el curso de su búsqueda heurística), en la partida siguiente el estado del generador de números aleatorios habrá cambiado (a menos que lo arreglemos para que se reinicialice), y por lo tanto se explorarán diferentes alternativas, en un orden diferente, lo que llevará ocasionalmente a la «elección» de movimientos distintos. Florecerá una variante de la partida, y luego una tercera que será diferente en otros aspectos, lo que dará como resultado una serie en la que no habrá dos partidas iguales, como sucede con los copos de nieve. Sin embargo, si apagáramos el ordenador y luego lo reiniciáramos con el mismo programa, obtendríamos exactamente el mismo variado catálogo de partidas.

Supongamos ahora que creamos un universo de ajedrez de este tipo con dos programas distintos, A y B, y que estudiamos los resultados de una serie de mil partidas, por ejemplo. Encontraremos gran cantidad de pautas altamente fiables. Supongamos que descubrimos que, en mil partidas distintas, A siempre gana a B. Tal vez queramos encontrar una explicación para esa pauta y decir simplemente: «Como el programa es determinista, A estaba predeterminado a ganar siempre a B» no contribuirá en nada a aplacar nuestra más que razonable curiosidad. Queremos saber qué hay en la estructura, los métodos y las disposiciones de A que explica su superioridad en el ajedrez. A posee una competencia o una capacidad que B no tiene, y queremos aislar el factor interesante. Para examinar la cuestión, debemos adoptar una perspectiva de alto nivel desde la que se hagan aparentes los objetos «macroscópicos» de la toma de decisiones ajedrecísticas: representaciones de piezas de ajedrez, posiciones sobre el tablero, evaluaciones de continuaciones posibles, decisiones acerca de qué continuaciones adoptar, y así sucesivamente. O también podría ser que la explicación se encontrara a un nivel inferior; podría resultar, por ejemplo, que el programa A y el programa B fueran idénticos por lo que respecta a la evaluación de los movimientos de ajedrez, pero que el programa A tuviera una codificación más eficiente, de manera que pudiera llegar más lejos en sus exploraciones que el programa B en el mismo número de ciclos de la máquina. A «piensa los mismos pensamientos» que B sobre el ajedrez, pero simplemente los piensa más rápido.

En realidad, sería más interesante si no ganara siempre el mismo programa. Supongamos que A gana casi siempre a B y supongamos que A evalúa los movimientos empleando un conjunto distinto de principios. En tal caso tendríamos algo más interesante por explicar. Para investigar esta cuestión causal, deberíamos estudiar la historia de las mil partidas diferentes en busca de pautas ulteriores. Podríamos estar seguros de encontrar muchas. Algunas de ellas serán endémicas en cualquier partida de ajedrez que se juegue (por ejemplo, la certeza casi absoluta de la derrota de B en cualquier partida en la que B tenga una torre menos) y algunas de ellas serán peculiares de A y B como jugadores particulares de ajedrez (por ejemplo, la tendencia de B a perder su reina pronto). Descubriríamos sus modelos básicos de estrategia ajedrecística, como el hecho de que cuando a B se le acaba el tiempo, examina menos a fondo las ramas restantes del árbol de posibilidades de la partida que cuando le queda más tiempo, estando en la misma posición. En resumen, encontraríamos gran abundancia de regularidades explicativos, algunas de las cuales no conocerían excepciones (en nuestra serie de mil partidas) mientras que otras tendrían un carácter estadístico.

Dichas pautas macroscópicas son momentos destacados en el desarrollo de un espectáculo determinista que, visto desde la perspectiva de la microcausalidad, viene a ser siempre el mismo. Lo que desde nuestra perspectiva parece el combate lleno de suspense entre dos programas de ajedrez puede verse bajo el «microscopio» (al contemplar el flujo de datos e instrucciones por la CPU del ordenador) como un sencillo autómata determinista que actúa de la única manera que puede hacerlo, con cambios siempre predecibles si se examina el estado preciso del generador de números pseudoaleatorios. No hay «auténticas» encrucijadas o ramificaciones en su futuro; todas las «elecciones» tomadas por A y B están predeterminadas. Según parece, no es posible que en este mundo ocurra nada distinto de lo que ocurre. Supongamos, por ejemplo, que en el tiempo tB se expone a un posible jaque mate, pero este no llega a producirse porque a A se le acaba el tiempo y da por concluida su búsqueda del movimiento clave un ciclo antes de encontrarlo. Aquel jaque mate nunca va a producirse. (Esto es algo que podríamos demostrar, por si teníamos alguna duda, con sólo ejecutar exactamente el mismo torneo otro día. En el mismo momento de la serie, a A se le acabaría el tiempo otra vez y daría por concluida su búsqueda exactamente en el mismo punto).

Así pues, ¿qué debemos decir? ¿Es este mundo de juguete un mundo donde no hay prevención, ni defensa, ni ataque, ni oportunidades perdidas, un mundo sin posibilidades genuinas, que no conoce el toma y daca de la agencia genuina? Es necesario admitir que nuestros programas de ajedrez, igual que los insectos o los peces, son agentes demasiado simples como para ser candidatos plausibles a un libre albedrío moralmente significativo, pero el determinismo de su mundo no les quita sus diferentes talentos, sus diferentes capacidades de aprovechar las oportunidades que se les presentan. Si queremos comprender lo que ocurre en ese mundo, podemos —o en realidad debemos— hablar sobre los cambios que introducen en sus circunstancias a través de sus elecciones informadas, y sobre lo que pueden y no pueden hacer. Si queremos desvelar las regularidades causales que explican las pautas que descubrimos en aquellas mil partidas, debemos tomarnos en serio la perspectiva que describe este mundo como si contuviera dos agentes, A y B, cada uno de los cuales trata de derrotar al otro al ajedrez.

Supongamos que amañamos el programa que supervisa el torneo para que siempre que A gane suene una campana y cada vez que gane B suene un timbre. Ponemos en marcha la maratón, y un observador que no sabe nada del programa observa que la campana suena con bastante frecuencia, mientras que el timbre apenas lo hace nunca. Quiere saber qué es lo que explica esta regularidad. La regularidad con la que A vence a B puede ser advertida y descrita con independencia de si adoptamos la perspectiva intencional, y necesita una explicación. La única explicación —la explicación correcta— sería que A genera mejores «creencias» sobre lo que B hará si… de las que B genera sobre lo que A hará si… En un caso como este, adoptar la perspectiva intencional es un requisito para encontrar la explicación.

Supongamos que encontramos dos partidas dentro de la serie en las que los primeros doce movimientos son iguales, pero en la primera A juega con blancas y en la segunda con negras. En el movimiento 13 de la primera partida, B «mete la pata» y, a partir de ahí, todo va cuesta abajo para A. En el movimiento 13 de la segunda partida, A, en cambio, encuentra el movimiento salvador, el enroque, y termina ganando. «B podría haberse enrocado en aquel punto de la primera partida», dice un observador, haciéndose eco de Austin. ¿Verdadero o falso? El movimiento, el enroque, era igual de legal la primera vez, de modo que en este sentido entraba dentro de las «opciones» disponibles para B. Supongamos que descubrimos, además, que el enroque no era sólo uno de los movimientos posibles que se había representado B, sino que B llegó a realizar una somera exploración de las consecuencias del enroque, que abandonó, por desgracia, antes de que se le revelaran sus virtudes. En tal caso, ¿podía haberse enrocado B? ¿Qué es lo que estamos tratando de descubrir? Mirar exactamente el mismo caso, una y otra vez, no resulta nada informativo: lo que lleva en realidad al diagnóstico es prestar atención a otros casos parecidos. Si descubrimos que, en otras circunstancias parecidas, B sí es capaz de llevar más lejos su evaluación y adivina las virtudes de movimientos como ese y los realiza efectivamente —si descubrimos, en el caso extremo, que cambiar un solo bit en el generador de números aleatorios daría como resultado el enroque de B—, habríamos confirmado (sobre la base de «experimentos ulteriores») la convicción del observador de que B podía haberse enrocado entonces. Diríamos que el hecho de que B no se enrocara fue pura chiripa, mala suerte con el generador de números aleatorios. Si, en cambio, comprobamos que descubrir las razones en favor del enroque requiere un análisis mucho más largo del que B puede ejecutar en el tiempo disponible (mientras que la superior potencia de A le permite realizar la tarea), tendremos base suficiente para concluir que B, a diferencia de A, no podía haberse enrocado. Tal vez descubriéramos que enrocarse era uno de esos movimientos que va seguido de un «(!)» en los problemas de ajedrez de los periódicos, un movimiento «profundo» que estaba fuera del alcance de B. Imaginar que B se enrocara requeriría demasiadas alteraciones en la realidad; estaríamos cometiendo el error antes mencionado de permitir que X abarcara demasiado.

En resumen, usar el método estrecho para escoger X no nos sirve de nada si lo que queremos es explicar las pautas que se manifiestan en los datos. Sólo obtendremos algún conocimiento si «removemos los hechos» (tal como ha dicho David Lewis) y examinamos no las «condiciones exactamente tal como se dieron», sino las de mundos vecinos. En cuanto ampliamos un poco X, descubrimos que B tiene opciones adicionales, en un sentido tanto informativo como moralmente relevante (si pasamos a otros mundos que van más allá del ajedrez). Muchos filósofos han dado por supuesto, sin aportar argumentos específicos para ello, que cuando preguntamos por las posibilidades que había en cierto momento, estamos —y deberíamos estar— interesados en saber si, en caso de darse exactamente las mismas circunstancias, volvería a producirse el mismo hecho. Hemos sostenido que, a pesar de la tendencia tradicional de los filósofos a suscribir esta estrategia, no ha sido nunca la que han seguido aquellos que han investigado seriamente las cuestiones relativas a la posibilidad, y no hay, en todo caso, motivo para adoptarla: en ningún caso se podría conseguir por esta vía una respuesta satisfactoria a nuestra curiosidad. La carga de prueba está ahora del lado de aquellos que piensan de otro modo; son ellos quienes deben explicar por qué las posibilidades «reales» requieren una elección estrecha de X… o por qué debería interesarnos una concepción de este tipo de la posibilidad, sea cual sea su «realidad».

Así pues, los mundos deterministas pueden dar cabida cómodamente a posibilidades en el sentido más amplio e interesante del término. En realidad, introducir el indeterminismo no añade nada a un universo en términos de posibilidades valiosas, oportunidades o competencias. Sustituir el generador de números pseudoaleatorios por un dispositivo genuinamente indeterminista no ayudará en nada al programa B en nuestro torneo determinista de ajedrez donde siempre gana A. El programa A seguirá ganando cada vez. Un algoritmo superior como el de A apenas notará un cambio tan insignificante, tan invisible a la práctica. Por más que los generadores pseudoaleatorios no puedan producir resultados genuinamente aleatorios, se acercan tanto a ello que la diferencia es casi despreciable a todos los efectos. Hay sin embargo un contexto en el que sí introduce una diferencia práctica: la criptografía. Los superordenadores son capaces de dar con la clave de la aparente falta de pauta de los algoritmos particulares pseudoaleatorios de generación de números, lo que da una importancia especial al uso de números genuinamente aleatorios en tales contextos especializados^[3]. Pero fuera de este contexto, donde debemos preocuparnos por la existencia de un oponente que puede tener acceso a nuestro particular modelo de generador de números pseudoaleatorios y usarlo para «leernos la mente», no tenemos nada que ganar con ser genuinamente indeterministas. Para expresarlo de forma más gráfica, el universo podría ser determinista los días pares del mes e indeterminista los días impares y nunca descubriríamos una diferencia en las oportunidades o las capacidades de los seres humanos; lograríamos los mismos éxitos —y los mismos lamentables fracasos— el 4 de octubre que el 3 o el 5 de octubre. (Si su horóscopo le hubiera aconsejado posponer cualquier decisión moralmente importante a un día impar, no tendría mayor motivo para seguir su consejo que si le dijera que esperara a la luna menguante).

EVENTOS SIN CAUSA EN UN UNIVERSO DETERMINISTA

El determinismo es una doctrina relativa a la suficiencia: si S_o es una proposición (inconcebiblemente compleja) que especifica con perfecto detalle la descripción del estado del universo en to, y si Si especifica del mismo modo la descripción del estado del universo en un momento posterior to entonces el determinismo establece que S_o es suficiente para Si en todos los mundos físicamente posibles. Sin embargo, el determinismo no nos dice nada sobre qué condiciones previas son necesarias para producir Si o cualquier otra proposición, en realidad. En consecuencia, como la causalidad presupone en general la necesidad, la verdad o falsedad del determinismo tiene poca o ninguna importancia para la validez de nuestros juicios causales.

Por ejemplo: según el determinismo, la situación exacta del universo un segundo después del Big Bang (llamemos S_o a la proposición correspondiente) es causalmente suficiente para producir el asesinato de John F. Kennedy en 1963 (proposición C). Sin embargo, no hay razón para decir que S_o causó C. Aunque sea una razón suficiente, no tenemos razón para creer que S_o sea necesario. Por lo que podemos saber, Kennedy podría muy bien haber sido asesinado en cualquier caso, aunque se hubieran dado condiciones distintas en el nacimiento del universo. ¿Cómo podríamos saberlo? Podemos imaginarnos cómo sería la investigación, aunque no podamos llevarla a cabo: imaginemos que tomamos una instantánea del universo en el momento del asesinato de Kennedy y luego alteramos la imagen en algún aspecto trivial (pongamos que movemos a Kennedy 1 milímetro hacia la izquierda). La proposición C: «John F. Kennedy fue asesinado en 1963 (en Dealey Plaza, cuando iba en su coche oficial…)» sigue siendo cierta, pero con una diferencia microscópica en las condiciones atómicas que la convierten en verdadera. Luego, partiendo de nuestra descripción de estado sutilmente revisada de 1963 y siguiendo las leyes (deterministas) de la física a la inversa, generamos una película que recorre toda la historia hasta el Big Bang, con lo que obtenemos un mundo en el que S_o no se aplica por una sutil diferencia. Hay mundos posibles muy parecidos al nuestro donde Kennedy muere pero S_o no se cumple, de modo que el estado del universo descrito por S_o no es la causa del asesinato de Kennedy. Otras más plausibles de aquel evento incluirían: «Una bala sigue un curso que se dirige al cuerpo de Kennedy»; «Lee Harvey Oswald apretó el gatillo de su arma». Los grandes ausentes de esta lista son las descripciones microscópicas del universo billones de años antes del incidente. Los filósofos que afirman que según el determinismo S_o «causa» o «explica» C pasan por alto la idea central de la investigación causal, y este es el segundo error capital.

En realidad, el determinismo es perfectamente compatible con la noción de que algunos eventos no tienen ninguna causa. Consideremos la proposición: «La devaluación de la rupia hizo que se desplomara el índice Dow Jones». Con razón miramos con recelo esta declaración; ¿estamos realmente seguros de que dentro del conjunto de los universos vecinos al nuestro el Dow Jones se desplomó únicamente en aquellos donde la rupia había caído primero? ¿Podemos imaginarnos siquiera que en todos los universos donde cayera la rupia se dispararan las órdenes de venta en el mercado de valores? ¿No es posible que se diera una confluencia de multitud de factores que bastaran en conjunto para hacer que se desplomara el mercado, sin que ninguno de ellos fuera esencial en sí mismo? Tal vez haya días en los que se pueda encontrar una razón válida para el comportamiento de Wall Street; pero al menos con igual frecuencia sospechamos que no hay ninguna causa particular que lo explique.

El lanzamiento de una moneda que no esté trucada es un ejemplo familiar de un evento que tiene un resultado (por ejemplo, cara) que propiamente no tiene causa. No tiene causa porque no importa cómo escojamos el conjunto X (ignorando el consejo erróneo de Austin de considerar las circunstancias tal como se dieron exactamente) no encontraremos ningún rasgo de C que sea necesario para que salga cara o para que salga cruz. ¿Ha pensado usted alguna vez en la aparente contradicción que supone usar una moneda como forma de generar un evento aleatorio? No hay duda de que el resultado del lanzamiento de una moneda al aire es la consecuencia determinista de la suma total de las fuerzas que actúan sobre ella: la velocidad y la dirección del lanzamiento que imparte el giro, la densidad vía humedad del aire, la rotación de la Tierra, la distancia entre Marte y Venus en aquel momento, y así sucesivamente. La cuestión es que esta suma total no contiene pautas predictivas. Tal es el truco que hay detrás de los mecanismos generadores de aleatoriedad del tipo de lanzar una moneda al aire: convertir en incontrolable el resultado al hacerlo sensible a tantas variables que no podemos señalar como causa ninguna lista finita o factible de condiciones. Ese es el motivo por el que pedimos que se lance la moneda bien alta, con mucho efecto, y no simplemente que se deje caer de los dedos una pulgada por encima de la mesa: ponemos en marcha una secuencia que prácticamente garantiza que nada será la causa de que el resultado sea cara o cruz. Nótese que la estrategia de lanzar la moneda utiliza la digitalización para garantizar que el resultado carece de causa (si se hace debidamente). Cumple exactamente la función contraria de la que cumple la digitalización en los ordenadores: en lugar de absorber todas las microvariaciones del universo, las amplifica, y garantiza que la suma inimaginablemente larga de fuerzas que actúan en aquel momento situará el digitalizador en uno de sus dos estados, cara o cruz, pero sin que haya condiciones necesarias destacables para ninguno de los dos resultados.

La práctica de «remover los hechos» en experimentos controlados es una de las grandes innovaciones de la ciencia moderna y, tal como señala Judea Pearl, depende de que usemos algo como el lanzamiento de una moneda para romper los lazos causales que de otro modo existen entre los eventos que queremos analizar:

Supongamos que queremos estudiar el efecto de cierto tratamiento farmacológico para la recuperación de pacientes aquejados de cierta enfermedad […]. Bajo condiciones no controladas, la elección del tratamiento está en manos de los pacientes y puede depender de su trasfondo socioeconómico. Esto crea un problema, ya que no podemos decir si los cambios en los índices de recuperación son debidos al tratamiento o a dichos factores de fondo. Lo que nos interesa es comparar pacientes de trasfondos parecidos, y eso es precisamente lo que consigue el experimento aleatorio de [sir Ronald] Fisher. ¿Cómo? En realidad consta de dos partes: aleatorización e intervención.

La intervención significa que alteramos el comportamiento natural del individuo: separamos a los sujetos en dos grupos, llamados tratamiento y control, y convencemos a los sujetos para que sigan las reglas del experimento. Asignamos tratamiento a algunos pacientes que, bajo circunstancias normales, no buscarían tratamiento, y damos placebo a los pacientes que sí recibirían tratamiento en otro caso. Eso, en nuestro nuevo vocabulario, es hacer cirugía: cortamos un vínculo funcional y lo reemplazamos por otro. La gran idea de Fisher fue que conectar el nuevo vínculo con el lanzamiento aleatorio de una moneda garantiza que el vínculo que deseamos romper se rompe realmente. La razón es que se presume que una moneda lanzada al azar no se ve afectada por nada que podamos medir a nivel macroscópico (incluido, por supuesto, el trasfondo socioeconómico de un paciente) (Pearl, 2000, pág. 348).

Nuestra práctica en estos casos revela una presunción de fondo que parece estar ampliamente aceptada (aunque nunca o raras veces es sometida a examen): la presunción de que la única forma de que un evento no tenga causa es que se encuentre estrictamente subdeterminado, que no tenga condición suficiente, por más difusa, compleja y poco interesante que sea esta. Esto puede llevar a graves distorsiones de nuestra agenda científica: ¿cuál fue la causa de la Primera Guerra Mundial? ¡Si queremos ser unos buenos investigadores científicos, lo menos que podemos hacer es encontrarle una causa! Declarar que la Primera Guerra Mundial no tuvo ninguna causa vendría a ser lo mismo que declararla o bien una violación de las leyes de la naturaleza —¡un milagro!— o bien (la física cuántica al rescate) el resultado de procesos cuánticos indeterministas. Pues bien, no es así. Podría ser que por más que los historiadores «removieran los hechos» en busca de los antecedentes necesarios de la Primera Guerra Mundial en mundos posibles cercanos, se encontraran con que aquellos universos donde se produce la Primera Guerra Mundial no comparten ningún antecedente común y necesario. Supongamos, por ejemplo, que en el universo A, el archiduque Fernando es asesinado y se declara subsiguientemente la Primera Guerra Mundial. ¿Significa eso que lo anterior es la causa de esta última (tal como algunos de nosotros «aprendimos» en la escuela)? Tal vez no; tal vez en un universo B, el archiduque Fernando sobrevive, pero la Primera Guerra Mundial estalla igualmente. Y, del mismo modo, podría darse el caso de que para cada «causa» que propusiera el historiador X, el historiador Y fuera capaz de imaginar un mundo en el que se produce la Primera Guerra Mundial sin venir precedida por dicha candidata a causa. La guerra podría haber sido un golpe de azar, en cuyo caso persistir en disputas sobre cuál fue «la causa» no sólo sería inútil, sino que casi garantizaría la creación de mitos artificiales sobre causas secretas que explorar. La búsqueda de tales condiciones necesarias es siempre racional, mientras tengamos presente que puede ser que en algún caso particular no haya nada que encontrar^[5]

Alguien podría preguntarse por qué nos preocupa tanto la necesidad causal. Volvamos por un momento a los programas de ajedrez A y B. Supongamos que nos llama la atención una de las raras partidas en las que B gana, y que queremos saber «la causa» de esta sorprendente victoria. La tesis trivial de que la victoria de B la «causó» el estado inicial del ordenador no resultaría nada informativa. Por supuesto, el estado total del universo del modelo en los momentos anteriores era suficiente para que se produjera la victoria; pero lo que queremos saber es qué rasgos eran necesarios, para así comprender qué tienen en común estos raros eventos. Queremos descubrir cuáles son estos rasgos, la ausencia de los cuales traería de manera más directa la derrota de B. el resultado normal. Tal vez descubramos un defecto hasta ahora inadvertido en la estructura de control de A, un fallo que no se ha manifestado hasta ahora. O tal vez descubramos un rasgo idiosincrásico de brillantez en la competencia de B, que una vez diagnosticado nos permitiría predecir exactamente qué circunstancias harían posible en el futuro otra victoria parecida de B. O tal vez la victoria es una coincidencia de múltiples condiciones que no justifican ninguna reparación, pues la probabilidad de que se reproduzcan es nula en la práctica. Esta última posibilidad, es decir, que en un sentido relevante simplemente no hubiera causa para la victoria de B —que fuera un golpe de suerte—, resulta fácil de comprender en un contexto simplificado como este, pero es más difícil de admitir, según parece, en casos reales.

La racionalidad requiere que evaluemos las condiciones necesarias al menos con el mismo cuidado que las condiciones suficientes. Consideremos el caso de un hombre que cae por el hueco del ascensor. Aunque no sabe exactamente en qué mundo posible habita, sí sabe una cosa: se encuentra dentro de un conjunto de mundos en todos los cuales en breve acabará en el fondo del hueco del ascensor. La gravedad se encargará de eso. El batacazo es en este sentido inevitable, porque se produce en todos los mundos consistentes con lo que conoce. Pero tal vez no sea inevitable el hecho de morir. Cabe la posibilidad de que en alguno de los mundos donde se pega el batacazo logre, sin embargo, sobrevivir. Dichos mundos no incluyen ninguno donde caiga, por decir algo, con la cabeza por delante o con los brazos abiertos como un pájaro, pero puede haber mundos en los que caiga con los pies por delante, amortigüe el golpe y sobreviva. Hay cierto margen. Puede planificar racionalmente sus acciones partiendo de la premisa de que es posible que viva e, incluso aunque no pueda descubrir condiciones suficientes que garanticen su supervivencia, puede al menos mejorar sus opciones al realizar todas las acciones que sean necesarias y, por lo tanto, con un poco de suerte, encontrarse en el Vasto número de mundos posibles en los que vive.

CONRAD: Una vez más, ¿qué sentido tiene hablar de mejorar sus opciones? Estamos presuponiendo el determinismo. No puede cambiar de mundo. Está en el mundo en el que está, el mundo presente, y en este mundo vive o muere, y ahí termina la cuestión.

De acuerdo, pero eso es cierto con independencia del determinismo y es irrelevante para la cuestión de la racionalidad de su acción. Supongamos que suspendemos temporalmente su caída y que le permitimos leer el Vasto rincón de la Biblioteca de Babel donde se encuentran las biografías de un hombre que responde a su mismo nombre, posee sus mismos rasgos, características e historia hasta la fecha: la historia de un hombre que cae accidentalmente por el hueco de un ascensor y se encuentra frente a una colección inimaginablemente grande de libros, cada uno de los cuales pretende ser la verdadera historia de su vida. En algunos de estos libros vive y en otros muere (y, tratándose de la Biblioteca de Babel, en algunos de ellos se convierte en una taza de oro y es arrojado a Cleopatra por un caracol gigante). El problema es que aunque puede descartar los libros fantásticos sobre la base de su conocimiento general de cómo funciona el mundo, no tiene ninguna forma de saber qué libro en concreto es el verdadero entre los que dicen que vive o muere tras su caída. Y suponer que el determinismo sea verdadero, o falso, no le ayudará a encontrar la aguja en este pajar. La mejor estrategia que puede adoptar frente a esta incertidumbre insuperable respecto a cuál de los libros dice la verdad es buscar pautas generales predictivas —causas y efectos— y dejarse guiar por las predicciones que sugieren. Pero ¿cómo va a hacer eso? No hay problema: eones de evolución le han diseñado para hacer precisamente eso. Si no tuviera estos talentos, no estaría allí. Es el producto de un proceso de diseño que ha creado una especie de previsores-evitadores en quienes este truco es como una segunda naturaleza. No son perfectos, pero obtienen resultados mucho mejores que el mero azar. Comparemos, por ejemplo, las perspectivas de unos seres que tienen ante sí la oportunidad de ganar un millón de dólares con un lanzamiento de moneda o una jugada a los dados en la que salgan dos unos. Algunos de ellos razonan en términos fatalistas: «No importa qué método escoja; las opciones de que salgan dos unos son 0 o 1. No sé cuál es el destino ya predeterminado, y lo mismo sucede con la moneda». Otros actúan guiados por la convicción de que la probabilidad de 1 entre 2 que tienen al escoger la moneda es mucho mejor que la probabilidad de 1 entre 36 de que les salga el doble uno, y optan por lanzar la moneda. No es ninguna sorpresa que la gente diseñada para hacerlo así haya obtenido mucho mejores resultados que los fatalistas, los cuales puede decirse que tienen un defecto de diseño, desde la perspectiva que da la historia.

¿SERA EL FUTURO IGUAL QUE EL PASADO?

Y ahora, por fin, estamos listos para enfrentarnos al tercer gran error en relación con el determinismo. Algunos pensadores han planteado que la verdad del determinismo implicaría uno o más de los siguientes desalentadores corolarios: todas las tendencias son permanentes, el carácter es en gran medida inmutable, y es improbable que uno pueda cambiar en el futuro la propia manera de ser, la propia fortuna, o la propia naturaleza básica. Ted Honderich, por ejemplo, ha sostenido que el determinismo destruye de algún modo lo que llama nuestras esperanzas vitales:

Si a una persona le han ido bien las cosas, todavía puede esperar más del futuro partiendo de la presunción de que su vida entera está prefijada […]. Si no le han ido bien las cosas, o no tan bien como esperaba, puede decirse cuando menos que no es insensato que tenga mayores esperanzas partiendo de la presunción de que el conjunto de la propia vida no está prefijado, sino que está vinculado a la actividad del yo […]. Dada la premisa optimista de nuestra razonabilidad, hay razones para pensar que no tendemos a la idea de un futuro personal prefijado (Honderich, 1988, págs. 388389).

No hay duda de que tales inquietudes tienen su origen en la vaga noción de que las verdaderas posibilidades (de mejorar nuestra fortuna, por ejemplo) desaparecen con el determinismo. Pero esto es un error. La distinción entre ser un ente con un futuro abierto y ser un ente con un futuro cerrado es estrictamente independiente del determinismo. En general, no hay paradoja alguna en la observación de que ciertos fenómenos están predeterminados para ser alterables, caóticos e impredecibles, un hecho evidente e importante que los filósofos curiosamente han ignorado. A Honderich le parece inquietante la idea de que podamos tener un «futuro personal prefijado», pero las implicaciones de esta idea son enteramente distintas de las implicaciones de tener una «naturaleza personal prefijada». El propio futuro personal «prefijado» —es decir, predeterminado— podría consistir perfectamente en la bendición de una naturaleza proteica, altamente sensible a la «actividad del yo». El conjunto total de los futuros personales, esté o no «prefijado», contiene toda clase de escenarios agradables, entre los cuales habrá victorias sobre la adversidad, superaciones de la debilidad, reformas del carácter e incluso cambios de fortuna. Tan determinado podría ser el hecho de que los perros viejos pudieran aprender trucos nuevos como que no pudieran. La cuestión que debemos preguntar es: ¿son los perros viejos el tipo de ente al que se le pueden enseñar trucos nuevos? Si no lo son, no queremos ser como los perros viejos. Es justo que nos preocupemos por si somos la clase de entes cuya trayectoria futura no repetirá las mismas pautas del pasado, y la tesis general del determinismo no tiene ninguna implicación respecto a estas cuestiones.

Consideremos los simples mundos deterministas Vida. En un nivel nada cambia nunca; los píxels hacen lo mismo una y otra vez eternamente, siguiendo la sencilla ley de la física. En otro nivel, vemos diferentes clases de mundos. Algunos mundos son tan inmutables a vista de pájaro como lo son al nivel atómico, un campo de naturalezas muertas y semáforos, pongamos por caso, que parpadean para toda la eternidad. No hay drama, ni suspense. Otros mundos «evolucionan» constantemente, sin pasar dos veces por el mismo estado, sea de una forma ordenada, con un crecimiento predecible, al crear por ejemplo un flujo constante de planeadores idénticos y separados por el mismo espacio, o bien de una forma aparentemente desordenada, con miríadas de masas de píxels que crecen, se mueven y colisionan entre sí. En esos mundos, ¿es el futuro igual que el pasado? Sí y no. La física es eternamente inmutable, de modo que los microeventos son siempre iguales. Pero, a un nivel superior, el futuro puede ser muy variado: puede contener pautas que sean iguales que las del pasado y otras que sean completamente nuevas. Es decir, que en algunos mundos deterministas hay cosas cuya naturales cambia con el tiempo, de modo que el determinismo no implica una naturaleza fija. Un hecho pequeño, pero alentador. Y aún nos faltan uno cuantos más.

Algunos mundos Vida contienen competiciones y, aunque el demonio de Laplace sabe exactamente cómo terminará cada competición, puede resultar auténticamente dramático e inquietante para inteligencias inferiores, que no pueden saber, desde su limitada perspectiva, cómo terminará la competición. Consideremos, por ejemplo, aquellos mundos Vida en los que hay una Máquina Universal de Turing que ejecuta nuestro programa de partidas de ajedrez de A contra B. El ajedrez es un juego de «información perfecta»; en este sentido es distinto de los juegos de cartas, en los que se ocultan las cartas al oponente (y en los que ningún oponente sabe qué carta saldrá a continuación de la baraja). Así pues, A y B tienen una información completa y compartida sobre el estado de la partida de ajedrez en curso y sobre las posibilidades que se abren a continuación. Sin embargo, acaban creando como resultado de sus esfuerzos diferentes inventarios de expectativas acerca de los probables movimientos futuros de sus oponentes, y de ellos mismos. La competición consiste en utilizar la información compartida para generar una información privada sobre la que basar la elección de los propios movimientos, y la explicación de por qué A gana a B (si lo hace, y cuando lo hace) debe formularse en términos de su superior capacidad para generar, y usar, información acerca de un futuro incierto y abierto (desde su perspectiva). Cada usuario finito de información tiene un horizonte epistémico; no lo sabe todo del mundo que habita, y esta ignorancia insuperable garantiza que tenga un futuro subjetivamente abierto. El suspense es una condición necesaria de la vida para cualquier agente de este tipo^[6].

Pero dejemos a un lado la cuestión del suspense subjetivo, y del cambio de naturaleza. ¿Qué pasa con la superación? ¿Puede haber no sólo superación, sino una superación causada por el propio agente en un mundo determinista? ¿Puede un agente de un mundo determinista tener una esperanza realista de prosperar? Una vez más, la respuesta a esta pregunta no tiene nada que ver con el determinismo y mucho que ver en cambio con el diseño. Los programadores han demostrado ya que algoritmos informáticos deterministas pueden adaptarse a cambios del entorno y aprender de sus errores. Hemos dejado para más adelante la posibilidad de atribuir capacidad de aprendizaje a los programas A y B, por no querer distraer la atención de otras cuestiones que estaban en discusión, pero consideremos lo que ocurre cuando incorporamos la capacidad de aprender de la experiencia en uno de los oponentes. Si el inicialmente mediocre B poseyera la capacidad de aprender y A no, podría ser que al final B saliera victorioso. Uno de los productos de la historia de las competiciones de B, podríamos decir que el fruto de sus esfuerzos, podría ser el desarrollo de una estructura que le diera una competencia mejor y, por lo tanto, una mejor posición en la vida. B pasaría de ser el eterno perdedor al ganador habitual. Supongamos que B posee esta clase de estructura capaz de aprender en un mundo determinista; su envidiable capacidad no experimentará ninguna mejora con la introducción de un generador de números aleatorios genuinamente indeterminista. La introducción del indeterminismo tampoco contribuirá a hacer más abierto el futuro de B, si le falta esta capacidad de aprender.

Las condiciones bajo las que se produce la superación personal (a falta de milagros) son precisamente las condiciones bajo las cuales algo —sea un dios-hacker, o la evolución, o el instructor de B, o el propio B— identifica las causas que hay detrás de la victoria y genera diseños que aumentan las probabilidades de que dichas causas estén presentes en el futuro en los momentos adecuados. Hay, pues, una razón familiar para diseñar un programa que aprenda de la experiencia: en el futuro puede encontrarse con una situación parecida, y lo que ocurra entonces podría verse influido por lo que aprenda ahora. Esto es así porque lo que ocurra entonces dependerá de lo que decida entonces; si enroca o no, por ejemplo, dependerá de él en un sentido importante. No dependerá de él si las reglas del ajedrez siguen siendo las mismas, como tampoco los movimientos de su oponente; sus propios movimientos, en cambio, dependerán de él en el sentido que nos interesa: serán el resultado de sus propios procesos exploratorios y deliberativos.

En este sentido, comparemos el caso de un pez enfrentado a un anzuelo con cebo y el de un pez enfrentado a una red que se le viene encima a gran velocidad; que el primer pez muerda el anzuelo es algo que depende de sí mismo, mientras que el hecho de que el segundo pez entre en la red probablemente no. Así pues, ¿son libres los peces? No en un sentido moralmente relevante, pero sí tienen sistemas de control que toman «decisiones» de vida o muerte, lo cual es al menos una condición necesaria para la libertad. En el capítulo 4 consideraremos si hay otro sentido más profundo de «depender de» que se nos pueda aplicar a nosotros (como agentes morales) pero no a los ordenadores deterministas que juegan al ajedrez, o a los peces.

Vivimos en un mundo que está subjetivamente abierto. Y hemos sido diseñados por la evolución para ser «informóvoros», seres epistémicamente hambrientos, buscadores de información, entregados a la interminable tarea de mejorar nuestro conocimiento del mundo, para poder tomar mejores decisiones respecto a nuestro futuro subjetivamente abierto. La luna está hecha de la misma materia que nosotros, obedece a las mismas leyes de la física, pero su naturaleza, a diferencia de la nuestra, está fijada. Es más, a diferencia de nosotros, no se preocupa por su naturaleza. No está preparada para preocuparse lo más mínimo por sí misma. La diferencia entre nosotros y la luna no es una diferencia que tenga que ver con la física; es una diferencia de diseño de un nivel superior. Somos el producto de un proceso competitivo a gran escala para la mejora de diseños; la luna no. Este proceso de diseño, la selección natural, se basa como es sabido en la mutación «aleatoria» como Generador de Diversidad último. Hemos visto que los programas informáticos —y en general los experimentos controlados— utilizan esta clase de generadores de diversidad en buena medida con el mismo objeto: para introducir nuevos modelos en los procesos indagatorios y hacer que superen los antiguos. Pero también hemos visto que esta bienvenida fuente de diversidad no tiene por qué ser verdaderamente aleatoria, en el sentido de ser indeterminista.

Decir que si el determinismo es verdadero, nuestro futuro está fijado, es decir… nada interesante. Decir que si el mundo es determinista, nuestra naturaleza está fijada, es decir algo falso. Nuestras naturalezas no están fijadas porque hemos evolucionado hasta convertirnos en entidades diseñadas para cambiar su naturaleza en respuesta a las interacciones con el resto del mundo. Toda la angustia acerca del determinismo tiene su origen en una confusión entre lo que supone tener una naturaleza fijada y tener un futuro fijado. La confusión surge cuando uno trata de mantener dos perspectivas simultáneas sobre el universo: la perspectiva del «ojo de Dios», ante la que se despliegan al mismo tiempo pasado y futuro, y la perspectiva situada de un agente integrado en el universo. Desde la perspectiva intemporal de Dios nada cambia jamás —la historia entera del universo se despliega «de una vez»— e incluso un universo indeterminista no sería sino un árbol de ramificaciones estáticas. Desde la perspectiva del agente situado, las cosas cambian con el tiempo, y los agentes cambian para hacer frente a dichos cambios. Pero por supuesto no todos los cambios son posibles para nosotros. Hay cosas que podemos cambiar y cosas que no podemos cambiar, y algunas de estas últimas son deplorables. Hay muchas cosas que están mal en nuestro mundo, pero el determinismo no es una de ellas, incluso aunque nuestro mundo esté determinado.

Así pues, una vez superado el miedo al determinismo físico, podemos dirigir nuestra atención al nivel biológico, desde el que tal vez podamos explicar cómo es posible que seamos libres, cuando otras entidades de nuestro mundo, hechas del mismo tipo de materia que nosotros, no lo son en absoluto. Como sucede habitualmente cuando se habla de biología, encontraremos que hay toda clase de categorías y grados diferentes de libertad. La libertad, tal como se manifiesta en un ordenador capaz de jugar al ajedrez que habita en el plano Vida, no es más que un juego, una mera caricatura de la clase de libertad que nos interesa. Pero estamos realmente interesados en esta clase de libertad, y resulta útil comenzar con el modelo más sencillo imaginable para confirmar si es compatible con el determinismo.

CONRAD: De acuerdo, ha demostrado usted que Austin estaba equivocado. Pero resulta que a él no le interesaba en absoluto cuáles eran las posibilidades reales; ¡lo que le interesaba era su tiro al hoyo! Y tiene razón en que la forma de comprobar eso es hacer algunos tiros y ver cuántos entran. Tal como usted sabe, hay un sentido de competencia, de poder hacer, que se aplica igualmente bien a los agentes humanos y a artilugios como los ordenadores que juegan al ajedrez (y a los abrelatas, si a eso vamos). Pero todo lo que esto demuestra es que responder a esa clase de pregunta no roza siquiera la pregunta que a mí me interesa: ¿podría Austin haber metido aquel tiro en concreto? Y la respuesta a esta pregunta debe ser «no» en un mundo determinista.

Muy bien, si insiste. Tal vez haya un sentido de «posible» en el que Austin no podía haber metido aquel tiro, si el mundo fuera determinista. Ahora bien, ¿por qué razón habría de preocuparnos esta cuestión? Aparte de una ociosa curiosidad metafísica, ¿qué interés puede tener para nosotros si Austin podía o no haber metido aquel tiro en el sentido que usted dice?

Los incompatibilistas tienen una respuesta a esta pregunta, y antes de que podamos volver cómodamente a la evolución, deberíamos darles la oportunidad de presentarla. El siguiente capítulo está dedicado a examinar la mejor respuesta que han dado hasta el momento. Aquellos que ya estén convencidos de que el determinismo simplemente no es la cuestión pueden pasar directamente al capítulo 4, pero se perderán algunos descubrimientos incidentales sobre la naturaleza de nuestra libertad que son hasta cierto punto independientes de la defensa del indeterminismo que los reveló.

Capitulo 3

Nuestra manera cotidiana de pensar en relación con la posibilidad, la necesidad y la causalidad parece entrar en conflicto con el determinismo, pero se trata de una ilusión. El determinismo no implica que, hagamos lo que hagamos, no podíamos haber hecho otra cosa, que todo evento tiene una causa, o que nuestra naturaleza está fijada.

Capítulo 4

Un examen constructivo de un ambicioso modelo indeterminista de toma de decisiones revela tanto los motivos como los problemas que rondan a cualquier teórico que vaya por aquel camino. Se puede dar respuesta a las tesis más plausibles de los libertaristas sin necesidad de suscribir el indeterminismo, y el indeterminismo no introduce nada que pueda suponer una diferencia moral.

NOTAS SOBRE FUENTES Y LECTURAS COMPLEMENTARIAS

El libro de Judea Pearl Causality: Models, Reasoning, and Inference (2000), que descubrí mientras preparaba el último borrador del presente libro, plantea cuestiones acerca del modelo Taylor/Dennett en términos de mundos posibles, al tiempo que abre alternativas tentadoras. No será una tarea fácil digerirlas y, en caso necesario, reformular nuestras conclusiones, que en nuestra opinión no se ven directamente cuestionadas. Es una tarea que queda para el futuro.

Para leer más acerca de la posibilidad, véase La peligrosa idea de Darwin (Dennett, 1995), capítulo 5, «Lo real y lo posible» y, especialmente, «La posibilidad naturalizada» (págs. 118-123). Véase también el experimento mental («Dos Cajas Negras», págs. 412-422), que deja claro que los científicos podrían tener un conocimiento completo de los procesos microcausales presentes (de manera determinista) en este fenómeno y sin embargo ser totalmente incapaces de explicar las regularidades macrocausales que observan y desean explicar.

Para leer más sobre números pseudoaleatorios y su utilidad para el control y la libertad, véase Elbow Room (Dennett, 1984), págs. 66-67, y el resto del libro.

Publicada en nueve volúmenes entre 1759 y 1766, la novela cómica de Lawrence Sterne Tristram Shandy pretende ser una autobiografía, pero se enreda en espirales recurrentes de reflexión, reacción y metarreacción que la convierten en una tarea inacabada e inacabable.