Teorema de Pitágoras

…

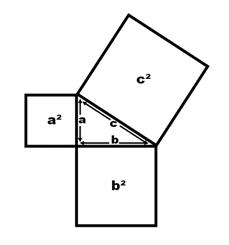
El Teorema de Pitágoras establece que, en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo del triángulo) es igual a la suma de los cuadrados de los catetos (los lados contiguos al ángulo recto).

En el diagrama: c²=a²+b²

Desde hace al menos cinco mil años, en el Antiguo Egipto y en otras civilizaciones de la Antigüedad se conocían ternas de valores que corresponden a los lados de un triángulo rectángulo. El ejemplo más sencillo es: 3, 4, 5. (5²=3²+4²). Al triángulo rectángulo en el que la longitud de sus lados tiene esos valores se lo conoce como triángulo sagrado egipcio. Se cree que se utilizó para diseñar múltiples construcciones, como la Pirámide de Kefrén (S. XXVI a. C.).

En la época de Pitágoras, muchos pueblos llevaban miles de años utilizando ejemplos prácticos del triángulo rectángulo. Sin embargo, no sabemos de nadie que, antes que Pitágoras, demostrara teóricamente la relación entre sus lados. Esto es: que c²=a²+b² se cumple siempre, y no sólo en algunos casos concretos como el del triángulo sagrado egipcio.

El Teorema de Pitágoras es otro de los descubrimientos de la escuela pitagórica que muestra, de un modo sublime e inequívoco, la relación entre la aritmética y la geometría; es decir: el vínculo entre los números y el espacio físico.

El Teorema contribuyó notablemente a la enorme confianza que los pitagóricos tenían en sus ideas, y a que Pitágoras fuera encumbrado definitivamente como uno de los mayores genios de la historia.

…