Números irracionales

…

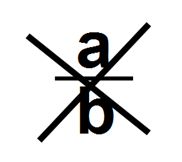
Son aquellos que no pueden expresarse como un cociente —o fracción— de dos números enteros. Una de sus características es poseer infinitas cifras decimales no periódicas.

Su descubrimiento conllevó la mayor crisis de la historia de las matemáticas.

Los babilonios y los egipcios hicieron aproximaciones a algunos números irracionales sin darse cuenta de que nunca podrían lograr un resultado exacto. También los griegos trabajaron de modo similar, pero ellos acabaron descubriendo la existencia de los irracionales.

Para los pitagóricos, las fracciones expresaban la proporción o razón entre dos números enteros. Esto reflejaba la realidad del mundo tal como lo concebían: todos los elementos de la naturaleza tenían que guardar entre sí una razón exacta. Esa conclusión se derivaba de que sólo conocían los números racionales —expresables mediante fracciones de números enteros— y de sus investigaciones empíricas. Habían hecho algunos descubrimientos donde la proporción sí era exacta y confiaban en desentrañar del mismo modo todos los misterios del universo.

Los detalles del descubrimiento de los irracionales son un misterio. Aristóteles afirma que se produjo al aplicar el teorema de Pitágoras a un triángulo cuya hipotenusa era la raíz de dos, que es un número irracional. De lo que sí estamos seguros es de que fue un descubrimiento dramático para toda la matemática griega, y en especial para los pitagóricos, cuya filosofía científica se basaba en la creencia de que sólo existían números racionales.

Los matemáticos griegos estaban siguiendo un camino que de repente encontraron cortado. El desconcierto fue absoluto, y cayeron en una parálisis creadora que tardaron varias décadas en superar.

…