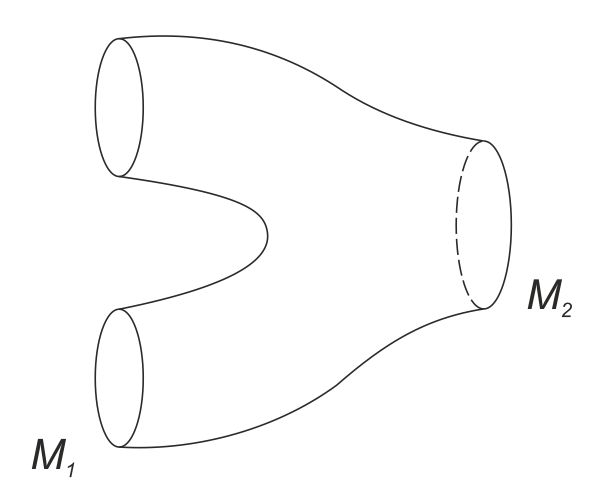
FIG. 1. Cobordismo de dos variedades M1 y M2. La imagen intuitiva más simple es la de un pantalón.
Popper dice: «Las disciplinas son diferentes, en parte, por razones históricas, por motivos de conveniencia administrativa (piénsese en la organización de la enseñanza y de los empleos) y, en parte, porque las teorías que construimos para resolver nuestros problemas tienden a desarrollarse en el interior de sistemas unificados». Pero «nosotros no somos estudiosos de ciertas materias, sino de problemas».[10] Aunque sea por conceder algo a las «razones administrativas», ¿cómo se califica René Thom con respecto a la tradicional división disciplinar?
Suelen decir que soy un matemático. O, mejor, desde un punto de vista sociológico, eso es lo que se me considera. Pero, claro, lo que importa es el tipo de matemática que he practicado.
¿Podría esbozar una breve autobiografía intelectual como matemático?
Mi vocación matemática no está muy clara. En la enseñanza secundaria era un alumno brillante, de ésos a los que se considera dotados tanto para las materias literarias como para las científicas. Fue el azar lo que me impulsó hacia las matemáticas, lo que hizo que me inscribiese en un curso de matemáticas elementales y, luego, en uno de matemáticas superiores. La guerra, por su parte, tuvo también su papel en esta elección: estábamos en 1939… los que habían conseguido la licence en matemáticas podían ir a artillería y no a infantería; esto, claro, contribuyó a hacerme optar por la matemática…
Pero eso no quiere decir que emprenda la carrera de matemático…
No, claro. La auténtica investigación en este campo la inicié en 1946, después de salir de la Ecole Normale.
¿Puede darnos una visión de conjunto?
En aquella época había seguido las clases de mi maestro, Henri Cartan,[11] en la Universidad de Estrasburgo: con él empecé a estudiar los trabajos de Oka,[12] el gran matemático japonés (teoría de las funciones de variables complejas). Mis contactos con la matemática se produjeron, pues, a través de estos trabajos, que eran entonces, en especial para un investigador occidental, un tema notable para la reflexión.
Fue éste un hallazgo intelectual destinado a marcar mis siguientes investigaciones. Por ejemplo: en su aproximación al célebre problema de Cousin[13] (que no hace al caso examinar aquí con rigor), Oka dice que, al tratar de resolverlo, tropieza con una «obstrucción» de carácter topológico. Dicho brevemente: se trata, a partir de piezas de una función, dadas localmente mediante mapas, de reconstruir una función global, es decir una función multiplicativa no nula: ello corresponde a una aplicación en el círculo unidad. Se dispone de toda una familia de aplicaciones en el círculo unidad y el problema consiste, entonces, en saber si se pueden sintetizar todas estas aplicaciones en una aplicación única. Oka había comprendido a la perfección que el problema tropezaba con un obstáculo, con una «obstrucción» de orden topológico. Exactamente en aquel momento —estábamos en 1946— había en Estrasburgo un seminario organizado por Charles Ehresmann,[14] extremadamente puesto al día: en particular en cuanto a las nociones más importantes de la topología algebraica —espacios fibrados, cohomología, operaciones de cohomología según módulo p, etc. Todas estas ideas eran entonces nuevas para muchos: la topología algebraica se estaba consolidando como un articulado y prometedor filón para la investigación. Ehresmann ha hecho mucho por darle, por una parte, una buena conceptualización y, por otra, por presentar sus aplicaciones.
Entonces fue cuando me di cuenta de que las obstrucciones de las que habla Oka se pueden considerar en realidad como obstáculos para la construcción de una sección de un espacio fibrado. En ese punto los problemas que interesaban a Oka eran problemas relativos a la obstrucción de una función analítica… Y en vez de ello tropezaba con una obstrucción de funciones diferenciables. Me planteé entonces un interrogante que hubiese podido devolver a Cartan: ¿por qué resolver en un dominio analítico un problema que no se sabe resolver en un dominio diferencial?[15] ¿No es mejor resolver antes el problema diferencial? Sobre la base de esta reflexión empecé a interesarme de una forma específica por la teoría de las funciones y aplicaciones diferenciales… pero no quiero apoyarme demasiado en el desarrollo de mis propias ideas en matemáticas. Baste decir que mi primer trabajo consistió en la sistematización de la teoría de Morse[16] y, más concretamente, en la demostración de que cuando se da una función en un espacio, tomando las trayectorias del gradiente de esta función en relación con una métrica, puede descomponerse el espacio dado en células, cada una de las cuales se asocia a un punto crítico de índice dado. Ésta es una observación que se manifestó de gran utilidad para mí y llegó a ser clásica en los años siguientes. También Samuel Eilenberg[17] llegó a resultados análogos.
Pero en mi carrera como matemático ha intervenido también la suerte…
¿Por qué?
El extraordinario desarrollo técnico de la topología algebraica entre 1945 y 1950 ha llevado a la introducción de todas aquellas ideas a las que aludía antes: espacio fibrado principal, grupo estructural de un espacio fibrado, espacio clasificador, clase característica, cohomología, operadores cohomológicos, evaluación de las obstrucciones como clases de cohomología… Estas nociones han formado, por así decirlo, un río que ha inundado el campo de la matemática,[18] permitiendo un desarrollo extremadamente rápido en las cuestiones vinculadas a la construcción de los diversos espacios y las diversas funciones… Es en esta perspectiva que he trabajado alrededor de los años cincuenta, interesándome en particular por las llamadas variedades cobordantes…[19]
Así nació la teoría del cobordismo…
Se trataba de saber cuándo dos variedades constituyen precisamente el límite común de una misma variedad: es un problema que, en principio, puede parecer bastante gratuito. Pero si lo pensamos un poco, nos damos cuenta de que es el caso particular de un problema que tiene incluso un aspecto filosófico. Tenemos dos espacios, dos variedades diferentes, y se trata de algún modo de unirlas con una especie de deformación continua. El mejor procedimiento consiste en la construcción de un «cobordismo» entre las dos variedades (fig. 1). Con la ayuda de este tipo de ideas he podido desarrollar toda una técnica sobre las aplicaciones diferenciabas, mediante la cual he conseguido resolver, por lo menos teóricamente, el problema de reconocer si dos variedades son cobordantes, reduciéndolo a términos puramente algebraicos. Pero no he conseguido encontrar la solución algebraica definitiva del problema. Ésta es, por otra parte, una situación generalizada, muy frecuente en topología: retrotraer el problema al álgebra es ya muy difícil y, además, no parece que haya nada que hacer. Esta reducción, en todo caso, se ha considerado muy interesante en sí misma.

FIG. 1. Cobordismo de dos variedades M1 y M2. La imagen intuitiva más simple es la de un pantalón.
¿Por qué?
Con este tipo de técnica he podido apoyar en 1951 mi tesis de doctorado, que trataba esencialmente de ciertos tipos característicos de variedad acerca de los cuales he mostrado la invariabilidad topológica. Tres años después (1954) resolví el problema del cobordismo en un artículo titulado Quelques propiétés globales des variétés differentiables, aparecido en «Commentarii mathematicae helveticae»,[20] donde proporcionaba procedimientos algebraicos para resolver el problema del cobordismo y para reconocer cuándo una variedad es una «buena» variedad. Por este motivo recibí de Heinz Hopf la medalla Fields en el Congreso Internacional de Edimburgo en 1958.[21] Pero, como he dicho ya, fue en parte un golpe de suerte. He cosechado, eso sí, en el momento adecuado, sabiendo hacer uso de las técnicas que Cartan, Ehresmann, J. P. Serre y muchos otros me habían enseñado.
¿Hay alguna otra novedad sobre estos protagonistas de la investigación matemática…?
Casi todos pertenecían al grupo Bourbaki. Al principio, yo también fui seleccionado por los Bourbaki[22] como «cobaya»: como era la costumbre, tenía que asistir a la preparación de las tesis y pedían mi opinión en caso de discusión. Pero, desgraciadamente para mí, ¡resulté un pésimo cobaya! Me cansaba de atender (¡era un poco aburrido!) y en ocasiones llegaba a quedarme dormido durante las sesiones. En cierto sentido, eso no me ha perjudicado: de hecho, poco después, me opuse a la concepción bourbakista de las matemáticas.
¿Por qué?
¡Eran unos auténticos ultraformalistas! Presentaban las matemáticas de una forma rigurosa, aséptica; pero, haciéndolo así, acababan sólo interesándose por aquellas partes de la matemática que se prestaban a tal presentación rigurosa. Y precisamente por esta razón, gran parte de la matemática que se estaba haciendo en ese momento escapaba a su atención.
«El formalismo niega el status de matemáticas a la mayor parte de lo que comúnmente se ha entendido siempre como matemática y no logra decir nada acerca de su desarrollo. Ningún período “creativo” y muy pocos períodos “críticos” de las teorías matemáticas se admitirían en el paraíso de los formalistas, donde las leonas matemáticas existen como serafines, purificadas de todas las impurezas de la incertidumbre terrena».[23] Ahora, nadie sueña poner en duda que algunos problemas de una teoría matemática sólo pueden enfrentarse desde su formalización, así como algunos problemas sobre los seres humanos, relativos por ejemplo a su anatomía, sólo pueden plantearse después de su muerte. Pero limitarse sólo a las teorías formales es como si, en los tiempos de Vesalio, cuando el método de la disección logró imponerse, se hubiese querido identificar el estudio de los seres humanos con el análisis de los cadáveres.
¡Me gusta esta comparación! Aún hoy hay partes de la matemática —cálculo de variaciones, ecuaciones en derivadas parciales, dinámica cualitativa, etc.— que aún no se consideran suficientemente «limpias» (¡o «muertas»!) como para figurar en la antología bourbakista. Existe, pues, una auténtica incompatibilidad entre el repertorio bourbakista y la matemática viva. ¡Bourbaki ha embalsamado la matemática, la ha reducido, por así decirlo, a una momia! Dicho esto, no hay que ser completamente negativo en cuanto a los Bourbaki: el grupo tiene sus propios méritos históricos. Asumió un papel de relevo antes de la guerra, introduciendo en Francia las matemáticas algebraicas de Alemania.
¿Está usted aludiendo en particular a la escuela de Hilbert?[24]
Sí, y sobre todo en oposición a la vieja escuela de la teoría de las funciones que entonces dominaba en Francia: la escuela de Borel, Picard, Hadamard, etc.[25] Pero, sin embargo, ¡no hay que asimilar demasiado los Bourbaki al movimiento «modernista» que triunfó en los años sesenta, que para mí no es otra cosa que una auténtica «perversión» del bourbakismo!
¿Cuál es la diferencia?
¡Yo diría que el movimiento modernista nació como una especie de pulsión en un sentido casi psicoanalítico! Se abrió camino en la comunidad de los matemáticos por una serie de razones que es difícil explicitar; a mí me parece que eran, en todo caso, razones sobre todo de historia local, de sociología de la matemática.
¿Y en el terreno de la didáctica matemática?
El movimiento modernista ha renovado en parte la enseñanza de la matemática, que sufría en Francia de una cierta esclerosis, debida a la presencia de los exámenes de las Grandes Ecoles. Desde el principio, el alumno era formado para superar estos exámenes; los programas quedaban fijados de una vez por todas, eran prácticamente eternos. Se aprendía la geometría descriptiva, por ejemplo, porque la había instaurado Monge,[26] el creador de la Ecole Polytechnique, etc.
Así que la exigencia de renovación era real…
Sí. Pero luego evolucionó en un sentido bastante absurdo. El logicista, para entendernos. Teoría de conjuntos, notación lógica, cálculo proposicional, teoría de la cuantificación, etc., son cosas que, tanto para el matemático profesional como para el estudiante corriente de matemáticas, tienen muy poca utilidad.
Ése es un punto de vista con el que muchos no estarían de acuerdo…
¡Son muy libres de ello! Pero, según mi opinión, la teoría de conjuntos no tiene de por sí mucho interés, por ejemplo, en matemáticas. Como máximo, se le encontrará un interés en el hecho de que aporta un simbolismo, una estenografía para ciertas articulaciones del razonamiento.
Hilbert hablaba en su tiempo del «paraíso cantoriano». Brouwer era algo más sospechoso.[27] Alguien, finalmente, ha definido la construcción cantoriana del transfinito como una catedral barroca.
Para mí, más que barroca, es fantasmagórica, es decir que está absolutamente montada en el aire. No posee ninguna relación con la matemática normal…
Pero ¿piensa usted lo mismo de teoremas como el de Gödel, el de Tarski, o de los resultados más recientes, de consistencia y de independencia de Gödel o de P. J. Cohen?[28]
Aparte de un cierto interés filosófico —innegable—, estos resultados demuestran tan sólo que es inútil trabajar en determinadas direcciones. Ésta es, y perdonen el juego de palabras, su utilidad. Son como guardacantones que nos indican que no hay que salirse de la carretera.
En suma: que no se puede (y no se debe) formalizarlo todo.
¡Exactamente! Incluso para responder a los así considerados fundamentos de la matemática. Ha sido una pretensión aberrante la de que la matemática pudiera basarse en sí misma. ¿Por qué, después de todo, debería ser la matemática la única ciencia que pudiese encontrar sus fundamentos en sí misma o en la lógica?
Entonces ¿está usted de acuerdo con Dieudonné[29] cuando dice que Bertrand Russell,[30] al promover su sistema logicista, ha hecho perder el tiempo a aquellos matemáticos —pocos— que le han seguido?
Estoy de acuerdo con el fondo de esta actitud. Por otra parte me satisface que Bourbaki haya cambiado de punto de vista. El propio Dieudonné lo ha reconocido. En 1935 Dieudonné estaba ideológicamente con Cantor[31] en contra de «aquellos viejos reaccionarios» (como Borel y Lebesgue)[32] que insinuaban que todas estas construcciones no llevarían a ninguna parte. Y hoy Bourbaki, por boca de Dieudonné, asume exactamente la misma posición que aquellos viejos reaccionarios. A este respecto, ¡yo también sería un reaccionario!
Pero ¿no se dan hoy nuevas aproximaciones al problema de los fundamentos? Aludo a la aproximación categorial, que cuenta ya con una larga historia, desde MacLane a Lawvere.[33]
Confieso que no siente mayor simpatía por la teoría de las categorías que por la teoría de conjuntos. Es verdad que también la teoría de las categorías ofrece, obviamente, un lenguaje en ciertos casos precioso; pero dudo de que se trate de algo más que de un lenguaje. El propio MacLane ha admitido que en la teoría de las categorías se ha producido mucho abstract nonsense:[34] Finalmente, sí, los categoristas han trabajado mucho, pero no lo suficiente como para reducirlo todo a abstract non-sense. Así pues, mientras no se haya reducido todo a abstract non-sense, queda bastante por hacer. Personalmente, no comparto esta visión negativa de la matemática. No creo que la matemática consista o deba consistir toda ella en una reducción a abstract non-sense.
Cerremos este paréntesis y volvamos a su historia de matemático profesional.
Después de los años 1958-60 pasé por un periodo más bien difícil; me encontré ante problemas de topología pura que estaban más allá de mis posibilidades: como, por ejemplo, problemas de la teoría de las variedades topológicas, de las estructuras PL,[35] etc. No conseguía siquiera dedicar mi tiempo a estos problemas, me agotaban. Finalmente, me replegué hacia una teoría en cierto sentido más simple, la de las aplicaciones diferenciables. Aquí es oportuno reconocer los grandes méritos de Hassler Whitney,[36] que ha aportado en este campo unas intuiciones esenciales acerca de la clasificación de las singularidades de las aplicaciones del plano sobre el plano (en 1954-1955). Por medio de estas ideas conseguí sistematizar sus construcciones e introducir una noción, convertida más adelante en clásica como noción de conjunto estratificado.[37] Ello me permitió desarrollar una técnica que permitía en cierta medida la clasificación de las singularidades de las aplicaciones diferenciables. Pero también aquí tropecé con dificultades que no me permitieron tener éxito en el sentido del término. Sólo en 1965-1966 pudo el matemático J. Mather llevar a término estas demostraciones.[38]
Sin embargo, no considero infructuosos estos trabajos míos: he derivado de ellos ideas importantes, como la del «despliegue universal» de una singularidad de una aplicación, idea clave de la que después será la teoría de las catástrofes.[39]
Y ¿qué es un despliegue universal?
Es difícil explicar en pocas palabras de qué se trata, a pesar incluso de que en un cierto sentido no es difícil de comprender. La base es que cuando se tiene un germen de una función[40] siempre es posible introducirlo en una familia maximal. Este germen analítico genera una familia, que es la familia de todas sus deformaciones. Debido a la misma estructura, por tanto, genera algo cualitativamente.
Un despliegue universal no es otra cosa que una forma de desplegar toda la información intrínseca encerrada en una singularidad. En mi opinión, una singularidad de una aplicación es siempre algo que concreta toda una estructura global en una estructura local.[41]
Gracias a los trabajos de B. Malgrange, que ha demostrado una generalización del «teorema de preparación de Weierstrass»,[42] he podido mostrar que esta idea del despliegue universal servía para las estructuras diferenciables.
Esta idea del despliegue universal es, pues, en mi opinión, un complemento muy importante de aquella constelación de ideas que acompañan el surgimiento del cálculo diferencial. En cierto sentido, es un regreso a la matemática del siglo XVIII, después de toda la gran elaboración analítica y formal del XIX.
La idea del despliegue universal contiene en cierto sentido toda la parte cualitativa de la fórmula de Taylor:[43] cuando se tiene un germen de función diferenciable, que localmente es un desarrollo de Taylor y que puede cerrarse racionalmente, truncando en un cierto punto el desarrollo de Taylor, este desarrollo truncado seguirá el mismo proceso, tendrá el mismo tipo topológico del germen de la función diferenciable.
Toda esta teoría de la singularidad permite resolver el problema de dar condiciones suficientes para que el germen truncado hasta el orden k sea equivalente, vía un cambio de variable, al germen de la función inicial. Es evidente que se trata de algo intelectualmente muy satisfactorio, en cuanto permite reducir localmente un germen, descrito por una serie infinita, a una serie que consta de un número finito de términos; así se da una gran economía de pensamiento: un medio único para describir todas las deformaciones posibles de este germen.
En 1966 di, un poco empíricamente, la lista de las siete singularidades que aparecen en un despliegue de dimensión inferior o igual a 4: éstas se interpretaron más adelante como las siete catástrofes elementales.[44]
¿Y luego? ¿Cuáles son los ulteriores desarrollos de su investigación matemática?
Desde ese momento me desinteresé un poco de las matemáticas. Dediqué mi esfuerzo a la teoría de las catástrofes, una investigación que aún está creciendo, y he dejado un poco de lado la matemática propiamente dicha…
Pero, la teoría de las catástrofes, ¿no es matemática?
Se inicia en la matemática, pero no es matemática. Ya hablaremos de esta ambigüedad. En cualquier caso, nunca me he considerado verdaderamente un matemático. El matemático, en mi opinión, ha de encontrar placer en las dificultades, en las estructuras hermosas, ricas y profundas. Yo no siento este placer. Las estructuras ultrarrefinadas por las que se apasionan mis colegas —grupos de Lie, grupos simples finitos, etc.; en resumen, toda esta especie de mitologías matemáticas— no me han interesado nunca en realidad. En su lugar, estimo las cosas que se mueven, las cosas flexibles que se pueden deformar y que puedo transformar a mi gusto.
Es un tipo de matemática muy diferente de la que practican los algebristas y soñaba Bourbaki: la matemática de las estructuras «limpias», con las que se sabe lo que se hace…
¡Prefiero el campo de la matemática en que no se sabe demasiado bien lo que se hace! Por eso considero hoy las matemáticas con una cierta distancia: no se puede decir que exista hoy un problema alguno estrictamente matemático por el cual sienta un apasionado interés. Es inevitable: ¡no se puede consagrar toda la propia vida a la matemática!
Pero ¿no es el propio René Thom quien acabó un artículo suyo con las siguientes palabras: «…Sólo el matemático, que sabe caracterizar y generar las formas estables a gran alcance, tiene el derecho de utilizar los conceptos (matemáticos); sólo él, en el fondo, tiene el derecho de ser inteligente»?[45]
No hay que exagerar. La matemática es difícil, pero creo que la física teórica también presenta auténticas dificultades. Mientras no se den similares dificultades intelectuales en otros campos de investigación, existe, según mi opinión, una diferencia cualitativa entre las matemáticas y la física teórica por un lado y las otras disciplinas, por otro. Estas últimas, creo, están a un nivel intelectual inferior.
El saber matemático se considera generalmente un saber a priori, mientras que las otras disciplinas son saberes a posteriori. ¿Cómo ha podido la física teórica situarse a tan gran proximidad con la matemática? ¿Cuál es la razón de su prestigio entre las distintas disciplinas «empíricas»?
La física teórica plantea, efectivamente, graves problemas. En la actualidad, estoy en un instituto en el que trabajan codo con codo físicos y matemáticos y a menudo se discute acerca de las respectivas dificultades. Le he oído decir a un colega mío, físico —un colega al que por otra parte tengo en gran estima— que es infinitamente más difícil hacer buena física que buena matemática. Creo que tiene razón. Hacer buena física exige de veras un tipo de intuición más sutil que la que es indispensable para la buena matemática.
¿Alude usted, en particular, a algún sector específico de la física teórica?
Pienso sobre todo en la mecánica cuántica; en particular en la llamada renormalización, que ha constituido uno de los grandes algoritmos de la teoría cuántica del campo. Pero este algoritmo ha sido durante mucho tiempo un enigma para los matemáticos profesionales; sólo ahora se empieza a entrever una descripción matemáticamente correcta. Éste se relaciona con la teoría de la bifurcación: en cierto sentido, la renormalización puede convertirse en algo similar a una forma canónica de bifurcación.[46]
¿Cómo se plantean, pues, las relaciones entre la física teórica y la matemática? El gran físico italiano Enrico Pérsico decía de una fase precedente a la mecánica cuántica: «Los físicos han encontrado el instrumental matemático ya dispuesto».[47] El ejemplo de la renormalización, como otros casos en el desarrollo de la mecánica cuántica (por ejemplo, la célebre «función» de Dirac, que ha precedido en más de veinte años la teoría rigurosa de las distribuciones debida a Schwartz)[48] parecería demostrar lo contrario. Dicho brevemente: ¿son los matemáticos los que proporcionan a los físicos sus «instrumentos para pensar»? ¿No serán los físicos quienes planteen a los matemáticos las cuestiones que ellos han de resolver, induciéndoles a forzar sus marcos conceptuales?
Ésta es una pregunta que me interesa mucho, en cuanto que se relaciona con un argumento suscitado por ciertos opositores a la teoría de las catástrofes, los cuales han sostenido que en las ciencias empíricas no hace falta utilizar esquemas matemáticos a priori. Al contrario, dicen, son estos esquemas los que se adaptan a las necesidades de la experiencia.
En una dura crítica a la teoría de las catástrofes y a sus aplicaciones a las ciencias biológicas y sociales, Sussmann y Zahler escriben: «… la teoría de las catástrofes es un intento de hacer ciencia tratando de imponer al mundo un sistema preconcebido de estructuras matemáticas, más que mediante el método experimental».[49]
Pero ¿existe el método experimental? Sussmann y Zahler son un ejemplo típico de los críticos a los que me refería. Históricamente, sin embargo, se constata que los esquemas matemáticos han preexistido siempre a las exigencias de la experiencia. De ello hay ejemplos notables: pensemos en las cónicas, estudiadas por Apolonio en el siglo III a. de J. C.: encontraron aplicación sólo con Kepler.[50] O el caso del cálculo tensorial, que encontró su aplicación en la relatividad general.[51] Por no hablar de la utilización —como ya decía Pérsico— de estructuras matemáticas «ya dispuestas» en la mecánica cuántica: cálculo de matrices, espacios de Hilbert, operadores en espacios de Hilbert, etc.
Para la tesis del carácter pre-formado, casi a priori, de las estructuras matemáticas aplicadas a la física teórica o a otras ramas del conocimiento de la realidad, hay un único y genuino contraejemplo: la teoría ondulatoria de Fourier. Resulta muy claro que la teoría de las series de Fourier está en realidad inspirada en la física, y precisamente en el estudio de las cuerdas vibrantes o en la teoría del calor.[52]
Éste es el motivo de que me horrorice un poco la teoría de la transformada de Fourier. Se trata de uno de esos algoritmos por los que la inmensa mayoría de los matemáticos y científicos se desviven, pero yo siempre lo he encontrado odiosamente lineal. ¡Demasiado lineal para ser serio!
Pero ¿no habrá quizá algún ejemplo de lo contrario? Pensemos en el cálculo de los operadores creado por Heavisid[53] o en la δ de Dirac. Dirac utilizaba la «función» δ antes de que Schwartz le abriese las puertas del «paraíso del rigor».[54]
Es cierto. Pero también aquí nos encontramos en un punto de vista similar al de la transformada de Fourier. En cuanto a esta última, como ya lo he dicho, estoy dispuesto a reconocer que ha sido sugerida por la mecánica, por la física.
Sin embargo, en muchos otros casos ha sucedido lo contrario. En cuanto a los desarrollos de la física teórica del siglo XX, en particular de la mecánica cuántica, la teoría cuántica del campo, la situación resulta bastante paradójica. De hecho es una paradoja que una teoría forjada en los años 1930-1935 y desarrollada en el marco de una matemática un tanto «barroca», supersofisticada, no haya desembocado hasta ahora en una auténtica matemática. Éste es un síntoma bastante inquietante. Quizá se me acuse de alimentar una especie de prejuicio «imperialista», pero me parece importante para una teoría física que conduzca a una matemática significativa. Sin embargo, no ha sido esto lo ocurrido con la teoría cuántica del campo.
En la práctica, siempre que se han introducido símbolos que en principio no parecían denotar nada, se ha presentado a continuación alguien que ha proporcionado un modelo que ha permitido ver que el procedimiento en cuestión tenía fundamento, era riguroso. Por ejemplo, los matemáticos han introducido los números negativos y luego han creado los números imaginarios mediante un puro simbolismo: de lo que se trataba era de manipular símbolos, sin preocuparse de si correspondían en realidad a algo. El rigor vino después, y me refiero con ello, por ejemplo, a la interpretación de los números complejos como vectores en el plano, es decir, al conocido modelo de Argand y Gauss.[55]
Pues bien, en la teoría cuántica del campo, se ha dicho que no se sabe multiplicar demasiado bien las distribuciones: pero se multiplican lo mismo, postulando la licitud de esta operación y se arreglan las cosas para derivar un cálculo, etc., pero la desgracia es que los esfuerzos por hacer de este cálculo algo riguroso, incluso en el caso mejor establecido físicamente de la electrodinámica cuántica, no han tenido éxito. Y también esto es un síntoma inquietante: quizá sea la primera ocasión en que los físicos han introducido verdaderamente un formalismo y los matemáticos no han sido capaces de justificarlo.
¡Al contrario de lo que ocurre con los números negativos y los imaginarios![56]. Pero lo que ahora está diciendo, ¿no contradice su predilección por «las cosas que se mueven», su tesis de que la investigación de los fundamentos es una desviación, y que el rigor no es lo más importante?
Por supuesto que estoy convencido de que las cosas que se mueven son fascinantes, mientras que no hace ninguna falta quedarse embobado con el rigor por sí mismo. Pero la desgracia es que los físicos razonan de una manera completamente distinta. Los físicos, en general, son personas que de una teoría mal planteada deducen resultados (numéricos) que llegan hasta la séptima cifra decimal, ¡y luego comprueban esta teoría intelectualmente poco satisfactoria buscando una concordancia hasta la séptima cifra decimal con los datos experimentales! Se da así un horrible batiburrillo entre la incorrección de los conceptos básicos y una fantástica precisión numérica. Y he aquí la laguna: si los físicos no fuesen globalmente rigurosos, es decir, si no fuesen rigurosos ni en la elaboración intelectual ni en el resultado numérico, no habría nada que objetar; pero, por desgracia, pretenden llegar a un resultado numéricamente muy riguroso a partir de teorías que conceptualmente no tienen ni pies ni cabeza.
Esta forma de practicar la ciencia, que según usted parece caracterizar una buena parte de la física teórica actual, ¿no tendrá quizá sus raíces en una tradición que se remonta hasta Newton o tal vez hasta Galileo?
Por lo menos en cierta medida, contestaría afirmativamente: es la herencia del hypotheses non fingo de Newton. Es verdad que Newton no solía aceptar de buen grado la falta de una genuina teoría explicativa, por el contrario… ¡pero hypotheses non fingo! Hacia finales del siglo XVII se había llegado así a decretar que, después de todo, ya no era necesario buscar explicaciones cuando se disponía de una fórmula que funcionaba. La física ha adoptado, pues, el punto de vista según el cual las fórmulas que tienen éxito se presentan sin más explicación. Los filósofos positivistas más radicales han sostenido que el papel de la ciencia es el de proporcionar una serie de recetas que funcionen, es decir que permitan hacer predicciones y actuar con eficacia.
¿Hay, pues, una clara contraposición entre explicación y predicción?
¡Explicación y predicción son objetivos bastante contrapuestos en la empresa científica! Pero de esto ya hemos hablado.
Volvamos a la física de nuestro tiempo. ¿Considera usted que toda la investigación física actual se encuentra en las condiciones de la teoría cuántica del campo? ¿O hay teorías intelectualmente más satisfactorias?
Creo que en la llamada física fundamental —física de las partículas elementales, física de las altas energías, etc.— se está pasando en la actualidad por un período de fermentación que no se presta a la realización de balances.
Me sentiría tentado de decir que la experiencia ha permitido recopilar una fenomenología considerable, aunque los esfuerzos teóricos por organizaría de forma coherente han quedado en un estadio más bien rudimentario: cada vez más rudimentario a medida que tal fenomenología ha ido enriqueciéndose.
¿En qué sentido?
En el sentido de que, mientras más «hechos» nuevos han ido apareciendo para ser ordenados, más necesario se hace disponer de unos marcos conceptuales adecuados. Pero éstos han ido revelándose cada vez más bastos. En mi opinión, la teoría de los quark[57] es, en el momento actual, una teoría notablemente basta. Un colega se manifestó al respecto de una forma más bien brutal, que no repetiré aquí. Otro, con no menor brutalidad, ha modificado esa opinión definiendo dicha teoría como un estercolero en el cual, sin embargo, podrán germinar nuevas y prometedoras teorías.
¿Y cuál es su opinión?
Yo creo que la mecánica cuántica, aparte de sus dificultades, plantea problemas filosóficos significativos, como por ejemplo el de comprender la naturaleza del espacio y del tiempo en relación con las entidades físicas. Cabría preguntarse si, otológicamente, lo primero es el espacio-tiempo de los entes físicos —materia y radiaciones— o bien si estos últimos no deberían considerarse como entidades primarias y el espacio-tiempo una especie de superestructura deducida de ellos de una manera —por otra parte— bastante misteriosa. Yo mismo me he planteado muchas dudas ante este problema: inicialmente, el planteamiento de la teoría de las catástrofes me impulsó a considerar el espacio-tiempo como entidad primaria y las partículas y las radiaciones como singularidades inmersas en esta especie de éter primitivo. Ésta era en el fondo la concepción de Einstein, subyacente a su teoría de la relatividad general. Él quería volver a ésta mediante una conveniente teoría del campo unificado.[58] Sin embargo, he de reconocer que el formalismo cuántico no se presta mucho para una resolución de este tipo y que quizá haya que aceptar la idea de que el espacio-tiempo no es la entidad primaria. Podrían darse entidades más fundamentales, en un cierto sentido más «psíquicas», es decir más relacionadas con el psiquismo del observador.
¿Contrariamente a Einstein, pues, una revalorización del «espíritu de Copenhague»?
Sí, desde este punto de vista quizá haya algo justo en la interpretación de Copenhague; incluso podría admitir que hay algo de verdad en esta visión del universo, según la cual la entidad primitiva es el fenómeno percibido por un observador. El problema consiste entonces en sintetizar las distintas visiones que tenga cada observador. Es en este sentido en el que he procurado investigar la fase compleja de la función de onda de la mecánica cuántica como expresión de una ruptura de la simetría de la intersubjetividad de los observadores. Ésta es una idea que nunca han explotado las diferentes filosofías de la ciencia, y sobre la cual habrá que volver. Es una idea que me vino sugerida por la teoría de las catástrofes…
¿Y…?
En la base está la idea de que la ciencia es conocimiento intersubjetivo. Para que sea objetiva, toda nueva adquisición ha de ser objeto de consenso: es imprescindible, pues, que los observadores se sumen y desempeñen un papel igual en la adquisición y en la interpretación de este saber.
Es una exigencia muy dura…
Sí, y si se la transfiere a un modelo geométrico o mecánico, se ve uno inmediatamente conducido a considerables restricciones respecto a la naturaleza de los entes matemáticos que pueden servir para la descripción de los fenómenos.
Es precisamente según este punto de vista que he llegado a pensar que se podía interpretar la fase de un fenómeno cuántico como una ruptura de la simetría de la intersubjetividad de los observadores.
¿Y en lo que se refiere al tiempo?
Otra de mis ideas preferidas es que el tiempo sigue siendo, a pesar de todo, algo fundamentalmente irreversible. Cuando los físicos afirman que todos los procesos físicos son reversibles, expresan lo que los ingleses llaman un wishful thinking, una intención piadosa; separan del fenómeno todos aquellos aspectos que exhiben una cierta irreversibilidad para conservar sólo el que es perfectamente reversible. Pero yo creo que no existe ninguna fenomenología sin alguna forma de irreversibilidad, dado que, para que se produzca un fenómeno, es necesario que algo penetre en nuestro ojo.
Los atomistas antiguos —Demócritof Epicuro, Lucrecio…— pensaban que unos entes pequeñísimos, los corpúsculos, penetraban de verdad en nuestro ojo…[59]
¡Es como si un objeto natural penetrase de verdad en nuestro ojo! En el acto mismo de nuestro conocimiento sea como sea, hay siempre algo fundamentalmente irreversible. Y sólo ha sido cancelando este aspecto irreversible como los físicos han podido decir que los fenómenos son regidos por leyes reversibles…
Pero en algunos campos podrían tener razón, como en la mecánica celeste.
Precisamente ésta constituye, por el contrario, uno de mis ejemplares favoritos. Si la mecánica celeste da lugar a una fenomenología es porque vemos los planetas, y los vemos porque los ilumina el sol.
Al acoplar la mecánica celeste (que en primera instancia es reversible) con ese fenómeno fundamentalmente irreversible que es la radiación solar (la transformación de la energía gravitacional del sol en energía luminosa), podemos ver los planetas y, en consecuencia, el fenómeno reversible se convierte en una fenomenología. Éste es un hecho fundamental.
¿Cómo evaluar entonces la dicotomía reversible/irreversible en la física y en la química? ¿No ha sido esta dicotomía lo que ha propiciado el nacimiento de la termodinámica como sector autónomo de investigación?
Para contestar hay que salir por un momento del marco de la física fundamental para entrar en el de la macroscópica. En la física macroscópica la irreversibilidad es con toda claridad, la reina. Y aquí está la paradoja: a un nivel macroscópico. Creo que una de las razones puede ser que, a nivel macroscópico, se da una permanencia de la validez de la descripción lingüística. En otros términos: la descripción cualitativa del fenómeno, en el lenguaje común, tiene un valor permanente. La idea de irreversibilidad queda, en cierto modo, englobada en la gramática; la irreversibilidad, por así decirlo, está en la gramática.
¿Por ejemplo?
Ya en la distinción entre substantivo y verbo en la frase se da una especie de germen de irreversibilidad. Recurramos a mi ejemplo preferido: el gato se come al ratón. Se trata claramente de un proceso fundamentalmente irreversible…
Pero no todos los verbos expresan acciones irreversibles…
De acuerdo. Sin embargo me parece que si la irreversibilidad se ha aceptado en el mundo físico, es decir que se ha hecho compatible con un consenso intersubjetivo, ello se ha producido como consecuencia de la utilización del lenguaje común. El lenguaje cotidiano ha permitido la existencia de un consenso intersubjetivo en cuanto a la descripción de procesos irreversibles, mientras la descripción matemática no lo permite. Pensemos en la usual teoría hamiltoniana, esto es en la mecánica reversible. Lo que se deseaba era un modelo cuantitativo e intersubjetivamente válido. Lo cual quiere decir válido no sólo para los hombres del presente, sino también para los del pasado y el futuro: un marco global válido con independencia de la época.
¿No es posible, pues, elaborar una matemática de la irreversibilidad?
Me parece difícil. Se puede elaborar un sistema diferencial que percuta atractores: se parte de una determinada situación inicial y se buscan los estado asintóticos de la trayectoria. Si estos estados presentan propiedades, en un cierto sentido, de estabilidad estructural, se puede caracterizar una determinada evolución hacia un límite, pero, y esto es lo curioso, el propio estado asintótico se convierte en reversible. Cuando se va a t = ∞, es decir cuando se considera el límite para t tendiendo al infinito, da igual que se tome infinito + 1 o simplemente infinito, se obtiene el mismo límite. Por tanto, en cierto modo, queda abolido el efecto del tiempo en el límite mismo: ésta es, según yo lo entiendo, una de las razones de la reversibilidad de las leyes físicas.
Aquí han quedado relegadas las situaciones transitorias, lo que es por otra parte, típico de la mecánica cuántica: lo único que se puede decir es que se «salta» de un estado inicial a uno final La transición no la conoce nadie ni nadie es capaz de describirla.
¿Pero qué decir entonces de la extrapolación de la irreversibilidad de la física a la biología?
Aquí estoy de acuerdo con Ilya Prigogine en decir que los fenómenos de los seres vivos son irreversibles. Se trata de una afirmación tan evidente que no creo que nadie se atreviese a insinuar lo contrario. Habría mucho que discutir, sin embargo, en cuanto a la metodología de Prigogine. Prigogine partió de la termodinámica; pero me parece que siempre que se han podido exhibir efectivamente las que Prigogine llama «estructuras disipativas» ha sido gracias a leyes específicas de la dinámica, en las cuales la termodinámica no aparece. Bajo esta perspectiva, me parece que su teoría resulta algo confusa, en cuanto se presenta como termodinámica en situaciones en que la termodinámica clásica no desempeña papel alguno. Nos reducimos siempre al estudio de un sistema explícito, si el sistema explícito no se conoce por completo podemos servirnos entonces de consideraciones cualitativas como las de la teoría de las catástrofes o la teoría de la bifurcación. Yo creo que mi posición es más coherente: siempre he procurado presentar modelos geométricos de las situaciones límite de las dinámicas irreversibles; precisamente en la teoría de las catástrofes me esforcé por dar en cualquier forma conceptualizaciones de los fenómenos irreversibles típicos, como por ejemplo el salto de un atractor a otro.
¿En conclusión?
En cuanto atañe a la investigación física, creo que junto a la física fundamental queda un notable lugar para la física macroscópica. Según este punto de vista, me parece legítimo concluir, aunque sea pecar un poco de optimista, que mi libro ha contribuido en algo a hacer que los físicos vuelvan a la física macroscópica, sustrayéndolos a la fascinación de la física fundamental. Y pienso en particular en la física de los sólidos y, sobre todo, en la física de los medios ordenados, de los cristales líquidos, etc. Se trata de un sector en el que en estos últimos años se han hecho muchos progresos. Una de las ideas más interesantes, en mi opinión, es la que se encuentra en la base del principio de Kleeman-Toulouse que permite reconocer, en una estructura ordenada, cuáles son sus defectos estructuralmente estables. Se trata de un principio que proporciona un criterio topológico en relación con la estabilidad estructural de estos defectos.
Quizá la idea no se derive directamente de la teoría de las catástrofes, pero concuerda bastante bien con su filosofía general, según la cual una estructura ordenada es algo así como un dato global y el defecto aparece como una obstrucción al prolongar este dato global a través del defecto. Quizá no quede muy claro, pero cuando se ven unos ejemplos se comprende enseguida de qué se trata. Presentemos algunos: pensemos en la orientación de las moléculas en un «neumático»;[60] nos encontramos aquí con un defecto que se denomina «curva de disclinación»; el vector constituido por la dirección de las moléculas gira cuando se dan vueltas en torno al defecto de la «curva de disclinación» y se obtiene un gradiente asociado a esta singularidad del campo vectorial; la no nulidad de este gradiente implica la estabilidad del defecto. Se trata de una idea de gran profundidad y ciertamente útil que demuestra, entre otras cosas, que las consideraciones topológicas, incluso las cualitativas, pueden intervenir en la morfogénesis de los medios inanimados.
Hasta aquí, la física. ¿Y en cuanto a la química?
Para mí la química representa una especie de zona intermedia entre las teorías matematizadas de la física teórica, como la mecánica y la física instrumental, y las teorías conceptualmente más fascinantes que se dan en biología y, hasta cierto punto, en las ciencias humanas. La química es un terreno en el que la materia actúa en cierto modo a su albedrío. En todo caso, la teoría general de la cinética química es una buena teoría que ha servido, entre otras cosas, como modelo básico para la teoría de las catástrofes, que en su forma biológica original se había inspirado en Max Delbrück[61]. Esta teoría se podía también interpretar en términos del campo de la cinética química local, y desde este punto de vista tal modelo químico ha desempeñado su papel en la elaboración de la teoría de las catástrofes. Sin embargo, he de confesar que la química propiamente dicha nunca me ha interesado mucho.
¿Por qué?
Quizá porque nociones como las de valencias, enlace químico, etc., nunca me han parecido demasiado claras desde el punto de vista conceptual. En cualquier caso, las conceptualizaciones vinculadas a la noción de densidad electrónica en las moléculas y una clasificación de las diversas bifurcaciones que experimenta la nube de densidad electrónica en el entorno de las moléculas podrían, quizá, permitir una conceptualización más satisfactoria de estas nociones.
Luego la química, por así decir, es morfológica. Por ejemplo, todo lo que se ha hecho recientemente a propósito de las reacciones del tipo de la Zabotinskij[62] puede dar origen a interpretaciones bastante interesantes, tanto más cuanto que hay bien pocas reacciones químicas que den origen a morfologías, por lo menos a morfologías fácilmente interpretables.
Y sin embargo, también en otros sectores este tipo de morfologías podría resultar prometedor…
Evidentemente, si consideramos las diversas cristalizaciones en los materiales, se presenta toda una interesante morfología. Pero esto es bastante difícil de interpretar.
Hay otro aspecto interesante: en los años 1910 Stéphane Leduc pretendió dar una teoría de la vida utilizando la morfología química. Producía células con membranas artificiales. Seguramente hay en todos estos trabajos elementos para llevar a cabo productivas reflexiones y quizá nos hayamos detenido demasiado pronto en este camino. En mi Stabilité structurelle et morphogenése he preconizado un estudio más sistemático de la formación de la morfología de los medios inanimados: racionalmente no se puede esperar comprender la morfología del viviente antes de haber comprendido bien la morfología de los medios inanimados. Me parece que en estos últimos años se ha hecho un esfuerzo apreciable en este sentido: hoy se acepta con más facilidad la idea de que ciertos medios inanimados generan de forma casi obligatoria, de forma extremadamente estable, morfologías extremadamente complejas. Y he aquí un orden de ideas que aportará con seguridad una nueva precisión conceptual… Obviamente, esto va contra las viejas creencias de la termodinámica, cuyo segundo principio nos dice que los sistemas van siempre de un estado ordenado a otro caótico. En realidad, si se considera de cerca la demostración del segundo principio de la termodinámica, no hay nada en absoluto que permita afirmar que la variación de la entropía esté necesariamente vinculada a una evolución hacia un estado caótico. La evolución de un sistema hacia un estado más estable podría estar relacionada con la aparición de un orden. Aquí hay evidentemente algo nuevo que los investigadores no han comprendido siempre del todo.
Habla usted, tanto respecto a la física como respecto a la química, de morfologías estructuralmente estables. Ya nos ha planteado las razones epistemológicas profundas que inducen a presuponer la estabilidad. Sin embargo, en cuanto a la mecánica, la mayor parte de los procesos no parecen estructuralmente estables.
Anticipemos aquí la que ha sido una de las más formidables objeciones a la teoría de las catástrofes. Se ha dicho que, después de todo, las leyes físicas, y en particular las de la mecánica, no son estructuralmente estables; por consiguiente, la hipótesis de la estabilidad estructural hecha a partir de modelos no es pertinente. Mi respuesta es, muy brevemente, ésta: si nos servimos en ciertos casos de la mecánica hamiltoniana, es decir de una mecánica conservativa y reversible, es porque existe un vínculo subyacente que obliga a tener en cuenta este tipo de dinámica.
¿Qué vínculo, por ejemplo?
El vínculo de la intersubjetividad. Como ya he dicho, hay que presentar una descripción válida tanto para el pasado como para el futuro. Lo curioso es que al nivel de lo macroscópico esta exigencia ya no se satisface: los modelos pierden, en cierto modo, su validez; pero siempre sigue siendo válida la descripción lingüística. Éste es un fenómeno de difícil explicación: ¿por qué la descripción lingüística mantiene su validez en nuestro universo? Con las mismas palabras describimos los mismos objetos y éstos tienen prácticamente siempre las mismas propiedades, la misma apariencia, la misma forma, la misma composición. Verdaderamente, se trata de uno de los grandes enigmas del mundo en que vivimos.
Nosotros no tenemos conciencia inmediata de este enigma porque nuestro espíritu está organizado de tal modo que nos basamos en la estabilidad de las cosas para poder hablar de ellas, para utilizarlas, etc., pero eso no impide que en un plano científico la estabilidad de las cosas constituya un enorme problema.
Esta cuestión está bastante vinculada a consideraciones extremadamente refinadas sobre los sistemas hamiltonianos; en un sistema de estas características se encuentran con frecuencia lo que yo llamo «atractores vagos». Un atractor vago es una especie de gran apertura cuyo comportamiento es más o menos caótico; y después además de éste, existen unos pequeños núcleos centrales, como por ejemplo el entorno de una trayectoria cerrada central, en la que el punto se encuentra prisionero y ya no puede escapar. El conflicto entre estos distintos atractores vagos quizá pudiera modelarse con consideraciones del tipo de la teoría de la bifurcación,[63] que se pueden describir lingüísticamente.
Finalmente, el hecho de que la mayor parte de los objetos con los que nos relacionamos en el mundo en que vivimos, en el mundo macroscópico, sean sólidos, corrobora a mi entender la idea de que la fase sólida sea de hecho la fase cristalina, fase que tiene una periodicidad estricta en oposición a las fases líquida y gaseosa, que son infinitamente menos ordenadas. Quizá una reflexión más profunda sobre el problema de la transición entre las fases permitiría comprender la estabilidad de la descripción lingüística, al menos parcialmente, ya que en la lengua interviene también el aspecto biológico, en particular la depredación.[64]
De la química, pues, pasemos a la biología.
La biología actual está dominada por la teoría molecular. Habría mucho que decir sobre la fascinación que ejerce la biología molecular estos últimos años. Hay algo que me parece cierto: la mayor parte de las ideas que se preconizaron en los inicios de la biología molecular han experimentado de forma repentina considerables replanteamientos. Verdad es que el célebre «dogma central» según el cual el DNA es útil para la síntesis de las proteínas sigue prácticamente inalterado,[65] pero las ideas que había acerca de los mecanismos que permiten esta síntesis han experimentado considerables modificaciones.
¿Por ejemplo?
Recuerdo que en cierta ocasión, en 1966, Waddington[66] me había invitado a un coloquio sobre biología teórica, celebrado cerca de la Villa Serbelloni, en Bellagio, donde me encontré con Francis Crick.[67] En esa ocasión tuve con él discusiones más bien duras, en particular sobre la cuestión de saber si una bacteria podía tener una morfología interna. Crick mantenía que la bacteria es una enzyme-bag, mientras que según, mi opinión, está dotada de una morfología interna extremadamente sutil y complicada. Creo que, como consecuencia de ello, la mayor parte de los bacteriólogos y de los microbiólogos abandonaron la idea de la enzyme-bag, reconociendo la existencia de un morfología interna de la bacteria.
En cuanto a los mecanismos que regulan la duplicación de DNA, resulta algo aún muy misterioso; nadie sabe —ni consigue describir de una forma explícita— cómo funcionan. En general, se relaciona el DNA con la conocida estructura de doble hélice: pese a que todavía no se haya encontrado una solución clara al problema de saber cómo es posible que dos filamentos logren desbobinarse sin romperse. Personalmente, soy de la opinión de que la estructura de doble hélice del DNA es una estructura más bien excepcional. Probablemente, in vitro, los dos filamentos no están «rebobinados» en una espiral, sino que son más bien bordes de una cinta algo plana, que puede abrirse para su lectura y experimentar muchas modificaciones. La misma continuidad lineal del genoma,[68] que es uno de los puntos clave de la biología molecular, es algo que me ha parecido siempre que pertenecía más al dominio de los postulados que al de la evidencia experimental. En todo caso, lo único que importa es que el genoma existe como cantidad formal y que puede producirse materialmente con un cierto número de condiciones, pero no siempre.
Pero también se puede sostener que el modelo de Watson y Crick responde exactamente a la exigencia que usted subraya constantemente de llegar a una descripción localmente finita de la correspondiente realidad… Más ampliamente, la biología molecular procede hoy como una combinatoria, debido precisamente al reducido número de moléculas que entran en juego…
Es completamente cierto que la morfología que la biología molecular evidencia hoy respecto a ciertas estructuras como el DNA responde a la condición de ser localmente finita y, en consecuencia, descriptible.
Permanece abierto, sin embargo, el gran problema de formalizar las conexiones entre el nivel molecular (o macromolecular) y los niveles superiores (célula, organismo, etc.).
El pensamiento biológico contemporáneo está aún demasiado fascinado por la molécula y no tiene consciencia suficiente de los vínculos globales que actúan en el metabolismo. En el terreno de la biología hay que hacer un enorme esfuerzo de educación, y no sé cuánto tiempo hará falta para llegar finalmente a una intuición de los vínculos globales. Personalmente, he propuesto en mi libro ciertas ideas, que han quedado en letra muerta, aunque sigo convencido de su validez, por lo menos como marco general de los vínculos que actúan en un metabolismo que se autorreproduce.
Ha habido ya quien le ha objetado que esa actitud «globalista» tiene precedentes precisos, como Lysenko…[69]
Citar el nombre de Lysenko resulta un poco tendencioso: Lysenko no tiene, por supuesto, el monopolio de las declaraciones holísticas en biología. Antes que nada quiero decir que la autorreproducción de un sistema, por ejemplo una célula que genera dos células que descienden de ella, apela necesariamente a vínculos de carácter topológico, e incluso la existencia del genoma, según mi punto de vista, es uno de los aspectos de estos vínculos topológicos.
Cuando creé la teoría de las catástrofes, pensé aplicarla inicialmente a la embriología. Como anécdota, creo que tuve esta intuición cuando visitaba en Bonn, en Alemania, en 1961, el Museo de Historia Natural del Poppelsdorfer Schloss. Se celebraba una recepción ofrecida por los matemáticos de la Universidad e iba visitando este museo cuando vi un modelo en yeso que representaba la gastrulación[70] del huevo de la rana. Al ver el surco circular que se formaba, para luego volver a cerrarse, vi, por asociación, la imagen de una cúspide truncada de una singularidad. Esta especie de «visión» matemática fue el origen de los modelos que a continuación propuse para la embriología. Claro que no creo haber creado escuela en este campo, ya que este tipo de investigación se ha quedado en letra muerta entre los biólogos. Quizá haya que esperar unos quince años para que este tipo de consideración consiga abrirse camino.
En su libro se ha vuelto usted contra los biólogos. ¿Cuál ha sido el obstáculo que ha impedido que sus ideas tuviesen buena acogida?
Resulta bastante paradójico que los comentaristas de mi libro se hayan atenido sobre todo a los aspectos matemáticos del texto, corriendo un tupido velo sobre mis consideraciones biológicas. Entre los diversos comentaristas, sólo Klaus Jänich ha tenido la valentía de presentar las cosas en sentido inverso, haciendo notar que, después de todo, el gran interés de mi libro podría residir precisamente en la interpretación de los fenómenos biológicos, y de los embriológicos en particular, y no tanto en la parte matemática, que ya está superada en cierta medida. Pero me habían preguntado ustedes por qué los biólogos no han comprendido o no han aceptado mi punto de vista. Pues bien, se pueden dar distintos motivos: el primero es que toda la biología contemporánea está dominada por la experiencia; por tanto, dado que las hipótesis avanzadas por mí no son susceptibles de verificación empírica —por lo menos en su forma actual—, los biólogos que piensan únicamente en términos de experiencia sostienen que mis ideas son «fábulas», que al no tener comprobación empírica no son de ningún interés. Pero la filosofía según la cual todo lo que no es justificable por la experiencia carece de interés está, a su vez, privada de interés: según mi opinión, es una filosofía limitada, «estrecha», si así se puede decir. Y hay una segunda razón: la utilización de conceptos un tanto abstractos como los de sistema dinámico, campo morfogenético, atractor, etc., plantea serios problemas al nivel de la inteligibilidad, tal vez debido a la tradicional insuficiencia de los biólogos en cuanto a la matemática.
¿Hay alguna otra razón?
Quizá ésta: los biólogos contemporáneos creen no tener necesidad de teorías. Ya que les parece que pueden trabajar con plena libertad sobre el material biológico, no sienten esa necesidad. Y, por otra parte, si se puede verdaderamente trabajar sin una teoría, ¿por qué buscar una?
Es decir, que en biología el trabajo empírico lo es todo…
Las investigaciones estimuladas por razones prácticas —como la clínica médica o el control de las epidemias— exigen una aproximación experimental importante. Lo curioso es que el pensamiento biológico ha llevado a un plano general una exigencia de acción procedente de la medicina y de las necesidades sanitarias. Así que los biólogos no sienten necesidad de teorías, y la prueba palmaria de ello es que nunca han instituido cátedras de biología teórica.
Hay algún ejemplo en sentido contrario…
Sí, pero por regla general estas cátedras de biología teórica no duran mucho. Por ejemplo, recuerdo que la Universidad de Buffalo, en USA, había instituido una, que muy pronto se vinculó a disciplinas «serias», como la biofísica o la bioquímica.
¿Simple conservadurismo académico?
No sólo eso. Aquí ha intervenido la circunstancia de que el pensamiento biológico contemporáneo ha tropezado por lo general con la idea de que los procesos vitales podrían quedar sometidos a un análisis de tipo conceptual, sin recurrir a un conocimiento químico profundo.
De manera que en biología hay dos campos «serios»: la biofísica y la bioquímica. Y no queda lugar para la biología teórica.
Exacto. El espacio para la teoría queda muy restringido, incluso a un nivel institucional.
¿Y no se corre el riesgo de que ocurra algo parecido con las ciencias humanas?
No; en mi opinión, en las ciencias humanas la situación es algo distinta. Al contrario que los biólogos, los investigadores de las llamadas ciencias humanas tienen perfecta conciencia de que no tienen auténticas teorías.
Los lingüistas son en parte una excepción…
Sí, respecto a los lingüistas la cosa es diferente; creen haber alcanzado ya los niveles supremos de la cientificidad y consideran las demás disciplinas un poco desde arriba. Pero los economistas, los sociólogos, los psicólogos, son conscientes de las dificultades con que se encuentran para producir modelos teóricamente satisfactorios. Así, se muestran extremadamente bien dispuestos para tomar en consideración cualquier cosa que los matemáticos puedan proporcionarles. Desde este punto de vista, el matemático tiene una gran responsabilidad: de lo que aquí se trata es de frenar los entusiasmos, más que de suscitarlos.
Los especialistas en ciencias humanas tienen un auténtico complejo de inferioridad con respecto a las ciencias exactas…
Así es.
Se trata de una verdadera necesidad de legitimación.
Sí. Todo lo que los matemáticos les dan es bien recibido. Es un desafío para la creatividad del matemático… Sin embargo, me siento perplejo y desilusionado porque los criterios más favorables confunden el sentido de la modelización matemática en las ciencias sociales.
Veamos, por ejemplo, toda la controversia sobre los modelos construidos por Zeeman via la teoría de las catástrofes.[71] Se trata de modelos que, en mi opinión, no se prestan mucho a un tratamiento cuantitativo. Si se les quiere hacer cuantitativos a la fuerza, se consigue sólo una espúrea cuantificación, spurious quantification, como han escrito Sussmann y Zahler.[72] El verdadero interés de estos modelos no reside en la buena o mala cuantificación que podrían eventualmente consentir. Pero de esto ya hablaremos más adelante.
Esta insistencia en los resultados cuantitativos ¿no está relacionada con la inflación experimental en la ciencia?
Sí. Éste es uno de mis temas preferidos. Gran parte de las cosas que se dicen en la actualidad sobre el progreso de la ciencia experimental es un diezmo que la corporación científica otorga a la opinión pública para que ésta siga subvencionando la investigación.
O sea que hay una especie de propaganda para el público no especialista…
…que se queda muy convencido de que lo que se hace es muy importante. En mi opinión, todos estos discursos sobre el progreso hay que tomarlos con muchas reservas. Creo incluso que los investigadores de la generación de nuestros padres o incluso de nuestros abuelos (es decir, hacia 1880-1900), conocieron e hicieron frente a problemas mucho más importantes que éstos con los que se está enfrentando la generación actual.
¿Cómo valora, pues, una de las afirmaciones predilectas de Jean Dieudonné, según la cual ha habido más progreso en matemáticas, desde digamos, el 1945 hasta aquí, que en el período de tiempo que va desde Tales de Mileto hasta el final de la Segunda Guerra Mundial?[73] ¿Es que quizá se da en las matemáticas un tipo de progreso o un ritmo de crecimiento distinto del de las ciencias empíricas?
A mi juicio, el criterio de Dieudonné es más válido en el terreno cuantitativo que en el cualitativo. No quiero menospreciar lo que se ha hecho en matemáticas en los últimos años, pero me resulta difícil advertir progresos verdaderamente notables en matemáticas después de 1964. Quiero decir que no vislumbro nada comparable al desarrollo de la topología abstracta de los años cincuenta, a los desarrollos de la dinámica cualitativa de Smale[74] en los primeros años sesenta. No comprendo muy bien a qué se refiere Dieudonné. Probablemente a los progresos de la geometría algebraica abstracta…
Aunque sí se ha producido algo muy importante en los últimos quince años, debido a Hironaka: la resolución de las singularidades de las variedades algebraicas.[75] En cuanto al resto, quiero recalcar que han sido progresos de carácter técnico más que otra cosa. Pero quizá sea un problema de ignorancia por mi parte… como decía antes, me he apartado en exceso de la investigación matemática de punta.
Así pues, ¿ni siquiera en matemáticas se produce una cosecha de éxitos deslumbrantes?
Seré prudente. Me parece que una afirmación como la de Dieudonné podrían aprovecharla aquellos especialistas que siguen proclamando que la ciencia consigue éxitos, sólo para justificar la importancia que se les atribuye y para lograr un mayor crédito social. Claro que no creo que ésta sea la actitud de Dieudonné: los matemáticos exigen poco.
Aludo sobre todo a la mala costumbre de ciertos «expertos» —en física, en biología, etc.— que enfatizan las «conquistas» de las respectivas disciplinas… Ésta es una actitud que, en mi opinión, deberían controlar rigurosamente los adictos a los mass media. Una de las grandes aportaciones de la epistemología de T. S. Kuhn ha consistido precisamente en mostrar que el progreso científico es automático. Por definición, un saber científico no puede hacer más que progresar; mientras el arte y la filosofía no progresan necesariamente, la ciencia progresa obligatoriamente.
Entonces, desde este punto de vista, decir que la ciencia progresa no es más que enunciar una simple tautología.
Eso es. El problema real no es saber si una ciencia progresa, sino evaluar la calidad del progreso. Y así, si consideramos en su conjunto lo que las ciencias han producido desde los años cincuenta hasta aquí, podremos llegar a la conclusión de que los progresos han sido cualitativamente mucho menos significativos de lo que cabría esperar de una forma razonable. Las estadísticas ponen bien de manifiesto que han habido más científicos desde 1950 en adelante que en toda la historia precedente de la humanidad. ¿Podemos por ello afirmar que el progreso que ha aportado esta leva masiva de científicos es comparable a los esfuerzos que la humanidad ha consagrado a la empresa científica en el pasado? En absoluto. Se ha producido un estancamiento en el crecimiento después de los años cincuenta…
Y sin embargo la opinión pública tenía la vaga sensación de un importante progreso científico, precisamente en aquellos años.
¡Es una ilusión! Incluso en la vida de cada día encontramos efectos del estancamiento. Pensemos, por ejemplo, en la utilización de la energía fósil. Ha hecho posibles muchos progresos: mejora de las comunicaciones, transporte más rápido, etc. Sin embargo, las reservas se agotarán un día u otro. La crisis del petróleo es un síntoma preocupante. ¿Cómo se reemplazarán, dentro de no mucho tiempo, las fuentes energéticas tradicionales?
O sea que la ciencia no ha cambiado nuestra vida en los últimos tiempos…
Sin duda. Pero en el terreno del bienestar no creo que haya dado los frutos esperados. La esperanza de prolongar la vida, por ejemplo, no se ha satisfecho en estos últimos años, ni siquiera en los países desarrollados. La medicina sigue mostrándose prácticamente impotente ante enfermedades degenerativas que detienen la vida humana en el umbral de los 70-80 años. Así pues, el desarrollo de la biología no ha tenido efectos radicales en cuanto a la cuestión del mejoramiento de la salud y de la longevidad.
Sin embargo, es innegable toda una serie de éxitos de la investigación física.
Hasta este momento, se trata de éxitos tecnológicos —física de los sólidos, física de los materiales— que en sí no significan aún bienestar. ¡Y eso por no hablar de la energía nuclear!
En cuanto a esta última: ¿promesa o amenaza?
Ya están bastante claras las dificultades relacionadas con la utilización civil y militar de la energía nuclear. No quiero extenderme en ello.
En general, ¿balance negativo?
No, positivo a pesar de todo: no puede ser de otra manera (por lo menos, si estamos de acuerdo con Kuhn). En todo caso, en el terreno de la eficacia y de las posibilidades de mejora de las condiciones de vida, se podría insinuar la duda de si el balance es negativo o no.
Hay alguna excepción…
El único punto en el que me parece que se da indiscutiblemente un progreso importante es en la investigación del espacio. Enviando observadores más allá de la atmósfera terrestre ha mejorado, con toda seguridad, nuestra capacidad de investigar los cielos: la astronomía derivará para sí beneficios de unas mejores observaciones. El descubrimiento de objetos celestes extraños, de «monstruos del espacio», no hace más que confirmarlo; pensemos en los púlsar, los quasar, los llamados agujeros negros. Estamos en una situación en la que la astronomía empieza a percibir una rica «patología» en los cielos; la investigación de esta patología se revelará preñada de enseñanzas, seguro.
Pero, aparte de eso, los críticos de los distintos programas espaciales sostienen que estas empresas no afectan mínimamente la calidad de la vida…
Pues claro; no se ve cómo la conquista del espacio externo podría ser útil para la humanidad. Sin embargo, diría que está en la lógica de la evolución y del destino terrestre tratar de «colonizar» todos los espacios posibles.
Y ahí está el hecho, en todo caso, de que bajo el aspecto del incremento del bienestar global de la humanidad se haya producido quizá un pecado de optimismo…
La opinión pública, a mi entender, ha sido en cierta medida engañada por las declaraciones optimistas de los especialistas, es posible que los mismos gobiernos hayan sido víctimas de este optimismo. Pero, éstos, claro está, tienen también otros motivos para interesarse por la ciencia, no desestimando la posibilidad de las aplicaciones energéticas y militares.
Quizá se podría plantear como «criterio» de progreso el incremento de nuestra comprensión del mundo, en una perspectiva «más desinteresada»…
Si se quiere sostener que el objetivo último de la ciencia es comprender mejor el mundo que nos rodea, hacerlo «más inteligible», tampoco me parece que desde este punto de vista se hayan producido últimamente grandes progresos. Claro que habrá alguno que objetará enseguida: ¡está la biología molecular! Como ya he dicho antes, me parece que la biología molecular ha dado más problemas que los que ha resuelto.
¿Y no podría ser precisamente esto el signo del auténtico progreso científico? Si los problemas son el pan de la ciencia (como decía André Weil, al menos para las matemáticas).[76] ¡que sean bienvenidos!
La biología molecular ha atraído la atención sobre ciertas morfologías de las moléculas en el interior de los procesos vitales y, con razón, ha mostrado que tales moléculas tenían un carácter extremadamente típico, simbólico, desempeñando un papel central en la regulación global del ser vivo. En el fondo, la biología ha procedido desde el punto de vista molecular de la misma forma que los neurofisiólogos lo han hecho respecto de la localización cerebral: si un proceso requiere la integridad de una determinada parte del cerebro, se produce la tendencia a decir que es aquella parte del cerebro la responsable. De forma análoga, ya que la síntesis de una proteína requiere la presencia del DNA, se tiende a decir que el DNA es responsable de la síntesis de las proteínas. Si se replanteasen las cosas en una perspectiva global, se caería en la cuenta de que la situación no es tan simple. En resumen: toda la biología molecular se basa en la idea de que para cada proceso se puede encontrar un agente químico responsable, ¡pero a esta mitología habría que renunciar de una vez por todas!
Por ejemplo, cuando se quiere combatir una enfermedad vírica, se intenta destruir el virus con un agente químico (al que se da el nombre de «interferente»). Hay que ser de una ingenuidad inaudita para creer que una sola sustancia química puede actuar sobre todos los tipos de virus… Pero toda la historia de la biología molecular no es más que una serie de ingenuidades de este estilo, contradichas por la experiencia. Se deseaba que un solo agente, un único encima, fuese el responsable de la duplicación del DNA, que hubiese una sola polimerasis, mientras que en lugar de eso lo que hay es un número enorme de polimerasis;[77] se deseaba que hubiese una correspondencia biunívoca entre el gen y el m-RNA (RNA mensajero), mientras que con respecto de los eucariotas no se ha encontrado nada de eso.[78] Se ha descubierto en su lugar que el m-RNA estaba compuesto a partir de segmentos pertenecientes a genes diferentes muy distantes uno de otro en el genoma, y así sucesivamente.
En resumen, que no acabaríamos nunca de enumerar todas las modificaciones que se han ido introduciendo al dogma central de la biología molecular.[79] En conclusión, el pseudoprogreso de la biología molecular ha sido un progreso de simple descripción, no de explicación. Y, después de todo, en lo que concierne a los procesos generales de la regulación de los seres vivos, me atrevo a afirmar que, paradójicamente, se los conocía mucho mejor antes del descubrimiento del DNA y de las moléculas químicas que caracterizan el genoma, salvo excepción de ciertos casos, pero muy particulares, muy locales. Todavía hay muchas lagunas en la comprensión general de los mecanismos de regulación; los progresos de los que se envanecen los biólogos son en realidad adquisiciones de nuevas descripciones. Es este aspecto de la cuestión el que se relaciona esencialmente, como decía, con el aspecto puramente empírico de la ciencia moderna. Hoy se cree que cualquier ciencia ha de ser experimental y que sin experimentos no es ciencia en realidad.
Existe, entonces, una tendencia antiteorética cada vez más clara.
Yo, sin embargo, sigo creyendo que sólo mediante el perfeccionamiento de las «entidades teóricas», como los llaman los positivistas, como una disciplina puede esperar la realización de progresos realmente significativos. Lo malo es que siempre cabe hacer experiencias, con cualquier cosa y con cualquier instrumento. Basta tener un instrumento, ponerlo a funcionar en tal o cual condición, en éste o aquel ambiente, etcétera, y se obtendrán, con toda seguridad, «datos» que luego pueden presentarse como «producción científica». La «inflación experimental» no es menos perniciosa que la inflación económica: se tienen unos instrumentos a disposición, se utilizan masivamente y se consigue un masa descomunal de datos, con los cuales, finalmente, no se sabe qué hacer. Los datos llenan bibliotecas enteras y se quedan en archivos polvorientos, y ya nadie se interesa por ellos.
¿Y qué remedios hay para este tipo de «inflación»?
Me parece que la única salida es un esfuerzo teórico extremadamente serio. Tal esfuerzo debería plantearse de algún modo la canalización de esta proliferación experimental. Es seguro que lo que digo no gustará a la casta de los científicos experimentales que basan su carrera en esta expérimentation routinière… Creo que un día u otro la sociedad caerá en la cuenta de esta situación y tratará de ponerle freno; ¡será un despertar amargo para los propios científicos! Deberían preocuparse ya desde ahora en orientar las investigaciones experimentales de modo que su utilidad y su interés sea a priori suficiente. Cuando la sociedad pase cuentas a los investigadores, entonces volverá a sentirse la exigencia de una armazón teórica que permita una valoración del trabajo experimental. Así es como veo las cosas en cuanto a la ciencia y a la orientación global de la investigación.
¿Y dónde buscar las raíces de este experimentalismo llevado al extremo?
También en este caso habría que partir del Hypotheses non fingo de Newton y de todo aquel planteamiento según el cual la investigación busca recetas eficaces, para encontrar el truco del éxito. Eso es, por ejemplo, lo que normalmente se hace en farmacología: se aíslan fármacos que actúan en ésta o aquella situación determinada y luego se intenta utilizarlos en situaciones análogas. Quede bien entendido que este procedimiento está perfectamente justificado desde un punto de vista práctico, y que desde este punto de vista no existe razón alguna para oponerse a la experimentación; pero reducir la ciencia a una serie de recetas eficaces significa no ver la verdadera importancia de la empresa científica. Esta consiste en el incremento de nuestra comprensión del mundo, en hacer las cosas más inteligibles. Si disponer de recetas eficaces no incrementa la inteligibilidad, on passe à coté.
¿Hay, pues, un cierto conflicto entre necesidades y comprensión del mundo y entre aplicaciones y teorías, entre razones prácticas y motivaciones teóricas?
Entre estos dos planteamientos fundamentales de la ciencia —comprender el mundo y actuar sobre él— creo que sería mejor subordinar el segundo al primero, más que el primero al segundo. Muchos son de la opinión de que estas dos finalidades son conciliables, incluso que van al mismo paso: para comprobar si algo se ha comprendido bien tiene que haber verificaciones mediante la acción, y sólo se puede actuar bien, por otro lado, en una situación que se comprende bien. Yo no creo en este tipo de «armonía preestablecida»; en realidad se plantean muchas situaciones en las que comprender y actuar están disociados de una manera bastante fundamental. Acabo de mencionar el ejemplo de la acción de los fármacos; en muchos casos un fármaco resulta eficaz sin que se comprenda la razón.
Al contrario de lo que afirman ciertas filosofías de la ciencia o ciertas «concepciones del mundo y de la historia», se podría auspiciar entonces una cierta autonomía de la investigación teórica…
En mi opinión, hay que poner otra vez el acento en las exigencias de comprensión de los fenómenos, sin imponer el vínculo de la acción eficaz. Y para comprender los fenómenos hay que substituir los métodos experimentales ciegos —típicos de muchas ciencias actuales— por un procedimiento que exija un poco más de inteligencia y reflexión. Yo creo que la matemática puede desempeñar aquí un papel importante.
Haber planteado dilemas como ciencia pura/aplicación y teoría/experiencia nos ha llevado de forma natural al terreno de la filosofía. ¿No aspira ésta a una explicación global del mundo? ¿No pretende también proporcionarnos normas de vida y ser una especie de «guía para perplejos»? ¿Cómo se concilian las aspiraciones de la filosofía con las de la ciencia?
Ahí está la célebre afirmación de Heidegger: «Die Wissenschaft denkt Nicht», la ciencia no piensa, a lo que añade, con razón: «porque no es su objetivo». Es cierto que se ha producido un divorcio entre ciencia y filosofía en el siglo pasado, debido esencialmente a que la ciencia llevaba a procedimientos eficaces, cosa que nunca consiguió la filosofía, si se excluye algún caso de sabiduría práctica. Por otra parte, los métodos utilizados por la ciencia resultan ahora de difícil comprensión para los filósofos: baste pensar en los métodos teóricos de la física fundamental que, como hemos visto, requieren matemáticas muy sofisticadas; el «lego» ya no puede controlar la enorme masa de datos de laboratorio que existen. Por todas estas razones, los filósofos han dejado a los científicos la indagación de la naturaleza, que tanto fascinaba a los presocráticos, y se han confiado en el campo de la introspección.
…y naturalmente la ciencia «oficial» ha marcado este campo como «divagación extracientífica»…
Habría mucho que decir al respecto. Creo que los métodos de la introspección no carecen de valor, pero no son suficientes. Tienen límites muy estrechos. Hay enormes dificultades que nos impiden la comprensión de nuestra estructura: el psiquismo humano no puede autosimularse sin modificarse, alienarse o alterarse. Hay barreras naturales que nos impiden ver los elementos constitutivos esenciales de nuestro yo. Sólo el análisis de la naturaleza nos permite ir más allá de estas barreras; sólo este análisis puede hacernos conscientes de mecanismos demasiado implícitos en nuestra actividad mental. En mi opinión la importancia del conocimiento científico consiste precisamente en que nos permite rodear ciertos obstáculos implícitos en la visión que proporciona la introspección. También la ciencia, pues, es una especie de «hermenéutica».
¿Y por qué este aspecto no se ha conceptualizado lo suficiente?
Ante la pretensión del saber científico de representar un conocimiento cierto e indudable, la filosofía tradicional ha tenido que renunciar a sus objetivos cognoscitivos, ya que, como máximo, podía proponer aserciones inciertas o conjeturales. Por otra parte, las dificultades relacionadas con la utilización de la deducción matemática en física y el carácter incontrolable por parte de los no expertos de los datos proporcionados por los experimentadores han expulsado literalmente a los filósofos de la empresa científica.
¿Y no era cometido de los científicos construir una nueva «filosofía de la naturaleza»? ¿No podían sacar a la luz pública los presupuestos «tácitos», los postulados «implícitos» que guiaban su práctica científica?
Excepto unas cuantas excepciones (Poincaré, Schrödinger…) esto no se ha producido. La articulación de la tarea investigativa en especializaciones claramente separadas (y a veces en competencia entre sí para obtener financiación pública) y la constitución de una auténtica «casta» de investigadores científicos en quienes los intereses corporativos sofocan con demasiada frecuencia las ambiciones intelectuales, han reprimido desde el nacimiento cualquier tentativa de pensamiento generalizados Preocupados por difundir y exaltar ante la opinión pública el mito de la ciencia (sobre todo experimental) como fuente exclusiva de conocimientos, la inmensa mayoría de los científicos se han contentado con una filosofía sumaria, en este momento de corte neopositivista o popperiano, según la cual sólo asertos comprobables o falsificables son «científicos»… Por otra parte, la Naturphilosophie ya había muerto; no pudo sobrevivir a Schelling o, si se prefiere, a la Teoría de los colores de Goethe,[80] que cometió el error de transponer a la física una teoría que tenía una cierta validez en la psicología de la visión, transfiriendo así al macrocosmos una estructura propia del microcosmos. Los grandes éxitos prácticos de la física y de la biología en el siglo pasado dieron por fin el golpe de gracia a cualquier intento serio de filosofía natural.
Existe un duro juicio de Helmholtz acerca de Hegel. Éste sería, según él, el responsable del divorcio entre ciencia y filosofía…[81]
No cabe duda de que el divorcio entre ciencia y filosofía fue resultado también de las irracionales ambiciones de filósofos que, como Hegel, pretendían con sus sistemas dar una explicación universal del curso completo de la historia. Los científicos, por su parte, han hecho suya la actitud opuesta, consistente en afirmar que el esfuerzo filosófico carece de todo interés: es suficiente examinar los hechos para ver aquello que necesitamos. Pero limitarse a los «hechos» no puede conducir más que a la acumulación de un conocimiento desprovisto de cualquier organización interna, un conocimiento caótico y anárquico. Si en lugar de eso se quieren organizar de veras los datos de la experiencia, hay que proceder necesariamente de una manera más teórica, es necesario disponer de marcos a priori.
Hay mucha epistemología actual que insiste en el hecho de que la experiencia está impregnada de teoría.[82] Esto es también una banalidad; exagerándola, se puede también sostener que los hechos no existen si no es en función de la teoría. En mi opinión, no hay que seguir en esta dirección hasta sostener que los hechos son, sin más, creaciones de la teoría; pero esto no quiere decir que existen hechos en sí, «hechos brutos». Los hechos se consideran en relación con una cierta problemática, son respuestas a un cierto tipo de preguntas.
En conclusión: sitúo el esfuerzo de la ciencia en la capacidad de organizar los datos de la experiencia según esquemas impuestos por estructuras teóricas. Como decía antes, soy de la opinión de que le corresponde a la matemática proporcionar estas últimas. A partir de aquí, se puede ya determinar también cuál es el papel de la teoría de las catástrofes en sentido estricto.