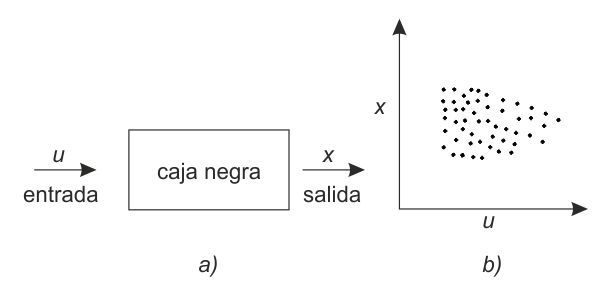
FIG. 2. a) El esquema de la caja negra, b) La nube de puntos.
Vayamos, pues, a la teoría de las catástrofes.
Ante todo hay que ver con claridad que la teoría de las catástrofes no es una teoría científica en el sentido corriente del término. Es decir que no es una teoría científica como lo son, por ejemplo, la teoría de la gravitación de Newton, la teoría del electromagnetismo de Maxwell o incluso la teoría de la evolución de Darwin. Respecto a teorías de este tipo cabe el derecho de decir que se han visto, en algún sentido, confirmadas por la experiencia, es decir que se pueden aducir argumentos experimentales en su favor.
Pero la teoría de las catástrofes no ha de satisfacer esta exigencia. El término «teoría» se entiende aquí en un sentido muy particular: yo diría más bien que se trata de una metodología, o acaso de una especie de lenguaje, que permite organizar los datos de la experiencia en las condiciones más diversas.
¿No es entonces un poco como el cálculo de fluxiones y fluentes para Newton o el cálculo diferencial e integral para Leibniz?
Yo diría que eso es una buena analogía. El cálculo diferencial fue creado esencialmente para describir la evolución de los estados de un sistema, en particular la evolución del movimiento de un cuerpo. Siempre quedaba una cierta unidad del sistema; en el caso del movimiento, por ejemplo, la unidad venía representada por el cuerpo material, que permanecía siempre igual a sí mismo. De forma análoga, cuando se describe la evolución de un sistema mecánico con una ley diferencial, se puede decir que existe un espacio de las fases que describe la totalidad de los estados posibles del sistema, un espacio del cual no se sale.[83] En la teoría de las catástrofes la situación es un poco más paradójica: se esfuerza por describir las discontinuidades que pudieran presentarse en la evolución del sistema. Intuitivamente, se admite que la evolución global de un sistema se presenta como una sucesión de evoluciones continuas, separadas por saltos bruscos de naturaleza cualitativamente diferente. En principio, para cualquier tipo de evolución continua subsiste una modelización de tipo diferencial clásico, pero los saltos hacen que se pase de un sistema diferencial a otro. El dato de la teoría de las catástrofes aparece entonces como una especie de «paquete» de sistemas diferenciales que, en la mejor de las hipótesis, se dan en número infinito. Así pues, el punto representativo «salta» de una evolución continua descrita por un sistema de ecuaciones diferenciales a otra evolución continua descrita por otro sistema y, en determinadas circunstancias, no se puede excluir que un número finito de sistemas no sea suficiente para describir la situación por completo. Éste es, brevemente, el esquema global de la teoría.
¿Cómo se presenta, pues, el intento «hermeneútico» de la teoría de las catástrofes?
Para hacerse una idea, creo que sería útil recurrir a un modelo clásico, el de la «caja negra». Una caja negra no es otra cosa que un sistema que comunica con el mundo exterior sólo mediante unas entradas (inputs) y una salidas (outputs). En cualquier momento, si se determina la entrada, el sistema da las salidas.
Se puede suponer que el espacio de las entradas es, por ejemplo, un espacio euclídeo[84] Rr de dimensión r y el espacio de las salidas un espacio euclídeo Rn de dimensión n. Entonces, en el espacio producto Rr × Rn, la correspondencia entrada-salida vendrá representada por un punto, y una serie de experimentos realizados sobre el sistema lleva a la construcción de una nube de puntos en tal espacio (fig. 2).

FIG. 2. a) El esquema de la caja negra, b) La nube de puntos.
Un problema de fondo de la teoría de sistemas y de la teoría de los autómatas es en general como se puede reconstruir conociendo las nubes de puntos que pueden generarse de este modo, el mecanismo interno —o el sistema de mecanismos internos— de la caja negra. Desde este punto de vista, se da con frecuencia una situación de este tipo: cualesquiera que sean los datos iniciales, o el procedimiento o el plan de las sucesivas entradas que llegan al interior de la caja negra, la nube de puntos tiende a una situación asintótica, con independencia de la selección de las entradas. Se trata, pues, evidentemente, de una situación un tanto particular, que en ciertas ocasiones puede ser falsa. Creo que para una clase muy amplia de sistemas debería existir un teorema que estableciese que para cualquier selección de la teoría de las entradas la nube de puntos tiende a una distribución de las probabilidades única y bien definida. Pero demostrar un teorema semejante exige consideraciones que, por lo menos en el momento presente, no están a nuestro alcance. Siempre hay casos excepcionales, en cuya correspondencia las salidas son asimismo excepcionales y en correspondencia con las cuales, a su vez, la nube de puntos tiene una forma muy especial, muy distinta de la acostumbrada. La selección de estas historias excepcionales es, por otra parte, muy importante, por cuanto, si pueden ser puestas en evidencia, se puede derivar información interesante de ellas acerca de la estructura interna del sistema. Sin embargo, lo que ocurre en general es que, a falta de datos a priori acerca de los mecanismos del interior de la caja cerrada, se vuelve a caer en el caso en el que se tiende hacia una nube de puntos que tiene una estructura asintótica relativamente bien definida. El problema, en este punto, consiste en interpretar los mecanismos internos que generan esa estructura asintótica, y es aquí, evidentemente, donde entra en juego el método de la teoría de las catástrofes. Tal método consiste en suponer, en una primera aproximación, que se puedan considerar en primera instancia casos muy particulares.
Veamos enseguida algún ejemplo. Hasta ahora, de hecho, la noción general de aplicación[85] es la que modela la idea intuitiva de una correspondencia entre las entradas (consideradas como elementos de un adecuado subconjunto U de Rr) y las salidas (consideradas como elementos de un adecuado subconjunto X de Rn)…
Una primera simplificación puede consistir en considerar sólo aquellas aplicaciones en las que a una entrada de U corresponde sólo un número finito de salidas, es decir de elementos de X.
Consideremos el grafo vinculado a la aplicación: este grafo está constituido por cualquier u de U de las parejas (u, x), tales que x es elemento de un conjunto finito Iu de puntos de X tal que cada Iu corresponde a u. El grafo C representa en cierto sentido la «característica» del sistema.
Para concretar las ideas, supongamos n = r = 1. Planteémonos ahora el caso de que C sea una curva lisa, cerrada, convexa (fig. 3) que admite dos puntos críticos (es decir, con tangente vertical) a, b. En el espacio de control U, sean a', b' las proyecciones de a y b. Consideremos en primer lugar valores u comprendidos entre a' y b': a éstos les corresponden dos salidas posibles, x(u) y x'(u). Supongamos que el sistema se encuentra en x(u) en la porción superior de C. Si incrementamos u, x(u) varía continuamente con u (en función del teorema de las funciones implícitas), por lo menos mientras u < b'; para u = b', x(u) coincide con b. Pero ¿y para u > b'? Si el experimentador insiste y da a u valores mayores que b' no cabe otra solución que destruir el sistema. Y he aquí la catástrofe en el sentido usual del término, como por ejemplo la explosión de una caldera si se lleva la presión del vapor más allá del límite de resistencia.
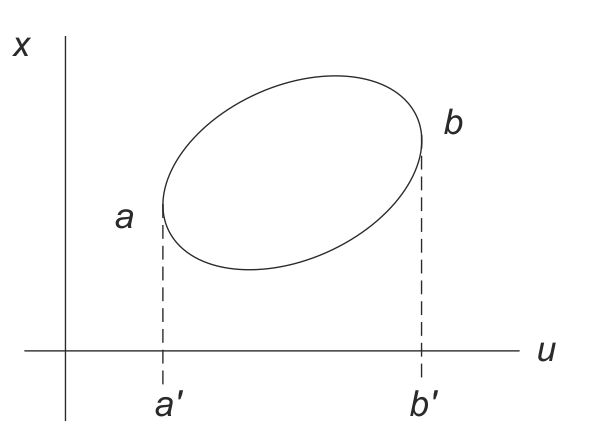
FIG. 3. La característica del sistema es una curva cerrada, lisa, convexa.
Pero, precisamente, la «catástrofe», en el sentido de la teoría de las catástrofes, no tiene esta connotación desastrosa…
Cierto. Pongamos un ejemplo un poco diferente del anterior. Se mantiene n = r = 1, pero en esta ocasión la característica C tiene la apariencia de una curva en forma de S mayúscula (véase fig. 4). Seguimos teniendo dos puntos críticos, a y b, y dos valores críticos, a' y b' en U. Imaginemos, como antes, que el valor u, comprendido entre a' y b' corresponde en la porción superior de C a x(u). Hagamos ahora que u crezca hasta alcanzar el valor b': x(u) describe por continuidad el tramo superior de C hasta llegar al punto b. Si u se prolonga más allá de b' el sistema escapa a la destrucción en cuanto permite a x(u) «saltar» con gran rapidez al tramo inferior de C, en b1. Si finalmente hacemos que u vuelva a bajar hacia a', x1(u) se mueve con continuidad en el tramo inferior de C hasta el punto crítico b. Aquí, si u sigue decreciendo, x(u) «salta» de nuevo al tramo superior de C en a, donde podrá reiniciar el proceso precedente (es lo que en física se denomina proceso de histéresis).
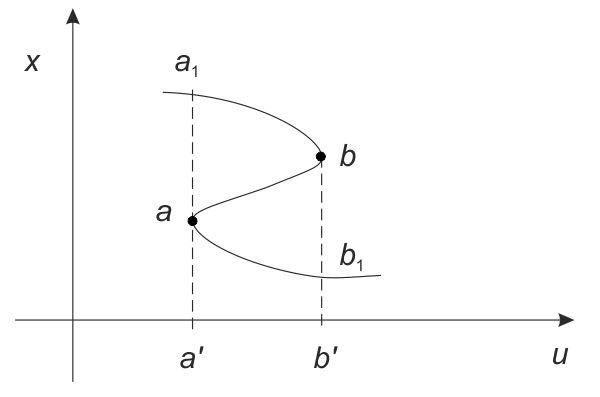
FIG. 4. La característica del sistema es una curva en S.
Estos «saltos» de un tramo a otro de C (para u = a' o para u = b') son las típicas catástrofes en el sentido en que yo he utilizado el término, pero, al contrario de lo que cabe esperar en la acepción intuitiva, no comportan la destrucción del sistema.
En cualquiera de los dos casos, como ya he dicho, se da una hipótesis «elemental» acerca de la aplicación considerada: a cualquier entrada u le corresponde un conjunto Iu finito de salidas. En el caso en que, una vez elegida la entrada u, se tiene una única salida x(u) es decir que x quede unívocamente determinado por u, nos encontramos, como caso aún más especial, con la noción clásica de función.[86] Nuestras aplicaciones pueden considerarse como un «paquete» de funciones…
Y así nos volvemos a encontrar con una de las más familiares nociones matemáticas…
…y también filosóficas. El mundo exterior, no lo olvidemos, se presenta ante nuestros ojos como una mezcla de determinismo e indeterminismo. En cualquier circunstancia hay que distinguir, para decirlo con el Manual de Epicteto,[87] aquello que «depende de nosotros» (ta eph hemin) y lo que «no depende de nosotros» (ta ouk eph hemin). Si esta distinción es importante desde el punto de vista de la ética, no lo es menos para la ciencia. Pues bien, el pensamiento matemático ha llevado hasta el extremo, por así decirlo, esta distinción: lo que depende de nosotros es la variable, el argumento de la función… Lo que no depende de nosotros es el determinismo rígido que, una vez asignado de una vez por todas un determinado valor a la variable, determina el correspondiente valor de la función…
Se trata de una idea que ha sido muy importante en el desarrollo de la tradición científica. De hecho, creo que en el origen de la revolución galileana se dio simplemente el hecho de que el espíritu científico estaba en condiciones de producir modelos, precisamente con ayuda de la idea de función, de un cierto número de fenómenos que hasta ese momento no se habían podido «modelizar» de una forma suficientemente fiel. Desde este punto de vista, según mi opinión, se han dado dos factores que han actuado conjuntamente: por una parte, una serie de necesidades prácticas —y pienso en especial en la artillería— que llevaban a estudiar la trayectoria de las balas de cañón, de los proyectiles y, en consecuencia, el movimiento de los cuerpos pesados; por otra parte, la idea de función que empezaba a germinar en el ánimo de los investigadores y que les permitió describir con exactitud y fidelidad precisamente la trayectoria de un cuerpo pesado. Creo que la formación de esta idea de función —y quiero decir imagen, ya que función es aquí más imagen que concepto— fue lo que dio origen a la gran revolución científica galileana.
Gracias a la idea de función —aún vaga— se hace posible establecer modelos de la caída de los cuerpos y de la refracción de los rayos luminosos. Una vez establecidas las leyes, se pueden construir los instrumentos que aprovechan esas leyes. Galileo construyó así su «lente» y, un tiempo después, el primer microscopio… Una vez en posesión de los instrumentos, empezó obviamente, a utilizarlos. Galileo observó los astros, Malpighi los tejidos de los seres vivos. Así nació la ciencia experimental. Pero el énfasis en la experiencia no ha sido la causa del progreso científico, sino el efecto. Efecto de la maduración, en el espíritu de la comunidad científica, de esa estructura teórica que es la idea de función.
La idea de función ha aparecido muy tarde en la escena científica, por lo menos en forma completa. Se trata de una noción prácticamente desconocida para la matemática antigua y que hizo tímida aparición sólo con el álgebra árabe, la cual, manipulando las ecuaciones lineales, introdujo en cierta medida la idea de función lineal. Cuando los algebristas italianos, en el año mil quinientos, empezaron a estudiar los polinomios y las ecuaciones algebraicas de grado superior, se sintió efectivamente la exigencia de elaborar una teoría de estas funciones particulares. El propio Newton, al describir los movimientos de los cuerpos, no conocía la función, a no ser en casos particulares, en que la variable era el tiempo. Esta aparece sólo con Leibniz: al propio Leibniz se deben también, de hecho, las definiciones generales de las nociones de variable, de argumento de una función y también de parámetro.[88]
Esto muestra con claridad que se ha cometido un error al infravalorar el papel de la imaginación en el desarrollo de las ciencias. Yo, por el contrario, mantengo que todos los progresos de la ciencia, por lo menos los decisivos, van siempre ligados a mejores posibilidades de creación de modelos, a una mayor capacidad de simulación interna de los fenómenos.
Así que, una vez más, estamos con Platón: las ideas (las estructuras matemáticas) son antes que las cosas…
Cierto, y en este sentido sirve todo lo que se ha dicho antes respecto a la física: las estructuras matemáticas, en general, han precedido a su utilización en física, y no al revés. Del mismo modo, creo que también en biología serán las estructuras matemáticas las que ordenarán los fenómenos más importantes. Los fenómenos de regulación, por ejemplo, exigen un gran número de parámetros y, por consiguiente, cualquier descripción un poco sutil de estos fenómenos exigirá la utilización de espacios multidimensionales. Creer que se pueda producir una teoría de la regulación manipulando simplemente diagramas cibernéticos con vértices y flechas resulta en mi opinión ilusorio. La importancia de la regulación consistirá siempre en que es un fenómeno de carácter fundamentalmente continuo y, así, exigirá relacionar con estas situaciones figuras multidimensionales. La teoría de las catástrofes puede ser muy útil en este caso, precisamente porque trata de interpretar las nubes de puntos que se dan experimentalmente, mediante construcciones matemáticas que sean a la vez las más simples y las más consistentes, es decir que satisfagan la propiedad de estabilidad estructural y resistan a las pequeñas perturbaciones debidas al ambiente y a los errores experimentales.
Toda la «filosofía» de la teoría de las catástrofes, su esquema general, es precisamente éste: se trata de una teoría hermenéutica que, ante cualquier dato experimental, se esfuerza por elaborar el objeto matemático más simple que pueda generarlo. Desde este punto de vista, resulta claro que la teoría de las catástrofes no coincide, como se tiende a pensar, con el elenco de las siete catástrofes elementales; quien piensa así, reduce, de hecho, toda la teoría de las catástrofes a lo que yo llamo la teoría de las catástrofes elementales.
Con todo, dada la resonancia del debate suscitado por Stabilité structurelle et morphogenése, será oportuno esbozar las ideas de fondo de la teoría de las catástrofes elementales.
Para dar una idea de lo que es la teoría de las catástrofes elementales, utilizaré antes que nada una metáfora: supongamos que los mecanismos del interior de la «caja negra» estén regidos por una especie de voluntad interna que se describe con un potencial. En los casos más simples podemos considerar una función F de un subconjunto X del espacio Rn que contiene un entorno del origen en el conjunto R de los reales; el potencial F dependerá de r parámetros, es decir de r «variables de control», es decir de una entrada u que corresponde a un entorno U con origen en RT. Pues bien, imaginemos que dentro de la caja negra hay una especie de «demonio» que trata de maximizar su «ganancia», representada por −F, es decir que trata de minimizar el potencial F. Si sobre esta «ganancia» se establecen hipótesis de estabilidad estructural, hipótesis de resistencia, en cierto sentido, entonces nos vemos llevados a clasificar los accidentes que se presentaban mediante las nubes de puntos y a dar una descripción algebraica. Éste es, el tema de la llamada teoría de las catástrofes elementales, que matemáticamente se reduce a la teoría de las singularidades de las funciones numéricas.[89]
¿Cuáles son, entonces, las características de los modelos obtenidos mediante la teoría de las catástrofes elementales?
Tales características, desde un punto de vista matemático, dependen substancialmente del potencial F. F es un germen de Rn × Rr en R que es C∞ en el origen 0 y que constituye el despliegue de un germen η de funciones de Rn en R, C∞ en el origen 0. Lo que quiere decir que F depende de las «variables de comportamiento» x1, …, xn y de los parámetros o «variables de control» u1, …, ur, por decirlo con Zeeman, y además vale F (x1, …, xn, 0, …, 0) = η (x1, …, xn). En resumen, un despliegue no es más que una familia de funciones reales de las «variables de comportamiento» que depende de r parámetros («variables de control»).
Pongamos un ejemplo.
Tomemos, para n = 1, la función (el germen) η(x) = x3: un despliegue es, por ejemplo, F (x, u) = x3 + ux donde r = 1.
O bien tomemos η(x) = x4: un despliegue es, por ejemplo, F(x, u, v) = x4 + ux2 + vx, donde r = 2.
Se trata, en todo caso, de privilegiar, en el modelo, despliegues «estables», es decir, dicho intuitivamente, que resistan pequeñas perturbaciones…
Consideremos, en el origen 0, la función (x) = x3 y perturbémosla añadiendo un término εx. Si tomamos ε positivo no encontramos punto crítico alguno, y si tomamos ε negativo tenemos dos, un máximo y un mínimo relativos (véase fig. 5). Análogamente η(x) = x4 perturbado con εx2 da un mínimo para ε > 0 y un máximo (relativo) y dos mínimos (relativos) para ε < 0 (véase fig. 6). Cuanto más subimos el exponente k, más complicado resulta el comportamiento de xk: de este modo, si perturbamos x5 podemos obtener cuatro puntos críticos (véase fig. 7), etc. Así pues, no todos los despliegues funcionan bien: y, por otra parte, en el caso n = 1, por ejemplo, no conseguiremos mucho según este perfil, pasando de x4 al despliegue x4 + ux2, ya que esto es todavía inestable, etc.
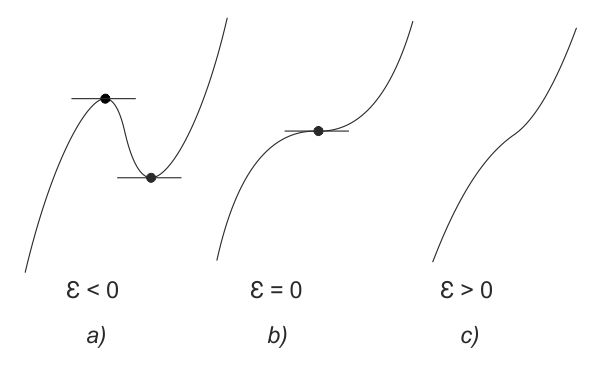
FIG. 5. Perturbaciones de x3 con εx. a) Para ε negativo tenemos un máximo y un mínimo; b) para ε nulo tenemos un punto de inflexión, como es sabido; c) para ε positivo no tenemos ni máximo, ni mínimo, ni punto de inflexión.
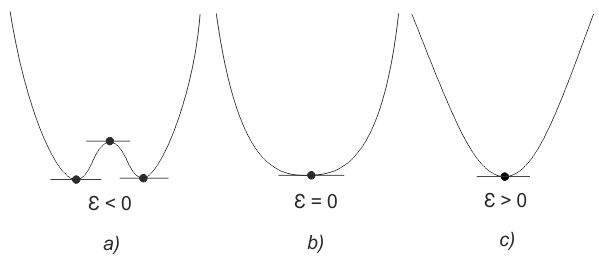
FIG. 6. Perturbaciones de x4 con εx2. a) Para ε negativo tenemos dos mínimos y un máximo; b) para ε nulo encontramos un mínimo; c) para ε positivo tenemos un mínimo.
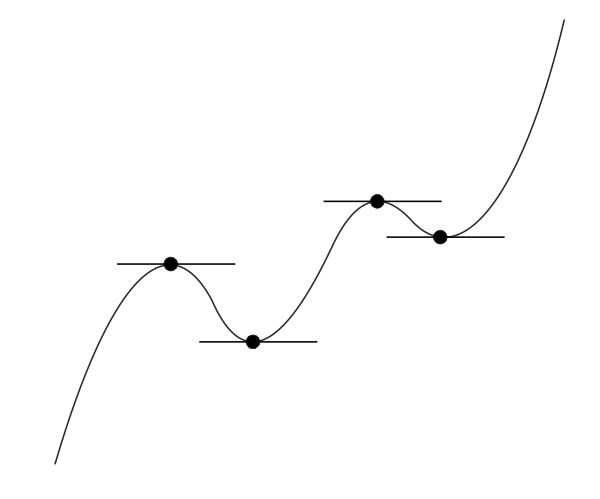
FIG. 7. Perturbaciones de x5.
Pero, una vez formulada convenientemente la noción de estabilidad respecto a un despliegue, individualicemos, para valores bajos de la dimensión r del «espacio de control», un elenco finito, suficientemente manejable, de potenciales standard que hagan «equivalentes» (como es obvio, definiendo la equivalencia de una forma natural) todos los despliegues estables. Volviendo al ejemplo, en el caso de x3, su despliegue universal (o potencial standard) es x3 + ux; en el caso de x4, es x4 + ux2 + vx; en el caso de x5, es x5 + ux3 + vx2 + wx, etc.
Pero usted atribuye a la noción de despliegue universal un cierto cariz filosófico…
¡Por supuesto! Esta idea rehabilita y puntualiza en cierto modo el par aristotélico potencia/acto. Cualquier situación inestable es una fuente de indeterminación; pero nosotros queremos establecer en forma de parámetros todas las posibles «actualizaciones» de las virtualidades contenidas en una situación inestable, que representamos matemáticamente con una singularidad η, de forma que cualquier actuación corresponda a un particular camino que parte del origen 0 en el espacio Rn de los parámetros de control…
Vayamos otra vez a un ejemplo.
Consideremos, en n = 1, el potencial F (x, u, v) = x4 + ux2 + vx, en donde r = 2. Si lo entendemos como función de la única variable de comportamiento x para encontrar los puntos críticos, se establece dF/dx = 0, es decir que se considera en primer lugar la derivada y se la iguala a cero: 4x3 + 2ux + v = 0, o, lo que es lo mismo, x3 + ax + b = 0, donde a = u/2 y b = v/4.
Aquí volvemos a encontrar manipulaciones algebraicas que nos resultan familiares desde la gran álgebra italiana del cinquecento, x3 + ax + b = 0 es una ecuación de tercer grado: tiene como mínimo un radical real y como máximo tres. La naturaleza de los radicales depende precisamente de los parámetros a y b, que aparecen en el factor discriminante de la ecuación cúbica D = 4a3 + 27b2. Como se ve, para D < 0 hay tres radicales reales diferentes; para D > 0 hay un solo radical real (y dos complejos conjugados); para D = 0 vuelve a haber tres radicales reales, pero algunos coinciden; para D = 0 y a ≠ 0 o b ≠ 0 dos de los radicales reales son iguales; para D = 0 y a = b = 0 los tres radicales son iguales.
Geométricamente, la situación se interpreta con facilidad en el «plano de control» (a, b) (véase fig. 8.) Dada la curva (parábola semicúbica) B de ecuación 4a3 + 27b2 = 0 es oportuno considerar el plano (a, b) dividido en cinco partes: el origen 0, las dos ramas de la curva B1 y B2, la región «interna» I de la curva y la región «externa» E de la curva. Si el punto (a, b) está en E, hay una única raíz real C que corresponde a un mínimo de F; por lo tanto, en nuestra «caja negra» hay un solo régimen posible. En I los radicales reales son tres, c1, c2, c3, y corresponden a dos mínimos —digamos c1 y c2— y a un máximo c3. En la hipótesis planteada, el demonio tiene ante sí dos regiones que corresponden a los mínimos estables para c1 y c2. Es decir que en el interior de la parábola semicúbica B hay dos regímenes estables en conflicto. Finalmente, en B1 y B2 (y no en el origen O) encontramos un mínimo y un punto de inflexión, y sólo un mínimo c1 = c2 = c3 en el origen O (véase fig. 9).
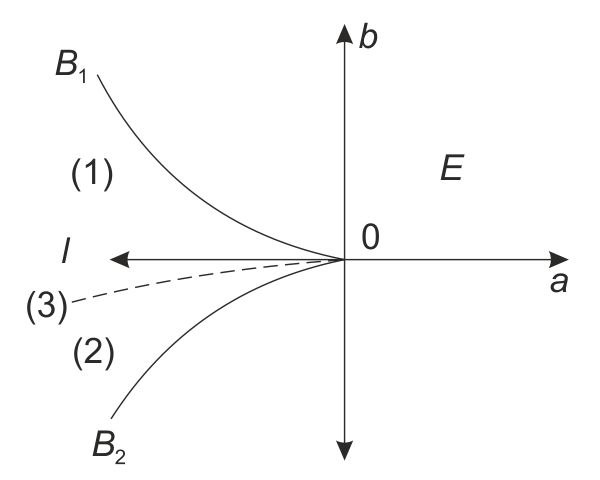
FIG. 8. La parábola semicúbica de ecuación 4a3 + 27b2 = 0 en el plano de control (a, b). En la región I la línea punteada (3) que sale del origen 0 (a = b = 0) indica los puntos de catástrofe, éste es el estrato de conflicto entre las dos regiones (1) y (2) (adoptando la convención de Maxwell).
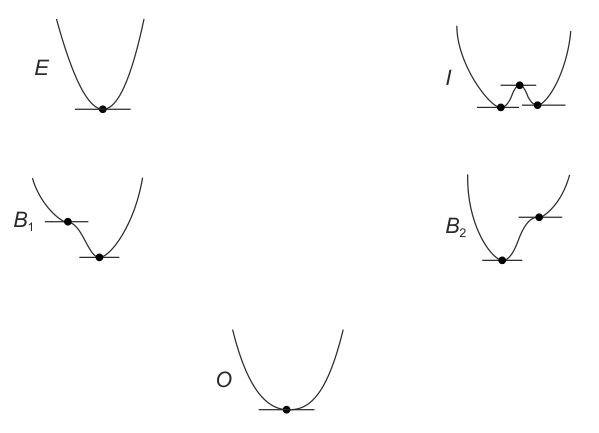
FIG. 9. Las diversas formas del potencial F (x) = x4 + ux2 + vx en relación con las cinco regiones en que se ha descompuesto el plano de control (a, b) (en el supuesto que a = u/2 y b = v/4).
¿Y cómo el demonio, siguiendo con la metáfora, escoge, en el interior de la «caja negra» entre dos regímenes estables?
En la perspectiva de la teoría de las catástrofes elementales, los mínimos del potencial F («pozos de potencial»), es decir los máximos de ganancia −F del «demonio» definen los regímenes locales estables. Pero, como ya habíamos visto en el caso precedente en la zona I, hay en general más de un mínimo y, evidentemente, sólo uno puede predominar en un punto regular.
¿Cómo escoger? Una solución consiste en adoptar una convención, llamada convención de Maxwell, que es bastante arbitraria pero que por lo menos tiene el mérito de la simplicidad. En el caso precedente, por ejemplo, en I hay dos valores de la variable de comportamiento x, digamos c1 y c2 para el mismo punto (a, b) del plano de control. Este conflicto entre los «atractores» c1 y c2 se resuelve conviniendo en que prevalezca el «atractor» de potencial mínimo, digamos c1, si F (c1) < F(c2).
Esta convención resulta, por otra parte, coherente con nuestra vieja idea heurística de que el «demonio» intenta maximizar su «ganancia» −F.
Maxwell había utilizado una regla similar para eliminar la indeterminación en v (volumen) de la ecuación de estado de van der Waals, F(p, v) = 0 en el intervalo de p (presión) en el que hay tres raíces reales en v, lo que describe una mezcla de fases gaseosas y líquidas. Obviamente, la validez de la «convención de Maxwell» según una perspectiva cuantitativa no nos interesa: lo que en su lugar nos interesa, aunque con ciertas limitaciones, es el tipo de descripción de la estructura topológica de los puntos catastróficos K en el entorno de una singularidad del potencial F que admita tal convención.[90]
De la convención de Maxwell se deriva que un punto K del espacio de control Rr puede ser catastrófico sólo en dos casos: o se alcanza el mínimo absoluto del potencial F (x1, …, xn, u1, …, un,) en dos puntos distintos c = (c1, …, cn) y c' = (c1, …, c'n), es decir dos puntos de conflicto; o bien el mínimo absoluto del potencial, llegado a un único punto c = (c1, …, cn) deja de ser estable (punto de bifurcación).
Apliquemos ahora la convención de Maxwell al interior I de la parábola semicúbica que hemos puesto como ejemplo. No es posible escoger un régimen continuo en el interior de tal parábola. El estrato de conflicto, es decir el conjunto de la función F para el que F(c1) = F(c2), se da por una elección de los parámetros a, b que describe en el plano de control (a, b) una curva (esbozada en la figura 8) que parte del origen 0. En el origen, es decir para a = b = 0, corresponde un mínimo del potencial no estable; el origen es, pues, un punto de bifurcación en el plano de control (a, b). En resumen ¡la bifurcación genera la catástrofe!
O sea que, para decirlo con Heráclito, «hay que saber que el conflicto es universal, que la justicia es una lucha y que todas las cosas se generan en la lucha y según una necesidad».
Exacto. Repetiré una de mis frases favoritas: una morfología se produce en el conflicto de dos (o más) atractores.
Volviendo a Sussmann y Zahler (y a otros críticos): gran parte de sus objeciones se relacionan con la naturaleza restrictiva de las condiciones para las que resulta válido el «teorema de Thom».[91] Pero la teoría de las catástrofes elementales, como ya se ha dicho, no agota la teoría de las catástrofes…
¡No es verdad! Por otra parte, aún permaneciendo en el contexto de la teoría de las catástrofes elementales, se puede decir que el establecimiento de modelos se ha limitado hasta ahora a la utilización de la cúspide, mientras las singularidades de orden superior —como la «cola de golondrina», la «mariposa» y los «ombligos»— no se han utilizado nunca.[92] Por lo que a mí respecta, he propuesto, por medio de «ombligos», algunas interpretaciones, de la refracción de las ondas, por ejemplo, pero estas interpretaciones no las han aceptado los especialistas, porque no han conseguido justificarlas a partir de ecuaciones, como las de Navier-Stokes.[93] El problema permanece, pues, abierto. Yo creo que muy probablemente, en tal caso, la teoría no puede conducir a un modelo via catástrofes elementales stricto sensu, sino más bien a un modelo «mixto», en el que se dará una dinámica en los filamentos y una dinámica en la base. El problema consiste precisamente en conseguir expresar una síntesis entre estas dos dinámicas. Pero esto no es más que una declaración de propósitos.
Las críticas de Sussmann y Zahler se dirigen a la naturaleza restrictiva de las condiciones que determinan una «dinámica de gradiente» en las que resulta válido el teorema de las siete catástrofes elementales. ¿Fallan el blanco?
No hay que pensar que la teoría de las catástrofes se relacione tan sólo con la utilización de la teoría de las singularidades de las funciones; en lugar de eso, creo que habría que utilizar todos los recursos de la teoría de la bifurcación.[94] Dado un campo continuo de dinámicas que se bifurcan en ciertos lugares del espacio de las entradas, del espacio de control, como lo llama Zeeman, el problema consiste en aclarar la naturaleza de las bifurcaciones genéricas, de las bifurcaciones estructuralmente estables. Se ha objetado que la teoría de las bifurcaciones no conduce, en general, a un despliegue de dimensión finita, contrariamente a lo que ocurre con las singularidades de funciones, que por lo general llevan a despliegues de dimensión finita. ¡Ésta es una auténtica dificultad! Pero la objeción, que es matemáticamente válida, no es igualmente válida desde el punto de vista, por así decirlo, de la fenomenología: ésta demuestra que la noción de estabilidad estructural es una noción demasiado sutil para la mayor parte de las situaciones concretas. Dos sistemas diferenciales pueden ser topológicamente bastante diferentes y conducir, a pesar de ello, a aspectos fenomenológicos muy próximos. El problema entonces consiste en expresar «termodinàmicamente» esta equivalencia fenomenológica de dos sistemas diferenciales. Se entra aquí en un campo que desgraciadamente es poco conocido: el problema de la estructura genérica de los atractores. Se da un sistema diferencial en una variedad compacta: en general casi cualquier trayectoria va hacia un atractor, y el problema es describir lo que un atractor resiste frente a una pequeña perturbación de los datos. En general, el tipo topológico del atractor no es estable —excepto en casos muy simples—, pero es posible que exista una cierta termodinámica del atractor que permanece estable. Por ejemplo, me parece verosímil que pueda existir una medida invariable del atractor que pueda eventualmente extenderse al espacio del atractor. Una teoría de la bifurcación basada en la consideración de estos atractores estructuralmente estables con la propiedad termodinámica, podría quizá llevar a algo bastante similar a la teoría de las catástrofes elementales y habría entonces que tener en cuenta el carácter particular de estas bifurcaciones. Permanece abierto el problema de saber si estas bifurcaciones conducen a configuraciones verdaderamente distintas de las de la teoría de las catástrofes elementales, o si llevan a configuraciones del mismo tipo.
¿Puede dar un ejemplo?
El ejemplo de las transiciones de fase es un ejemplo bastante típico. Se sabe que la transición líquido-gas se rige por el modelo de las catástrofes elementales. El modelo de las catástrofes elementales coincide en este caso con el modelo de van der Waals,[95] llamado por los físicos modelo del campo medio de Landau. Se sabe que este modelo no funciona desde el punto de vista de la descripción local de los fenómenos críticos, pero si se consideran las cosas desde un punto de vista cualitativo, es decir, desde el punto de vista de la configuración de lo que ocurre en un espacio, el modelo funciona muy bien. La situación resulta un tanto paradójica: una teoría que en principio se reconoce como inexacta conduce, sin embargo, a una descripción cualitativa correcta. Es ésta una situación que los físicos no son capaces de explicar con los modelos rigurosos de la mecánica estadística y la renormalización. Así pues, el problema sigue abierto y está muy lejos de haber sido explicitado por completo. Esto pone de manifiesto en todo caso que, cuando se hayan reducido a las medias las situaciones topológicamente demasiado complicadas, se llegará a bifurcaciones cuyo carácter en el espacio de control resultará relativamente simple. Desde este punto de vista, precisamente, sigo creyendo que el esquema general de la teoría de las catástrofes elementales conserva una validez que va más allá de la teoría «estricta» de las singularidades de las funciones.
Pero ¿ha sido verdaderamente considerado por sus críticos este aspecto del esquema general?
No; ni por los críticos ni por los seguidores del punto de vista catastrofista. En este sentido, la teoría de las catástrofes no se ha comprendido aún. Se han limitado a utilizar de una forma sistemática las fuerzas canónicas de las singularidades de las funciones y basta. La evolución más reciente de la teoría de las catástrofes (elementales) se ha producido bajo el signo de una especie de degradación utilitarista, que ha consistido en la imposición de un cierto número de formas típicas sobre los fenómenos para dar cuenta de ellos. Por supuesto que no tengo nada contra la imposición de estructuras a priori a los fenómenos, como he admitido hace un momento, pero me opongo a que se reduzca la teoría de las catástrofes a la burda utilización de un cierto número de «recetas».
Cuando habla de degeneración de la teoría de las catástrofes, ¿se refiere a la escuela de Zeeman?
Al contrario, yo diría que Zeeman ha aportado mucho a la teoría de las catástrofes; en su formulación de la teoría se ha servido de variables de control que no aparecían en mi libro. Yo no he considerado nunca de un modo sistemático la utilización de la teoría de las catástrofes según una óptica de la teoría general de los sistemas. Siempre me he limitado al caso en que las variables de control eran las coordenadas espacio-temporales: en el fondo, he sido víctima de un prejuicio análogo al de Newton, que creía que todas las funciones tenían el tiempo como variable independiente. Del mismo modo, yo creía que las catástrofes debían de tener el espacio-tiempo como variables de control. Indudablemente, el punto de vista de Zeeman, de la teoría de los sistemas, resulta preferible, y en este punto he de reconocer sus grandes méritos al haber vehiculado una considerable ampliación del campo conceptual de la teoría.
Una limitación de Zeeman es que se preocupa enseguida por los resultados, es decir que pretende que la teoría de las catástrofes (¡la acuñación es suya!) esté inmediatamente en disposición de producir modelos eficaces, previsiones y acciones efectivas. Como muestra la discusión que tuve con él, incluida en su libro. Catastrophe theory,[96] yo no estoy de acuerdo en eso.
¿Por qué?
Haciendo eso, Zeeman ha creado modelos que tenían una precisión ilusoria, fácil presa para la crítica. Pero no hay que ser demasiado drástico: a propósito de los modelos de Zeeman para la etología y las ciencias humanas, como el modelo de la agresividad del perro o el modelo del conflicto entre estados,[97] en los que se ha concentrado el fuego de las críticas de Sussmann y Zahler, yo sería bastante más prudente que ellos.
Pero si la precisión es «ilusoria» y la cuantificación «espuria», ¿cuál puede ser el valor de unos modelos como ésos?
Según mi opinión, estos modelos tienen un valor real en cuanto son vehículos de la imaginerie, de la imaginación científica. Porque la imaginación, como ya hemos visto, tiene un papel en la empresa científica. Es un lugar común decir que no hay que recurrir a ella en la teorización: yo sostengo la opinión contraria. Aportar una imagen es un bien y no un mal. Así, por ejemplo, el modelo elaborado por Zeeman de la agresividad del perro es un buen modelo (véase fig. 10) desde este punto de vista.
Muestra una situación paradigmática, cuya analogía encontramos en otras situaciones muy diversas. Es, pues, interesante en la medida en que deviene representativo de todo un tipo de situaciones análogas.
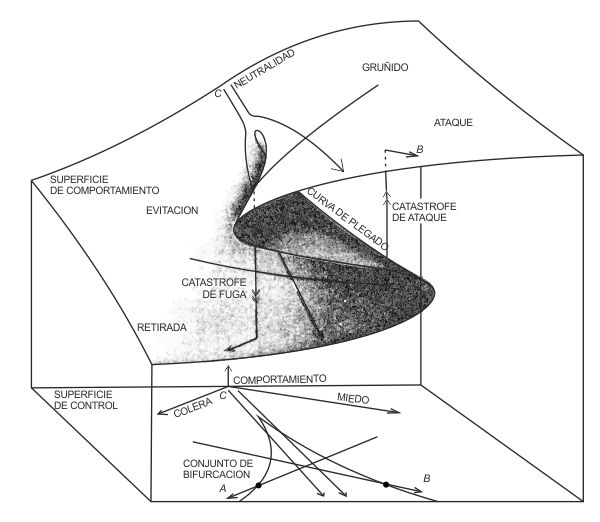
FIG. 10. El modelo, ideado por Zeeman, de la agresividad del perro. Se supone que el comportamiento agresivo viene determinado por dos factores en conflicto entre sí, cólera y miedo, a) En el plano de control representamos estos factores, mientras que el comportamiento del perro, que va del ataque a la retirada, lo representamos en el eje vertical. Para cada combinación de cólera y miedo existe por lo menos una forma probable de comportamiento: se tiene, pues, una superficie de comportamiento. En la mayoría de los casos existe una sola forma de comportamiento; pero en una cierta zona se presentan dos formas posibles. En el plano de control la cúspide señala el umbral en el que el comportamiento empieza a ser biforme. Si el perro encolerizado está asustado, su humor seguirá la trayectoria A de la superficie de control. El correspondiente recorrido en la superficie de comportamiento se va hacia la izquierda del plano superior de la superficie de comportamiento hasta encontrar la curva de pagamiento; aquí el plano superior se acaba y el recorrido cae de golpe al plano interior. Es aquí cuando el perro interrumpe su ataque y se retira de improviso. Análogamente, un perro asustado que se encoleriza sigue la trayectoria B. El perro permanece en el plano inferior hasta que dicho plano se acaba y entonces, en cuanto salta al plano superior, cesa de retirarse y ataca de forma imprevista. En resumen, un perro que simultáneamente está asustado y encolerizado debe seguir una de las dos trayectorias C. b) El hecho de que el perro, si se halla en el plano superior, devenga más agresivo o bien que, si se halla en el plano inferior (de la superficie de comportamiento) devenga más sometido depende de forma crítica de los «valores» de la cólera y del miedo. Según Zeeman, que retoma una idea de Lorenz, la cólera y el miedo pueden revelarse por la expresión del animal: la cólera por el grado de apertura de la boca, el miedo por el grado de acercamiento de las orejas a la a la nuca [Le Scienze, n. 96, agosto 1976, págs. 17-18].

Zeeman parece pretender algo más con este modelo.
Si se utiliza una óptica skinneriana en la que se pretende controlar el modelo con experiencias concretas y cuantitativas, se plantearán notables dificultades. Como se hace notorio, en este modelo es necesario un plano de control en el que miedo y rabia son llevados a dos ejes de coordenadas; pero para un control experimental hace falta una interpretación cuantitativa de estos dos parámetros, de estas dos variables de control —miedo y rabia—, es decir una interpretación independiente del temperamento individual del perro en cuestión. Ésta es, claro, una dificultad importante para la experimentación: llevando a un perro a un estado de miedo o de furor, tenemos que utilizar protocolos experimentales muy definidos, que no pueden ser otra cosa que discretos. Después hay que tener la capacidad de ordenar estos protocolos discretos, cualificarlos en cierto modo. ¿Y no se trata ya de algo que va más allá del alcance del procedimiento experimental acostumbrado? Además, ni siquiera estamos seguros de que todos los puntos del plano (de control) puedan reunirse mediante un procedimiento experimental.
De hecho, es posible que ciertos puntos del plano de control (u, v) no se puedan reunir mediante procedimientos de este tipo. Quizá el estado de miedo, por ejemplo, sea algo fundamentalmente discreto en cuanto al propio animal. Así, al hacer un gesto de amenaza a un perro, si el gesto es poco amenazador el animal no nos hará ningún caso, y sólo a partir del momento en que le atribuya una interpretación amenazadora podrá entrar en un estado de miedo y de rabia. Esto es una especie de limitación que hace, en cierta forma, que no se pueda alcanzar cualquier punto del plano. Aquí encuentro, en cierto sentido, los motivos de las críticas de Sussmann y Zahler,[98] según las cuales disponer los estados de miedo y de furor en un plano (w, v) de control lleva a una cuantificación espúria.
Pero usted no acepta las consecuencias extremas que Sussmann y Zahler han derivado de este punto…
Creo que es algo perfectamente legítimo representar en un plano los estados de furor y miedo, mientras se tenga muy en cuenta que el procedimiento experimental quizá no tenga la capacidad de asumir todos los puntos del plano, es decir mientras se esté de acuerdo en que se plantean dificultades técnicas que es bastante difícil superar. Pero la cuestión de fondo es: ¿hay que convertir estas dificultades técnicas en dificultades de principio, como lo han hecho Sussmann y Zahler, negando en bloque toda validez a este tipo de modelo? A mí me parece que aquí se han equivocado. Es un hecho absolutamente generalizado, en la organización de los seres vivos, que a pesar de que el parámetro que se considera es continuo, el individuo actúa tan sólo mediante operaciones discretas en el interior de este parámetro continuo.
¿Por ejemplo…?
Consideremos el acto de andar. Es un proceso de tipo periódico, cuya célula base es el paso; incluso aunque el parámetro de nuestra experiencia, la longitud del recorrido, sea continuo, un paso tiene como norma una amplitud definida y, en particular, no se puede dar pasos infinitamente pequeños…
Por otra parte, se trata de una situación absolutamente generalizada: incluso si los parámetros son continuos, los seres vivos se ven obligados por su propia organización biológica a proceder mediante campos discretos, una especie de «creodos» (recorridos obligados), por decirlo como Waddington,[99] que llevan a una construcción en cierto modo discreta de este campo continuo, construcción que puede dejar ciertas zonas inaccesibles. Es difícil rehuir este tipo de dificultad y ésta es la razón por la cual el modelo de Zeeman de la agresividad del perro seguirá siendo de difícil control utilizando los métodos experimentales tradicionales. Pero esto no le quita valor como analogía de muchas situaciones.
Ahora somos más capaces de definir mejor la naturaleza hermenéutica de la teoría de las catástrofes…
De hecho, el interés esencial de la teoría de las catástrofes es precisamente este intento hermenéutico de explicar las nubes de puntos con las entidades matemáticas más simples posibles…
Y aquí se abre un enorme campo para la indagación.
El propio término «nube de puntos» exige de forma inmediata consideraciones estadísticas…
La aproximación estadística tradicional ha descuidado por completo, según mi opinión, tal punto de vista. Pero estoy convencido de que en el futuro éste se manifestará extraordinariamente útil.
¿Incluso en las ciencias humanas?
Incluso en las ciencias humanas la estadística es notablemente importante. Pero los espacios con que en ellas se trata son espacios muy artificiales: las coordenadas tienen significaciones muy distintas.
Las variables de control tienen, de hecho, una naturaleza ontológica radicalmente diferente; en consecuencia, los espacios en que se extienden las nubes de puntos (cualquier estadística, como hemos dicho, lleva evidentemente a una nube de puntos) no tienen grupos de equivalencia que actúen en forma transitiva en cualquier punto del modo en que lo hace el grupo euclídeo en el espacio ordinario.
He aquí, pues, una diferencia importante entre las ciencias humanas y las demás ciencias.
Sí, en las ciencias humanas tropezamos con una noción de forma más bien diferente, precisamente por este motivo. Ello hace extremadamente delicado el establecimiento de modelos via teoría de las catástrofes en estas disciplinas. También creo que la situación es distinta cuando las estadísticas se refieren a situaciones naturales, como ocurre con frecuencia en geología y paleontología. Aquí los métodos interpretativos de la teoría de las catástrofes pueden ser útiles de una forma inmediata.
Antes hemos hablado de la ciencia como descripción de formas y después hemos discutido la cuestión de la explicación científica. Aquí aparece de nuevo…
Sí. Supongamos que partimos de una nube de puntos. Para explicarla, introduzcamos coordenadas suplementarias, unos parámetros ocultos.
En el espacio producido se crea un gran sistema dinámico de carácter ergódico,[100] que, por proyección en el espacio de los fenómenos observables, generará la nube de puntos dada. Se trata de una técnica de carácter general, compendiada en la célebre frase del físico francés Perrin:[101] sustituir por lo visible complicado un invisible simple.
En el fondo, éste es precisamente el modo de proceder hermenéutico por excelencia. En el caso de Perrin se trataba de átomos, y por tanto de una explicación de tipo reduccionista, pero creo que su fórmula podría aplicarse también en otro sentido, es decir, en el sentido de la introducción de los parámetros ocultos, mediante los cuales se pueden proyectar en el espacio de los fenómenos observables entidades simples del espacio producido. Se trata evidentemente de un método tentativo diferente del reduccionista clásico; precisamente por esto es una actitud combatida por el pensamiento científico contemporáneo, pero equivocadamente.
¿Por qué?
Estoy convencido de que la aproximación reduccionista falla en un gran número de situaciones, en particular ante el fenómeno casi universal de una jerarquía de los niveles de organización, en un gran número de fenómenos morfológicos. La explicación de la existencia de niveles morfológicos apelará necesariamente a entidades matemáticas del mismo tipo de las que preconiza la teoría de las catástrofes, cosas tales como los espacios de potencial, etc., que no aparecen inmediatamente en la aproximación reduccionista y que, según el planteamiento reduccionista, se pueden considerar sólo después de haber recurrido a procedimientos extremadamente largos y complejos. Aunque no sea más que para dar un ejemplo, digamos que la teoría del estado sólido es bastante difícil de explicar en términos de interacción molecular…
Y sin embargo, como usted mismo reconoce, la actitud reduccionista parece aún hoy muy difundida en el ambiente científico… ¿Cómo ha hecho para sobrevivir a sus graves fracasos?
El problema es un poco de naturaleza psicológica, de «psicología de la investigación» en el sentido de Kuhn: se olvidan los fracasos y se tienen en cuenta sólo los éxitos…
Lakatos[102] ha dado un correlato de un comportamiento de este tipo al nivel de una «lógica del descubrimiento»…
Cualquiera que sea la que se acepte de estas dos aplicaciones, lo que sigue en pie es el hecho de que la aproximación reduccionista también ha tenido éxitos, incluso un gran número de éxitos. Pensemos, por ejemplo, en que se han aislado entidades como el electrón o el protón. Por decirlo de algún modo, son entidades inmutables con carácter permanente. Es cierto que cuando consigue ponerles la mano encima a elementos de este tipo la empresa científica gana mucho. Los peros empiezan cuando se pasa a la teoría de la organización molecular. La teoría de los núcleos atómicos ya es una teoría extremadamente fenomenológica, de la que es difícil dar una formulación rigurosa; si luego, sobre esta base, se construye una teoría general de las moléculas, de la organización molecular, se ve uno llevado a aproximaciones que corrigen notablemente las pretensiones de la aproximación reduccionista.
Pero la teoría de las catástrofes y la aproximación reduccionista ¿no tienen precisamente en común la idea de Perrin, de la que usted hablaba antes? ¿No se trata, en el fondo, de dos variantes del mismo «recorrido» intelectual, de la misma actitud filosófica?
Digamos que la substitución de lo visible complicado por un invisible simple es un objetivo muy natural. Creo que teoría de las catástrofes y reduccionismo son planteamientos opuestos: en la aproximación reduccionista se conserva siempre el mismo espacio, el espacio sustrato en el que tiene lugar la fenomenología que se quiere explicar al principio. Los átomos, por ejemplo, se consideran como corpúsculos que ocupan un pequeño lugar del espacio y que están provistos de unas ciertas propiedades de interacción; cuando haya un gran número de ellos, se podrá reconstruir la fenomenología global utilizando estas interacciones. Esencialmente, se trata de una aproximación combinatoria; se quiere llegar a una solución global en un «paquete» de situaciones locales, de elementos inmutables, reduciendo la dinámica a una combinatoria que en principio tiene lugar en el mismo espacio que el inicial. Pero en realidad la situación es infinitamente más compleja; por ejemplo, incluso en la mecánica cuántica nos vemos obligados a recurrir a un espacio auxiliar, un espacio de Hilbert que es de dimensión infinita, el espacio de las funciones de onda.
El punto de vista de la teoría de las catástrofes es diferente. Pensemos en el mito platónico de la caverna:[103] como los hombres de la caverna, no vemos nada más que los reflejos de las cosas y para pasar del reflejo a la cosa misma hay que multiplicar la dimensión del espacio y proveerse de una fuente que en el caso de Platón es el fuego, el fuego que ilumina. La teoría de las catástrofes supone precisamente que las cosas que vemos son sólo reflejos y que para llegar al ser mismo hay que multiplicar por un espacio auxiliar y definir en este espacio producido el ser más simple que por proyección da origen a la morfología observada. Así pues, la metodología es muy diferente de la reduccionista.
Pero la metodología reduccionista, ¿no es en todo caso más eficaz?
En ciertos casos puede serlo. En biología, por ejemplo, existe una tentación de proporcionar modelos basados en la descomposición de un tejido en sus células, cada una de ellas provista de una estructura automática, de un automa, y de un programa interno. En casos muy simples —pienso por ejemplo en el modelo de Lindenmayer sobre el crecimiento de las algas— estos modelos han dado un resultado. Pero está claro que, en biología, tropiezan con el grave problema de la regulación. Cuando existe un embrión, se le pueden añadir o retirar unas células, por lo menos mientras la perturbación no sea demasiado importante, y el embrión se formará, será igualmente apto para vivir. Se le puede también dividir en dos y en la mayor parte de los casos, si el plano de la sección se ha elegido bien, se conseguirán dos animales. Los fenómenos de regulación reducen a mi entender en gran parte las posibilidades de establecer modelos discretos, basados en una «contabilidad» de las células, que son muy sensibles a las variaciones en el número de las células. Para dar cuenta de los fenómenos de regulación hay que recurrir a teorías continuistas: la desgracia es que los biólogos no están aún convencidos de eso…
¿Por qué?
Las metodologías reduccionistas funcionan hasta que los elementos tienen una individualidad bien definida, hasta que presentan caracteres de inmutabilidad muy manifiestos. Cuando son más «flexibles» y no tienen una individualidad muy clara, la descomposición del sistema en elementos no se manifiesta muy eficaz.
¿Puede dar algún ejemplo?
La neurofisiología constituye un ejemplo patente. Se han adquirido conocimientos muy importantes acerca de la anatomía del cerebro y sobre la fisiología misma de las neuronas, y sin embargo eso no ha sido de gran utilidad para comprender el funcionamiento del cerebro. Ni siquiera se ha conseguido comprender demasiado bien el origen, por así llamarlo, de las variaciones eléctricas en el encefalograma; aparece como una especie de fenómeno sobrepuesto, cuyo significado no se comprende bien. Por otra parte, la situación resulta típica: no es suficiente saber cómo está construido un sistema para saber cómo funciona, sobre todo cuando los elementos tienen una estructura interna más bien complicada.
¿Fracaso, pues?
Decir que la aproximación reduccionista es un fracaso me parece excesivo; yo creo que en muchas ocasiones resulta válida. Puede ser interesante descomponer un sistema en sus elementos, mientras estos últimos presenten propiedades de estabilidad e inmutabilidad bien definidas. En caso contrario, hay que recurrir, en mi opinión, a una teoría continuista.
Pero ¿existen en biología modelos continuistas?
Podría citar los modelos que yo mismo he planteado para la embriología, pero han tenido un éxito muy limitado entre los embriólogos… Se trata de una cuestión de paradigmas, como diría Kuhn. Las ideas que he avanzado tropezaron con los paradigmas tradicionales, y de esa manera se ha preferido no tenerlas en cuenta. Por otra parte, ideas como las mías, en cierto modo basadas en unas analogías entre procesos embriológicos y procesos lingüísticos, son declaradamente escandalosas para el buen sentido del científico positivista tradicional. Identificar la estructura triploblástica del embrión con la estructura ternaria de la frase transitiva sujeto-verbo-objeto puede parecer sólo una metáfora difícil de sostener. En todo caso es exactamente lo que propongo cuando identifico el ectodermo con el objeto, el mesodermo con el verbo y el endodermo con el sujeto, al menos respecto de los vertebrados, porque respecto de los insectos la situación es un poco diferente.[104]
En cuanto a esto, usted ha sostenido que el interés esencial de la teoría de las catástrofes, en cuanto a la metodología, es la posibilidad de proveer un modelo de los procesos lingüísticos y semánticos. ¿Cree usted que en este campo la teoría de las catástrofes tiene posibilidades?
En mi opinión, es precisamente en esta dirección en la que la teoría de las catástrofes resulta más prometedora: mucho más que en el uso que se ha hecho de ella en mecánica o en óptica, por lo menos hasta ahora. La teoría de las catástrofes ofrece una metodología que permite, en cierta medida, enfrentarse a problemas de carácter filosófico con métodos de carácter geométrico y científico, que apelan a las técnicas de la topología diferencial y de la geometría diferencial.
Kurt Lewin, en los años treinta, había utilizado técnicas similares para la psicología.[105] ¿Cuál es su opinión al respecto?
He vuelto a leer recientemente, por sugerencia de un psicólogo americano, algunos trabajos de Kurt Lewin, y creo que muchos de sus intentos revelan una intuición psicológica extremadamente válida.
Lewin fundó una psicología topológica en la que había introducido también la noción de campo; el problema es que, en su tiempo, la topología aún no se había creado en realidad. Sin embargo, Lewin fue capaz de encontrar un cierto número de situaciones típicas cuya validez psicológica no deja dudas. A él le debemos, por ejemplo, la idea de gate-keeper, es decir, de la persona que controla el tráfico; se trata sin lugar a dudas de una noción muy importante en nuestra sociedad que tiene notoriamente, un origen topológico. Las personas que controlan los flujos se colocan generalmente en un punto angosto de una corriente y son capaces de producir notables modificaciones en el régimen de la corriente mediante una pequeña acción en ese punto. Hay, pues, una idea topológica sobreentendida en el poder de ciertos elementos de la organización social…[106]
Por este mismo procedimiento podríamos ahora intentar puntualizar cuáles son los problemas filosóficos a los que usted cree que se puede aplicar con éxito la teoría de las catástrofes…
Sí. Personalmente diría que lo que Lewin tenía en la cabeza era la noción que los psicoanalistas llamarían pulsión o tendencia. Kurt Lewin lo interpretaba en los términos de «poder de atracción», es decir de potencial atractivo en un espacio. Un modelo de este tipo, en mi opinión, puede comportar no pocas intuiciones en un cierto número de casos.
Pero sus motivaciones son distintas de las de Lewin…
Sin duda. Personalmente, lo que me interesa es, en esencial, el problema de la gramática universal y de la semántica; se trata de comprender cómo funciona el lenguaje, aislando ante todo los mecanismos comunes a todas las lenguas (lo cual es el objetivo de lo que se llama gramática universal). Una vez aislada la gramática universal, se podrá hacer el intento de pasar de la estructura profunda a la estructura de superficie, tratando de aislar los mecanismos lingüísticos específicos presentes en la distintas lenguas que no aparezcan explícitamente en la gramática universal.
Pero éste es el aspecto más propiamente lingüístico…
Sí, éste es el aspecto más propiamente lingüístico; el que observa el aspecto filosófico advierte que el problema de una gramática universal va unido al problema de lo que una vez se llamó las grandes categorías del espíritu humano. Aristóteles, Kant… Recordemos que Aristóteles es el primero que dio una tabla de las categorías que después recogió y modificó Kant. Curiosamente, estos intentos de caracterizar las categorías fundamentales del espíritu humano han experimentado una cierta detención. ¡En el siglo XIX quizá haya sido tan sólo Peirce quien propuso un cuadro de categorías! En todo caso, no cabe duda de que una gramática universal sólo se puede elaborar si se relaciona con un cuadro de las categorías del espíritu.
¿Y qué es en el fondo un cuadro de las categorías? Es un cuadro de las grandes preguntas que es razonable plantear. En todo caso, Aristóteles lo planteaba exactamente así al hacer la lista de las preguntas: ¿quién?, ¿qué?, ¿dónde?, ¿cuándo?, ¿por qué?[107] La legitimación de este punto de vista es evidente: ¿por qué se plantean las preguntas?, para conseguir una información de la que tenemos necesidad. ¿Y por qué tenemos necesidad de tal información? Porque la necesitamos para llevar a cabo una cierta acción reguladora: algo que se nos plantea para la salvaguarda de nuestros intereses. Cualquier mecanismo de regulación se asienta, en cierta medida, en la asimilación de una determinada información… Ya se ha dicho que cuando hacemos unas preguntas queremos conseguir una información que necesitamos, y la naturaleza de las preguntas se relaciona de una manera bastante fundamental con el conjunto de parámetros en los que se juega el proceso de regulación. Si se considera tal proceso esencialmente como un proceso de mantenimiento de una forma, es decir un proceso de homeóstasis, se puede decir que estas formas están «desplegadas» en un cierto espacio de regulación.
Las preguntas que se pueden formular entran precisamente en la clasificación topológica de estos grandes espacios contenidos en los parámetros de regulación. Tomemos un ejemplo sencillo: ¿dónde? y ¿cuándo?, son preguntas con las que se relaciona la localización espacio-temporal. Se trata, evidentemente, de un elemento muy importante, porque nuestro cuerpo, la integridad física de nuestro organismo, pasa por el mantenimiento de estos límites espacio-temporales. La integridad de la piel, por ejemplo, que nos separa del mundo externo, diferencia lo interior de lo exterior… Así pues, es absolutamente natural que haya categorías ligadas a la localización espacio-temporal. En lo que se refiere a las preguntas ¿quién?, ¿qué?, la cuestión es un poco distinta, porque en este caso se hace referencia a la idea de sujeto que los lingüistas han complicado notablemente en estos últimos tiempos. ¿Quién?, se refiere más precisamente al sujeto, y ¿qué?, al objeto. También en este caso hay categorías, o más bien funciones, que presentan un cierto carácter de universalidad vinculado, creo, al hecho de que ciertas regulaciones biológicas, como por ejemplo la depredación, requieren la presencia de agentes distintos del propio sujeto.
¿Pero cómo se configura la relación entre depredación y lingüística?
En la depredación hay dos protagonistas: el depredador y la presa.
El depredador se asimila gramaticalmente al sujeto, la presa al objeto. En la base de estas grandes categorías hay, creo, una especie de descomposición de los espacios substratos en la que tiene lugar la regulación de los seres vivos, de nuestro ser, de nuestro psiquismo. La elucidación de estos grandes parámetros, de estos grandes espacios substratos de la regulación, no cabe duda de que es una tarea fundamental si se quiere comprender cómo funciona nuestro espíritu en el lenguaje, mediante el lenguaje. Es una tarea ambiciosa, pero el interés es tan grande que tenemos todo el derecho de arriesgarnos al reproche de ser ambiciosos.
Así que, como ha quedado dicho, en el conocimiento hay que valorar, no sólo la verdad sino también el interés…
Exacto. Hay muchas adquisiciones de la ciencia que sin duda alguna son verdaderas, pero cuyo interés es muy pequeño, casi nulo. El verdadero problema es el de encontrar la fuente del interés. En algunos casos se trata de una fuente sociológica local: un resultado es interesante simplemente porque quien financia la investigación ha sugerido al científico un problema que éste tiene todo el interés del mundo en resolver, si no por otra razón, para hacer carrera…
Por lo tanto, Kuhn está en lo cierto; así va la investigación…
Ésta es una fuente inmediata de interés; sin embargo, creo que se podría encontrar otra, más vinculada a la gran empresa hermenéutica a la que se consagra la ciencia, que consiste en descifrar el mundo, hacerlo inteligible. Según este punto de vista, el interés de una investigación reside en su capacidad de desvelar una estructura subyacente que hace inteligibles los fenómenos.
Pero ¿qué quiere decir hacer inteligible una situación?
Cuando se trabaja sobre una fenomenología, hacer inteligible una situación significa más que nada aislar en esta fenomenología, en la morfología dada en el espacio substrato, elementos identificables, reconocibles, estables. Yo considero que el objetivo de cualquier teoría científica es la explicación de una morfología empírica (o experimental)… Haciendo variar las condiciones iniciales de un proceso de una determinada clase, se consigue, en un espacio definido, un cuerpo de datos empíricos, archivados bajo la forma de documentos escritos, tablas numéricas, imágenes fotográficas, etc. El medio en el que se presentan estas formas es, precisamente, el espacio substrato de la morfología. Se llamará entonces, «explicación» a cualquier procedimiento cuyo resultado consista en reducir la arbitrariedad de la descripción…
Basta considerar el punto de partida de la Gestalt-Theorie para darse cuenta de que precisamente discontinuidades de la morfología constituyen los elementos más evidentes y los más estables. Puede parecer paradójico que las discontinuidades sean estables, pero es un dato de la experiencia: basta pensar en el contorno de un objeto sólido, por ejemplo, que es a todas luces algo que permanece estable. Desde este punto de vista se puede decir que el objetivo primario de cualquier interpretación morfológica es la determinación de las discontinuidades de una morfología y de las partes estables de estas discontinuidades. En esta interpretación interviene la noción de singularidad, de la cual, de hecho, la discontinuidad es un caso particular. Se trata evidentemente de una noción muy importante, ya que es uno de los dos instrumentos, actuantes en sentido inverso el uno con respecto al otro, de que dispone el matemático para pasar de lo local, a lo global: un paso que se requiere en cualquier deducción. El primero de estos instrumentos, el que va de lo local a lo global, es la prolongación analítica en la que puede decirse que se basan, en última instancia, todos los métodos existentes de predicción cuantitativa.[108] El segundo, que va de lo global a lo local, es precisamente el de las singularidades: en una singularidad, de hecho, se concentra en un punto un ente global que luego se puede reconstruir por despliegue o por desingularización.
Hacer inteligible una situación significa, pues, en muchos aspectos, definir un conjunto de singularidades que generan, por su combinatoria, por su disposición recíproca, una configuración global estable, no sólo en el espacio substrato, sino también en un espacio de parámetros desconocidos añadidos como factor. Una vez más: sustituir lo visible complicado por lo invisible simple.
Por el contrario, aquéllos que se preocupan por la acción, aquéllos que, como Karl Marx, pretenden transformar el mundo en lugar de interpretarlo, tratan de actuar en el espacio substrato. Si el espacio substrato es el espacio ordinario, cualquier posibilidad de predicción está siempre ligada a una buena localización espacio-tiempo de los fenómenos que se predicen: de este modo, se ven obligados a contar con algoritmos «capaces de predecir», es decir a ampliar una situación medida en el pasado a una situación prevista en el futuro. Así pues, cualquier método predictivo se vincula a la posibilidad de ampliar una función por extrapolación del pasado hacia el futuro.
Ahora bien, como antes se decía, en matemáticas hay un solo procedimiento de extrapolación canónica, la prolongación analítica. Por prolongación analítica es como se procede de hecho cuando se hacen predicciones. Se llega en consecuencia al resultado de que las posibilidades de realizar acciones eficaces en el porvenir, ante una situación determinada, están siempre vinculadas a la posibilidad de disponer de un modelo analítico de los fenómenos.
Así pues, ¿reside aquí la razón profunda del «milagro de la física»?
Sí. Lo que caracteriza a la física es que sus entidades derivadas son todas ellas extraídas del espacio usual con un procedimiento canónico de naturaleza matemática. En la mecánica cuántica, por ejemplo, el estado del universo para un observador A puede venir representado por un vector XA de un espacio vectorial E. Las visiones de dos observadores diferentes A, B difieren de un automorfismo lineal hAB (matriz) que en principio no depende más que de la posición y del movimiento relativo de B con respecto a A. Toda la física está así contenida en la representación del grupo de las equivalencias (grupo de Galileo, grupo de Lorentz) del espacio E. Aunque estos grupos de equivalencia no sean compactos, desde el momento en que lo que nos interesa son sólo los estados «estacionarios» del universo (para t y |x| tendentes a infinito), tal cosa puede llevarnos de nuevo al caso en que el grupo G de equivalencia es compacto. Ya se sabe que en este caso (teorema de Peter-Weyl) la representación hAB es necesariamente analítica: cualquier término de la matriz hAB es una función analítica de las coordenadas del observador B, y ello es suficiente para explicar de dónde procede, en este caso, la posibilidad de predicción: de hecho, partiendo del conocimiento de la función en el entorno de un punto, se puede ampliar por prolongación analítica una función a todo su dominio de existencia: la posibilidad de «predecir» es, pues, en el caso de la física, algo íntimamente ligado a la naturaleza de espacio analítico del espacio usual (o en cualquier caso de los grandes grupos de equivalencia que operan en él).[109]
Me parece sin embargo, que tal «milagro» es algo muy limitado y que no es fácil ampliar los métodos de extrapolación de la física a situaciones en las que no se da un soporte analítico natural.
Así pues, es éste un punto en el que difieren la física y las demás ciencias empíricas.
Si, aquí aparece algo que limita de una forma drástica las posibilidades de ampliar, por ejemplo, a las ciencias humanas, o incluso a la biología, unos formalismos derivados de la mecánica y la física. Creo que, en un amplio sentido, habrá siempre dos tipos de ciencia: unas ciencias que permiten efectuar predicciones eficaces —es decir, predicciones cuantitativas eficaces— y que por ahora se limitan, creo, a la mecánica y la física; y otras ciencias en las que no se puede predecir en forma cuantitativa, pero en las que se podrá proceder mediante clasificaciones de carácter cualitativo y topológico. Obviamente, estas clasificaciones podrán utilizar también algoritmos matemáticos y no sólo taxonomías de carácter conceptual.
Por otra parte, el problema de la inteligibilidad está ligado en la ciencia al de la localización. Es difícil por ejemplo, considerar inteligible una acción a distancia. Como he repetido una y otra vez, las objeciones que le hacían a Newton los críticos de su tiempo son, en mi opinión, todavía válidas. Tanto es así que, incluso hoy, se busca la forma de poner de manifiesto unas ondas gravitacionales que se propaguen en el espacio. Es decir que hay una relación más bien estrecha entre los fenómenos de localización/no localización de las teorías físicas y la cuestión de la inteligibilidad; en el sentido de que la mayor parte de las leyes, de los grandes éxitos de la empresa científica, están relacionados con la formulación de acciones no locales.
La gravitación newtoniana es un ejemplo de ello. También lo es la interacción coulombiana entre dos cargas eléctricas y la interacción entre una corriente y un imán. En principio todas ellas eran acciones no locales, que se formalizaron matemáticamente. Newton formalizó la gravitación y Coulomb, Ampère y otros formalizaron las otras acciones. Los progresos teóricos han llevado luego a reemplazar estas acciones no locales por acciones locales; sólo más tarde han aparecido las teorías locales. La relatividad general de Einstein es lo que ha hecho local la gravitación; Maxwell hizo lo mismo con el electromagnetismo.
Es, pues, importante poder sustituir las teorías globales con teorías locales: desde este punto de vista, el formalismo de la teoría de las catástrofes tiende a la inteligibilidad de los fenómenos, en cuanto es fundamentalmente un formalismo local: no hay situaciones no locales en el esquematismo de la teoría de las catástrofes.
¿Cómo se articula entonces la dialéctica local/global?
En la física —y pienso, por ejemplo, en el electromagnetismo y, en cierta medida, en la mecánica cuántica— hay teorías locales, que, sin embargo, tienen también efectos globales a causa de la analiticidad global del esquema.
Y viceversa: hacer local una teoría global, una teoría inicialmente concebida como teoría de la acción a distancia, es una operación que, en sí misma, no supone un gran progreso desde el punto de vista de la eficacia práctica. Es un progreso teórico, pero, por lo menos en principio, no es un progreso en el sentido de la eficacia de la acción.
A partir del análisis del par local/global nos encontramos otra vez con una motivación profunda para la necesidad de distinguir entre teorización y acción eficaz o, para decirlo con un léxico filosófico más familiar, entre teoría y praxis.
Ciertamente.
La tensión local/global aparece como fundamental no sólo para las matemáticas, sino también para el conjunto de la tarea científica.
Habría aún mucho que decir acerca de la distinción entre local y global. Así, creo que uno de los teoremas más profundos de la matemática es el teorema de Stokes, del que se puede dar tanto una expresión local como una global.[110] Gracias a este paso de lo local a lo global se puede, en los formalismos físicos, jugar efectivamente entre las distintas formas de una teoría, dándole tan pronto una forma global como una local.
Pero es cierto que la forma local se conforma más a la inteligibilidad: como se ve en las aplicaciones del teorema de Stokes, pongamos por caso, para pasar de la forma local a la global hay que conocer las invariantes globales del espacio, las invariantes topológicas globales; el hecho por ejemplo, de que el dominio del espacio sea contractivo o simplemente conexo; en tal caso se puede dar una forma global.
Éste es un aspecto bastante interesante en la cuestión de la representación de las dinámicas, que se vincula necesariamente, por lo menos en cierta medida, con la estabilidad estructural. Hay teoremas sobre la estabilidad de los sistemas hamiltonianos que tienen este sentido, pero no voy a insistir en este punto.
Podríamos ahora presentar un cuadro de la génesis y la historia de la teoría de las catástrofes, para volver luego a la utilización que hace de ella Zeeman y a las polémicas que a partir de allí se han derivado.
Yo escribí mi libro Stabilité structurelle et morphogenése en los años 1966-67. Tropecé con no pocas dificultades para su publicación, dado el escaso entusiasmo de los editores por un texto que les parecía difícil y también un poco extravagante. Sólo en el 71-72 el editor que había substituido a Benjamin cayó en la cuenta de que mi libro no se había publicado todavía y se propuso la tarea de darlo por fin a conocer. El libro, sin embargo, ya había circulado en forma de manuscrito entre numerosos investigadores, y fue precisamente gracias a este manuscrito informal cómo Zeeman fue capaz de desarrollar la teoría de las catástrofes en la dirección que le interesaba, ocupándose en particular del establecimiento de modelos para un gran número de situaciones, desde la mecánica y la física hasta la biología y las ciencias humanas. Estos modelos quedan ampliamente expuestos en su Catastrophe theory.
De ello se derivó un amplísimo interés por la teoría de las catástrofes. Sobre todo después del Congreso de Vancouver,[111] en 1974, la teoría de las catástrofes empezó a ponerse de moda incluso en los mass-media. El hecho de que, a continuación, se desencadenaran las críticas contra ella, es también un contragolpe, por así decirlo, de esa moda. Ha habido también críticas serias, entre ellas el artículo de Sussman y Zahler publicado en «Synthese» en 1978.[112]
Las críticas, como ya se ha dicho, se dirigieron sobre todo contra los modelos de Zeeman… ¿Las comparte?
Las críticas de Sussman y Zahler se basan en el punto de vista tradicional de la modelización cuantitativa. La mayor parte de los modelos considerados por Zeeman no es susceptible de una formulación cuantitativa rigurosa, en especial los que se refieren a las ciencias humanas o el particularmente típico del estallido de revueltas en las cárceles.[113] Por otra parte, la aproximación de Sussman y Zahler me parece, a su vez, mucho menos seria, pues juega un poco excesivamente con la ambigüedad local/global que se debe tomar necesariamente en consideración en este tipo de modelos. Está claro que los modelos derivados de la aplicación de la teoría de las catástrofes elementales son modelos locales; en cualquier caso, para derivar de ellos conclusiones que tengan una cierta validez, habrá que completar siempre este carácter local con hipótesis de globalidad suficientemente verosímiles. Me parece que buena parte de las críticas de Sussman y Zahler se produce por el hecho de que este carácter al infinito, por así decirlo, de la dinámica en el espacio de control no surge directamente del modelo, sino que viene impuesto en cierto modo a priori por el modelizador. En otros términos: los modelos de Zeeman serían modelos locales, pero para derivar de ellos conclusiones sería necesario establecer hipótesis al infinito, hipótesis marginales, y precisamente el hecho de que estas hipótesis no estén claramente explicitadas en los modelos de Zeeman justificaría las críticas de Sussman y Zahler. Éstos, por ejemplo, mantienen, refiriéndose al modelo de la agresividad del perro, que un perro enfurecido acaba siempre por atacar, mientras que el modelo de Zeeman conduce a la hipótesis de que el perro sigue enfureciéndose siempre, sin llegar a atacar nunca. El razonamiento no me parece muy importante, precisamente porque revierte en la dinámica al infinito, que, en cierto sentido, es algo que se deriva del modelo. También la objeción acerca del comportamiento del mercado de la Bolsa es del mismo orden…[114]
A pesar de que en el artículo de «Synthese» Sussman y Zahler declaran «tener como principal objetivo a Zeeman», hacen sin embargo una crítica que se dirige a usted cuando afirman que los modelos proporcionados por la teoría de las catástrofes atribuyen una morfogénesis a un conflicto, «a la lucha entre dos o más atractores», e impugnan la tesis según la cual, para usted, la teoría de las catástrofes no debe atender a una confirmación experimental. Finalmente, se critica el énfasis sobre el par continuo/discontinuo y se contraponen a la teoría de las catástrofes métodos discretos, como la teoría de los grafos, etc.[115]
Aquí se plantean muchas objeciones en una. Ante todo, una objeción acerca de la originalidad de la teoría de las catástrofes. Se trata de una observación que se encuentra, mejor articulada, en la recensión de Smale al libro de Zeeman, publicada en el «Bulletin of American Mathematical Society».[116] Smale afirma que, después de todo, las nociones de discontinuidad, de onda de choque, de bifurcación, etc., son nociones ya definidas y puestas en práctica por la escuela soviética, en especial por Andronov, uno de los fundadores de la noción de estabilidad estructural.
Mi respuesta es que, ciertamente, la noción de bifurcación se utilizó mucho antes que la teoría de las catástrofes. Prueba de ello es el hecho de que el término «bifurcación» (Abwegung) aparece, por lo menos, en Jacobi.[117] Por tanto, ¿quién podría pretender que la «teoría de las catástrofes» ha generado la «teoría de la bifurcaciones»? Nueva es, sin embargo, la idea de utilizar de forma sistemática la teoría de las bifurcaciones para explicar las discontinuidades de la naturaleza. Creo que ésta es la aportación esencial de la teoría de las catástrofes en cuanto metodología y, sinceramente, no veo cómo se podría afirmar que esta idea se había formulado antes de una forma tan sistemática como se ha hecho en mi Stabilité structurelle et morphogenése.
Quede claro que muchos han utilizado antes que yo la noción de bifurcación y han utilizado incluso los umbrales a priori, Sussman y Zahler dicen que el método de los umbrales es por lo menos tan bueno como el de las catástrofes… ¡estupendo! Yo creo que todo depende de la situación que se considere. Si se quiere comprender de dónde procede un umbral, se ve uno obligado a asumir una perspectiva ontogenética, una perspectiva diacrónica que explique la génesis del umbral. Pero si se quiere explicar la génesis de un umbral, se ve uno llevado casi automáticamente a considerar una situación de tipo catastrófico. Evidentemente, se puede también prescindir de la génesis del umbral y proponerse simplemente ver cómo funciona un umbral ya constituido: en tal caso, no es necesario introducir un formalismo como el que lleva a la cúspide para explicar la presencia de tal umbral.
Las críticas de Sussman y Zahler afectan también al status general de la teoría de las catástrofes. En muchas ocasiones, ha afirmado usted que la teoría de las catástrofes procede de las matemáticas, pero que no es matemática.
Fue Zeeman quien acuñó el término «teoría de las catástrofes», de manera que le correspondería a él decir en qué consiste efectivamente. Después de todo, la cuestión de lo que pueda ser la teoría de las catástrofes es una cuestión de definiciones. En lo que a mí respecta, la teoría de las catástrofes no es una teoría que forme parte de las matemáticas. Es una teoría matemática en el sentido de que utiliza instrumentos matemáticos en la interpretación de algunos datos experimentales. Es una teoría hermenéutica o, mejor aún, más que una teoría una metodología, que se preocupa por la interpretación de datos experimentales, utilizando para ello instrumentos matemáticos cuyo repertorio, por otra parte, no está definido a priori. Ya me guardaré muy mucho de utilizar este o aquel tipo de algoritmo matemático si no veo la necesidad de ello. Éste es un punto muy delicado, de comprensión muy sutil. Vuelvo ahora a una de las críticas de Sussman y Zahler. Según algunos, la teoría debería ser, como cualquier teoría física válida, controlable por la experiencia; una teoría puramente matemática, una teoría de la matemática, en la que, a partir de ciertos axiomas, se demuestran unos teoremas, y todo acaba ahí. La idea de que la teoría de las catástrofes pueda ser una metodología que se apoye en las matemáticas y que considere como su material los datos experimentales es algo que, a primera vista, parece escapar al punto de vista tradicional. En resumen, se trata de una metodología que escoge, en el conjunto de los algoritmos matemáticos, el que le parece más adecuado a la situación considerada.
Pero ¿cuál es el criterio según el cual distinguiremos, entre los diversos algoritmos, el mejor para la interpretación de una fenomenología dada? Positivistas y popperianos contestarían a la vez (aunque con distintas motivaciones) que el control empírico permite discernir las explicaciones más adecuadas, las que precisamente conseguirían «sobrevivir» al control empírico. ¿Cuál es su opinión? Hay quien le acusa de negar cualquier posibilidad de control.
He dicho multitud de veces que la teoría de las catástrofes no puede quedar confirmada ni negada por la experiencia. El biólogo Lewis Wolpert me decía en un congreso: «En resumen, que su teoría lo explica todo; ahora bien, una teoría que lo explique todo no explica nada». De momento, quedé escandalizado. Pero después de reflexionar sobre ello, encuentro que la crítica de Wolpert, inspirada en el más puro empirismo anglosajón, está bastante fundada… Los empiristas más rigurosos siempre podrán atribuir a la teoría de las catástrofes el mismo estatuto que Evans-Pritchard atribuía a la magia. En sus estudios[118] de las prácticas mágicas de los Nuer del Alto Nilo y de los Azandi, mostró cómo el sistema explicativo de la magia es un sistema que no falla nunca. Si cualquier acto o cualquier procedimiento mágico no surte efecto, la opinión pública siempre podrá explicarse un fracaso de este tipo con razonamientos de orden local: la eficacia del acto se ha visto reducida o anulada por completo debido a un vicio de forma, a la incapacidad o a la impureza del oficiante, a un contra-sortilegio de la víctima o del enemigo, etc.
En resumen, que de una forma análoga a las creencias Nuer, la teoría de las catástrofes sería una especie de magia, una sofisticada magia de nuestro tiempo…
Hay quien tiene esa sospecha… Por otra parte, es bien sabido que Popper ha sostenido que el psicoanálisis, al no poderse «falsar», no se puede considerar «científico». Pues bien, no debemos ocultar que también la teoría de las catástrofes puede ser objeto de objeciones de este tipo…
¿Queda excluida por lo tanto del campo de las teorías científicas?
En cuanto a esto procederé con cautela. El problema de la diferenciación entre «ciencia» y «no ciencia» es un problema epistemológico que todavía se debate… Por otra parte, en este caso concreto, es falso decir que no hay forma de control para la teoría de las catástrofes. Se da un control, porque se parte siempre de datos. Todo el problema reside en que para muchos, sean científicos o filósofos de la ciencia, no es suficiente partir de un dato para hacer ciencia, sino que es necesario, además, hacer predicciones cuya contrastación con la experiencia dirá después si hemos tenido éxito… Por eso se insiste tanto en el «poder predictivo» de las teorías. Según mi opinión por el contrario, se puede hacer un buen trabajo científico a partir de un dato, sistematizando una teoría que concuerde con este dato, sin que haya que hacer necesariamente una nueva predicción a partir de ahí. Para dar un simple ejemplo, Michael Ventris, que descifró la escritura lineal B en Creta y descubrió que era griego vertido en una especial escritura alfabética,[119] tenía a su disposición un cuerpo de inscripciones, y a partir de este cuerpo de inscripciones, mediante un análisis bastante profundo, fue capaz de edificar una teoría: el control experimental quedó representado simplemente por el hecho de que las inscripciones adquirían sentido… Verdad es que no fue capaz, ni se lo planteaba, de encontrar nuevas inscripciones…
Un popperiano y sin embargo, podría contraargumentar que el propósito de Ventris no era el de encontrar una nueva inscripción en lineal B; su teoría debería más bien «vetar» que se encontrasen inscripciones en lineal B que no fuesen inscripciones en griego. Existe, pues, una posibilidad (teórica) de invalidar (falsar) una teoría hermenéutica del estilo de la de Ventris.
Es verdad que si se admite el concepto de «falsabilidad virtual» también los modelos proporcionados por la teoría de las catástrofes resultan en algún sentido «falsables».
Quizá se dé una cierta analogía con los principios de la termodinámica, un célebre ejemplo de Popper por cuanto concierne a la «falsabilidad» de las hipótesis científicas. Popper «no exige, de hecho, que, antes de ser aceptada, cualquier aserción científica haya de ser, de hecho, controlada. Exige más bien que cada aserción de este tipo sea susceptible de ser controlada». Y además: «Las llamadas leyes naturales tienen la forma de aserciones estrictamente universales; así pues, pueden venir expresadas en forma de negaciones de aserciones estrictamente existenciales, o bien en forma de aserciones de no-existencia (o aserciones “no hay”). La ley de la conservación de la energía, por ejemplo, puede expresarse en la forma “No existe ninguna máquina de movimiento continuo” o la hipótesis de la carga eléctrica elemental en la forma “No existe ninguna carga eléctrica que no sea múltiplo de la carga eléctrica elementar”. En esta formulación vemos que las leyes naturales pueden compararse a “prohibiciones”. No afirman que algo existe u ocurre: lo niegan… Y precisamente porque lo hacen son “falsables”. Si aceptamos como verdadera una sola aserción singular que, por así decir, infrinja la prohibición afirmando la existencia de una cosa (o el acaecer de un evento) excluida por la ley, la ley resulta refutada (un ejemplo de ello podría darlo la aserción “En tal lugar hay un aparato que es una máquina de movimiento continuo”)».[120] Esto es lo que Popper quiere dar a entender con su noción de «falsador potencial» de una teoría científica. Por otra parte, todos los intentos realizados de hecho para construir un mecanismo de movimiento continuo han fallado, y se interpretan así como «corroboraciones» de la teoría. ¿Quién por otra parte está más convencido de la profunda falsedad del primer principio de la termodinámica que uno de los muchos «inventores» de las máquinas de movimiento continuo? En resumen, ¡se intenta «sinceramente» falsar la teoría, aunque no se consigue!
Diré entonces que ciertos modelos de Zeeman son verdaderamente susceptibles de ser falsados virtualmente en el sentido que hemos aclarado aquí. Se puede imaginar, por ejemplo, una actuación en el espacio de control para producir una u otra transformación y ver si tal transformación se produce efectivamente, Pero el hecho de que ciertos modelos propuestos por Zeeman sean «falsables» (en el sentido de Popper) no quiere decir que estén «bien corroborados» (en el sentido de Popper).
¿Está usted de acuerdo entonces en considerar la «teoría» de las catástrofes como un «generador» de modelos?
Por supuesto.
El hecho de que los diferentes modelos sean falsables o, sin más, que hayan sido de hecho falsados, no quiere decir, pues, que la teoría de las catástrofes quede eliminada ipso facto. Contra cierto falsacionismo «ingenuo», una falsación «local» no implica el rechazo «global» de un generador de modelos de este tipo…
Seguramente: si consideramos el estado presente de cierta modelización inspirada en la teoría de las catástrofes, hay que convenir en que se han producido notables fracasos, debidos al hecho de que ciertos investigadores han aplicado esta modelización como una routine, de una forma pedestre y no inteligente. En mi opinión, existen pocos ejemplos de una utilización pertinente de la metodología de la teoría de las catástrofes. El mejor uso que se puede hacer de ella, según mi parecer, consiste de hecho en el hallazgo de parámetros pertinentes. Por el contrario, una modelización pseudo-cuantitativa que impone un modelo catastrofista a una situación empírica determinada, puede tener interés como «matemática de aproximación», exactamente como puede tener interés en ciertos casos representar una función continua con un polinomio de interpolación.
Todo esto no dice mucho, sin embargo, acerca de los mecanismos profundos de los fenómenos, y tiene una validez local que es imposible extrapolar más allá de ciertos límites difíciles de especificar. Ello hace que, en conjunto, todo lo que se ha presentado como «aplicación» de la teoría de las catástrofes no haya dado hasta ahora resultados convincentes. En particular, no ha habido ejemplos en los que se haya podido hacer una predicción efectiva, confirmada después por la experiencia, con excepción de los experimentos realizados por M. Berry en óptica geométrica, sobre las «cáusticas».[121] En este caso, sin embargo, se trata de fenómenos tan evidentes y previsibles a priori, que la sorpresa no ha sido muy grande… Desde este punto de vista, se puede decir que la teoría no ha tenido hasta ahora grandes aplicaciones prácticas y no está claro que vaya a tenerlas en el futuro, aunque obviamente ello no quede excluido. Es una situación bastante parecida a la utilización de las distribuciones gaussianas en estadística. ¿La utilización de las distribuciones gaussianas ha llevado quizás a buenas posibilidades de predicción? La cuestión no es demasiado evidente en mi opinión, y me parece que los modelos de las catástrofes se encuentran en parte en el mismo status, si puede decirse así. Sobre todo los proporcionados por la teoría de las catástrofes elementales —en los que se utilizan de forma sistemática las formas canónicas de las singularidades— y sus despliegues. Es verdad que la situación resulta un tanto ingrata, ya que hace difícil defender la teoría de las catástrofes, mientras todo el mundo se pregunta qué es efectivamente esta teoría. Se podría responder que consiste en las siete catástrofes elementales en el espacio-tiempo de dimensión cuatro, pero éste es un punto de vista que no acepto porque, en mi opinión, la teoría de las catástrofes es mucho más general. Pero si no es eso, entonces ¿qué es? Podría responder que es un método general, pero un «método general» no hace apelación a teoremas precisos: así pues, no es «substancia matemática». Ésta es, en el fondo, la objeción de Smale cuando escribe que no hay una substancia matemática real fuera de las catástrofes elementales. En un cierto sentido, Smale tiene razón. Por otra parte, me parece que sería absurdo quedar confinado en un esquema matemático único, mientras intento utilizar todos los recursos ofrecidos por la teoría de la bifurcación y estos recursos están muy lejos de conocerse y haberse analizado, incluso desde el punto de vista matemático. En general, desde el momento en que no se conoce la estructura de los atractores, a fortiori tampoco se conoce la estructura de la bifurcación: es térra ignota. Es cierto que en muchos casos se han utilizado técnicas análogas a las de Stabilité structurelle et morphogenése, pero creo que en mi libro se da por primera vez una metodología sistemática de este tipo de modelización.
Parece que muchas de las críticas se articulan en dos frentes: sobre el control empírico de la teoría de las catástrofes, y también sobre su rigor matemático.
En lo que se refiere al control empírico, ya he respondido. En cuanto al rigor, es cierto que como matemático he escrito algunos artículos no muy rigurosos; soy el primero en admitirlo. Por ejemplo, mi comprometido artículo sobre los conjuntos estratificados tenía algunas lagunas en la axiomatización (que arregló Mather después), y he enunciado muchos teoremas que no podía demostrar efectivamente. Pero creo que, en conjunto, no he cometido nunca errores clamorosos. Tengo la intuición suficiente como para no cometerlos.
Por lo demás, cuando Sussman y Zahler hablan, por ejemplo, de «modelización poco rigurosa», critican ciertos aspectos de la presentación de Zeeman que son un tanto discutibles. Recuerdo muy bien que Zeeman consideraba lícito, basándose en ciertos «teoremas», afirmar, digamos, que en ciertos procesos reales se mueve una frontera y luego se estabiliza.
Es preciso que seamos precisos: soy de la opinión de que no se puede nunca «deducir» un fenómeno concreto de un teorema. Creo que existe una distinción fundamental entre el mundo de las matemáticas, en el que se procede por deducción, y el mundo de la realidad. En resumen, Zeeman quería deducir fenómenos naturales de una proposición matemática. Ello es lícito sólo si a priori se sabe que un fenómeno viene regido por un determinado modelo. Pero esto sólo se puede saber en virtud de una ley física o algo similar.
Así pues, usted está de acuerdo aquí con la crítica de Sussman y Zahler…
Sí. Naturalmente, mi acuerdo con Sussman y Zahler es sólo sobre un punto particular. Por otra parte, es lo que le objetaba a Zeeman: en ningún caso la matemática tiene el derecho de dictar cosa alguna a la realidad.
¿Se agota aquí la cuestión del rigor?
Para volver a cuestiones personales, es éste un aspecto que ha sorprendido mucho a algunos matemáticos, precisamente a propósito de las catástrofes elementales.
Algunos representantes de la escuela de Warwick y muchos investigadores que han seguido su intento, han llamado a esta clasificación «teorema de Thom».[122] Pero yo nunca he enunciado un teorema de ese género, sólo he dado la lista de las siete singularidades que se presentan genéricamente en un espacio-tiempo de dimensión cuatro. Un cierto número de puristas, en particular matemáticos de la escuela soviética como Arnold, han seguido manteniendo que era incorrecto denominarlo teorema de Thom, dado que yo no había enunciado ni demostrado nada de ese tipo. Respondí a Arnold que nunca había tenido tal pretensión y que, por el contrario, me guardo mucho de reivindicar los teoremas cuando no dispongo de demostraciones completas. Pero estas cuestiones de prioridad pertenecen a ese tipo de controversia técnica que resulta de muy escaso interés para quienes no son profesionales.
Planteémonos entonces la cuestión sobre el rigor matemático. En un artículo suyo se lee que «todo lo que es riguroso es insignificante»: ¿No le parece que la insistencia sobre la confirmación experimental y sobre el rigor absoluto serían las dos caras de una misma moneda, de un «compromiso justificacionista», como lo denominan los filósofos anglosajones?
Sí. Existe, en efecto, un cierto parentesco entre las dos exigencias. Se da además un tercer factor, a mi entender, que actúa sobre la justificación de los modelos, que los que han caracterizado las otras dos características han olvidado: me refiero a la economía intelectual.
¿Por qué este término? ¿Se trata de una alusión al clásico punto de vista de Mach?
¿Mach? Quizá, si no a la navaja de Occam. Está claro que, dada cualquier fenomenología, siempre se puede dar un modelo que la describa. En otros términos: si se utilizan los suficientes parámetros, funciones de grado suficientemente elevado, siempre se puede construir un modelo matemático de lo que sea. Pero el auténtico problema no es evidentemente éste, sino que reside en la construcción de un modelo que no recurra a «demasiados» entes matemáticos. Por lo tanto, se plantea un problema entre la adhesión rigurosa al dato empírico, es decir aquello que los anglosajones llaman fit, y la cantidad de parámetros que comparecen en el modelo: si se introducen muchos parámetros, se da un buen fit, pero se tiene un modelo complicado; y si se introducen pocos, el modelo es simple, pero el fit es malo. De manera que lo mejor será conseguir aquellos modelos que concilien, mediante un compromiso, pocos parámetros y un buen fit.
He aquí, pues, un criterio en cuanto a la validez de los modelos…
…pero, que depende fundamentalmente de lo que se quiera hacer. Si, por ejemplo, se buscan modelos cuantitativos locales, es decir si se quieren modelizar cuantitativamente situaciones locales (pensemos, por ejemplo, en fenómenos biológicos bien definidos, como la circulación de la sangre o la eliminación del gas carbónico de los pulmones), hay que introducir un número suficiente de parámetros. Pero si de lo que se trata es de aislar los grandes parámetros subyacentes a los fenómenos, entonces será interesante contentarse con un número pequeño de parámetros, pasando por alto, por lo menos parcialmente, la concordancia cuantitativa con la experiencia. Cuando construí, por ejemplo, mis modelos para la embriología, nunca me preocupé por esta concordancia cuantitativa…
¿Y por qué no es relevante aquí la concordancia con la experiencia?
Según mi opinión, el problema más relevante para un modelo del desarrollo embriológico es el enlace de ciertos fenómenos locales con su ambiente (environnement). Plantearé un ejemplo específico que permita aclarar también la cuestión general acerca de la que estamos discutiendo: qué tipo de matemática hay que utilizar para explicar una determinada fenomenología.
Tomemos, por ejemplo, en la embriología de los vertebrados, el fenómeno de la gastrulación, una etapa del desarrollo embrional en el transcurso de la cual el ectodermo recubre la superficie del embrión, el endodermo se sitúa en el interior y el mesodermo en una situación intermedia. Ante una situación de este tipo se puede elegir entre un cierto número de modelizaciones matemáticas. Se puede, por ejemplo, como lo hizo Zeeman, tomar un modelo con tres mínimos correspondientes a tres regímenes estables (endodermo, ectodermo y mesodermo) y razonar a partir de una singularidad de estilo «mariposa». He respondido a Zeeman que considero que es preferible partir de una cúspide y suponer después que por efecto de una ulterior complicación en la dinámica se produzca un ciclo de histéresis que, eventualmente, se puede pulir y dar origen a un auténtico ciclo estable que pueda explicar la presencia del mesodermo. En este caso, se puede elegir entre dos singularidades típicas: la mariposa o la cúspide. Yo he optado por la segunda interpretación. Ciertas porciones del mesodermo dan origen, por ejemplo, al tejido cardíaco, el cual desarrolla después, a partir de sí mismo, un ciclo típico de evolución, de contracción periódica; hasta tal punto que, como se sabe, si se le impide al corazón formarse, se da entonces un gran número de pequeños corazones que se constituyen en una especie de cápsulas que pulsan, cada una por su cuenta. Se da en este caso la típica situación en la que la elección puede depender de una morfología determinada, puede venir determinada por lo que suceda en ambientes lejanos del proceso considerado.
En otros términos: hay que retrotraer el fenómeno a su ambiente, considerarlo en su génesis y en su desarrollo. De hecho son estas consideraciones vinculadas al ambiente las que pueden decidir sobre la elección de la dinámica a utilizar en el modelo.
No tengo prejuicios en cuanto a cómo construir los modelos: creo que habría que considerarlo todo, no sólo los objetos modelizados en sí, sino también los ambientes. Uno de los méritos de la teoría de las catástrofes es precisamente que permite esta flexibilidad, este mirar alrededor, relacionar las cosas… mientras que, por el contrario, la modelización más tradicional establece el modelo de un ser muy específico, muy delimitado, sin preocuparse por lo que ocurre inmediatamente después.
¿Pero no es típico de la ciencia moderna como forma específica de conocimiento este cortar los lazos? ¿Por qué, por ejemplo, Galeno, aun habiendo aplicado un método de experimentación análogo al de Harvey (la conexión) no consiguió determinar el mecanismo de la circulación sanguínea? La respuesta es que ello se debió a la incapacidad por parte de Galeno de considerar el movimiento de la sangre como un simple problema de hidráulica, de estudiar este movimiento en sí y por sí. Para la biología galénica la circulación no podía ser considerada como un sistema mecánico cerrado, ni la sangre se podía tratar con independencia del conjunto del cuerpo, del problema de la salud, de las relaciones entre el organismo y sus propios ecosistemas, de los problemas de la alimentación, etc. Lo que Harvey pudo individualizar, no era individualizable para Galeno.
No cabe duda de que el método experimental ha favorecido en amplia medida esta disociación de los fenómenos: para describir los fenómenos parece cómodo disociarlos, aislarlos. Hay que ser capaz de disponer de una situación que sea repetible, reproducible y en la medida en que se requiere una situación reproducible, hay, evidentemente, que «recortarla». Pero en mi opinión esto de recortar las cosas es una considerable mutilación de la realidad, sobre todo en biología. En física, de hecho, se puede sostener, y no sin razón, que muchos fenómenos están ya disociados por sí mismos o vinculados de una manera muy laxa: la gravitación y el electromagnetismo, por ejemplo, están vinculados muy débilmente: en biología, por el contrario, los fenómenos están más relacionados y las disociaciones son siempre algo muy artificial.
¿Y cómo puede la teoría de las catástrofes superar semejante dificultad?
La ventaja del esquema de la teoría de las catástrofes es la idea según la cual, cuando se tiene un proceso morfológico en un espacio substrato, se puede suponer que todos los procesos locales que se dan en un área pequeña, en un pequeño abierto del entorno de un punto, forman cada uno una especie de caja negra con una «ventana», y el color de la ventana es la salida del sistema. Toda la morfología se convierte así en un campo de «cajas negras con ventanas»; el problema se convierte entonces en cómo interpretar los saltos de color, y por lo tanto la morfología, en términos de una dinámica subyacente, de una dinámica interna.
Supongamos entonces que una cierta región D del espacio-tiempo sea la sede de un proceso natural (físico, químico, biológico, etc.); D se divide en células, y en cada una de ellas hay una caja negra con una ventana, de la cual «surge» un color…
Exacto: el dominio D es la base de un campo de automas locales, en los que la entrada es simplemente la posición espacio-temporal, mientras de cada «ventana» sale un color, de manera que D aparece como una especie de cuadro coloreado. Si en un punto a de D el automa local se encuentra en un ramal regular de la característica C del sistema y permanece ahí para una pequeñísima variación de a, a constituye un punto regular de la morfología. Los puntos regulares constituyen un abierto cuyo complementario es, precisamente, el conjunto cerrado K de los puntos de catástrofe. Y son estos puntos, en los que el color es discontinuo, los que constituyen los soportes de las formas visuales que percibimos en D. Así, en la distinción figura/ fondo, cara a los gestaltistas, K se representa como el borde de la figura…
Pero en esta idea de una morfología como campo de cajas negras con ventanas y de dinámica subyacente, la teoría de las catástrofes ¿no recupera alguno de los temas de fondo de la antigua filosofía de la naturaleza?
Efectivamente, hay en la teoría de las catástrofes una exigencia de síntesis que, en cierta medida, recupera la herencia de la vieja Naturphilosphie. En mi opinión, si se observan los fenómenos con un cierto distanciamiento, se constatará que muchos accidentes morfológicos aparecen de una forma por completo independiente de la naturaleza de los entes involucrados. La clasificación de estos fenómenos generales ubicuos permite aislar «entidades» que actúan, localmente en esta dinámica y que yo he llamado λόγοι, arquetipos. En principio, estos arquetipos se manifiestan en cualquier substrato. Ésta es una idea que escandaliza a los científicos positivistas que parten del principio, por otra parte discutible, de que las morfologías están vinculadas de una manera fundamental a la naturaleza de los elementos constituyentes.
Tenemos por ejemplo la teoría de las fases: todos los líquidos tienen prácticamente el mismo comportamiento, todos los gases tienen prácticamente el mismo comportamiento, todos los sólidos tienen comportamientos en gran medida similares, aunque las propiedades de rigidez, viscosidad y resistencia sean evidentemente muy distintas. La teoría de las catástrofes elementales es, en cierto sentido, una teoría del substrato más general, del substrato indiferenciado, podríamos decir de la materia prima de los escolásticos. Pero si al substrato le imponemos propiedades de invariancia, como dejar el volumen constante o la distancia constante, etc., la teoría se modifica y estas modificaciones implican un cambio en la naturaleza de los accidentes morfológicos. La materia impone vínculos suplementarios: rigidez, simetría, invariabilidad de ciertos volúmenes, etc., y debido a estos vínculos la teoría de las singularidades se modifica. Esta modificación aparece empíricamente en la naturaleza específica de las singularidades; las singularidades de las nubes, por ejemplo, no son las de un iceberg o las de una roca…
Parece, pues, que su punto de vista une la noción de forma y la de crecimiento tal como lo plantea D’Arcy Thompson.[123] Por otra parte, revaloriza el papel de la causa formal… ¿No indica eso, en cierto modo, una vuelta a Aristóteles?
Con ocasión de una convención sobre Aristóteles, he tenido oportunidad hace poco tiempo (1978) de sostener en mi intervención que con la teoría de las catástrofes reaparece una idea aristotélica, la del encadenamiento hilomórfico, según la cual la materia aspira a la forma. Creo que en esta idea hay un elemento nuclear muy justo; en mi opinión, es posible un resurgimiento de la causalidad formal.
Si bien se suele contraponer la ciencia de Newton a la ciencia aristotélica, Kuhn, en lugar de ello, ha subrayado que en Newton queda aún algo que sigue vinculado a la idea de causa formal de Aristóteles.[124] Se podría hablar, más bien, entonces, de una contraposición entre el modelo científico cartesiano y una tradición que va de Aristóteles a Newton. ¿Está usted de acuerdo con esto?
Desde este punto de vista se da, en efecto, una oposición entre Descartes y Newton. En un cierto sentido, sin embargo, en el esquema newtoniano se conserva la noción de fuerza como causa activa, más que formal; pero si Newton «envejece» un siglo y se une a Hamilton, se ve con toda claridad que las leyes de Newton se pueden expresar mediante una hamiltoniana dotada de un cierto potencial y el sistema diferencial que se obtiene hereda entonces una cierta forma, y también los accidentes locales que se obtienen, como las trayectorias cerradas, las curvas de las órbitas, el espacio de fases, etc., se ven forzados a heredar una cierta forma. Así pues, se puede decir que a partir del momento en que se utilizan formalismos hamiltonianos nos vemos llevados automáticamente a considerar ciertas envolventes de trayectorias que presentan una forma determinada, aunque en general estas formas sean, desde un punto de vista geométrico, terriblemente complicadas. Ello no impide que aparezca una disociación fundamental de las trayectorias que cumple un papel muy importante en toda la interpretación de la dinámica: existen algunas dinámicas que permanecen ergódicamente cerradas en el espacio, mientras que otras navegan caóticamente, ergódicamente en el espacio. En cierto sentido, se puede decir que ciertas formas tienden a realizarse automáticamente al nivel de una dinámica general.
¿Por ejemplo?
Consideremos un oscilador lineal. Su movimiento viene definido por la ecuación diferencial q = −kq con k > 0. Tenemos inmediatamente una interpretación en términos de causa eficiente: existe una fuerza de atracción que es proporcional a la distancia q y el modelo oscila indefinidamente en torno al origen según una ley sinusoidal. Pero si aplicamos el formalismo hamiltoniano se puede transformar el sistema introduciendo una «variable oculta» p que nos da el momento. Y entonces nos vemos llevados en el espacio de fases (p, q) a considerar una hamiltoniana cuadrática de la forma:
donde m es la masa del oscilador. Las trayectorias pueden interpretarse entonces como elipses alrededor del origen (véase fig. 11). Se da un mínimo cuadrático para la hamiltoniana H en el origen p = q = 0 y, en general, para H = E, con E constante; se definen, pues, las trayectorias elípticas
de manera que el mismo sistema dinámico puede tener una interpretación en términos de causa eficiente por medio de los flujos o una interpretación morfológica en términos de singularidades de una hamiltoniana. Decir qué interpretación es la más profunda, cuál es la más física, es una cuestión de libre elección.
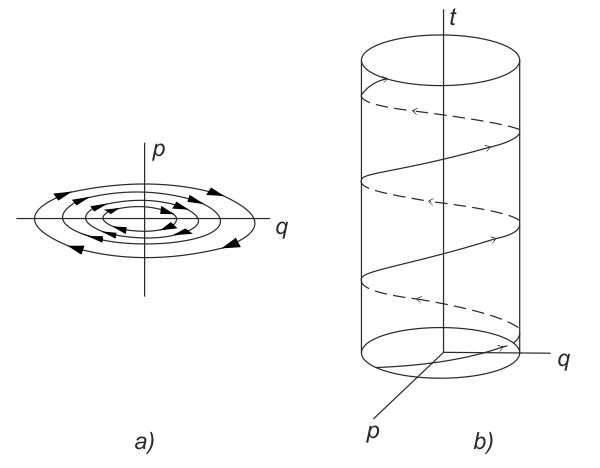
FIG. 11. El oscilador lineal, a) El espacio de fases (p, q). b) El espacio de los estados (p, q, t), en los que el tiempo t se considera como una variable adicional.
En conclusión, sobre este punto…
…quisiera citar las palabras de un colega economista, de quien no daré el nombre, que ha querido dar su interpretación a propósito de la teoría de las catástrofes. Dice textualmente: «cuando René Thom, de quien nos guardaremos mucho de discutir los méritos evidentes, afirma por ejemplo que la estabilidad de una forma como el vórtice del río heraclitiano del curso universal, reposa en definitiva en una estructura de carácter algebraico-geométrico dotada de la propiedad de estabilidad estructural respecto a las incesantes perturbaciones a las que está sujeta, ¿no parece invitarnos quizá a trasladar nuestra atención del análisis de las fuerzas al análisis de las formas, y a infravalorar, por ejemplo, la importancia de los fenómenos de afinidad química que fijan en el tiempo las estructuras de su encuentro aleatorio?». A lo que yo respondo: no existe razón alguna para pensar que la fuerza tenga en principio un estatuto ontológico más profundo que la forma. Si se ha atribuido en general a la fuerza un estatuto ontológico más profundo que a la forma, ello puede haberse debido a una especie de antropocentrismo ingenuo que depende del hecho de que actuemos sobre los objetos externos a través de la fuerza que aplicamos en ellos con el concurso de nuestros músculos.
Es cierto que también en la física newtoniana las fuerzas aparecen como agentes eficientes. Podemos entonces considerar que si la fuerza tiene un estatuto ontológico superior con respecto a la forma, ello se debe al paradigma fisicalista de tipo newtoniano… Pero que esta opinión la defienda un economista es algo más bien sorprendente.
Por mi parte, yo considero que la forma, entendida en una acepción extremadamente general, es un concepto infinitamente más rico y sutil que el concepto de fuerza, que es un concepto bastante antropocéntrico que reduce prácticamente un ser a un vector. Pero, sean físicos o economistas, hay que convencer a los investigadores de que es verdad que el análisis morfológico puede poner de manifiesto más cosas que un análisis en términos de fuerzas. Resta todo un programa de educación por cumplir.