Límites de cuencas fractales

El límite es donde un programa del conjunto de Mandelbrot pasa la mayor parte del tiempo y explota sus compromisos. En él, cuando no se interrumpen cien, mil o diez mil repeticiones, el programa no tendrá la seguridad de que un punto caiga dentro de la fase. ¿Quién sabe qué aportará la millonésima repetición? Por eso los programas que rendían las imágenes más asombrosas y más detalladamente ampliadas del conjunto se ejecutaban en ordenadores principales de gran resistencia, o en los dedicados a procesos paralelos, con millares de cerebros individuales, que efectuaban las mismas operaciones aritméticas en fase de bloque. Los puntos se escapaban más despacio, en el límite, de la fuerza del conjunto, como si vacilaran entre atractores contrarios, uno en cero y otro que llamaba al conjunto desde distancia infinita.

Cuando los científicos fueron del hallazgo de Mandelbrot al problema de representar los fenómenos físicos reales, las cualidades del límite del conjunto ocuparon el primer plano. El que había entre dos o más atractores, en un sistema dinámico, se presentó como una especie de umbral que existe, al parecer, en muchos procesos ordinarios, desde la rotura de materiales hasta la toma de decisiones. En tal sistema, cada atractor posee una cuenca, como las que recogen las aguas de los ríos. Y cada cuenca tiene un límite. Un campo desconocido y prometedor de las matemáticas y la física fue, al principio de los años ochenta, para un grupo influyente, el estudio de los límites de las cuencas fractales.

Esta rama de la dinámica no se interesaba en el comportamiento estable definitivo de un sistema, sino en cómo elegía éste una de las opciones que se le ofrecían. Uno, como el modelo ya clásico de Lorenz, tiene un solo atractor —un comportamiento que prevalece cuando el sistema se estabiliza—, y es caótico. Otros sistemas tal vez acaben en un comportamiento de estado estable no caótico, pero en más de un estado estable posible. El estudio de los límites de las cuencas fractales era el de los sistemas que finalizaban en uno de varios estados finales no caóticos, y proponía la cuestión de averiguar cuál era. James Yorke, que había iniciado aquella investigación a los diez años de dar nombre al caos, propuso un billar romano imaginario. Como casi todos estos juegos, tiene un tirador, provisto de un muelle, que se estira y se suelta para enviar la bola al campo. Éste está inclinado y tiene bordes elásticos y topes eléctricos, que proporcionan a la bola energía adicional. El impulso es importante, pues implica que la energía no se consume regularmente. En pro de la simplificación, el billar carece de aletas en la parte inferior, pero tiene dos rampas de salida. La bola ha de desaparecer por una de ellas.

Es un billar romano determinista, porque no sufre sacudidas. Un parámetro único rige el destino de la bola; es la posición inicial del tirador. Supóngase que la máquina está constituida de forma tal, que un tirón flojo hace siempre que la bola termine su carrera en la rampa de la derecha, y uno fuerte en la de la izquierda. En el período intermedio, el comportamiento es complicado, ya que la bola rebota en los topes con energía, ruido y lapso temporal variables, antes de elegir una salida.

Imagínese que se indica con una línea el gráfico del resultado de cada posible posición de partida del tirador. Márquese un punto rojo cuando una posición lleve a una salida en la derecha, y uno verde en el caso de la izquierda. ¿Qué se averiguará sobre esos atractores como función de la posición inicial?

El límite es un conjunto fractal, no autosemejante por necesidad, pero infinitamente detallado. Algunas porciones de la línea aparecerán encarnadas o verdes, sin mezcla, y otras, cuando se amplían, muestran regiones encarnadas tachonadas de verde, o verdes tachonadas de encarnado. En algunas posiciones del tirador, un cambio leve no incluye diferencia alguna; en otras, un pequeño cambio arbitrario señalará una clara diferencia de color.

James A. Yorke

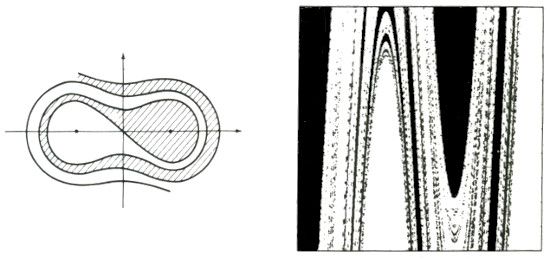
LÍMITES DE CUENCAS FRACTALES. Incluso cuando no es caótico el comportamiento a largo plazo de un sistema dinámico, el caos puede surgir en el límite que hay entre una clase de comportamiento estable y otra. A menudo un sistema dinámico tiene más de un estado de equilibrio, como el péndulo que puede detenerse en uno de los dos imanes colocados en su base. Cada equilibrio es un atractor. El límite entre dos atractores puede ser complicado, aunque regular (izquierda). O puede ser complicado e irregular. La mezcolanza enormemente fractal de blanco y negro (derecha) es el diagrama de un espacio de fases de un péndulo. El sistema alcanzará seguramente uno de dos estados estables posibles. Dadas ciertas condiciones iniciales, el resultado se predice bastante bien: negro es negro, y blanco, blanco. Pero, cerca del límite, la predicción es imposible.

El empleo de una segunda dimensión representa la adición de otro parámetro, de otro grado de libertad. En un billar romano, por ejemplo, puede considerarse el efecto de modificar la inclinación del campo de juego. Se topará con una complejidad tan laberíntica, que proporcionaría pesadillas a los ingenieros responsables de la estabilidad de sistemas energéticos reales y sensitivos, provistos de más de un parámetro, como redes de fuerza eléctrica y plantas nucleares generadoras, que se convirtieron en blanco de la investigación sobre el caos en el decenio de 1980. Para un valor del A, el parámetro B proponía un comportamiento ordenado y tranquilizador, con regiones coherentes de estabilidad. Los ingenieros efectuaban estudios y gráficos de la clase que concertaba con su educación de orientación lineal. Pero, junto a él, A podía tener otro valor que transformase la importancia de B.

Yorke mostró en conferencias imágenes de límites de cuencas fractales. Algunas representaban el comportamiento de péndulos forzados, que podían alcanzar uno de dos estados finales. Como su auditorio sabía, el péndulo forzado es un oscilador básico, que tiene muchos aspectos variables en la existencia cotidiana.

—Nadie podrá acusarme de que he influido fraudulentamente en el sistema al elegir un péndulo —dijo Yorke en tono jovial—. Cosas como él abundan en la naturaleza. Pero su comportamiento discrepa de cuanto figura en la bibliografía. Es fractal de género turbulento.

Las imágenes podían ser fantásticos torbellinos de blanco y negro, como si un cazo hubiese borbotado varias veces durante la fusión incompleta de leche y chocolate. Su ordenador las había hecho recorriendo una rejilla de mil puntos por lado, cada uno de los cuales representaba un punto de partida del péndulo, y había trazado el resultado en blanco y negro. Eran cuencas de atracción, barajadas y dobladas por las conocidas ecuaciones del movimiento newtoniano, y lo obtenido era sobre todo límite. Más de las tres cuartas partes de los puntos trazados estuvieron en el límite.

Aquellas imágenes guardaban una lección para los investigadores e ingenieros, una lección y un aviso. Con demasiada frecuencia había que colegir, de una reducida colección de datos, el ámbito potencial del comportamiento de sistemas complejos. Cuando éste actuaba con normalidad, manteniéndose dentro de un espacio reducido de parámetros, los ingenieros llevaban a cabo sus observaciones y esperaban extrapolarlas, más o menos linealmente, a un comportamiento de regularidad inferior. Mas los científicos, con el estudio de los límites de las cuencas fractales, pusieron en evidencia que la frontera entre la calma y la catástrofe podía ser más complicada que lo que cabía imaginar.

—Toda la red eléctrica de la costa oriental es un sistema oscilatorio, casi siempre estable, y nos gustaría saber qué ocurre cuando se lo perturba —dijo Yorke—. Necesitamos conocer cuál es el límite. En realidad, nadie tiene idea de su aspecto.

Los límites de las cuencas fractales planteaban graves cuestiones de física teórica. Las transiciones de fases se referían a umbrales y Peitgen y Richter examinaron una de las mejor estudiadas, la magnetización y la no magnetización de materiales. Sus imágenes mostraron la bella complejidad peculiar que empezaba a aceptarse como algo natural, figuras semejantes a coliflores, en las que aparecían protuberancias y surcos cada vez más enmarañados. Variaron los parámetros y aumentaron la ampliación de los detalles. Y se presentó una imagen, constantemente más sometida al azar, hasta que, de pronto, sin aviso, surgió; en el meollo de una región desconcertante, una forma conocida, de pelos deprimidos y tachonada de bultitos: el conjunto de Mandelbrot, sin que le faltase un zarcillo o un átomo. Era otro poste indicador de la universalidad. «Debiéramos creer en la magia», escribieron.