Sorpresa en el método de Newton

John Hubbard, matemático estadounidense aficionado a las camisas llamativas, había enseñado tres años antes cálculo elemental a los estudiantes universitarios del primer curso en Orsay (Francia). Entre las materias corrientes que había expuesto figuró el método de Newton, esquema clásico para resolver ecuaciones por medio de tanteos cada vez más aproximados a la realidad. Sin embargo, aburrido de lo corriente, decidió enseñar el procedimiento newtoniano de manera que obligase a sus alumnos a pensar.

El método citado es antiguo (lo era cuando Newton lo inventó). Los griegos usaron una versión de él para encontrar raíces cuadradas. Se inicia con una conjetura, ésta conduce a otra mejor, y el proceso de iteración se enfoca en una respuesta como un sistema dinámico que busque el estado estable. El procedimiento es rápido. La cantidad de dígitos decimales correctos suele doblarse en cada paso. Hoy día, desde luego, las raíces cuadradas sucumben a métodos más analíticos, lo mismo que todas las ecuaciones polinómicas de segundo grado, o sea en aquellas que las variables se elevan sólo a la segunda potencia. Pero el método de Newton también se utiliza en ecuaciones polinómicas de grado superior, que no pueden resolverse directamente. Se aplica también con éxito en una variedad de algoritmos en informática, porque, como siempre, la iteración es la fuerza de los ordenadores. Una pequeña contrariedad del método newtoniano es que las ecuaciones acostumbran tener más de una solución, particularmente cuando se incluyen las complejas. Cuál de ellas se encuentra depende del supuesto inicial. En la práctica, los estudiantes no lo consideran una dificultad. Por lo general, se tiene una idea clara de dónde se ha de empezar, y si la conjetura parece llevar a una solución errónea, se comienza la operación de otro modo.

Cabía preguntarse qué clase exacta de ruta traza el método de Newton cuando se encamina hacia una raíz de un polinomio de segundo grado en el plano complejo. Podía contestarse, pensando geométricamente, que el procedimiento sólo busca cuál de las dos raíces está más próxima a la conjetura inicial. Así lo dijo Hubbard a sus alumnos de Orsay cierto día en que surgió la cuestión.

—Ahora bien, en lo referente a las ecuaciones, por ejemplo, de tercer grado, la situación se complica. Pensaré sobre ello y se lo explicaré la semana que viene —prometió Hubbard con acento de confianza.

Estaba persuadido de que lo difícil sería enseñar a los estudiantes a calcular la iteración, y de que la conjetura no exigiría grandes esfuerzos. Pero cuanto más reflexionó menos supo qué constituía una conjetura inteligente, o, lo que venía a ser lo mismo, qué efectuaba el método de Newton. La suposición geométrica evidente consistía en dividir el plano en tres cuñas, con una raíz en el interior de cada una; pero Hubbard descubrió que aquello no servía. Sucedían cosas extrañas cerca de los límites. Encima, Hubbard averiguó que no era el primer matemático que daba de cabeza con dificultad tan sorprendente. Lord Arthur Cayley había intentado, en 1879, ir del manejable caso de segundo grado al tercero, pavorosamente ingobernable. Pero Hubbard, un siglo después, tenía a mano un instrumento del que Cayley careció.

Hubbard pertenecía al género de matemático riguroso que desprecia los supuestos, aproximaciones y medias verdades, basados más en la intuición que en las pruebas. De acuerdo con ello, insistía, a los veinte años de que el de Edward Lorenz se hubiese incorporado a la bibliografía, que nadie sabía de veras si aquellas ecuaciones daban origen a un atractor extraño. La conocida espiral doble, aseveró, no era demostración, sino mero indicio, algo que producían los ordenadores.

A despecho de ello, Hubbard empleó uno para efectuar lo que las técnicas ortodoxas no habían hecho. El ordenador no probaría nada. Pero quizá desvelase al menos la verdad, para que un matemático supiera qué debía intentar demostrar. Trató el método de Newton no como un medio de solventar problemas, sino como un problema en sí mismo. Consideró el ejemplo más simple de una ecuación polinómica de tercer grado: x³ − 1 = 0. Es decir, había que hallar el cubo de 1. Con números reales, se tiene, desde luego, la solución vulgar: 1. Sin embargo, el polinomio posee otras dos complejas: −1/2 + i√−3/2 y −1/2 − i√−3/2. Trasladadas al plano complejo, las tres raíces forman un triángulo equilátero, con un punto —pensando en un reloj— en las tres, otro en las siete y otro en las once. Dado un número complejo como lugar de partida, la cuestión era averiguar a cuál de las tres soluciones llevaría el procedimiento newtoniano, como si éste fuese un sistema dinámico y las tres soluciones otros tantos atractores. O como si el plano complejo fuera una superficie lisa que se inclinase a tres valles hondos. Una canica, partiendo de cualquier situación de aquella pendiente, caería en un valle. Pero ¿en cuál?

Heinz-Otto Peitgen, Peter H. Richter

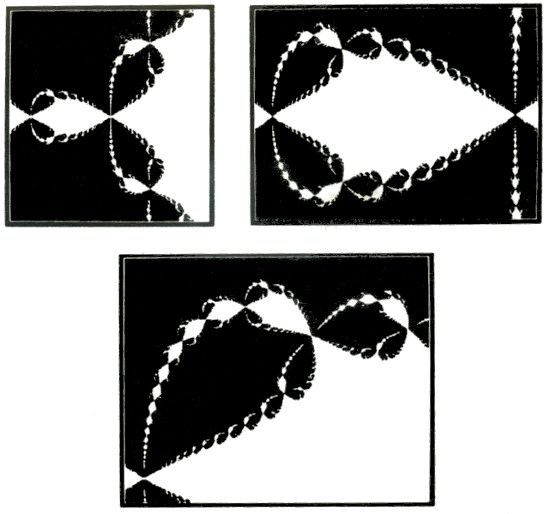
LÍMITES DE COMPLEJIDAD INFINITA. Cuando se corta en tres una tarta, las tres partes coinciden en un solo punto, y los límites entre dos de ellas son sencillos. Pero muchos procesos de matemáticas abstractas y de la física del mundo real crean límites de complicación casi inimaginable.

El método de Newton, aplicado para hallar la raíz cúbica de −1, divide el plano en tres regiones idénticas, una de las cuales se muestra en blanco. Todos los puntos de este color se sienten «atraídos» por la raíz que se halla en el área blanca más grande; todos los negros son atraídos por una de las otras dos raíces. El límite tiene la curiosa propiedad de que cada uno de sus puntos bordea las tres regiones. Y, como se aprecia en la ilustración, los segmentos ampliados revelan una estructura fractal, que repite la pauta básica a escalas cada vez más reducidas.

Hubbard exploró muchos de los puntos infinitos que componen el plano. Hizo que el ordenador fuera de uno a otro, calculando el flujo del método de Newton para cada uno, y los coloreó. Los puntos de partida que llevaban a una solución recibieron el color azul; los que llevaban a otra, el encarnado, y los que llevaban a una tercera, el verde. En la aproximación más elemental, averiguó que la dinámica del procedimiento de Newton dividía, ciertamente, el plano en tres cuñas. Por lo común, los puntos cercanos a determinada solución conducían rápidamente a ella. Pero la exploración sistemática con ordenador evidenció una complicada organización subyacente, que jamás los matemáticos anteriores, capaces sólo de calcular un punto acá y otro allá, habrían visto. Si unas conjeturas iniciales convergían en seguida en una raíz, otras se movían en apariencia al azar antes de converger en una solución. En ocasiones, parecía que un punto incidiría en un ciclo que se repetiría sin tregua —uno periódico— y sin llegar nunca a un resultado.

Cuando obligaron al ordenador a explorar el espacio cada vez con mayor detalle, Hubbard y sus alumnos se desconcertaron ante la imagen que se insinuaba. Vieron, por ejemplo, manchas verdes ensartadas como joyas, en lugar de una cresta definida entre los valles azul y encarnado, como si la canica, apresada en las atracciones contrapuestas de los dos valles cercanos, hubiese de acabar en el tercero y más distante. Jamás se formó del todo un límite entre un par de colores. Una inspección aún más atenta halló manchas encarnadas en la línea que había entre una verde y el valle azul. Y así sucesivamente. El límite enseñó a Hubbard una característica peculiar, que habría azorado incluso a alguien ducho en los fractales monstruosos de Mandelbrot: ningún punto servía de separación de dos colores solos. Cuando éstos intentaban juntarse, el tercero se entremetía siempre con series de intrusiones nuevas y autosemejantes. Inverosímilmente, cada punto limítrofe bordeaba una región de cada uno de los tres colores.

Hubbard se embarcó en el estudio de aquellas formas complicadas y lo que podía inferirse de ellas para las matemáticas. Su trabajo y el de sus colegas pronto se convirtieron en nueva línea de ataque en el problema de los sistemas dinámicos. Comprendió que la plasmación del diagrama del método de Newton no era sino una de la familia inexplorada de imágenes que reflejaban el comportamiento de las fuerzas en el mundo real. Michael Barnsley buscaba otros parientes. Benoît Mandelbrot, como no tardaron en saber ambos investigadores, estaba descubriendo el abuelito de todas aquellas formas.