El delicado triunfo de Albert Libchaber
Libchaber eligió helio líquido para su experimento, pues, por tener viscosidad bajísima, se movería al más mínimo impulso. El experimento equivalente con un fluido de viscosidad media, como el agua o el aire, habría impuesto una caja mucho más grande. Aquella característica del helio hacía que el experimento fuese muy sensible al calor. Para que surgiese la convección en su celdilla milimétrica, le bastaba crear, entre la superficie inferior y la superior, una diferencia térmica de una milésima de grado. Por eso el recipiente era tan minúsculo. En uno mayor, en que el helio tendría más espacio para moverse, la convección hubiese exigido menos, mucho menos, calentamiento. Y en uno diez veces más grande en cada dirección, del tamaño de una uva —de volumen mil veces superior—, el movimiento habría empezado con una diferencia calórica de una millonésima de grado. Variaciones tan exiguas de la temperatura no podían controlarse.
Tanto en el planteamiento como el diseño y la construcción, Libchaber y su ingeniero se esforzaron por eliminar cualquier sombra de confusión. De hecho, hicieron lo posible por eliminar el movimiento que se proponía estudiar. El de un fluido, desde el flujo suave a la turbulencia, se concibe como movimiento en el espacio. Su complejidad se muestra como espacial, y sus trastornos y torbellinos, como caos espacial. Pero Libchaber buscaba ritmos que se revelasen como cambios en el tiempo. El tiempo era el campo de juego y la vara de medir. Redujo el espacio casi hasta lo unidimensional. Llevaba a la exageración una técnica que habían utilizado sus precursores en la experimentación con fluidos. Todo el mundo sabía que un flujo aprisionado —convección de Rayleigh-Bénard en una caja, o rotación de Couette-Taylor en un cilindro— tenía mejor comportamiento que uno libre, como las olas en el océano o las ondas en el aire. Un flujo exento posee superficie limítrofe libre y su complejidad se multiplica.
La convección en una caja rectilínea produce rollos de fluido semejantes a salchichas calientes —o, en este caso, a semillas de sésamo—. Eligió cuidadosamente las dimensiones de la celdilla con el fin de que diese cabida a dos rollos únicos. El helio líquido se elevaría en el centro, ascendería, se encorvaría en lo alto y bajaría por los lados externos de la celdilla. Era una geometría confinada. El balanceo estaría preso. Las líneas limpias y las proporciones cuidadosas evitarían fluctuaciones espurias. Libchaber dominó el espacio para jugar con el tiempo.
Así que comenzara el experimento, con el helio agitándose en el interior de la celdilla, ésta dentro del recipiente sometido al vacío, y éste metido en el baño de nitrógeno, Libchaber observaría lo que ocurriese. Introdujo dos sondas microscópicas de la temperatura en la superficie del zafiro que cubría la celdilla. Registró los resultados una plumilla trazadora. Así comprobó las temperaturas en dos lugares de la superficie del fluido. Fue algo tan sensible, tan inteligente, comentó un físico, que Libchaber logró engañar a la naturaleza.
Aquella obra maestra en miniatura de la precisión empleó dos años en su exploración total, pero fue, como dijo el experimentador, el pincel que necesitaba para su cuadro, ni muy grande ni muy complicado. Acabó por ver todo. Efectuando el experimento hora tras hora, de día y de noche, Libchaber descubrió, en el inicio de la turbulencia, una pauta de comportamiento más intrincada de lo que jamás se había atrevido a imaginar. Apareció en su plenitud la cascada de la duplicación de período. Libchaber había confinado y purificado el movimiento de un líquido que asciende al ser calentado. El proceso empieza con la primera bifurcación, el principio del movimiento en cuanto se calienta la lámina inferior, de cobre de gran pureza, con la intensidad requerida para romper la tendencia del fluido a permanecer inmóvil. A poca distancia del cero absoluto, una mera milésima de grado lo consigue. El líquido del fondo se caldea y expande lo suficiente para ser más ligero que el que pesa sobre él. La parte fría ha de hundirse para que suba la cálida. En seguida, para que ambos movimientos se cumplan, el líquido se organiza en dos cilindros o rollos giratorios, que adquieren velocidad constante, y el sistema se asienta en un equilibrio, en uno móvil, porque la energía térmica se convierte sin cesar en movimiento, se disipa, a consecuencia de la fricción, en calor y se escapa por la lámina fría superior.
Libchaber repitió hasta aquel punto un experimento harto conocido en la mecánica de los fluidos, tan conocido que se desdeñaba.
—Era física clásica —dijo Libchaber—. Lo que significaba, por desgracia, que tenía muchos años y que, por lo tanto, no interesaba.
Daba la casualidad, al propio tiempo, de que era el mismo flujo que Lorenz había modelado con su sistema de tres ecuaciones. Pero un experimento práctico y real —líquido verdadero, caja construida adrede, laboratorio expuesto a las vibraciones del tráfico de París— hacía que la tarea de cosechar datos fuese empresa mucho más ardua que la de generar simples cifras en un ordenador.
Los experimentadores como Libchaber empleaban una plumilla trazadora para registrar la temperatura, tal como la medía una sonda introducida en la superficie superior. Durante el movimiento equilibrado que sigue a la primera bifurcación, la temperatura permanece estable en cualquier punto —más o menos—, y la plumilla marca una recta. La inestabilidad se acrecienta, si se intensifica el calor. Cada cilindro muestra un retorcimiento, que se agita adelante y atrás. Esa vacilación u oscilación señala un cambio de temperatura, que sube y baja entre los valores. Y la plumilla traza en el papel una línea sinuosa.
Es una línea térmica sencilla, que se modifica continuamente y se estremece con el ruido experimental, resulta imposible leer el momento exacto en que aparecerán nuevas bifurcaciones, o deducir su índole. La línea dibuja cumbres y valles caprichosos, que parecen casi tan fortuitos como la gráfica de la trayectoria bursátil en período de altibajos. Libchaber analizó aquellos datos convirtiéndolos en un diagrama espectral que revelara las frecuencias principales ocultas en las temperaturas mutables. Obtener un diagrama espectral de un experimento se parece a la tarea de trazar el gráfico de las frecuencias acústicas de un acorde complejo en una sinfonía. Una línea irregular de imprecisión recorre siempre la parte inferior del gráfico: el ruido o confusión experimental. Los tonos principales aparecen como púas verticales: cuanto más fuerte el tono, tanto más alta será la púa. Asimismo, si los datos producen una frecuencia dominante —un ritmo que se destaca una vez cada segundo, por ejemplo—, esa frecuencia aparecerá como una púa en el diagrama espectral.
Ocurrió que, en el experimento de Libchaber, la primera longitud de onda surgió alrededor de los dos segundos. La bifurcación siguiente aportó un cambio sutil. El rollo continuó oscilando y la temperatura bolométrica no modificó su ascenso y descenso, sometidos a un ritmo dominante. Pero, en los ciclos impares, subió algo más que antes, y en los pares, descendió algo más. De hecho, la temperatura máxima se dividió en dos, por lo que hubo dos máximas y dos mínimas. La línea de la plumilla, difícil de interpretar, trazó una oscilación encima de otra: una metaoscilación. Aquello se apreció mejor en el diagrama espectral. La antigua frecuencia acusó todavía su presencia, pues la temperatura crecía aún cada dos segundos. Sin embargo, una frecuencia distinta apareció exactamente en la mitad de la anterior, porque el sistema había desarrollado un componente que se repetía cada cuatro segundos. Como las bifurcaciones no cesaron, se distinguió una pauta extrañamente consistente: las nuevas frecuencias doblaban las antiguas, de suerte que el diagrama se llenó en las partes cuartas, octavas y decimosextas, y fue adquiriendo el aspecto de una valla en las que se alternasen tablas cortas y largas.
Incluso para quien buscaba formas escondidas en datos confusos, fueron necesarias decenas y, después, centenares de pruebas antes de que se precisaran los hábitos de la celdilla. Sobrevenían cosas singulares cuando Libchaber y el ingeniero aumentaban despacio la temperatura y el sistema pasaba de un equilibrio a otro. En ocasiones, comparecían frecuencias transitorias, se deslizaban lentamente por el diagrama espectral y desaparecían. En otras, pese a la geometría definida, se desarrollaban tres rollos en lugar de dos. Por consiguiente, ¿cómo sabrían lo que pasaba en realidad en el interior de la celdilla?
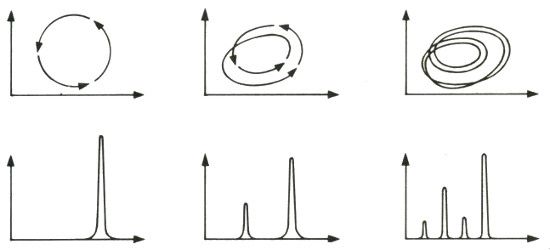
E. Brotman / Adolph Predrag Cvitanović
DOS MODOS DE VER UNA BIFURCACIÓN. Cuando un experimento como el de Libchaber con la celda de convección produce una oscilación uniforme, la imagen de su espacio de fases es una curva, que se repite a intervalos regulares (arriba, izquierda). El experimentador que mida las frecuencias en los datos obtendrá un diagrama espectral con una púa acusada para este ritmo único. Después de una bifurcación de duplicación de período, el sistema describe dos curvas antes de repetirse de modo exacto (centro). Entonces el experimentador observa un nuevo ritmo de la mitad de la frecuencia —dos veces el período— del original. Las nuevas duplicaciones de período llenan el diagrama espectral con más púas.
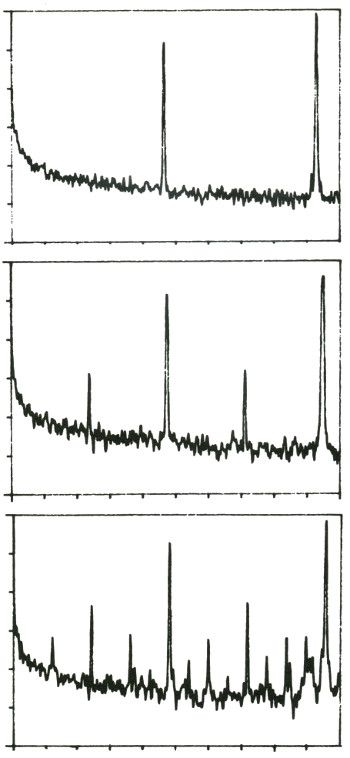
Albert Libchaber
LOS DATOS DEL MUNDO REAL CONFIRMAN LA TEORÍA. Los diagramas espectrales de Libchaber mostraron la pauta precisa de la duplicación de período que la teoría había pronosticado. Las púas de las nuevas frecuencias se destacan con claridad sobre el ruido experimental. La teoría escalar de Feigenbaum predijo no sólo cuándo y dónde surgirían las nuevas frecuencias, sino también su fuerza, o sea su amplitud.

