La idea de David Ruelle sobre la turbulencia
David Ruelle decía que había dos clases de físicos: una que creció desmontando aparatos de radio —aquello sucedía en la era anterior al estado sólido, cuando se contemplaban cables y tubos de vacío que resplandecían con color anaranjado, y se imaginaba cualquier cosa sobre la circulación de los electrones—, y otra que jugaba con equipos químicos. Ruelle jugó con ellos, o con ninguno, en el posterior sentido estadounidense. Fueron sustancias químicas, explosivas o venenosas, que vendían sin reparos, en el septentrión de Bélgica donde había nacido, los farmacéuticos locales. El mismo Ruelle las mezclaba, removía, calentaba, cristalizaba y, a veces, hacía estallar. Había venido al mundo en 1935, en Gante, hijo de un maestro de gimnasia y de una profesora universitaria de lingüística, y aunque pensó en consagrarse al reino de la ciencia abstracta, siempre sintió debilidad por las sorpresas que oculta la naturaleza en las setas venenosas, o en la combinación del salitre con azufre y carbón.
No obstante, aportó una perdurable contribución a la exploración del caos con la física matemática. Ingresó en 1970 en el Institute des Hautes Études Scientifiques (Instituto de Altos Estudios Científicos), situado en las afueras de París e inspirado en el Institute for Advanced Study de Princeton. Ya había iniciado lo que se transformaría en hábito constante en su existencia: abandonar el instituto y su familia periódicamente para emprender excursiones solitarias, que llegaban a durar semanas, con una simple mochila, por los espacios desiertos de Islandia o México. A menudo no encontraba a nadie. Cuando hallaba seres humanos y aceptaba su hospitalidad —tal vez un yantar de tortillas de maíz, sin grasa animal o vegetal—, pensaba que contemplaba el mundo tal como había sido hacía dos milenios. De vuelta al instituto, reemprendía la vida científica, con el rostro más flaco y la piel más ceñida a su frente redonda y su agudo mentón. Había asistido a conferencias de Steve Smale sobre la herradura y las posibilidades caóticas de los sistemas dinámicos. Había reflexionado sobre la turbulencia de los fluidos y la imagen clásica de Landau. Sospechó que aquellas ideas estaban emparentadas… y que eran contradictorias.
Ruelle no poseía experiencia de las corrientes fluidas, pero aquello no le desanimó, como no había desanimado a sus muchos predecesores desafortunados.
—La gente no especializada siempre descubre las novedades —dijo—. No hay una sólida teoría natural de la turbulencia. Todas las preguntas que pueden hacerse sobre ella son de índole más general, y, por consiguiente, accesibles a los que no son expertos.
Se comprendía sin esfuerzo por qué la turbulencia se resistía a ser analizada. Las ecuaciones de la corriente de los fluidos son diferenciales parcialmente no lineales, insolubles excepto en casos especiales. A pesar de ello, Ruelle ingenió una alternativa abstracta de la imagen de Landau, expuesta en el léxico de Smale, con representaciones del espacio parecidas a una materia moldeable, que podía ser apretada, estirada y plegada en figuras tales como las herraduras. Escribió en el instituto un artículo en colaboración con Floris Takens, matemático holandés visitante, y lo publicaron en 1971. Su expresión fue inconfundiblemente matemática —¡mucho ojo, físicos!—, o sea, encabezaron los párrafos con vocablos tales como definición, proposición o prueba, a los que seguía la inevitable arremetida: Sea…
«Proposición (5.2). Sea X μ una familia de un parámetro de Ck campos vectoriales en un espacio H de Hilbert tal que…».
En cambio, el título prometía relación con el mundo real: «On the Nature of Turbulence» (Sobre la naturaleza de la turbulencia), eco deliberado del célebre de Landau, «On the Problem of Turbulence». La clara finalidad de la argumentación de Ruelle y Takens iba más allá de las matemáticas; se proponían ofrecer un sustituto del criterio tradicional sobre el arranque de la turbulencia. En lugar de amontonar frecuencias, lo que llevaba a una infinidad de movimientos traslapados independientes, declararon que tres movimientos independientes bastaban para generar la complejidad total de la turbulencia. Desde el punto de vista de las ciencias exactas, parte de su lógica resultó ser oscura, equivocada o tomada en préstamo, o todo al mismo tiempo. Las opiniones al respecto variaban todavía quince años más tarde.
Pero la intuición, el comentario, las cosas marginales y la física entretejidos en el artículo la convirtieron en don inagotable. Lo más seductor fue lo que los autores denominaron atractor extraño. Ruelle meditó después que tal denominación era psicoanalíticamente «sugestiva». Su importancia en el estudio del caos fue tal que él y Takens se disputaron, con apariencia cortés, el honor de haber inventado el nombre. Era la verdad que ninguno de ambos lo recordaba bien.
Takens, alto, rubicundo y fieramente nórdico, decía:
—¿Acaso se pregunta a Dios si ha creado este maldito universo?… No recuerdo nada… Creo a menudo sin acordarme de ello.
Ruelle, el autor más calificado del artículo, comentaba sin alterarse:
—Takens visitaba el Institut des Hautes Études Scientifiques. Cada persona trabaja a su modo. Algunas prefieren escribir los artículos sin colaboradores, para que el mérito sea sólo de ellas.
El atractor extraño vive en el espacio de fases, una de las invenciones más vigorosas de la ciencia moderna. Dicho espacio proporciona el modo de convertir los números en imágenes, abstrayendo cada miga de información esencial de un sistema de partes móviles, mecánicas o fluidas, y trazando un diagrama flexible de caminos que conducen a todas sus posibilidades. Los físicos trabajaban ya con dos clases simples de «atractores»: puntos fijos y ciclos límites, que representaban el comportamiento a que llegaba un estado estable, o que se repetía continuamente.
En el espacio de fases, el conocimiento completo de un sistema dinámico, en un instante temporal único, se transforma en un punto. Éste es el sistema dinámico…, en aquel instante. Pero, en el siguiente, el sistema habrá cambiado, aunque sea muy poco. Por lo tanto, el punto se mueve. La historia del sistema temporal puede registrarse con el punto móvil, que describe su órbita a través del espacio de fases en el transcurso del tiempo.
¿Cómo se almacena en un punto toda la información sobre un sistema complejo? La respuesta es simple, si tiene sólo dos variables. Se deriva de la geometría cartesiana que se explica en la segunda enseñanza: una variable en el eje horizontal y otra en el vertical. Si es un péndulo, que oscila sin fricción, una variable será la posición y otra la velocidad; las dos cambian continuamente, creando una línea de puntos que traza una curva más o menos cerrada, la cual se repite una y otra vez, siempre. El mismo sistema, con mayor índice de energía —a saber, oscilando más de prisa y más lejos—, forma en el espacio de fases una curva similar a la descrita, aunque más amplia.
Algo de realismo, con el aspecto de fricción, cambia la imagen. No se necesitan las ecuaciones del movimiento para comprender la suerte de un péndulo expuesto a fricción. Cada órbita acabará, al fin, en el mismo sitio, en el centro: posición 0, velocidad 0. Ese punto fijo central «atrae» las órbitas. En vez de formar curvas para siempre, describe una espiral hacia el interior. La fricción disipa la energía del sistema, y la disipación se revela en el espacio de fases como un impulso hacia el centro, desde las regiones externas de alta energía a las internas de baja energía. El atractor —del género más sencillo posible— es como un imán del tamaño de una cabeza de alfiler metido en una lámina de goma.
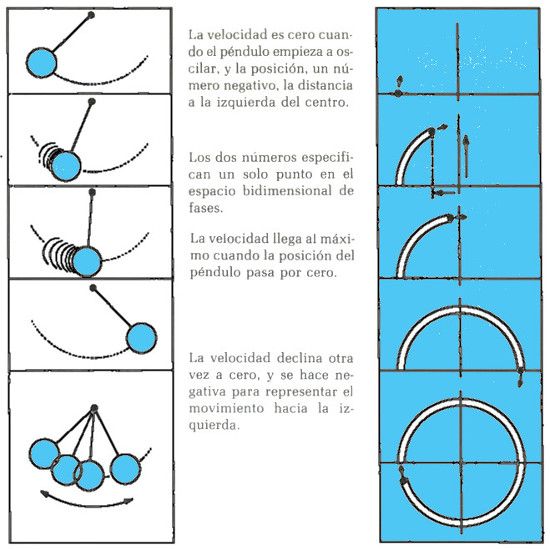
Adolph E. Brotman
OTRA MANERA DE VER EL PÉNDULO. Un punto en el espacio de fases (derecha) contiene toda la información sobre el estado de un sistema dinámico en cualquier instante (izquierda). En un péndulo sencillo, dos números —velocidad y posición— es cuanto se requiere saber.
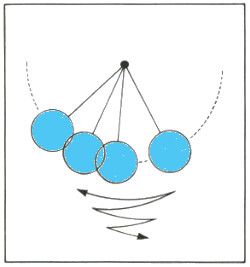 |
El punto traza una trayectoria, la cual proporciona una manera de visualizar el comportamiento continuo, a largo plazo, de un sistema dinámico. Un arco reiterado representa un sistema que se repite para siempre a intervalos regulares.
Si el comportamiento repetido es estable, como en el péndulo de un reloj de pared, el sistema regresa a su órbita tras pequeñas perturbaciones. En el espacio de fases, la órbita arrastra las trayectorias que pasan cerca de ella: es un atractor.
|
| |
|
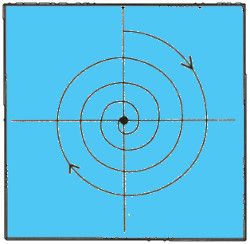 |
Un solo punto puede ser un atractor. En un péndulo que pierde constantemente energía a causa de la fricción, todas las trayectorias decrecen en espiral hacia un punto interior, que representa el estado estable, en este caso, el de la inmovilidad absoluta.
|
Una ventaja de concebir los estados como puntos en el espacio es que facilita la observación del cambio. El sistema cuyas variables se modifican, arriba y abajo, incansablemente, se transforma en un punto móvil, en algo así como la mosca que revolotea en una habitación. Si nunca ocurren algunas combinaciones de variables, el científico puede, en resolución, imaginar que una parte de la habitación queda fuera de los límites. La mosca nunca va a ella. Si el sistema se comporta periódicamente, volviendo al mismo estado en una ocasión, en otra y en otra, la mosca se mueve en una curva más o menos cerrada y pasa una y otra vez por la misma posición en el espacio de fases. Las imágenes del espacio de fases de sistemas físicos exponían pautas de movimiento que, de otra manera, hubieran sido invisibles, así como la fotografía infrarroja de un paisaje revela formas y detalles existentes del alcance de la percepción. Examinando la imagen de unas fases, el científico podía utilizar la imaginación para pensar en todo el sistema. Esta curva corresponde a esa periodicidad. Este sesgo pertenece a tal cambio. Este vacío significa esa imposibilidad física.
Incluso las imágenes bidimensionales de espacios de fases reservaban muchas sorpresas, y hasta los ordenadores de mesa podían demostrar algunas de ellas, mudando las ecuaciones en trayectorias móviles llenas de color. Algunos físicos rodaron películas y cintas de vídeo para mostrarlas a sus colegas, y algunos matemáticos de California publicaron libros con diseños verdes, azules y rojos por el estilo de los dibujos animados, que ciertos de sus cofrades definieron, con un toque de malicia, como «historietas del caos». Las dos dimensiones no satisficieron las exigencias de los sistemas que los físicos necesitaban estudiar. Requerían más de dos variables, y eso demandaba más dimensiones. Cada porción de un sistema dinámico capaz de moverse con independencia es otra variable, otro grado de libertad. Y cada uno de éstos exige otra dimensión en el espacio de fases, con el fin de asegurarse de que un solo punto contiene información suficiente para determinar de modo único el estado del sistema. Las ecuaciones sencillas que estudió Robert May eran unidimensionales: se contentaban con un solo número, que podía representar la temperatura o la población, y ese número definía la posición de un punto en una línea, unidimensional por su naturaleza. El sistema simplificado de Lorenz de la convección de los fluidos tenía tres dimensiones, no porque el fluido se moviera por ellas, sino porque se necesitaron tres números diferentes para precisar el estado del fluido en un instante dado.
Los espacios de cuatro, cinco o más dimensiones abruman la imaginación visual de los topólogos más dotados. Pero los sistemas complejos tienen muchas variables independientes. Los matemáticos habían de aceptar el hecho de que los sistemas con infinitos grados de libertad —la naturaleza indomeñada que se expresa en la cascada turbulenta o en el cerebro impredecible— requerían un espacio de fases de dimensiones infinitas. Pero ¿quién podía manejar aquello? Era una hidra, despiadada e ingobernable, y se trataba de la imagen de Landau de la turbulencia: modos infinitos, infinitos grados de libertad, dimensiones infinitas.


