Bifurcaciones ahorquilladas y un paseo por el Spree
Ocurría que May había llegado a la biología por la puerta trasera. Dio los primeros pasos como físico teórico en la ciudad australiana de Sydney, que le había visto nacer. Era hijo de un distinguido abogado. Llevó a cabo su trabajo posdoctoral en matemáticas aplicadas en Harvard. En 1971, pasó un año en el Institute for Advanced Study, en Princeton; en lugar de cumplir su deber, contrajo el hábito de visitar la universidad princetoniana para conversar con los biólogos.
Incluso al presente, estos últimos no dominan las matemáticas más allá del cálculo diferencial. Las personas a quienes gustan las ciencias exactas y tienen aptitudes para ellas, se inclinan a seguirlas, o se deciden por la física, antes que por las que estudian la vida. May era una excepción. Sus intereses le acercaron, de momento, a los problemas abstractos de la estabilidad y la complejidad, explicaciones matemáticas que permiten que coexistan los competidores. Pronto empezó a concentrarse en la cuestión ecológica más sencilla de cuál es el comportamiento de cada población en el transcurso del tiempo. Los modelos, inevitablemente simples, parecían un compromiso menor. Cuando se unió definitivamente al cuerpo académico de Princeton —en el que llegaría a ser decano de la actividad investigadora—, había pasado ya muchas horas estudiando una versión de la ecuación de diferencia logística, con la ayuda del análisis matemático y, también, de una primitiva calculadora manual.
Cierta vez había escrito, en Sydney, en una pizarra colocada en un pasillo, la ecuación como problema destinado a los estudiantes graduados. Principiaba a encocorarle. «¿Qué diablos sucede cuando lambda se hace mayor que el punto de acumulación?». O sea, qué ocurría cuando la razón de crecimiento de una población, su tendencia a aumentar y prosperar, excedía de un punto crítico. Durante el ensayo de diferentes valores para ese parámetro no lineal, May reparó en que podía cambiar de forma asombrosa el carácter del sistema. Acrecentar el parámetro equivalía a acrecentar la no linealidad, y eso alteraba no sólo la cantidad del resultado, sino su cualidad. Afectaba no sólo a la población en equilibrio, sino al hecho de si la población se equilibraría.
El modelo simple de May adquiría estado estable si el parámetro era bajo. Si era alto, se rompía el estado estable, y la población oscilaba entre dos valores alternantes. Si era altísimo, el sistema —el mismísimo sistema— comenzaba a portarse de forma impredecible. ¿Por qué? ¿Qué acaecía exactamente en los límites de las distintas clases de comportamiento? May no acertó con ello. (Ni tampoco los estudiantes graduados).
Puso en práctica un programa de exploración numérica intensa sobre el proceder de esta ecuación, la más sencilla de todas. El programa era análogo al de Smale: quería entender aquella simple ecuación de golpe, global y no localmente. Era mucho más sencilla que todo lo que Smale había estudiado. Parecía increíble que sus posibilidades para crear orden y desorden no se hubieran agotado mucho antes. Seguían ternes. Ciertamente, el programa de May acababa de empezar. Investigó centenares de valores distintos del parámetro, dando movimiento al bucle del feedback o realimentación, y esperando ver dónde —y si— la sarta de números se detenía en un punto dado. Se centró cada vez más en el límite crítico entre la estabilidad y la oscilación. Fue como si poseyera un vivero en el que ejerciese delicada autoridad sobre el aumento y la prosperidad de los peces. Utilizando todavía la ecuación logística, xpróx=rx(1 − x), acrecentó el parámetro con la mayor lentitud posible. Si era 2,7, la población sería 0,6292. Mientras el parámetro ascendía, la población final se acrecentó levemente, trazando una línea que se elevó de forma imperceptible, en tanto que se movía de derecha a izquierda en la gráfica.
Mas, de pronto, cuando el parámetro pasó a 3, la línea se partió en dos. La imaginaria población íctica de May se negó a permanecer en un solo valor y osciló entre dos puntos en años alternos. Cuando partía de un número bajo, la población crecía y fluctuaba hasta que aleteaba adelante y atrás. La oscilación se rompía girando el mando algo más —aumentando algo más el parámetro—, y así se produjo una serie de cifras que se resolvió en cuatro valores diferentes, cada uno de los cuales reaparecía cada cuatro años.[2] Por consiguiente, la población subía y bajaba según un programa cuatrienal regular. El ciclo se había vuelto a doblar: primero de un año a dos, y entonces a cuatro. Y de nuevo el comportamiento cíclico resultante fue estable; distintos valores de partida convergían siempre en el mismo ciclo de cuatro años.
Como Lorenz había descubierto hacía una década, la única manera de interpretar números como aquéllos, y conservar la vista, era recurrir a una gráfica. May diseñó un perfil escueto, destinado a sumar todo el conocimiento de la conducta de tal sistema en diferentes parámetros. El nivel de éstos se proyectó en sentido horizontal, de izquierda a derecha, y la población, verticalmente. May estableció para cada parámetro un punto que indicaba el resultado final, después de que el sistema alcanzara el equilibrio. A la izquierda, donde el parámetro era bajo, ese resultado sería un punto, de suerte que todos se significarían con una línea que ascendería lentamente de derecha a izquierda. Cuando el parámetro hubiese dejado atrás el primer punto, May tendría que señalar dos poblaciones: la línea se dividiría en dos en forma de Y inclinada u horquilla. La partición correspondería a una población que se deslizaba de un ciclo anual a otro bianual.
James P. Crutchfield / Adolph E. Brotman
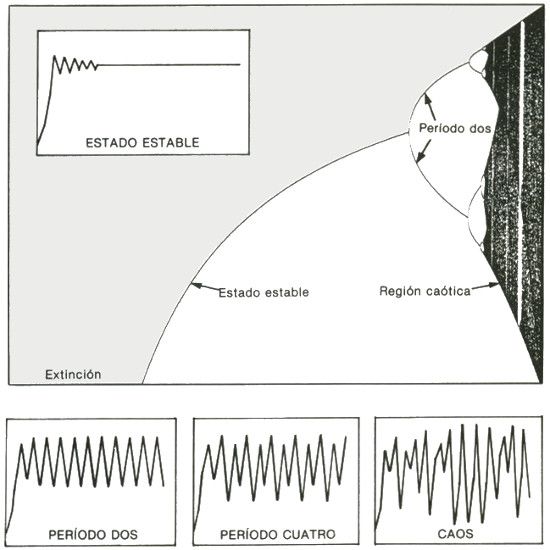
DUPLICACIÓN DE PERÍODO Y CAOS. En vez de utilizar gráficas para representar el comportamiento de poblaciones con grados distintos de fecundidad, Robert May y otros científicos recurrieron a un «diagrama de bifurcación» para reunir toda la información en una sola imagen.
El diagrama muestra cómo los cambios en un parámetro —en este caso, «el florecimiento y la proliferación» de una población silvestre— transformarán el comportamiento definitivo de un sistema tan simple. Los valores del parámetro se representan de izquierda a derecha; la población final se indica en el eje vertical. En cierto sentido, dirigir el valor del parámetro hacia arriba significa influir mucho más en el sistema, aumentando su no linealidad.
La población se extingue donde el parámetro es bajo (izquierda). Así que aumenta, también se acrecienta el nivel de equilibrio de la población (centro). Si sigue creciendo, el equilibrio se divide en dos, de la misma manera que intensificar el calor en un fluido en convección hace que aparezca la inestabilidad; la población principia a alternar en dos niveles distintos. Las divisiones, o bifurcaciones, se hacen cada vez más rápidas. Entonces el sistema se vuelve caótico (derecha), y la población pasa por muchos valores, infinitamente diferentes. (En las dos siguientes ilustraciones se presenta una ampliación de la región caótica).
Pues bien, a medida que el parámetro siguió elevándose, el número de puntos se dobló una vez, y después otra, y luego otra. Era desconcertante un comportamiento tan complejo y, al mismo tiempo, tan regular. May lo definió como «la serpiente en la hierba matemática». Las duplicaciones eran bifurcaciones, y cada una de ellas indicaba que la pauta de iteración se descomponía de nuevo. Una población estable alternaría entre diferentes niveles un año no y otro sí. La que había alternado durante un ciclo de dos años variaba en el tercero y el cuarto, mudándose al período cuatro.
Las bifurcaciones se aceleraban —4, 8, 16, 32, etc.— y se interrumpían de pronto. Allende cierta situación, el «punto de acumulación», la periodicidad se somete al caos, a fluctuaciones que jamás se asientan. Regiones enteras del gráfico se ennegrecen. Si se examina una población gobernada por la más sencilla de estas ecuaciones lineales, llega a creerse que los caminos anuales dependen del azar, como si los anulase el alboroto ambiental. No obstante, en el seno de esta complejidad reaparecen de súbito los ciclos estables. A pesar de que el parámetro ascienda, como prueba de que la no linealidad se adueña del sistema con intensidad creciente, aparece de repente una ventana con un período irregular: uno excéntrico, como 3 o 7. La pauta de la población cambiante se repite en un ciclo de tres o siete años. A renglón seguido, las bifurcaciones propias del período de duplicación se reinician con rapidez mayor, de manera que recorre velozmente ciclos de 3, 6, 12, etc., o de 7, 14, 28, etc., tras lo cual se interrumpe de golpe y el caos se renueva.
May no pudo, al principio, abarcar de una mirada la totalidad de lo antes descrito; pero eran bastante desconcertantes los fragmentos accesibles a sus cálculos. En un sistema del mundo real, el observador vería cada vez la tajada vertical de un solo parámetro, únicamente una clase de comportamiento, ya un estado estable, ya un ciclo de siete años, ya azar aparente. No tendría forma de saber que el mismo sistema, con algún cambio imperceptible en un parámetro, podía exhibir pautas de género por completo distinto.
James Yorke analizó con rigor matemático este comportamiento en su artículo «Period Three Implies Chaos» (El período tres implica caos). Probó que cualquier sistema unidimensional, si aparece un período regular de tres, mostrará no sólo ciclos regulares de extensión diferente, sino otros completamente caóticos. Tal fue el descubrimiento que afectó como una «descarga eléctrica» a físicos de la categoría de Freeman Dyson. Era algo tan contrario a la intuición… Se hubiera imaginado como trivial la presentación de un sistema que se repitiese a sí mismo en una oscilación de período tres, sin generar caos ni por asomo. Yorke demostró que se trataba de algo imposible.
Estaba convencido de que el valor en relaciones públicas de su artículo sobrepasaba el de su sustancia matemática, bien que fuera detonante. Acertó en parte. Pocos años después, mientras asistía a una conferencia internacional en el Berlín oriental, aprovechó la ocasión para visitar los alrededores y tomó una embarcación que recorría el Spree. Se le acercó de sopetón un ruso, con el ánimo evidente de comunicarle algo con urgencia. Gracias a la ayuda de un amigo polaco, Yorke consiguió enterarse de que el ruso pretendía haber probado el mismo resultado. Su inesperado interlocutor se negó a proporcionar más detalles; sólo se comprometió a enviarle su artículo. Yorke lo recibió, en efecto, cuatro meses después. A. N. Sarkovski se le había anticipado con un artículo titulado «Coexistencia de ciclos de un diagrama continuo de una línea en sí mismo». Pero Yorke había ofrecido más que un resultado matemático. Había despachado un mensaje a los físicos: el caos es ubicuo, estable y estructurado. También proporcionó motivo para creer que los sistemas complejos, que, tradicionalmente, se modelaban con arduas ecuaciones diferenciales continuas, se entenderían en términos de diagramas individuales fáciles.
James P. Crutchfield / Nancy Sterngold
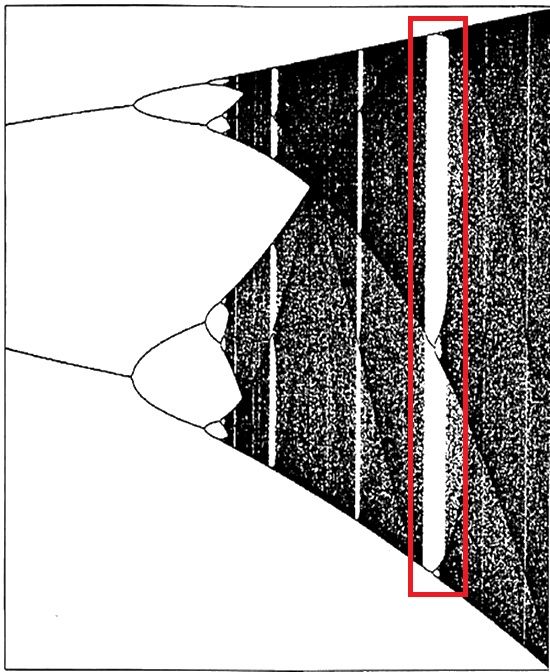
VENTANAS DE ORDEN EN EL INTERIOR DEL CAOS. Incluso con la ecuación más elemental, la región de caos en un diagrama de bifurcación tiene una estructura intrincada, pero mucho más ordenada de lo que Robert May sospechó al pronto. Ante todo, las bifurcaciones producen períodos de 2, 4, 8, 16, etc. Después empieza el caos, sin períodos regulares. Luego, cuando se fuerza aún más el sistema, aparecen ventanas con períodos impares. Surge un período 3 estable (ampliación arriba), y a continuación se reinicia la duplicación de períodos: 6, 12, 24, etc. La estructura tiene profundidad infinita. Cuando se amplían porciones de ella (como la parte central de la ventana del período 3, —ampliación abajo—), se asemejan al diagrama entero.
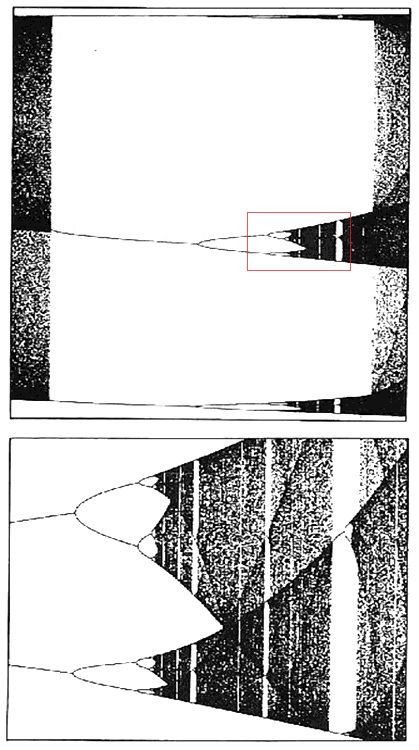
ampliaciones
El encuentro turístico de dos matemáticos, gesticulantes e impotentes para comunicarse, era síntoma de la falta de comunicación entre la ciencia soviética y la occidental. En parte por culpa del idioma, y, en parte, por culpa de las restricciones impuestas a los ciudadanos de la URSS deseosos de viajar, notables científicos de Occidente habían repetido a menudo trabajos que ya figuraban en la bibliografía soviética. El florecimiento del caos en los Estados Unidos y Europa ha inspirado una enorme cantidad de trabajo paralelo en la Unión Soviética; y asimismo ha provocado perplejidad y desorientación indescriptibles, porque un buen retazo de la nueva ciencia no era novedad en Moscú. Los matemáticos y físicos soviéticos disfrutan de sólida tradición en la investigación del caos, desde la obra de A. N. Kolmogorov, en el decenio de 1950. Además, tienen el hábito de colaborar, con el cual se han salvado de la divergencia que separa a los de otras naciones.
Por consiguiente, los científicos de la URSS estaban preparados a escuchar a Smale: su herradura provocó notable conmoción en los años sesenta. Un distinguido físico matemático, Yasha Sinai, tradujo en seguida sistemas similares a expresiones termodinámicas. De manera parecida, cuando la actividad de Lorenz llegó por fin a la física occidental, en la década de 1970, se divulgó también por la Unión Soviética. Y en 1975, cuando Yorke y May se esforzaban en encender el interés de sus colegas, Sinai y otros congregaron prontamente un poderoso grupo de físicos con centro en Gorki. En los últimos años, algunos expertos occidentales en el caos han convertido en norma las visitas regulares a la URSS, con el fin de estar al corriente de los nuevos avances; con todo eso, los más han de darse por satisfechos con la versión de su ciencia en Occidente.
Yorke y May fueron los primeros en el mundo occidental en sentir el pleno impacto de la duplicación de período y en transmitirlo a la comunidad científica. Los escasos matemáticos que habían advertido el fenómeno lo trataron como asunto técnico, como rareza numérica, casi como un juego. No lo juzgaron insignificante, pero sí algo que pertenecía a su universo personal.
Los biólogos no habían tenido en cuenta las bifurcaciones que llevan al caos, tanto porque carecían de refinamiento matemático, como porque no les asistían motivos para explorar el comportamiento desordenado. Los matemáticos habían reparado en las bifurcaciones, pero sin detenerse en ellas. May, que tenía un pie en cada mundo, comprendió que entraba en un campo asombroso y hondo.


