Los pitagóricos

Al tratar a autores como Parménides o Protágoras, que no eran científicos, poco o nada podemos inferir acerca de la eficacia científica de los puntos de vista extremos que mantenían. El prototipo de una escuela de pensadores de clara orientación científica tendente a reducir el edificio de la naturaleza a la razón (aunque al mismo tiempo con un sesgo bien marcado, que rozaba el prejuicio religioso) lo constituyeron los pitagóricos. Su asentamiento principal se encontraba en el sur de Italia, en las ciudades de Crotona, Síbaris y Taranto, situadas en la bahía que se forma entre el «talón» y la «punta» de la península. Sus partidarios formaban algo muy parecido a una orden religiosa con curiosos ritos relativos a la comida y otras cosas, obligados al secretismo con los extranjeros, al menos en lo referente a parte de las enseñanzas^[7]. El fundador, Pitágoras, quien tuvo su actividad en la segunda mitad del siglo VI a. C., debió de ser una de las personalidades más notables de la Antigüedad, y en su entorno se tejieron toda clase de leyendas relativas a sus poderes sobrenaturales, como la de que era capaz de recordar todas las vidas anteriores de su metempsicosis (transmigración del alma); o la de que alguien, por un cambio accidental de vestimenta, se percató de que su fémur era de oro puro. Parece no haber dejado una sola línea escrita. Su palabra era infalible para sus pupilos, como lo evidencia la conocida frase αὐτὸζ ἐϕα («el Maestro lo ha dicho»), con la que se zanjaba cualquier disputa entre ellos. Se dice también que tenían prohibido pronunciar su nombre, refiriéndose a él como «ese hombre» (ἐκεῖνοζ ἀνἠρ). Pero no siempre nos resulta fácil decidir cuándo una doctrina particular proviene de él y cuándo no, habida cuenta del carácter y actitudes de la comunidad.

Su perspectiva apriorística la retomaron claramente Platón y la Academia, profundamente impresionados e influidos por la escuela del sur de Italia. De hecho, desde el punto de vista de la historia de las ideas bien podríamos presentar la escuela ateniense como una rama de la pitagórica. El hecho de que no se hallarán formalmente vinculados a la «Orden» tiene poca relevancia y menos relevante aún es su preocupación por velar, más que enfatizar, su dependencia respecto de la escuela pitagórica con vistas a resaltar la propia originalidad. En cualquier caso, la mejor información acerca de los pitagóricos se la debemos, como tantas otras informaciones, a las sinceras y honestas referencias de Aristóteles, aunque la mayoría de las veces el Estagirita está en desacuerdo con los puntos de vista de los pitagóricos y los critica por su infundadas tendencias apriorísticas, a las que él mismo sin embargo se inclinaba.

La doctrina básica de los pitagóricos, se nos dice, era que las cosas son números, aunque algunos transmisores tratan de encubrir la paradoja, diciendo que «son como números» o análogos a éstos. Estamos lejos de conocer el alcance real de esta afirmación. Muy posiblemente se originó como una generalización a partir del impactante descubrimiento que hizo Pitágoras de las subdivisiones integrales o racionales (por ejemplo, 1/2, 2/3, 3/4) de una cuerda, produciendo intervalos musicales que, al componerse en la armonía de una canción, puede conducimos al borde de las lágrimas, como si hablaran, de alguna manera, directamente al alma. (A la Escuela se debe un hermoso símil de la relación entre el alma y el cuerpo, probablemente proveniente de Filolao: se denomina alma a la armonía del cuerpo, vinculándose a este del mismo modo en que lo está un instrumento musical con los sonidos que produce.)

Según Aristóteles, las «cosas» (que eran números) eran en primer lugar objetos sensibles, materiales; por ejemplo, después de que Empédocles desarrollara su teoría de los cuatro elementos, éstos también «se convertirían» en números; pero también «cosas» tales como Alma, Justicia, Oportunidad tenían sus números, o «eran» números. Un aspecto relevante era la atribución de algunas propiedades simples de la teoría de los números. Por ejemplo, los números cuadrados (4, 9, 16, 25,…) tenían que ver con la Justicia, particularmente identificada con el primero de ellos, concretamente el 4. La idea implícita sería la posibilidad de dividir el número en dos factores iguales (compárense palabras como «equidad», «equitativo»). Un número cuadrado de puntos puede ser ordenado en un cuadrado, como por ejemplo en el juego de bolos. En el mismo sentido los pitagóricos hablaban de triangulares como 3, 6, 10,…

El número se origina multiplicando el número de puntos de un lado (n) por el número siguiente (n + 1) y dividiendo el producto (que siempre es par) por dos: n(n + 1)/2 (Lo que puede apreciarse con mayor claridad yuxtaponiendo un segundo triángulo invertido y desplazando la figura hasta formar un rectángulo).

En la teoría moderna el «cuadrado del momento orbital del momentum» es n (n + 1) h², no n²h², donde n es un entero. Señalamos esto únicamente para ilustrar el hecho de que la distinción de los números triangulares no era una mera ilusión, pues estos aparecen en matemáticas con relativa frecuencia.

El número triangular 10 merecía singular respeto, posiblemente por ser el cuarto y, por tanto, el que designaba a la justicia.

Ilustramos a partir del testimonio fiable —y nunca despectivo— de Aristóteles, el cúmulo de sinsentidos que inevitablemente acarreaba tal tesis.

La primera propiedad de un número es la de ser impar o par. (El matemático está familiarizado con la distinción fundamental entre números primos impares y pares, aunque esta última clase sólo contenga el número 2.) Pero se suponía que el número impar determina el límite o el carácter finito de una cosa, haciéndose así al par responsable del carácter ilimitado o infinito de otras cosas. Simboliza la infinita (!) divisibilidad, puesto que un número par puede ser dividido en dos partes iguales. Otro comentarista señala un rasgo defectivo o de incompletitud (apuntando al infinito) del número par por el hecho de que al dividirlo en dos

. . . | . . .

queda en medio un espacio vacío carente tanto de posesor como de número (ἀδέσποτοζ καὶ ἀνάριθμοζ).

Los cuatro elementos (fuego, agua, tierra, aire) parecen haber sido concebidos como si se hubieran construido a partir de cuatro de los cinco poliedros regulares, mientras el quinto, el dodecaedro, se destinaba a simbolizar el receptáculo del universo entero, probablemente por aproximarse a la esfera y por estar formado por pentágonos; el pentágono tenía por sí mismo un papel místico, así como esta misma figura más sus cinco diagonales (5 + 5 = 10), que forma el conocido pentagrama. Uno de los pitagóricos más antiguos, Petron, afirmaba que existían alrededor de 183 mundos, configurados en un triángulo —aunque, dicho sea de paso, 183 no sea un número triangular—. ¿Resultaría muy irreverente recordar en esta ocasión que recientemente un eminente científico nos comunicaba que el número total de partículas elementales en el mundo es de 16 X 17 X 2²⁵⁶, donde 256 es el cuadrado del cuadrado del cuadrado de 2?

Los pitagóricos tardíos creían en la transmigración del alma en un sentido muy literal. Es habitual afirmar que Pitágoras también lo creía. Jenófanes nos cuenta esta anécdota acerca del maestro en un par de dísticos. Viendo golpear cruelmente a un perrito, sintió lástima de él y dijo al que así lo atormentaba: «Deja de golpearlo; es el alma de un amigo, al que he reconocido al oír su voz». En boca de Jenófanes se trataba probablemente de ridiculizar al gran hombre por su creencia extravagante. Hoy día no podemos evitar interpretar la anécdota de manera diferente. Suponiendo que sea cierta, uno buscaría un significado mucho más simple en las palabras de Pitágoras, algo así como: basta, oigo la voz de un amigo atormentado, pidiendo mi ayuda, («nuestro amigo el perro» se convirtió en una frase hecha con Charles Sherrington).

Permítaseme retornar por un momento a la idea general, mencionada al principio, de que los números se encuentran detrás de todas las cosas. He dicho que ello obviamente partió de los descubrimientos acústicos sobre las longitudes de las cuerdas en vibración. Pero, en justicia (pese a sus extravagantes derivaciones), uno no debería olvidar que es la época y el lugar de los primeros grandes descubrimientos en aritmética y geometría, que estuvieron corrientemente vinculados a algún tipo de aplicación real o imaginada sobre objetos materiales. La esencia del pensamiento matemático es abstraer números del soporte material (longitudes, ángulos y otras cantidades) para operar con ellos y sus relaciones. Por la naturaleza de tal procedimiento, las relaciones, modelos, fórmulas y figuras geométricas a las que se llega por esta vía muy a menudo resultan inesperadamente aplicables a entidades materiales muy diferentes de aquéllas de las que fueron abstraídas originalmente. De pronto, la fórmula matemática proporciona orden en un dominio para el cual no estaba previsto y en el que nunca se había pensado cuando se derivó el modelo matemático. Esta experiencia sorprendente es idónea para que surja la creencia en el poder místico de las matemáticas. Al encontrárnoslas de manera inesperada allí donde no las habíamos aplicado, las «Matemáticas» parecen hallarse en el fondo de todas las cosas. Este hecho, que debió de impresionar profunda y reiteradamente a los jóvenes amantes de la matemática, retorna como un singular evento para marcar el progreso de la ciencia física. Así, para dar al menos un ejemplo famoso, Hamilton descubrió que el movimiento de un sistema mecánico general se regía exactamente por las mismas leyes que un rayo de luz al propagarse en un medio no homogéneo. Hoy la ciencia se ha sofisticado, ha aprendido a ser cauta en tales casos y a no tener por conocimientos garantizados e intrínsecos lo que podría ser simplemente una analogía formal, resultado de la naturaleza misma del pensamiento matemático. Pero no debe extrañamos encontrar, en la infancia de las ciencias, conclusiones precipitadas de carácter místico a las que nos hemos referido.

Un caso moderno, divertido, aunque irrelevante, de un modelo aplicado a un asunto completamente diferente es el de la denominada curva de transición en la planificación de una pista o carretera. La curva que conecta dos tramos rectos de la pista no es simplemente un arco de círculo, pues eso supondría que el conductor tendría que girar de repente el volante al entrar en el círculo desde la recta. La condición para una curva de transición ideal se presenta por sí misma: requiere una proporción uniforme del giro del volante en la primera mitad, y la misma proporción uniforme de giro contrario en la segunda mitad de la transición. La formulación matemática de esta condición conduce a la exigencia de que la curvatura sea proporcional a la longitud de la curva. Se trata de una curva muy especial, denominada espiral de Cornu, que era conocida mucho antes de la aparición de los vehículos de motor. Su única aplicación anterior, que yo sepa, fue en un problema simple de óptica, concretamente la interferencia tras una rendija iluminada por una fuente luminosa puntiforme; este problema condujo al descubrimiento teorético de la espiral de Cornu.

Un problema muy simple, conocido por todo escolar, es el de intercalar entre dos longitudes (o números) dadas, p y q, una tercera, x, tal que la razón entre p y x sea la misma que entre x y q.

p:x = x:q

La cantidad x es la que se conoce como «media geométrica» de p y q. Por ejemplo, si q fuera 9 veces p, x sería 3 veces p y por tanto un tercio de q. De lo cual se puede apreciar mediante sencilla generalización que el cuadrado de x es igual al producto pq,

x² = pq

(Esto puede también inferirse de la regla general de las proporciones, según la cual el producto de los medios o miembros «interiores» es igual al producto de los extremos o miembros «exteriores»). Los griegos habrían interpretado esta fórmula geométricamente como la «cuadratura del rectángulo», en la que x es el lado de un cuadrado de área igual a la del rectángulo con lados p y q. Conocían la fórmula algebraica y las ecuaciones únicamente en una interpretación geométrica, puesto que en general no había número que se adaptara bien a la fórmula. Por ejemplo, si se dan a q los valores 2p, 3p, 5p,… (siendo p para simplificar igual a 1) entonces x es lo que denominamos √2, √3, √5,…, pero para ellos éstos no eran números, no los habían inventado todavía. Cualquier construcción geométrica que verifique la fórmula anterior es, pues, una extracción de la raíz cuadrada.

La manera más simple consiste en situar los segmentos p y q a lo largo de una línea recta; a continuación erigir una perpendicular en el punto donde se unen (N) y cortarla (en C) mediante una circunferencia trazada desde el centro O (el punto medio de p + q) que pase por los puntos finales A y B de p + q.

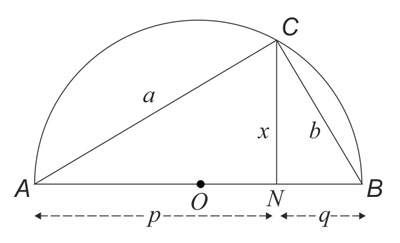
Fig. 1.

La proporción (1) se sigue del hecho de que ABC es un triángulo rectángulo, dado que C es un «ángulo en una semicircunferencia», configurándose tres triángulos ABC, ACN, CBN geométricamente semejantes. Tales triángulos exhiben dos nuevas «medias geométricas», a saber (tomando p + q = c, como hipotenusa).

De donde se sigue:

a² + b² = (p + q)c = c²,

lo que constituye la demostración más simple del denominado teorema de Pitágoras.

La proporción (1) podría habérseles ocurrido a los pitagóricos partiendo de algo completamente diferente. Si p, q, x son longitudes que uno delimita sobre la misma cuerda mediante soportes, o simplemente presionando con el dedo como lo hacen los violinistas, entonces x producirá un tono que será la «media proporcional» de los producidos por p y q; los intervalos musicales entre p y x y entre x y q serán iguales. Esto puede conducir fácilmente al problema de dividir un intervalo musical dado en más de dos intervalos iguales. A primera vista esto parece apartamos de la armonía, en la medida en que, por más que el cociente inicial p : q fuera racional, las relaciones intercaladas podrían no serlo. Precisamente este procedimiento de intercalar distancias es el empleado en el sistema temperado de los tonos del piano, con los doce grados. Se trata de un compromiso, condenable desde el punto de vista de la armonía pura, pero difícilmente evitable en un instrumento con tonos prefabricados.

Arquitas (también conocido por su amistad con Platón en Tarento hacia mediados del siglo IV) solucionó geométricamente el problema de hallar dos medias geométricas (δύο μέσαζ ἀνὰ λόγον εὑρεῖν), o dividir un intervalo musical en tres partes iguales. Lo que, por otra parte, equivale a encontrar geométricamente la raíz cúbica de un cociente dado q:p. Bajo esta última forma —hallar una raíz cúbica—, el asunto era conocido como el Problema Délico; a los sacerdotes de Apolo en la isla de Delos el oráculo les encargó en cierta ocasión duplicar las medidas de la piedra que servía de altar. Ahora bien, esta piedra era un cubo, y un cubo de doble volumen debería tener una arista de magnitud ³√2 veces la del cubo inicial.

Con símbolos modernos el problema se plantea así:

p : x = x : y = y : q,

de donde se deduce

x² = py, xy = pq

Multiplicando miembro a miembro y eliminando el factor y:

La solución de Arquitas consiste en repetir la construcción anterior,

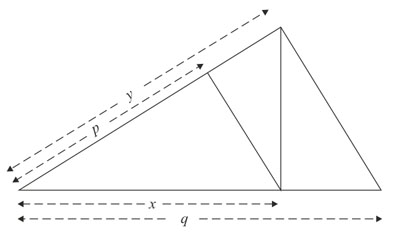
Fig. 2.

pero usando el segundo tipo de proporción antes mencionada, lo que aquí conduce a:

No obstante, esto es sólo el resultado final de la construcción de Arquitas, una construcción muy elaborada que utiliza intersecciones de una esfera, un cono y un cilindro —tan complicadas que en mi primera edición del Presocráticos de Diels la figura que debía ilustrar el texto era absolutamente errónea—. De hecho, la figura anterior, aparentemente simple, no puede construirse directamente con regla y compás a partir de los datos p y q. Y es que con una regla únicamente pueden construirse líneas rectas (curvas de primer orden), con un compás una circunferencia, que es una curva particular de segundo orden; pero para extraer una raíz cúbica es preciso disponer de al menos una curva particular de tercer orden. Arquitas lo resolvió de la manera más ingeniosa mediante curvas de intersección. Su método para solucionar el problema no supone, como cabría imaginar, una complicación añadida, y es una verdadera hazaña el que lo consiguiera aproximadamente medio siglo antes de Euclides.

El último aspecto de las enseñanzas pitagóricas que consideraremos aquí es el relativo a su cosmología. Resulta de particular interés para nosotros, puesto que nos revela la inesperada eficiencia de un punto de vista tan lastrado por ideales de perfección, belleza y simplicidad preconcebidos e infundados.

Los pitagóricos sabían que la Tierra era esférica y fueron probablemente los primeros en saberlo. Ello se infería posiblemente a partir de las sombras circulares de la Luna durante los eclipses lunares, fenómeno que interpretaban más o menos correctamente (véase más adelante). Su modelo del sistema planetario y de las estrellas queda recogido sumaria y esquemáticamente en la siguiente figura:

Fig. 3.

Para ellos la Tierra esférica tarda veinticuatro horas en girar en tomo a un centro fijo, F. C. (¡el fuego central, no el Sol!), hacia cuyo centro presenta siempre el mismo hemisferio —como lo hace la Luna respecto a nosotros—, no habitable puesto que es demasiado caliente. Se supone que existen nueve esferas, todas ellas centradas en F. C.: (1) la Tierra, (2) la Luna, (3) el Sol, (4-8) los planetas, (9) las estrellas fijas; todas se mueven alrededor del centro, cada una de ellas rotando a una velocidad relativa peculiar con respecto al centro (de tal modo que la posición sobre una línea recta de nuestra figura es puramente esquemática; nunca habría aparecido así). Hay además una décima esfera, o al menos un décimo cuerpo, el antichthon o anti-Tierra, del que no queda demasiado claro si se encontraba en permanente conjunción o en oposición a la Tierra con respecto al Fuego Central (nuestra figura muestra las dos alternativas). En cualquier caso, estos tres cuerpos —Tierra, Fuego Central, anti-Tierra— se suponían situados siempre en línea recta, pues el antichthon no se veía nunca; se trataba de una hipótesis gratuita. Podría haber sido inventado para redondear el número de cuerpos y llegar al número sagrado de diez, o bien como causa para explicar cierto tipo de eclipses lunares, como los que se dan cuando el Sol y la Luna resultan visibles en dos puntos opuestos cercanos al horizonte. Ello es explicable por la refracción de los rayos en la atmósfera, al igual que vemos la ubicación de una estrella cuando en realidad lleva ya unos minutos tras el horizonte. Puesto que eso no se sabía en la época, el tipo de eclipses en cuestión presentaba sin duda dificultades, lo que habría contribuido a la necesidad tanto del invento del antichthon como de la afirmación según la cual no sólo la Luna, sino también el Sol, los planetas y las estrellas fijas eran iluminados por el fuego central, siendo los eclipses de Luna producidos al interceptarse por la Tierra o el antichthon la luz del Fuego Central.

A primera vista este modelo parece tan erróneo que difícilmente justificaría que se le dedique la menor reflexión. Considerémoslo, sin embargo, cuidadosamente, recordando que no se sabía nada acerca de las dimensiones de (a) la Tierra y (b) las órbitas. La parte entonces conocida de nuestro planeta, la región mediterránea, se mueve en círculo en veinticuatro horas en torno a un centro invisible, ante el cual presenta siempre la misma cara. Esto causa, precisamente, el rápido movimiento diurno común a todos los cuerpos celestes. Reconocer este último como movimiento meramente aparente es en sí mismo un logro enorme. El punto erróneo respecto al movimiento de la Tierra sólo era tal en lo que concierne al periodo (se le atribuía una revolución en el mismo periodo) y al centro de revolución. Estos errores, por considerables que nos parezcan, pesan poco en comparación con el espectacular descubrimiento de que la Tierra es uno más entre los planetas (como la Luna, el Sol y los otros cinco cuerpos a los que nosotros denominamos planetas). Estamos ante un admirable ejercicio de autoliberación del prejuicio según el cual el hombre y su morada deben situarse en el centro del universo, el primer paso hacia el punto de vista actual, que reduce nuestro globo a un planeta más de una de las estrellas en una de las galaxias del cosmos. Es sabido que este paso, tras ser completado por Aristarco de Samos hacia el 280 a. C., fue a continuación rápidamente desandado y el prejuicio se mantuvo —al menos oficialmente en algunos sectores— hasta principios del siglo XIX.

Cabría preguntarse por qué se inventó el Fuego Central. La dificultad de explicar los evocados eclipses excepcionales, en los que tanto la Luna como el Sol resultan visibles, difícilmente parecería suficiente^[8]. Que la Luna no tiene luz por sí misma, sino que es iluminada por otra fuente, es algo que se conoció muy pronto. Ahora bien, los dos fenómenos más llamativos en los cielos, el Sol y la Luna, son bastante similares en sus movimientos diurnos, en aspecto y en tamaño; esto último debido a la coincidencia de que la Luna se encuentra aproximadamente tantas veces más cerca de nosotros como veces es más pequeña que el Sol. Lo que induce necesariamente a otorgar el mismo estatus a ambos, a proyectar sobre el Sol lo que se conoce acerca de la Luna, y de este modo a considerar que ambos están iluminados por la misma fuente, que no sería sino el hipotético Fuego Central. Éste, al no ser visible, no podía ser ubicado más que «bajo nuestros pies», oculto a nuestros ojos por nuestro propio planeta.

Este modelo, quizás equivocadamente, se ha atribuido a Filolao (segunda mitad del siglo V). Un vistazo a sus desarrollos posteriores muestra que incluso grandes errores, resultado del influjo de ideas preconcebidas sobre perfección y simplicidad, pueden resultar relativamente inocuos. Es más: cuanto más arbitraria e infundada sea una afirmación, tanto menor será el daño mental que pueda causar, ya que la experiencia la eliminará más rápidamente. Como alguna vez se ha dicho, es mejor tener una teoría equivocada que no tener ninguna.

En el presente caso, ni los viajes de los mercaderes cartaginenses, más allá de las «columnas de Hércules», ni, poco más tarde, la expedición de Alejandro a la India revelaron nada acerca del Fuego Central o del antichthon, ni tampoco sobre que la Tierra se hiciera menos habitable más allá de los límites de la cultura mediterránea. De modo que todo ello debía ser olvidado. Desaparecido el centro ficticio (el Fuego Central), resultaba natural abandonar la idea de la revolución diurna de la Tierra y reemplazarla por una pura rotación sobre su propio eje. Los historiadores de la filosofía antigua disienten a la hora de decidir a quién se debe la «nueva doctrina de la rotación de la Tierra». Algunos hablan de Ecfanto, uno de los pitagóricos más jóvenes, mientras que otros se inclinan a considerarlo un personaje de un diálogo de Heráclides Póntico (un nativo de Heraclea en el Mar Negro, asiduo de las escuelas de Platón y Aristóteles) a quien de hecho atribuyen la «nueva doctrina» (que, por cierto, Aristóteles menciona pero rechaza). Pero quizá conviene poner de relieve que no se trata de una doctrina nueva. La rotación de la Tierra ya estaba contemplada en el sistema de Filolao: de un cuerpo que gira alrededor de un centro y se mantiene rotando siempre con la misma cara hacia este centro —como lo hace la Luna con respecto a la Tierra— no debe decirse que carece de rotación, sino que gira con un periodo exactamente igual a su periodo de revolución. No se trata de una sofisticada descripción científica, como tampoco es una coincidencia la igualdad de los periodos en el caso de la Luna (y de otros cuerpos similares); se debe a la fricción de las mareas, bien en un océano o envoltura atmosférica previamente existentes, bien en la masa del cuerpo celeste^[9].

Así, como afirmábamos antes, el sistema de Filolao atribuye a la Tierra, con respecto al Fuego Central, exactamente este tipo de movimiento: una rotación y una revolución con el mismo periodo. El abandono de esta última no debe vincularse al descubrimiento de la primera, puesto que ya estaba descubierta. Nos inclinamos más bien a calificarlo de paso en la dirección errónea, puesto que la revolución se articula en torno a otro centro.

Pero, según parece, hay que atribuir al antes mencionado Heráclides, en contacto con los pitagóricos tardíos, el paso más importante hacia el reconocimiento de la situación efectiva. Los llamativos cambios de luminosidad de los planetas interiores, Mercurio y Venus, ya se habían constatado. Heráclides los atribuyó correctamente a cambios de distancia con respecto a la Tierra. Por tanto no podía ser que se movieran en circunferencias alrededor de esta última. El hecho adicional de que en su movimiento principal siguieran la trayectoria solar ayudó probablemente a inspirar la hipótesis correcta de que ambos se movieran en circunferencias alrededor del Sol. Se harían pronto consideraciones similares sobre Marte, que también muestra cambios apreciables de luminosidad. Finalmente, como es bien sabido, Aristarco de Samos estableció (hacia el 280 a. C.) el sistema heliocéntrico, tan sólo un siglo y medio después de Filolao. No tuvo demasiado eco, y alrededor de 150 años más tarde fue desechado por la autoridad del gran Hiparco, «rector de la Universidad de Alejandría», como diríamos en nuestros días.

Constituye un hecho sorprendente, no poco desconcertante para el científico de nuestros días, el que los pitagóricos, con todos sus prejuicios y sus ideas preconcebidas acerca de la belleza y la simplicidad, progresaran más que otros hacia una intelección de la estructura del universo, más que la sobria escuela de los physiologoi jónicos, de los que hablaremos a continuación, y más también que el de los atomistas, sus sucesores espirituales. Por razones que veremos enseguida, los científicos tienden a considerar a los jónicos (Tales, Anaximandro) y, sobre todo, al gran atomista Demócrito como sus ancestros espirituales, a pesar incluso de que este último se mantuviera aferrado a la idea de una Tierra plana y configurada como un tambor, idea perpetuada entre los atomistas por Epicuro y prolongada hasta el poeta Lucrecio, en el siglo I a. C. Las infundadas y excéntricas fantasías y el arrogante misticismo de los pitagóricos podrían haber contribuido a que un pensador lúcido como Demócrito rechazara toda la enseñanza pitagórica como una construcción arbitraria o artificial. Pero el poder de sus observaciones, a partir de simples experimentos acústicos con cuerdas vibrantes, debería haber permitido reconocer, a través de la niebla de sus prejuicios, algo tan próximo a la verdad que sirviera de fundamento sólido sobre el que establecer la perspectiva heliocéntrica. Es triste decirlo, pero ésta también fue rechazada rápidamente bajo la influencia de la escuela de Alejandría, cuyos componentes se tenían a sí mismos por sobrios científicos, libres de prejuicios y guiados únicamente por los hechos.

No he mencionado en este rápido repaso los descubrimientos anatómicos y fisiológicos de Alcmeón de Crotona, un joven contemporáneo de Pitágoras; descubrió los principales nervios sensibles y siguió su curso hasta el cerebro, en el que reconoció el órgano central, la sede de la actividad de la mente. Hasta entonces —y durante mucho tiempo después, pese a su descubrimiento— el corazón (ητορ, καρδία), el diafragma (ϕρένεζ) y la respiración (πνεῦμα, lat. anima > animus) se consideraban conectados a la mente o el alma, como lo evidencian las expresiones que en todas las lenguas modernas utilizamos metafóricamente para designarlos. Pero con esto basta para nuestro propósito. El lector puede encontrar fácilmente información más completa sobre ello en los documentos médicos de la Antigüedad.