(Del Manual para empleados de la ADE, ADE TFX, Colorado. 2053).
Parecería ineficiente proceder a la geoformación en una secuencia de muchos saltos cortos en lugar de menos saltos más largos. Sin embargo, es algo que se deriva inevitablemente de la matemática de la Traslación Levant-Meyer.
Para apreciarlo, no es necesario tener una descripción técnica completa de la TLM; de hecho, no hay uno entre mil de los empleados de la ADE que entienda todas las sutilezas del proceso. Pero es instructivo comparar los requerimientos energéticos del cristal para saltos de diversa duración.
(Los lectores que no manejen matemáticas de un primer curso universitario quizá quieran consultar el cuadro final).
La ecuación básica para describir la energía necesaria para un salto dado es:
E = C (et/k cosh s1/2) / ((1/t) + 1)
t ≥ 0.01356, s ≥ 9.4095
donde C y k son constantes, t es la duración del salto, y s es la distancia. Los cálculos normalmente se hacen con el sistema metro-kilogramo-segundo, pero por razones de claridad consideraremos a t en unidades de días, y a s en unidades de años-luz.
Las limitaciones que figuran a la derecha de la ecuación se deben a un fenómeno de energía mínima del cristal TLM. Los saltos no pueden hacerse para destinos más cercanos que 9,4095 años-luz, y un salto no puede durar menos de diecinueve minutos y medio. La primera limitación nos impide explotar el prometedor sistema de Alfa Centauri.[1] La segunda nos imposibilita explorar planetas a más de 100 años-luz de distancia.
Considerar que esa ecuación es continua para toda la escala de valores que implica es una ficción conveniente. Sin embargo, la TLM no puede trasladar un objeto a cualquier punto del espacio que desee; sólo traslada de un cuerpo material a otro cuerpo material. Tiene que haber un objeto con una superficie diferenciada y relativamente fría —un planeta o asteroide— «cerca» del punto al que se apunta el cristal TLM (las tentativas de trasladar sondas a la superficie de estrellas sin planetas siempre han fracasado). El margen de error permitido está descrito en una ecuación diferencial de cuarta categoría donde intervienen la distancia, la energía, y el desplazamiento angular de la aplicación energética a partir del eje del cristal TLM.[2]
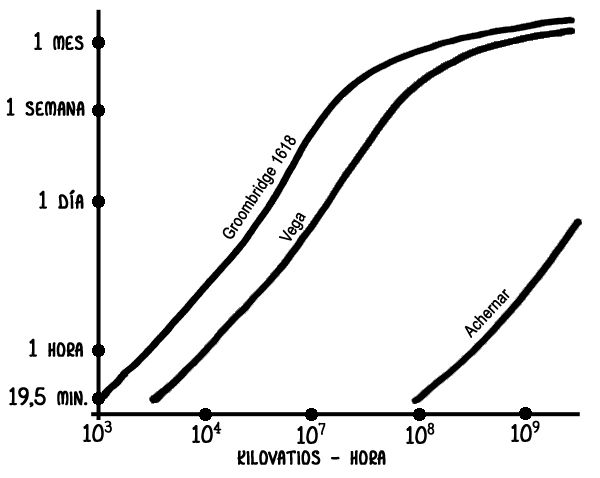
Esta familia de curvas muestra la relación entre requerimiento energético y duración del salto en distancias representativas:

Nótese que un incremento de diez veces en la distancia se transforma en un incremento de mil veces en la energía requerida.
La energía es dinero, por supuesto, y la ADE es la mayor consumidora de energía del mundo. Como cualquier otro consumidor, pagamos una tarifa fija a Westinghouse Interplanetaria por cada kilovatio-hora, aunque nuestra tarifa está reducida a causa del volumen y a causa de los tratados de intereses mutuos concertados con los equipos de investigación de WI.
Es instructivo comparar el costo de los saltos a varios planetas por duraciones diferentes:
| Nombre | Distancia | Duración del salto (Días) | ||||||
| (años luz) | 0.02 | 0.1 | 1.0 | 5.0 | 10 | 30 | 70 | |
| Ross 2481 | 10.3 | 0.48 | 2.24 | 13.6 | 34.7 | 64.8 | 589.0 | 43,301.4 |
| 61 Cygnus A | 11.2 | 0.55 | 2.58 | 15.6 | 39.9 | 74.3 | 675.3 | 49,654.5 |
| Groombridge 16182 | 15.0 | 0.93 | 4.37 | 26.5 | 67.7 | 126.0 | 1,145.2 | 84,200.0 |
| Vega | 26.0 | 3.17 | 14.86 | 89.9 | 229.9 | 428.3 | 3.891.0 | 286,000 |
| Achernar3 | 115 | 87,97 | 4,113.82 | 24,913 | 63,717 | 119,000 | 1,079E3 | 52,440E3 |
| Canopus4 | 240 | 10,354 | 484,200 | 2,932E3 | 7,499E3 | 13,970E3 | 127E6 | 9,330E6 |
| (Las cifras representan el costo en miles de dólares.) | ||||||||
| 1. La estrella más cercana adonde se puede efectuar un traslado TLM | ||||||||
| 2. Planeta donde se descubrió el Puente de Groombridge. | ||||||||
| 3. En este momento se prepara una breve expedición a Achernar. | ||||||||
| 4. Es sólo a modo de ejemplo; nunca se efectuó un salto a Canopus, y quizá no se efectúe nunca. La energía requerida para el salto de setenta días (si tuviéramos un modo de producirlo y mantenerlo) agotaría las reservas energéticas que la Tierra consumiría en diez mil años. | ||||||||
Un estudio detenido de este cuadro permitirá apreciar qué compleja es la tarea de planear los saltos (coordinándolos de tal modo que el cristal esté siempre despejado cuando alguien regresa).
Como ejemplo ilustrativo, considérese el curso de una misión de fecundación en Cygni A. Una Domadora embarazada pasará unos ciento cincuenta días de su preñez fuera del planeta. El costo energético de varias combinaciones de saltos es la siguiente:
150 saltos de un día = 2.340.000 dólares
30 saltos de 5 días = 1.197.000 dólares
15 saltos de 10 días = 1.114.500 dolares
5 saltos de 30 días = 3.376.500 dólares
De manera que una secuencia de saltos breves en realidad puede costar más que un número menor de saltos más largos. Lo que sucede en la práctica es que se calcula la combinación menos costosa, y luego se ajusta la secuencia para compaginar mejor los horarios de empleo del cristal…