«Las cosas sencillas tienen una demostración sencilla», escribió Feynman en sus apuntes para la conferencia. Luego tachó la segunda sencillez y en su lugar puso «elemental». La cosa sencilla que tenía en la cabeza era la primera ley de Kepler, la ley de las elipses. La demostración que iba a presentar era ciertamente elemental, en el sentido de que no empleaba matemáticas más avanzadas que la geometría del bachillerato, pero distaba mucho de ser sencilla.
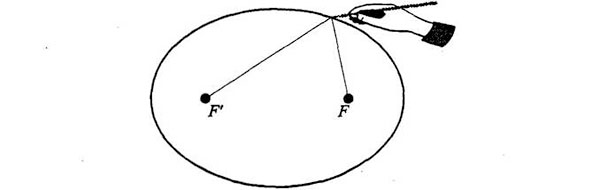
Para empezar, Feynman nos recuerda que una elipse es una especie de círculo estirado que puede trazarse con dos tachuelas, un cordel y un lápiz, del siguiente modo:

Las tachuelas son los dos focos de la elipse. El cordel traza una línea entre un foco y un punto de la elipse y a continuación va hacia el otro foco. La longitud total del cordel no varía mientras el lápiz traza la curva. He aquí un diagrama geométrico algo más exacto:
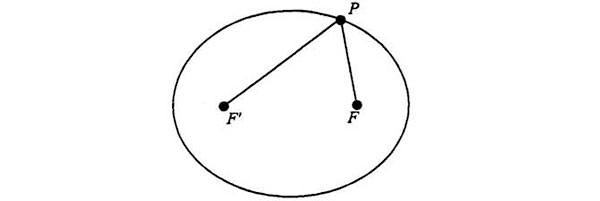
F’ y F son los dos focos y P puede ser cualquier punto de la curva. La distancia entre F’, P y F es siempre la misma, sea cual fuere el punto de la curva donde esté P.
He aquí ahora una bagatela que conviene recordar: si el cordel se acorta un poco y las tachuelas se dejan donde están, podemos trazar otra elipse dentro de la primera, y si el cordel se alarga y las tachuelas siguen sin moverse, podemos trazar una elipse por fuera de las otras dos. De aquí se sigue que cualquier punto del plano —por ejemplo, q— situado de tal modo que la distancia entre F’, q y F sea inferior a la distancia entre F’, P y F (es decir, cualquier punto que pueda alcanzarse con un cordel más corto) queda dentro de la primera elipse. Del mismo modo, cualquier punto q tal que F’Q + QF (otra forma de decir la distancia de F’ a Q más la distancia de Q a F) sea mayor que F’P + PF (la longitud del primer cordel) queda fuera de la elipse primera. He aquí un dibujo para ilustrar la idea:
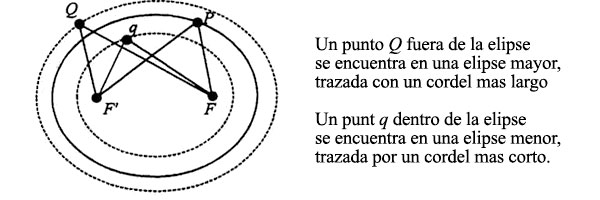
Feynman se sirve de esta idea ya en plena conferencia, pero no la prueba como nosotros. Por el contrario, indica a los estudiantes que la prueben por su cuenta.
Una elipse tiene otra propiedad particular. Si en F se encendiera una bombilla, y si la superficie interior de la elipse reflejara la luz como un espejo, todos los rayos reflejados acabarían concentrándose en F', como sigue:
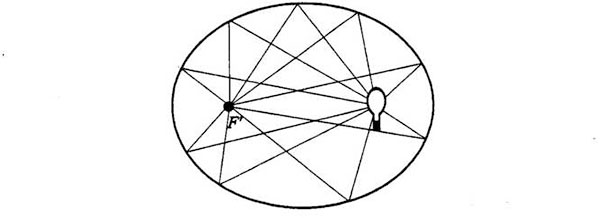
Y viceversa: todos los rayos luminosos que partan de un foco se concentrarán en un punto del otro foco. Feynman formula estas palabras como segunda propiedad elemental de la elipse y se pone a probar que las dos propiedades en realidad son equivalentes. (Su estrategia consiste aquí en conducimos hacia una propiedad más misteriosa de las elipses y que será después indispensable.) Dibújese un punto P cualquiera en la elipse. Por ese punto (como por cualquier otro) de la elipse (o de cualquier otra curva) pasa una sola línea recta que roza la curva sin cortarla, del siguiente modo:
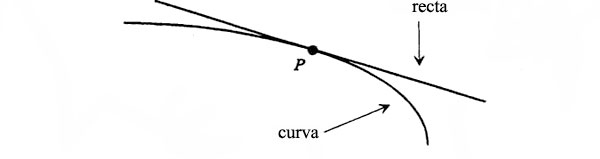
Esta línea es tangente a la curva en dicho punto. Un rayo luminoso, reflejado por la curva en cualquier punto, del siguiente modo:
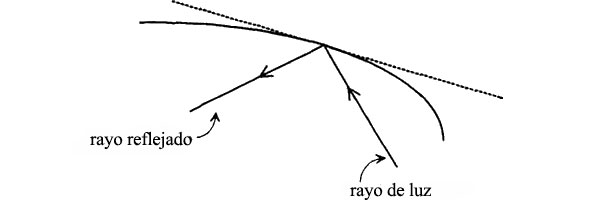
Seguiría la misma trayectoria si fuera la tangente la que lo reflejase en el mismo punto, así:
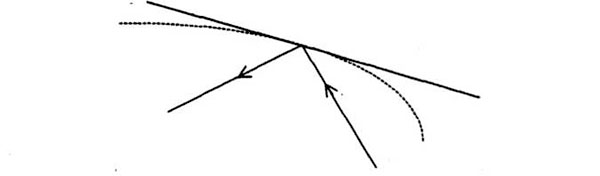
El motivo de que la luz se refleje en la curva tal como lo haría en la tangente en el mismo punto es que la tangente señala la dirección de la curva en ese punto concreto. Si se parte con una curva y su tangente en determinado punto,
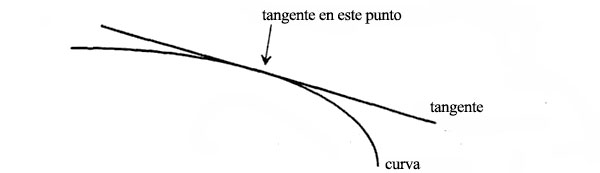
y se amplía la imagen en los alrededores del punto, la curva se estira y se vuelve casi tan recta como la tangente:
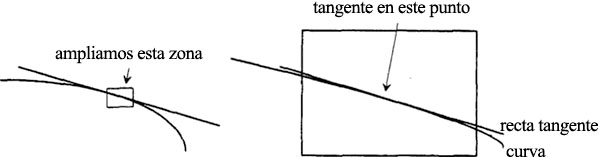
Cuanto más de cerca miremos, menos diferencia habrá entre la curva y su tangente en ese punto. Así, si la luz se refleja en una curva en un solo punto, refleja sólo lo que reflejaría la tangente en ese punto. Por el mismo motivo, la tangente tiene otra propiedad que será importante para nosotros más adelante: si la curva es en realidad la trayectoria de un objeto móvil, la tangente muestra la dirección del movimiento del objeto en cada punto. Cuando decimos que la elipse es la figura que describe un planeta en su órbita alrededor del Sol, la tangente a la elipse en cada uno de los puntos estará en la dirección de la velocidad instantánea en ese punto.
La ley de reflexión en un espejo plano dice que el rayo toca el espejo y sale reflejado en el mismo ángulo, como sigue:
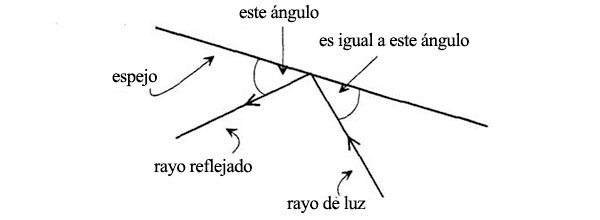
He aquí pues la propiedad aplicada a los rayos luminosos:
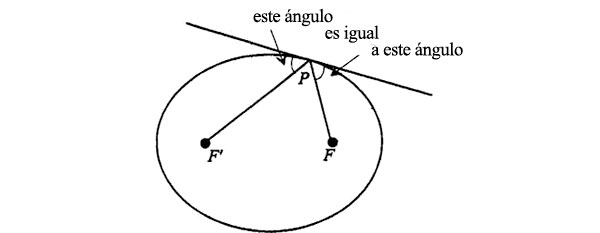
El rayo incidente de F a P forma el mismo ángulo con la tangente en P que el rayo reflejado, que va a F’. Nuestra misión es probar que esta afirmación equivale a decir que la distancia F’P más la distancia PF es la misma para cualquier punto P de la curva.
La prueba necesita algunas operaciones. Tracemos una línea desde F’ que sea perpendicular a la tangente, de este modo:
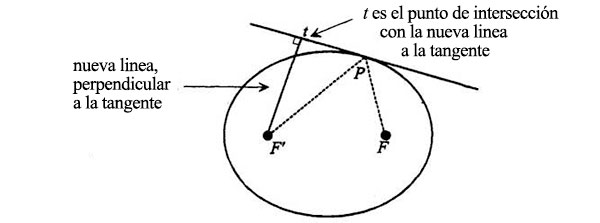
A continuación prolongamos la perpendicular hasta duplicar su longitud, hasta el punto llamado G’.
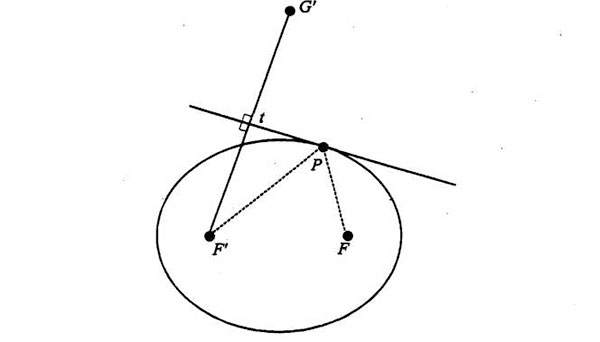
La línea F’G’ se ha trazado de tal modo que la tangente a la elipse en el punto P es su bisectriz perpendicular. Feynman llama G’ al punto reflejo de F’. Lo que quiere decir es que si la tangente fuera en realidad un espejo, y si el punto F’ se viera a sí mismo en dicho espejo, su reflejo parecería estar en G’, a la misma distancia detrás del espejo.
Hace falta otra línea. Conectemos los puntos G’ y P con una recta:
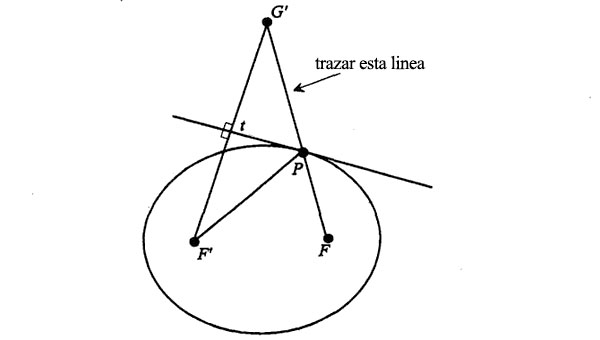
Veamos ahora los dos triángulos que hemos formado; uno aparece con líneas gruesas y el otro con líneas de puntos:
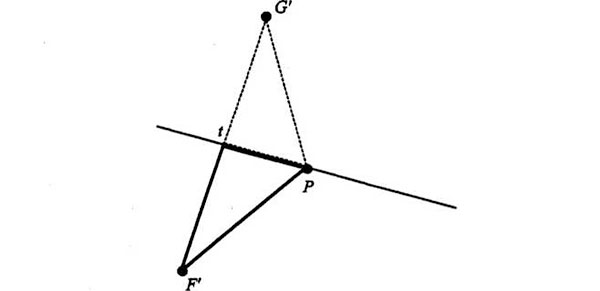
Los dos triángulos son congruentes, es decir, son idénticos en todos los aspectos menos en la orientación. He aquí la prueba. Puesto que hicimos que el cruce en t fuera un cruce de perpendiculares, los dos triángulos tienen un ángulo recto:
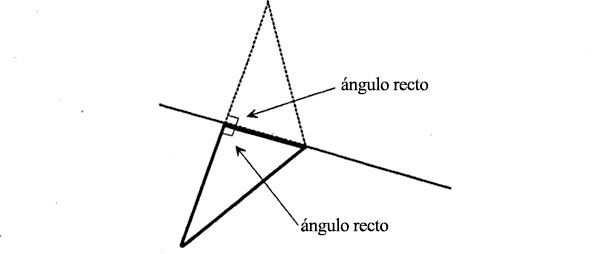
Tienen un lado común:
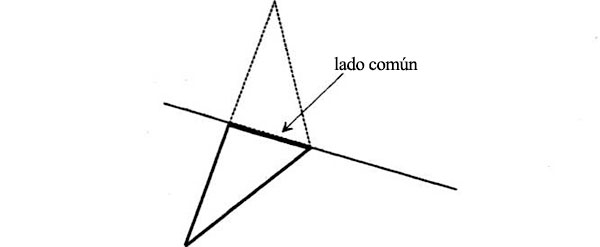
Los dos triángulos tienen además un lado que se trazó de la misma longitud (la tangente que corta F’G’ por la mitad):
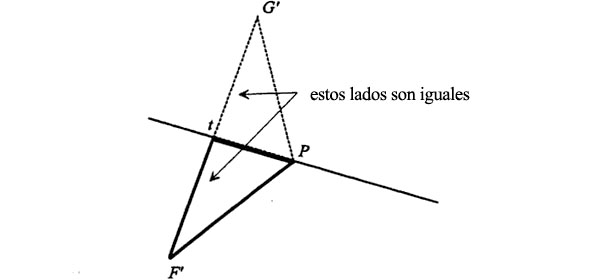
Dos triángulos cualesquiera que tengan iguales un ángulo y dos lados son congruentes: QED[1], como solíamos decir en el instituto. Lo cual significa que todos los lados correspondientes son iguales. Observemos en concreto que el lado G’P es igual al lado F’P:
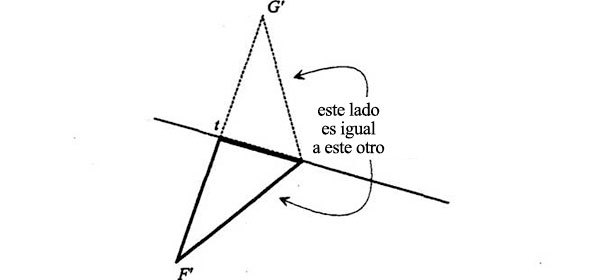
Y los ángulos F’Pt y G’Pt son iguales:
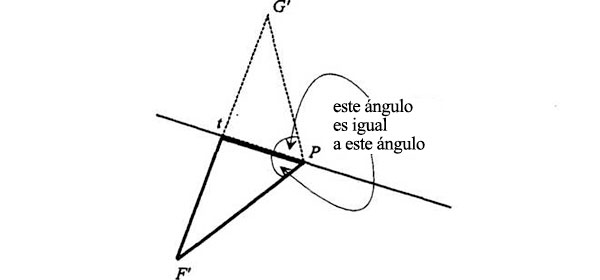
Bien, volvamos al diagrama completo para ver qué hemos aprendido.
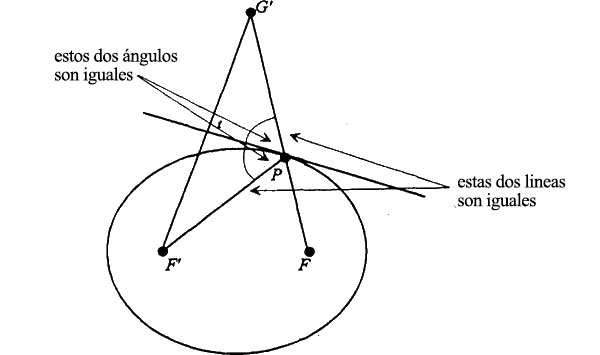
A estas alturas es fácil que hayamos perdido de vista lo que suponemos y lo que queremos probar. Para aclarar la situación, reconstruyamos el diagrama partiendo de cero. Dibujaremos dos puntos, F’ y F, que por el momento no tendrán especial protagonismo. Son dos puntos cualesquiera en un plano:
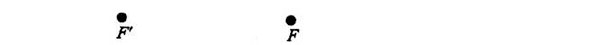
Partiendo de F’, trazamos una recta en cualquier dirección:
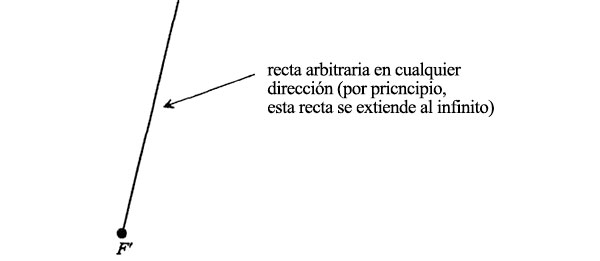
Dibujemos ahora un punto t y tracemos una perpendicular que pase por él. El punto t estará alejado de F’ lo suficiente para que la perpendicular no pase entre F y F’:
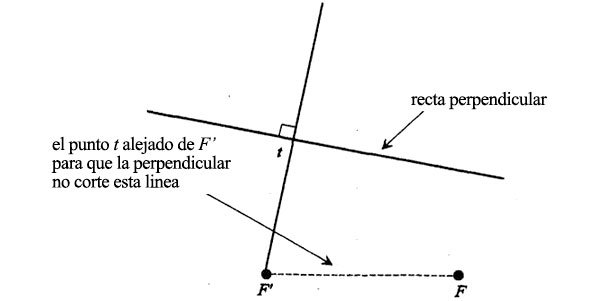
Dibujemos en la recta arbitraria un punto G’ tal que F’t sea igual a tG’. La perpendicular que trazamos será pues la bisectriz de F’G’:
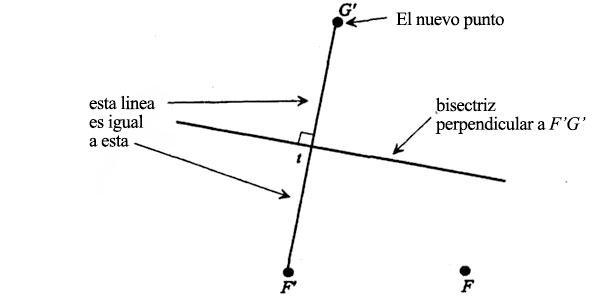
Tracemos ahora una recta que una G’ con F:
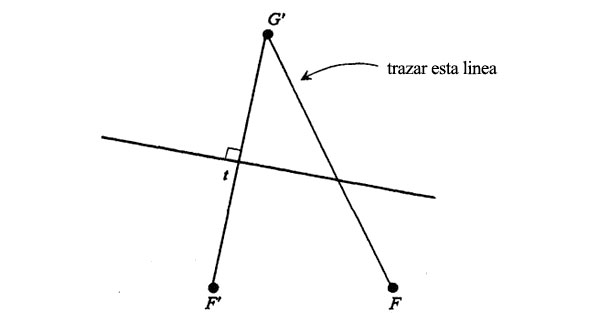
Llamemos P al punto donde esta última línea se cruza con la bisectriz perpendicular y tracemos la línea que une P con F’:
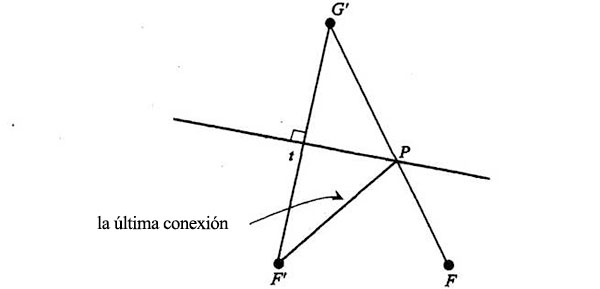
Los dos triángulos son congruentes, lo mismo que antes; luego los ángulos F’Pt y G’Pt son iguales:
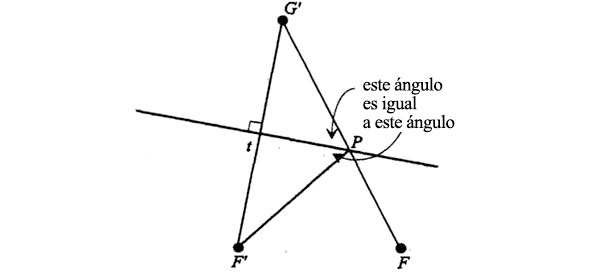
Y el ángulo G’Pt es asimismo igual al ángulo opuesto que se forma cuando G’PF se cruza con la bisectriz (cuando dos rectas se cruzan, los ángulos opuestos son siempre iguales):
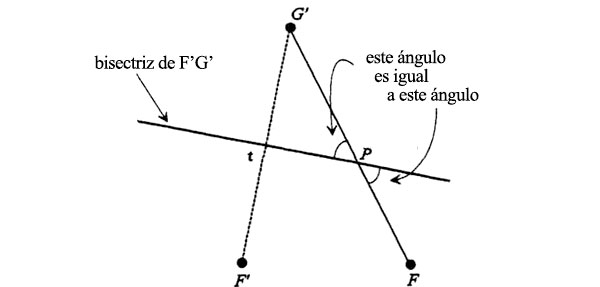
Por lo tanto, todos estos ángulos son iguales:
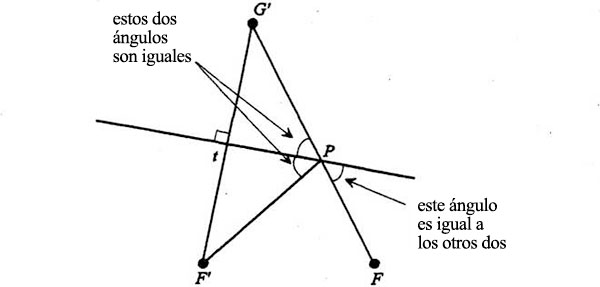
Esto significa que la bisectriz reflejaría la luz de F a F’ en el punto P (pues en ese punto el ángulo de incidencia y el de reflexión son iguales). Más aún: la línea FPG’ tiene una propiedad realmente espectacular que podemos ver volviendo a los triángulos congruentes:
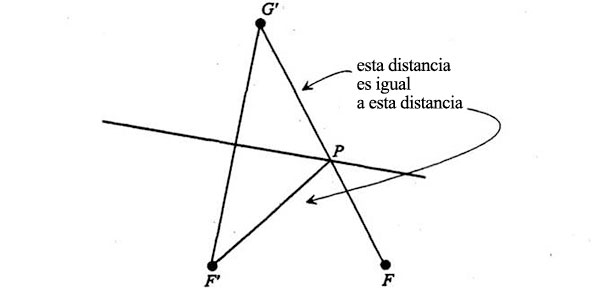
A causa de la congruencia de los triángulos, la longitud F’P es la misma que la longitud G’P. De aquí se sigue que la distancia de F’ a P y de aquí a F es la misma que la de la recta FG’. Pero dicha distancia no es más que la longitud del cordel que utilizamos para trazar la elipse del principio. En otras palabras, si trazamos una elipse con el método del cordel, G’ será el punto al que llegaremos estirando el cordel.
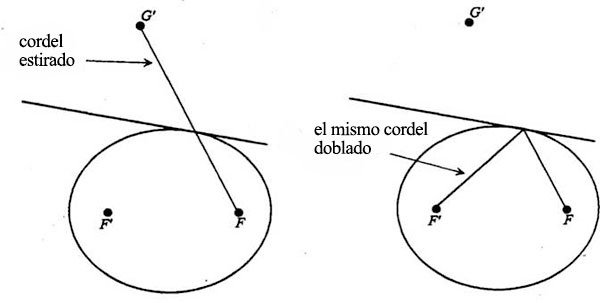
De esta manera hemos descubierto una modalidad nueva, extraña y sorprendente de construir una elipse. He aquí cómo funciona. Tomemos dos puntos en un plano, F’ y F. Tomemos luego un cordel de longitud constante (más largo que la distanciaF’F) y conectemos un extremo al punto F. Estiremos el cordel hasta que quede recto en cualquier dirección y señalemos su extremo con un punto que llamaremos G’:
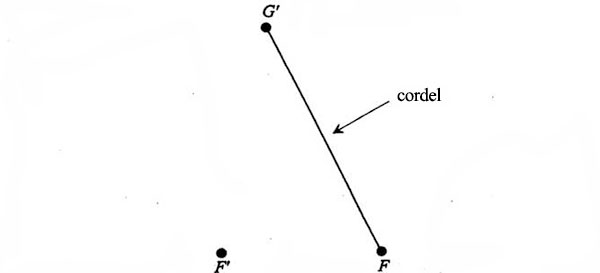
A continuación unamos F’ y G’, y tracemos la bisectriz perpendicular deF’G’. La bisectriz se cruza con la línea FG’ en un puntoP:
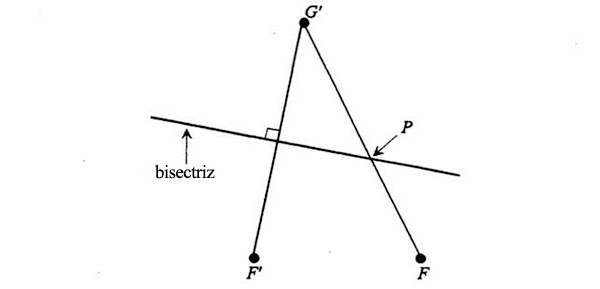
Hagamos ahora que el punto G’ del extremo del cordel se mueva trazando un círculo de radio constante, con el centro en F:
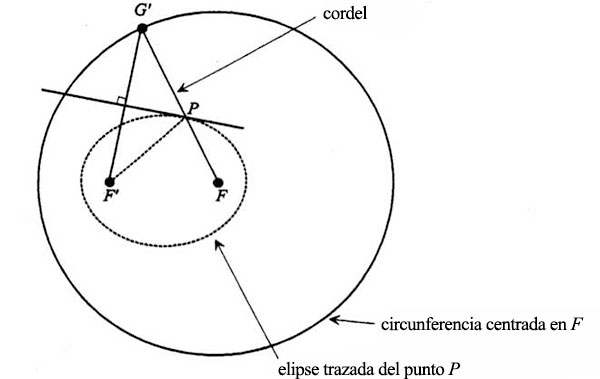
Así pues, el punto P, formado por el cruce de FG’ y la bisectriz perpendicular de F’G’, traza la misma elipse que se habría formado empleando el cordel con los extremos sujetos con tachuelas en F’ y F. Lo sabemos porque hemos probado ya que cuando P se determina de este modo, la distancia FPG’ (que va de F al círculo) es siempre igual a la distancia FPF’ (que construye la elipse):
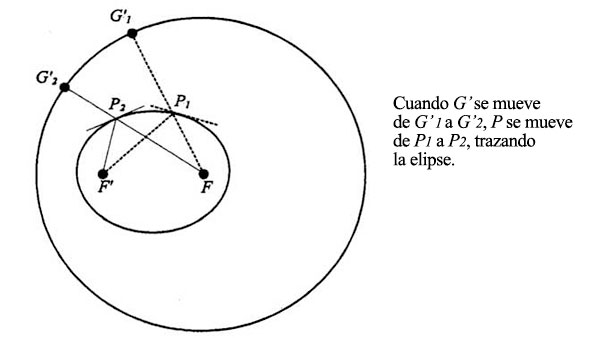
Así, por cada punto excéntrico interior a un círculo anda al acecho una elipse excéntrica. Sin embargo, aunque esto es muy interesante (y luego nos será muy valioso), no es la propiedad que queríamos probar.
Lo que queríamos probar es que la construcción de la elipse con tachuelas y cordel es equivalente a su propiedad de reflejar rayos luminosos de F a F’. Lo que tenemos por el momento es una elipse que obedece el método constructor de las tachuelas y el cordel (es decir, F’P + PF no varía en toda la longitud de la elipse), y la línea que refleja en el punto P y desvía hacia F’ la luz que llega de F con el ángulo de incidencia y el de reflexión iguales. Da la casualidad de que la línea de reflexión es la bisectriz perpendicular de F’G:
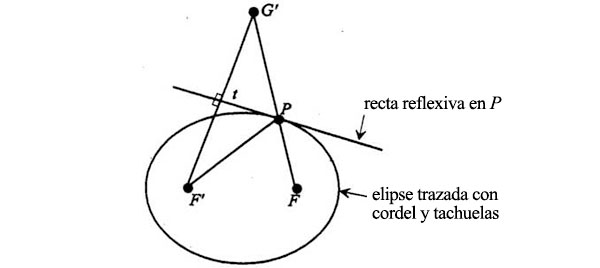
Lo único que nos queda por probar es que la línea de reflexión en el punto P es además tangente a la elipse en el punto P. Sabemos que todos los puntos de la elipse tienen las mismas propiedades de reflexión que una tangente que pase por ese punto. Así, si la línea de reflexión en P es también tangente a la elipse en P, la elipse reflejará la luz de F a F’ en cualquier punto P, y así se demuestra que las dos propiedades (método de tachuelas y cordel y luz refleja que va de un foco a otro) son equivalentes. La prueba se hace mostrando que, aunque el punto P está (por construcción) a la vez en la línea y en la elipse, todos los demás puntos de la línea quedarán fuera de la elipse. Es la propiedad característica de las tangentes a las curvas: que tocan la curva en un punto sin cortarla. Si la línea cortara la elipse en P, parte de la línea quedaría forzosamente dentro de la elipse:
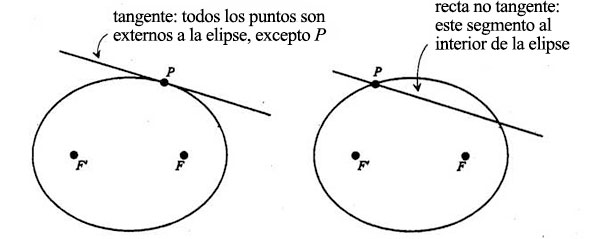
Volvamos a la construcción y tomemos cualquier punto de la línea que no sea P. Llamémosle Q y unámoslo a F’ y a G’:
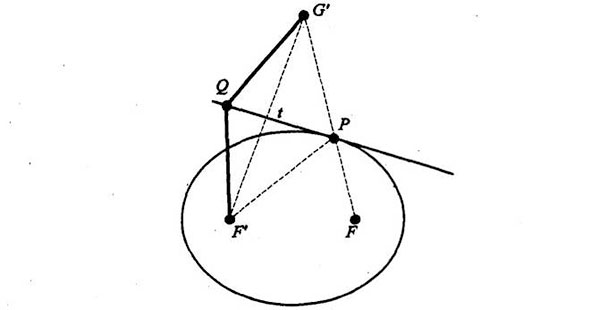
Se verá fácilmente que las distancias F’Q y G’Q son iguales (PQ es la bisectriz de F’G’, los triángulos F’tQ y G’tQ son congruentes, etc., QED). Tracemos ahora la línea QF:
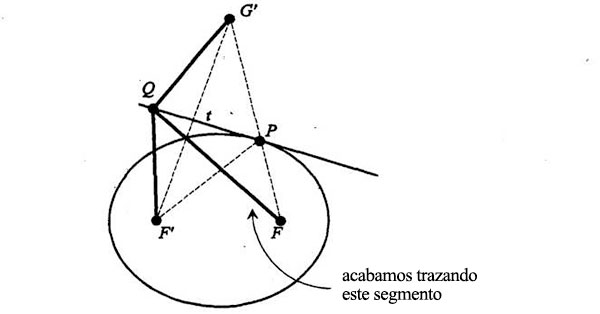
La distancia de F’ a Q y a F es igual a la distancia de G’ a Q y a F; lo sabemos porque sabemos que los primeros segmentos trazados (F’Q y G’Q) son iguales y que el segundo segmento trazado es el mismo en ambos casos (QF). Comparemos ahora las longitudes FQ + QG’ (líneas negras) con FP + PG’ (línea de puntos):
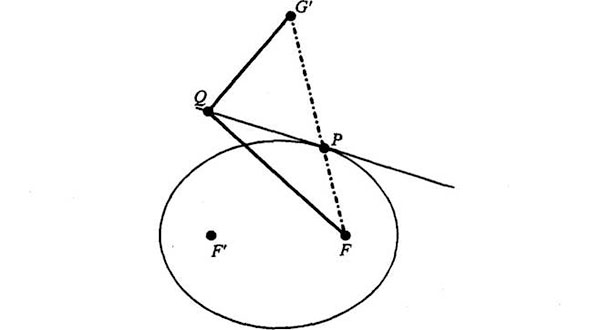
Evidentemente, FPG’ es más corta, porque es una línea recta, y la línea recta es la distancia más corta entre dos puntos. Pero acabamos de ver que las líneas negras G’QF del dibujo de arriba tienen la misma longitud que las líneas negras F’QF del dibujo de abajo, y las líneas de puntos también (ya lo vimos antes: la línea de puntos es la longitud del cordel):
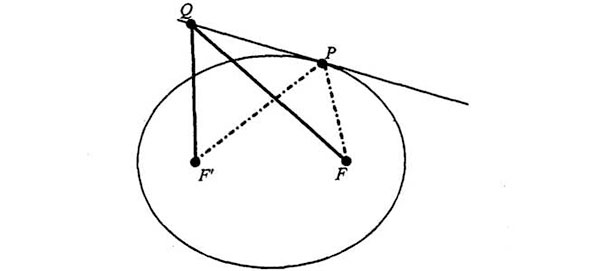
Hemos probado que las líneas negras son más largas que las de puntos. En otras palabras: si queremos llegar al punto Q con un cordel sujeto por los extremos con tachuelas en F’ y F, el cordel tendría que ser mayor que el que se necesitaba para llegar al punto P. Ya vimos antes que esto significa que todos los puntos así están fuera de la elipse. Así pues, la línea es tangente a la elipse en el punto P. QED.
Hablando de QED, hay algo muy interesante en este método de demostración cuando lo utiliza Feynman. Hemos visto en efecto que la trayectoria más corta de F’ a la tangente y de aquí a F es la que sigue la luz que se refleja en el punto P. Es un caso particular del principio de Fermat (la luz sigue siempre la trayectoria más rápida entre dos puntos) y está estrechamente relacionado con la concepción feynmaniana de la electrodinámica cuántica, que en inglés se conoce también por QED (quantum electrodynamics) y que le hizo ganar el Nobel. El principio de Fermat es un caso particular del principio de mínima acción.
De todos modos, Feynman nos ha contado ya todo lo que necesitábamos saber sobre la elipse. A continuación pasa a la dinámica, esto es, a las fuerzas y a los movimientos que resultan de ellas. El diagrama que Feynman dibujó en sus apuntes para la conferencia está copiado directamente de los Principia de Newton. Salta a la vista cuando cotejamos los dos diagramas:
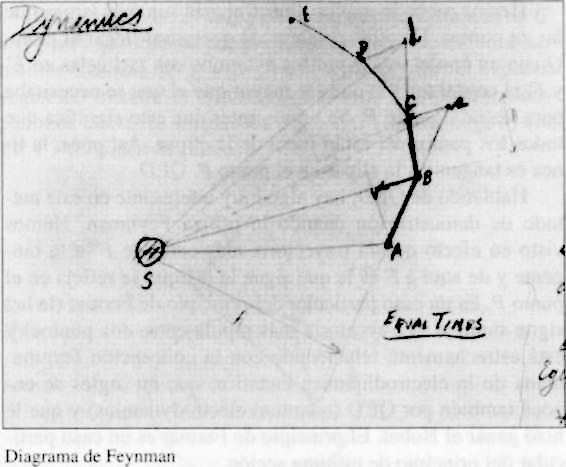
Diagrama de Feynman
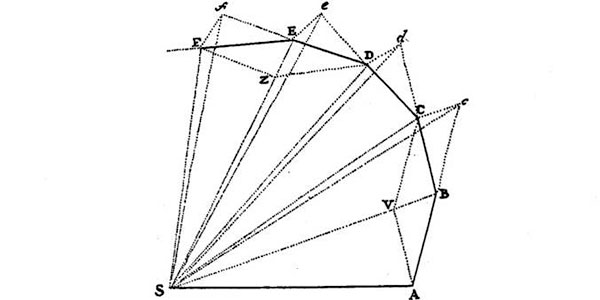
Diagrama de Newton
En el diagrama de Newton, S representa la posición del Sol (el centro inmóvil de fuerza), mientras que A, B, C, D, E y F son posiciones sucesivas, a intervalos de tiempo iguales, de un planeta en órbita alrededor del Sol. El movimiento del planeta es el resultado de una pugna entre la tendencia del planeta a moverse a velocidad constante en línea recta mientras no se ejerza ninguna fuerza sobre él (ley de inercia) y el movimiento debido a la fuerza que se ejerce sobre el planeta, es decir, la tracción gravitatoria del Sol. La verdad es que la combinación de estos efectos produce una órbita de curva lisa, pero para satisfacer las necesidades del análisis geométrico del siglo XVII, Newton los representó con una serie de segmentos rectos debidos a la inercia, interrumpidos por cambios bruscos de dirección debidos a las impulsivas (esencialmente instantáneas) intervenciones de la fuerza solar. Así, la primera etapa del diagrama comienza de este modo:
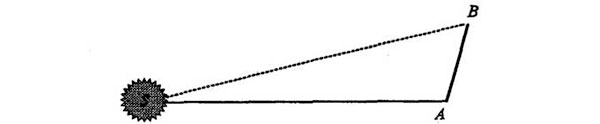
En determinado intervalo de tiempo el planeta se moverá de A a B si no se ejerce sobre él ninguna fuerza. En el siguiente intervalo de igual duración, si no se ejerciera ninguna fuerza sobre él, el planeta recorrería una distancia igual siguiendo una trayectoria recta, Bc:
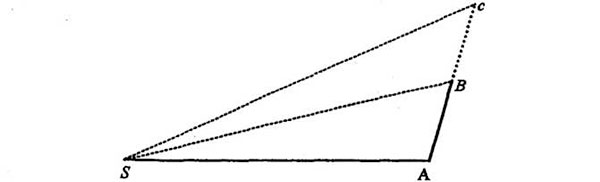
Sin embargo, la fuerza del Sol (que se ejerce de manera continua) se representa mediante un impulso ejercido en el punto B, que se traduce en un componente de movimiento dirigido hacia el Sol, BV:
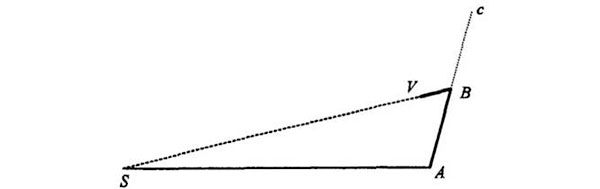
El movimiento que tendría el planeta sin la fuerza, Bc, y el movimiento debido a la fuerza, BV, están contenidos en un paralelogramo; su diagonal es el movimiento «real»:
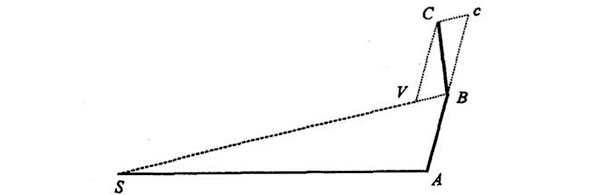
Así, el planeta sigue «realmente» la trayectoria ABC. Adviértase que Cc no se dirige hacia el Sol. Es rigurosamente paralela a VB, que sí se dirige hacia el Sol. Por cierto, todos estos puntos están en un plano; tres puntos cualesquiera. S, A, B, definen un plano. El segmento BV se encuentra en el mismo plano, porque está en la línea BS. El segmento Bc está en el plano porque prolonga la línea AB. La línea BC está en el plano porque es la diagonal del paralelógramo formado por BVy Bc. El mismo procedimiento se repite en cada punto, de modo que la siguiente etapa tiene este aspecto:
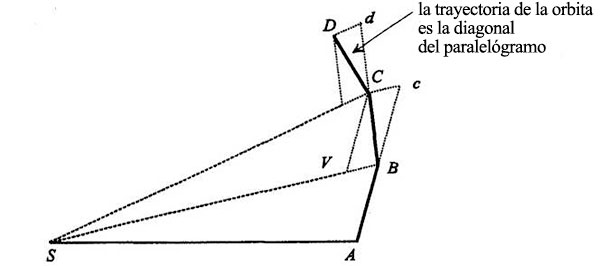
Y así sucesivamente. Al final, Newton repite el mismo análisis para intervalos de tiempo decrecientes, y la trayectoria resultante, ABCD…, se aproxima arbitrariamente a una órbita lisa, sobre la que se ejercen a la vez y de manera continua la inercia y la fuerza del Sol. La órbita está siempre en un solo plano.
Antes de reducir el intervalo de tiempo, Newton (y Feynman) pasa a probar que la órbita del planeta barre áreas iguales en tiempos iguales. En otras palabras: el triángulo SAB barrido por el planeta en el primer intervalo, tiene la misma área que el triángulo SBC, barrido en el segundo intervalo de igual duración, y así sucesivamente. La primera etapa, sin embargo, nos da a entender que el triángulo SAB tiene la misma área que SBc, el triángulo que se habría barrido en el segundo intervalo si el Sol no hubiera ejercido ninguna fuerza. He aquí el aspecto de los tres triángulos:

El área de un triángulo es igual a la mitad de su base por su altura. Una forma de averiguar el área del triángulo SAB sería tomar SA por base, en cuyo caso la altura sería la perpendicular que podría trazarse entre la prolongación de SA y el punto más alto del triángulo:
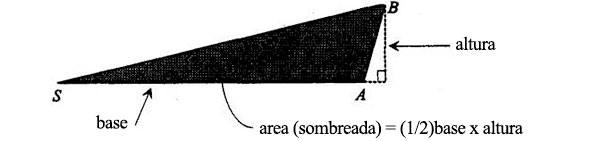
Obtenemos el mismo resultado si tomamos SB por base y trazamos la altura así:
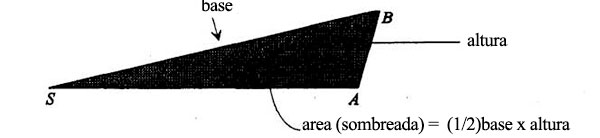
Comparemos ahora esta área con el área de SBc:
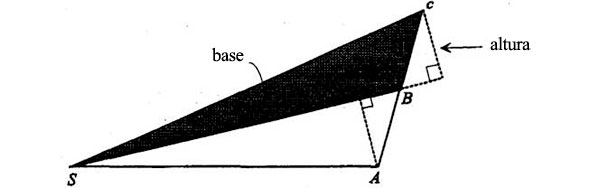
donde SB es la base y la altura se traza como se ha visto. Fijémonos en el diagrama que resulta del trazado de la altura de los dos triángulos:
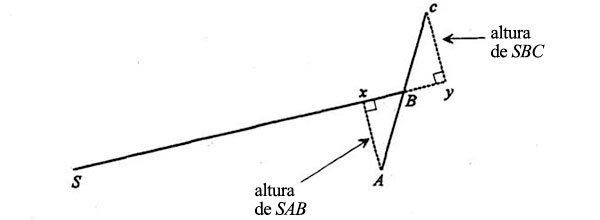
Llamemos por el momento x e y a los rincones donde se han formado ángulos rectos. Los triángulos ABx y cBy son congruentes porque tienen un lado y dos ángulos iguales. Los lados iguales son AB y Bc (son iguales porque son las distancias que el planeta recorrería en tiempos iguales si no sintieran la fuerza del Sol), y los ángulos iguales son los ángulos rectos (AxB y Byc) y los ángulos opuestos formados por el cruce de las dos rectas xBy y ABc. Puesto que los triángulos son congruentes, las dos alturas, Ax y cy, son iguales; y como los triángulos SAB y SBc tienen la misma base (SB) e igual altura, sus áreas son iguales. QED[2].

A continuación (siguiendo a Newton y a Feynman) demostramos que el área de SBc (líneas negras) es también igual al área de SBC (líneas discontinuas):

Los dos triángulos tienen la misma base, SB. La altura de SBC es la perpendicular que se traza desde c hasta la prolongación de SB:
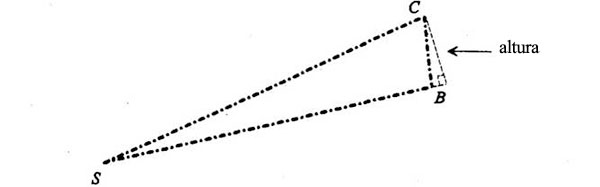
La altura de SBc es la perpendicular que se traza desde c hasta una prolongación más larga de SB:
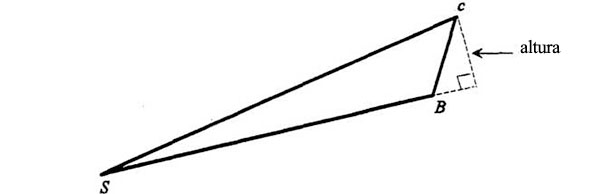
Volvamos a juntar los dos diagramas y recordemos que Cc es rigurosamente paralela a SB:
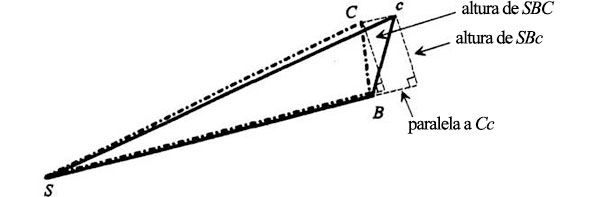
Las dos alturas son perpendiculares que unen dos paralelas y, por tanto, son iguales. Así pues, los triángulos SBC y SBc tienen la misma base e iguales alturas, y por lo tanto la misma área. Una vez más, QED.
Aparte de ser una geometría preciosa, la última prueba es muy importante en física. Si no se ejerciera ninguna fuerza en absoluto, la trayectoria del planeta sería Bc. Pero hay una fuerza, dirigida hacia S. Esta fuerza hace que se cambie la trayectoria Bc por BC, pero no cambia las áreas barridas en un tiempo dado. Tiempo después de Newton (pero mucho antes de Feynman) se averiguó que el área en cuestión era proporcional a una cantidad llamada momento angular. Dicho en el lenguaje de la última física, hemos probado que una fuerza ejercida sobre un planeta y dirigida hacia S no cambia el momento angular del planeta medido en relación a S. Aunque Newton no utilizó la expresión «momento angular», es evidente que entendió el significado de esta cantidad y que sólo podría cambiarse mediante una fuerza ejercida en una dirección que no fuera el centro S.
En cualquier caso, hemos demostrado ya que el área de SAB es igual al área de SBc, y que el área de SBc es igual al área de SBC. De aquí se sigue que SAB y SBC tienen la misma área. Si volvemos al primer diagrama de esta última serie.
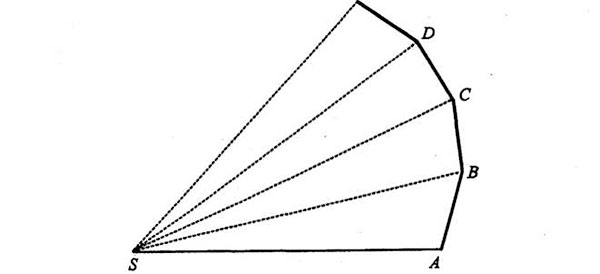
Salta a la vista que podríamos aplicar los mismos argumentos a los triángulos siguientes, SCD, SDE, etc. Son los triángulos barridos por el planeta en tiempos iguales. De este modo hemos probado la segunda ley kepleriana del movimiento planetario: que un planeta barre áreas iguales en tiempos iguales.
Ya que sabemos adonde hemos llegado, vale la pena volver atrás y ver cómo hemos llegado. ¿Qué había que saber en concreto de dinámica (es decir, de las fuerzas y de los movimientos que generan) para llegar tan lejos?
La respuesta es la siguiente: hemos aplicado la primera ley de Newton (ley de la inercia), la segunda ley de Newton (cualquier cambio de movimiento se verifica en la dirección de la fuerza ejercida) y la idea de que la fuerza gravitatoria sobre el planeta se dirige hacia el Sol. Nada más. Por ejemplo, no hemos aplicado la idea de que la fuerza de la gravedad es inversamente proporcional al cuadrado de la distancia. Así pues, el carácter «inverso cuadrático» no tiene nada que ver con la segunda ley de Kepler. Cualquier otra fuerza produciría el mismo resultado, con la única condición de que se dirigiera hacia el Sol. Lo que hemos aprendido es que si la primera y segunda leyes de Newton son ciertas, la observación kepleriana de que los planetas barren áreas iguales en tiempos iguales significa que la fuerza de gravedad ejercida sobre el planeta se dirige hacia el Sol.
Podríamos preguntarnos en qué momento exacto hemos aplicado la primera y segunda leyes de Newton. Aplicamos la primera al decir que el planeta se movería de A a B y de B a c si no se ejerciera ninguna fuerza sobre él, y la segunda al decir que el cambio en el movimiento, BV debido a la fuerza solar, se dirigía hacia el Sol. A propósito, también hemos utilizado el primer corolario newtoniano de estas leyes: que el movimiento neto producido por ambas tendencias en el intervalo de tiempo lo da la diagonal del paralelogramo de los movimientos correspondientes que se habrían producido:
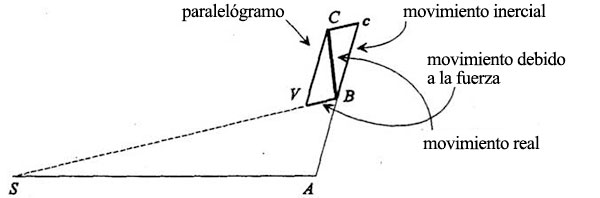
En este punto de la charla, dice Feynman que «la prueba que acabáis de ver es una reproducción exacta de la que figura en los Principia Mathematica de Newton», pero añade que no pudo ir más allá con la argumentación newtoniana y que «inventó» el resto de la prueba de la ley de las elipses. Antes de pasar a la prueba de Feynman, introduzcamos otro argumento que baraja al principio de su conferencia: ¿dónde entra la ley de la inversa del cuadrado?
La proporcionalidad inversa al cuadrado de la distancia (en lo sucesivo R-2) de la gravedad se deduce de la tercera ley de Kepler, que dice que el tiempo que tarda un planeta en completar una órbita (es decir, un año de la vida del planeta) es proporcional a la potencia 3/2 de la distancia planetaria al Sol. En realidad, puesto que las órbitas de los planetas son elipses con el Sol en un foco, un planeta dado no siempre está a la misma distancia del Sol:
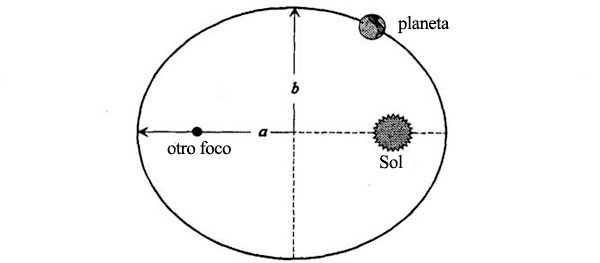
La distancia desde el centro de la elipse (no desde el Sol, que es excéntrico) hasta el punto más lejano de la elipse es el semieje mayor, y lo llamaremos a (el eje más corto, que llamaremos b, es el semieje menor). El semieje mayor se denomina así porque es la mitad del eje más largo de la elipse. La tercera ley de Kepler dice que el tiempo que tarda un planeta en completar una órbita es proporcional a la potencia 3/2 de a, el semieje mayor.
Para asegurarnos de que el significado de esta afirmación está claro, imaginemos un sol alrededor del cual evolucionan dos planetas (o un planeta con dos satélites a su alrededor, ya que se seguiría la misma ley):
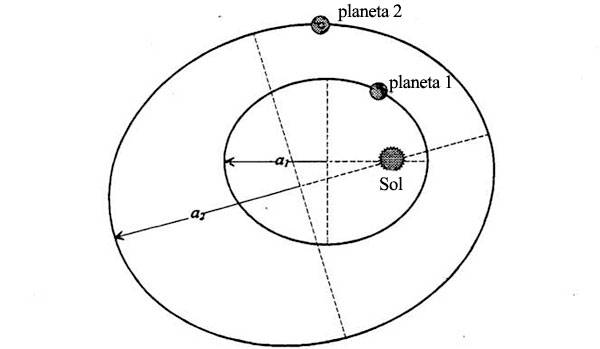
Las flechas señalan las distancias desde los centros de las dos elipses hasta el punto más lejano de cada una. Estas distancias son los semiejes mayores, a1 y a2. Supongamos ahora que a2 es dos veces mayor que a1. La tercera ley kepleriana dice entonces que el tiempo que tarda el planeta 2 en completar una órbita es mayor que el periodo orbital del planeta 1 en un factor 2 elevado a la potencia 3/2; es decir; partiendo de 2, lo elevamos al cubo y obtenemos 8, luego sacamos la raíz cuadrada de 8 y obtenemos 2,83. El año del planeta 2 es 2,83 veces más largo que el del planeta 1.
Esta ley sería cierta, y la conducta de todos los planetas sería mucho más sencilla (aunque mucho menos interesante), si Platón hubiera tenido razón y las órbitas planetarias fueran círculos perfectos. Un círculo puede considerarse una elipse particularmente sencilla.
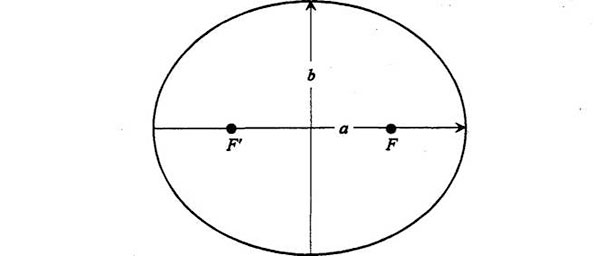
Partiendo de una elipse se puede construir un círculo desplazando los dos focos, F’ y F, hacia el centro:
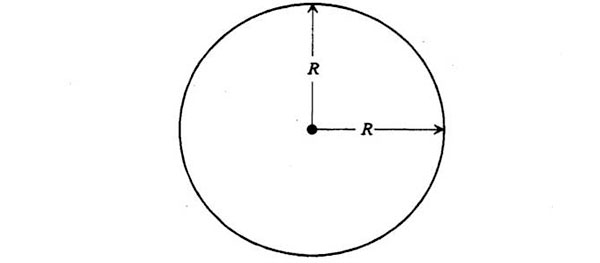
El semieje mayor a tendrá así la misma longitud que el semieje menor b, y podremos llamar a los dos R. Adviértase que, puesto que un círculo es una elipse (un caso especial de elipse, para ser exactos), las leyes keplerianas permiten que las órbitas planetarias sean círculos, pero no lo exigen. En realidad, las órbitas de los planetas de nuestro sistema solar son casi (pero no totalmente) circulares, pero otros objetos que obedecen las leyes keplerianas (el cometa Halley, por ejemplo) tienen órbitas que distan mucho de la circularidad.
Volviendo a nuestro tema, nos gustaría demostrar que la tercera ley de Kepler significa que la fuerza gravitatoria del Sol disminuye con el cuadrado de la distancia a este. Siguiendo a Feynman, simplificaremos el argumento suponiendo que las órbitas planetarias son en realidad círculos. El tiempo que se tarda en completar una órbita lo llamaremos T. Así, la tercera ley kepleriana dice que T~R3/2 (léase «T es a, o es proporcional a, R3/2), donde R es la distancia al Sol. ¿Cómo se relaciona esto con la ley R-2?
Al igual que Feynman, somos incapaces de seguir aquí la argumentación de Newton, y como también la argumentación de Feynman es algo críptica, formularemos otra por nuestra cuenta. Esta argumentación tiene por objeto no sólo explicar la tercera ley kepleriana y la ley newtoniana R-2, sino también introducir algunas técnicas geométricas que necesitaremos en la apoteosis final.
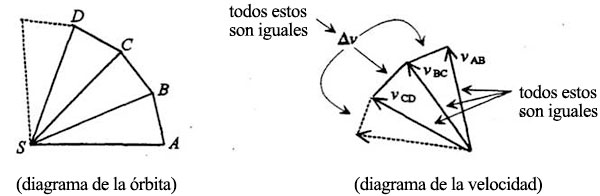
El diagrama que nosotros (y Feynman) hemos copiado de Newton muestra posiciones sucesivas de un planeta en el espacio:
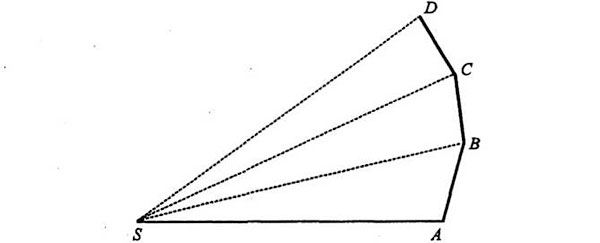
Empleando tiempos iguales, el planeta se mueve de A a B, de B a C, etc. También podemos representar en el diagrama la velocidad del planeta durante cada segmento (debido a la inercia, el planeta pasa de A a B a velocidad constante, de B a C a velocidad constante, etc.). La velocidad puede representarse por una flecha que apunte en la dirección del movimiento (recordemos que en física, velocidad significa rapidez y dirección):
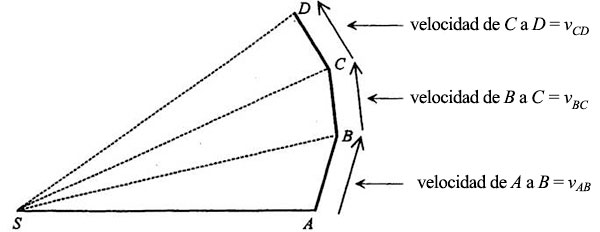
No hay razón para que las flechas de la velocidad se tracen junto al correspondiente segmento de la órbita; las podemos poner juntas al lado, con un origen común:
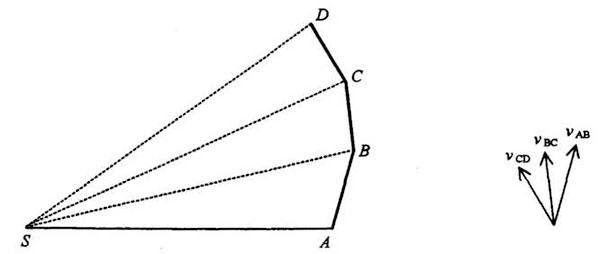
El nuevo diagrama es un diagrama de velocidades y no de posiciones. La dirección de la flecha señala la dirección del movimiento del planeta, de modo que vAB tiene que ser paralela a AB,
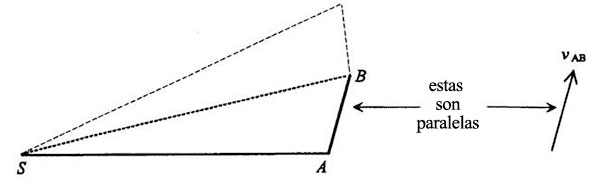
y la longitud de la flecha es proporcional a la aceleración. En otras palabras, cuanto más aprisa se mueva el planeta en ese tramo, más larga será la flecha. Si el planeta se mueve en el segmento de B a C más despacio que de A a B, podríamos dibujar un diagrama así:
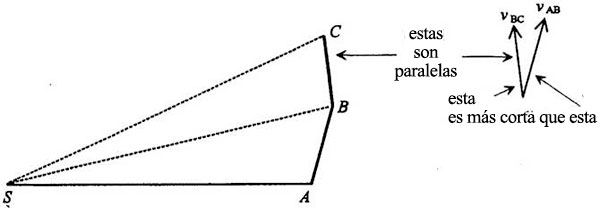
Sin embargo, el cambio de velocidad, según la segunda ley de Newton, ha de darse en dirección al Sol, en el punto B, donde la fuerza de tracción cambia la velocidad:

Si vAB es la velocidad antes del cambio, y vBC es la velocidad después del cambio,

entonces el cambio de velocidad es también una flecha

que debe apuntar en la dirección de la línea de B a S:
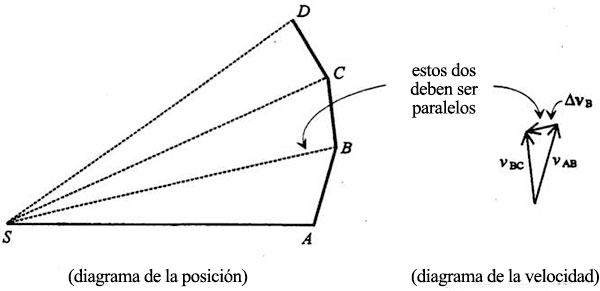
El cambio de velocidad en el punto B ΔvB, se hace pues en la dirección de la tracción solar y es además proporcional a la magnitud de la fuerza. Si la tracción solar fuera el doble de fuerte en el punto B, ΔvB sería dos veces mayor. Tal es el significado de la segunda ley de Newton. El cambio de velocidad en cada uno de los puntos (imaginarios) A, B, C… del diagrama de Newton depende también de los intervalos de tiempo (iguales) entre esos puntos. Newton supuso que se calculaba la misma órbita reduciendo los intervalos a la mitad para aproximarse a la curva lisa real que describe la órbita en el espacio. Si se hace lo mismo en todos los demás casos y los tiempos se reducen a la mitad, cada cambio de velocidad se tendrá que dividir por dos igualmente, pero habrá el doble de cambios:
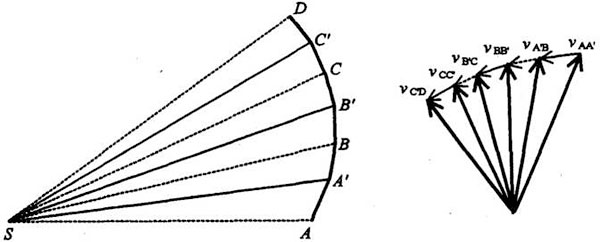
Es la misma órbita, originada por la misma fuerza que en el diagrama anterior. La fuerza es proporcional al cambio de velocidad en cada punto (reducido a la mitad en este diagrama) dividido por el tiempo (también reducido a la mitad): F ~ Δv/Δt, donde F es la fuerza y Δt el tiempo. La fuerza, en este diagrama, es la misma que la del diagrama anterior.
Como hemos visto, hay una correspondencia real de las direcciones entre el diagrama de posiciones y el de velocidades. Sin embargo, el tamaño de un diagrama no guarda ninguna relación con el tamaño del otro. Aunque aumentáramos el doble el diagrama de velocidades (operación que no modificaría ninguna dirección), seguiría siendo correcto:
Busquemos el ejemplo concreto más sencillo que se nos ocurra. Supongamos que la órbita fuera un círculo de radio R. El diagrama de Newton sería entonces como sigue:
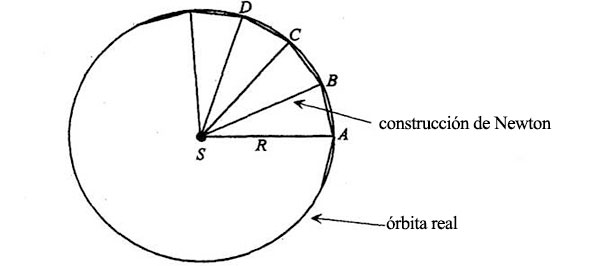
Todas las distancias (SA, SB, SC, etc.) serían iguales a R, el radio del círculo. Además, los cambios de velocidad debidos a la fuerza de tracción en A, B, C, D, etc., serían iguales al margen de que la fuerza solar dependa de la distancia, dado que todos los puntos en cuestión están a la misma distancia del Sol. Se sigue de aquí que las aceleraciones en AB, BC, etc., tienen que ser iguales, y que las longitudes de los segmentos AB, BC, etc., también son iguales. Es la única forma de que el planeta siga siempre la misma trayectoria, una y otra vez. En otras palabras: la figura dibujada por Newton es un polígono regular, una figura con los lados y los ángulos iguales, inscrito en un círculo, que es la órbita real.
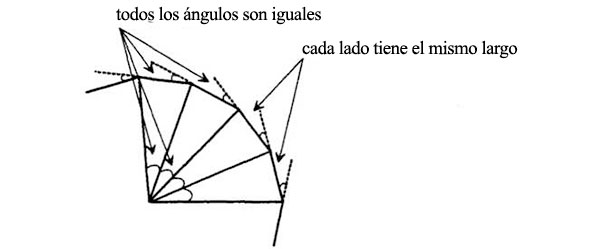
Los polígonos regulares son el triángulo equilátero, el cuadrado, el pentágono, el hexágono, etc., Cuantos más lados tenga un polígono regular, más se parecerá a un círculo. Newton imaginó que empleaba tiempos menores en su diagrama, que obtenía un polígono regular con más lados
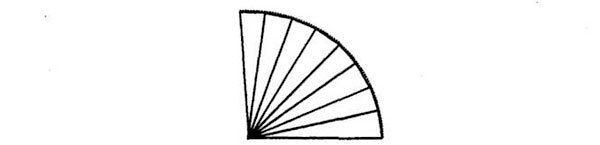
y que se iba aproximando al círculo real, en el infinito, hasta obtener la órbita real.
En el diagrama de velocidades de una órbita circular, todas las velocidades tienen la misma longitud y están separadas por los mismos ángulos, de modo que todos los cambios Δv son iguales:
Así, el diagrama de velocidades es también un polígono regular, que además se convierte en círculo cuando la órbita se vuelve circular (después de llegar al infinito):
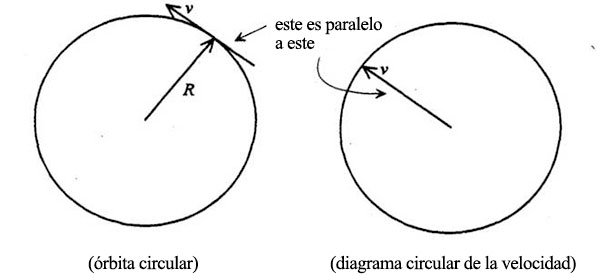
El radio del círculo, en el diagrama de velocidades, es v, la rapidez uniforme del planeta en toda la órbita. Esta rapidez viene dada por la distancia que recorre el planeta dividida por el tiempo que tarda. La distancia recorrida por el planeta es la longitud de la circunferencia orbital, es decir, 2πR, y el tiempo que tarda el planeta en recorrerla es lo que hemos llamado T, el periodo de la órbita. Por lo tanto, v es igual a 2πR/T.
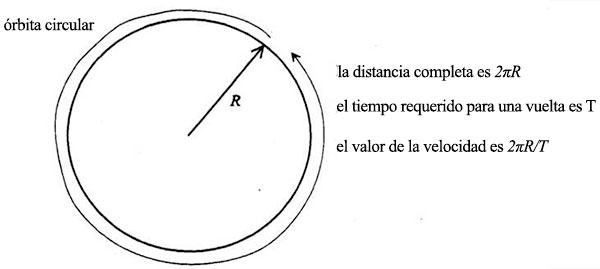
Cada vez que el planeta completa una órbita, la flecha de la velocidad recorre igualmente un ciclo completo:
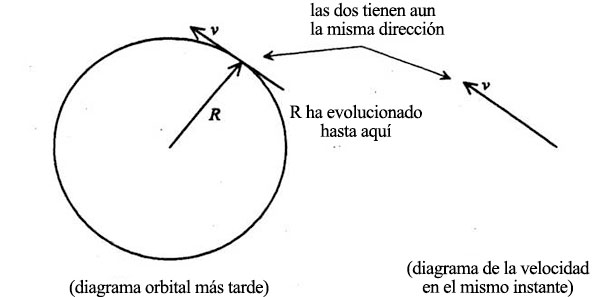
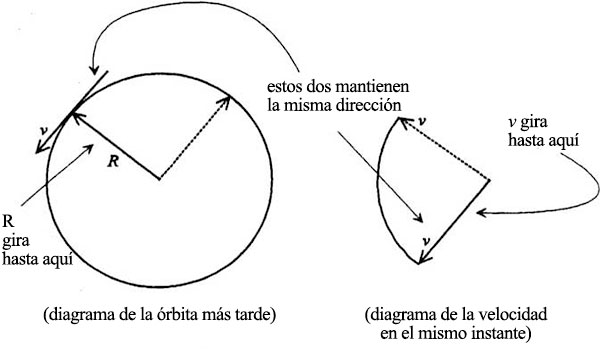
Cuando la flecha de la velocidad traza un círculo completo, la punta de la fecha recorre una distancia dada por 2πv:
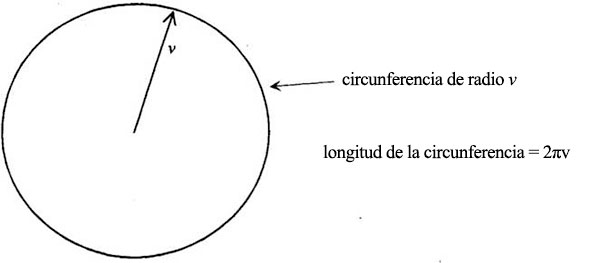
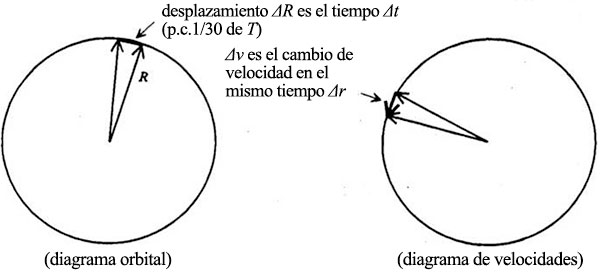
Recordemos que el cambio de velocidad viene dado por el movimiento de la punta de la flecha de la velocidad:
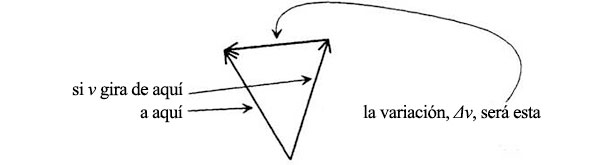
Pongamos que el círculo se ha dividido en 30 partes y que cada una representa 1/30 del periodo orbital T.

La fuerza, como hemos visto, es proporcional a Δv/Δt, donde Δv es el cambio de velocidad, igual a 1/30 del perímetro del círculo de velocidades, y Δt el tiempo empleado, 1/30 de T. Evidentemente, 1/30 del perímetro dividido por 1/30 del tiempo es lo mismo que dividir todo el perímetro por todo el tiempo. Así, Δv/Δt es igual al perímetro (o circunferencia, es decir,2πv) dividido por el tiempo T.

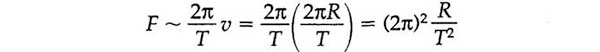
Esto significa, por ejemplo, que si hubiera un planeta que distara el doble del Sol (que estuviera a una distancia 2R en vez de R) y que completara su órbita en el mismo tiempo, entonces la fuerza de tracción del Sol, que es proporcional a R, tendría que ser el doble de intensa. Sin embargo, los planetas no suelen hacer estas cosas. Hemos visto que si un planeta estuviera en 2R, su tiempo sería 2,83T. Esto viene dado por la tercera ley de Kepler:
T~ R3/2 (el periodo de un planeta es proporcional a su distancia del Sol elevada a la potencia 3/2)
La fuerza F es proporcional a la distancia R dividida por T2. Ahora bien, T2 es el cuadrado de R3/2 , y (R3/2)2=R3. Luego la fuerza es proporcional a la distancia R dividida por el cubo de la distancia R3. Pero R partido por R3 es lo mismo que 1 partido por R2. La fuerza es proporcional a 1 partido por el cuadrado de la distancia al Sol. He aquí la conexión que buscábamos para la ley de la fuerza proporcional a R-2.
Antes de continuar, este es un buen sitio para detenernos un momento y ver de dónde venimos y adonde vamos.
Kepler nos ha dado tres leyes y Newton otras tres. Las leyes de Kepler, sin embargo, son muy diferentes de las de Newton. Las leyes keplerianas son generalizaciones de observaciones celestes. Lo que hacen es ajustar una curva, como diríamos hoy. Kepler tomaba unos cuantos puntos en el espacio (las posiciones observadas del planeta Marte en momentos conocidos) y decía: «¡Ajá! Todos estos puntos están contenidos en una línea curva llamada elipse». Esta descripción trivializa la obra de toda la vida de uno de los grandes genios de la historia, pero es bastante exacta. Es la naturaleza básica de las tres leyes de Kepler.
Las leyes de Newton son muy distintas. Son verdaderas hipótesis sobre la naturaleza profunda de la realidad física: las relaciones entre materia, fuerza y movimiento. Si la conducta deducida de estas hipótesis se observa en la naturaleza, las hipótesis pueden ser ciertas y, si tal es el caso, entonces hemos visto el alma de la naturaleza, o la mente de Dios, según el gusto metafórico de cada cual. En el importantísimo terreno de los movimientos planetarios, la prueba de que las hipótesis newtonianas son ciertas es que den lugar a las leyes de Kepler, las cuales resumen con admirable precisión gran cantidad de datos astronómicos.
La conexión entre leyes newtonianas y leyes keplerianas es más compleja, pues aún nos falta un eslabón. Para determinar los movimientos planetarios que ordenaban sus leyes, Newton tuvo que descubrir la naturaleza de una fuerza concreta, la fuerza de gravedad. Para ello recurrió a la segunda y tercera leyes de Kepler. Luego, una vez deducida su naturaleza estuvo en situación de demostrar que la gravedad, dirigida por sus leyes, explicaba el resto de la observación kepleriana, la ley de las elipses. Esta es la serie lógica de los acontecimientos tal como la presenta Newton en los Principia. Ahora estamos en un punto de su argumentación en el que hemos deducido la naturaleza de la gravedad recurriendo a las leyes newtonianas y a la segunda y tercera leyes de Kepler. Repasemos cómo lo hemos hecho antes de que se levante el telón y empiece el acto final, la primera ley de Kepler, la ley de las elipses.
Aplicada a los movimientos planetarios, la primera ley de Newton, la ley de la inercia, dice que si sobre un planeta no se ejerce ninguna fuerza, entonces permanecerá en reposo si ya lo estaba o, si estaba en movimiento, viajará eternamente en línea recta a velocidad constante. Por qué es así es un misterio, aunque Newton se refiere a veces al mecanismo llamándolo «fuerza interior» del planeta. Lo que importa de las leyes de Newton, sin embargo, no es por qué son verdaderas, sino sólo si lo son.
La segunda ley de Newton dice que si se ejerce una fuerza F sobre un planeta, su efecto lo desvía de la línea recta que habría seguido a velocidad constante en virtud de la inercia. En concreto, si se ejerce una fuerza durante un tiempo dado Δt, se produce un cambio de velocidad (es decir, una desviación de la trayectoria inercial) Δv, proporcional a la fuerza y en la misma dirección de la fuerza. Esto significa que si ejerce una fuerza doble (2F), se producirá un cambio de velocidad doble (2Δv). También significa que 2Δv puede obtenerse ejerciendo la misma fuerza el doble de tiempo (2Δt). Algebraicamente lo escribiríamos Δv ~ FΔt. Lo cual significa a su vez que, si la fuerza apunta al Sol, el cambio de velocidad será hacia el Sol.
La tercera ley de Newton dice que las fuerzas que se ejercen mutuamente las partes de un planeta no generan ninguna fuerza sobre el planeta entero, de modo que para analizar los movimientos planetarios podemos olvidamos del hecho de que los planetas son cuerpos complejos grandes y tratarlos como si su masa estuviera concentrada en un punto matemático situado en su centro.
La imagen que bosqueja Newton a continuación es la de que el Sol, hipotéticamente inmóvil, ejerce sobre los planetas una fuerza, la gravedad, que los desvía de las rectas inerciales que de otro modo seguirían hacia las órbitas que describen en la realidad.
Una propiedad de estas órbitas reales, descrita por la segunda ley de Kepler, es que la línea hipotética que une el Sol con un planeta barre áreas iguales en tiempos iguales mientras el planeta evoluciona en su órbita. Newton demuestra, como hemos hecho ya nosotros, que el sentido de la observación kepleriana es que la gravedad se ejerce en la dirección de la línea que une el Sol con el planeta.
Otra propiedad del movimiento planetario es que cuanto más lejos esté del Sol la órbita de un planeta, más despacio la recorrerá éste. En concreto, el tiempo que tarda el planeta en completar una vuelta aumenta con la potencia 3/2 de la distancia de la órbita al Sol. Newton demuestra, como lo hemos hecho ya nosotros, que para generar este resultado la fuerza desviadora de los planetas debe disminuir proporcionalmente al cuadrado de la distancia al Sol. En otras palabras, si un planeta está el doble de lejos del Sol, la fuerza gravitatoria que lo mantiene en su órbita será cuatro veces más débil.
Adviértase que la segunda ley de Kepler (áreas iguales) trata del movimiento de un solo planeta en diferentes partes de la órbita, mientras que la tercera ley compara las órbitas de diferentes planetas. Es extraño pero cierto que la masa de los planetas no tenga ninguna influencia en la rapidez de sus trayectorias respectivas. Un año (una órbita completa) del planeta Tierra es más corto que un año del planeta Júpiter sólo en proporción a la potencia 3/2 de sus distancias respectivas al Sol, y eso que la masa de Júpiter es más de trescientas veces la de la Tierra.
En cualquier caso, sabemos ya que la fuerza ejercida por la gravedad solar sobre un planeta se dirige hacia el Sol, y que su intensidad disminuye proporcionalmente al cuadrado de la distancia al Sol. Hemos empleado para averiguarlo la segunda y tercera leyes de Kepler. La triunfante hazaña final será demostrar que una fuerza como la gravedad, comportándose de acuerdo con las leyes de Newton, hace elípticas las órbitas planetarias.
En la conferencia, éste es el punto en el que Feynman no puede seguir la argumentación de Newton y decide inventar otra. Su primera desviación de Newton se parece mucho a un movimiento brillante e inesperado de un maestro de ajedrez. En vez de dividir la órbita en segmentos imaginarios que representen intervalos de tiempo iguales, como hace Newton, Feynman divide la órbita en segmentos que formen ángulos iguales con centro en el Sol. Tendremos que hacer algunos dibujos para ver qué significa esto.
Recordemos el diagrama de los Principia que Feynman copió en sus apuntes para la conferencia:
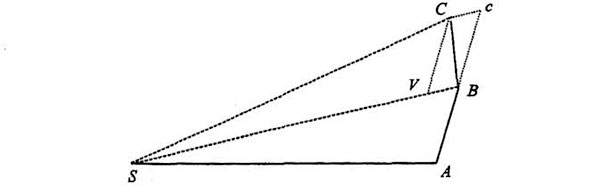
En un tiempo dado, si el Sol no ejerciera ninguna fuerza un planeta se trasladaría de A a B. El tiempo podría ser, por ejemplo, un segundo, un minuto o un mes. En el siguiente intervalo recorrería una distancia igual de B a c. Pero la fuerza del Sol produce una tracción en B que obliga a un desplazamiento en dirección al Sol igual a BV. Durante el segundo intervalo el planeta combina realmente la trayectoria Bc exigida por la inercia, y la trayectoria BV, exigida por la gravedad solar: el planeta sigue la diagonal del paralelo gramo formado por los dos movimientos y llega a C. Ya demostramos que los triángulos barridos en tiempos iguales, SAB y SBC, tienen áreas iguales. Newton calcula así la órbita como una serie de puntos equidistantes en el tiempo (A, B, C…), en cada uno de los cuales el planeta se desvía de la recta inercial en virtud del tirón instantáneo del Sol. Cuanto menores sean los tiempos, más frecuentes serán los tirones solares y más se parecerá la trayectoria a la órbita real, que es una curva lisa, ya que la gravedad solar tira continuamente del planeta. La órbita lisa del final conserva la propiedad que nosotros (y Newton y Feynman) hemos demostrado en el caso de la órbita esquemática: que barre áreas iguales en tiempos iguales, lo que significa que el planeta se mueve más aprisa cuando está más cerca del Sol.
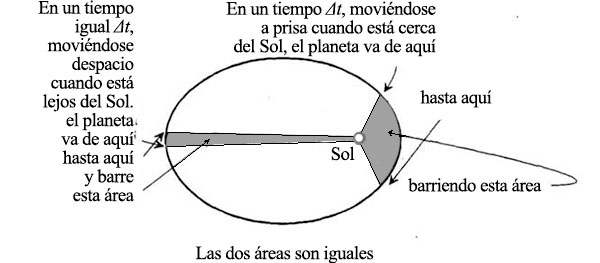
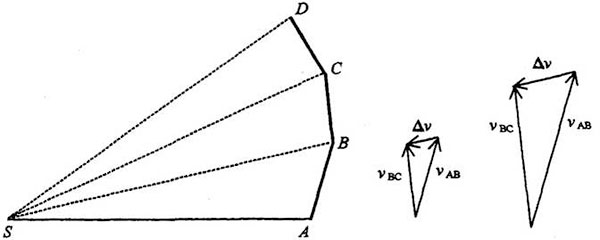
Feynman ha empleado el mismo argumento, tomándolo directamente de Newton, para probar esta ley de las áreas iguales. Ahora, sin embargo, prefiere dividir la órbita en ángulos iguales y no en áreas iguales.
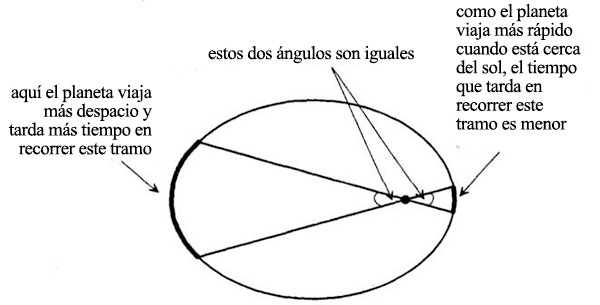
Los dos segmentos de la órbita que acabamos de ver tienen ángulos iguales, pero barren áreas diferentes y por lo tanto no tardan lo mismo. La ley dice que el planeta barre áreas iguales en tiempos iguales. Esto significa que si barre la mitad del área, tarda la mitad de tiempo, es decir:
Δt ~ (área barrida)
Representemos provisionalmente estos segmentos equiángulos en un diagrama newtoniano en el que el planeta tiene movimientos inerciales en línea recta, jalonados por cambios de velocidad causados por la gravedad. Para simplificar las cosas, dibujemos directamente los cambios de velocidad, Δv, en el diagrama de la órbita:
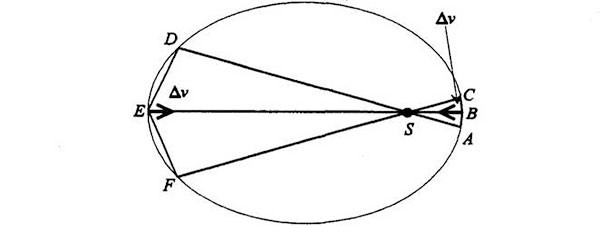
En el lado orbital más cercano al Sol, el planeta se desplaza de A a B, se desvía Δv a causa del Sol y sigue de B a C. En el otro extremo de la órbita, el planeta se desplaza de D a E, sufre un tirón equivalente a Δv y sigue de E a F.
Sabemos que el planeta es más rápido en BC que en EF. Para ver cuánto más tenemos que comparar el área de los triángulos SBC y SEF porque los tiempos son proporcionales a las áreas barridas. Recordemos que los dos triángulos tienen el mismo ángulo central en S. Dando la vuelta a SEF y superponiéndolo a SBC vemos que:
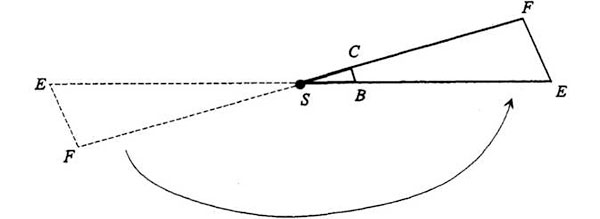
El área de cada triángulo es 1/2 (base) x (altura). Además, son triángulos semejantes. Esto significa que si la base del triángulo mayor mide el doble que la base del menor, la altura debe medir también el doble; en tal caso, el área del triángulo mayor rebasaría al menor en 2 x 2 = 4. La norma general es que el área es proporcional al cuadrado de la distancia al Sol[3]. Así, el tiempo invertido en recorrer una parte cualquiera de la órbita es proporcional al área barrida, que es proporcional al cuadrado de la distancia al Sol. He aquí una comparación de la división de la órbita en segmentos, según Newton y según Feynman:
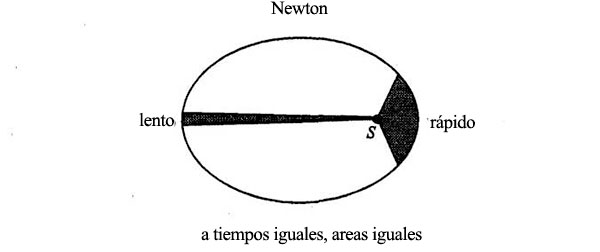
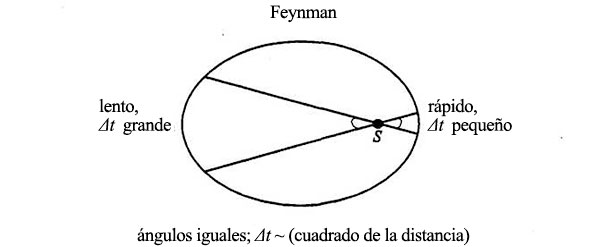
Algebráicamente, Δt ~ R2 en el diagrama de Feynman, donde R es la distancia del planeta al Sol. Pero sabemos además que la fuerza solar disminuye con la distancia, según la ley de la inversa del cuadrado, es decir, F ~ 1/R2 . Volvamos al diagrama que muestra el cambio de velocidad, Δv, en cada punto particular de la órbita:
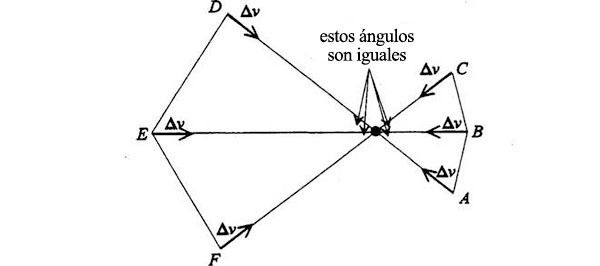
En cada punto de la órbita (A, B, C… D, E, F…, y todos los que hay entre ellos) hay un Δv hacia el Sol. Cuanto mayor es la fuerza F, mayor es Δv, y asimismo, cuanto más largo sea el tiempo Δt mayor será el cambio de velocidad Δv:
Δv ~ F Δt
Pero como: F ~ 1/R2 y Δt ~ R2,
Δv ~ (1/R2)xR 2= 1
Esto significa que Δv no depende de R en absoluto. En todos los puntos de la órbita, estén éstos cerca o lejos del Sol, el Δv producido en un ángulo dado es el mismo. Esto sucede, como ya hemos visto, porque conforme el planeta se aleja del Sol la fuerza que se ejerce sobre él disminuye (en razón del cuadrado de la distancia), pero el tiempo durante el cual la fuerza se ejerce sobre el planeta se dilata (también en razón del cuadrado de la distancia). El resultado es que todos los Δv producidos en toda la trayectoria orbital son los mismos. Este es, dice Feynman en su charla, «el núcleo central del que se deducirá todo, que se producen cambios de velocidad iguales cuando la órbita describe ángulos iguales».
Para comprender con exactitud lo que esto significa, volvamos otra vez a la modalidad del diagrama dibujado por Newton y copiado por Feynman. En vez de representar con él posiciones de los planetas, representemos velocidades:
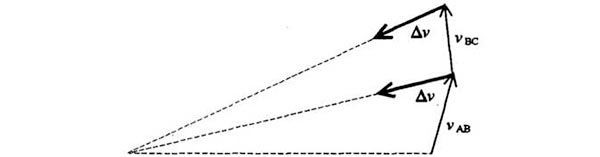
Según el estilo newtoniano, los tiempos eran iguales y todos los Δv estaban dirigidos hacia el Sol, pero unos Δv eran mayores que otros (los mayores se producían cuando el planeta estaba más cerca del Sol). En el esquema de Feynman, los ángulos centrales son iguales, de modo que los tiempos son distintos. Todos los Δv están orientados hacia el Sol (es necesario, según la segunda ley de Newton) y ahora tienen todos exactamente el mismo tamaño durante toda la trayectoria orbital. Esto tiene consecuencias que se verán en seguida.
En este punto Feynman dibuja en sus apuntes el diagrama de la órbita y el correspondiente diagrama de velocidades para los segmentos de ángulos iguales. He aquí el resultado:
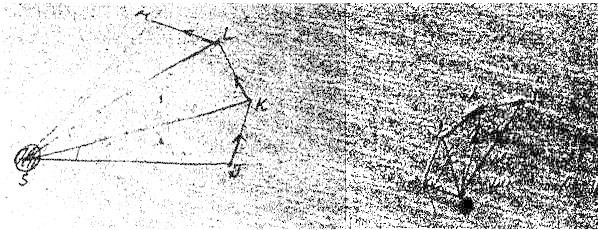
La órbita parte de la posición J, sigue hasta K formando un ángulo con el Sol, sufre un Δv que cambia su dirección, luego continúa, formando un ángulo idéntico, de K a L, y a continuación de L a M:
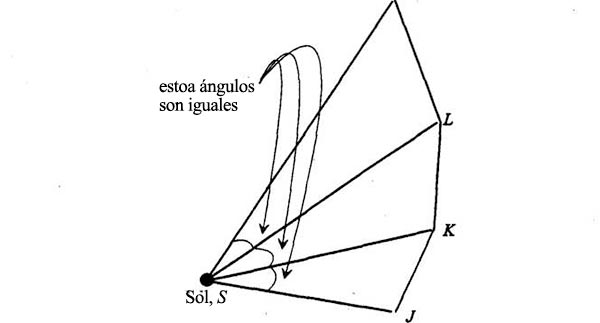
A diferencia de la versión newtoniana de este esquema, los tiempos de estos segmentos no son necesariamente iguales. Las velocidades tienen la dirección JK, KL, etc. Son, en general, de magnitud diferente en diferentes segmentos. Los cambios de velocidad sufridos en los puntos J, K, L y M se dirigen todos hacia el Sol y son todos de la misma magnitud. En otras palabras, en Jhay un Δv en la dirección JS; en K se produce el mismo Δv en la dirección KS, y así sucesivamente. Sirviéndose de estos datos, Feynman construye el diagrama de velocidades:
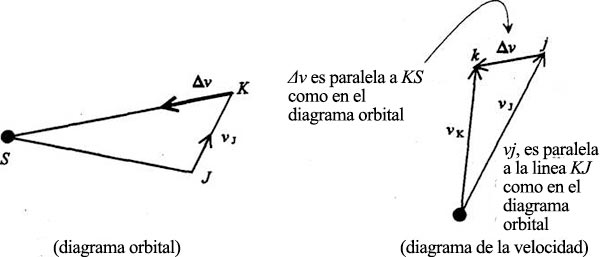
En el diagrama orbital, el planeta va de J a K a velocidad vj. En el diagrama de velocidades, vj tiene la misma dirección, pero no la misma longitud que JK. En el punto K hay un Δv en la dirección KS, recorriendo en el diagrama de velocidades una distancia Δv entre el punto j y el punto k, donde la velocidad se vuelve vg. Este proceso se reproduce en el siguiente paso: se traza desde K, paralelo a vg, el segundo segmento del diagrama orbital, hasta el punto L, y el ángulo resultante, KSL, será igual al ángulo JSK:
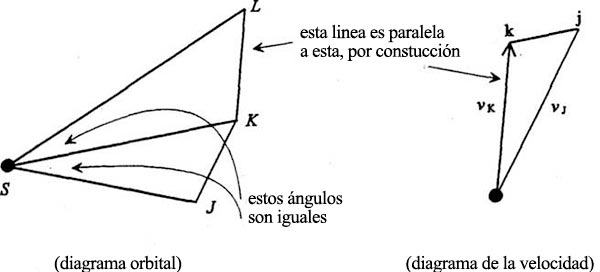
Ahora encontramos el punto l del diagrama de velocidades añadiendo un Δv igual en magnitud a jk, pero paralelo a LS:
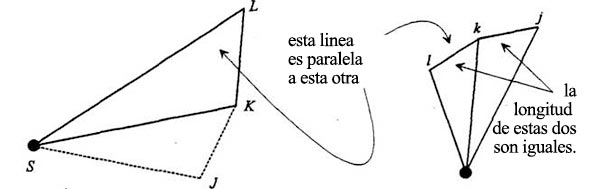
El mismo procedimiento puede repetirse en toda la órbita. El siguiente paso da el diagrama que dibujó Feynman en sus apuntes:
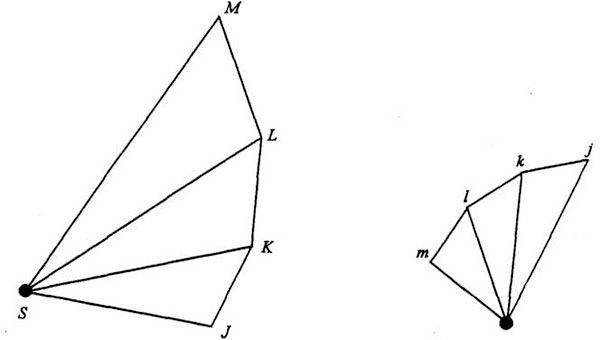
Como escribió Feynman en sus apuntes, jk es paralela a KS, lk es paralela a LS, lm es paralela a MS y lk = jk = lm.
Cada uno de los lados del diagrama de velocidades (jk, kl, lm…) es paralelo a una de las líneas que salen del Sol en el diagrama orbital. Como las líneas que salen del Sol se construyen con ángulos iguales, los lados de la figura del diagrama de velocidades tienen también ángulos exteriores iguales:
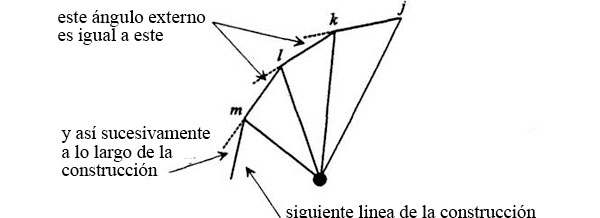
Cuando se complete el diagrama de velocidades, será una figura con lados y ángulos (exteriores) iguales:
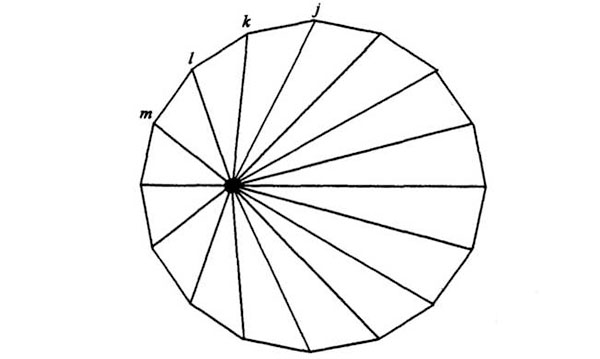
Adviértase que las velocidades, que son las distancias respectivas del origen a j, k, l, etc., son desiguales, pero que los lados (los Δv) son iguales. La figura resultante es un polígono regular. El origen de las velocidades no está en el centro, pero el contorno es un polígono regular.
Si pasamos ahora a dividir, como de costumbre, el diagrama orbital en una cantidad mayor de segmentos con ángulos iguales pero más pequeños, la órbita se aproximará a una curva lisa, y lo mismo pasará en el diagrama de velocidades. Como el diagrama de velocidades es un polígono regular, la curva lisa a la que se aproxima es un círculo. Pero el origen de las velocidades no está necesariamente en el centro del círculo.
En este punto, Feynman dibuja en sus apuntes unos diagramas orbitales y velocidades en forma de curva lisa. Primero la órbita. Parte del punto J y Feynman la dibuja de forma convencional, con la línea que parte del Sol prolongándose horizontalmente; al contrario que en el diagrama orbital segmentado, la velocidad en el punto J es una vertical, perpendicular a la línea que parte del Sol:
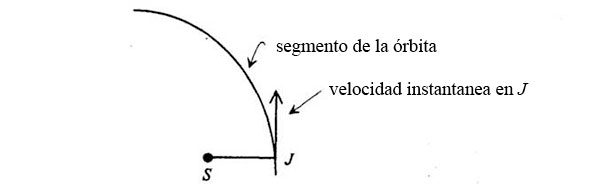
Al cabo de un tiempo, el planeta llega al punto P y forma un ángulo Φ en el Sol:
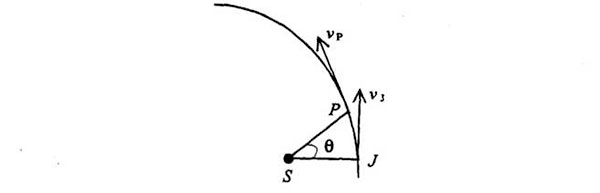
En cada punto, la velocidad instantánea es tangente a la curva lisa.
Construyamos ahora el correspondiente diagrama de velocidades. Será un círculo y el origen será excéntrico. La longitud de la línea que trazaremos para representar vj, dependerá de la aceleración del planeta en el punto J de la órbita. Recordemos que, en un diagrama de velocidades, cuanto mayor sea la línea más rápida será la aceleración. El punto J del diagrama orbital de Feynman es también el punto más cercano al Sol (Feynman lo resuelve en su cabeza sin mencionarlo en la conferencia), punto donde la aceleración orbital es mayor. Por lo tanto, la línea vj debe pasar por el centro del círculo, dado que debe ser la línea más larga del diagrama de velocidades:
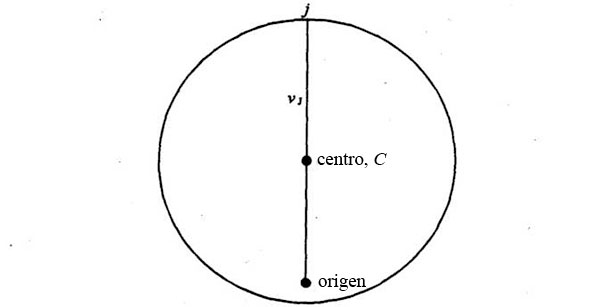
Trazada así, vj es vertical (paralela a la vj del diagrama orbital) y es la distancia más larga entre el origen y un punto del círculo. La velocidad en el punto P del diagrama de velocidades, correspondiente al punto P del diagrama orbital, es una línea que sale del origen y es paralela a vp:
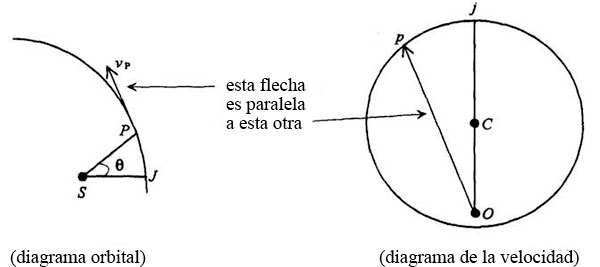
Es verdad igualmente que el ángulo jCp del diagrama de velocidades es el mismo ángulo, Φ, que JSP en el diagrama orbital:
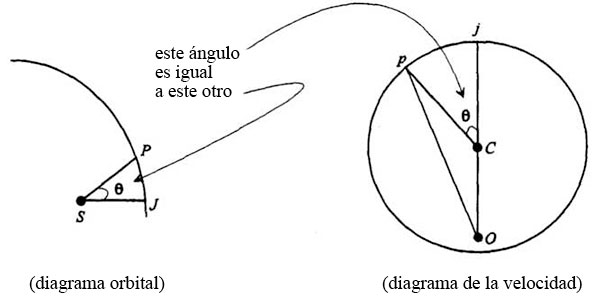
La razón de que sea así se comprende cuando volvemos al diagrama completo de las velocidades de los segmentos de la órbita, al polígono regular, y trazamos líneas desde el centro y no desde el origen de velocidades:
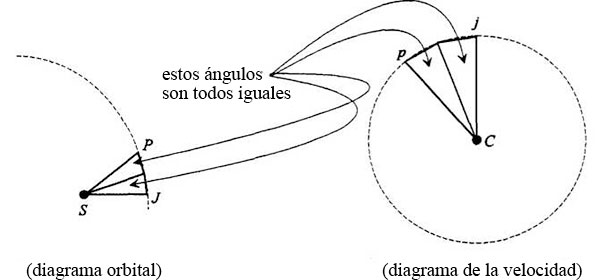
La órbita se ha dividido en cierta cantidad de ángulos iguales, que en total deben sumar 360°. El polígono tiene por fuerza la misma cantidad de lados iguales, y todos han de estar en la misma fracción de 360°. Por lo tanto, el ángulo que forme SJ con un punto cualquiera de la órbita será igual al ángulo que forme Cj con el punto correspondiente del diagrama de velocidades.
El resultado neto se muestra en estos dos diagramas dibujados por Feynman:
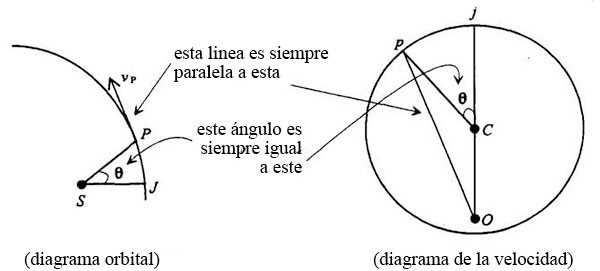
Puesto que ya hemos establecido todas las correspondencias entre ambos diagramas, construyamos la órbita partiendo del diagrama de velocidades. Es un punto de partida más sencillo, pues sabemos que se trata sólo de un círculo:
Toda órbita permitida por las leyes de Newton y la fuerza de la gravedad tendrá siempre este diagrama de velocidades. La forma concreta de la órbita dependerá del lugar donde pongamos el origen de las velocidades. Elijamos un punto cualquiera del interior del círculo, pero que no esté en C, el centro (ya veremos lo que ocurre, en el círculo o fuera de él, si el punto está en C):
Sólo por razones de familiaridad, giremos el diagrama hasta que el punto elegido quede exactamente debajo de C:
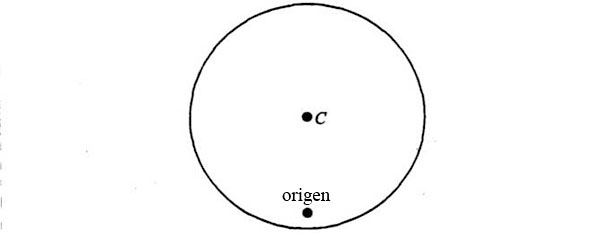
El punto elegido hace de origen de las velocidades, lo que quiere decir que una línea trazada desde aquí hasta cualquier punto de la circunferencia tendrá una longitud proporcional a la aceleración del planeta en ese punto de la órbita y estará en la misma dirección que el movimiento del planeta en ese mismo punto. Como ya se advirtió, la línea que vaya del origen a la circunferencia del círculo pasando por el centro será la más larga, y en consecuencia representará el punto de la órbita donde el planeta se moverá más aprisa.
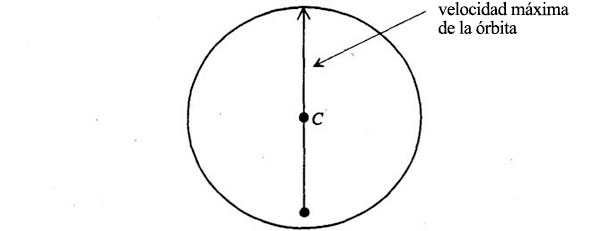
Según la ley de las áreas iguales, este será el punto de la órbita más próximo al Sol. Tal como hace Feynman, dibujemos la órbita de modo que la línea desde ese punto hasta el Sol sea horizontal y la velocidad vertical (por eso dimos la vuelta al diagrama de velocidades y pusimos el origen debajo del centro):
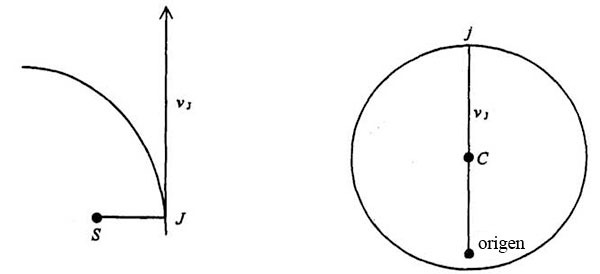
Tracemos ahora una línea desde el origen hasta otro punto cualquiera del círculo, p:
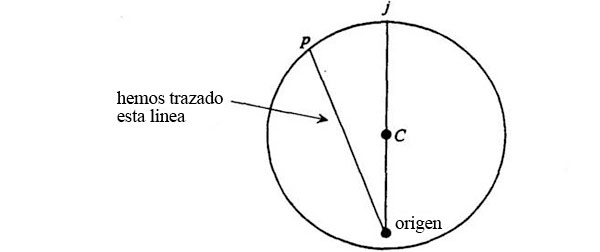
Este punto corresponde a un punto P de la órbita que tiene las siguientes propiedades: la línea entre el origen y p, en el diagrama de velocidades, es paralela a la tangente al punto P del diagrama orbital, y el ángulo jCp es el mismo que JSP:
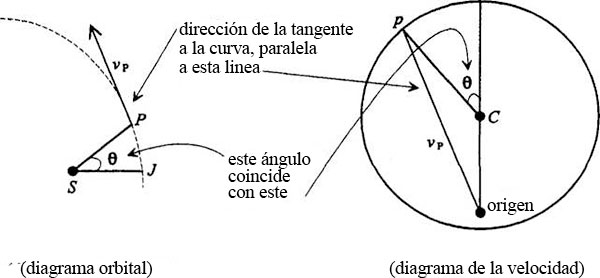
Así, en cada ángulo Φ conocemos la dirección de la tangente a la órbita que queremos construir. ¿Cómo construiremos la curva?
Más adelante nos dice Feynman que éste fue el paso más difícil de descubrir. El truco es girar 90° el diagrama de velocidades en el sentido de los relojes, para que las direcciones que aparecen en él sean las mismas que las del diagrama orbital:
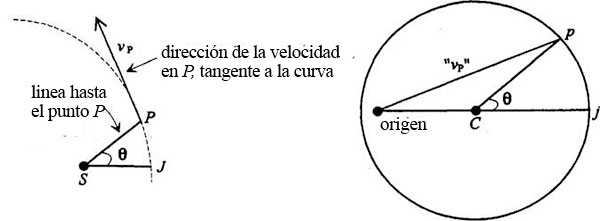
Ahora el ángulo central Φ es el mismo en ambos diagramas, pero la línea denominada vp, que era paralela a la velocidad en P en la órbita, ahora es perpendicular a ella, porque hemos girado 90° el diagrama de velocidades. Ahora conocemos, por el diagrama de velocidades, la dirección desde el Sol hasta el punto P de la órbita, y conocemos la dirección de la tangente a la órbita en ese punto. Es perpendicular a la línea denominada vp. Pero aún no sabemos con exactitud dónde está dicho punto.
La forma más sencilla de construir la curva, con todas las propiedades necesarias, es dibujarla directamente sobre el diagrama de velocidades. El tamaño de la órbita será entonces arbitrario, pero todas las direcciones, y por tanto la forma de la órbita, serán correctas. Para obtener la órbita, basta con construir la bisectriz de la línea que va del origen a p:
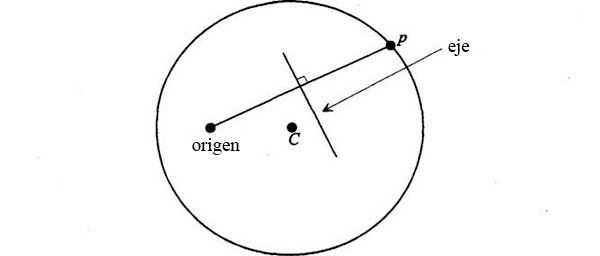
Como es perpendicular a la línea del origen a p, sabemos que es paralela a vp, la velocidad en el punto P de la órbita. En determinado punto, la bisectriz corta la línea que une P con el centro C:
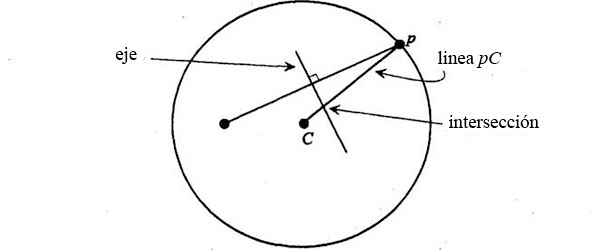
Como el punto P se mueve por la circunferencia del círculo, la intersección depC y la bisectriz se mueve describiendo una curva propia:
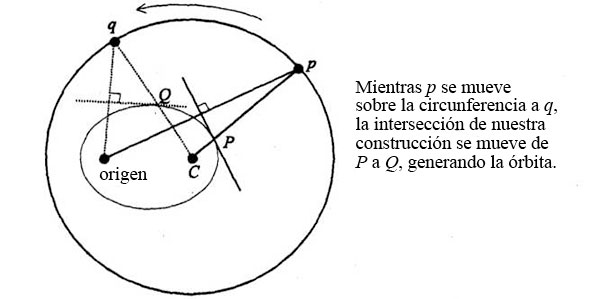
La verdad es que ya habíamos hecho esta misma construcción. Partiendo de dos puntos del plano, denominados F’ y F (correspondientes al origen y a C, respectivamente), dibujamos una línea de F’ a un punto G’ (p en el último diagrama):
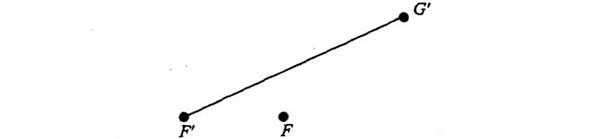
Luego unimos G’F y trazamos la bisectriz de F’G’, que corta FG’ en el punto P:
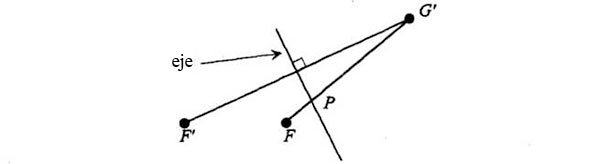
Así demostramos que cuando el punto G’ describe un círculo con centro en F, el punto P describe una elipse, y en cada punto P la bisectriz es tangente a la elipse.
Ahora hemos construido la misma figura que en la página 86, solo que con otras denominaciones. He aquí el aspecto del nuevo diagrama:
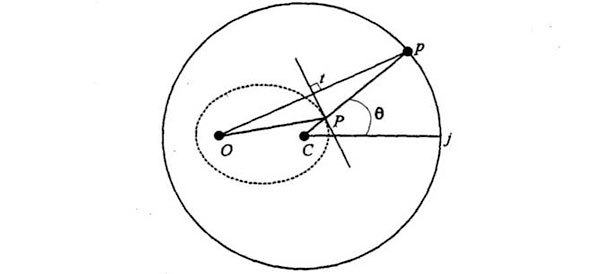
Aquí, p es un punto de un círculo con centro en C. Hay también un punto excéntrico: el origen del diagrama de velocidades, que ahora denominamos O. El segmento Op tiene una bisectriz perpendicular en t, que corta la línea Cp en un punto P. Ahora demostraremos otra vez que todos los puntos P creados de este modo, mientras p se mueve por la circunferencia del círculo, están en una elipse, y que la línea tP es tangente a la elipse en P. Puesto que tP es paralela a la velocidad del planeta cuando éste está en el punto P de la órbita, habremos construido la curva única que describe el planeta al desplazarse en la dirección correcta en todos los puntos de la órbita.
Para demostrar que esta curva es una elipse, advirtamos que los triángulos OtP y ptP son congruentes:
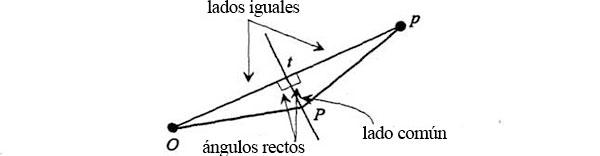
Por lo tanto, OP = pP. Y en el diagrama completo,
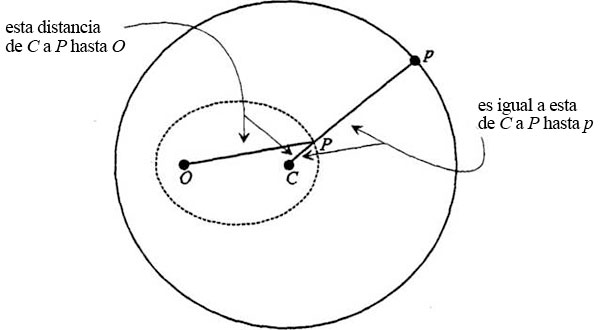
CPp, que es el radio del círculo, y por tanto el mismo para toda la circunferencia, es igual a CP + PO, la longitud de la cuerda de los focos C y O que construye la elipse. La curva trazada (la órbita) es por lo tanto una elipse, QED. Para demostrar que P es la tangente en P,volvamos a los triángulos congruentes:
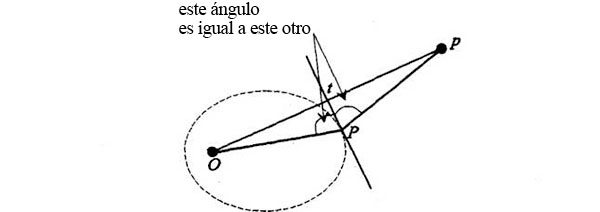
Hagamos ahora que las líneas Pp y tP se crucen:
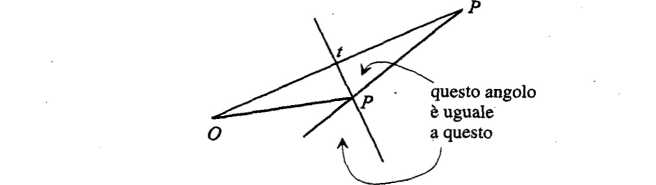
Por lo tanto,
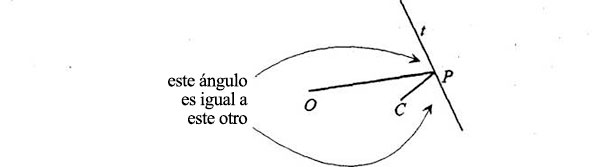
La línea tP es en consecuencia la que refleja en el punto P la luz que va de C a O. Más atrás demostramos que la línea tP que posee esta propiedad es la tangente. Por última vez, QED.
La demostración se ha completado. Feynman no ha terminado aún, pero por nuestra parte hemos expuesto lo que nos proponíamos. Las leyes de Newton, junto con una fuerza gravitatoria proporcional a R-2 y orientada hacia el Sol, hacen que los planetas tengan órbitas elípticas. Antes de abandonar el tema, volvamos una vez más a la lógica de los argumentos que nos han permitido (con la ayuda de Newton y Feynman) realizar esta hazaña heroica.
Newton viene a decir: partiendo del hecho de que los planetas barren áreas iguales en tiempos iguales, he aplicado mis leyes para deducir que la fuerza de gravedad solar sobre un planeta apunta directamente hacia el Sol. Luego, partiendo del hecho de que los periodos orbitales de los planetas son proporcionales a la potencia 3/2 de su distancia al Sol, he aplicado mis leyes para deducir que la fuerza de gravedad disminuye según R-2. Por último, mis leyes, junto con estos dos hechos sobre la gravedad, producen órbitas elípticas.
En realidad Newton no razonó así. Sabemos, por versiones anteriores de su obra (por ejemplo, el breve texto que envió a Halley en 1684), que ensayó varias formulaciones de los axiomas de la dinámica. Al final los redujo a tres y los llamó «leyes». Reducir toda la dinámica a tres leyes fundamentales fue de importancia suprema, porque, como Newton y sus seguidores demostrarían en el curso de los tres siglos siguientes, dichas leyes podían emplearse para explicar no sólo el movimiento de los planetas, sino también casi todos los demás fenómenos del mundo físico. Las leyes de Newton nos dicen cómo se comporta la materia cuando se ejercen fuerzas sobre ella. Las dos únicas cosas que necesitamos conocer sobre el mundo físico y que las leyes de Newton no nos dicen son la naturaleza de la materia y la naturaleza de las fuerzas que actúan entre pedazos de materia. Estas dos incógnitas son todavía el problema central de las ciencias físicas.
Esta tremenda reestructuración general de nuestro conocimiento del mundo comienza con la prueba de las órbitas elípticas. Para esto no necesitamos saber mucho de la naturaleza de la materia, porque la gravedad afecta a toda la materia del mismo modo. No obstante, la naturaleza de la fuerza de gravedad es muy importante, y Newton la deduce sirviéndose de dos leyes de Kepler.
Por último, hemos visto la prueba de las órbitas elípticas, no la versión de Newton, sino la de Richard Feynman. Feynman divide la órbita en ángulos iguales. En cada segmento angular, el cambio de velocidad se orienta al Sol y es proporcional a la magnitud de la fuerza y al tiempo durante el que se ejerce. Es la segunda ley de Newton. El tiempo es proporcional al área barrida, que (por geometría pura y simple) es proporcional al cuadrado de la distancia, y la fuerza está en razón inversamente proporcional al cuadrado de la distancia (tal es la naturaleza de la fuerza de gravedad); así, al margen de la forma de la órbita y de la distancia al Sol del planeta, éste sufre cambios iguales de velocidad en ángulos iguales. Se sigue de aquí que el diagrama de velocidades es un polígono regular (lados iguales en ángulos iguales) que en el caso de las órbitas lisas se convierte en círculo. Sin embargo, el origen del diagrama de velocidades no está en el centro del círculo. A continuación, con ayuda de una construcción geométrica astutamente preparada de antemano, se demuestra que la órbita tiene forma de elipse y que sus focos son el origen del diagrama de velocidades y el centro del círculo de velocidades.
El diagrama de velocidades es un potente instrumento geométrico. Las leyes newtonianas de la dinámica, más una fuerza R-2, dan siempre un diagrama de velocidades circular:
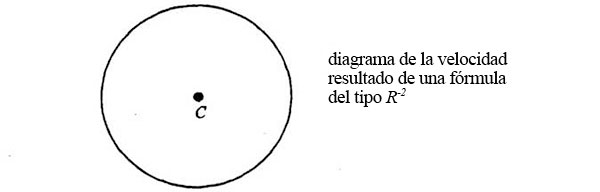
La forma de la órbita depende de dónde esté O, el origen del diagrama de velocidades. Si coincide con C, el centro del diagrama, entonces los dos focos de la elipse coincidirán y el planeta tendrá la misma rapidez en todas las partes de la órbita:
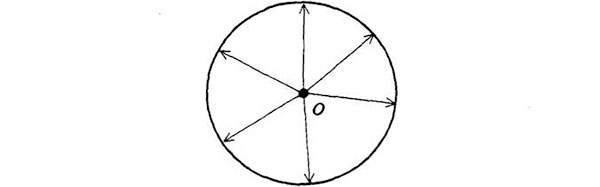
En este caso, la órbita no es más que un círculo.
Si el punto O está en algún lugar situado entre C y la circunferencia del diagrama, la órbita es entonces una elipse. Cuanto más cerca esté O de C, más circular será la elipse. Cuanto más alejados estén ambos puntos, más alargada será:
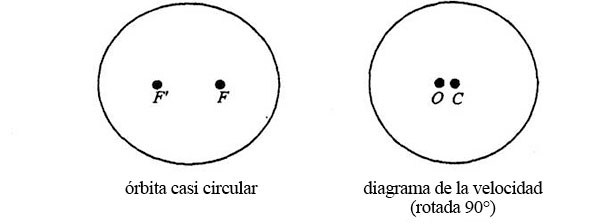
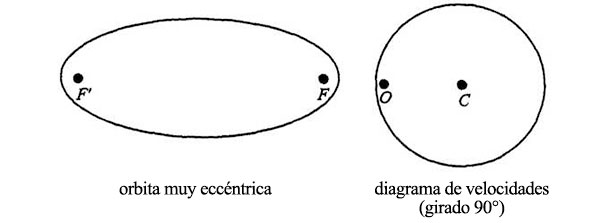
Todas las órbitas planetarias de nuestro sistema solar son casi circulares. En la órbita de la Tierra, la distancia entre focos viene a ser 1/100 del diámetro de la órbita; en la de Marte es alrededor de 9/100; en las de Mercurio y Plutón (las más excéntricas), algo más de 20/100. El cometa Halley, por el contrario, tiene una órbita elíptica muy excéntrica. La distancia entre focos es 97/100 del diámetro de su órbita.
¿Qué sucede cuando O está fuera del círculo? Volvamos al diagrama de velocidades antes de girarlo 90°. Todavía tenemos la mayor velocidad en el punto más cercano de la órbita:
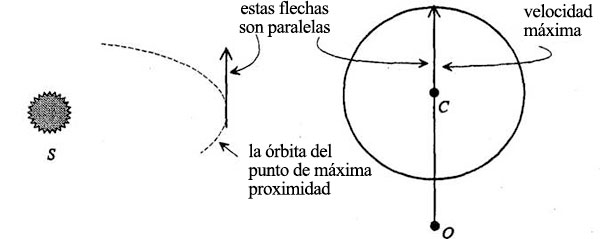
Conforme aumenta el ángulo 0, las velocidades evolucionan en el círculo del diagrama:
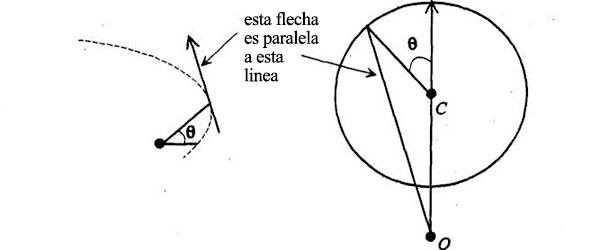
Para algún valor de Φ la línea de O será tangente al círculo de velocidades:
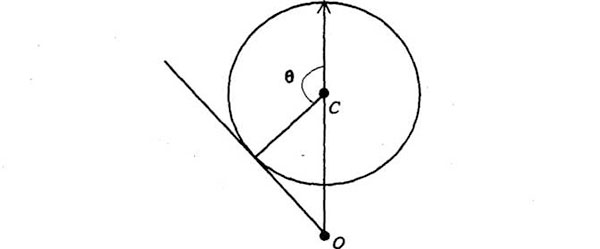
Recordemos que esta línea es además paralela a la velocidad instantánea de la órbita y que la tangente al diagrama de velocidades tiene la dirección de los Δv del diagrama orbital, que representa los cambios de velocidad. En otras palabras: para este ángulo Φ, el cambio de velocidad se produce en la misma dirección que la velocidad misma. Esto significa que la velocidad ya no cambia de dirección. La trayectoria no es ya una curva, es una línea recta. La «órbita» no será por tanto una elipse, figura imposible de trazar con una línea recta. Por el contrario, será una hipérbola, otra sección cónica, que tiende a alejarse del foco en línea recta:
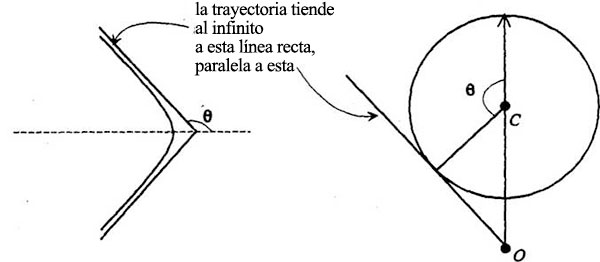
En esta trayectoria, el «planeta» cae hacia el Sol desde el infinito, da una vuelta alrededor suyo y huye otra vez hacia el infinito. Esta trayectoria no es en realidad una órbita. Cuando parte del infinito y cuando vuelve, su velocidad no es cero; la velocidad es proporcional a la longitud de la línea que va de O al punto de tangencia con el círculo de velocidades.
Si el punto O está en la circunferencia, el «planeta» huye igualmente hacia el infinito, pero cuando llega tiene velocidad cero; su trayectoria será una parábola. Así, la dinámica newtoniana, más una fuerza cuadrática inversa, genera diagramas de velocidades circulares. Según dónde esté el origen del diagrama de velocidades, la órbita será un círculo, una elipse, una parábola o una hipérbola, las curvas que llamamos secciones cónicas.
Al final de la conferencia (y porque tiene tiempo para ello, según dice). Feynman transforma la maquinaria que ha desarrollado en un problema totalmente distinto, y una vez más de importancia histórica.
En 1910 los investigadores Ernest Marsden y Hans Geiger, dirigidos por Ernest Rutherford, descubrieron que si se proyectaba un rayo de partículas alfa (núcleos de átomos de helio) sobre una delgada lámina de oro, algunas rebotaban en vez de atravesar la lámina. El experimento podría compararse a grandes rasgos con un alienígena que lanzase un cometa contra el sistema solar para saber si la masa del sistema solar estaba distribuida de manera uniforme por todas partes o más bien concentrada en un objeto compacto (el Sol), situado en el centro. Sólo un objeto compacto podría hacer que el cometa diera la vuelta alrededor de él para alejarse a continuación. En vez de cometa, el grupo de Rutherford manejó partículas alfa, y en vez de sistema solar, átomos de oro. La incógnita era si la materia del interior del átomo estaba dispersa más o menos uniformemente (como se pensaba entonces) o, por el contrario, estaba concentrada en el centro. El que algunas partículas alfa rebotasen demostró que la masa estaba concentrada en el centro, y con este experimento se descubrió el núcleo atómico.
La fuerza que operaba aquí entre el proyectil y los componentes del sistema no era la gravedad, sino la electricidad. La electricidad es una fuerza que opera entre cargas eléctricas positivas y negativas (términos acuñados por un científico newtoniano y autodidacta del siglo XVIII, Benjamín Franklin). Al igual que la gravedad, la electricidad es una fuerza tipo R-2 que actúa a lo largo de la línea que une las cargas; a diferencia de la gravedad, puede hacer que las cargas se atraigan entre sí (cargas opuestas) o que se repelan (cargas iguales). La fuerza de la gravedad siempre es atractiva, nunca repulsiva. La fuerza eléctrica es muchísimo más potente que la de gravedad. En realidad, es tan potente que se neutraliza a sí misma. Todos los átomos de la lámina de oro tienen exactamente la misma cantidad de cargas positivas y negativas, por eso el átomo es neutro por fuera, ya que si no es perturbado no ejerce ninguna fuerza eléctrica. La cuestión es: ¿qué sucede cuando un proyectil con carga eléctrica (la partícula alfa, que es eléctricamente positiva) se lanza dentro de un átomo? La respuesta dice que lo repele el núcleo atómico, que contiene toda la carga positiva y casi toda la masa del átomo. De vez en cuando, por pura casualidad, una partícula alfa se acercará tanto al núcleo que saldrá rebotada por el mismo camino de entrada, y eso es lo que Marsden y Geiger observaron.
Dado que la electricidad es una fuerza proporcional a R-2 que actúa siguiendo la línea que une las cargas, y si las partículas obedecen la dinámica de Newton todos los argumentos geométricos utilizados por Feynman son aplicables a este problema. Se trata de averiguar la probabilidad de que un proyectil salga despedido hacia atrás, de modo que el experimento pueda compararse con una teoría cuantitativa. El punto de partida es el diagrama de velocidades (válido para toda fuerza tipo R~2 a lo largo de la línea que une las partículas) con el origen fuera del círculo. Las «órbitas» de las partículas alfa no serán elipses atrapadas para siempre en los alrededores del núcleo, sino más bien hipérbolas que enviarán las partículas alfa hacia el infinito después de curvar su trayectoria en un ángulo mayor o menor. No seguiremos todos los pasos aquí, porque Feynman ya no se siente obligado a ceñirse a los argumentos geométricos. Antes bien, se salta todos los semáforos con objeto de llegar a lo que, por emplear sus propias palabras, es una fórmula celebérrima.
Dicha fórmula merece esta celebridad porque condujo directamente al descubrimiento de la mecánica cuántica, y de aquí al derrocamiento de la dinámica newtoniana empleada para llegar a ella. Pero esta historia da para otro libro. Ha llegado el momento de ponernos en manos del maestro. Entra Feynman.