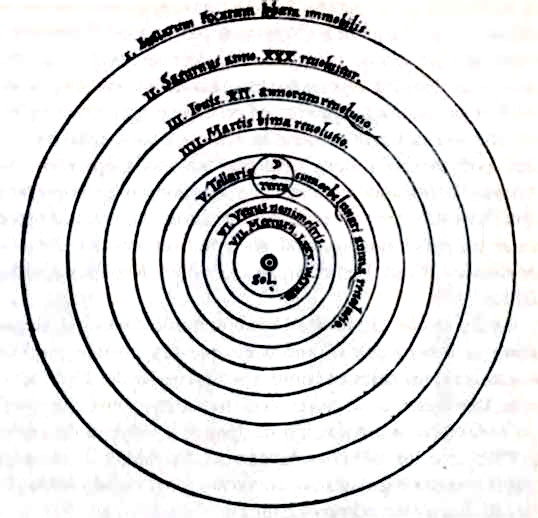
Concepción copernicana del sistema solar, según el
De revolutionibus orbium coelestium. de 1543.
En 1543, cuando ya estaba en el lecho de muerte, el canónigo polaco Nicolás Copérnico pudo ver los primeros ejemplares de su libro sobre Las revoluciones de las esferas celestes. Había retrasado adrede su publicación hasta el momento en que ya no tuviera que afrontar las consecuencias. Aquella obra sugería algo impensable: que el Sol y no la Tierra era el centro del universo. Hablaba de revoluciones, de revoluciones reales en el cielo, y representó el inicio de lo que dio en llamarse, metafóricamente, revolución científica. En la actualidad, cuando llamamos revoluciones a los grandes cambios, políticos y de otra especie, rendimos homenaje a Copérnico cuyo libro sobre las «revoluciones» inició la primera de ellas.
Antes de Copérnico, nuestra concepción del mundo procedía de los antiguos filósofos y matemáticos griegos, perpetuada en el tiempo gracias a los escritos de Platón y Aristóteles, que vivieron y enseñaron en el siglo IV a. C. Toda la materia del mundo aristotélico estaba compuesta de cuatro elementos: tierra, agua, aire y fuego. Cada elemento tenía su lugar natural: la tierra, rodeada por el agua, en el centro del universo, y luego el aire y el fuego, en esferas ascendentes. El movimiento natural se producía porque los elementos buscaban su lugar natural. Así los cuerpos pesados, básicamente terrestres, tendían a caer, mientras que las burbujas de aire subían en el agua y el humo ascendía por el aire. Los movimientos restantes eran violentos y necesitaban una causa inmediata. Por ejemplo, una carreta de bueyes no se podía mover salvo que un buey tirase de ella. Más allá de las esferas de tierra, agua, aire y fuego, los cuerpos celestes giraban en esferas cristalinas autónomas. Las esferas celestes, a las que sólo se permitía la perfección del movimiento circular, eran imperturbables, armónicas y eternas. Sólo aquí en la Tierra había cambio, muerte y degeneración. Era un sistema coherente, indiscutiblemente ideado para ponemos en el lugar en que estábamos, pero dicho lugar era el centro del universo y pese a todos nuestros defectos, era fácil imaginar que éramos la finalidad de la creación. «Estábamos la mar de contentos con el cosmos de Aristóteles», dice un personaje de la Arcadia de Tom Stoppard, que se burla de historiadores y científicos por igual. «Personalmente hablando, era mi preferida. Cincuenta y cinco esferas cristalinas girando y Dios dándole a la manivela es lo que yo llamo un universo satisfactorio.»
Pero incluso en los cielos imperturbables del cosmos aristotélico había algunos problemas. El Sol, la Luna y las estrellas ejecutaban bien sus movimientos (casi siempre), pero había unos cuantos cuerpos excepcionales llamados planetas (planeta en griego significa «errante») que no se comportaban como es debido. Predecir la posición de dichos cuerpos (en qué lugar del cielo aparecerían en una noche dada) era el cometido profesional de los astrónomos. La información tenía cierta importancia para la agricultura y la navegación y, por encima de todo, para trazar horóscopos en un mundo inmerso en la astrología. La idea de que los planetas daban vueltas alrededor de la Tierra describiendo círculos perfectos no coincidía con la observación, pero Platón había dicho que en los cielos sólo era posible el movimiento circular. Por eso, los astrónomos hicieron que los planetas describieran circunferencias, llamadas epiciclos, que eran a su vez el centro de otros círculos, llamados deferentes. Si la observación de un planeta en el cielo no coincidía del todo con el sistema vigente de círculos deferentes y epiciclos, se podía añadir otro epiciclo para ajustar los cálculos y mejorar la seguridad de las predicciones, una práctica que se llamaba «salvar las apariencias». Este sistema antiguo quedó codificado en el Almagesto de Ptolomeo, un astrónomo alejandrino del siglo II d. C. El Almagesto fue el principal manual de astronomía durante mil cuatrocientos años, hasta la época de Copémico.

Concepción copernicana del sistema solar, según el
De revolutionibus orbium coelestium. de 1543.
En su libro sobre las revoluciones. Copérnico señalaba que todo el complicado sistema de epiciclos y círculos deferentes se simplificaba si, por conveniencia matemática, se ponía el Sol en el centro del universo y no la Tierra. Lo decía en el primer capítulo. El resto del libro estaba lleno de tablas astronómicas, calculadas después de trazar epiciclos y círculos deferentes centrados en el Sol. El truco de la conveniencia matemática no engañó a nadie, aunque fueron pocos los que prestaron atención a Copérnico después de su muerte y menos aún los que se molestaron en leer su libro. Es verdad que en las décadas siguientes los misioneros jesuitas ya enseñaban astronomía copernicana en China, pero en la metrópoli romana del cristianismo la Iglesia estaba más preocupada por Martín Lutero que por Nicolás Copérnico. No obstante, hubo unos cuantos que lo tomaron en consideración. Tres hombres en particular estaban llamados a representar un papel fundamental en la subversión del universo geocéntrico. Eran Tycho Brahe, Johannes Kepler y Galileo Galilei.
Tycho Brahe (1546-1601) era un noble danés que de pequeño se enteró con asombro de que era posible predecir acontecimientos celestes como el eclipse solar del 21 de agosto de 1560; más tarde supo, con mayor asombro aún mientras observaba la conjunción de Júpiter y Saturno de agosto de 1563 que las tablas astronómicas (incluidas las copernicanas) estaban equivocadas en varios días, seguramente por falta de datos astronómicos exactos.
Después de estudiar Derecho, viajar por Europa, perder la nariz en un duelo y sustituirla por otra de oro plata y cera, Brahe escandalizó a la sociedad danesa casándose con una plebeya y dedicándose a la astronomía. Instaló un pequeño observatorio en unos terrenos de la familia y allí, el 11 de noviembre de 1572, descubrió una brillante estrella donde no había habido ninguna hasta entonces, en la constelación de Casiopea. En teoría no podían aparecer estrellas nuevas en el inmutable cielo aristotélico. El escrito de Brahe De nova stella ofendió a la Iglesia, cimentó su reputación y le valió el mecenazgo de Federico II de Dinamarca.

Tycho Brahe a los cuarenta años. Frontispicio de la Astronomiæ instauratæ mechanica, edición de 1602.
Federico dio a Brahe la isla de Hveen, próxima a Copenhague, y dinero para construir allí el mayor observatorio astronómico que el mundo había visto hasta entonces. Se construyeron instrumentos colosales (la «gran armilla ecuatorial» tenía dos metros y medio de diámetro, y el diámetro del «gran cuadrante mural» era de cuatro metros) para hacer mediciones de exactitud sin precedentes y edificios fabulosos donde vivir y trabajar, imprentas para publicar los hallazgos y muchas cosas más. Brahe dio al lugar el nombre de Uraniborg, por Urania, la musa de la astronomía. Comenzado en 1576, estuvo en funcionamiento hasta 1597. Unos años después, en 1610, la invención del telescopio acabó para siempre con la observación astronómica a simple vista. Sin embargo, las observaciones que se hicieron en Uraniborg durante su breve existencia redujeron la inexactitud de las tablas astronómicas de diez minutos de arco a dos minutos. (El dedo índice, con el brazo estirado, abarca un ángulo de un grado aproximadamente: diez minutos de arco es la sexta parte de un grado; dos minutos es la quinta parte de diez minutos.)
Tras la muerte de Federico II en 1588 le sucedió su hijo Cristián IV. Al nuevo rey le incomodaban las incesantes peticiones de patrocinio generoso que le hacía Brahe, y en 1597 la situación estaba ya tan deteriorada que Brahe clausuró Uraniborg, abandonó Dinamarca y se instaló en Praga, donde pasó a ser matemático imperial de Rodolfo II, rey de Hungría y Bohemia y soberano del Sacro Imperio Romano.
Cuando Brahe se fue a Praga ya había hecho una imperecedera contribución a la astronomía. Sin embargo, no estaba satisfecho. Aún tenía que poner sus valiosas (y en buena medida todavía secretas) observaciones al servicio de la nueva cosmología. Pero no de la cosmología copernicana y, desde luego, tampoco la tolemaica; Brahe había ideado un cosmos propio. En el sistema de Brahe todos los planetas daban vueltas alrededor del Sol y éste, con los demás planetas, daba vueltas alrededor de la Tierra, que volvía así a ser el centro del universo. Para la mentalidad moderna el sistema de Brahe parece una solución de compromiso entre Aristóteles y Copérnico, pero en aquella época supuso un alejamiento de Aristóteles aún más audaz que el del canónigo polaco, ya que pulverizaba las esferas cristalinas que en teoría llenaban los cielos, al margen de que en su centro estuviera la Tierra o el Sol. La cuestión era: ¿apoyaban los datos de Brahe el sistema de Brahe? Para responder esta pregunta hacía falta un talento matemático aún mayor que el del matemático imperial. Puede que en toda Europa no hubiera más que un matemático con la capacidad requerida. Pero uno había por lo menos. Era Johannes Kepler.
Kepler nació en 1571. Era hijo de un soldado mercenario que se esfumó muy pronto y de una mujer de armas tomar, hija de un posadero, que luego sería procesada por bruja. De corta estatura, salud frágil y ningún patrimonio, la evidente inteligencia de Kepler le mereció una beca que le permitió ingresar en la universidad de Tubinga. Allí estudió con uno de los primeros defensores europeos del sistema copernicano, Michael Mastlin. Después de obtener los títulos de bachiller y maestro, el profesorado de Tubinga lo salvó de la teología luterana y lo recomendó para un puesto de profesor de matemáticas en la Escuela Superior de la ciudad austriaca de Graz.
Según la leyenda, cierto día de verano de 1595, mientras el cuerpo de Kepler hablaba de geometría a una clase llena de adolescentes aburridos, su mente repasaba los datos clasificados de la astronomía copernicana, la pasión de su vida. Al trazar dos círculos, uno por fuera y otro por dentro de un triángulo equilátero, se dio cuenta de pronto de que la proporción que guardaban los diámetros de los dos círculos (el exterior mide el doble que el interior) era básicamente la misma que la de los diámetros de las órbitas de Júpiter y Saturno. El descubrimiento puso al mismo Kepler en órbita. No tardó en idear un modelo en el que las seis esferas invisibles que regían las órbitas de los seis planetas conocidos estaban acopladas, por dentro y por fuera, a los cinco «sólidos perfectos» de la antigüedad (sólidos con todas las caras iguales: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro), metidos unos dentro de otros. Poniendo los sólidos en el orden justo, los diámetros de las esferas guardaban casi la misma proporción que los diámetros de las órbitas planetarias.
El modelo kepleriano explicaba por qué había seis planetas y sólo seis (porque había cinco, y sólo cinco, sólidos perfectos) y por qué sus órbitas guardaban las proporciones que guardaban. Milagrosamente todo encajaba. Kepler pensó, y no por última vez en su vida, que había visto el interior de la mente de Dios. En 1596 hizo público el motivo de su inspiración en el Mvsterium cosmographicum, obra que llamó la atención de Tycho Brahe.
A Brahe no le fascinaban las ideas copernicanas de Kepler, pero su talento matemático le impresionó. Invitó a Kepler a trasladarse a Praga. Kepler se había labrado ya una sólida reputación de astrólogo perspicaz (sus predicciones sobre la peste, el hambre y las invasiones turcas solían dar en el blanco), pero su economía seguía siendo precaria y, como era luterano, se sentía acosado en la católica Graz. El primero de enero de 1600 partió hacia Praga para reunirse con el astrónomo danés.
El apocado Johannes Kepler no hizo buenas migas con el ruidoso Tycho Brahe y su nariz metálica, pero los dos se necesitaban. El primero necesitaba los datos del segundo para crear la obra de su vida, y Tycho necesitaba del genio de Kepler para organizar sus observaciones y confirmar su propio sistema. El desencuentro duró dieciocho meses, hasta que en 1601 Tycho Brahe murió repentinamente de una infección urinaria aguda. Se cuenta que las últimas palabras que dijo a Kepler fueron: «Que no haya vivido en vano». Pero Kepler, el abnegado copernicano, no tenía intención de continuar la cosmología de Tycho.
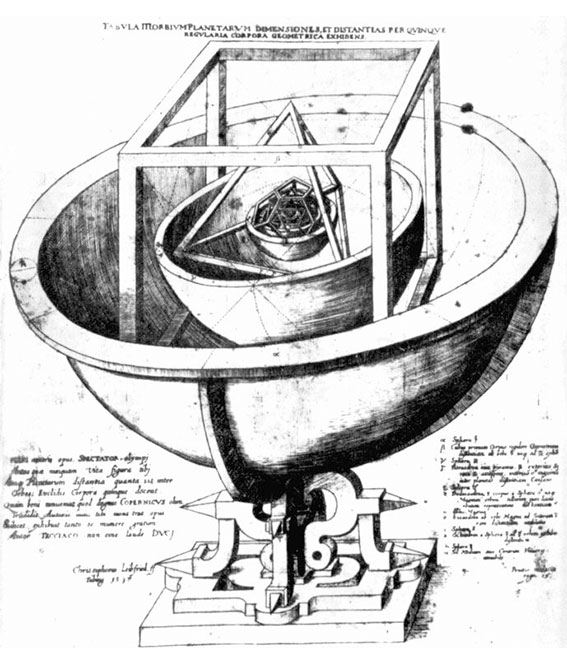
Los sólidos acoplados (la esfera exterior es la de Saturno): del Mysterium cosmographicum de Johannes Kepler, de 1596.
A la muerte de Brahe, Kepler consiguió, con algunas dificultades (nada fue fácil en la vida de Kepler) que lo nombraran matemático imperial (un título más honorífico que rentable) y que los herederos de Brahe le cedieran los fabulosos datos del difunto. Además, publicó un libro de astrología. (Consideraba charlatanes y farsantes a los demás astrólogos, pero no podía dominar la tentación de creer que había cierta armonía entre el destino humano y el paisaje celeste.) Y en 1604, mientras observaba una rara conjunción de Marte, Júpiter y Saturno, vio aparecer una supernova, una estrella nueva que fue visible en el cielo durante diecisiete meses.
La mayor contienda de Kepler fue su propia «guerra con Marte», la búsqueda de una órbita para el planeta que coincidiera con las observaciones de Tycho Brahe. La órbita marciana habría podido ser un círculo si en las observaciones la incertidumbre hubiera sido de diez minutos de arco, como antes de Brahe. Pero la magnífica herencia de Brahe pedía algo distinto. Kepler hizo cálculos prodigiosos, utilizando un método ingenioso para deducir la órbita de la Tierra, la insegura plataforma celeste desde la que Tycho había hecho sus observaciones. La órbita terrestre podía pasar por un círculo, con el Sol algo desplazado del centro. Pero la órbita de Marte no. Por más empeño que ponía, ningún círculo encajaba. En su Astronomía nova, publicada en 1609, Kepler cita unos versos de Virgilio para describir su búsqueda:
La lujuriosa Galatea
me busca con picardía:
corre hacia el bosque,
pero espera que la vea primero.
En el sistema copernicano, la Tierra es un planeta más. Pero siendo un lugar de cambio, muerte y degeneración, no se encuentra en estado de perfección platónica, como en teoría tenían que estar los planetas, de modo que es posible que las órbitas de los planetas no necesiten ser círculos platónicos. («¡Necio de mí!», exclama Kepler por no haberse dado cuenta antes; pero ya no nos expresamos así en las publicaciones científicas.) La órbita de Marte no era un círculo. Era una elipse, con el sol en un foco (Kepler tomó esta palabra de la latina focus, que significa fogón).
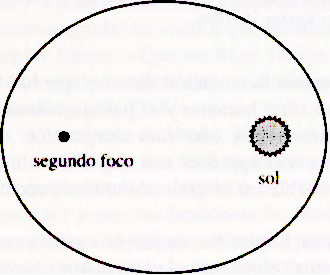
Elipse con el sol en un foco (la órbita de Marte es mucho más circular).

Izquierda: El plano corta el cono y origina un círculo visto desde arriba (abajo). Derecha: El plano inclinado corta el cono y origina una elipse vista desde arriba (abajo).
La elipse es una curva cerrada ya conocida en la antigüedad. Apolonio de Perga (hacia 262 - hacia 190 a. C.) demostró que cortando un cono con un plano se obtenían dos curvas cerradas, el círculo y la elipse, y dos curvas abiertas, la parábola y la hipérbola.

Izquierda: El plano corta el cono en sentido paralelo al lado opuesto del cono. Desde arriba se ve una parábola {abajo). Derecha: El plano corta los dos miembros de un cono extendido. Desde arriba se ve una hipérbola (abajo). A diferencia de las demás secciones cónicas, la hipérbola tiene siempre dos ramas.
Estas figuras se conocen con el nombre genérico de secciones cónicas. La elipse en concreto se puede dibujar con ayuda de un cordel y dos tachuelas situadas en los dos focos:
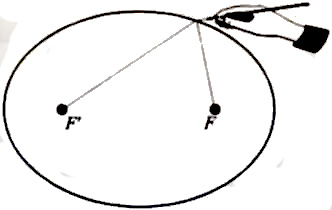
Volveremos sobre las especiales propiedades de la elipse en el capítulo 3.
En su Astronomía nova, Kepler nos dice que, en realidad, las órbitas de todos los planetas son elipses, con el Sol en un foco; esta afirmación acabó conociéndose como primera ley de Kepler, la ley de las elipses. También nos dice que un planeta se mueve más aprisa cuando está en la parte de la órbita más próxima al Sol y más despacio cuando está en la parte más lejana. Además, esta aceleración y esta dilatación del movimiento planetario poseen una regularidad muy especial: una línea trazada entre el Sol y el planeta barrería áreas iguales en tiempos iguales. Esta propiedad pasó a conocerse como segunda ley de Kepler. Diez años más tarde, en 1619, Kepler publicó un nuevo libro. Harmonices mundi, «Ciencia de la armonía del mundo», en el que exponía otra ley, la tercera. Las dos primeras describen el movimiento de un solo planeta en su órbita. La tercera compara las órbitas de los planetas. Dice que cuanto más alejado está un planeta del Sol, más despacio se mueve en su órbita. En concreto, un año de vida de un planeta (el tiempo que tarda en completar una órbita) es proporcional al tamaño de la órbita elevado a la potencia 3/2 (teóricamente, el diámetro mayor de la elipse). En conjunto, estos enunciados son la mayor contribución de Kepler, las tres leyes del movimiento planetario. En 1627 publicó las Tablas rudolfinas, llamadas así por el nombre del mecenas de Kepler, Rodolfo II. Estas tablas astronómicas, basadas en las minuciosas observaciones de Tycho Brahe, combinadas con las tres leyes de Kepler hicieron avanzar la astronomía como en ningún otro momento del pasado.
Aproximadamente por entonces, en Italia, Galileo Galilei escribía en Il saggiatore: «El libro de la naturaleza, quiero decir el universo, está siempre abierto ante nuestros ojos, pero no lo descifrará nadie que no aprenda y entienda antes el idioma y las letras con que está escrito. El idioma es matemático y las letras son figuras geométricas». Galileo no escribía para elogiar las leyes de Kepler, que, paradójicamente, no llegó a conocer y mucho menos defender. Escribía, por el contrario, en defensa del sistema de Copérnico. En 1616, el primer teólogo de la Iglesia Católica, el cardenal Roberto Belarmino había dicho que el sistema copernicano era «falso y erróneo» y había incluido la obra de Copérnico en el índice de libros prohibidos. Pero he aquí que había subido al solio pontificio un nuevo papa, Urbano VIII, antiguo amigo y defensor de Galileo y éste esperaba impedir que la Iglesia chocara de frente con la ciencia. No lo consiguió.

Frontispicio de las Tubular Rudolphinæ. de 1627. Dibujado por Kepler. este complejo grabado retrata a los gigantes de la astronomía reunidos en el templo de Urania. En el panel izquierdo de la base se encuentra el mismo Kcpler y el titulo de cuatro libros suyos.
Galileo nació en 1564 en Pisa; su padre. Vincenzio Galilei, era músico. (Entre las familias toscanas estaba entonces de moda bautizar al primogénito con el apellido gentilicio.) Galileo estudió medicina en la Universidad de Pisa, pero abandonó los estudios sin llegar a titularse por falta de dinero. Aprendió matemáticas él solo, publicó algunos ensayos y se ganó la vida dando clases de matemáticas en Pisa. En esta ciudad descubrió la ley del péndulo (un péndulo tarda siempre el mismo tiempo en completar un ciclo, sea cual fuere la amplitud de su arco) y la ley de la caída de los cuerpos (todos los cuerpos, sea cual fuere su masa, caen en el vacío con la misma aceleración constante), y realizó diversos experimentos cinéticos con bolas y planos inclinados que condujeron nada menos que a la invención de la ciencia experimental tal como la concebimos actualmente. (La palabra saggiatore se traduce tradicionalmente por «ensayador», pero el moderno término «experimentador» describe mejor la intención de Galileo.) Al parecer se convirtió al sistema copernicano en fecha temprana, pero mantuvo su fe en secreto por temor al ridículo. En una de sus escasas cartas a Kepler (en realidad, una nota de 1597 para agradecerle el envío de un ejemplar del Mysterium cosmographicum) escribió: «Me felicito por tener un aliado en el estudio de la Verdad que es amigo de la Verdad». La Verdad con mayúscula es una velada pero inconfundible alusión a Copérnico.
El sistema de Copérnico no era sólo un insulto a los principios aristotélicos y eclesiásticos: parecía igualmente un insulto al sentido común. Cualquier necio se daba cuenta de que la Tierra estaba en firme reposo. Si la Tierra giraba sobre su eje y corría por el espacio, como afirmaba Copérnico, ¿por qué no percibía nadie estos movimientos? Para hilar más fino, medítese el siguiente experimento mental: supongamos que tiramos un objeto pesado desde lo alto de la torre de Pisa. Al margen de nuestra orientación cosmológica, todos estaremos de acuerdo en algo: en que el objeto caerá al pie de la torre (olvidándonos por el momento de su famosa inclinación). Ahora bien, según los copernicanos la Tierra gira sobre su eje mientras el objeto cae. Si la gravedad hace que el objeto caiga hacia el centro de la Tierra, el objeto deberá caer en línea recta mientras la torre se aleja con la rotación terrestre. ¿Cuánto se aleja? Un objeto arrojado desde lo alto de la torre tarda unos dos segundos en llegar al suelo. Dados el tamaño de la Tierra y el hecho de que tarda un día en completar una rotación, la distancia no es difícil de medir. Mientras el objeto cae, la torre debería alejarse unos ochocientos metros. En otras palabras, si Copérnico tenía razón y la Tierra completaba una rotación cada día, un objeto arrojado desde lo alto de la torre inclinada de Pisa debería tocar el suelo a ochocientos metros de ella. El que esto no ocurra parece una muy tajante refutación del sistema copernicano.
El problema que tenían ante sí los copernicanos renacentistas no era que costase mucho rebatir estas objeciones, sino algo peor aún: que no parecía haber punto de partida para enunciar una réplica. Cuando Copérnico arrancó la Tierra del centro del universo, arrancó también el alma de la mecánica aristotélica, la argamasa intelectual que lo cohesionaba todo. Por ejemplo, ¿por qué había de caer un objeto pesado, si no iba en pos de su lugar natural? Responder que caía a causa de la gravedad, como se hizo y se sigue haciendo, no es más que dar otro nombre a lo desconocido. Para los seguidores de Copérnico, el aristotelismo estaba en ruinas y no había nada para reemplazarlo. Tal fue el dilema al que se enfrentó Galileo.
Para averiguar cómo funcionaba el mundo, Galileo concibió la idea de hacer experimentos cuyos resultados pudieran analizarse matemáticamente. Fue una idea que cambió para siempre el curso de la historia humana. No podía observar directamente los cuerpos que caían, dado que caían demasiado aprisa y no había relojes buenos: los primeros cronómetros exactos, basados en su descubrimiento de la isocronía del péndulo, aparecerían mucho después. Para retrasar el movimiento de los cuerpos que caían, midió el tiempo que empleaban en su caída unas bolas rodando por planos ligeramente inclinados, que se habían alisado al máximo para minimar la fricción. (En el Museo de Historia de la Ciencia de Florencia hay reproducciones de estos instrumentos, hechas por hábiles artesanos.) Probó muchos métodos para medir el tiempo que transcurría mientras rodaban las bolas. El mejor fue una especie de cronómetro de agua. El agua corría por un tubo (que el experimentador tapaba y abría con el dedo) y caía en otro recipiente mientras la bola estaba en movimiento. Luego pesaba el agua vertida. El peso del agua equivalía al tiempo transcurrido. Las reproducciones modernas de estos experimentos han demostrado que con un poco de práctica Galileo llegaba de este modo a una precisión de unas dos décimas de segundo. Salvo en contadísimos casos, estas mediciones no se mejoraron hasta el siglo XX.
Gracias a este método, Galileo descubrió la ley de la caída de los cuerpos. Vio que, duplicando el tiempo, la bola recorría una distancia cuatro veces mayor. Fuera cual fuese la inclinación del plano, el resultado no cambiaba, y con un gigantesco alarde de imaginación supuso que seguiría siendo el mismo si la pendiente era vertical, si el cuerpo caía de veras. Al experimento añadió el análisis matemático: si la distancia era proporcional al cuadrado del tiempo, esto significaba, como él mismo demostró con argumentos geométricos que el movimiento tenía una aceleración uniforme. Por último imaginó que el cuerpo caía en el vacío. En la mecánica aristotélica, hay lugar donde hay algo. Imaginar un lugar donde no hay nada, el vacío, es una contradicción en los términos, un absurdo lógico impensable. Pero Galileo rompió todas o al menos algunas de las amarras del pensamiento aristotélico. Imaginó el vacío y comprendió que la aceleración de un cuerpo que caía en el vacío no podía depender de su peso; sólo la resistencia del aire hace que los cuerpos más ligeros caigan más despacio que los pesados. Esta observación completó la ley de la caída de los cuerpos.
Sin embargo, no explicaba por qué un cuerpo caía al pie de la torre de Pisa y no a ochocientos metros de distancia. La solución del dilema salió, sin embargo, de los experimentos con los planos inclinados y las bolas. Galileo descubrió que si se hacía que la bola bajase por un plano y subiera por otro, tendía a subir por el segundo plano hasta alcanzar la misma altura de partida. Si la pendiente del segundo plano era más pronunciada que la del primero, la bola subía menos trecho, y si era menos pronunciada, subía más trecho, alcanzando en ambos casos la misma altura del principio. Hoy sabemos que esta conducta es una manifestación de lo que llamamos conservación de la energía. Pero Galileo comprendió algo más. Con otro prodigioso alarde de imaginación, razonó que, si el segundo plano fuera horizontal, la bola no dejaría de rodar nunca, porque nunca alcanzaría la altura del principio. Así llegó a la conclusión de que el estado natural de un objeto dotado de movimiento horizontal era seguir moviéndose horizontalmente, a velocidad constante y para siempre. La idea representaba un alejamiento radical de la filosofía aristotélica, donde todo movimiento horizontal necesitaba una causa inmediata. Al final se transformaría en la primera ley newtoniana del movimiento, la ley de la inercia. Era también lo que hacía falta para solucionar el dilema del objeto arrojado desde la torre de Pisa y, por otra parte, el problema, más general, de por qué no percibimos el movimiento de la Tierra. La superficie de la Tierra y todo lo que contiene están en movimiento horizontal, a causa de la rotación del planeta. Su estado natural es seguir así, de suerte que para un observador situado en la superficie de la Tierra, todo, por moverse al mismo tiempo, parece estar en reposo. Si un observador que estuviera realmente en reposo observara el experimento de la torre de Pisa, vería que tanto la torre como el objeto se movían a la vez en sentido horizontal, incluso mientras caía el objeto. Por eso aterriza el objeto al pie de la torre, y no más atrás.

Retrato de Galileo aparecido en Il Sagiatore, 1623.
El mismo razonamiento era válido, decía Galileo, para cualquier proyectil, por ejemplo una bala de cañón. Con una trayectoria horizontal, una bala de cañón (olvidándonos de la resistencia del aire) conservaría la velocidad inicial aportada por la explosión de la pólvora. Con una trayectoria vertical sería igualmente válida la ley de la caída de los cuerpos, incluso durante el ascenso de la bala. Combinando las dos clases de movimiento y barajando matemáticas, Galileo demostró que la trayectoria de cualquier proyectil próximo a la superficie de la Tierra describía una parábola. «Se ha observado», escribió en sus Consideraciones y demostraciones matemáticas sobre dos nuevas ciencias, de 1638, «que los proyectiles describen una trayectoria curva, pero nadie ha demostrado que sea una parábola. Que lo es lo demostraré juntamente con otras muchas cosas, también dignas de conocerse, y lo que es todavía más importante, que se abren las puertas de una inmensa e importantísima ciencia.» Una vez más, Galileo tenía razón: era una ciencia inmensa e importantísima. El descubrimiento de que su ley de la inercia (la tendencia de un cuerpo a moverse a velocidad constante en sentido horizontal), en combinación con la gravedad (representada por su ley de la caída de los cuerpos), originaba trayectorias próximas a la superficie de la Tierra con la forma de una sección cónica, la parábola, fue el mismo que Isaac Newton empleó más tarde para exponer cómo funcionaba el universo.

Portada del Dialogo… sopra i due massimi sistemi del mondo, Tolomaico e Copernicano de 1632. Por defender en este libro la teoría copernicana, Galileo fue procesado por la Inquisición romana y condenado arresto domiciliario perpetuo. La obra estubo en el índice de libros prohibidos hasta 1823.
Los conflictos de Galileo con la Iglesia (toda una epopeya pero no es el tema de este libro) tuvieron como resultado la expulsión de la revolución científica de suelo italiano. Se afincaría en Inglaterra, en la persona de Isaac Newton. Mientras viajaba al norte, sin embargo, se detuvo brevemente en Francia, donde encontró a René Descartes. Descartes sabía de líneas rectas. Las coordenadas cartesianas, con su conocido sistema x-y-z, se llaman así por él. La versión galileana de la inercia funcionaba sólo en sentido horizontal. Pero, según Galileo, cuando se prolongaba ilimitadamente, el movimiento horizontal a velocidad constante se convertía en movimiento circular alrededor del centro de la Tierra. A pesar de su inteligencia. Galileo no pudo desembarazarse de este rezagado ideal platónico. Descartes puso las cosas en su sitio. Describió la ley de la inercia tal como la emplearía Newton: si no se ejerce ninguna fuerza sobre los cuerpos, el cuerpo en reposo seguirá en reposo y el cuerpo en movimiento seguirá moviéndose, a velocidad constante, en línea recta.
Suele decirse que Isaac Newton nació en 1642, el año de la muerte de Galileo como si fuera necesario que hubiera siempre en el mundo un genio de estas características. La verdad es que nació el 4 de enero de 1643, según el calendario moderno y el que se empleaba en la Italia de Galileo. En Inglaterra no se había adoptado aún la última reforma papal del calendario por culpa de los problemas conyugales (o conceptuales) del rey Enrique VIII, de manera que el nacimiento se fechó el 25 de diciembre de 1642. En cualquier caso, Newton fue hijo póstumo y prematuro, una combinación insólita. El padre, llamado también Isaac Newton, falleció tres meses antes de nacer su hijo, y éste era una criatura frágil que no parecía destinada a vivir ochenta y cuatro años.

René Descartes
La madre de Isaac esperaba que, cuando se hiciese mayor administrase las cuantiosas propiedades que le había legado su segundo marido, fallecido cuando Isaac tenía unos once años. La verdad es que si el padre de Isaac hubiera vivido, o si su padrastro hubiera sido un individuo más humano el futuro físico habría sido de mayor un terrateniente razonablemente adaptado y muy industrioso. Pero las cosas no ocurrieron así. Por el contrario, de adulto fue un hombre cuya cólera desenfrenada lo ponía a veces al borde de la locura y que al final de sus días afirmaba que aún no había perdido la virginidad. No obstante, también fue un hombre que cambió la historia humana hasta un punto reservado sólo a unos cuantos.
En 1661, el joven Isaac se matriculó en el Trinity College de Cambridge, donde los planes de estudios seguían aún bajo la égida de Aristóteles, pero donde la revolución científica flotaba en el aire. Recibió el título de bachiller en 1665 y poco después, para huir de la peste bubónica, se refugió en las propiedades familiares de Lincolnshire. Se cree que durante los dos años que pasó allí hizo muchos de sus descubrimientos más importantes, pero el mundo no los conocería hasta mucho después.
Entre las numerosas hazañas de Newton, la más importante fue formular los principios dinámicos que sustituirían la concepción aristotélica del mundo. En 1687, cuando publicó su obra maestra, los Principia, lo había reducido todo a tres leyes, enriquecidas con una serie de definiciones y corolarios. La primera ley era el principio de inercia, heredado de Galileo y Descartes:
LEY 1
Un cuerpo no sometido a la acción de ninguna fuerza que le haga cambiar de estado permanece en reposo o en movimiento rectilíneo uniforme.
La segunda ley de Newton, auténtica piedra angular de su dinámica, explica lo que le ocurre a un cuerpo cuando está sometido a alguna fuerza:
LEY 2
El cambio de movimiento es proporcional a la fuerza motriz ejercida y se produce en el sentido de la línea recta en que se ejerce la fuerza.
Al comienzo de los Principia, Newton definía la cantidad de movimiento diciendo que era el producto de la velocidad (esto es la rapidez más la dirección) por la cantidad de materia, o dicho más exactamente, lo que los físicos actuales llaman momento. Mucho después de la muerte de Newton la segunda ley se resumió en la fórmula F = ma (fuerza igual a masa por aceleración); pero Newton no la expresó nunca de este modo.
La tercera ley de Newton se denomina ley de acción y reacción:
LEY 3
A toda acción se le opone siempre una reacción igual; o lo que es lo mismo, las acciones recíprocas de dos cuerpos son siempre iguales y tienen direcciones contrarias.
La tercera ley elimina una complicación potencialmente embarazosa que había en el problema del movimiento planetario. Los planetas (incluida la Tierra) son cuerpos muy grandes y complejos cuyas partes internas ejercen fuerzas entre sí. Según la tercera ley de Newton, estas fuerzas se anulan recíprocamente, sea cual fuere su naturaleza. Toda fuerza debida a un punto de un planeta que se ejerce sobre otro punto queda compensada por otra fuerza igual y opuesta que el segundo punto ejerce sobre el primero. El resultado neto es que la naturaleza bruta del planeta puede pasarse por alto completamente al calcular su trayectoria alrededor del Sol. El planeta se comporta como si su masa estuviera concentrada en un punto geométrico situado en su centro.
La tercera ley da a entender además que los planetas ejercen sobre el Sol fuerzas iguales y opuestas a las que ejerce el Sol sobre los planetas. Para soslayar los problemas que esta afirmación podría originar. Newton en su demostración formal, no se refiere al Sol, sino a «un centro inmóvil de fuerza». Newton supone (acertadamente) que el Sol tiene tanta masa que apenas se entera del tirón de las fuerzas gravitatorias de los planetas. La tercera ley sería tiempo después de importancia capital en otras áreas de la física, pues está en la base de las leyes de la conservación del momento, del momento angular y de la energía. En lo que respecta al problema del movimiento planetario, sin embargo, su principal virtud es que todos sus efectos pueden pasarse por alto.
Las tres leyes de Newton son los principios dinámicos que reemplazaron los movimientos «naturales» y «violentos» de la mecánica aristotélica. A estas leyes, válidas para todas las fuerzas y todos los cuerpos, Newton añadió la naturaleza concreta de una clase particular de fuerza que operaba entre el Sol y los planetas, o entre un planeta y sus satélites,o entre dos puntos materiales cualesquiera del universo. Era la fuerza de gravedad, y para deducir sus propiedades recurrió, como veremos después, a la segunda y tercera leyes de Kepler. Luego demostró que sus tres leyes, en combinación con la fuerza de gravedad, originaban las órbitas elípticas de los planetas.

Isaac Newton. Grabado de B. Reading, 1799, según un retrato de sir Peter Lely.
Isaac Newton inventó el cálculo diferencial y el integral. Es indudable que empleó estas potentes herramientas analíticas para hacer sus grandes descubrimientos. Sin embargo, cuando escribió los Principia no había publicado aún sus trabajos sobre el cálculo. (Más tarde se desataría una típica y aburrida polémica sobre quién había sido el verdadero inventor, si Newton o el filósofo y matemático alemán Gotfried Wilhelm Leibniz, que había hecho los mismos descubrimientos matemáticos por su cuenta.) Los Principia están escritos en dos idiomas clásicos, el latín y la geometría euclidiana. El motivo es evidente: Newton tenía que dirigirse a sus contemporáneos en un lenguaje que éstos entendieran. Puede que este método de presentación tuviera otra ventaja. Muchos años después, Richard Feynman (un hombre que no se parecía en nada a Newton, salvo en las cuestiones científicas) sintió tanta curiosidad que ideó su propia demostración geométrica de la ley de órbitas elípticas. «Es difícil descubrir cosas con el método geométrico», dijo en su conferencia sobre el tema (capítulo 4 de este libro), «pero la elegancia de la demostración, una vez hechos los descubrimientos, no tiene precio.»
Es notorio que Isaac Newton dijo que «si he alcanzado a ver tan lejos es porque me subí a hombros de gigantes». Los gigantes fueron Copérnico, Brahe, Kepler, Galileo y Descartes. Antes de Newton no había más que la confusión producida por el hundimiento de la concepción aristotélica del mundo y ningún indicio sobre cómo llenar el vacío que había dejado. Los gigantes de Newton pusieron algunos ladrillos o parte de los andamios, pero la forma y estructura del nuevo edificio no eran visibles aún. (Descartes creyó verlo, pero se equivocó.) Entonces llegó Newton y el mundo, de repente, estuvo otra vez en orden y se hizo previsible y comprensible. Newton había averiguado cómo funcionaba todo, y la demostración de que no se equivocaba fue su forma de probar la ley kepleriana de las elipses. No tardaremos en ver nuestra propia prueba de la ley de las elipses; no será exactamente como la de Newton, sino la ideada por Richard Feynman casi trescientos años después.
Primero, una ojeada a Richard Feynman.