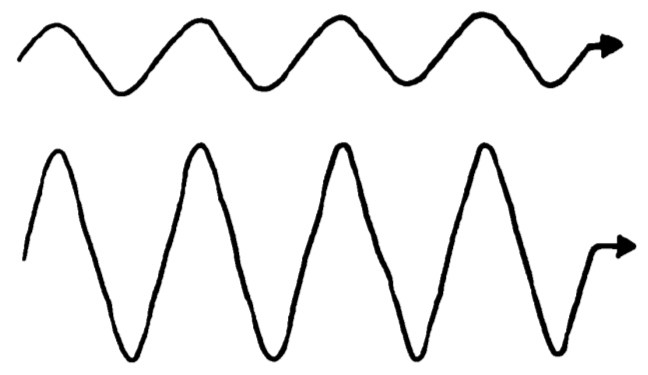
Patrones de ondas de la misma nota, con un volumen bajo (arriba) y alto (abajo). La frecuencia de la nota no ha cambiado, pero la nota más fuerte conlleva unas mayores variaciones de presión.
Todos notamos cuando el volumen de la música sube o baja, pero es extremadamente difícil precisar con exactitud la diferencia de volumen entre dos sonidos. Tratar de saber si un sonido tiene exactamente el doble de volumen que otro es tan difícil como tratar de decidir si un chiste te hace exactamente dos veces más gracia que otro.
Una de las rarezas más grandes del volumen tiene que ver con la suma de sonidos. Normalmente, cuando sumamos cosas, el resultado tiene sentido. Si le doy a Pepe una naranja y usted le da otra, entonces el suertudo de Pepe tiene dos naranjas; si yo le doy tres y usted le da dos, tiene cinco, y así sucesivamente. La suma de sonidos no funciona así. Cuando escuchamos a un solista tocando un concierto de violín con una orquesta, puede variar el número de personas que tocan en cada momento, entre uno y cien, en un segundo, pero no nos llevamos las manos a los oídos diciendo Vaya, el volumen de la música se ha multiplicado por 100. Es difícil generalizar sobre cuánto sube el volumen en estos casos; depende de qué instrumentos se usen y si el compositor ha dado instrucciones para que todos toquen fuerte o suave. Sería posible, por ejemplo, que la orquesta entera tocara más suave que un solo instrumento tocando fuerte.
Si sumamos el sonido de diez violines tocando juntos (y esto es cierto de cualquier otro instrumento), no oímos un volumen diez veces superior al de un solo instrumento. De hecho, es muy difícil estimar exactamente cuántas veces mayor es el volumen, aunque la mayor parte de la gente estará de acuerdo en que diez violines (tocando la misma nota con la misma fuerza) producen un volumen aproximadamente dos veces superior al de un solo violín. ¿Y cien por uno? El resultado es más o menos cuatro, obviamente.
Bien: entonces diez instrumentos suenan sólo el doble de fuerte que uno, y cien instrumentos cuatro veces. Estas afirmaciones, extrañas pero ciertas —como se suele decir—, requieren alguna explicación. Por fortuna, yo me había preparado una…
Antes de empezar nuestro análisis, quiero señalar que para simplificar hablaré de un solo tipo de instrumento cada vez —en la siguiente sección hablaré de flautas—, pero los datos son igualmente ciertos con grupos de distintos instrumentos.
Pues bien, imaginémonos que hemos conseguido reunir una orquesta de cien flautistas. Para empezar, hay silencio. Entonces una de las flautas empieza a emitir una nota. La diferencia entre el silencio y una flauta es impresionante, algo parecido a cuando estás a oscuras y enciendes una vela. Entonces otra flauta empieza a tocar la misma nota. Se nota la diferencia, pero no es tan grande como la diferencia entre el silencio y la primera flauta. Cuando se les une la tercera flauta, tocando la misma nota, hay poca diferencia en el volumen, y con la cuarta todavía menos. A medida que cada uno de los flautistas se une, tocando la misma nota, llega un momento en el que es imposible percibir el momento en el que empieza a tocar una flauta nueva, ya que la diferencia entre, por ejemplo, 62 y 63 flautas es muy pequeña.
Todo esto es muy extraño, ya que podríamos haber pedido al flautista número 63 que fuera el primero en tocar, en cuyo caso habría sido el que más diferencia habría marcado. De hecho, podríamos pedir a cada flautista que tocara solo, tan fuerte como fuera capaz, después de un silencio, y el volumen de todos ellos sonaría igual.
Hay dos razones por las que nuestros cien flautistas suenan menos fuerte de lo que cabría esperar. Una de ellas tiene que ver con la manera en que se combinan las ondas de sonido, y la otra tiene relación con el funcionamiento de nuestro sistema auditivo. Veamos cada una por separado.
Ya sabemos de sobra que una nota musical es un patrón regular de cambios en la presión del aire que hace que los tímpanos se flexionen hacia adentro y hacia afuera. El número de veces que se flexiona cada segundo informa al cerebro sobre el tono de la nota. Además, las notas más fuertes implican mayores cambios de presión, lo que hace que se flexione más el tímpano (y si se oye un sonido excesivamente fuerte, como una explosión, la alta presión flexionará tanto el tímpano que lo rasgará, una condición que se llama perforación del tímpano).
La siguiente ilustración nos indica lo que sucede. Ambos patrones de ondas tienen la misma frecuencia, pero uno implica mayores cambios de presión, por lo que deforma más el tímpano y tiene más volumen.

Patrones de ondas de la misma nota, con un volumen bajo (arriba) y alto (abajo). La frecuencia de la nota no ha cambiado, pero la nota más fuerte conlleva unas mayores variaciones de presión.
¿Qué le parece si vamos de compras? Usted vaya a una tienda de música y compre dos glockenspiels idénticos mientras yo voy a comprar un medidor de presión acústica. Este dispositivo tiene un micrófono que funciona exactamente como un oído: las ondas de presión presionan sobre una parte de modo que se flexiona hacia adentro y hacia afuera. También cuenta con un ordenador que mide la potencia de dichas ondas. Estoy utilizando un medidor de presión acústica porque responde de forma muy directa a los cambios en la presión del sonido —si se duplica la presión del aire, se multiplica por dos la lectura que da el ordenador.
Ahora lo único que necesitamos es un hotel grande y unos gemelos idénticos (confíe en mí, esto se va a poner interesante). Empezamos en una habitación donde pedimos al primer gemelo que golpee cualquier nota del glockenspiel a la vez que medimos la potencia de las ondas de presión que se producen. Digamos que el ordenador nos indica que el volumen de la nota justo después de golpear es de 10 unidades de presión.
Ahora llevamos al segundo gemelo a otra habitación del hotel y le pedimos que golpee la misma nota en el otro glockenspiel con la misma fuerza que su hermano (hemos escogido gemelos idénticos precisamente porque queremos que los dos golpeen con la misma fuerza). Como sería de esperar, cuando medimos las ondas de presión el ordenador nos indica que el máximo volumen es nuevamente diez.
Ahora los reunimos a los dos en la misma habitación. Primero hacemos que se turnen golpeando la nota. No es extraño que no haya diferencia entre las lecturas que obtenemos; mientras sigan golpeando la misma nota con la misma fuerza, el volumen es de diez unidades.
Finalmente, hacemos que los dos golpeen la misma nota a la vez. Podríamos esperar que el ordenador indique que diez más diez da veinte. Pero no. Podemos repetir la prueba varias veces, y la lectura media de la combinación de ambas notas será más o menos catorce. Una parte de nuestro sonido ha desaparecido.
Y si fuéramos a comprar más glockenspiels y contratáramos a más gemelos, resultaría que para cuarenta instrumentos, en lugar de obtener una lectura de cuatrocientos el resultado es de apenas sesenta y tres.
Vaya desilusión. Tenemos una habitación llena de costosos gemelos y glockenspiels y resulta que una gran parte del sonido simplemente desaparece. Vamos a pedirles que se vayan a la cafetería del hotel a tomarse algo mientras explico lo que está sucediendo.
Cuando usamos un solo instrumento, obtenemos los mejores resultados por nuestro esfuerzo. Golpeamos la barra, que empieza a deformarse hacia arriba y hacia abajo y transmite esas vibraciones al aire como ondas de presión. Así que con ese golpe obtenemos el 100% de lo que hemos pagado.
Sin embargo, con dos instrumentos conseguiríamos el doble del efecto únicamente si las ondas de presión estuvieran exactamente sincronizadas entre sí. En ese caso, actuarían juntas para generar una onda de presión que va ARRIBA-ABAJO-ARRIBA-ABAJO.
Pero cuando golpeamos ambos instrumentos, es prácticamente imposible que los golpeemos al mismo tiempo exactamente, así que las ondas de ambos instrumentos no estarán sincronizadas cuando lleguen al micrófono. El resultado será que en ciertos momentos, una onda estará intentando subir la presión del aire a la vez que la otra está intentando bajarla. De hecho, si las notas de ambos instrumentos estuvieran exactamente desincronizadas, el movimiento arriba-abajo-arriba-abajo de uno se vería cancelado por el movimiento abajo-arriba-abajo-arriba del otro, y la nota quedaría totalmente anulada.
Esto es extraño, pero cierto. Así es como algunos agricultores se protegen los oídos cuando conducen un tractor ruidoso todo el día. Se compran unos protectores, que son auriculares que en el interior llevan un micrófono y un altavoz. Estos van conectados a un dispositivo electrónico que recoge el sonido que está a punto de llegar al oído y genera una onda de presión idéntica pero perfectamente desfasada con la original. En teoría, cuando ambas ondas se encuentran, una de ellas intenta subir la presión mientras la otra la intenta bajar, así que no sucede nada y el tímpano no recibe ninguna agresión. En la práctica, las ondas de sonido son demasiado complicadas para que esto funcione a la perfección, pero sí es verdad que se reduce la mayor parte del ruido.
Volviendo a nuestros glockenspiels, las vibraciones no se cancelan de forma perfecta porque sería algo demasiado difícil de organizar: las ondas sonoras vienen desde distintos lugares de la habitación y rebotan contra las paredes, además de que es prácticamente imposible golpear ambos instrumentos en el momento preciso para que las ondas estén perfectamente desfasadas justo en el momento en que alcanzan el micrófono. Lo que sucede en la realidad es que aunque se genera más presión sonora con dos instrumentos que con uno, hay un determinado grado de interferencia entre las secciones de baja presión de un conjunto de ondas con las de alta presión del otro, de modo que se cancelan mutuamente en parte.
Si participa un mayor número de instrumentos, el grado de cancelación es más importante. La presión del aire junto al micrófono puede ser mayor de lo normal (lo que empuja el micrófono) o menor que lo normal (lo que tira de él), pero no las dos cosas a la vez. Todos nuestros cuarenta glockenspiels pueden subir o bajar la presión en un momento determinado, pero su influencia es contrarrestada por otros en gran medida. Si el glockenspiel número cuarenta y uno se incorporase a nuestra pequeña fiesta, su nota quedaría cancelada casi en su totalidad, pero una pequeña parte sí se mantendría y contribuiría al volumen total.
Así que esa es la razón por la que las combinaciones de instrumentos hacen menos ruido del que se podría esperar. Pero este no es el único factor en nuestra percepción del volumen. Por este efecto exclusivamente, 100 instrumentos tendrían un volumen de 10, pero como he señalado anteriormente, nosotros percibimos su volumen como cuatro veces el de un solo instrumento. Esta mayor disminución es el resultado de la manera en que estamos diseñados los seres humanos. Vamos a echarle un vistazo.
¿Por qué nuestro cerebro no suma de forma normal el sonido? La respuesta puede resultar sorprendente: nuestro cerebro y oídos suman los sonidos de forma extraña para ayudarnos a seguir vivos. Desde los tiempos de los primeros cavernícolas hasta nuestros días, hemos utilizado los oídos para evitar el peligro. De hecho, esta es una de las causas principales por las que tenemos oídos (aunque también son útiles para llevar gafas de sol[*]). Para ser eficaces, los oídos tienen que ser capaces de detectar sonidos muy suaves (como el sonido de alguien que se te acerca a hurtadillas), pero a la vez no deben ser dañados por los ruidos fuertes (como un trueno). No serviría de nada si tuviéramos un oído excelente para los sonidos suaves pero que dejara de funcionar al primer ruido fuerte que oyéramos.
Si un sonido es suave, el funcionamiento de nuestro sistema auditivo permite que lo oigamos nítidamente, pero a medida que sube el volumen, el ruido tiene cada vez menos incidencia. Esto sucede también con el resto de nuestros sentidos: el olfato, el gusto, la vista y el tacto. Seis calcetines apestosos no nos resultan seis veces más apestosos que uno solo (incluso si cada calcetín despide la misma cantidad de olor) y diez cacahuetes salados no nos resultan cinco veces más salados que dos (aunque ahora tenemos cinco veces más sal en la lengua). Si encendemos cien velas en una habitación oscura se producirá el mismo efecto que con las flautas: la primera es la que más diferencia marca; la número ochenta y siete casi no se nota. Y si estamos tan locos como para clavarnos un alfiler en el dedo, nos dolerá; pero si nos clavamos otro (junto al primero), no sentiremos el doble de dolor.
Alguien me preguntará por qué he señalado específicamente que los alfileres deben estar juntos. Bueno, sí hay una razón, y es sorprendentemente relevante para nuestro análisis sobre el volumen del sonido. Imaginemos que accidentalmente piso una chincheta con el dedo gordo del pie. Obviamente sentiría mucho dolor y probablemente juraría en arameo. Si pisara dos chinchetas con el dedo gordo, la sensación global sería un poco peor, pero ni de lejos sentiría dos veces más dolor. Si, por el contrario, me clavara una chincheta en el dedo gordo izquierdo y otra en el derecho, el dolor que sentiría sería mucho mayor que si me las clavo las dos en un solo dedo (por favor, que nadie haga la prueba; sencillamente créanme). La causa de este aumento de dolor es el hecho de que mi cerebro recibirá dos señales de dolor, una de cada pie, en lugar de una sola señal de haberme clavado dos chinchetas en un dedo.
¿Y qué tiene que ver todo esto con la música? Bueno, al principio dijimos que el sistema formado por el oído y el cerebro hace el cálculo según el cual diez flautas tienen aproximadamente el doble de volumen que una flauta. Esto es así sólo si todas ellas tocan la misma nota. Si las dividimos en dos grupos y pedimos al grupo 1 que toque una nota con un tono mucho más agudo o mucho más grave que el grupo 2, entonces las dos notas tocadas simultáneamente serán más fuertes que cuando todo el mundo toca la misma nota. Pero para que esto se cumpla, la diferencia de los dos tonos tiene que ser mayor que la diferencia entre pa y ni en Campanita del lugar. Una razón de este aumento de volumen es el hecho de que el cerebro estará recibiendo entonces dos señales sonoras distintas (como las dos señales de dolor). La otra razón es que cada una de las notas se verá menos cancelada por las ondas simultáneas, al ser más pequeño el grupo.
La sensibilidad de nuestro sistema auditivo no es igual en todas las frecuencias. La demostración más extrema de esto es que hay sonidos que no podemos oír en absoluto porque tienen un tono demasiado agudo (por ejemplo, los de un silbato para perros) o demasiado grave (por ejemplo, los infrasonidos que a veces experimentamos cuando el motor de un gran camión hace vibrar las ventanas del edificio donde nos encontramos). Tanto el silbato para perros como la vibración de las ventanas producen un sonido, pero nuestros oídos no están hechos para percibirlos. Incluso dentro del rango de sonidos que puede percibir el oído humano, hay diferencias de sensibilidad. Nuestra máxima sensibilidad es a los sonidos bastante agudos, chillones, que se corresponden a las notas más altas del flautín, que es la razón por la que en una orquesta o banda oímos ese instrumento claramente por encima de todos los demás. De hecho, los libros de texto de música aconsejan a los compositores que utilicen poco el flautín, ya que es difícil de mezclar con los demás instrumentos.
A frecuencias más altas o más bajas de este rango agudo, chillón, nuestros oídos van perdiendo sensibilidad. La mayoría de las notas musicales están por debajo. Eso significa que si aspiramos a conseguir un sonido que equilibre un instrumento grave, como el fagot y un instrumento más agudo, como el clarinete, es posible que el fagotista tenga que tocar tan fuerte como pueda mientras que el clarinetista se lo toma con tranquilidad. De igual manera, si dos instrumentos idénticos tocan juntos pero uno toca notas altas y el otro bajas, este último debe tocar más fuerte para que su volumen se perciba como parecido al de las notas altas.
Otra peculiaridad más del volumen tiene relación con la duración de las notas. El volumen normal de una nota se aprecia si dura un segundo más o menos, pero si se toca durante medio segundo o menos sonará menos fuerte. Hay que tener en cuenta que muchas piezas de música contienen notas que duran menos de medio segundo. Por ejemplo, cuando en Campanita del lugar cantamos del lugar, la única sílaba que dura más de medio segundo es gar.
Por otro lado, si una nota se toca durante varias decenas de segundos, su volumen parece disminuir a medida que el cerebro empieza a notarla menos. Este efecto de disminución de intensidad en un estímulo continuado también se da con el resto de nuestros sentidos, sobre todo el olfato (de lo cual podemos estar contentos a veces). La razón por la que el sonido parece disminuir después de un rato es que el cerebro está constantemente monitorizando los sentidos en busca de señales de peligro. Si un sonido es continuo y no está sucediendo nada malo, el cerebro pierde interés porque obviamente no es importante para nuestra seguridad. A nuestro cerebro le interesa sobre todo cualquier cambio en los sonidos que oímos. Esa es la razón por la que nos ponemos alerta cuando un sonido de larga duración cesa de golpe —el efecto del silencio ensordecedor.
A los humanos nos encanta medir las cosas. Medimos nuestra estatura, nuestro peso, la velocidad de nuestros coches y el tamaño de nuestros baños. Las medidas nos ayudan a hablar de las cosas con más precisión y claridad. Por supuesto, hay muchas cosas a las que no les podemos aplicar un sistema preciso de medidas, como la habilidad para besar o las destrezas sociales de un hámster, pero siempre que podemos, inventamos y utilizamos un sistema de medición. Como veremos a continuación, la invención de un sistema para medir el volumen fue casi tan complicado como lo sería para medir los besos (y probablemente fue mucho menos divertido). Antes de empezar esta sección, quisiera repasar un par de cuestiones sobre los sistemas de medición en general.
Hay dos tipos básicos de sistemas de medición: el absoluto y el comparativo (o relativo). Si usamos el tipo absoluto, decimos: El granjero González tiene ocho vacas y el granjero Rodríguez tiene cuatro vacas. Si usamos un sistema comparativo, diremos: El granjero González tiene el doble de vacas que el granjero Rodríguez. Como se puede ver, ambos sistemas nos dan información útil, si bien el sistema absoluto es más preciso, razón por la que solemos utilizarlo normalmente. Sin embargo, hay casos en los que no podemos usar un sistema absoluto y hemos de recurrir a uno comparativo. Sí, lo ha adivinado… el volumen es uno de esos casos incómodos.
Puesto que nuestros oídos responden a los cambios de presión, cualquier sistema para medir el volumen debería estar basado en la medición de la presión. Por desgracia, sin embargo, el primer sistema de medición del volumen se adaptó de un método para medir la disminución de fuerza en las señales eléctricas tras recorrer un cable eléctrico de una milla. Así que acabamos teniendo un sistema basado en la intensidad en vez de la presión. Esto equivaldría a medir la distancia en litros de gasolina (si entre Londres y Nottingham hay 35 litros de gasolina, entonces la distancia entre aquí y Bolton es de 27 litros). Dichas cifras son útiles y precisas a su manera, pero se trata de un sistema bastante engorroso. El sistema de intensidad de energía para medir el volumen del sonido tiene ventajas y desventajas, como veremos a continuación.
¿Recuerda nuestros gemelos con sus glockenspiels? Se cansarían igual de golpear el instrumento en habitaciones separadas que al tocar juntos. En ambos casos, utilizarían la misma cantidad de energía, y no es culpa suya que las ondas de presión rehúsen colaborar completamente. El sistema de intensidad se fija en cuánta energía ambos han dedicado a dar sus golpes y no al sonido que producen. Este sistema dice: la energía dedicada a golpear no se modifica por el hecho de que estén en la misma habitación; un golpe más un golpe, igual a dos golpes de intensidad energética. Esta comodidad para utilizar una suma simple es la principal ventaja del sistema de medición del volumen basado en la intensidad.
Si tomamos un micrófono, lo conectamos a un ordenador y le pedimos que convierta las lecturas de la presión en medidas de intensidad energética, podemos sumar los sonidos con las reglas normales de la aritmética. A un ordenador se le puede pedir que detecte que los diez flautistas están trabajando igual de duro para producir diez veces más potencia acústica que un solo flautista. Así que, por ejemplo, podríamos decir: Diez violines producen diez veces más potencia acústica y dos veces más volumen que un solo violín.
Digamos que vamos a utilizar un ordenador y un micrófono para medir la potencia acústica que hay entre el silencio absoluto y un doloroso daño a los oídos. Después de algunos experimentos minuciosos, podríamos encontrar el silencio más suave que puede oír un ser humano. Entonces podríamos configurar el ordenador para que a esta intensidad le asignara el valor de uno, y a esto lo podríamos llamar umbral auditivo. Este sonido podría ser, quizá, equivalente al de una persona suspirando a diez metros de distancia. Pues bien, si diez personas estuvieran a diez metros de distancia, suspirando (no entraremos aquí en las causas de tanta infelicidad), entonces el ordenador le asignaría a este sonido un valor de diez, si bien nosotros lo oiríamos a sólo el doble de volumen.
Ahora dejemos a esos pobres desgraciados y midamos el sonido de unas motos y de unas bandas de música. Nos podemos imaginar que para cuando lleguemos a los niveles de ruido que producen dolor (por ejemplo, colocar el oído a unos centímetros de una taladradora de las que usan en las carreteras), estaremos midiendo intensidades sonoras varias veces mayores que nuestro suspiro original. Bueno, prepárese para quedarse boquiabierto. La intensidad que produce dolor es 1.000.000.000.000 de veces mayor que la del sonido más suave que podemos oír. Sí, la potencia acústica generada por una taladradora de obras públicas es un billón de veces más grande que la del suspiro. Así que si está insatisfecho como operador de taladro y quiere que se aprecien sus suspiros, acuérdese de apagar el taladro.
Pero ahora necesitamos poner los pies sobre la tierra. Como he dicho antes, nuestros oídos no miden la intensidad, sino que monitorizan las diferencias de presión. Estas diferencias sí tienen relación con las intensidades, pero para convertir la intensidad en presión necesitamos hacer un cálculo. El resultado de la conversión es que la diferencia de presión entre el silencio casi absoluto y el dolor no es de 1.000.000.000.000, sino apenas de 1.000.000 —un millón. Sigue tratándose de un número enorme, pero no es un número ridículamente enorme.
Volvamos al mundo de la medición de la intensidad. Ya sabemos que cada vez que multiplicamos la potencia acústica por diez (cuando tocan diez violinistas en vez de uno) el volumen del sonido se duplica. Así que hagamos una lista de sonidos que abarquen desde el más suave hasta el más fuerte que podemos oír. Cada uno de estos sonidos tiene el doble de volumen que el anterior.
Lista de sonidos desde el umbral auditivo hasta el umbral del dolor
| Ejemplo | Volumen relativo | potencia acústica relativa |
|---|---|---|
| Casi silencio (suspiro a diez metros) | 1 | 1 |
| Mosca pequeña en la habitación | 2 | 10 |
| Abeja grande en la habitación | 4 | 100 |
| Alguien tarareando una melodía | 8 | 1.000 |
| Conversación tranquila | 16 | 10.000 |
| Violín solo —a medio volumen | 32 | 100.000 |
| Restaurante bullicioso (o diez violines) | 64 | 1.000.000 |
| Tráfico urbano en hora punta | 128 | 10.000.000 |
| Orquesta tocando fuerte | 256 | 100.000.000 |
| Discoteca muy ruidosa | 512 | 1.000.000.000 |
| Cerca de los altavoces, concierto de rock | 1.024 | 10.000.000.000 |
| Gran explosión de fuegos artificiales | 2.048 | 100.000.000.000 |
| Dolor —a unos centímetros de una taladradora | 4.096 | 1.000.000.000.000 |
(Todos estos ejemplos son meramente orientativos, naturalmente. Quizá en la zona donde usted vive haya abejas ruidosas y bulliciosas, o quizá su hermana tenga un volumen extraordinariamente alto cuando tararea.)
Esta tabla ilustra algunas de las ideas más importantes sobre el volumen y proporciona dos métodos para comparar los sonidos fuertes y los suaves. Sin embargo, ninguno de los dos nos brinda una escala numérica útil, ya que se trata de unas cifras excesivamente altas. Las cifras referidas a la potencia acústica relativa, en la columna de la derecha dice que una mosca tiene un valor de 10 y el violín 100.000. Si esto es así, entonces necesitaríamos casi 10.000 moscas pequeñas en la habitación para producir la misma potencia acústica que la de un violín. Esto es un dato muy útil si usted es un granjero que se dedica a la cría de moscas y además toca el violín, pero seguimos necesitando un sistema para medir el nivel del ruido que utilice un rango de cifras más reducido.
La búsqueda de un sistema con un rango pequeño de cifras le dio a alguien, en algún momento de la primera mitad del siglo XX, la ingeniosa idea de una escala de volumen basada en cuántos ceros había después del 1 en la columna de potencia acústica relativa de la tabla de arriba. Esta es la escala de belios, según la cual una intensidad de 1.000 tendría un volumen de 3 belios, 1.000.000 sería 6 belios, etc. (en cada caso es cuestión de contar los ceros). Esto se consideró una idea brillante durante unos siete minutos y medio, hasta que alguien todavía más listo señaló que eso sólo nos da doce cifras para medir el rango de volúmenes que va entre extremadamente silencioso hasta dolorosamente fuerte y eso no iba a ser un sistema muy útil, ya que ahora no contaríamos con suficientes cifras.
Así que finalmente se decidió que un sistema con ciento veinte medidas de volumen prometía ser más útil, y que eso se conseguiría multiplicando por diez todos los números del sistema de belios, con lo que el volumen se mediría en décimas de belios, o decibelios. Así que ahora tenemos un sistema en el que una potencia acústica de 1.000 equivale a 30 decibelios, 1.000.000 es 60 decibelios, etc. (se trata de contar el número de ceros y multiplicar por 10). Un esquema sencillo de lo que significa para nuestros oídos el sistema de decibelios (decibelio se suele abreviar como dB).
Potencia, decibelios y volumen
| Potencia acústica relativa | Decibelios | Volumen relativo | |
|---|---|---|---|
| 1 | 0 | 1 | (casi silencio —suspiro) |
| 10 | 10 | 2 | (mosca pequeña) |
| 100 | 20 | 4 | (abeja grande) |
| 1.000 | 30 | 8 | (tarareo) |
| 10.000 | 40 | 16 | (conversación tranquila) |
| 100.000 | 50 | 32 | (violín solo) |
| 1.000.000 | 60 | 64 | (restaurante bullicioso) |
| 10.000.000 | 70 | 128 | (tráfico en hora punta) |
| 100.000.000 | 80 | 256 | (orquesta tocando fuerte) |
| 1.000.000.000 | 90 | 512 | (discoteca) |
| 10.000.000.000 | 100 | 1.024 | (altavoces en un concierto de rock) |
| 100.000.000.000 | 110 | 2.048 | (petardo grande) |
| 1.000.000.000.000 | 120 | 4.096 | (dolor —taladro de obras públicas) |
Ahora tenemos un sistema que sirve para medir el volumen desde el sonido más suave hasta el más fuerte y que sólo incluye valores entre 0 y 120. Pero me temo que, aunque los números son sencillos, la utilización de esta escala es complicada. Parece muy simple hasta que nos damos cuenta de que no sólo 20 dB es el doble de volumen que 10 dB (algo que parece obvio), sino que 90 dB es el doble de volumen que 80 dB (lo que parece una locura, pero es verdad: basta con mirar la tabla).
En este momento es necesario que yo haga una confesión: no me gusta en absoluto el sistema de medición de volumen. No es fácil de usar incluso si has estudiado matemáticas o física a nivel universitario. Incluso un científico profesional necesitaría una calculadora y varios minutos para poder indicarnos la diferencia de volumen entre 53 y 87 decibelios. No tengo pruebas de esto, pero me parece que el decibelio fue inventado en un bar, a altas horas de la madrugada, por un comité de ingenieros eléctricos borrachos que querían vengarse del mundo porque no tenían con quién bailar. Además de los problemas de cálculo, la utilización de la intensidad para medir sonidos es indirecta y excesivamente complicada.
Al principio de este libro prometí que no habría fórmulas matemáticas y tengo la intención de cumplir mi promesa. Sin embargo, no puedo explicar cómo calcular la diferencia entre 53 y 87 decibelios sin usar fórmulas. Si a algún lector le gustaría contar con más información sobre el sistema de decibelios, podrá encontrarla en la parte B de la sección sobre Detalles Engorrosos, al final del libro. Sin embargo, pienso que deberíamos dejar detrás los horrorosos decibelios y seguir adelante para echar un vistazo a los sistemas más sencillos desarrollados en la década de 1930 por una serie de investigadores estadounidenses, con el psicólogo experimental Stanley Smith Stevens a la cabeza.
Mientras los ingenieros eléctricos se reían entre ellos sobre cómo nos habían endilgado el sistema del decibelio, los diseñadores de salas de conciertos y los psicólogos especializados en la percepción auditiva decidieron contraatacar. Puesto que se pasaban el día trabajando con mediciones del volumen, sabían que el decibelio tenía dos grandes defectos.
Gran Defecto 1: Como he señalado anteriormente, el sistema auditivo humano es más sensible a unas frecuencias que a otras. Esto significa que una nota aguda de una flauta a 32 dB sonará más fuerte (para un humano) que una nota grave de un contrabajo a 32 dB, así que como sistema de medir el volumen para los seres humanos no es fiable.
Gran Defecto 2: antes del nacimiento de las calculadoras de bolsillo, tenías que pasarte la noche entera con seis lápices y tres gomas para calcular cosas como, ¿Qué diferencia de volumen hay entre 49 y 83 dB? Incluso cuando ya había calculadoras, te tenías que comprar una con un número absurdo de botones y un manual de instrucciones tan gordo como el listín telefónico.
¡Ajá!, dijeron los psicólogos experimentales, podemos prescindir del decibelio y desarrollar un sistema que se corresponda más con la respuesta del oído humano. (Los psicólogos experimentales hablan con este tono de superioridad y pedantería siempre que tienen la ocasión.)
La única forma de desarrollar un sistema basado en la respuesta subjetiva del oído humano es efectuar pruebas con muchísimas personas. Por eso el trabajo lo hicieron psicólogos: medían las opiniones de las personas más que cosas que se puedan medir con instrumentos.
El primer conjunto de pruebas tenía como fin contrarrestar el Gran Defecto 1, y en él participaron muchas personas a las que pidieron que compararan notas de distintas frecuencias y que dijeran cuándo les parecía que tenían el mismo volumen. A partir de estas observaciones, que se realizaron con una gama amplia de volúmenes y frecuencias, se desarrolló una unidad de volumen llamada fonio.
Para explicar la diferencia entre los fonios y los decibelios, imaginemos que hemos programado un robot para que toque el piano para nosotros. Primeramente le pedimos que produzca un volumen de 50 decibelios para cada nota y que toque todas las notas, una a una, empezando por la más aguda.
Puesto que nuestros oídos pierden sensibilidad a medida que nos movemos de las notas más agudas a las más graves, nos parecería que las notas perdían volumen a medida que el robot avanzaba por el teclado. Por otro lado, un ordenador que contara con un micrófono para escuchar las notas, detectaría que todas ellas tienen la misma intensidad de energía.
Ahora le pedimos al robot a repetir las notas, pero en esta ocasión produciendo un volumen de 50 fonos para cada nota. Esta vez nuestro amigo mecánico aumentaría la fuerza con la que golpea las teclas a medida que avanza por el teclado. Nosotros oiríamos todas las notas al mismo volumen, puesto que el robot estaría compensando el hecho de que no podemos oír los graves del piano tanto como los agudos. Por otro lado, el ordenador detectaría exactamente lo que hace el robot y registrará que está tocando más fuerte las notas graves.
El sistema del fono es, simplemente, el sistema del decibelio, pero compensando el hecho de que el oído humano es menos sensible a las notas graves.
Habiendo conquistado el Gran Defecto 1, los psicólogos abordaron el Gran Defecto 2. Puesto que el sistema del fono es básicamente una versión del sistema del decibelio, tenemos el mismo problema cuando intentamos que las cifras signifiquen algo. ¿Qué diferencia de volumen hay entre 55 y 19 fonos? Que alguien me pase la calculadora y unas galletas de chocolate.
Así que los psicólogos decidieron prescindir por completo de los decibelios y buscar una manera de utilizar una escala basada en volumen relativo, causando gran consternación entre los ingenieros eléctricos que habían desarrollado el sistema del decibelio. No ha habido intercambio de invitaciones a fiestas entre los dos grupos desde 1936.
Si volvemos a mirar la última tabla, vemos que la escala de volúmenes relativos va desde 1 (suspiro) hasta 4.096 (taladradora de obras públicas) y que, como hemos señalado, maneja cifras demasiado abultadas como para constituir una escala útil. Pero… un momento… los sonidos fuertes son así de grandes únicamente porque hemos empezado asignando el número 1 al sonido más suave que podemos oír. Eso sería como calcular el precio de todo en céntimos. No decimos, el coche me costó 800.000 céntimos. No necesitamos utilizar la moneda más pequeña posible como nuestra unidad de medida. Los psicólogos lo pensaron y decidieron pasar el 1 de un sonido extremadamente suave a algún punto en el centro de nuestro rango auditivo. Lo asignaron al nivel de una conversación bastante tranquila. Así, el rango actual sitúa el 1 donde antes estaba el 16. Esto significa que tenemos que dividir todas las cifras de nuestra columna de volumen relativo entre 16, de modo que actualmente las cifras que se manejan sólo suben hasta 256, como se puede apreciar en la siguiente tabla. Aunque tenemos que utilizar fracciones para los sonidos suaves, esto no presenta una gran dificultad, ya que no necesitamos fijarnos en los sonidos muy suaves muy frecuentemente.
Así que ahora tenemos un sistema que realmente funciona para los seres humanos. Se basa en el sonio como unidad de medida, y no hay que preocuparse por grandes cifras o por operaciones matemáticas complejas: 8 sonios tienen el doble de volumen que 4 sonios y 5 sonios suenan la mitad de fuerte que 10 sonios.
Sistema de medida de volumen basado en el sonio
| Ejemplo | (después de compensar la frecuencia) | Sonios |
|---|---|---|
| Casi silencio (un suspiro a 10 metros) | 1 | 0,06 |
| Mosca pequeña en la habitación | 2 | 0,12 |
| Abeja grande en la habitación | 4 | 0,25 |
| Alguien tarareando en la proximidad | 8 | 0,5 |
| Una conversación bastante tranquila | 16 | 1,0 |
| Violín solo —volumen moderado | 32 | 2,0 |
| Restaurante bullicioso (o diez violines) | 64 | 4,0 |
| Tráfico urbano —hora punta | 128 | 8,0 |
| Orquesta tocando a alto volumen | 256 | 16,0 |
| Discoteca muy ruidosa | 512 | 32,0 |
| Proximidad de los altavoces, concierto de rock | 1.024 | 64,0 |
| Explosión de un gran petardo | 2.048 | 128,0 |
| Dolor —a unos centímetros de una taladradora de obras públicas | 4.096 | 256,0 |
Los medidores de volumen modernos deberían medir los distintos niveles en sonios, ya que se trata del sistema más sensato para monitorizar y analizar el volumen desde el punto de vista del ser humano. Por ejemplo, si una guitarra acústica tiene 4 sonios de volumen y el nivel de una banda de rock es de 40 sonios, eso significa que la banda tiene diez veces el volumen de la guitarra para un oyente humano. Puesto que este sistema está basado en la audición humana, los instrumentos de medición en sonios realizan automáticamente las compensaciones necesarias para las distintas frecuencias. Este tipo de medidores ayudan a los ingenieros a desarrollar mejores altavoces y materiales de aislamiento acústico.
Habrá notado, sin embargo, mi utilización de la palabra deberían al principio del párrafo anterior. De hecho, la mayoría de las mediciones de volumen que se realizan hoy en día utilizan los decibelios, aunque normalmente se realiza un ajuste según la sensibilidad humana a las distintas frecuencias. Esto sucede así sencillamente porque el sistema basado en el decibelio fue el primero en establecerse y es al que hacen referencia los documentos oficiales y la legislación respecto a los niveles de ruido y la insonorización. Así que no nos queda más remedio que usarlo.
Pero un día nos alzaremos todos y, empalando nuestras calculadoras científicas en taladradoras de obras públicas especialmente puntiagudas, nos liberaremos de los malvados grilletes opresores del ridículo y abominab…
Pero quizá estoy perdiendo un poco mi objetividad fría de autor… cambiemos a un tema con menos carga de controversia: el arte y la ciencia de la armonía.