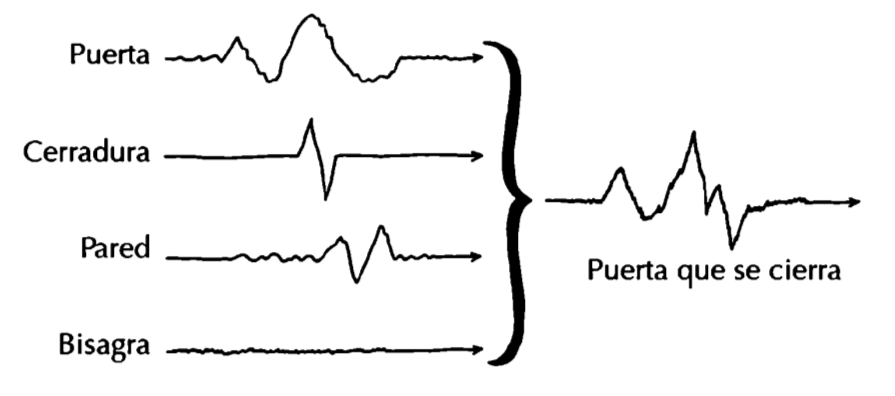
Para formar un ruido se unen varios conjuntos de ondas de presión. Las ondas generadas por una puerta, una cerradura, una pared y una bisagra se unen para formar el ruido completo de una puerta que se cierra.
Cada día oímos millones de sonidos y sólo unos pocos son notas musicales. Normalmente, las notas musicales se crean deliberadamente a partir de un instrumento musical, pero también pueden producirse en situaciones ajenas a la música, como cuando golpeas ligeramente una copa de vino o haces sonar el timbre de una puerta. Al margen de cuándo y cómo se produzcan, las notas musicales tienen un sonido distinto al de otros sonidos.
¿Cuál es la diferencia entre una nota musical y cualquier otro tipo de sonido? Todas las personas que usted conoce responderán a esto de alguna forma, pero la mayoría se basará en la idea de que las notas musicales suenan… mmm… musicales y los otros sonidos no son… mmm… musicales.
La música nos afecta emocionalmente y puede amplificar o transformar nuestro estado de ánimo. Un buen ejemplo de esto es la manera en que la banda sonora de una película nos da pistas de cómo debemos responder emocionalmente a la escena que estamos viendo: el romance, el humor o la tensión se ven potenciados por la música que los acompaña. Esta vinculación entre música y emoción nos podría hacer pensar que las propias notas poseen un contenido emocional y que, de alguna manera, son sonidos misteriosos y mágicos. Pero aunque sí existe una genuina diferencia entre las notas musicales y todos los demás sonidos, no tiene nada que ver con la emoción, y un ordenador podría detectar dicha diferencia sin vacilar.
Si arroja una piedra a un estanque tranquilo, agitará la superficie del agua y creará ondas que se irán alejando del impacto inicial. De manera parecida, si chasquea los dedos en una habitación silenciosa, agitará el aire y se generarán ondas de aire que se irán alejando de sus dedos.
En el caso de la piedra en el estanque, las ondas significan un cambio en la altura del agua, y nosotros podemos ver claramente lo que está sucediendo: la altura del agua sube, baja, sube, baja, sube, baja, etc., y las ondas se alejan del lugar del impacto.
Cuando chasqueamos los dedos (o hacemos cualquier otro sonido, incluida una nota musical), las ondas de sonido que viajan hasta nuestros oídos son cambios de presión del aire. No podemos ver esas ondas, pero nuestros oídos las detectan. Cuando las ondas llegan hasta nuestros oídos, la presión del aire baja, y luego sube y baja y sube y baja, lo que hace que los tímpanos se muevan hacia adentro y afuera y adentro y afuera y adentro y afuera al mismo ritmo, ya que nuestros oídos son como unas minúsculas camas elásticas que fácilmente son empujadas hacia adentro o hacia afuera por los cambios de la presión del aire. Entonces nuestro cerebro analiza esos movimientos del tímpano y descifra lo que está sucediendo: ¿es el momento de echar a correr o el momento de pedir el postre?
A medida que crecemos, vamos desarrollando una enorme habilidad para identificar e interpretar los sonidos: el agua hierve, alguien extiende mantequilla sobre una tostada, alguien más corta leña, el cajero automático hace un simpático clic mientras se come nuestra tarjeta de crédito. Vamos acumulando una enorme biblioteca de sonidos que nos ayudarán a entender lo que sucede a nuestro alrededor.
Si pudiéramos ver las ondas de presión de estos sonidos no musicales, notaríamos que son muy complicados. La onda básica se creará por todo tipo de cosas que suceden al mismo tiempo; el sonido de una puerta que se cierra puede incluir las vibraciones producidas por la puerta, por la cerradura, por la pared y por las bisagras, y cada una de estas complejas vibraciones individuales se combina con las demás para producir un conjunto todavía más complicado de ondas de presión de aire.
Imaginemos que podemos ver las ondas de presión producidas por una puerta que se cierra. En la parte izquierda de la siguiente ilustración he dibujado unas posibles representaciones de las ondas[3] de la puerta, la cerradura, la pared y las bisagras por separado. A la derecha de la ilustración las he combinado para indicar la forma de la onda principal que hace que nuestros tímpanos se muevan hacia adentro y hacia afuera cuando se cierra la puerta.

Para formar un ruido se unen varios conjuntos de ondas de presión. Las ondas generadas por una puerta, una cerradura, una pared y una bisagra se unen para formar el ruido completo de una puerta que se cierra.
La forma de las ondas que finalmente llega al tímpano del oído a partir de un ruido es extremadamente compleja porque está constituida por un grupo caótico de ondas individuales que no tienen relación entre sí. Esto es cierto de todos los ruidos que no son notas musicales.
Las notas musicales son distintas a los sonidos no musicales en que cada nota musical está formada de un patrón de ondas que se repite una y otra vez. En la siguiente ilustración se presentan algunos ejemplos de los patrones de ondas de notas producidas por distintos instrumentos. Para considerarla una nota musical, no importa lo complicadas que sean las ondas individuales, sino el hecho de que el patrón se repita.
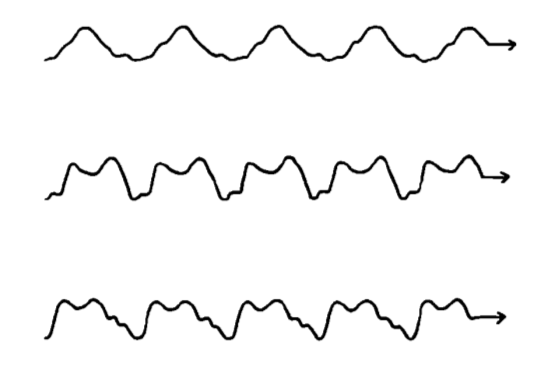
Las notas musicales se forman de patrones de ondas que se repiten una y otra vez. Aquí se representan notas reales producidas por una flauta (superior), un clarinete (medio) y una guitarra (inferior). (Fuente: Exploring Music, de C. Taylor (Taylor & Francis, 1992))
Nuestros tímpanos se flexionan hacia adentro y hacia afuera cuando las ondas de presión actúan sobre ellos. Pero los tímpanos no pueden responder adecuadamente si el patrón de ondas se repite demasiado rápida o lentamente; solamente oímos patrones que se repiten entre más de veinte veces por segundo y menos de veinte mil veces por segundo.
No es necesario que las notas musicales las produzca un instrumento musical. Cualquier cosa que vibre o agite el aire de forma repetitiva entre veinte y veinte mil veces por segundo produce una nota, sea una moto a gran velocidad o un taladro de dentista. En la canción The Facts of Life, la banda Talking Heads usa lo que parece ser un taladro accionado por aire comprimido para producir una de las notas del acompañamiento de fondo. Esta combinación de música e ingeniería encaja bien con la letra, que nos dice que «el amor es una máquina sin conductor».
Los instrumentos musicales son simplemente dispositivos que han sido diseñados para producir notas de forma controlada. Un músico usa el movimiento de sus dedos o la potencia de su soplo para que algo vibre a las frecuencias elegidas, y se producen las notas.
Cuando las cosas vibran, normalmente lo hacen de muchas maneras diferentes a la vez. Por ejemplo, si está cortando un árbol, cada vez que el hacha golpea el árbol las diversas ramas vibran a velocidades distintas y en diferentes direcciones. Cada una de estas vibraciones genera un patrón de ondas en el aire, pero éstos no se suman para crear un patrón general repetitivo, de modo que oímos un ruido en vez de una nota. Las notas musicales se producen únicamente cuando todas las vibraciones contribuyen a generar un patrón repetitivo como los de la ilustración anterior. Para que esto suceda, el objeto que vibra debe producir únicamente ondas que están fuertemente relacionadas entre sí y se pueden unir de forma organizada. Es más fácil que esto suceda cuando el objeto que vibra tiene una forma muy simple. Una de las formas más sencillas posibles es una columna o barra como la que se muestra en la siguiente ilustración. Como veremos en breve, las columnas vibran de la manera exactamente adecuada para generar notas musicales, y esta es la razón de que la mayoría de los instrumentos musicales utilicen la vibración de una columna de aire en el interior de un tubo (la flauta, el clarinete, etc.) o la vibración de cuerdas, que no son más que columnas largas y finas hechas de plástico o de acero.

Una columna es una forma simple que vibra de la manera justa para producir notas musicales. Esa es la razón por la que la mayoría de los instrumentos musicales utilizan columnas de aire que vibran dentro de un tubo (como la flauta o el clarinete) o la vibración de cuerdas (que son largas y delgadas columnas de acero o plástico).
En cuanto a las cuerdas, las notas más puras y con mayor volumen se consiguen con cuerdas nuevas, cuando su forma se acerca lo más posible a una columna. Cuando llevan usándose un tiempo adquieren raspaduras y daños y su forma de columna se hace más imperfecta. Cuando esto sucede, su sonido es más apagado y las notas tienden a hacerse más ambiguas en cuanto a su tono. Los músicos profesionales cambian de cuerdas cada pocas semanas, pero cuando yo era estudiante siempre esperaba a que las cuerdas fueran casi imposibles de afinar antes de comprar un juego nuevo, ya que se pueden comprar muchas patatas fritas, refrescos y salsa curry con el precio de un juego de cuerdas de guitarra. Generalmente, hay que comprar el juego completo, ya que si reemplazas solamente las dos peores vas a tener dos cuerdas nuevas que suenan con más volumen y brillantez que las otras. Y no funciona lo de intentar hacer trampa comprando dos cuerdas nuevas y envejeciéndolas artificialmente con aceite de patatas fritas y salsa curry: la columna perfectamente simétrica de las cuerdas nuevas acabará sobreponiéndose a esas admirables técnicas caseras para intentar ahorrar.
Podemos aprender mucho sobre las notas musicales si nos fijamos en la manera en que vibra una sola cuerda. Cuando pulsamos una cuerda de guitarra, se mueve hacia delante y hacia atrás cientos de veces por segundo. Naturalmente, ese movimiento es tan rápido que no lo vemos: únicamente vemos la imagen borrosa de la cuerda en movimiento. Las cuerdas que vibran solas no hacen mucho ruido, ya que son muy finas y no desplazan demasiado aire, pero si se une a la cuerda una gran caja hueca (como un cuerpo de guitarra), entonces la vibración se amplifica y la nota se oye con toda nitidez. La vibración se transmite a las superficies de madera de la caja, que se ponen a vibrar a la misma velocidad que la cuerda. La vibración de la madera crea ondas de presión de aire más potentes. Cuando las ondas emitidas por la guitarra alcanzan el oído, el tímpano se flexiona hacia adentro y hacia afuera tantas veces por segundo como la guitarra original. Finalmente, el cerebro analiza el movimiento del tímpano y piensa, el vecino de al lado ya está ensayando con la guitarra, el muy pesado.
El número de veces que vibra la cuerda en un segundo se llama la frecuencia de la nota, y el término se refiere precisamente a con cuánta frecuencia vibra. Uno de los primeros en realizar un estudio científico serio sobre las frecuencias, en la década de 1880, fue un alemán de barba poblada llamado Hertz. Los científicos y músicos que realizaban trabajos sobre acústica se encontraban con que les hacía falta una manera breve de decir la cuerda tenía una frecuencia vibracional de 196 ciclos de movimiento hacia delante y hacia atrás. Primeramente lo acortaron a la cuerda tenía una frecuencia de 196 ciclos por segundo[4], pero incluso los científicos de barba poblada se dieron cuenta de que no se trataba de una forma muy atractiva de expresarlo. Por fin, en 1930 se le ocurrió a alguien la idea de utilizar el nombre de Hertz para expresar el número de ciclos por segundo, así que en la actualidad decimos esta cuerda tiene una frecuencia de 196 hercios. Normalmente acortamos hercio a Hz cuando lo escribimos: la cuerda tenía una frecuencia de 196 Hz. (Estoy seguro de que tanto el doctor Hertz como su barba habrían estado encantados de dicho honor; a mí ya me gustaría que se me ocurriera algo que se pudiera medir en Powells.)
En el capítulo 1 expliqué que el tono (o frecuencia) de cada nota que utilizamos se decidió en un comité en 1939. Aunque no hablaron concretamente de guitarras, las decisiones que tomaron afectaban a todos los instrumentos. Así, hoy sabemos que la segunda cuerda más gruesa de una guitarra, la cuerda La, debe vibrar 110 veces por segundo.
Así que John Williams (el guitarrista clásico por excelencia) acaba de pulsar la cuerda La de su guitarra y, en una guitarra bien afinada, la cuerda La tiene una frecuencia fundamental de 110 Hz. Una forma simplificada de expresarlo es decir que la cuerda ahora se mueve hacia adelante y hacia atrás 110 veces por segundo y nuestros tímpanos hacen lo mismo. Pero esta no es la historia completa. La cuerda está vibrando en realidad a muchas frecuencias simultáneamente, y la de 110 veces por segundo, o 110 Hz, es apenas la más baja de las frecuencias. Las otras frecuencias son múltiplos de ésta: 220 Hz (2x 110), 330 Hz (3x 110), 440 (4x 110), 550 Hz (5x 110), y así sucesivamente. Cuando se hace sonar la cuerda, oímos todas esas frecuencias simultáneamente, pero el efecto en nuestro sistema auditivo es de un único patrón de ondas que se repite 110 veces por segundo.
Esto nos plantea varias preguntas muy interesantes:
Vamos a contemplar este tema desde el punto de vista de la cuerda. Antes de ser pulsada, la cuerda vivía feliz en un estado de estabilidad: cuando estaba estirada ocupaba la ruta más corta entre dos puntos, la línea recta. Al pulsarla la hemos estirado un poco más antes de soltarla. Esto es extremadamente incómodo para la cuerda e inmediatamente intenta volver a ser una línea recta, aunque pasa de largo una y otra vez hasta que agota la energía. A la cuerda se le agota la energía porque al moverse de un lado para otro, tiene que abrirse camino a través del aire, además de que transfiere su energía vibratoria al cuerpo de madera de la guitarra o el violín.
Se podría pensar que la cuerda simplemente se desplazaría de un extremo a otro, desde una curva suave hasta otra curva suave, como se muestra en la siguiente ilustración. Pero no puede hacer eso porque para ir de una curva a otra sin más, la cuerda tendría que empezar su trayecto como curva suave. Pero de hecho cuando se pulsa una cuerda, se forma una línea quebrada —dos rectas que se unen en el dedo que la pulsa— como se muestra en la segunda figura de la ilustración. Cuando se suelta, la cuerda no tendrá tiempo para organizarse en forma de una suave curva gradual, sino que sus distintas partes se desplazarán tan rápidamente como sea posible.
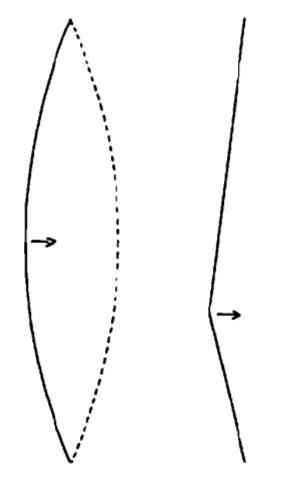
Si quisiéramos hacer que una cuerda vibrara solo a su frecuencia fundamental, tendríamos que iniciar su movimiento con la forma correcta: una curva suave como la de la figura de la izquierda. Lo que en realidad sucede es que cuando pulsamos una cuerda, iniciamos el movimiento a partir de dos líneas rectas que se encuentran en el dedo que la pulsa, como se puede ver en la figura de la derecha.
Así que ahora nuestra cuerda se encuentra en un conflicto. Necesita moverse apenas sea soltada, pero no se puede mover como una curva sencilla porque no ha empezado a desplazarse como una curva sencilla. La solución a este problema es que la cuerda empieza a vibrar de varias maneras a la vez.
Esto quizá suene extraño. ¿Cómo puede una cuerda hacer varias cosas a la vez? En realidad no es tan difícil. Imagine que está sentado en un columpio del parque, uno de esos de tipo tradicional que constan de un asiento de madera suspendido de dos cadenas. Si se columpia suavemente hacia adelante y hacia atrás, cada uno de los eslabones de cada cadena también se desplazará hacia adelante y hacia atrás. Es verdad que los eslabones más cercanos al asiento son los que más se mueven y los que están próximos al travesaño del que cuelga el columpio se mueven muy poco, pero podemos decir que la cadena en su totalidad está respondiendo a una orden única: muévete suavemente hacia adelante y hacia atrás. Ahora, mientras esto sucede, dé un golpe a la cadena más o menos a la altura de su vista. Entonces, empezará a vibrar rápidamente hacia adelante y hacia atrás además de desplazarse suavemente. La cadena estará obedeciendo dos órdenes distintas: 1. Muévete suavemente hacia adelante y hacia atrás; y 2. Vibra rápidamente hacia adelante y hacia atrás. Además, mientras se columpia, podría iniciar un movimiento rotatorio, con lo que se le daría otra instrucción adicional. Y si lo que quiere es marearse, puede añadir muchos otros movimientos distintos. Esto pone de manifiesto que una cadena o una cuerda pueden obedecer varias órdenes a la vez.
Aunque nuestra obediente cuerda de guitarra puede seguir varias instrucciones simultáneamente, solo acepta, sabiamente, las que le permiten que los extremos se mantengan estacionarios, ya que se encuentran sujetos al instrumento y por tanto no se pueden mover.
Echemos un vistazo a la ilustración de abajo: junto a una foto de mi guitarra clásica favorita hay tres dibujos de algunas formas en las que podría vibrar una cuerda. Lo primero que hay que notar es que, sea cual sea el patrón de vibración que haya dibujado, me he tenido que asegurar de que los extremos se mantenían en el mismo sitio, ya que los extremos de las cuerdas están sujetos a la guitarra y no se pueden mover. Esto se traduce automáticamente en el hecho de que sea cual sea la manera en que vibra la cuerda, su longitud se tiene que dividir en una, dos, tres partes, o cualquier otro número entero de partes, pero no se puede dividir de ninguna forma más complicada. No se puede dividir en cuatro partes y media, por ejemplo, porque eso supondría que uno de los extremos se mueve con la vibración.
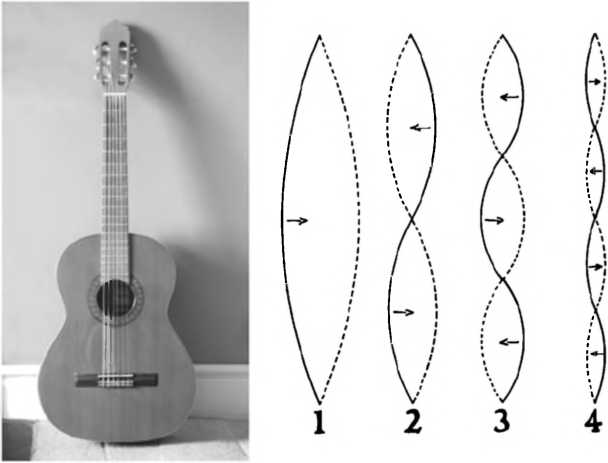
Algunos ejemplos de cómo podría vibrar una cuerda: 1. La cuerda entera vibra a 110 Hz. 2. La cuerda se divide en dos mitades que vibran a 220 Hz. 3. La cuerda se divide en tres tercios que vibran a 330 Hz. 4. La cuerda se divide en cuatro cuartos que vibran a 440 Hz. Todas estas vibraciones, y muchas más, se realizan simultáneamente en una especie de danza compleja que repite un ciclo entero en la frecuencia más baja de todas, 110 Hz.
Así que, cuando está vibrando de un lado para otro, la cuerda no sólo se comporta como una cuerda larga que se mueve a la frecuencia fundamental, sino que participa en una compleja danza ondulante en la que muchas vibraciones distintas se realizan simultáneamente: el movimiento de la cuerda entera se ve acompañado por algunas vibraciones de media cuerda, de un tercio de cuerda o de un cuarto de cuerda.
Las cuerdas cortas vibran a una frecuencia mayor que las largas, si se trata del mismo tipo de cuerda sujeto al mismo grado de tensión. Es más, hay una relación directa entre la longitud de la cuerda y la frecuencia en la que vibra. Si dividimos por la mitad la longitud de la cuerda, estaremos duplicando la frecuencia. De igual manera, si usamos una cuerda con una sexta parte de longitud, estamos multiplicando la frecuencia por seis.
Todos los segmentos más cortos que resultan cuando la cuerda se divide, vibran a frecuencias que se corresponden a su longitud: las mitades vibran al doble de 110 Hz, los tercios vibran a tres veces 110 Hz, y así sucesivamente. Aunque las mitades, tercios y cuartos vibran de forma independiente, hacen lo que las parejas en un baile de salón tradicional: a intervalos regulares vuelven a la primera posición para volver a empezar. El patrón global de la danza se repetirá a la misma frecuencia, que es la más baja de todas, 110 Hz en este caso. Por eso llamamos a la frecuencia más baja la frecuencia fundamental de la nota. Este es el tono de la nota global que oímos, que es por lo que cuando hablamos de las notas musicales nos referimos sólo a su frecuencia más baja. Todas las demás frecuencias se unen y apoyan a la fundamental (algo muy parecido a los cantantes del coro que apoyan al solista), y esto produce una mayor riqueza de sonido.
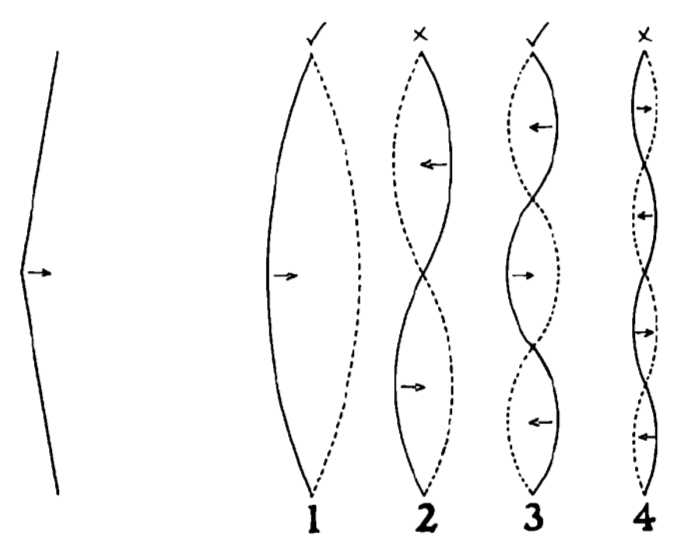
Si se pulsa la cuerda en el centro, todas las vibraciones que requieren que se mueva el centro de la cuerda se pueden sumar al movimiento que produce la nota. Sin embargo, estarán ausentes las vibraciones que requieren que el centro de la cuerda permanezca estático. A la izquierda se representa una cuerda pulsada en el centro; solamente las vibraciones que permiten que el centro de la cuerda se desplace —identificadas por un tick en la parte superior— pueden formar parte de la nota cuando la cuerda se pone a vibrar.
Lo que sucede en realidad cuando se suelta la cuerda es que todos los tipos de vibración relacionados con el veloz desplazamiento de la cuerda en torno al punto en que se ha pulsado empiezan a la vez. Por ejemplo, si se pulsa por el centro, se producirán vibraciones en la frecuencia fundamental y en la que es el triple de la fundamental, ya que ambos tipos de vibración implican mucho movimiento en el centro, como se puede apreciar en la siguiente ilustración. Por otro lado, estarán ausentes las vibraciones dos o cuatro veces la frecuencia fundamental, ya que estas requieren que el centro de la cuerda no se desplace.
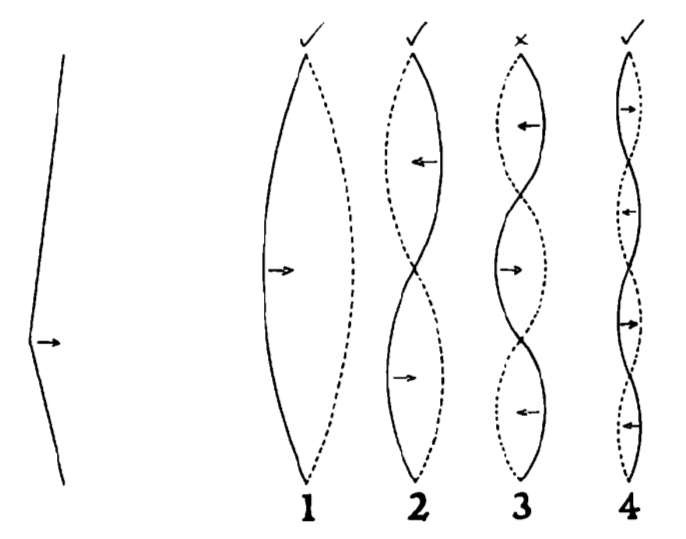
Cuando se pulsa la cuerda a un tercio de su longitud, solo los tipos de vibración que requieren que la cuerda se mueva en ese punto (señaladas por un tick) pueden incorporarse a la nota, mientras que las que exigen que esté inmóvil en ese punto no podrán hacerlo.
Pongamos otro ejemplo: si se pulsa la cuerda a un tercio de su longitud, se producirá una gran cantidad de vibraciones a la frecuencia fundamental y a dos y cuatro veces la fundamental, pero ninguna al triple, puesto que estas últimas no pueden incorporarse si la cuerda se mueve en ese punto, como se puede observar en la anterior ilustración.
Ahora es cuando nos ilumina la deslumbrante luz del entendimiento. Si pulsamos una cuerda, producimos muchas vibraciones simultáneas, y dependiendo del punto en el que la pulsamos se añadirá a la mezcla una determinada proporción de cada tipo de vibración. Esto explica por qué es diferente el sonido de las cuerdas de guitarra en función de que se pulsen cerca del centro o de los extremos. La frecuencia fundamental se mantiene, independientemente del punto donde se pulse la cuerda, pero se verá complementada por distintas proporciones del resto de las vibraciones. Hemos cambiado el patrón de la danza sin modificar la cantidad de veces que se produce el ciclo completo de movimiento. Para producir otra nota distinta, o bien se pulsa otra cuerda o se acorta la misma con la utilización de los trastes[5] del mástil. En esos casos se genera otra vibración fundamental distinta, con su propio acompañamiento de frecuencias relacionadas.
Hay, naturalmente, un grupo de instrumentos musicales cuyos sonidos no implican la colaboración de armónicos, de modo que lo que producen son ruidos. Se trata de los instrumentos de percusión no afinados, como los címbalos, gongs y bombos. Están entre los instrumentos más antiguos del mundo puesto que su origen se remonta a un tiempo muy anterior a la invención de los buenos modales en la mesa. En aquellos tiempos maravillosos las personas que iban a las danzas tribales aporreaban cualquier cachivache que tuvieran a mano. Hoy en día las cosas son ligeramente más sofisticadas, y no está bien visto usar el cráneo de tus enemigos o parientes cercanos, ni siquiera entre los jugadores de rugby. Las bandas de rock, pop o jazz utilizan tambores y platillos casi continuamente para crear un impulso rítmico para la música y ésa es la razón por la que se usan instrumentos que generan ruidos, no notas. Si un batería estuviera produciendo una o dos notas todo el tiempo, dichas notas dominarían la canción y ocasionalmente desentonarían con sus armonías. Un ruido repetitivo, el rataplán de un tambor o el chisss de un platillo, proporciona información rítmica sin secuestrar la música.
Los tambores son circulares y muy parecidos a columnas cortas, así que tienen tendencia a producir notas si no los disuades (algunos tambores, como los timbales de las orquestas se afinan deliberadamente para producir notas). Un bombo tiene dos membranas, una en cada extremo del cilindro, y lo que hay que hacer para impedir que produzcan notas es afinarlas a notas distintas. Cuando se golpea una de las membranas, se comprime el aire dentro del tambor y eso hace que ambas membranas empiecen a vibrar. Sin embargo, ya que no producen patrones de movimiento que se apoyen entre sí, el sonido no tiene un tono identificable. La falta de apoyo mutuo es asimismo la razón por la que el sonido muere rápidamente, algo que es muy útil si quieres producir ritmos claros.
La razón por la que escogí la cuerda La para el ejemplo de este capítulo es que su frecuencia fundamental es 110 Hz, y es muy fácil reconocer a simple vista que 220 Hz es el doble y 330 Hz es el triple. Pero este libro se refiere a todas las notas, así que no podemos usar siempre el mismo ejemplo. La regla general es que cualquier nota está compuesta de una frecuencia fundamental y otra serie de frecuencias que son el doble, el triple, el cuádruple y así sucesivamente. Todas estas frecuencias se llaman los armónicos de la nota. La frecuencia fundamental es el primer armónico, pero normalmente la llamamos sencillamente la fundamental. La frecuencia que es el doble que la fundamental es el segundo armónico, la que es el triple se conoce como tercer armónico, y así sucesivamente.
Aunque hasta ahora solamente hemos hablado de las cuerdas de guitarra, estos principios son ciertos para todas las notas musicales: cada nota contiene una familia de vibraciones relacionadas entre sí por números enteros, y son las distintas combinaciones de estas vibraciones las que dan a la nota un carácter propio sin cambiar la frecuencia fundamental.
El principio de que las cuerdas producen distintas combinaciones de armónicos en función del punto desde donde se hacen vibrar también es cierto en los instrumentos en los que en lugar de pulsar las cuerdas se utiliza un arco, como el violín y el violonchelo. Este principio proporciona una forma muy útil para controlar el sonido del instrumento si se ejecuta una pieza que tiene repeticiones, como sucede en casi todas las piezas. Se puede ejecutar la melodía primeramente pulsando o frotando con el arco en la zona central de la cuerda, lo que producirá un agradable sonido dulce. Cuando se repita la melodía, se pueden ejecutar las mismas notas más cerca de un extremo de las cuerdas, para generar un sonido mucho más áspero. Esta es una buena manera de potenciar el interés musical de la pieza, aumentando o disminuyendo la tensión. El guitarrista puede empezar con una sensación de dulce resignación cuando el cantante le dice a su novia que se da cuenta de que no es del todo feliz; más tarde, se puede tocar de modo que se dé a entender que ya está mucho menos relajado, cuando está cantando la parte que cuenta que ella se fugó con un pedicuro de Vigo.
Las ondas de presión que hemos visto al principio de este capítulo tienen un aspecto muy complicado, mientras que las ilustraciones que reflejan los patrones de las vibraciones de una cuerda son muy sencillas. Nos podemos preguntar cómo es que la suma de cosas sencillas produce una cosa compleja. Las vibraciones individuales de una cuerda producirían ondas sencillas en el aire, como se refleja en la izquierda de la siguiente ilustración, pero las combinaciones de los diversos ingredientes pueden resultar en una variedad amplísima de formas de onda. La persona que descubrió que se puede construir casi cualquier módulo repetitivo a partir de ondas sencillas fue un francés llamado Fourier, uno de los más importantes colaboradores de Napoleón en tres campos intelectuales íntimamente relacionados entre sí: la egiptología, las matemáticas y el drenaje de pantanos. Utilizando operaciones matemáticas complejísimas consiguió crear casi cualquier patrón repetitivo imaginable a partir de estos ingredientes. Por fortuna, aquí no nos hace falta hablar en detalle de eso. Nos basta con saber que si introducimos en un ordenador cualquier forma de onda, se podrían encontrar los componentes necesarios para generarla: determinada cantidad de la fundamental, un poquito del segundo armónico, con una pizca del séptimo armónico y un chorrito del decimonoveno, o lo que hiciera falta para conseguir esa forma general de onda.
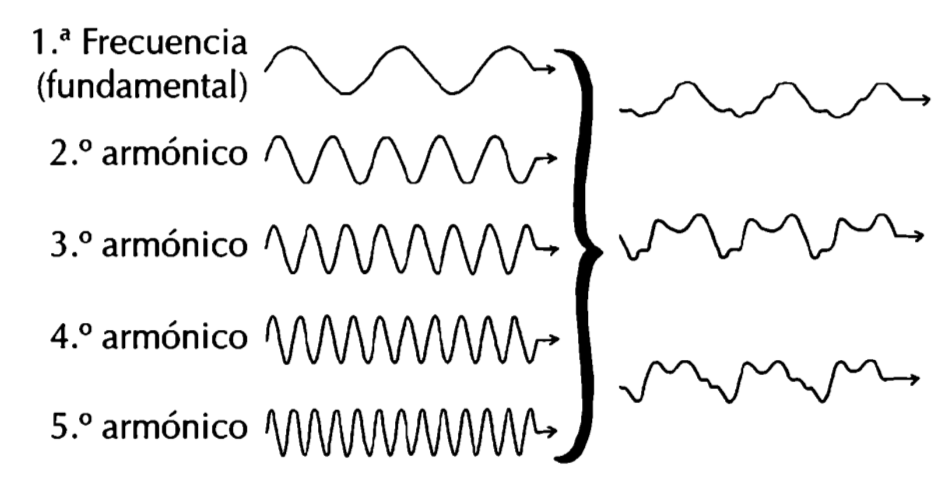
Las diversas ondas relacionadas con una nota se pueden combinar en distintas proporciones para producir distintas formas de onda con la misma frecuencia fundamental. Las proporciones dependen tanto de los instrumentos que se utilicen como de las distintas formas de interpretar un instrumento concreto. El resultado es la misma nota, pero con un sonido diferente (dulce, áspero, etc.). Las ondas combinadas de la derecha son las vibraciones de la flauta, el clarinete y la guitarra que hemos visto anteriormente.
Así que ya tenemos la respuesta a nuestras tres preguntas:
Si rompemos un plato o arrugamos una bolsa de papel, oímos un ruido compuesto de muchas frecuencias sin relación entre sí, pero todas las notas musicales están compuestas de patrones repetitivos. Nuestro cerebro es capaz de identificar si un sonido está compuesto de un patrón de ondas repetitivo o no repetitivo, y gracias a eso distinguimos entre notas y ruidos.
Sabemos por experiencia que las mismas notas tocadas en instrumentos diferentes no tienen el mismo sonido, aunque tengan la misma frecuencia. Por ejemplo, la nota a 110 Hz que se produce cuando pulsamos la cuerda La de una guitarra, contiene distintas proporciones de los diversos armónicos que se suman a la mezcla. Estas distintas mezclas son las responsables de que haya diferencias entre los sonidos de los diversos instrumentos. Ese será el tema del próximo capítulo.
Además de controlar los sonidos de los diferentes instrumentos, los armónicos también influyen sobre cuáles notas escogemos para que suenen bien juntas en las armonías y melodías. Si, por ejemplo, oímos una nota cuya frecuencia fundamental es de 110 Hz y simultáneamente otra cuya frecuencia es el doble, 220 Hz, suenan estupendamente juntas. La nota a 110 Hz está compuesta de armónicos con frecuencias a 110, 220, 330, 440, 550, 660 Hz etc., y la nota a 220 Hz contiene armónicos a 220, 440, 660 Hz etc. La razón por la que las notas suenan bien juntas es que sus armónicos tienen mucho en común, puesto que los armónicos de la nota más aguda son iguales capítulo 1 a algunos de la más grave. Cuando la frecuencia fundamental de la nota más aguda es el doble que la más grave, decimos que está a una octava de ella. Este intervalo, la octava, es la piedra angular de todos los sistemas musicales, y se mencionará frecuentemente en el resto del libro. Las notas que están a una octava entre sí están tan relacionadas que se les da el mismo nombre. Ya hemos visto que la nota cuya frecuencia fundamental es a 110 Hz es un La, pero es que la que tiene el doble, 220 Hz, también es La, y la nota que tiene el doble que esta, 440 Hz, también es La, y así sucesivamente. De hecho, hay ocho notas La en el teclado del piano, y para distinguirlas entre sí las numeramos (como se puede ver en la página 8). La que ya conocemos, la de 110 Hz, recibe el nombre de La2, y el siguiente La, con frecuencia fundamental a 220 Hz, se conoce como La3.