En el crepúsculo de este relato, del que nunca ha estado del todo ausente, el ciclista vuelve a ser protagonista destacado. Porque nuestra querida y admirada bicicleta —que ha ocupado buena parte de las páginas que nos han traído hasta aquí— cuando se queda sola, tal vez exhibiéndose en el escaparate de una tienda, vestida con sus mejores galas, tratando de despertar la concupiscencia de quienes desearían poseerla, nuestra querida y admirable bicicleta, inmóvil e inanimada, es muy poca cosa. Hasta que llega el ciclista y la monta, inyectándole la energía que necesita para iniciar su resurrección.
El cuerpo del ciclista es, desde luego, almacén y transformador de energía. Pero contiene, también, la estructura que cobija y sostiene el motor que lo mueve y sus complejísimos componentes. La bicicleta es, realmente, un pedestal estructural, por el que se encaminan las fuerzas que nacen en el cuerpo del ciclista hasta que alcanzan el suelo en el que reposan.
El cuerpo en movimiento del ciclista debe ineludiblemente cumplir, como todos los objetos animados o inanimados que pueblan nuestro planeta, las tres leyes que, como descubrió Newton, explican y gobiernan su comportamiento. Como cualquier otra parte de la estructura que forma con su bicicleta, el cuerpo del ciclista y cada uno de sus miembros deben estar, a cada instante, en equilibrio. Y, para ello, las fuerzas gravitatorias, las aerodinámicas y las de inercia que actúan sobre él, estarán contrarrestadas por las reacciones que aparecen en los puntos de contacto —sillín, manillar, pedales— del cuerpo del ciclista con su montura.

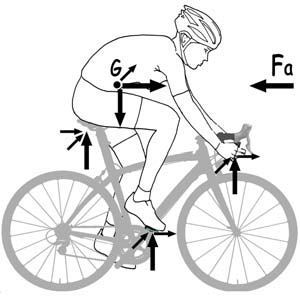
En síntesis, sobre el cuerpo del ciclista de masa, m, actuarán las fuerzas gravitatorias, m · g, así como las de inercia, m · av, cuando existan aceleraciones verticales, av, debidas al movimiento. Actuarán, también, las fuerzas aerodinámicas, Fa y las de inercia, m · aL, originadas por las aceleraciones longitudinales del cuerpo del ciclista. Y finalmente, intervendrán las fuerzas transversales de inercia, m · aT, debidas a las aceleraciones, aT, asociadas a la movilidad transversal del cuerpo del ciclista, así como a la componente, en dicha dirección, de las fuerzas aerodinámicas.
Las reacciones en los tres posibles apoyos —el del contacto de sus manos con el manillar, de sus glúteos con el sillín y de sus pies con los pedales— deben fluir por la estructura del cuerpo para alcanzar cada punto de su masa. Aunque al haber considerado un modelo muy simplificado en el que toda ella se concentra en su centro de gravedad, éste será la diana hacia la que apuntarán los itinerarios por los que discurrirán las reacciones de apoyo.
La estructura del cuerpo humano, que puede parecer de concepción sencilla es, sin embargo, de una enorme complejidad real. Está constituida, como tantas celosías estructurales que utilizamos en la ingeniería civil y en la arquitectura, por robustas y rígidas piezas —los huesos— que pueden trabajar esencialmente en flexocompresión y por flexibles tirantes que sólo pueden hacerlo en tracción: los músculos con sus tendones, que los prolongan y anclan a los huesos. Y en las zonas donde confluyen las extremidades de huesos y tendones, se ubican las esenciales y especialmente complejas articulaciones en cuyo equilibrio colaboran los ligamentos que, sin impedir su movilidad, la limitan a rangos funcionalmente útiles.
Por tratarse de una estructura articulada puede ser relativamente sencillo, a partir de las reacciones del cuerpo en las superficies en las que se apoya, estimar los esfuerzos a que podrían verse sometidos huesos, y músculos, y evaluar su respuesta a las solicitaciones que reciben. Pero, como en las estructuras de la ingeniería, las articulaciones son las zonas más críticas del entramado estructural, las de funcionamiento más complejo y las de evaluación más incierta.
En todo caso, hay que reiterarlo, cada hueso y cada músculo con sus tendones, tienen que estar en equilibrio y si se aíslan virtualmente, las fuerzas aplicadas en uno de sus extremos deben contrarrestarse con la que actúa en el otro, y, para que así suceda, deben de estar en prolongación unas de otras.
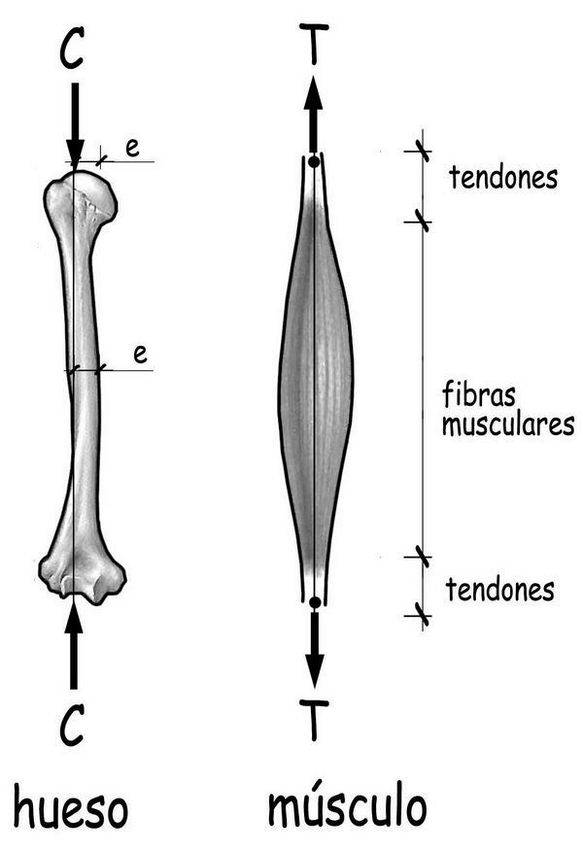
Los huesos suelen estar solicitados en flexocompresión y no en compresión pura. Porque, por una parte, su geometría nunca es perfectamente recta y en algunos casos está notoriamente curvada. Y porque las cargas que se introducen en las articulaciones, en el contacto con los huesos contiguos, suelen tener una cierta excentricidad que, además, varía con el movimiento de la articulación. Por tanto, en cualquier sección perpendicular a la directriz del hueso, por exigencias de equilibrio, actuará un esfuerzo de compresión, un cortante y un momento flector.
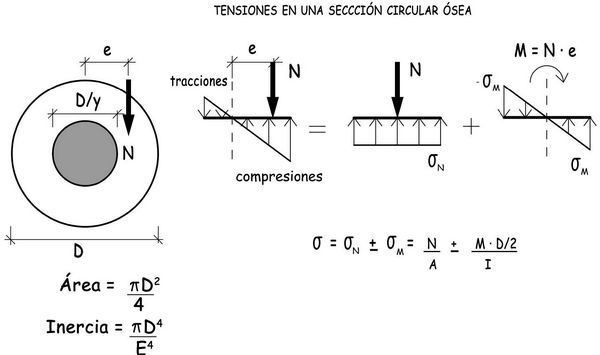
Para que los huesos estuviesen exclusivamente comprimidos, la línea de acción de las fuerzas de compresión que se transfieren de una extremidad a la otra, debería situarse dentro del núcleo central de cualquier sección perpendicular a su directriz. En una sección cilíndrica de diámetro D, el borde de dicho núcleo central está definido por un círculo, de radio muy reducido, D/8. Por eso, la línea de acción de los esfuerzos de compresión que solicitan a los huesos, se sitúan habitualmente fuera de su núcleo central y, en consecuencia, la zona del hueso, más alejada de la línea de acción de la compresión estará habitualmente traccionada, dentro de unos límites aceptables para el material óseo.
Los músculos, en cambio sólo pueden trabajar en tracción. Son como tirantes estructurales constituidos por un cuerpo central de fibras paralelas envueltas en tejido muscular. En sus extremidades los músculos se convierten en tendones que los anclan, a un hueso en un extremo y a otro diferente en el otro. Entre los músculos y los tendones existe una zona de transición en la que se imbrican para transferirse las fuerzas entre ellos.
Todo ello expuesto de forma muy elemental. Porque el cuerpo humano, ese gran desconocido para la inmensa mayoría de los seres humanos, es de una extraordinaria y fascinante complejidad. Quien esto escribe, tuvo que estudiar y aprender en un bachillerato ya remoto, algunas nociones de biología y de química y, desde entonces, ha mantenido una cierta curiosidad e interés, por estas disciplinas, como por tantas otras. Y ahora, en la preparación de este elemental texto, ha huroneado por las páginas de algunas enciclopedias y de algunos prestigiosos textos de anatomía, fisiología y, sobre todo, de biomecánica. En los capítulos introductorios de estos últimos se suelen exponer los principios de la mecánica racional. Y, de hecho, en el resto de los capítulos, llenos de informaciones y esquemas de indudable interés, las exigencias de equilibrio, formuladas por Newton en sus leyes centenarias, suelen tener una presencia, generalmente implícita, pero relevante.
Y no he podido dejar de preguntarme si el contenido de estos capítulos introductorios será suficiente para aportar a unos estudiantes, a los que, probablemente, en su gran mayoría, se les podrían calificar de «letras», los sólidos conocimientos que se requieren para comprender realmente la mecánica del comportamiento de un cuerpo humano.
No es probable que así ocurra porque he tenido incluso la impresión que los saberes estructurales de los autores de estos especializados libros de texto, en tantos aspectos tan valiosos, parecían insuficientes para explicar en profundidad las exigencias que imponen las insoslayables leyes de Newton en el comportamiento de todas y cada una de las partes en que podemos, virtualmente, deconstruir la compleja estructura de un ser humano.
Así, en uno de los prestigiosos textos a los que me refiero, se asegura, que el concepto de trabajo, como producto de la fuerza por el desplazamiento, que está tan arraigado en la física, no es aplicable en biología. Y para justificar tan insólita afirmación se utilizan argumentos que, cuando menos, producen perplejidad y que pueden ser manifestación de la lamentable ausencia de diálogo entre profesionales de diferentes especialidades y, por otra parte, esperanzadora manifestación de las posibilidades que se abrirán en la investigación y en la educación de estas materias cuando existan auténticas colaboraciones interprofesionales.
Aunque, por otra parte, este confuso estado de cosas, podría tener una cierta justificación por la existencia de una aparente paradoja, de las que tanto agradaban al gran Niels Bohr: «Es magnífico, dijo, que hayamos dado con una paradoja. Ahora tenemos la esperanza de realizar progresos».
Y es que como la física newtoniana nos enseña, y nos enseña bien, el trabajo es, desde luego, el producto de la fuerza por el desplazamiento de dicha fuerza siguiendo su línea de acción. Pero si sostenemos un peso en la palma de la mano de un brazo estirado que mantenemos inmóvil, no se produciría trabajo: el cuerpo no necesitaría generar energía y no tendría por qué cansarse. Lo que, evidentemente, no es cierto. El cuerpo se cansa y, cuando el peso es grande, sólo es capaz de sostenerlo un tiempo limitado.
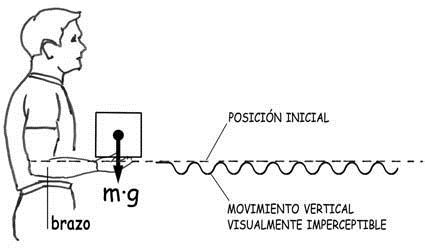
Acaso se pueda explicar esta paradoja considerando que la inmovilidad del peso es tan solo aparente, y que, en realidad, está moviéndose cíclicamente, con amplitudes muy reducidas, que suelen pasar desapercibidas. Porque, tal vez, el músculo bajo un esfuerzo sostenido —como ocurre con la relajación de los aceros de pretensar y con la fluencia de los hormigones— se distienda y el peso comience a descender muy ligeramente hasta que el músculo recibe instrucciones para acortarse y devolverlo a su nivel inicial. De manera que el peso subiría y bajaría innumerables veces y realizando en cada ciclo un trabajo y consumiendo energía generada por el cuerpo humano. Este hecho se puede apreciar, por ejemplo, entre los levantadores de grandes pesos que en situaciones límite, mueven, instintivamente, los músculos con movimientos un tanto espasmódicos que concluyen cuando suelta el peso y dejándolo caer al suelo. Y entre los «castellers»…

Los huesos, que conforman el esqueleto de un ser humano, son componentes esenciales de su estructura. Una persona de constitución normal suele tener unos 208 huesos de muy variadas geometrías: largos y cortos, grandes y pequeños, rectos, planos y curvados. Su masa conjunta es de unos 9 kilogramos, de los que el 70% aproximadamente está constituido por una sustancia que contiene calcio, fósforo, oxígeno e hidrógeno, en proporciones que responden a la formulación de los hidroxiapetitos [3Ca3 (PO4)2 · Ca (OH)2], así como sales de magnesio y otras sustancias menos relevantes en inferiores proporciones. El 30% restante lo forman fibras de colágeno (una mezcla de aminoácidos) que envuelven, desordenadamente, a los cristales microscópicos de hidroxiapetito.
Desde un punto de vista estructural, se puede considerar que los huesos están constituidos por un material compuesto por cristales de hidroxiapetito envueltos en una matriz de colágeno. Según la proporción de cristales, las características mecánicas de los huesos varían considerablemente. Como ocurre, en cierto modo, con los materiales compuestos por fibras de carbono de los que se ha tratado en el apartado 5.5. Aunque en este caso el componente más resistente no se encuentre en forma de fibras sino de cristales.
Como consecuencia de todo ello, los huesos tienen características mecánicas muy heterogéneas y son marcadamente anisótropos. Trabajan, como ya se ha comentado, fundamentalmente a flexocompresión y están constituidos por una parte interior más esponjosa por la que discurren las arterias que los mantienen con vida y otra, externa, más resistente.
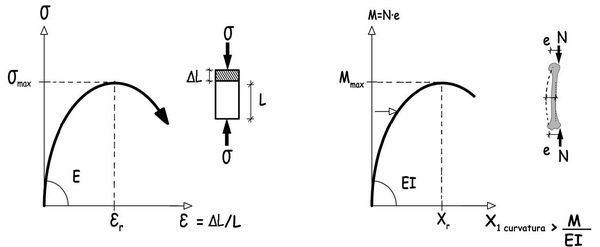
Los huesos largos tienen sección tubular cuya área resistente útil es sensiblemente inferior a la encerrada por el perímetro externo de la sección. Pequeñas probetas extraídas de la parte más externa de los huesos largos, y ensayadas a compresión para determinar sus diagramas σ-ε, manifiestan módulos de elasticidad longitudinal que puede superar los 1.500 N/mm2, reduciéndose a la mitad cuando se ensayan transversalmente. La tensión máxima de compresión puede superar puntualmente los 100 N/mm2, en zonas que están previsiblemente confinadas. Es, como la piedra o el vidrio, un material esencialmente frágil, que rompe bruscamente con deformaciones muy pequeñas, y lo hace sin avisar. Sus diagramas cualitativos de tensiones-deformaciones, deducibles del ensayo de una probeta pequeña tomada del hueso, y el de momentos-curvaturas que se pueden obtener del ensayo de un hueso completo aplicando cargas excéntricas en sus bordes, deberían mostrar geometrías lineales en el origen, que se irían incurvando progresivamente al aproximarse a las cargas límites, en la frontera de la rotura frágil.
Los músculos a los que corresponde un elevado porcentaje, del orden del 40%, de la masa corporal son, por el contrario, esencialmente dúctiles. Se deforman significativamente antes de romper y cuando se los solicita en exceso avisan, mediante el dolor muscular, que se está aproximando el límite de su capacidad resistente.
Se suelen clasificar en lisos y estriados. Los «músculos lisos» aseguran la pausada movilidad que necesita para su funcionamiento el sistema digestivo, por ejemplo. Pero los que interesan, desde la perspectiva de este texto, son los denominados «músculos estriados» que, responden con gran rapidez, a los impulsos voluntarios que provienen del sistema nervioso conectado con el cerebro, contrayéndose y provocando, al hacerlo, los movimientos que se desea que haga el cuerpo humano y los que necesita el corazón para alimentarlo con la sangre oxigenada.
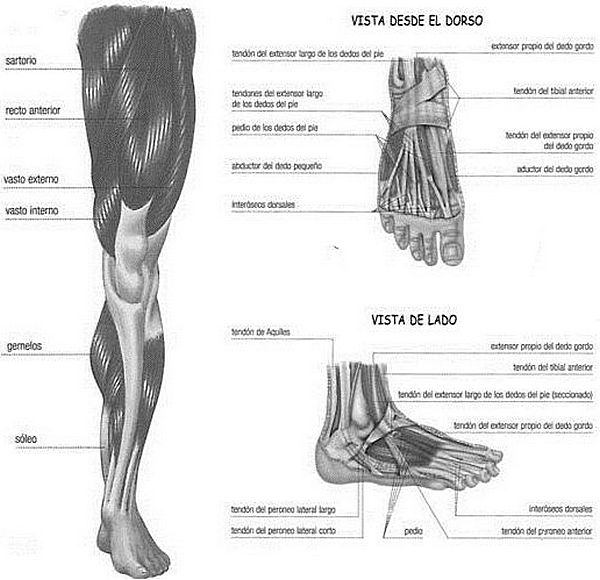
Los músculos estriados están constituidos por fibras paralelas, cada una de ellas conformadas por una sucesión de eslabones biológicos que se contraen cuando reciben las señales del sistema nervioso y vuelven, a su posición inicial al cesar el estímulo. No tienen la geometría simple y recta —propia de los tirantes tradicionales en las estructuras de la ingeniería— con las que se suelen representar en algunos confusos croquis que aparecen en algunas publicaciones. No hay más que palparse una pierna o bien observar las expresivas imágenes que abundan en cualquier atlas de anatomía, para confirmar que la geometría de los más de 600 músculos que configuran el cuerpo humano es espacial y compleja, que se abren y se estrechan, se entrecruzan y envuelven a los huesos, protegiéndolos.
En las extremidades de los músculos se encuentran los tendones que se pueden considerar, muy esquemáticamente, como los anclajes que transfieren las tracciones a los huesos. De ellos brotan, en efecto, los tendones que salen a recibirlos, para insertarse en la masa muscular.
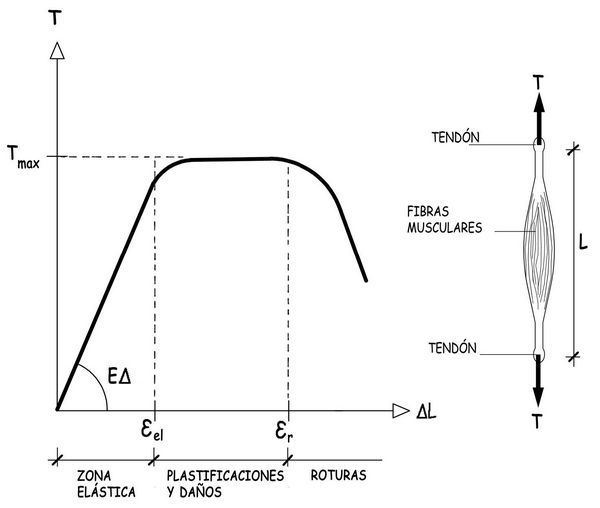
Han existido intentos, infructuosos, para caracterizar con generalidad, el comportamiento de los tirantes constituidos por músculos y tendones. Cada persona es un mundo y cada conjunto muscular tiene su propia vida, variable con la edad y las circunstancias. Pretender establecer un diagrama tensiones-deformaciones, como los que se utilizan para caracterizar materiales estructurales convencionales, no parece que pueda conducir a resultados útiles y fiables. Los progresos tecnológicos son los que podrán facilitar información precisa del comportamiento de músculos y tendones cuando se les solicita con fuerzas o con desplazamientos impuestos cuya cuantificación se desconoce. En todo caso, el tirante constituido por el paquete central muscular y por los tendones que lo anclen a los huesos, cuando esté solicitado por fuerzas de tracción se comportará, probablemente, de acuerdo con lo mostrado en el diagrama fuerzas-desplazamientos.
Los huesos y los músculos con sus tendones son fundamentales en la conformación de la bioestructura del cuerpo humano. Pero aún lo son más, las conexiones entre ellos, las articulaciones, nudos estructurales esenciales, que canalizan las fuerzas que llegan a ellos provenientes de los tendones musculares y de los huesos y aseguran las rotaciones flexionales y torsionales que imponen los movimientos del cuerpo. Y en el entorno de las articulaciones y formando parte de ellas, se encuentran los ligamentos, y, protegiendo las superficies de las rótulas, los cartílagos permeables.
Muy esquemáticamente, y distorsionando notoriamente la realidad, podremos representar la función estructural de huesos y músculos en los croquis siguientes:
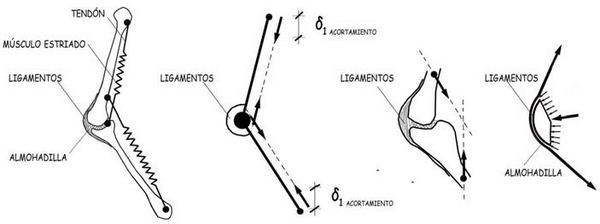
Los ligamentos tienen una composición material y unas características mecánicas en cierto modo similares a los tendones. Son esenciales tanto para generar los esfuerzos de tracción, que demanda el equilibrio de la articulación, como para limitar los giros de las rótulas en las extremidades de los huesos. Algunos ensayos de ligamentos sitúan su módulo de elasticidad, en rangos de unos 10.000 a 20.000 N/mm2, y su rigidez longitudinal en valores del orden de 75 N/mm. La carga de rotura puede alcanzar los 300 N con una capacidad última de alargamientos muy notable que puede superar los 4 mm, en ligamentos que no superan los 12 mm de longitud.
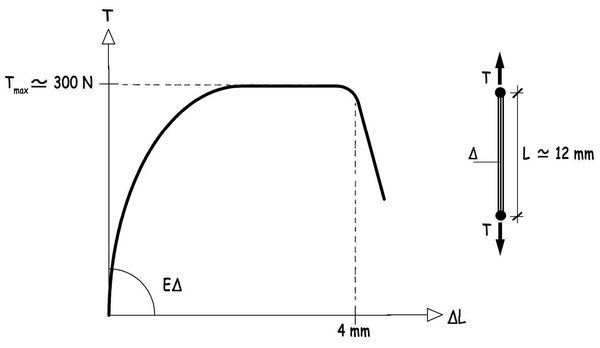
Las máximas tensiones que se producen en el conjunto del sistema óseo están localizadas, obviamente, en las zonas de contactos de los dos huesos que configuran una articulación.
Para proteger las superficies en contacto las rótulas suelen ir recubiertas de capas cartilaginosas de pocos milímetros de espesor que, siendo permeables, permiten además el acceso al líquido sinovial almacenado en las proximidades de las superficies que tienen que lubricar para permitir el giro relativo de las rótulas de uno y otro hueso, con coeficientes de rozamiento asociados muy bajos, del orden del 1%.
Las rótulas de las articulaciones óseas suelen estar constituidas por dos superficies aproximadamente esféricas, una cóncava de radio –R2 y otra convexa de radio menor R1. Hacia 1881 Hertz publicó en el libro «Über die Berühung fester elasticher Körper» la fórmula que lleva su nombre y que permite determinar la tensión máxima en el contacto de las dos superficies que transfieren una fuerza N. Suponiendo que el módulo de elasticidad de los dos huesos que configuran la rótula es el mismo, E, y que el coeficiente de Poisson del material es ν = 0,30, tendremos una ley de tensiones máximas de contacto aproximadamente parabólica, con un valor máximo
σmax = 1,5 · N / (π · a2)
siendo a, el coeficiente que figura en el croquis adjunto.

Las rótulas no solamente deben permitir las rotaciones del sistema en un plano, el del papel en los croquis dibujados. Los giros de tipo torsional son también habituales. Por eso, los músculos y ligamentos deben tener una configuración espacial para que sean posibles, al tiempo, que deben controlar que se mantienen dentro de límites tolerables. Los ligamentos cruzados, por ejemplo, tienen una función en cierto modo análoga, aunque mucho más evolucionada, que las barras de acero a 45° que solemos disponer en las vigas o soportes de hormigón estructural para asegurar el equilibrio de las fuerzas que generan los esfuerzos cortantes y de torsión.
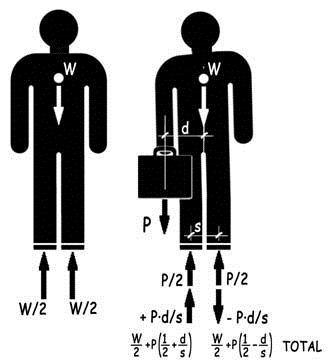
Podría ser interesante, llegados a este punto, contrastar el equilibrio de las fuerzas que actúan en el codo de un brazo extendido horizontalmente y soportando un peso dispuesto sobre su mano extendida, con el de una pieza, en cierto modo equivalente, de hormigón armado, en forma de L soportando también en su extremo una carga vertical. Comencemos por subrayar algunos rasgos característicos en el comportamiento de la estructura en L de hormigón armado. Pongamos para ello en equilibrio la barra vertical que se empotra en cabeza, la barra horizontal que sostiene en su extremo al peso P y el nudo de encuentro entre ambas.
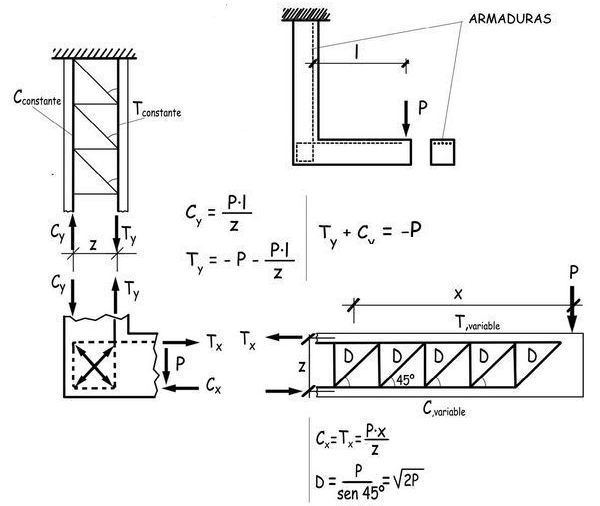
La pieza vertical, solicitada por un esfuerzo de tracción P y por el momento flector concomitante, P · L, transferirá estos esfuerzos desde el nudo hasta la sección de empotramiento, por la tracción Ty que se mantendrá constante a todo lo largo de la barra vertical y por la compresión Cy =Ty – P que permanecerá también constante.
La pieza horizontal se comportará como una celosía, de acuerdo con un modelo tradicional ampliamente utilizado en estructuras. Las armaduras conformarán el tirante traccionado. Gracias a su adherencia con el hormigón que le rodea, podrá ir reduciendo su esfuerzo de tracción entre un valor máximo
Tmax = P · x / z
en las proximidades del nudo y un mínimo Tmin = P, en el otro extremo. Tendremos, además, las diagonales comprimidas
D = P / sen 45° = (2 · P)½
que equilibrarán, el cortante P que no varía a lo largo de la viga.
Tanto la pieza horizontal como la vertical, a partir de una distancia suficientemente alejada del nudo, se comportan en razonable conformidad con la hipótesis clásica de Bernouilli-Navier (secciones planas antes de la deformación se mantienen planas después de la deformación), lo que simplifica notablemente los análisis numéricos de este tipo de estructuras constituidas por piezas prismáticas.
El comportamiento del nudo es mucho más complejo. Es una zona singular, cuya capacidad resistente, de incierta evaluación, condiciona la del conjunto de la estructura de la que forma parte. Aquí no es aplicable la cómoda hipótesis de Bernouilli-Navier y hay que esforzarse en identificar un modelo del tipo «strut and tie», con barras comprimidas y tirantes traccionados, que sea coherente con la disposición adoptada para las armaduras dispuestas en el interior del nudo.
En el elemental ejemplo que estamos considerando, podremos lograrlo si la armadura horizontal traccionada que penetra en el nudo hiciese en su interior un bucle, como el esquematizado, y volviese a surgir del nudo en la posición que ocupa la armadura traccionada de la barra vertical que conduce la tracción Ty hasta el empotramiento. El bucle de la armadura genera, por otra parte, bielas comprimidas, cruzadas en el interior del nudo, que son esenciales para la transferencia de los esfuerzos de compresión, Cx, de la barra horizontal y, Cy, de la vertical y del esfuerzo P, que es tracción en ésta y cortante en aquella. Consideremos ahora el caso del brazo horizontal sosteniendo en el extremo de la mano la carga P. Y para visualizar el equilibrio, aislemos el brazo, el antebrazo y el codo en el que confluyen. El modelo para el antebrazo puede ser asimilable al de la barra vertical de la estructura de hormigón. El músculo toma la tracción y el hueso asume la compresión necesaria para el equilibrio. No hay cortantes.
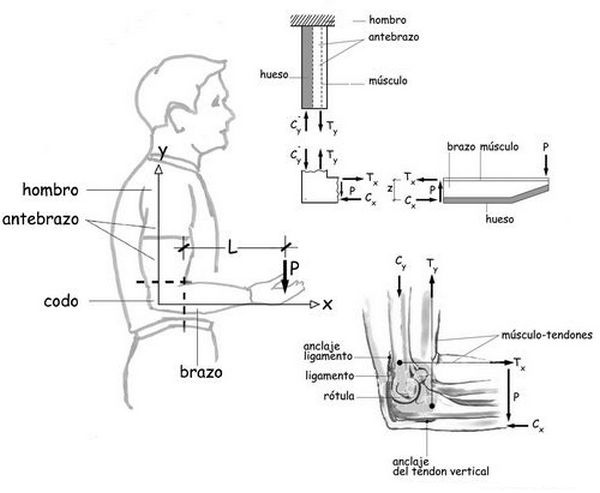
El posible modelo para el brazo plantea más interrogantes. Es evidente que, para equilibrar el momento P · d en una sección perpendicular, muy próxima al codo, tendremos la tracción Tx, y una compresión Cx. Pero, además, existe un esfuerzo cortante Q = P que cambia sustantivamente el panorama en relación con lo que ocurriría en el antebrazo.
El valor de Tx se puede deducir de la siguiente expresión en la que z es el brazo de palanca, o distancia a la fuerza de compresión Cx.
Tx = M / z = P · x / z
Pero, al aceptar este valor, estaríamos implícitamente considerando que el brazo se comporta como una estructura mixta, de músculos traccionados y huesos comprimidos trabajando al unísono. Y, consiguientemente estaríamos aceptando que la tracción Tx se va reduciendo progresivamente a medida que la sección estudiada se aleja del codo, porque el esfuerzo rasante entre músculo y hueso, también se iría reduciendo linealmente, al ser proporcional al momento flector, hasta anularse al alcanzar la mano. Para que así pudiera ser, debería existir una, poco probable, adherencia perfecta entre músculos y huesos.
También existiría otro posible modelo para la estructura del brazo, en el que músculos y huesos trabajasen independientemente y no se produjese rasante entre ellos. En este caso, la tracción constante del músculo sería igual a T = P · tg 45° = P, suponiendo que la carga, a partir de su punto de contacto con la mano, se difunde a 45°. En este hipotético modelo, el hueso trabajaría a flexocompresión y estaría pretensado por la fuerza P aplicada con la excentricidad correspondiente a la distancia entre el eje del músculo y el del hueso.
¿Cuál de los dos modelos expresa mejor el comportamiento real del brazo? No he encontrado respuesta a esta pregunta en los limitados documentos que, sobre estas cuestiones, he podido brevemente consultar.
En todo caso, la complejidad de un hipotético modelo para la estructura del brazo, es poca cosa en comparación con la que tiene una pieza tan esencial como es el codo. En él se anclan, por intermedio de los tendones respectivos, los músculos del brazo y del antebrazo. A él llegan, también, los huesos que se encuentran en la rótula compartida, con su superficie cóncava en la extremidad de uno de ellos, convexa, y complementaria en la del otro. Y, entre ambas superficies de contacto, se encuentran los cartílagos protectores y permeables al líquido sinovial. En la zona de la rótula encontraremos, también, andados a los huesos por un mecanismo de adherencia, los esenciales ligamentos que traccionados generan en sus superficies curvadas, adaptadas a la geometría de los huesos con los que están en contacto, tensiones de compresión que contribuyen al equilibrio de la articulación. Me he atrevido a esbozar un esquema muy impreciso de la estructura del codo —que, en todo caso, debería ser espacial y no plano— poniendo de manifiesto al hacerlo una ignorancia a la que sería injusto calificar de culpable. Porque he buscado respuestas a mis dudas y no las he tenido a mi alcance.
Tal vez porque hasta ahora no ha sido posible modelizar con rigor la compleja estructura de un ser humano ni caracterizar los diversos materiales que lo constituyen. Las metodologías que utilizamos para modelizar las estructuras de la ingeniería civil, de la arquitectura y de la industria, algunas complejas y de gran responsabilidad, no parecen las adecuadas para modelizar la estructura del cuerpo humano. Los cada día más sofisticados programas de cálculo de elementos finitos que tan profusamente se utilizan, aunque no siempre acertadamente, no sirven, por ejemplo, para analizar el comportamiento del cuerpo de un ciclista en acción. Y no parece que existan tendencias nuevas que abran vías serias de progreso.
Yo he tenido la impresión, tras lecturas, sin duda someras y superficiales, de algunos prestigiosos textos que se utilizan en la formación de especialistas, que la ciencia de la biomecánica está en sus albores. Y me ha sorprendido el interés que parecen despertar los modelos «tensegrid», bien conocidos en la ingeniería, para explicar una estructura, la de un ser humano, constituida por huesos que no trabajan sólo a compresión, por músculos que no son, desde luego, tirantes rectos, y por articulaciones extremadamente complejas que permiten el milagro de la movilidad. Su impulsor B. Fuller fue un personaje extraordinario y fronterizo, ingenioso y seductor que, realmente, poco aportó a la ingeniería estructural. En el magnífico documental, no exento de sombras, que sobre la vida de Norman Foster, el más ingeniero de los arquitectos estrella, se proyecta estos días de octubre de 2010 en las pantallas de los cines de Barcelona, nuestro admirable arquitecto y apasionado esquiador, le hace un hueco a su lado y le toma prestado el título, no demasiado afortunado, del film.
El progreso de la biomecánica, especialidad que parece tener más futuro que presente requerirá, creo yo, que quienes investiguen, enseñen o practiquen tengan, desde luego, unos sólidos conocimientos de anatomía. Pero que, además, conozcan a fondo el significado de las leyes de Newton. Los especialistas en este campo complejo y fascinante, al que me he asomado, con mi bagaje de conocimientos e ignorancias, deberían ser, idealmente también ingenieros. Y algunos ingenieros con las ideas claras, que no todos las tienen, debería ser estrechos colaboradores de los profesionales de esta rama de la medicina, de la salud y del deporte.
El ser humano nace con el sentido de equilibrio genéticamente instalado. El concepto de equilibrio debería presidir todo intento de comprender y de mostrar la estructura de su cuerpo. Equilibrio que, solo excepcionalmente, suele ser estático. Porque el cuerpo humano es esencialmente dinámico. Se desplace o no sobre una bicicleta.
Desde la perspectiva del equilibrio, que ha presidido muchas de las reflexiones anteriores, me permito para concluir este apartado unos breves comentarios: