El progreso en los materiales y en las tecnologías de fabricación, han multiplicado, con el paso del tiempo, las tipologías de los cuadros que se utilizan para las bicicletas de paseo o de competición en carretera. Además, en las últimas décadas, se han popularizado las bicicletas de montaña, las «mountain bikes», y con ellas han surgido una multitud de geometrías, que se adaptan a una gran diversidad de usos a los que se conocen con denominaciones anglosajonas que recuerdan su origen («cross country», «freeride», «dirt-bikes», «downhill»…) y de las que no existe aún aceptadas traducciones al castellano. Entre las «mountain bike» se pueden distinguir las de cuadro rígido, dotadas de un amortiguador de impactos incorporado en la rueda delantera, y las de doble cuadro, con suspensión trasera que exigen configuraciones especiales para las vainas y tirantes que permitan a la rueda posterior desplazarse en relación con el triángulo rígido de la parte delantera del cuadro.
Las bicicletas de montaña suelen estar sometidas a condiciones mucho más exigentes que las tradicionales de carretera, pensadas para desplazarse por superficies bien pavimentadas. Las irregularidades y obstáculos que encuentran en sus singulares recorridos provocan impactos que afectan a la bicicleta y al ciclista, que se manifiestan por importantes incrementos de las reacciones de apoyo, en el contacto de las ruedas con el terreno, y que afectan al itinerario que siguen las fuerzas para configurar el equilibrio dinámico que se ha de producir en cada instante. Los amortiguadores delanteros y suspensiones traseras mitigan los efectos de los impactos reduciendo el factor de amplificación de las reacciones de apoyo y reduciendo las aceleraciones y vibraciones que afectan al cuerpo del ciclista.
En las bicicletas convencionales, con el ciclista sentado, las aceleraciones que se producen como consecuencia de la dinámica del movimiento, tanto las de componente horizontal, longitudinal o transversal, debidas a frenadas o cambios de velocidad, como a las de componente vertical que se producen cuando el ciclista se levanta del sillín y su centro de gravedad se desplaza hacia arriba y hacia abajo, tienen valores reducidos que, en general, no superarán los 0,5 g. Por el contrario, en las bicicletas de montaña los valores de las aceleraciones pueden ser mucho más importantes. Cuando en las competiciones acrobáticas el ciclista salta despegándose del suelo la aceleración vertical supera el valor de g y cuando vuelve a tomar contacto con el suelo, el impacto correspondiente está asociado a aceleraciones verticales que pueden superar muchas veces el valor de la aceleración de la gravedad.
Los protagonistas de esta sorprendente y atractiva evolución son las suspensiones que van incorporadas en las horquillas delanteras, y los amortiguadores ubicados en diversas posiciones en la parte posterior de las bicicletas de doble cuadro. Se fabrican con sistemas de una o de cuatro articulaciones que permiten la movilidad relativa buscada entre los dos cuerpos del cuadro de lo que resulta, por otra parte, geometrías variadísimas e inéditas de un gran interés visual.
Además, la funcionalidad de este tipo de bicicletas, su razón de ser, ha exigido cambios significativos en relación con las soluciones que utilizan las bicicletas tradicionales. Los manillares son específicos y las alturas a las que se colocan, también. La posición del ciclista debe estar más próxima al suelo, para reducir el riesgo de caídas, paliar sus consecuencias si se producen y lograr, además que las magnitudes de los impactos, que dependen de la altura de caída, se reduzcan también. Todo un mundo, nacido en muy pocos años en sociedades prósperas de allende los mares, que evoluciona cada día teniendo como referente lo que ocurre en el campo de las motocicletas, sus hermanas mayores.

Las bicicletas de montaña de cuadro rígido, las denominadas «hard tail» (de «cola dura», podría ser la traducción literal al castellano), integran la suspensión, en las barras laterales de la horquilla. Las más tradicionales y económicas constan de un muelle de acero en el interior de uno de los cilindros, y de una cámara con aceite para amortiguar la respuesta posterior al impacto. Las más modernas sustituyen el muelle de acero, por un sistema de aire a presión, buscando y logrando la reducción de peso.
Las de cuadro doble, las «fullis» en el lenguaje coloquial del ciclismo, cuentan además con un amortiguador trasero que enlaza el triángulo delantero rígido, con los tirantes y vainas de la parte posterior del cuadro, lo que permite que la rueda trasera se desplace horizontal y verticalmente adaptándose a las irregularidades del terreno y contribuyendo a mitigar, también, impactos inevitables. La distancia entre las ruedas delantera y trasera podría, en consecuencia variar, lo que, entre otras cosas, influirá en la velocidad de transmisión de la fuerza de los pedales a los piñones.
Los sistemas de suspensión de la rueda delantera y de amortiguación de la trasera se han ido sofisticando con el tiempo para optimizar el comportamiento de la bicicleta en recorridos con curvas bruscas, pendientes pronunciadas de subida o bajada, y superficies de rodadura, de tierra o fango, con baches, piedras y obstáculos frecuentes. Existen, para ello, sistemas para bloquear y ajustar el recorrido de los muelles de acero o de la presión del aire que el ciclista puede activar con sus manos, así como para variar el grado de amortiguación que proporciona el aceite. Un mundo crecientemente complejo y eficiente que, por otra parte, responde a unos conceptos muy sencillos de la dinámica de las estructuras, que expondremos, someramente, a continuación.
Analicemos, para ello, el comportamiento de una masa, m, que cae desde una altura, h, sobre un muelle elástico, de rigidez k, y masa despreciable. Como consecuencia del impacto, el muelle se acortará una cantidad xdin. La energía potencial correspondiente a la masa desplazada una altura h + xdin debería ser igual a la energía elástica acumulada por el muelle (área rayada del diagrama fuerzas-desplazamientos, F-x)
m · g · (h + xdin) = ½ · k · x2din
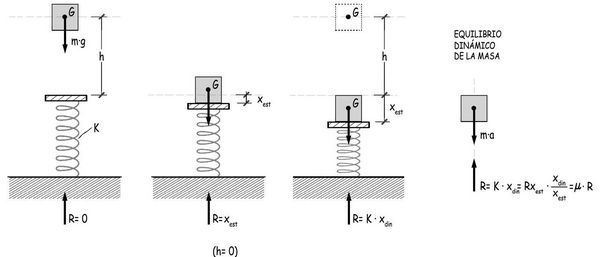
Como xest = m · g / k, es el desplazamiento elástico que hubiese tenido el muelle si la masa se hubiese posado suavemente, sin impactos, sobre él, tendremos
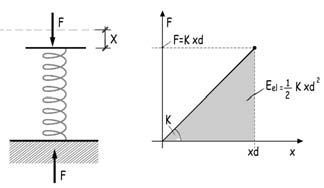
xest · (h + xdin) = ½ · x2din
de donde resulta, xdin = xest · [1 + (1 + 2 · h / xest)½]
El coeficiente de impacto, γ, factor de amplificación también de los desplazamientos y de las reacciones provocados por dicho impacto, valdrá
γ = Rdin / Rest = xdin / xest = [1 + (1 + 2 · h / xest)½]
Por otra parte, la masa aun teniendo velocidad nula al final de su recorrido estará sometida en ese instante a una aceleración, a, distinta de la gravitatoria, de manera que la correspondiente fuerza de inercia, m · a, equilibrará a la reacción dinámica
Rdin = k · xdin
En consecuencia, el coeficiente de impacto, γ, se podrá interpretar también como la relación entre las aceleraciones a y g, γ = a / g, y por lo tanto
a = g · [1 + (1 + 2 · h / xest)½]
Si, a modo de ejemplo, consideramos que la altura de caída es de 50 mm y el desplazamiento estático del muelle fuese de 10 mm, tendríamos un coeficiente de impacto
γ = 1 + (1 + 2 · 50 / 10)½ ≈ 4,3
y la aceleración consiguiente sería también 4,3 veces la de la gravedad.
Una reacción estática en la rueda delantera de aproximadamente 250 N, hubiese aumentado hasta 4,3 · 250 N = 1.075 N, como consecuencia del impacto.
Cuando h = 0, porque la masa se aplica bruscamente sobre el muelle con el que estará inicialmente en contacto, se obtiene el conocido valor de γ = 2.
Podemos representar, en términos cualitativos, la variación del coeficiente de impacto γ = Rdin / Rest —para distintos valores de h— en función de la rigidez del muelle representado por el parámetro xe = m · g / k.
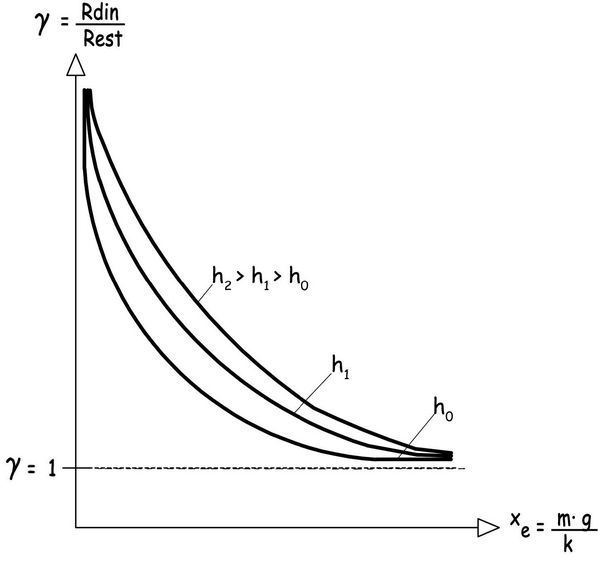
Cuando el valor de xe es muy pequeño, y por consiguiente, la rigidez del muelle muy grande, los valores de γ y de Rd tienden a infinito. Tenderán, por el contrario, a la unidad cuando la rigidez del muelle sea muy reducida y el desplazamiento estático, xe, muy elevado. En el caso de una bicicleta sin amortiguadores «externos» será la propia rueda delantera y la horquilla curvada la que actuarán a modo de amortiguador «intrínseco». La reacción de apoyo generará una pequeña deformación en la cubierta de la rueda, a la que se sumarán la provocada en su estructura (llanta más radios) y la debida a la flexión de la horquilla, que suele ser la más importante. En conjunto dicho desplazamiento puede ser de pocos milímetros para reacciones estáticas de apoyo de pocos centenares de newtons. La rigidez intrínseca podría situarse en el entorno de los 50 o 100 N/mm, muy superior a la que proporcionan los amortiguadores externos que, suelen situarse en rangos de 5 a 10 N/mm, pudiendo variar al incrementarse el desplazamiento.
Realmente el sistema global de amortiguación podría modelizarse mediante dos muelles en serie: el del amortiguador «externo» de rigidez ka, dispuesto a continuación del que representa la rigidez, kr, de la rueda y horquilla. El conjunto de los dos muelles equivale a un muelle único de rigidez keq, tal
1 / keq = 1 / ka + 1 / kr
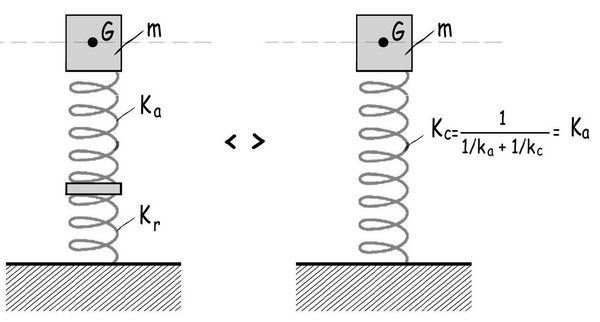
Como ka suele ser mucho mayor que kr la rigidez equivalente, keq coincidirá prácticamente con ka. Por ello, la existencia de un sistema de amortiguación incorporado a las horquillas hace innecesario el curvado característico de las bicicletas de carretera. No así la excentricidad de la horquilla en relación con el eje de la rueda delantera (para facilitar el giro controlado del manillar) que se logra con la geometría que se adopte para las punteras.
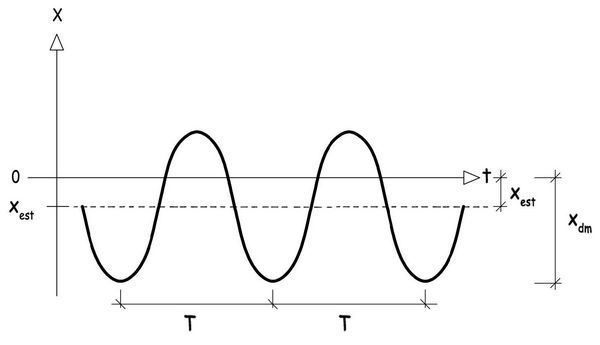
Si no existiese amortiguación en el sistema, la masa m, una vez alcanzado su descenso máximo xa, comenzaría a ascender debido al alargamiento del muelle y se movería indefinidamente con un movimiento armónico de expresión
x = A · sen (ω · t)
en donde A = xd – xe será la amplitud del sistema, y ω su pulsación.
La ecuación de equilibrio dinámico será
m · ∂2x/∂t2 = k · x
fuerza de inercia, fi = fuerza elástica, fe
es decir
∂2x/∂t2 = (k / m) · x = ω2 · x
siendo ω = 2 · π · f = 2 · π / T = (k / m)½, la pulsación del sistema, cuyo periodo de vibración valdrá
T = 2 · π · (m / k)½
del que resulta la conocida y útil expresión para el periodo propio del sistema:
T ≈ 0,2 · (xest)½
siendo xest, el desplazamiento estático en centímetros.
En el caso que hemos supuesto con xest = 10 mm, T valdría 0,2 segundos y la frecuencia del sistema sería de 5 hertzios.
Una situación como la descrita sería intolerable para el ciclista. El movimiento que provoca un impacto debe ser rápidamente amortiguado. El aceite dispuesto en el interior de los tubos de la horquilla tiene esta finalidad, y crea una fuerza de amortiguamiento, fc = c · ∂x/∂t, que por ser de naturaleza viscosa es proporcional a la velocidad de desplazamiento. La ecuación del equilibrio dinámico de las fuerzas, siendo c el coeficiente de amortiguamiento, se convierte en
fuerza de inercia, fi = fuerza de amortiguación, fc + fuerza elástica, fe
m · ∂2x/∂t2 = c · ∂x/∂t + k · x
La solución de esta ecuación diferencial es del tipo x = eλ·t, expresión que introducida en la anterior de equilibrio permite deducir el exponente, λ
λ = [c ± (c2 – 4 · m · k)½] / c2
El amortiguamiento crítico, Ccr, será el que anule el radical,
c2cr – 4 · m · k = 0
o lo que es lo mismo
c2cr – 4 · m2 · ω2 = 0
Por lo tanto,
ccr = 2 · m · ω
Para que el movimiento se amortigüe rápidamente el valor de c debe estar próximo al de ccr. Los esquemas del movimiento amortiguado son los siguientes. Cuando c << ccr (es lo que ocurre en las estructuras de la ingeniería civil, en las que, en general, sólo se cuenta con la amortiguación de la propia estructura), la amplitud de la vibración se irá amortiguando progresivamente. En el otro extremo, cuando c > ccr, el desplazamiento no cambiará de signo y el sistema volverá, sin vacilaciones, a su posición estática original.