
Los sistemas de engranajes, con sus múltiples variantes, tienen una larga y bien conocida historia detrás. Hace más de 3.000 años que se utilizaban en los molinos para transformar el giro de las palas movidas por el viento, en rotación de las piedras que molían el grano. En el Renacimiento, los mecanismos de engranaje —protagonistas de muchas de las invenciones de Leonardo da Vinci, en el siglo XVI— fueron la base del desarrollo de los relojes que permitían medir el tiempo con gran sencillez y precisión. Con la revolución industrial llegaron los motores de explosión y con ellos las máquinas de todo tipo que convertían el desplazamiento de los émbolos del motor en movimientos de otra naturaleza, mediante mecanismos crecientemente sofisticados.

Es natural que con estos antecedentes, somerísimamente expuestos, los primeros fabricantes de bicicletas incorporasen mecanismos de transmisión que fueron evolucionando hasta llegar al actual sistema de pedal-biela-plato-cadena-piñón-rueda, que permite convertir tan eficientemente cada pedalada del ciclista en movimiento de la bicicleta.
Por cada vuelta que dan los pedales, y por tanto el plato del pedalier, el piñón trasero dará un número de vueltas igual a la relación de dientes del plato y del piñón, unidos por la cadena. Y a cada vuelta que da el piñón, la rueda trasera a la que está rígidamente unida, dará también una vuelta. De manera que el número de vueltas, n, de la rueda trasera, y lógicamente de la delantera también, se deduce de la sencilla relación:
n = dientes del plato / dientes del piñón
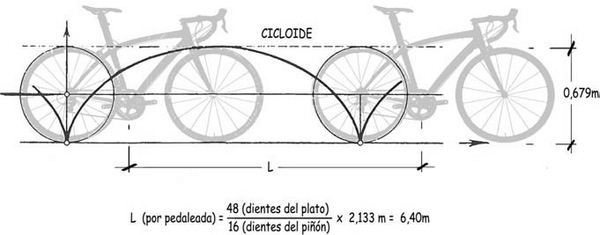
Así, si la cadena solidariza un plato de 48 dientes con un piñón de 16, por cada pedalada las ruedas darán 3 vueltas recorriendo una longitud igual a n veces su perímetro. A las más habituales de carretera se les atribuye un diámetro de 70 cm que, en realidad es un valor aproximado que traduce en centímetros el nominal de 28 pulgadas. Aunque en realidad, con un neumático bien hinchado, su diámetro exterior es de 0,679 m y su perímetro de 2,133 m.
Abramos aquí un paréntesis para comentar que las de 29", las «twenty-nine» en el lenguaje de ultramar desde donde se está impulsando fuertemente su uso, ya tienen una presencia destacada en el mundo de la bicicleta, siquiera como motivo de conversación. Y que las de 26" son protagonistas, hasta ahora, en todas las modalidades de «mountain-bike».
En el caso que estamos considerando, con la cadena uniendo un plato de 48 dientes con un piñón trasero de 16, cada pedalada del ciclista, provocará un desplazamiento de la bicicleta de
L1 = (48 / 16) · 2,133 ≈ 6,40 m
Para una cadencia de 60 pedaladas por minuto —una por segundo—, la velocidad de recorrido será
v = 6,40 m/pedalada · 1 pedalada/s = 6, 40 m/s ≈ 23 km/h
Si la cadencia, fuese de 90 pedaladas/minuto (1,5 p/s) la velocidad de desplazamiento sería
v = 1,5 · 6,40 = 9,60 m/s ≈ 34,5 km/h
Cuando un ciclista excepcional (tal vez, un Cipollini), mueve un plato de 53 dientes, con un piñón de 11 y una cadencia de 120 pedaladas por minuto, la velocidad correspondiente resulta:
v = (53 / 11) · 2,133 m/pedalada · 120 / 60 pedaladas/s = 20,55 m/s ≈ 74 km/h
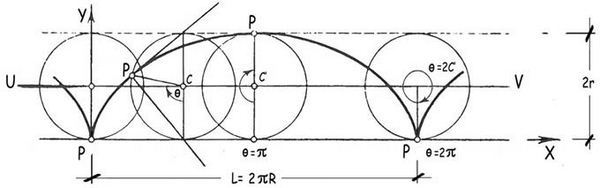
Cuando la bicicleta se desplaza, sin deslizarse, siguiendo una línea teórica perfectamente recta, el punto que en un instante preciso será el de contacto de la rueda con el pavimento comenzará a describir una curva que se conoce con el nombre de cicloide.
Es a Galileo a quien se debe la denominación de esta curva que él mismo descubrió hacia 1590, al tratar de comprender la trayectoria de un punto de una rueda que se desplazaba, sin deslizar, a lo largo de una recta. Su alumno Torricelli, y otros sabios, se ocuparon, también, del estudio matemático de la cicloide. Pero fue Pascal quien realizó un estudio exhaustivo de sus propiedades y las dio a conocer en 1659 («Historia de la cicloide»). A partir de entonces sabios como Huygens, Newton, los Bernouilli o Leibnitz trabajaron sobre numerosas aplicaciones prácticas.
La ecuación de la cicloide ordinaria, a la que nos estamos refiriendo, tiene por ecuaciones en coordenadas paramétricas
x = R · (Φ – sen Φ)
y = R · (Φ – cos Φ)
siendo Φ el ángulo de rotación de la rueda.
Entre sus numerosas y notables peculiaridades se encuentra el que la longitud del arco que describe la cicloide es igual a ocho veces el radio, R, de la rueda que la genera y que la superficie de un bucle es tres veces la de la rueda.
Hagamos, ahora, a modo de primerísima aproximación, algunas reflexiones acerca de las geometrías que dibujan las ruedas delantera y traseras cuando el ciclista gira el manillar para «negociar» la curva de una carretera. Debe ser, sin duda, una cuestión compleja que ha tenido que ser muy estudiada, sobre todo, en relación con los automóviles y las motocicletas.
La bicicleta, a estos efectos y muy elementalmente se puede considerar que está constituida por dos cuerpos rígidos. Por una parte, el que forman la rueda motriz posterior, con el cuadro, el sillín y el sistema de transmisión. Por otra, el de la rueda delantera con el sistema de dirección, incluida la horquilla y el manillar. Los dos cuerpos estarán enlazados por la barra de dirección del cuadro en cuyo interior se alojan los dos rodamientos, que permiten el giro relativo entre los dos cuerpos y transfieren las fuerzas entre ellos. Muy esquemáticamente los dos cuerpos se pueden representar, para mayor claridad, separados y vistos en planta.
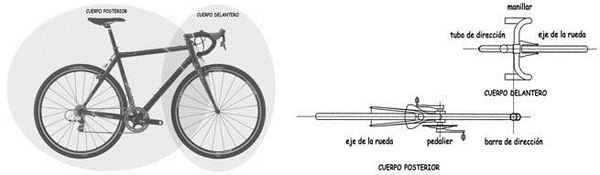
Aún más esquemáticamente, podemos representar el conjunto de la bicicleta con el manillar girando un ángulo a, por la acción de las manos del ciclista.
Suponiendo que los puntos de contacto de las ruedas con el pavimento coinciden con la vertical de sus bujes, observamos en el esquema que la perpendicular a la alineación del eje de rueda trasera se encontrará con la del eje de la rueda delantera en el punto C, que será el centro instantáneo de rotación del movimiento de las ruedas. La posterior, se desplazará, en el instante considerado, por una circunferencia de radio, Rt, y el de la rueda delantera por otra ligeramente mayor, de radio Rd. Si el ciclista mantuviese fija la posición del manillar, su centro de gravedad daría, en efecto, vueltas por el perímetro de un círculo de radio intermedio entre Rt y Rd. Al modificar el giro del manillar iría variando, simultáneamente, el radio de los círculos, de manera que el recorrido real de cada rueda se haría tangente a cada uno de los sucesivos círculos instantáneos que jalonarán el movimiento.
Por otra parte, el ciclista para girar el manillar habrá tenido que aplicar con sus manos un par de fuerzas iguales y contrarias. Y para equilibrar dicho par torsor aparecerán unas fuerzas transversales en el contacto con el pavimento de la rueda delantera y otra, igual pero de sentido contrario en la rueda trasera, de manera que se verifique la condición de equilibrio.
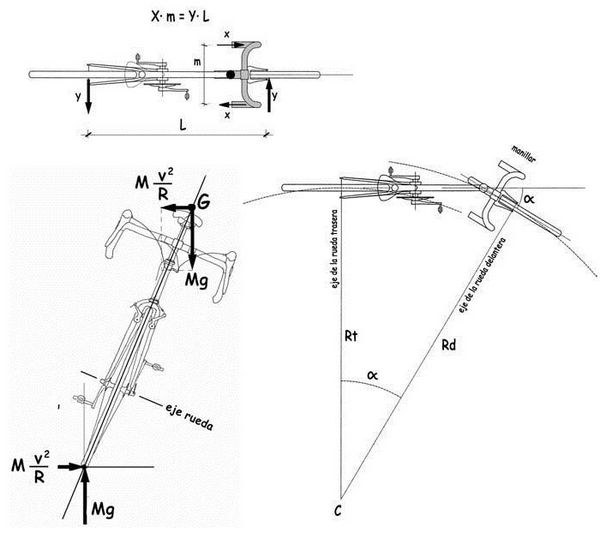
Sin embargo, con estos planteamientos, estamos olvidando al ciclista, indiscutible protagonista de esta historia. Su centro de gravedad, en el que muy simplificadamente, consideramos que se concentra toda la masa del ciclista y de su bicicleta, también se desplazará describiendo una circunferencia cuyo radio no coincidirá con el que habrán dibujado en el pavimento las ruedas delantera y trasera.
Y como consecuencia de este movimiento circular del centro de gravedad, aparecerá una fuerza centrífuga transversal, que es una fuerza de inercia, de valor
Ft = M · at = M · v2 / R
siendo at, la fuerza centrífuga asociada al movimiento e igual a v2 / R.
El ciclista y su bicicleta se inclinarán lo suficiente para que, a cada instante, se produzca el equilibrio dinámico de fuerzas.
Por lo tanto, el giro del manillar, y la consiguiente modificación de la trayectoria de la bicicleta, exigirá que el cuerpo del ciclista y de su bicicleta se inclinen lateralmente. En los contactos de las ruedas delantera y trasera con el pavimento aparecerán fuerzas transversales, de diferentes orígenes, que se relacionarán entre ellas a través de las reacciones en los rodamientos de la barra de dirección, así como de las debidas al propio cuerpo del ciclista situadas en los puntos en los que se apoya en la bicicleta. El cuadro de la bicicleta estará, también, solicitado por esfuerzos torsionales consecuencia de la transferencia de las fuerzas transversales entre los dos cuerpos delantero y trasero de la bicicleta, cuya geometría en planta se quiebra, al girar el manillar alrededor del eje de dirección.
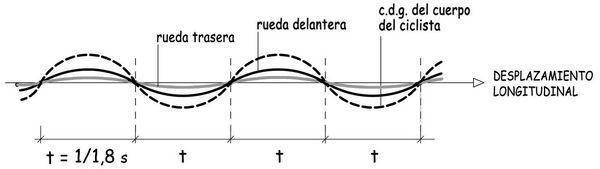
Los movimientos de un ciclista cabalgando sobre su bicicleta tienen su componente de misterio. Aun cuando pretenda seguir una trayectoria recta en una carretera sin curvas, su pedaleo no producirá fuerzas simétricas. La aplicada en uno de los pedales será, en un instante dado, mayor que en el opuesto. Instintivamente el cuerpo del ciclista se moverá transversalmente en el sentido del pedal más cargado y, consiguientemente, aparecerá una fuerza transversal de inercia que se opondrá a dicho movimiento hasta anularlo e iniciar el cambio de sentido, lo que hará posible un mayor esfuerzo en el pedal opuesto. Y así sucesivamente, con el ritmo correspondiente al de la cadencia del pedaleo. En este proceso, la geometría del recorrido de la bicicleta no será una recta, sino una línea de aspecto senoidal que cambiará de curvatura 1,5 veces por segundo, cuando la cadencia sea de 90 pedaladas por minuto. Las trazas que dibujarán, por otra parte, las ruedas delantera, trasera y el centro de gravedad del cuerpo del ciclista serán similares pero no idénticas. Las amplitudes máximas podrían ser del orden de pocos centímetros en el cuerpo del ciclista y de imperceptibles milímetros en las ruedas.
Entre las reflexiones que suscita el sistema de dirección no puede faltar la que tratan de explicar su geometría. La barra de dirección suele formar un ángulo de 72°-73° con una línea horizontal y su eje está situado de tal manera que su prolongación virtual encuentra al pavimento ligeramente por delante, unos 50 o 60 mm, del punto de contacto con la cubierta de la rueda delantera. En consecuencia, la respuesta al momento torsor que aplica el ciclista en el manillar para hacer girar la rueda delantera, será una fuerza transversal que tendrá por valor
Ft = MT / r
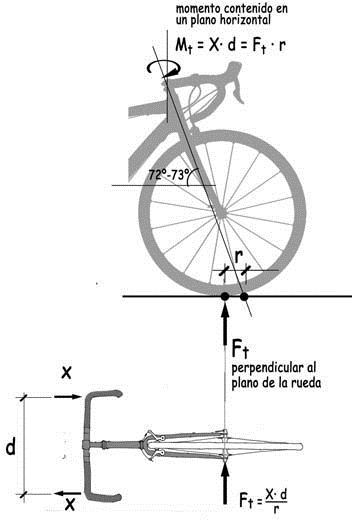
Si no existiese este decalaje y el valor de r fuese próximo a cero, la fuerza Ft sería mucho más grande y costaría girar el manillar. Si, en el otro extremo, la distancia r fuese excesiva la fuerza asociada al giro del manillar sería muy pequeña, y cualquier pequeño obstáculo provocaría su rotación y la bicicleta sería difícil de controlar.
La bicicleta está plagada de sabios detalles geométricos avalados por las experiencias vividas por centenares de millones de ciclistas.
Por otra parte, el curvado de la horquilla del sistema de dirección y la esbeltez habitual de su geometría contribuye, además, a dotar a la rueda delantera de una flexibilidad que mitigue los pequeños impactos que puede padecer una bicicleta de carretera debidos a las irregularidades del pavimento. La rigidez vertical que se consigue de esta manera, debida en parte a la deformación de la rueda y en mayor medida a la flexibilidad de la horquilla puede ser del orden de 100 N/mm.
Además, la rueda delantera puede ser, en ocasiones, origen de sorprendentes y perturbadoras vibraciones transversales a las que, en la terminología anglosajona, se conoce con el término «shimmy», y para las que no existe, a lo que parece, una explicación del todo convincente. Tal vez entre las causas que pueden provocar estas vibraciones esté la que se aventura a continuación. Los radios de la rueda delantera están inclinados sucesivamente a un lado a un lado y otro de su plano de simetría con una inclinación aproximada de
H / V = 1/8
Si imaginamos que la totalidad o buena parte de la reacción de apoyo se transmitiese a un único radio, como consecuencia de su inclinación aparecería una fuerza transversal que valdría la octava parte de la reacción de apoyo. Al continuar girando la rueda, se cargaría (o se descargaría, para ser más precisos) el radio siguiente, que tendría una inclinación opuesta al anterior.
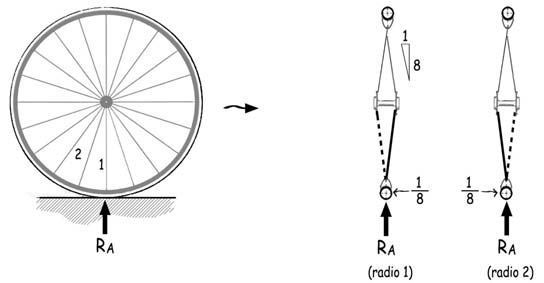
La fuerza transversal pasaría a tener, por tanto, el mismo valor pero de sentido contrario y así ocurriría sucesivamente en cada uno de los radios. Por tanto, transversalmente a la rueda irían apareciendo fuerzas alternativas con una frecuencia que, tratándose por ejemplo de una rueda de 36 radios que giran 3 veces por segundo (plato de 48 dientes piñón de 16) sería de 3 · 36 = 108 hertzios, valor que puede coincidir con alguna de las frecuencias propias de la bicicleta y, consiguientemente provocar un efecto de resonancia.
Podría ser, en cierto modo, algo pareado a lo que sucedió con la pasarela del Millenium que se construyó en Londres sobre el Támesis para festejar el tránsito entre los siglos XX y XXI, y que se clausuró a los pocos días de su inauguración para proceder a su refuerzo. Un peatón puede producir, al apoyarse sucesivamente en uno u otro pie fuerzas alternativas transversales del orden de 25 N, aproximadamente un 3% de su peso, con frecuencias del orden de 1 hertzio (T = 1 s) que pueden ser similares a alguna de las frecuencias propias de vibración, en el modo transversal, que tenía la pasarela original. Cuando el número de peatones circulando sobre el tablero fue suficientemente importante, del orden de 200, y cuando cada uno de ellos, estimulados por las vibraciones incipientes, ajustaron, instintivamente, su paso con el de todos los demás, se produjo una notable amplificación de los movimientos transversales con aceleraciones entre 0,2 y 0,3 g que justificó su clausura y la colocación de numerosos amortiguadores que resolvieron el problema al año de haberse planteado. Las aceleraciones máximas que se suelen considerar tolerables por un ser humano no superan los 0,05 g o 0,5 m/s2.

También, en los modernos aerogeneradores eólicos, se produce un efecto similar, más sistemático y relevante, porque es determinante en el dimensionamiento de las torres que sostienen los aerogeneradores. Al girar las palas, pasan por delante de la torre con una frecuencia que es la del giro del eje del aerogenerador multiplicado por 3 que es el número de palas. Dicha frecuencia debe mantenerse alejada de la frecuencia propia de la torre para evitar amplificaciones indeseables
