
Como ya se ha comentado en apartados precedentes, la consideración del equilibrio de la bicicleta permite identificar con sencillez y razonable precisión las reacciones de apoyo, longitudinales y transversales, que se producen en el contacto entre las cubiertas de las ruedas y el pavimento sobre el que circula. Y como en cualquier estructura, si se conocen las reacciones provocadas por las acciones que actúan sobre una bicicleta, se dispone de la información esencial para evaluar su comportamiento y confirmar el acierto de las geometrías y de los materiales utilizados en su fabricación.
Para establecer las fuerzas que intervienen en el equilibrio, hemos supuesto, hasta ahora, que las masas de la bicicleta y del ciclista estaban concentradas en sus centros respectivos de gravedad. Y hemos admitido también que la superficie de rodadura era suficientemente lisa, sin baches o resaltos de una u otra naturaleza. No se producirían, por tanto, impactos asociados a bruscas aceleraciones que influirían notablemente en el valor de las acciones, incrementarían las reacciones máximas, reducirían las mínimas, y modificarían así mismo el reparto de cargas entre las dos ruedas. Al contrario de lo que sucede cuando se circula por caminos o senderos de montaña, lo que explica la sofisticación de las «mountain-bike», con sus suspensiones delanteras, y sus eventuales amortiguadores traseros, integrados en dobles cuadros, articulados entre sí. En este apartado 5, nos referiremos exclusivamente a las bicicletas de carretera dejando el 8 para bicicletas de montaña.
Es evidente que la masa de la bicicleta y del ciclista no está concentrada en sus respectivos centros de gravedad. Esta suposición es solamente una simplificación muy útil que permite localizar y cuantificar las reacciones de apoyo. Porque, realmente, la estructura de la bicicleta, en toda su sencillez conceptual y su complejidad tecnológica, se puede entender y describir como un entramado de elementos estructurales que relacionan las acciones o fuerzas actuantes con las reacciones de apoyo. Dichas fuerzas fluyen desde el cuerpo del ciclista por los distintos componentes de la bicicleta hasta alcanzar el suelo. En cada punto infinitesimal de este conjunto se producen tensiones y deformaciones unitarias, relacionadas entre ellas por los módulos de elasticidad longitudinal, y transversal que caracterizan el material estructural. Tensiones y deformaciones fluyen inseparables a través del material que van encontrando en su camino, cambiando a cada instante, dado el dinamismo del conjunto, pero preservando siempre la insoslayable exigencia de equilibrio. La similitud hidráulica salta a la vista. Los puntos de contacto con el suelo, en los que se concentran las reacciones de apoyo, son como los sumideros hacia los que afluyen los caudales que se han ido generando en cada minúsculo trozo de materia del cuerpo del ciclista y de su bicicleta. Cada caudal infinitesimal que brota de cada punto material se suma a otros caudales que circulan por los cauces, que definen la geometría estructural. Y la armonía de los itinerarios por los que discurren los caudales acumulados es una manifestación de la eficacia de la geometría estructural. Como en el caso de una canalización de agua, los recodos, las pendientes excesivas, los estrechamientos bruscos, limitan la capacidad de transferencia de los caudales tensionales y deformacionales, provocando, también, flujos irregulares y turbulencias indeseables. A través de la bicicleta y del cuerpo del ciclista fluyen tensiones y deformaciones, y la ausencia de zonas singulares en las que se amplifican unas y otras es manifestación de armonía y de eficiencia en la concepción estructural. O, de otra manera, como en las estructuras de la ingeniería civil, las zonas singulares de la bicicleta —y del ciclista— que son muchas, son las estructuralmente críticas, las que definen los límites de las cargas que se pueden transferir, como las zonas singulares de una conducción determinan los caudales máximos del fluido que puede transportar.
Iniciaremos ahora un viaje virtual acompañando a las fuerzas en su recorrido a través de la estructura de la bicicleta y a través del cuerpo del ciclista.
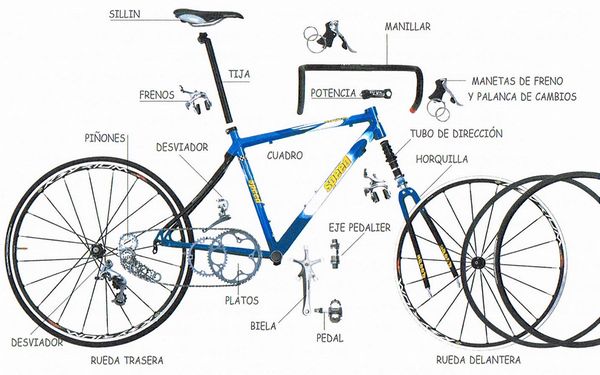
El primer tramo del recorrido, se inicia en el punto de contacto de la rueda delantera (la trasera no es idéntica) con el pavimento y concluye en el buje que la permite girar. El itinerario de fuerzas, tensiones y deformaciones recorre la cubierta, utiliza el aire a presión para alcanzar la llanta, fluye después por los esbeltos y tensos radios, hasta llegar al buje, meta de esta primera etapa.
La siguiente se inicia donde acaba la primera y discurre por la subestructura que forman el conjunto de la horquilla y la potencia, y concluye en el contacto de las manos del ciclista con el manillar y en la bifurcación señalada por los rodamientos de la barra de dirección que conducen parte de las fuerzas hacia la estructura del cuadro.
El cuadro de la bicicleta, la siguiente subestructura, se apoya en la barra de dirección y en el buje de la rueda trasera. Recibe al sillín, en la tija prolongación de la barra vertical que en su encuentro con la diagonal y la desdoblada vaina del cuadro, deja el hueco por el que penetra el eje de los pedales y de los platos del sistema de transmisión de la bicicleta. El desdoblamiento de las vainas y tirantes que confluyen en el buje de la rueda trasera procura el espacio para acomodarla. La particular geometría del cuadro de la bicicleta con numerosas singularidades es manifestación de un itinerario, más justificado por su función que por su eficiencia estructural.
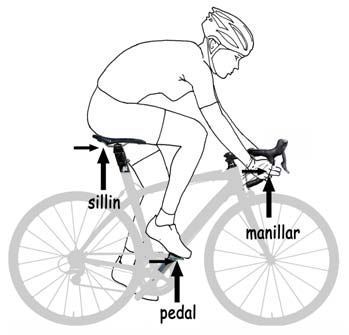
La última etapa de este recorrido virtual por la estructura de la bicicleta que nos aprestamos a realizar incluye el conjunto del mecanismo de transmisión —pedales, platos, cadena y piñones— que permiten insuflar energía a la bicicleta, asegurando su movilidad. Pero, además, tenemos el flujo itinerante de las fuerzas que nacen en el cuerpo del ciclista, con tres posibles zonas de contactos con la bicicleta: manillar, sillín y pedales. El cuerpo del ciclista es también una estructura, ciertamente muy especial y evidentemente esencial a la que en una primerísima aproximación, podría describirse como una celosía, con elementos comprimidos, los huesos, y elementos traccionados que serían los músculos. Los huesos estarían articulados para permitir su movimiento relativo, provocado por la tracción de músculos, ligamentos y tendones que se activan por el sistema nervioso gestionado por un cerebro que gobierna la transformación de la energía química en la energía mecánica que hace posible la asombrosa movilidad del cuerpo del ser humano, distinguidísimo miembro de la especie animal.
El conjunto ciclista-bicicleta se puede considerar, por tanto, como un ensamblado de subestructuras cada una de las cuales tiene que estar en cada instante en equilibrio dinámico.
La rueda ha sido una de las invenciones más importantes en la historia de la humanidad y de las que más trascendencia han tenido. Su utilización por el hombre primitivo le permitió mejorar su movilidad; lo que fue esencial en su desarrollo individual y social. Los animales nunca utilizaron la rueda. Lo que probablemente explique, también, su retraso.
Pero tal vez no sea la rueda una invención trascendente del ser humano. En todo caso, hubiese sido un descubrimiento, porque la posibilidad de desplazarse rodando está muy presente en la naturaleza: en las piedras que se encuentran en los cauces de algunos ríos, en los troncos de árboles sin ramas, o en las vueltas que da un niño en su cuna mientras duerme. Porque lo que verdaderamente transformó el mundo fue el eje, sin el cual la rueda hubiera tenido muy limitadas aplicaciones. La invención, en el Renacimiento, del reloj moderno facilitó la medición sencilla y sistemática del tiempo, y contribuyó a una profunda transformación del orden de valores en los que se asentaban las sociedades medievales. Su desarrollo estuvo íntimamente ligado a la utilización de mecanismos de pequeñas ruedas dentadas que giran alrededor de minúsculos ejes.
El nacimiento y evolución de la bicicleta fue también posible por el progreso de la rueda, su componente quizás más tecnológico. Y, tal vez, el más sutil siendo, de hecho, una maravilla estructural, ejemplo de estructura pretensada en que los esbeltos radios, fuertemente traccionados, enlazan el colchón toroidal de aire presurizado, que conforman cubierta y llanta con el eje, al que transfieren las reacciones de apoyo localizadas en el contacto del neumático con el pavimento.
Aislemos la rueda delantera de la bicicleta —la posterior posee algunos rasgos específicos— y analicemos el equilibrio entre la reacción de apoyo y la fuerza, igual y contraria, que se localiza en el eje alrededor del cual rota. En el plano de la rueda, la reacción de apoyo tendrá una componente vertical Rv, y otra horizontal Rh, en general, significativamente menor aunque sea la responsable de la movilidad de la bicicleta. La inclinación de la resultante de ambas fuerzas en relación con la vertical será tal que
tg α = Rh / Rv
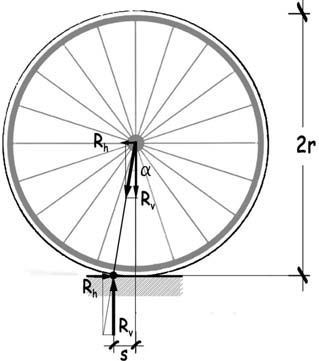
Para que dicha resultante pase por el eje de la rueda, el contacto entre el neumático y el pavimento estará desplazado en el sentido contrario al movimiento, una distancia
s = r · α
siendo r el radio de la bicicleta.
Si, a modo de ejemplo, suponemos que Rv = 200 N y Rh = 10 N, la inclinación de la resultante sería del 5%, y en una rueda de 350 mm de radio el desplazamiento del punto de contacto sería aproximadamente
s ≈ 5/100 · 350 mm = 17,5 mm
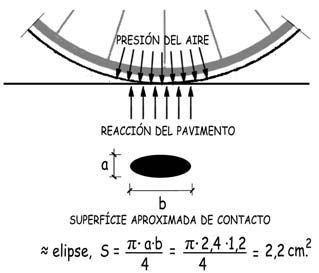
La magnitud de la superficie de contacto entre la rueda y el pavimento dependerá fundamentalmente del valor de la reacción vertical Rv, de la presión P, del neumático y de la rigidez del pavimento. En el caso de una carretera bien asfaltada o con firme rígido de hormigón, la deformabilidad del pavimento será insignificante. Por tanto, la cubierta adoptará la geometría del pavimento, y la superficie de contacto valdrá
S = Rv / p
En una bicicleta de carretera de competición, la presión de hinchado suele alcanzar los 9 bares, (1 bar ≈ 10 N/cm2). Para una reacción vertical de 200 N la superficie de contacto sería:
S= 200 N / 90 N/cm2 = 2,2 cm2
Tendría el aspecto de una elipse, inscrita, tal vez, en un rectángulo de 2,4 x 1,2 cm.
Si, como ocurre con frecuencia en los caminos de rodadura utilizados por las bicicletas de montaña, el terreno es muy deformable y su «tensión admisible» muy inferior a la de la presión de hinchado de las ruedas, que en este tipo de bicicletas no suele exceder de los 3 bares, será el terreno el que se adapte a la forma circular de la rueda que, al avanzar, irá abriendo surco, siendo la superficie de contacto en un instante determinado de
S = 200 N / 30 N/cm2 = 6,66 cm2
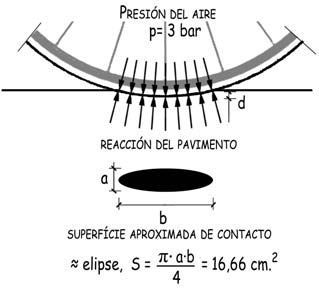
Si la deformabilidad del terreno, caracterizada por un coeficiente de balasto, o coeficiente de reacción del terreno (relación entre la presión y el desplazamiento, esto es k = P / d) fuese, pongamos por caso, de 10 N/cm3 la profundidad de la huella sería
d = p / k = 30 N/cm2 / 10 N/cm3 = 3 cm
El comportamiento real será, en general, intermedio entre los dos anteriores y de análisis, desde luego, mucho más complejo. Localmente, en la zona de contacto con el pavimento, la cubierta de la rueda estará sometida a la presión externa de contacto y a la presión interna de hinchado, que no serán idénticas. Para acomodar estas diferencias de presión, la cámara se habrá de deformar tanto en sentido longitudinal como transversal y su compleja estructura de capas hará posible la adecuada respuesta a los esfuerzos consiguientes.
La industria que concibe y fabrica las cubiertas de las ruedas de la bicicleta (y de las motos y coches, sus hermanos mayores) es un sector altamente especializado que ha evolucionado extraordinariamente, desde que Dunlop, un veterinario de Belfast, primero, y Pirelli, poco después, estableciesen sus fundamentos, hace más de 120 años.
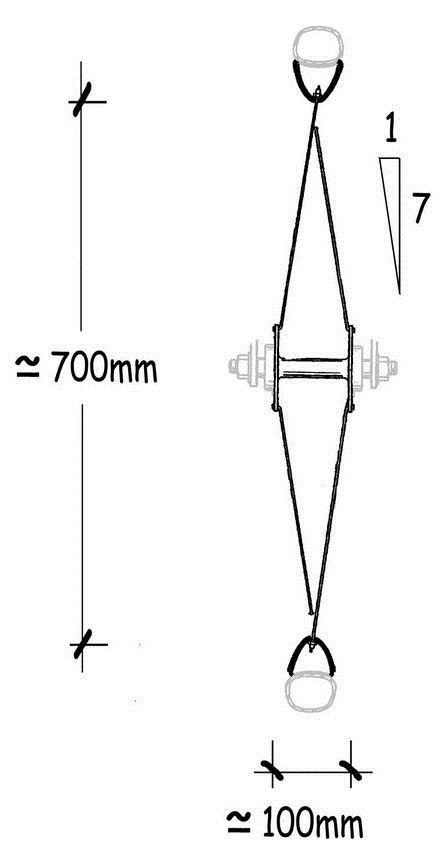
Las ruedas de las bicicletas de carretera más habituales tienen un diámetro nominal de 700 mm (28 pulgadas), aunque últimamente parece que se extiende el uso de las de 29", las «twenty nine». Tradicionalmente sus llantas estaban construidas con aceros inoxidables y en la actualidad lo están con perfiles de aluminios aleados fabricados por extrusión. Y más recientes, con materiales compuestos por fibras de carbono con una matriz de resina epoxi. Existen, también, llantas fabricadas por combinación de estos dos últimos materiales.
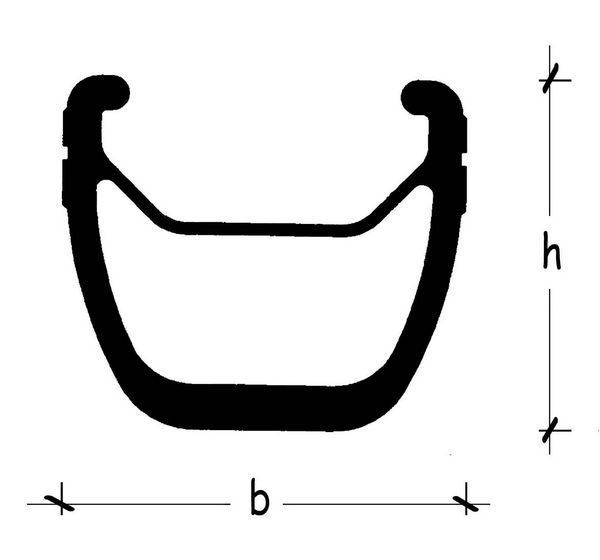
Su sección transversal suelen tener una anchura, b, del orden de 20 mm y alturas, h, de unos 20 mm también en las de perfil bajo, que puede llegar a 50 mm en los de perfil alto. La cubierta neumática forma con la llanta un conjunto inseparable. En la figura adjunta se muestra la composición de uno de los modelos que comercializa un prestigioso fabricante.
En las bicicletas de los ciclistas profesionales las cubiertas «tubeless», sin cámara, han desplazado totalmente a las tradicionales, en las que un pinchazo era reparado por el propio ciclista que portaba, para ello, su cámara de repuesto. Las cubiertas sin cámara deben ir muy bien ajustadas a las alas interiores de las llantas para asegurar una impermeabilidad, que, antes, proporcionaban las cámaras de goma.

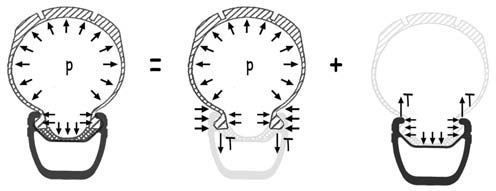
En los croquis adjuntos se muestra el equilibrio de la cubierta y de la llanta. Como orden de magnitud, las fuerzas de tracción T que se transfieren entre ambos componentes, supuesta la presión de 9 bares y la anchura de la llanta de 20 mm será
T ≈ 90 N/cm2 · 2 cm / 2 = 90 N/cm
Suponiendo, también, que el espesor del aluminio de la llanta, en la zona de transferencia de T, fuera de 1 mm, la tensión correspondiente sería del orden de
σ = 90 N/cm / 0,1 cm = 900 N/cm2
valor muy reducido, de dirección radial, y que poca influencia tendrá en el comportamiento de la estructura de la llanta.
Las tensiones más importantes serán las circunferenciales y tendrán por causa principal la tracción de los radios, que inducirán compresiones circunferenciales considerables.
Suponiendo que se trate de una rueda de 32 radios, separados en el perímetro de la llanta unos 6,5 cm y solicitados cada uno de ellos por una tracción de 1.000 N, la presión inducida que supondremos uniformemente repartida, valdría:
P ≈ 1.000 N / 6,5 cm = 150 N/cm
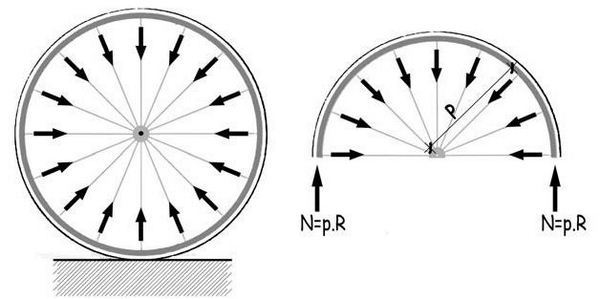
Esta presión induce a su vez una compresión en la llanta que valdrá
N = p · R = 150 N/cm · (70/2) cm = 5.250 N
La sección de una llanta de aluminio, de 430 gramos de masa, debe situarse en el entorno de 0,8 cm2 (0,8 cm2 · 200 cm · 2,7 g/cm3 ≈ 430 g).
La tensión de compresión circunferencial en la llanta, consecuencia de las presiones radiales provocadas por los radios, valdrá
σ = 5.250 N / 0,8 cm2 = 6.562 N/cm2
Dicho valor es muy inferior al que admiten los aluminios aleados que se utilizan en la fabricación de las llantas. La máxima tensión admisible estará limitada por el riesgo de pandeo que existe siempre en un anillo estructural solicitado por tensiones radiales contenidas en su plano. La carga crítica de pandeo, cuya deducción se encuentra en publicaciones especializadas, tiene por expresión:
pcr = α · E · Iy / r3
siendo E, el módulo de elasticidad del material, Iy la inercia de la sección de la llanta o anillo, en relación con un eje perpendicular a su plano, r el radio del centro de gravedad de dicha sección y α un coeficiente que, principalmente, depende de la relación entre las rigideces a flexión y torsión de la sección de la llanta y el anillo, cuyo modo de pandeo adoptará la forma de ocho esquematizada.
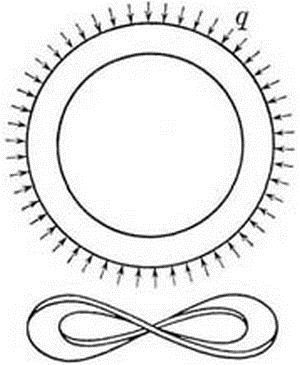
En realidad la situación es más favorable. La mitad de los radios de una rueda tienen una inclinación en un sentido y la otra mitad en el otro (ver figura adjunta), lo que hace que en la deformación transversal de la llanta, su tendencia al alabeo, esté coaccionada. Es como si se encontrase envuelta en un medio elástico, con virtuales muelles que pueden generar fuerzas transversales estabilizadoras en todo el perímetro de la rueda, que serán del orden de
1/8 · 150 N/cm ≈ 19 N/cm
lo que incrementará sensiblemente la capacidad del pandeo lateral, por flexión y torsión.
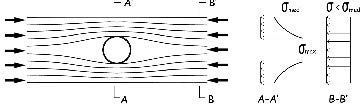
Estos valores recuerdan, por otra parte, la importancia de que los radios estén uniformemente tensionados y la rueda perfectamente alineada. Cualquier imprecisión al respecto afecta sensiblemente al comportamiento de la rueda, por la aparición de fuerzas transversales consecuencia de los desequilibrios asociados a las variaciones de tensión entre radios.
Entre las zonas críticas de la llanta, se encuentran las del entorno de las perforaciones, del orden de 2,5 mm, asociadas al dispositivo de anclaje roscado de los radios y sobre todo la de unos 6,5 mm que exige la presencia de la válvula de hinchado de las ruedas. Dichas perforaciones provocan por una parte, una reducción muy significativa, que puede llegar al 50%, del área del ala interna del perfil de la llanta y, además, una distorsión del flujo tensional que puede provocar puntas de tensiones 2 y 3 veces superiores al de su valor medio. Lo que explica la necesidad de sobredimensionar el perfil de la llanta, reforzando los entornos de las perforaciones.
Los radios de las ruedas («spokes» en la terminología anglosajona) son elementos esenciales para configurar la delicada y eficiente estructura de las ruedas. Aunque conceptualmente son similares a las que ya utilizaron las primeras bicicletas fabricadas hace más de 100 años, se han producido mejoras sustanciales debido a los progresos en los materiales utilizados, en los procesos de fabricación y en los procedimientos de tensado y control.
Antaño, todos los radios de las bicicletas eran, como muchos de los actuales, cilindros macizos de acero de gran esbeltez que se tensaban anclándolos por un extremo al perfil de llanta y por el otro a las alas del buje. En realidad se comportaban como cables tensos, que no tenían práctica capacidad para soportar esfuerzos de compresión, pues, dada su esbeltez, pandeaban. La rueda, ocupa, por ello un destacado lugar entre las estructuras constituidas por cables traccionados y barras comprimidas, de las que existen notables realizaciones en la ingeniería civil y en la arquitectura. Los primigenios aviones en que los dos planos de las alas se unían por una estructura de cables tensos son también ejemplo paradigmático de este tipo de estructuras y no es casualidad que sus inventores, los hermanos Wright, fuesen mecánicos de bicicletas.

En las imágenes de arriba, el transbordador del Niágara de Leonardo Torres Quevedo. Abajo, imagen del primer avión de los hermanos Wright.
La rueda, conceptualmente, forma parte de la prestigiosa familia de las estructuras pretensadas y postensadas que, en la actualidad, dominan el panorama de las construcciones de hormigón a gran escala. El notable ingeniero francés Eugène Freyssinet (1879-1962) afirmó con indiscutible fundamento y autoridad, que la invención del hormigón pretensado, debido en buena medida a su inteligencia y tenacidad, supuso una auténtica revolución en el arte de construir. Una gran parte de las grandes estructuras de hormigón que se han construido en los últimos cincuenta o sesenta años son pretensadas: puentes de muy diferentes tipologías, recintos para centrales nucleares, depósitos para materiales granulares, líquidos y gases. Es una eficientísima tecnología que con el paso del tiempo no ha perdido un ápice de interés. Sin haber cambiado nada en lo esencial, ha ido progresivamente mejorando los materiales utilizados, así como los dispositivos de tensado y anclaje de los cables de acero fuertemente tensionados contra el hormigón que comprimen, y al que dotan, así, con una capacidad para aceptar esfuerzos de tracción de la que carece el hormigón, como piedra artificial que realmente es. Y que, además, contribuye a evitar fisuras para las cargas de servicio o, en todo caso, permite controlar su apertura y mantenerla dentro de unos límites que se establecen por razones de perdurabilidad, permeabilidad, o incluso aspecto estético.
En la rueda —espléndido ejemplo de estructura pretensada— los radios traccionados equivalen a los cables del hormigón pretensado, la llanta al hormigón que se comprime, y la rosca en un extremo y la sujeción con el ala de los bujes en el otro, corresponden a los dispositivos de anclaje.

Estructura de cubierta con membrana textil en Kufstein, Alemania.
Los radios más convencionales están constituidos por cilindros de unos 2 mm de diámetro
A = π · Φ2 / 4 = 3,14 mm2
y unos 300 mm de longitud. Se tensan con fuerzas que pueden alcanzar y aun superar los 1.000 N. La tensión de tracción correspondiente será
σt = 1.000 N / 3,14 mm2 = 318 N/mm2
Es una cifra considerable que explica la utilización de materiales, aceros inoxidables o aluminios aleados, de alto límite elástico, aun cuando con ello se reduzca el escalón de fluencia, y por consiguiente, su alargamiento en rotura, es decir su ductilidad.
El alargamiento del radio de 300 mm de longitud, supuesto de acero, (Ea ≈ 210.000 N/mm2) será del orden de
ΔL = ε · L = 318/210.000 · 300 = 1,5 · 10–3 · 300 mm = 0,45 mm
Con radios de aluminio, cuyo módulo de elasticidad es del orden de la tercera parte del que caracteriza al acero, el alargamiento del radio sería aproximadamente tres veces mayor: ≈ 3 0,45 = 1,35 mm.
Reflexionemos ahora sobre el comportamiento estructural de una rueda considerando, solamente, como reacciones de apoyo, las fuerzas vertical y la longitudinal contenidas en su plano, cuya resultante, como ya hemos visto, se encuentra ligeramente retrasada en relación con la vertical del eje.
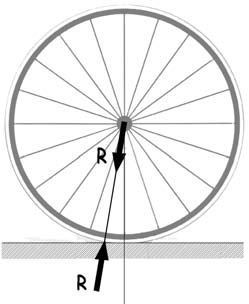
Aunque la rueda es una estructura altamente hiperestática y son muchos los caminos que tiene la reacción de apoyo para alcanzar el buje donde le espera la fuerza que la contrarresta, los que se activan en primer lugar serán los radios que estén más próximos al punto de contacto en el que se localiza la reacción en un instante dado. Como consecuencia del giro de la rueda, cada uno de sus radios irá coincidiendo, sucesivamente, con la línea de acción que une el contacto con el pavimento y el buje. Dicho radio podría recibir, hipotéticamente, la totalidad de la fuerza de reacción de apoyo. Pero al hacerlo se reduciría la tensión a la que estaba, previamente, sometido. Se acortaría, y al hacerlo, provocaría una ligerísima deformación en la llanta, suficiente para transferir a los radios contiguos una parte de la carga del radio más solicitado, en una proporción, de incierta determinación, que dependerá en gran medida de la rigidez flexional de la llanta. Supongamos, en todo caso, que un único radio, de acero, tensado inicialmente a 1.000 N recibe, en efecto, la totalidad de los 200 N de la reacción de apoyo.
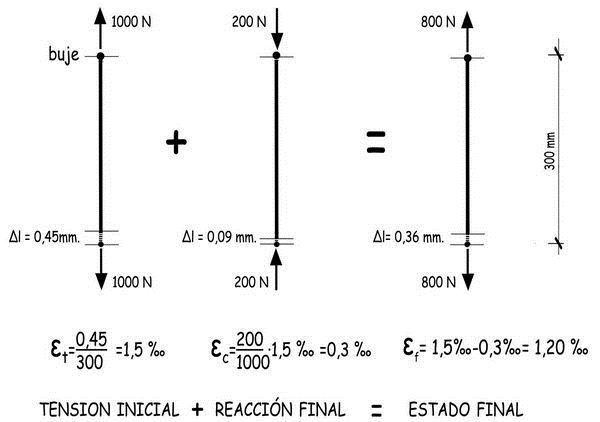
En su «estado final» el radio que transfiere la reacción de apoyo al eje de la rueda continuarán tensionado, aunque se haya reducido la tracción a 800 N y disminuido simultáneamente su alargamiento, para lo que se habrá tenido que producir una flexión localizada de la llanta.
Si imaginamos un ensayo de laboratorio, en el que aumentemos progresivamente el valor de la reacción R, llegaría un momento en que uno de los radios, el más cargado, recibiría una compresión de 1.000 N anulándose su tracción. A partir de ese momento, para aumentar la carga de transferencia, el radio debería comprimirse, pero su gran esbeltez le impediría hacerlo.
En efecto, la carga crítica de pandeo deducida en el siglo XVIII por el gran matemático alemán Leonard Euler (que está enterrado en el cementerio de San Petersburgo cerca de otro extraordinario personaje, Agustín de Betancourt, fundador hacia 1802 de la Escuela de Ingeniero de Caminos, Canales y luego Puertos de Madrid, y que acabó siendo, el equivalente a Ministro de Fomento en la ilustrada corte del zar Alejandro II) responde a la bien conocida expresión
NE = π2 · E · I / L2
que en términos de tensión se puede escribir como
σE = NE / A = π2 · E · I / (L2 · A) = π2 · E / λ2
siendo, λ, la esbeltez del radio, de longitud L
λ = L / i
El radio de giro, i, de una sección de inercia I y área A tiene por expresión:
i = (I / A)½
y en una sección circular con I = π · d4 / 64 y A = π · d2 / 4, tendremos
i = d / 4
La esbeltez, por tanto, del radio de longitud 300 mm y diámetro 2 mm, al que estamos suponiendo articulado en los dos extremos, será
λ = 300 mm / 0,5 mm = 600
esbeltez propia de cables y no de elementos comprimidos. En ingeniería civil es poco habitual que dicha esbeltez supere el valor de 100.
La tensión crítica del pandeo de Euler, en el caso del radio de acero, sería
σE = π2 · 210.000 N/mm2 / 6002 ≈ 5,7 N/mm2
cifra prácticamente irrelevante
El radio, por tanto, es prácticamente incapaz de trabajar a compresión. Al comenzar a hacerlo «pandearía», esto es se desplazaría transversalmente, acortándose longitudinalmente con la consiguiente deformación adicional de la llanta que trataría de transmitir la reacción de apoyo a los radios contiguos que mantuviesen todavía un cierto nivel de tracción.
Incrementos sucesivos de la reacción de apoyos, o de la carga en el buje, provocarían el pandeo de los radios en el entorno del punto de contacto, lo que llevaría consigo un cambio radical, aunque progresivo, en el mecanismo de transferencia.
La rueda se comportaría como si los radios destensados, del entorno del punto de contacto, no existiesen. En el hipotético ensayo de laboratorio que estamos realizando, con la rueda inmóvil, la carga del ensayo, aplicada en su eje, se transferiría a la parte alta de la llanta sobretensando para ello los radios correspondientes, más verticales. La ovalización de la llanta provocaría la sobretensión, también, de los radios más horizontales de la rueda. Finalmente, por caminos heterodoxos poco deseables, la carga aplicada al eje de la rueda llegaría a su punto de contacto con el pavimento, lo que provocaría una deformación significativa del tramo de la llanta que no podría contar con la ayuda de los radios destensados. La geometría final de la rueda conllevaría un rodar irregular y no sería apta para ser utilizada.
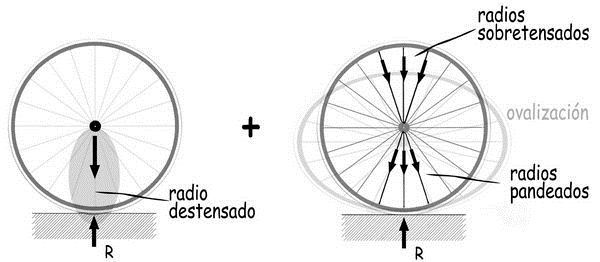
Todo ello pone de manifiesto la necesidad de que los radios dispongan de una importante reserva de seguridad para evitar que se destensen, como consecuencia del proceso de transferencia de la reacción de apoyo con el buje. Y como para moverse la bicicleta las ruedas deben girar, cada uno de sus radios se encontrará sucesivamente con la necesidad de transmitir una buena proporción de las reacciones de apoyo. Por consiguiente, todos los radios deben estar con análoga tensión y con margen de seguridad suficiente para evitar que sean destensados. Y, por otra parte, las dimensiones de la llanta deberían ser suficientes para permitir que la distensión de un radio o su rotura por las causas que sean, deje a la rueda fuera de servicio. Las diferencias de tensión entre unos radios y otros deberán ser suficientemente pequeñas para evitar ovalizaciones significativas de la rueda en su plano y también desplazamientos fuera del mismo.
El conjunto de la rueda de la bicicleta es una estructura sutil, altamente hiperestática. La gestión de las incertidumbres asociadas a su comportamiento es un ingrediente del arte de «afinar» una rueda de bicicleta, que recuerda también al arte del afinador de pianos, cuyo cometido es suma de ciencia y sensibilidad de quien manipula artesanalmente la rueda, o de quienes conciben y programan los modernos aparatos que permiten el montaje y control más industrializado de muchas de las ruedas del presente.
En el comportamiento real de un radio juegan, por otra parte, un papel determinante los dispositivos de conexión con el ala del buje por un extremo y con la llanta, por el otro, por medio de un sistema de roscado que permite, además, su puesta en tensión.
Estas esenciales conexiones de los radios plantean análogos problemas a los que nos enfrentamos con los anclajes de los tirantes que utilizamos en las estructuras de la ingeniería civil. Las soluciones que han prevalecido para los radios de las bicicletas estén basadas en experiencias acumuladas durante muchísimos años. Si cada año se venden, según parece, 50 millones de bicicletas en el mundo (4 millones en Alemania, 2 en Francia, 0,8 en España) tal vez en la historia de la humanidad se hayan construido más de 1.000 millones de ruedas con el objetivo de que sean al tiempo flexibles, resistentes y fáciles de sustituir. Y, para ello, la solución de las conexiones de los radios con las llantas y los bujes son fundamentales.
A la mirada de un ingeniero de caminos, familiarizado con las estructuras de la gran escala, le llama la atención, muy positivamente, la solución que se adopta en la actualidad para las zonas roscadas de radios cilíndricos, al menos por las marcas más prestigiosas. La rosca se mecaniza en un cabezal cilíndrico de mayor diámetro que el del resto del radio. De esta manera, el inicio de la rosca deja de ser el punto crítico en el que se alcanzaría la tensión máxima que limitaría la capacidad resistente y deformacional del radio. Toda la longitud del radio, entre las dos zonas singulares extremas podrá plastificarse, de manera que su alargamiento potencial será considerable por estar asociado a deformaciones plásticas generalizadas. Lo que en definitiva significa que el comportamiento de este tipo de radios es dúctil, que se ha resuelto el problema de la fragilidad de los radios, eliminando las roturas inesperadas por las roscas y haciéndolos más tolerantes a las imperfecciones inevitables y mal conocidas con las que los radios, también, han de convivir.
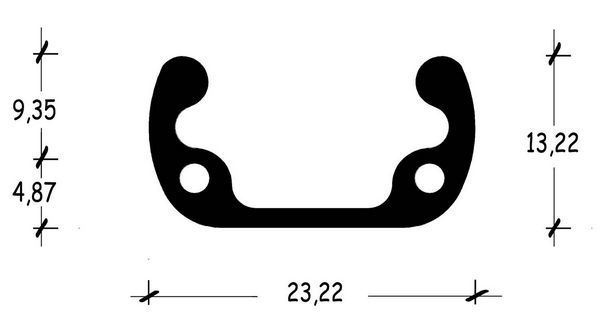
En su otra extremidad, los radios tradicionales para unirse al ala del buje suelen formar un brusco codo aproximadamente perpendicular al eje que acaba en un cabezal. La geometría de un radio correspondiente al catálogo de la prestigiosa firma DTswiss, es el representado en el esquema.
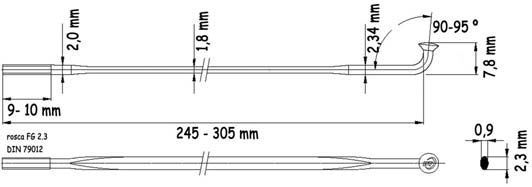
En la actualidad se utilizan también espectaculares radios planos, más aerodinámicos, en los que su parte central adopta formas rectangulares de ángulos redondeados y anchuras que pueden superar los 5 mm.
La solución del codo de unión con el buje de la rueda que proviene de los orígenes de la bicicleta ya ha demostrado, por tanto, su eficacia práctica, sorprende, sin embargo, vista desde la ortodoxia estructural.
Al conformar el codo, con un radio de doblado muy pequeño, se habrán producido en dicha zona plastificaciones del material. Serán necesarias deformaciones unitarias muy superiores a las correspondientes a su límite elástico lo que determina las características del material con el que se fabrican los radios y que se obtienen, mejorando el material específico de base, por procesos de transformación mecánicos y térmicos que les dotan de la dureza superficial, de la capacidad resistente y de la deformabilidad adecuada para absorber las tensiones y deformaciones que se concentrarán en el codo.
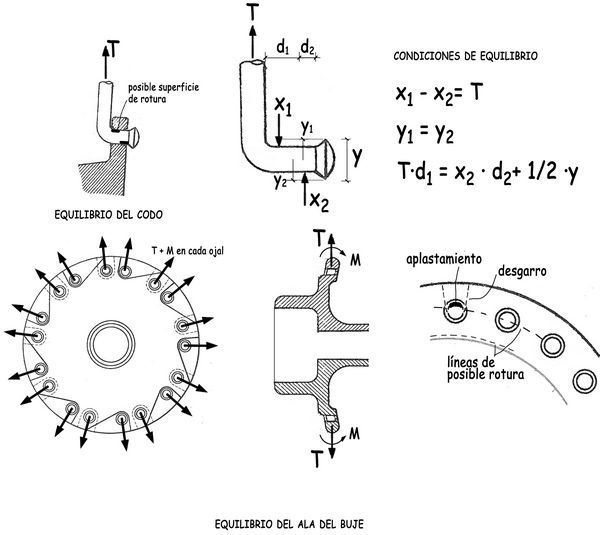
Para tener unos órdenes de magnitud de lo que ocurre en el entorno del radio en su encuentro con el ala del buje, consideraremos un radio tensado a 1.000 N, siendo las distancias d1 y d2 de 4 mm, (espesor del ala del buje de 6 mm). Tomando momentos respecto a la posición de la reacción X1 tendremos
X2 = 1.000 N · 2 mm / 4 mm = 500 N
y el valor de X1 sería
X1 = T + X2 = 1.000 + 500 = 1.500 N
Como la superficie de contacto del codo del radio con el ala del buje puede ser de unos 3 mm2, la tensión de contacto sería
σ = 1.500 N / 3 = 500 N/mm2
cifra considerable que requiere unas características específicas de dureza superficial tanto en el material del codo como en el del ala del buje. Por otra parte, una superficie probable de rotura del radio será la perpendicular inmediatamente próxima al ala del buje. La tensión tangencial media, que se acumula a las tensiones normales provocadas en dicha sección por la flexión localizada, supuesto que el área transversal del codo es de 4 mm2, será del orden de
τ ≈ 1.000 N / 4 mm2 ≈ 250 N/mm2
cifra también muy significativa.
La tensión media de comparación de Von Mises sería, en consecuencia,
σco = (σ2 + 3 · τ2)½ = (5002 + 3 · 2502)½ ≈ 660 N/mm2
lo que confirma la exigencia de disponer de características mecánicas del material del radio muy elevadas y explica que, esta zona, junto con la roscada en el otro extremo, sean las más críticas de un radio y donde de hecho se suelen producir la mayor parte de sus roturas.
La tradicional solución del codo, como dispositivo de anclaje, no es, por tanto, muy eficiente estructuralmente. Su heterodoxia está justificada por la facilidad del montaje y desmontaje de los radios y por la posibilidad de hacer ajustes en las tensiones para lograr equilibrarlas. Ya existen, en otras estructuras de la ingeniería, uniones entre elementos que se resuelven con disimetrías y para las que se aceptan concentraciones de tensiones que pueden ser soportadas con geometrías y materiales cuidadosamente escogidos.
Así ocurre, por ejemplo, con las juntas horizontales de las torres metálicas de hasta 80 m de altura utilizadas para soportar aerogeneradores de energía eólica.
La excentricidad de la unión genera sobreesfuerzos en los pernos pretensados y obligan a sobreespesores de las chapas de contacto y a alejar las soldaduras de la zona más solicitada de la unión. Pero, con todo, es una solución aceptada y ampliamente utilizada por sus ventajas funcionales. Las alas de los bujes son anillos con una geometría adecuada a la inclinación transversal de los radios, que brotan de su potente cuerpo central que alberga en su interior los diferentes componentes que lo constituyen: rodamientos, eje tubular, barra de cierre rápido. Están solicitadas por las fuerzas que le transmiten los radios y por los momentos provocados por la excentricidad de dichas fuerzas, que actúan a lo largo de la circunferencia definida por las perforaciones en las que se alojan los codos de los radios. La geometría de las alas y las características mecánicas del material utilizado en su fabricación deberán permitir la transferencia de dichas fuerzas desde las alas hacia el cuerpo del buje. Como ocurre cuando se utilizan los tornillos sin pretensar como medio de unión en las estructuras metálicas de edificación, las alas de los bujes podrían quedar fuera de uso por el aplastamiento del ojal circular en el contacto con el radio; o por el rasgado por cizalladura de las dos superficies radiales tangentes al ojal; o por rotura del anillo externo de las alas o de la superficie de encuentro entre el ala y el cuerpo central del buje debido a la acción simultánea de las fuerzas radiales de tracción y de los momentos transversales concomitantes.
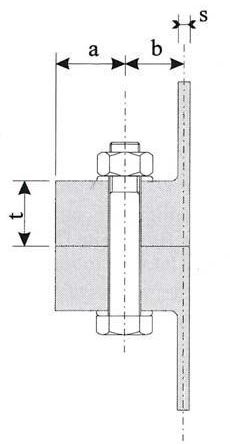
La rigidez de una llanta moderna de aluminio de unos 80 mm2 de sección unicelular, a la que nos hemos referido anteriormente, y que podría responder a una geometría como la representada en el esquema adjunto, podría tener una rigidez de 50 o 100 veces superior a la de un radio que hemos estimado en unos 660 N/mm. Tendría, por tanto, una gran capacidad para repartir la reacción puntual del apoyo de la rueda entre 3, 4 o 5 radios, lo que es manifestación también de la reserva de seguridad que atesora una rueda bien concebida y con los radios bien tensados. Y explica, también, la posibilidad de reducir el número de radios en ruedas con llantas de hasta 50 mm de altura y secciones aerodinámicas.
Las modernas tecnologías que se han ido incorporando a la fabricación de llantas nos permite disponer, en la actualidad, de secciones cerradas, mucho más eficientes que las abiertas que se utilizaban hace veinte años de las llantas de acero, y que como la esquematizada, fue objeto de algún trabajo de investigación.
Tenía unos 140 mm2 de sección y pesaba unas 5 veces más que una llanta moderna de aluminio. A pesar de ello, su inercia no superaría los 1.500 mm4 y el rendimiento
ρ = 1 / (A · v · v')
sería del orden de 0,24, confirmando la ineficiencia de las secciones abiertas para trabajar a flexión y, aún más, en torsión.
La sección de una llanta moderna tendría una inercia de unos 4.000 mm4, casi tres veces mayor y el rendimiento ρ podría superar 0,50.
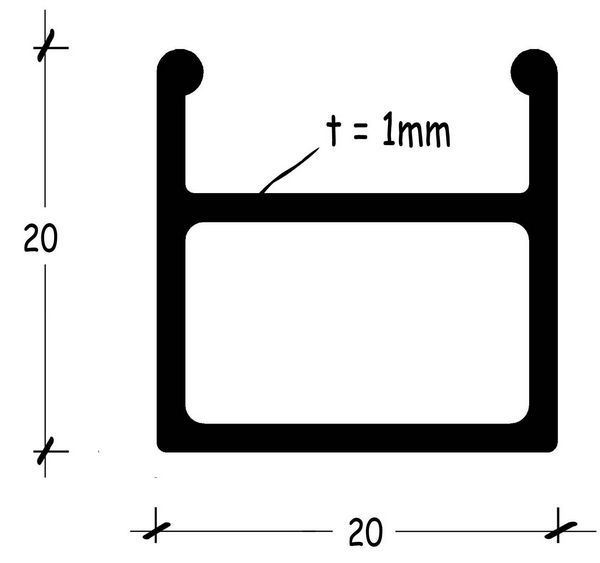
Por cierto que, desde un punto de vista estructural, no parece que disponer un tabique intermedio, como se hace en algunos casos, sea una iniciativa con futuro. El rendimiento de la sección a flexión disminuiría, sin que la rigidez torsional fuese a aumentar.
Las ruedas tradicionales, y todavía algunas de las que se utilizan en las «bicicletas de montaña» que deben soportar situaciones muy exigentes, solían estar dotadas de 36 radios. Dividían, por tanto, la rueda en sectores con ángulos de diez grados sexagesimales. En la actualidad la oferta de ruedas es amplísima y los catálogos de los fabricantes incluyen desde las que disponen de 32 radios hasta las que se reducen a 16. Los aluminios y aceros, aleados y mejorados superficialmente, son los materiales más empleados en la actualidad. Existen propuestas, también, de radios tubulares fabricados con fibra de carbono, capaces de resistir compresiones y que se enfrentan al delicado problema de su anclaje en las dos extremidades. Lo que por otra parte, si se llega a resolver eficientemente, podría servir de referencia e inspiración para los anclajes de tirantes con fibra de carbono que se podrían desarrollar, asimismo, para su uso en las estructuras de la ingeniería civil y de la edificación.
Las ruedas modernas más avanzadas, con llantas, radios y bujes integrados y suministrados por un único fabricante, van eliminando el heterodoxo codo del sistema de anclaje de los radios con las alas de los bujes. La posición de sus radios ya no apunta exclusivamente hacia el eje. Son frecuentes, también, las configuraciones con radios tangentes a un círculo concéntrico con el buje, lo que obligan a entrecruzar dos, tres y cuatro veces los radios en las proximidades de las alas de anclaje. Si en los puntos de cruce se sujetan los radios entre sí, la rigidez de la rueda en su conjunto puede incrementarse significativamente al reducirse la longitud de pandeo, mejorando su comportamiento en caso de sobreesfuerzos.
La rigidez de las llantas que se fabrican en la actualidad permite asimismo agrupar radios y aumentar notablemente la longitud de los tramos libres entre radios, lo que conlleva esfuerzos de flexión en la llanta muy superiores a los de las ruedas tradicionales.
Como ya se ha comentado en el apartado 4.4 las ruedas con gran número de radios, 32 o 36, tienen coeficientes aerodinámicos de arrastre, CD, significativamente más elevados que las ruedas con un número reducido, según se ha demostrado en ensayos en túnel aerodinámico. Cuando además, se aplanan los radios, se reduce, aún más, su oposición al viento. Desde el punto de vista puramente aerodinámico, las más eficientes pueden ser, en determinadas condiciones, las modernas ruedas lenticulares de fibra de carbono que cubren la totalidad de su superficie y que se utilizan preferentemente como rueda trasera en las pruebas contrarreloj de las competiciones entre profesionales, cuando los recorridos son predominantemente llanos, de trazados amables y sin viento meteorológico significativo. Los inconvenientes de su mayor peso, y coste, quedan así compensados. También son habituales, con esta finalidad, y para ser utilizadas como ruedas delanteras, las de 3 o 4 parejas de amplias láminas, también de fibra de carbono.

En estos casos las reacciones de apoyo se transmiten al buje de la rueda por compresión de las láminas. Las tensiones localizadas en su encuentro con el buje y con la llanta, la flexión de ésta, y el riesgo de pandeo por flexión de las láminas, condicionan el dimensionamiento de este tipo de ruedas, conceptualmente muy diferente de las tradicionales.
Existen, por tanto, en la actualidad, una amplia gama de ruedas caracterizadas por los materiales que se emplean en la fabricación de llantas y radios, por el trenzado de éstos, por los ingeniosos sistemas que permiten su unión con el buje, y por la sofisticación de las lenticulares o las que utilizan láminas de fibra de carbono. Configuran un panorama muy variado y atractivo.
En otro orden de cosas, es imprescindible constatar que las reacciones de apoyo, en el contacto de los neumáticos con el terreno, tienen también una componente transversal, que será suma de las fuerzas centrifugas no compensadas por la inclinación del ciclista, las debidas al viento, y las que puedan ser consecuencia del giro que impone el ciclista al manillar para cambiar la dirección del movimiento. Y, de cuando en cuando, las que se producen como consecuencia del impacto de la rueda con algún inesperado obstáculo que se encuentre en su camino.
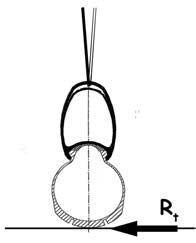
De manera que la estructura de la rueda debe tener capacidad para transferir estas reacciones transversales a los bujes, desde donde se dirigirán hacia el cuadro de la bicicleta. El esquema estructural de la rueda solicitada por esta reacción transversal será el representado en el esquema. Algunos de los radios, entre los más próximos al punto de aplicación de la carga RT, se comprimirán y los inclinados en sentido opuesto, se traccionarán. El equilibrio de fuerzas, suponiendo que la inclinación de los radios esté en la proporción 1:8, exige que
C = –T = (RT / 2) · 8 = 4 · RT
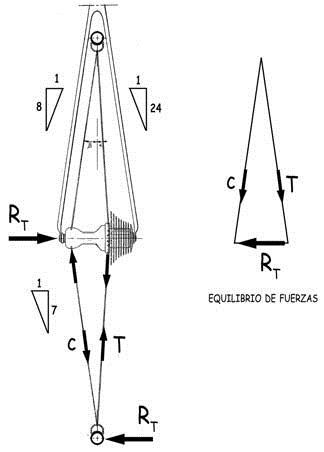
A estas fuerzas, C y T, que debido a la rigidez transversal de la llanta y la cubierta, se repartirán entre algunos radios, se añadirían las provocadas por las componentes verticales y longitudinales de las reacciones de apoyo y las tracciones previas inducidas por el pretensado.
Como veremos en el apartado 6, en el ensayo normalizado para una rueda trasera se impone una fuerza transversal de 370 N aplicada en la llanta. Si suponemos que una fuerza análoga se aplica también en la llanta de una rueda delantera y aceptamos que en su transferencia al buje se activan 4 radios, dos inclinados en un sentido y los otros dos en el opuesto, tendríamos un sobreesfuerzo, por radio, de:
Cr = –Tr = 4 · 370 / 2= 740 N
valores considerables que reducirían la tensión en algunos radios de los 1.000 N iniciales a los 1.000 – 740 = 260 N y que incrementarían sustancialmente, los esfuerzos de otros radios, hasta cifras de 1.740 N de tracción. En la práctica es muy improbable que se lleguen a alcanzar los valores de los ensayos normalizados si no fuese como consecuencia de algún choque o impacto de la rueda con algún obstáculo inesperado.
Conviene también observar, que la posición de la fuerza transversal se sitúa en la superficie de contacto de la cubierta con el terreno. Por consiguiente, dicha fuerza debe ser transferida, en primer lugar, desde la cubierta hasta la llanta para luego proseguir su peregrinaje a través de los radios hacia el buje de la rueda. La capacidad de la cubierta para transferir estas fuerzas transversales, es limitada, probablemente significativamente inferior a la capacidad que tiene la estructura constituida por la llanta, los radios y el buje. En todo caso, dicha transferencia produciría desplazamientos transversales de la cubierta y podría llegar a provocar el brusco deshinchado de la rueda con todas sus indeseables secuelas. Lo que, en definitiva, confirma que como bien sabe todo aficionado que se precie, la cubierta es un componente, muy sensible y esencial en el comportamiento de la bicicleta. Por lo que se ha de escoger y cuidar con esmero.
El buje es el último componente que nos queda por analizar de una rueda delantera. Hasta él, llegan las fuerzas que generan o canalizan los radios, y él los transfiere a las patillas de las horquillas del sistema de dirección. Está constituido por un cuerpo externo hueco de acero o aluminio aleado, fabricado por moldeado, del que forman parte las dos alas a las que se anclan los radios. El eje del buje suele ser un tubo hueco de unos 12 mm de diámetro, y algún milímetro de pared, en el que se introduce la barra cilíndrica que en sus extremos dispone de los dispositivos de cierre rápido que permiten la fijación de las patillas de la horquilla de dirección al eje del buje. Entre el eje interior y el cuerpo externo del buje se disponen, en la proximidad de las alas del buje, los rodamientos de bola que hacen posible la rotación de la rueda y transfieren las fuerzas provenientes de los radios a las patillas de la horquilla de dirección.
Los esenciales rodamientos de bolas equivalen en cierto modo a los estáticos aparatos de apoyo (de neopreno zunchado o teflón, por ejemplo) que utilizamos en las estructuras de la ingeniería civil. Están constituidos por dos anillos concéntricos, el externo unido al cuerpo del buje y el interno incorporado a su eje. Y entre ellos, un rosario de bolas que aseguran la rotación relativa de los dos conjuntos y la transferencia de fuerzas entre ellos.
Los dos modelos de rodamientos más utilizados en las bicicletas son los de bolas de contacto —los de más sencilla colocación y más incierto comportamiento— y los rígidos de bolas, que suelen estar premontados, se lubrican con grasas de larga duración y van sellados. Una bicicleta cuenta con numerosos rodamientos de bolas: en los bujes delantero y trasero, en la barra de dirección, en el eje del pedalier, en los pedales. Los rodamientos son, por consiguiente, componentes fundamentales de la bicicleta y entre los que más han contribuido a su progreso. Están, también, entre los más delicados, y los que, con mayor frecuencia, se han de sustituir.
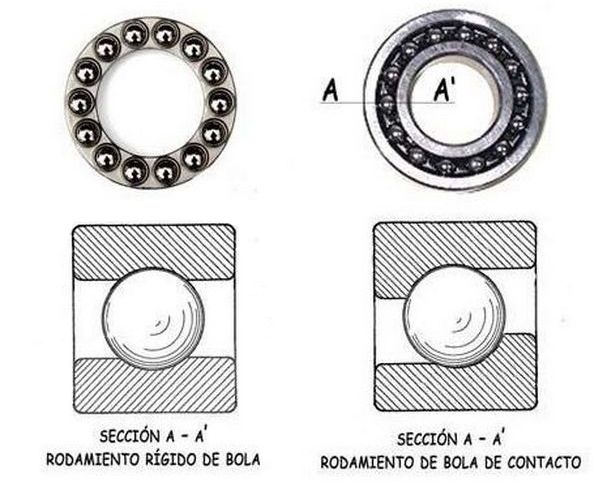
Sus dimensiones externas, que dependen lógicamente de su función, suelen ser de pocos centímetros y el diámetro de las bolas suele ser de milímetros. Las tolerancias de fabricación garantizadas se especifican en micras.
Las puntas de tensiones en el contacto de las bolas con los anillos de rodamiento pueden alcanzar valores elevadísimos, del orden de 3.500 N/mm2. Por ello en su fabricación se utilizan los aceros, aleados y tratados para aumentar su dureza superficial. En algunos modelos avanzados se emplean también materiales cerámicos. Los rodamientos son un prodigio tecnológico que a quienes provenimos de campos ajenos a la mecánica nos asombra por su esencialidad, por su sencillez conceptual, por el ingenio, y la belleza incluso, de los procesos de fabricación y montaje, por las características de los materiales empleados, por su universalidad e incluso por los moderados costes con los que se fabrican industrialmente. Probablemente, el coste del conjunto de rodamientos de acero de una bicicleta rondará los 30 euros.
Nos referiremos ahora a la estructura que posee el buje de una rueda delantera, como el sintetizado en el esquema.
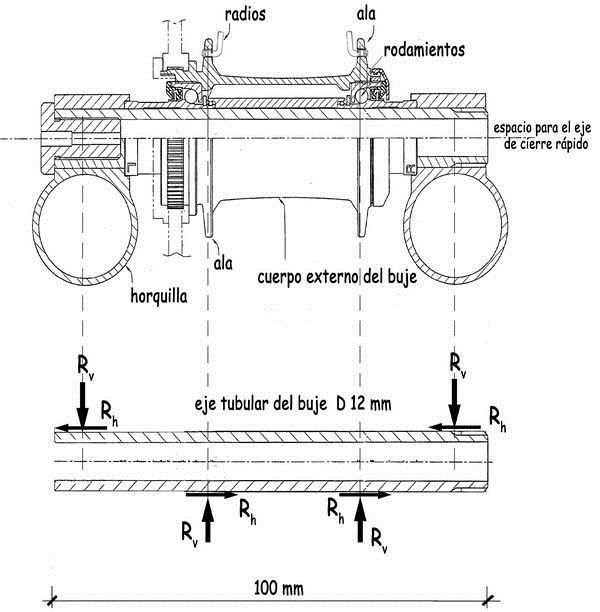
Las reacciones de apoyo, verticales y transversales que nacen en el contacto de la cubierta con el terreno, llegan tras su viaje a través de la estructura de la rueda hasta las alas del buje. De éstas pasan por los rodamientos hasta su eje tubular que, a su vez, por flexión y cortante, las transfiere a las patillas de las horquillas de la bici, desde donde continúan el peregrinaje que las conducirá hasta el cuadro de la bicicleta y su manillar.
El buje de las ruedas traseras, tiene, además, otras funciones que determinan su geometría. En el lado derecho de la bicicleta, vista desde su parte posterior, se instalan el paquete con los piñones del sistema de transmisión, que incorpora también el dispositivo de «rueda libre» que permite a los pedales y a la cadena rotar libremente en sentido opuesto al que provoca el movimiento hacia adelante de la bicicleta. Por ello, la separación entre horquillas suele ser superior al de los 100 mm de las ruedas delanteras. Y el cuerpo externo y el eje tubular del buje trasero deben tenerla capacidad para transferir las fuerzas originadas por el sistema de transmisión de las bicicletas, además de las que le llegan por la estructura de la rueda.
Para dejar espacio a los piñones y para transmitir más eficientemente las fuerzas que introducen al sistema, el ala derecha del buje se desplaza transversalmente. La distancia entre alas, que en la rueda delantera era de unos 60 mm, se reduce a 40 mm aproximadamente; la derecha se aproxima a 10 mm del eje de la rueda trasera, mientras que el ala izquierda mantiene la distancia de 30 mm, como en la rueda delantera.
Consiguientemente la inclinación de los radios (30 / 240 = 1/8, suponiéndolos de 240 mm de longitud) próximos a los piñones pasarían a ser del orden de 1/24 en los radios opuestos.
Los radios del lado derecho, próximo a los piñones, reciben, por tanto, más carga que los radios dispuestos en la parte opuesta y, llama la atención, que, a pesar de ello, en algunas ruedas traseras actuales con tecnologías avanzadas el número de radios sea la mitad, por ejemplo, que los del lado opuesto en ruedas traseras de 24 radios.
Los bujes de las ruedas delantera y trasera pueden acomodar también las piezas de los frenos de disco que en algunas bicicletas de montaña en general, se instalan como alternativa a los frenos tradicionales de zapatas. Consiguientemente, la estructura del buje debe tener capacidad también para transferir los esfuerzos que se producen cuando se activan dichos frenos, que, lógicamente difieren en magnitud y posición de las fuerzas que se generan en las superficies laterales de las llantas de las ruedas con frenos tradicionales.
El conjunto de la horquilla, de la potencia del manillar y del propio manillar constituye una subestructura que se macla con el tubo de dirección del cuadro de la bicicleta y permite el intercambio de las fuerzas que provienen de las patillas de las horquilla y del manillar con las del conjunto del cuadro. Aislaremos virtualmente la subestructura en cuestión, porque nos ayudará a comprender los itinerarios que recorrerán las fuerzas en dicho intercambio y a formular las condiciones del equilibrio, estático o dinámico, que gobernarán su relación.
En las punteras de la horquilla actuarán, básicamente, las fuerzas equivalentes a las reacciones de apoyo, que provienen del área de contacto de la cubierta de la rueda delantera con el pavimento.
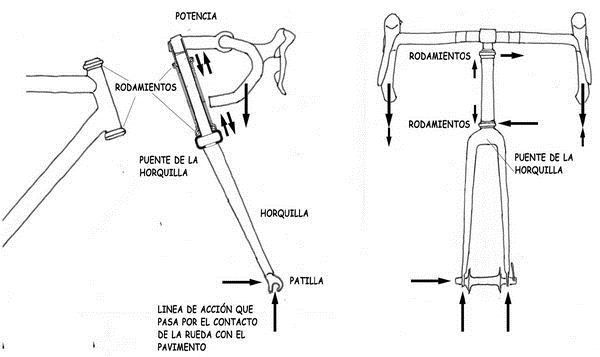
La barra vertical, que arranca del puente con el que se unen las dos patas de la horquilla, penetra en el tubo de dirección del cuadro. Los dos rodamientos de bolas, que se disponen entre la barra y los bordes del tubo de dirección, permiten la rotación relativa de la subestructura de la dirección y, por ende, de la rueda delantera, en relación con el cuadro de la bicicleta. Además, los rodamientos deben transferir o canalizar —misión también esencial— las fuerzas entre la subestructura de dirección y el cuadro. Todos los rodamientos que se disponen en una bicicleta, reiterémoslo, equivalen a los aparatos de apoyo que utilizamos en las estructuras de la ingeniería civil y la edificación, para transferir fuerzas entre diferentes componentes estructurales; por ejemplo, entre el tablero y las pilas de un puente de carretera o ferrocarril.

Por ello, los rodamientos pueden representarse con el símbolo clásico que se utiliza para representar las articulaciones fijas que permiten giros pero no desplazamientos. De manera que, esquemáticamente, el conjunto de la subestructura de la horquilla, barra de dirección, potencia y manillar, será el siguiente:
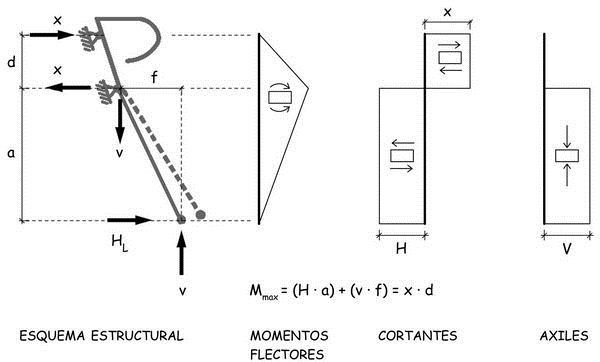
Las fuerzas externas, que actúan sobre esta subestructura serían las que se localizan en las punteras de la horquilla provenientes del contacto de la rueda con el pavimento y aquellas provocadas por las manos del ciclista que se apoyan en el manillar. En los esquemas se ha supuesto que, transversalmente, las fuerzas se reparten por igual entre las dos barras de las horquillas y los dos laterales del manillar, lo que, en la realidad no será siempre así. Porque, por ejemplo, para girar la bicicleta el ciclista aplicará fuerzas diferentes, de escasa magnitud en general, en uno y otro brazo del manillar.
Evaluemos, en primer lugar, los esfuerzos correspondientes a las componentes vertical, V, y longitudinal HL, de la fuerza aplicada en las punteras. Las leyes de momentos flectores, esfuerzos cortantes y axiles serían los representados en el esquema
La componente vertical, V, ascenderá por las barras de las horquillas, flexionándolas debido a la excentricidad asociada a su geometría ligeramente curvada. Continuará, después, por la barra de dirección hasta alcanzar el rodamiento superior en el que concluirá su peregrinaje estructural. La excentricidad, f, de dicha componente vertical, generará un momento V · f, al que se añadirá el debido a la fuerza longitudinal que valdrá H · a, siendo a la distancia vertical al rodamiento inferior.
Para equilibrar la suma de estos dos momentos V · f + H · a, aparecerán, en los rodamientos inferior y superior que están separados una distancia vertical, d, dos reacciones de apoyo, X, iguales y contrarias, de valor
X = ± (H · a + V · f) / d
La ley de momentos flectores, del conjunto de las dos barras de la horquilla crecerá linealmente hasta alcanzar, junto al rodamiento inferior, el valor máximo
Mmax = V · f + H · a = X · d
El esfuerzo cortante tendrá por valor H en el tramo de la horquilla y X entre los dos rodamientos.
En la barra-puente horizontal que conecta las dos patas de la horquilla y de la que arranca la vertical de dirección, el recorrido de fuerzas, y de los esfuerzos asociados, cambiará bruscamente de dirección y volverá a hacerlo al encontrarse con la barra vertical. Estos cambios bruscos, indispensables funcionalmente, alertan de la complejidad de análisis de esta barra esencial. La flexión de las dos barras laterales de la horquilla se hará aquí torsión antes de volver a hacerse flexión en la barra vertical de dirección. Los esquemas de esfuerzos debidos a las fuerzas V y HL son los siguientes:
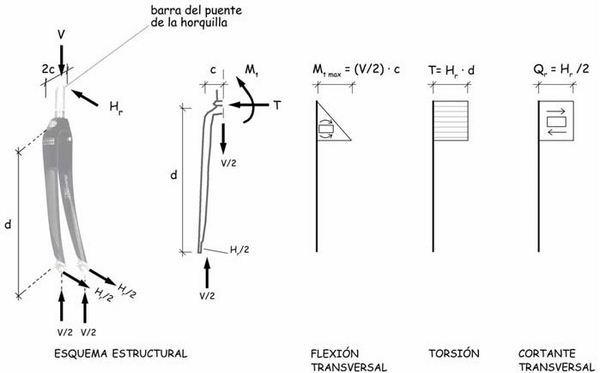
Además, la barra a la que nos estamos refiriendo sirve de dintel al pórtico, que es también, la horquilla y permite la transferencia hacia los rodamientos de la reacción de apoyo transversal. Los radios inclinados a un lado y otro del plano de la rueda, provocarán en las punteras de la horquilla un par de fuerzas verticales iguales y contrarias que equilibrarán el momento HT · r (siendo r, el radio de la rueda) y se sumarán o restarán a los valores de V. Se generarán, además, esfuerzos adicionales en el plano transversal del pórtico, como los esquematizados en el croquis adjunto.
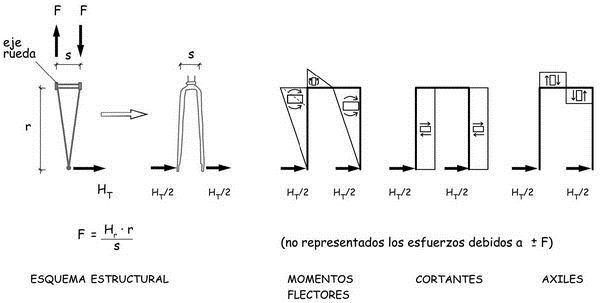
Consideremos ahora los esfuerzos que se producen como consecuencia de las fuerzas que introduce un ciclista que aferra con sus manos la parte inferior del manillar de competición de una bicicleta de carretera.
Las fuerzas provocadas por cada mano, que supondremos iguales, tendrán una componente vertical Vm, hacia abajo, y otra horizontal, Hm, hacia afuera. La condición de equilibrio exige que en los rodamientos aparezcan unas «reacciones de apoyo» que neutralicen las fuerzas aplicadas. Como los rodamientos, equivalen a articulaciones fijas, toda la carga vertical, Vm, estará equilibrada por la reacción del más próximo a la potencia del manillar. La carga vertical, Vm, no habrá pasado el filtro del primer rodamiento que encuentra tras haber recorrido toda la geometría del manillar y de la barra de potencia. Ambos rodamientos, como consecuencia de las fuerzas Hm y Vm provocadas por la presión de las manos sobre el manillar tendrán que transmitir, además, las reacciones horizontales Xm,s, en el superior y Xm,i, en el inferior, que asegurarán el cumplimiento de las condiciones de equilibrio.
Ym,s = Vm ; Ym,i =0
Xm,i · d = Vm · b – Hm · I
Xm,i + Hm = Xm,s
En consecuencia, los esquemas de los esfuerzos en el tubo de dirección son los representados en el esquema siguiente.
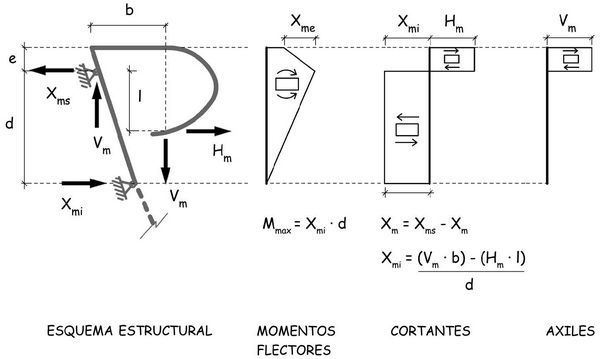
Las reacciones totales que deben soportar los dos rodamientos de la dirección, serán la suma de los provocados por las fuerzas aplicadas en las punteras de las horquillas en contacto con el eje y por las introducidas por el ciclista al apoyarse sobre el manillar de su bici, que, lógicamente desaparecerán cuando suelte las manos del manillar. Conociendo, por lo tanto, las reacciones de apoyo en el contacto de la rueda con el terreno por el que circula la bicicleta y las fuerzas que introducen las manos del ciclista en el manillar, se podrían determinar esfuerzos, y también deformaciones, de la subestructura constituida por la horquilla, la barra de dirección, la potencia y el manillar, así como establecer el valor de las fuerzas que llegan a los dos rodamientos de dirección y que se difunden desde allí, a la estructura del cuadro de la bicicleta. Pero la determinación teórica de las reacciones máximas de apoyo que se pueden producir en una bicicleta es, realmente, imposible. A ello se hace referencia en el apartado 6, en el que, además, de algunas reflexiones sobre métodos de cálculo y criterios de seguridad estructural, se describen, en síntesis, algunos de los ensayos estableados en las Normas, con las cargas, en diferentes escenarios estáticos y dinámicos, que debe soportar la estructura de la bicicleta.
En el ensayo normalizado de flexión estática se aplica una carga transversal de 1.500 N en las punteras de la horquilla. Suponiendo que la distancia de la carga al primer rodamiento sea de 450 mm y la separación entre ellos de 150 mm, el esquena estructural correspondiente al ensayo será el representado en la figura adjunta.
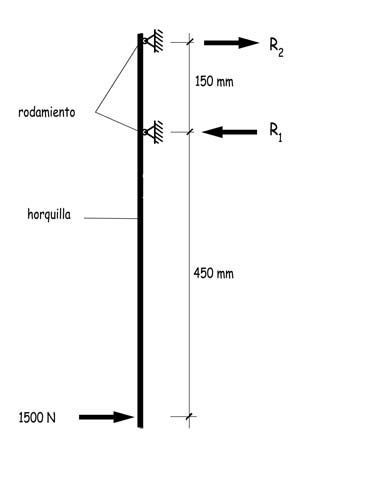
Las reacciones en los rodamientos de la barra de dirección serán
R1 = 1.500 N · (450 + 150) / 150 = 6.000 N
R2 = –6.000 + 1.500 = –4.500 N
Y el momento máximo, en la sección próxima a la posición del rodamiento inferior, será:
Mmax = 1.500 N · 0,45 m = 675 N·m
Estos valores son relevantes. La fuerza de 1.500 N utilizada en el ensayo incorpora, sin duda, importantes coeficientes de seguridad, por cuanto el valor de la máxima reacción horizontal de apoyo que se produce en el contacto de la cubierta de la rueda delantera con el pavimento suele ser de algunas decenas de newton solamente. De manera que el ensayo corresponde a un estado límite último, que busca verificar la capacidad máxima de la horquilla, de su puente y de la barra de dirección y de los rodamientos que recibe la carga y le transfieren al cuadro. Solo en caso de impactos considerables podrán alcanzarse valores próximos a los 1.500 N del ensayo.
En todo caso, para que la horquilla en su conjunto supere el ensayo estático de flexión, la barra de dirección deberá estar dimensionada para recibir un momento flector de 675 N·m y un esfuerzo cortante de 4.500 N. Si suponemos que la barra de dirección tiene un diámetro de 30 mm y sus paredes son de 2 mm de espesor, sus características mecánicas serían:
A = π · 30 · 2 = 188 mm2
I ≈ ρ · A · v · v' ≈ 0,50 · 0,88 · (30 / 2)2 = 21.150 mm4
La tensión máxima debida a la flexión elástica sería
σmax = M / W = 675.000 N·mm / 1.410 mm3 = 478 N/mm2
Y la tensión tangencial debida al cortante
τ ≈ 1,5 · Q / A = 1,5 · 4.500 N / 188 mm2 ≈ 36 N/mm2
Este último valor es prácticamente despreciable, pero para que la tensión máxima de flexión, 478 N/mm2, sea aceptable, el tubo en cuestión debería ser fabricado con aluminios aleados de altos límites elásticos o doblar el espesor de sus paredes considerado en este ejemplo.
Es interesante, evaluar, también, la flecha máxima de la horquilla ensayada, bajo la carga de 1.500 N aplicada. Considerando un voladizo empotrado de 450 mm, tendremos
fmax = P · L3 / (3 · E · I) = 1.500 N · (450 mm)3 / (3 · 70.000 N/mm2 · 21.150 mm4) ≈ 30 mm
cifra considerable, que equivale a L/15, y que realmente será aún mayor porque la estructura de la horquilla, junto al primer rodamiento probablemente habrá iniciado su plastificación. De hecho la norma acepta el ensayo si la deformación remanente, tras eliminar la carga, no supera los 5 mm, mientras que en el ensayo correspondiente de impacto, la flecha admisible podría alcanzar los 45 mm, lo que sorprende un tanto.
El somerísimo análisis realizado pone de manifiesto también que el rodamiento inferior es el más solicitado en el ensayo, como también lo es en la práctica. De hecho, suele ser el que padece más patologías y el que debe ser sustituido con mayor frecuencia. Lo que explica, por otra parte, la tendencia a conificar el tubo de dirección del cuadro, con un diámetro en la parte superior de 1 1/8 pulgadas (28,6 mm) y de 1 1/4 pulgadas (31,7 mm) en su nivel inferior para así poder disponer de un rodamiento más capaz abajo que arriba.
Si aislamos el cuadro de una bicicleta de carretera nos encontraremos con una geometría que se suele denominar de doble diamante. El triángulo principal, cuyo vértice delantero se ha truncado con el tubo de dirección, está constituido por el tubo superior, el vertical y el diagonal. Las barras de los tirantes y vainas —desdobladas para habilitar espacio para la rueda trasera y los mecanismos de transmisión— completan la estructura del cuadro.
Las fuerzas que actúan en el plano del cuadro —no se han representado las transversales— serían las siguientes:
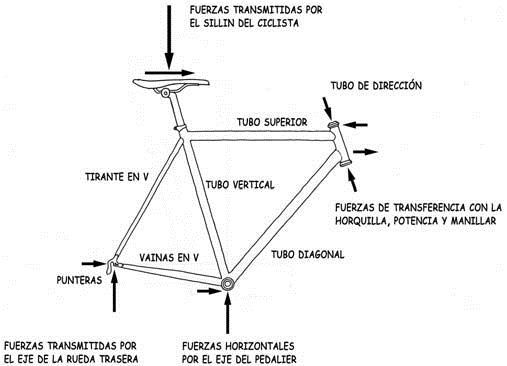
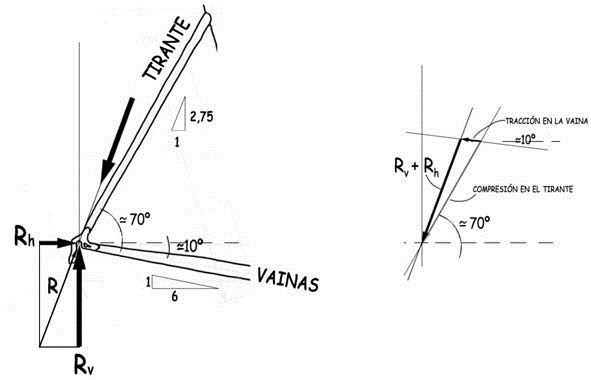
Sorprende que a las barras en V que nacen en el eje de la rueda trasera y apuntan hacia arriba, con un ángulo de unos 70°, se las denomine tirantes, porque, prácticamente, siempre estarán trabajando en compresión, con un valor ligeramente inferior al de la reacción de apoyo de la rueda trasera. Por el contrario, las barras en V que configuran la vaina que une el buje trasero con el eje del pedalier —y que se inclinan unos 10° hacia abajo en relación con la horizontal— estarán siempre ligeramente traccionadas porque, en otro caso, en el esquema de equilibrio, la componente horizontal RH, de la reacción tendría que superar el valor de
0,36 · Rv (≈ Rv / tg 70°)
lo que solo se producirá en circunstancias excepcionales.
El cuadro de una bicicleta está constituido por un conjunto de tubos, generalmente cilíndricos, unidos entre sí, que están solicitados por cargas que se introducen, en general, en sus dos nudos extremos. Con excepción de las que son debidas a su peso propio, muy poco relevantes, y las que pueden ser consecuencia de algún impacto o de la colocación de un peso: el de una persona sentada en su barra superior, por ejemplo.
El esquema de las barras aisladas que constituyen el esqueleto de una bicicleta convencional es el de la figura siguiente.
En general, los tubos del cuadro de una bicicleta suelen tener diámetros que varían entre 15 y 45 mm, con espesores de pared entre 0,5 y 2,0 mm.
La masa de un cuadro desnudo, sin horquilla, fabricado con aluminio de densidad 2,70 kg/dm3, puede ser del orden de 1,35 kg y el volumen del material necesario será de 1,35 / 2,70 = 0,500 dm3, es decir medio litro.
Para estimar algunos órdenes de magnitud dimensionales, consideraremos que las dos vainas equivalen a una única barra y otro tanto supondremos para los dos tirantes. El cuadro estará conformado por cinco barras que en conjunto tendrán una longitud de unos 2,50 metros. Para que el volumen del material necesario para construir el cuadro fuese, como hemos estimado, de 500 cm3, la sección del tubo característico tendría que ser de 2,0 cm2 (250 cm · 2 cm2= 500 cm3), lo que correspondería, por ejemplo, a un tubo de 40 mm de diámetro y 1,6 mm de pared constante. Sus características mecánicas serían:
A = 2,0 cm 2
I ≈ ρ · A · v · v' ≈ 0,50 · 2,0 · (4,0 / 2)2 = 4,0 cm4
W = I / v = 4,0 / 2,0 = 2,00 cm3
i = (I / A)½ = (4 / 2)½ = 1,41 cm (≈ 0, 35 · 4,0)
Si consideramos que el límite elástico del aluminio empleado es de 255 N/mm2, las capacidades resistentes de referencia para la sección del tubo característico (Φ = 40, t = 1,6) serían
Para disponer, asimismo, de órdenes de magnitud de los esfuerzos máximos que podrían solicitar a los tubos del cuadro, tomaremos como referentes las cargas de uno de los ensayos que se describen en el apartado 6. Las máximas aplicadas en las punteras de la horquilla son de +1.200 N, hacia afuera, y de –600, hacia adentro.
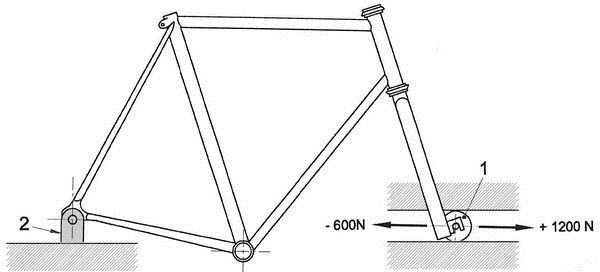
En el eje fijo del ensayo, en el que confluyen vainas y tirantes, las reacciones máximas de sentido opuesto al de las cargas aplicadas serán –1.200 N y + 600 N. En consecuencia, las vainas estarían solicitadas por una tracción aproximada de 1.200 N, muy inferior a la capacidad resistente de referencia de 51.000 N. Por otra parte, la compresión de 600 N tendería a pandear las barras que constituyen las vainas. Y, a este respecto, tendríamos que considerar el comportamiento individualizado de una de las dos barras. Suponiendo, en coherencia con lo expuesto anteriormente, que cada una de ellas tiene un diámetro de 20 mm, un área de 1 cm2, y una longitud de 400 mm, que aceptamos coincide con la longitud de pandeo, la esbeltez, λ, de la barra sería
λ = lp / I ≈ 400 mm / (0,35 · 20) = 57
La tensión crítica de pandeo de Euler, σE, será (para el aluminio E = 70.000 N/mm2)
σE = π2 · E / λ2 = π2 · 70.000 / 572 ≈ 210 N/mm2
Considerando un coeficiente de reducción de 0,50 para tener en cuenta las imperfecciones inevitables de la barra, tendremos una capacidad a compresión de la vaina compuesta por 2 barras de
N = 2 barras · 0, 50 · 210 N/mm2 · 100 mm2 = 21.000 N
muy superior, también a la solicitación de 600 N.
Estos valores y los que se han deducido anteriormente al tratar de la horquilla, ponen de manifiesto que ni las barras de los cuadros ni las del sistema de dirección están fuertemente solicitadas axilmente. No son ni los esfuerzos de compresión ni los de tracción lo que condicionan su dimensionamiento. Más determinantes son los de flexión, aunque su influencia declina rápidamente a medida que nos alejamos de los nudos. Porque, obviamente son estas zonas, en las que se reúnen las barras individuales, las más críticas de la estructura del cuadro de una bicicleta. Y las de más incierto análisis. En ellas, los flujos tensionales y deformacionales discurren por caminos torturados, con quiebros bruscos, en los que se amplifican notablemente tensiones y deformaciones, y, en cuyos entornos, se inician con más probabilidad fisuras o plastificaciones localizadas que preludian el colapso estructural. Y de los cuatro nudos de un cuadro, los más problemáticos son los del tubo de dirección y el que aloja el eje del pedalier, y cuyas superficies más delicadas son las de contacto de los rodamientos con los tubos que configuran los nudos.
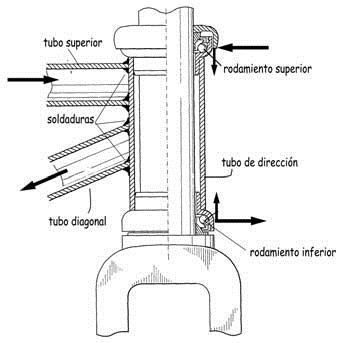
En el nudo del sistema de dirección, las fuerzas del tubo interno se transfieren a los rodamientos, y de éstos a la barra externa del cuadro que los difunde a los tubos diagonal y superior a través de los cordones de soldadura que han permitido su conexión y que como toda soldadura de fuerza, puede ser una zona especialmente crítica, porque su comportamiento es muy dependiente de la calidad de la ejecución: pueden existir «entallas geométricas», que amplifican tensiones y deformaciones y «entallas metalúrgicas», en la zona térmicamente afectada, en las que se pueden producir pequeñas fisuras difíciles de detectar, que se propagan hasta provocar la rotura frágil de la unión.
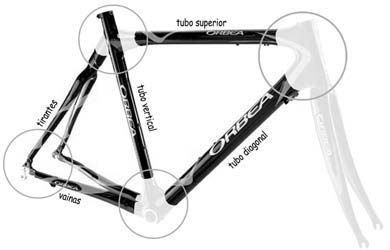
En algunos cuadros de fibra de carbono la concepción del nudo de dirección muestra con especial claridad que la transferencia de la fuerza del rodamiento inferior tiene lugar preferentemente en la parte más baja del tubo diagonal y la del otro en la parte alta del tubo superior. Por ello los extremos de los tubos superior y diagonal se configuran para que el flujo de fuerzas se produzca lo más directamente posible mientras que la parte baja del tubo superior y la alta del diagonal no llegan al tubo de dirección y se unen en una pronunciada curva, como se puede observar en la imagen adjunta.

Las secciones circulares huecas son muy adecuadas para transmitir esfuerzos centrados de compresión o tracción. No ocurre lo mismo, cuando los esfuerzos determinantes que actúan sobre una sección son los de flexión. En este caso, como una buena parte de su área se concentra en torno a la fibra neutra, en donde las tensiones debidas a la flexión se anulan, el rendimiento (ρ = I / (A · v · v')) de una sección tubular, índice de su eficacia para trabajar en la flexión, se reduce a 0,50.
Por contraste en una sección rectangular hueca, de más altura que anchura, y espesores mayores en las alas que en las almas, dicho rendimiento podría ser un 30% superior (ρ= 0,65). Y, en el hipotético caso, de una sección desalmada (que carece de almas), el rendimiento alcanzaría la unidad y se aproximaría a este valor ideal cuando las almas tienen espesores muy pequeños: tal como se muestra en el croquis adjunto, en el que todas las secciones tienen igual área.
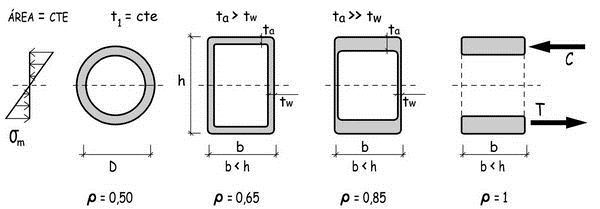
Y si las cosas son tal como han sido expuestas, ¿por qué han tenido tanto protagonismo y aún lo tienen los tubos cilíndricos de sección constante en la construcción de cuadros de bicicletas? Probablemente, porque la industria metalúrgica desarrolló en su momento tecnologías muy eficientes para fabricar tubos de acero y poder atender la enorme demanda de un producto que tenía infinidad de aplicaciones prácticas. Y, por ello, los primeros fabricantes de bicicletas, y cuantos les siguieron después, tuvieron a su disposición, a precios muy asequibles, tubos de acero que, tras cortarlos a la medida adecuada, se acabaron convirtiendo en cuadros de bicicletas.
En tiempos mucho más cercanos, el progreso en la metalurgia impulsó la utilización generalizada del aluminio. Su obtención, a partir de un mineral muy abundante, la bauxita, requería un consumo energético considerable —hasta 30 kWh eran necesarios para producir 1 kg de material—, lo que conllevaba un precio elevado y poco competitivo en relación con el del acero. Con el paso del tiempo la industria del aluminio fue optimizando sus procesos de producción. La energía necesaria para fabricar un kilogramo de este metal se redujo hasta menos de 14 kWh, con la consiguiente reducción de precios. Las posibilidades que ofrecían las aleaciones de aluminio, contribuyeron también a ampliar la gama de productos y sus aplicaciones. La bicicleta acabó por beneficiarse, también, de estos progresos, hasta el punto que, en la actualidad, para la fabricación de cuadros y otros componentes, los aluminios aleados se han hecho los principales protagonistas desplazando al acero. Sus 2,7 kg/dm3 de densidad es del orden de la tercera parte de la que caracteriza a los aceros (7,85 kg/dm3). Como contrapartida, otra característica fundamental, como es su módulo elástico E, se reduce también a un tercio y los aproximadamente 210.000 N/mm2 del acero pasan a ser 70.000 N/mm2 en los aluminios, aleados o no. En consecuencia, la deformabilidad del material es sensiblemente mayor, y la rigidez de los tubos fabricados con este material se reducen considerablemente, salvo que se aumenten, como suele hacerse, sus diámetros. Por ello, las esbelteces de los tubos de aluminio suelen ser apreciablemente menores y su aspecto más robusto que en los tradicionales tubos de acero.
Los aluminios débilmente aleados tienen capacidades resistentes muy reducidas, con límites elásticos en el entorno de los 30 N/mm2, aunque como contrapartida, son muy deformables (con un εu de hasta el 35%), lo que explica que sea un material tan útil para fabricar, por extrusión, piezas de geometrías muy variadas, con escasas exigencias resistentes.
Existen, por otra parte, una amplísima gama de aluminios aleados con características mecánicas equiparables y aún superiores a las que tienen los aceros al carbono. En la fabricación de cuadros de bicicletas se suelen emplear, los de la serie 6.000, según la terminología internacional, con aleaciones de sílice y magnesio, que con tratamientos térmicos específicos, permiten alcanzar límites elásticos de 250 N/mm2 y de rotura de 290 N/mm2 con deformaciones unitarias del 8% o 10%. Son aleaciones resistentes a la corrosión. También se utilizan aluminios aleados con zinc, a los que se les identifica por la denominación 7.000, que tratados térmicamente pueden alcanzar, como en el 7004T6, límites elásticos de 360 N/mm2 (valor correspondiente a una deformación unitaria del 0,2%) y tensiones de rotura superiores a los 400 N/mm2 con deformaciones unitarias límites que alcanzan también el 10%. Con este tipo de aleación, que no es resistente a la corrosión, es más problemático conseguir unas buenas uniones soldadas.
Existen, en definitiva, una gran diversidad de aleaciones con cualidades específicas que se utilizan en la fabricación de cuadros de las bicicletas y otros componentes. Además, al progreso en los materiales se han unido los avances tecnológicos que permiten transformar los tubos, por hidroformado, prensado o forjado u otros procedimientos y configurar sorprendentes cuadros con tubos de muy variadas geometrías con paredes conificadas de espesor variable, que permiten optimizar su comportamiento aerodinámico y su capacidad resistente.

No conviene olvidar, sin embargo, que la gran mayoría de los campeones que ganaron un Tour de Francia, lo hicieron sobre bicicletas con cuadros de acero. Los últimos, probablemente, fabricados con los míticos tubos Reynolds. Los que lo han logrado más recientemente —y en los últimos años prácticamente todos los componentes del pelotón— recurren a los materiales compuestos con fibras de carbono. Y antes que ellos, entre unos y otros, hubo otro puñado de vencedores que debieron emplear cuadros de aluminio. La historia del Tour, y la del ciclismo en general, puede narrarse también desde la perspectiva de los materiales utilizados en la fabricación de las bicicletas. Y en muchas de estas historias del pasado el acero sería protagonista. Y, tal vez, volverá a serlo, porque la industria siderúrgica, la que se ocupa del acero, ha hecho progresar este material extraordinariamente. El acero no es un material del pasado y acabará renaciendo, genéticamente modificado, con otros elementos que con su presencia discretísima, en muy pequeñas proporciones, pueden mejorar extraordinariamente las características de los aceros tradicionales al carbono, que son también una aleación de hierro con porcentajes de carbono inferiores al 0,4%, y que aportan la ductilidad indispensable para ser utilizado en tantísimas aplicaciones. La densidad del acero, 7,8 kg/dm3, es casi tres veces superior al del aluminio y éste es su gran inconveniente. Pero su capacidad resistente es muy superior. Los modernos aceros aleados con cromo y molibdeno, por ejemplo, pueden alcanzar tensiones límites de 1.000 N/mm2 y aún existen otras aleaciones, más modernas, que pueden llegar a los 1.400 N/mm2, cifras cuatro o cinco veces superiores a las que consiguen los más avanzados aluminios aleados. Los aceros para pretensar que utilizamos en las estructuras de la ingeniería civil, en forma de hilos obtenidos por estiramiento, o de cables construidos entrelazando hilos individuales, pueden superar los 1.600 N/mm2. El acero volverá y, tal vez, lo haga para fabricar, por moldeo, los nudos más delicados de los cuadros, a los que se soldarán los tubos que armarán un cuadro. La gran capacidad resistente de algunos aceros microaleados, permitirán secciones más esbeltas, con espesores más reducidos que los que necesitan los tubos de aluminio, con lo que los pesos de los cuadros de ambos materiales tenderán a aproximarse aportando los de acero su mayor rigidez, una cualidad que ha de ser muy valorada.
Y ahora, sobre todo para quienes puedan pagarlo, la fibra de carbono —como imprecisamente se la conoce— ha adquirido un protagonismo destacado. Los materiales compuestos por fibras de carbono envueltos en una matriz de resina epoxi se han convertido en los más valorados y se utilizan crecientemente en la fabricación de cuadros, llantas, manillares y otros componentes de las bicicletas más avanzadas. Todas las grandes marcas tienen sus modelos más prestigiosos fabricados con «fibras de carbono» como simplificadamente se conoce a un material complejo de elaborar y cuyas características mecánicas no son fáciles de establecer. Lo cierto es que, tras unos titubeantes comienzos, con frecuentes problemas que pusieron en tela de juicio su adecuación como material para las bicicletas, las mejoras introducidas en los procesos de producción, en los controles consiguientes y en el conocimiento de sus características mecánicas, explica su presencia tan extendida, el prestigio de que gozan en la actualidad y el precio tan elevado que se suele pagar por su utilización.
Se trata de un material sumamente especializado que se elabora tras laboriosos procesos, que demandan, paradójicamente, mucha mano de obra artesanal. Y por ello, la mayoría de los cuadros con fibra de carbono, que suelen estar concebidos y dimensionados por los departamentos de ingeniería de las grandes marcas; se fabrican, por encargo, en unas pocas industrias de las que algunas de las más importantes están ubicadas en China y Taiwán. Un mundo, de geometrías, que pueden ser sorprendentes, bellas y eficientes y que está, por otro lado, atiborrado de patentes y «secretos de fabricación», que filtra escasa información técnica y fiable y se adorna con un lenguaje digno del que utilizan, en sus descripciones, los más refinados catadores de vino.
En rasgos generales, el material al que nos estamos refiriendo está compuesto por delgadísimas fibras de carbono dispuestas paralelamente e integradas en una matriz de resina epoxi. Las fibras de carbono, son hilos o filamentos con densidades en el entorno de 1,80 kg/dm3, 4,3 veces inferior a la del acero (7,80 kg/dm3) e inferior también a la del aluminio (2,70 kg/dm3). Su módulo de elasticidad puede variar entre 250.000 y 390.000 MPa, superior al del acero (210.000 MPa) y al del aluminio (70.000 MPa) y su capacidad resistente puede alcanzar los 2.500 MPa, superando incluso al de los aceros de pretensado (1.600 MPa).
El polímero, resina epoxi, que se suele utilizar como matriz, tiene aún menor densidad (1,2 a 1,4 kg/dm3), es muy deformable y poco resistente. Su módulo de elasticidad puede variar entre los 2.100 y 5.500 MPa —unas 100 veces inferior al de las fibras de carbono— y la tensión máxima que puede resistir se sitúa entre los 40 y 80 MPa, 50 o 60 veces inferior al de las fibras.
El comportamiento mecánico del material compuesto dependerá por una parte de la orientación de las fibras de carbono, y, por otra, de su proporción en la masa de la matriz polimérica.
En cierto modo, el concepto es similar al del hormigón armado: las barras de acero proporcionan la capacidad resistente en tracción de la que carece la matriz del hormigón en la que aquéllas están embebidas. El comportamiento de un tirante de hormigón depende, lógicamente, de la cuantía de las armaduras y de su orientación, que debe aproximarse a la dirección de la carga aplicada. Análogamente una capa de material compuesto tendrá un comportamiento muy diferente cuando el esfuerzo se aplique en la dirección en que se han dispuesto las fibras de carbono o en una dirección perpendicular. Es, por tanto, un material marcadamente anisótropo.
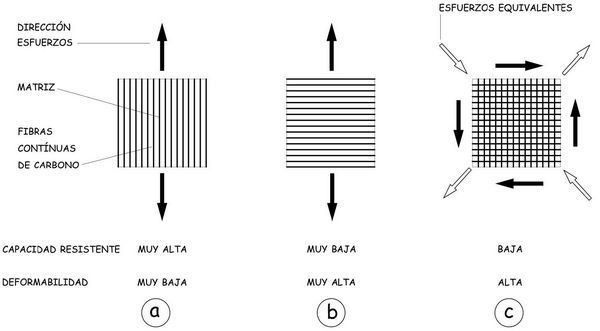
El diagrama tensiones-deformaciones del material compuesto en el supuesto de esfuerzos de tracción actuando en la dirección de las fibras de carbono será el representado en el esquema. Las fibras tienen gran capacidad resistente pero son frágiles, rompen bruscamente cuando alcanzan su máxima tensión. La resina, en cambio, es muy deformable y alcanza pronto su capacidad máxima para luego continuar deformándose pero sin romper. El diagrama tensiones-deformaciones, σ-ε, que caracteriza el comportamiento mecánico del material compuesto será intermedio entre uno puramente elástico y frágil debido a las fibras y el elástico-plástico que caracteriza a la resina.
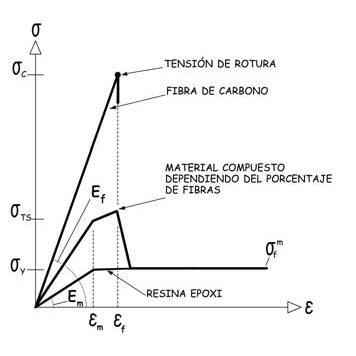
La definición del tramo elástico, del diagrama σ-ε del material compuesto que se muestra en el esquema, dependerá del porcentaje o cuantía, ρ, de las fibras de carbono.
Si consideramos una sección, de área total AT, en la que Af será la parte correspondiente a las fibras y Ar, la de la resina, tendremos
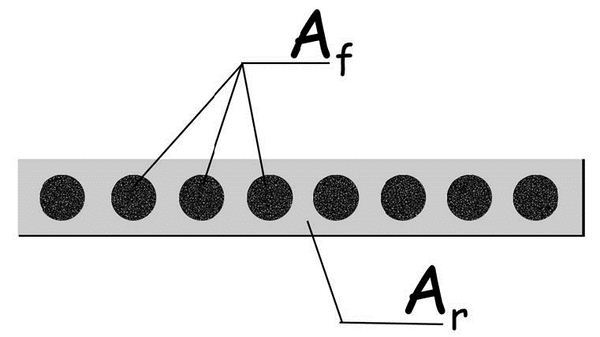
AT = Af + Ar
1 = Af / AT + Ar / AT = ρ + (1 – ρ)
siendo ρ = Af / AT
La resistencia máxima de la sección para esfuerzos de tracción paralelos a las fibras (siendo σf la tensión máxima de las fibras, σr, la de la resina y σT la del material compuesto) será
Tmax = σT · AT = σf · Af + σr · Ar
Por lo tanto,
σT = σf · ρ + σr · (1 – ρ)
Por otra parte, las deformaciones unitarias del material compuesto, εT coincidirán, —admitiendo que exista una adherencia perfecta—, con las de las fibras, εf, y con las de la resina, εr. Y, en consecuencia tendremos
εT = εf = εr
es decir
σT / εT = σf / εf = σr /εr
En definitiva, podemos escribir la expresión de σT como
σT = (σT / εT) · [σf · ρ + σr · (1 – ρ)]
Cuando se haya alcanzado la tensión máxima de la fibra de carbono, para la deformación unitaria, εf, se producirá un escalón brusco en el diagrama σT-εT y la tensión residual descenderá hasta el valor proporcionado por la resina:
σT = σf · (1 – ρ), para εT > εf
Cuando los esfuerzos se aplican perpendicularmente a la orientación de las fibras de carbono (esquema «b»), la capacidad resistente del material resistente será la debida exclusivamente a la resina (40 a 80 MPa) aplicada al área que ocupa este material en la sección, es decir, el valor de σT será el que se deduce la expresión anterior porque la resina es isotrópica y su resistencia a compresión coincide con la de tracción.
Los esfuerzos cortantes y de torsión provocan tensiones tangenciales que equivalen (esquema «c») a la combinación de tracciones inclinadas a 45° y de compresiones perpendiculares a ellas. Por tanto, en estas situaciones el material compuesto tiene también muy reducida capacidad resistente, cualquiera que sea la orientación de las fibras de carbono.
Un material compuesto, con un porcentaje, que puede ser habitual, del 58% de fibra de carbono, tendrá una densidad de 1,5 kg/dm3, muy inferior a la del acero (7,8 kg/dm3). La resistencia a tracción en la dirección de las fibras, estará en el entorno de los 1.000 MPa (70 MPa en el aluminio) y su módulo de elasticidad será ligeramente inferior, 190.000 N/mm2, al del acero.
En vista de ello, la estrategia que se sigue para aprovechar las extraordinarias cualidades mecánicas de los materiales compuestos con fibras de carbono (peso muy reducido, alta capacidad resistente, elevada rigidez en la dirección de las fibras) y paliar sus inconvenientes, consiste en superponer capas con espesores de pocas décimas de milímetro del material compuesto, cada una de ellas con orientaciones de las fibras de carbono alternadas, perpendiculares o cruzadas, para adecuar el material resultante multicapa a los esfuerzos que previsiblemente pueden solicitarlo. Y disponiendo suficiente número de capas para alcanzar un espesor suficiente para transferir las tensiones de compresión que inevitablemente siempre existirán.
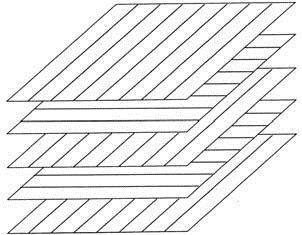
Para la producción de las capas de material compuesto se han desarrollado diferentes sistemas. En el procedimiento denominado «poltrusion» en la terminología anglosajona, las fibras de carbono que provienen de un conjunto de bobinas de eje vertical, pasan por un baño y después por unas cámaras de preformado y curado. En el procedimiento «prepreg» las fibras de carbono se incorporan a bandas de papel que se impregnan de resina tras pasar por rodillos calientes. Para la fabricación de tubos se utiliza el sistema denominado «filament winding», que permite el enrollado de las fibras de carbono con varias geometrías.
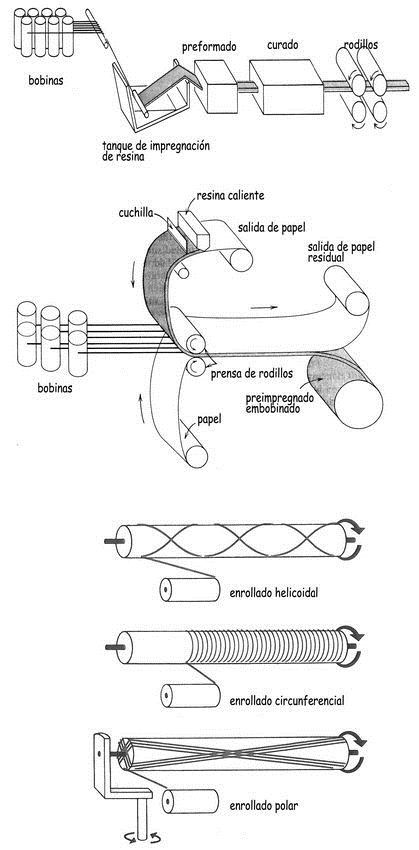
La evolución en los materiales empleados en la fabricación de bicicletas, cuadros y componentes, no concluirá jamás. Entre los que se han incorporado, en los últimos años, se encuentran el titanio, un metal descubierto hace más de 200 años que empezó a ser utilizado cuando, hacia 1936, se descubrió el procedimiento para producirlo industrialmente a partir de minerales como el rutilo (Ti O2) o la ilmenita (FeO TiO2).
El titanio tiene una densidad de 4,5 kg/dm3 y en estado puro posee características mecánicas similares a las del acero, que pesa un 73% más. Atesora una gran ductilidad εult = 35%. Es muy resistente a la corrosión y mantiene sus cualidades a temperaturas elevadas. Aleado, por ejemplo, con un 6% de aluminio y un 4% de vanadio, alcanza tensiones límites de 1.000 N/mm2 (con, σ0,2 = 900 N/mm2), con alargamientos en rotura aún considerables (εu = 15%).
Se ha convertido en un material indispensable en las industrias aeronáutica y aeroespacial. Por ser biológicamente compatible con los tejidos óseos del cuerpo humano, es material también de referencia en la preparación de prótesis dentales y óseas.
Ya existen aplicaciones generalizadas del titanio en componentes de bicicletas, como en piñones del cambio de marchas y en tornillería diversa. Existen también algunas realizaciones de cuadros construidos con titanio aleado. Como el del precioso modelo Lollobrigida, fabricado por una innovadora firma italiana.

En el futuro, parece previsible una creciente cooperación entre materiales para crear cuadros más eficientes. Ya se recurre a esta cooperación para reforzar las barras de dirección en las zonas de contacto con los rodamientos o en la fabricación de nudos a los que confluyen barras de otros materiales. El mestizaje estructural tendrá, probablemente, una presencia creciente en el futuro de la bicicleta.
Para la unión de los tubos que configuran el cuadro de una bicicleta, se utiliza la soldadura, técnica que ha experimentado también en las últimas décadas unos progresos extraordinarios. El más utilizado, tanto para unir tubos de acero, de aluminio o de titanio, es el procedimiento TIG, (Tungsten Inert Gas). Para producir la fusión de las piezas a unir y del metal de aportación, se utiliza como electrodo un hilo de tungsten que no funde. El baño de fusión se protege mediante un gas inerte, como el argón, que fluye a baja presión por el conducto tubular de la extremidad de la pistola de soldadura.
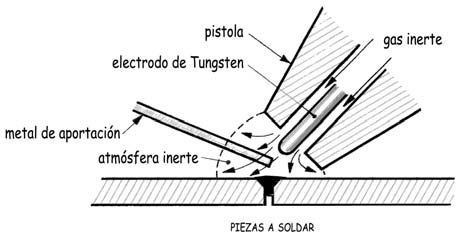
El pedal, la biela, los platos grandes, la cadena y los piñones traseros, son los componentes del sistema de transmisión de la bicicleta y hacen posible su desplazamiento. Desde una perspectiva estructural interesa evaluar la magnitud de las fuerzas que ponen en movimiento la bicicleta y el itinerario que recorren desde que nacen en los pedales hasta que alcanzan el contacto del neumático de la rueda trasera con el pavimento.
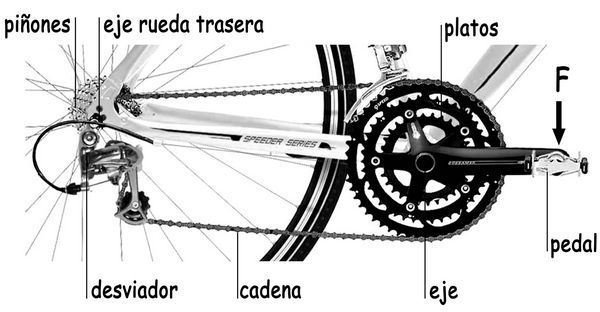
Si aislamos el subconjunto formado por pedal-biela-plato grande-cadena y el eje que lo conecta con el cuadro, observaremos que la fuerza F aplicada en el pedal, y que supondremos perpendicular a la biela situada horizontalmente, induce en la parte superior de la cadena una tracción T que la equilibra.
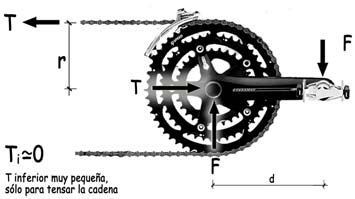
Si la fuerza F introducida por el pedaleo del ciclista fuera de 1.000 N (en el ensayo normalizado de fatiga de la biela, que se describe en el apartado 6, este valor es de 1.800 N aunque aplicado con la biela a 45°), la distancia, d, entre el pedal y el eje fuera de 17,5 cm, y el diámetro del plato de 20 cm, la tracción T en la cadena sería
T = 1.000 N · 17,5 cm / 10 cm = 1.750 N
Si los extremos de los cinco brazos que unen, en el esquema representado, la biela con el plato, y que se encuentran en el itinerario que recorre la fuerza F hasta hacerse tracción T en la cadena estuviesen situados en una circunferencia de 11 cm de diámetro, el esfuerzo cortante o de cizallamiento que deberían transmitir cada uno de los cinco tomillos de sujeción sería
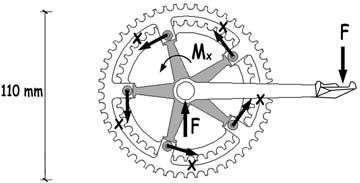
X = 1.000 N · 17,5 cm / (5 torn · 11/2 cm) ≈ 630 N/tornillo
y el correspondiente momento flector en el encuentro de cada una de las cinco barras radiales, con el eje del pedalier, valdría
Mx ≈ 630 N · 11/2 cm = 3.465 N·cm
En realidad los esfuerzos para los que habría que dimensionar tomillos y brazos radiales podría ser significativamente más elevado. La hipótesis de idéntica distribución de fuerzas circunferenciales entre los cinco tomillos radiales que unen cada uno de los cinco brazos de la «araña» con los platos (uno, dos o tres) del sistema motriz de la bicicleta, presupone una rigidez infinita del conjunto que no corresponde a la realidad. Y, de hecho, la distribución de fuerzas que equilibran el «par motor», F · d, no será uniforme.
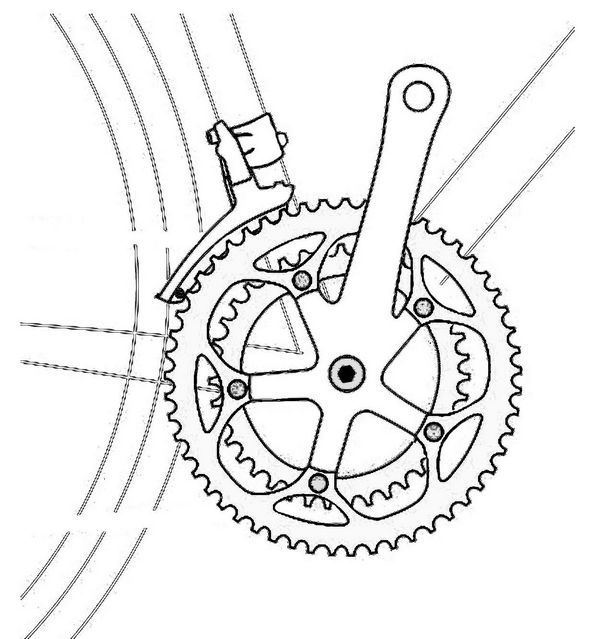
Algo similar se pone también de manifiesto cuando se enfoca la atención a la transferencia de fuerzas que se producen entre los eslabones de la cadena y los dientes del plato en el que se engranan. Solamente unos pocos entre ellos estarán en contacto, en la parte superior del plato y, por consiguiente, la transmisión de la fuerza aplicada por el ciclista a los pedales no estará uniformemente distribuida en todo el perímetro del plato, sino que se concentrará en una zona muy localizada que irá variando a cada instante. Por eso, el anillo externo del plato actuará también como estructura de reparto de las fuerzas de contacto de sus dientes y los eslabones de la cadena con los tomillos de la araña de sujeción de la biela, siendo lógicamente los más solicitados los que se encuentren más próximos a la zona de contacto de la cadena y el plato.
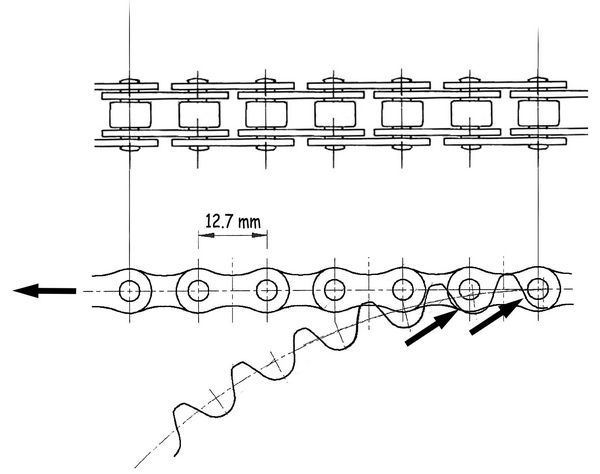
La cadena, obviamente, es un componente esencial del sistema de transmisión. Las que se utilizan en las bicicletas, de características normalizadas, suelen tener 114 eslabones, con un paso o distancia entre ejes de 12,70 mm. Con el progresivo aumento del número de piñones, su anchura se ha ido reduciendo. La que requieren los ultramodernos de 11 piñones tienen anchuras de 5,5 mm. En el esquema adjunto figuran las dimensiones aproximadas de un módulo.
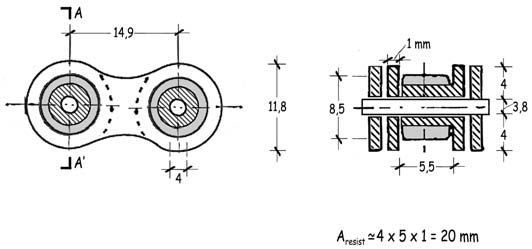
La capacidad resistente de la cadena será la correspondiente a su sección más reducida, que se sitúa en el plano del eje de cualquiera de los eslabones que configuran la cadena.
Si la carga de rotura, establecida en la normativa es de 17.850 N, la tensión media de tracción sería del orden de
σ ≈ 17.850 N / 20 mm2 ≈ 900 N/mm2
lo que exige aceros aleados muy resistentes y con tratamientos para mejorar la dureza superficial, por cuanto las tensiones de contacto entre eslabones de la cadena y dientes del plato serán aún más elevadas. El eje de los eslabones a través de los que se transfieren, por simple cizalladura, los esfuerzos de tracción de la cadena, es también un elemento crítico con tensiones tangenciales muy elevadas.
En la práctica habitual del ciclismo, la fuerza de tracción en la cadena estará lejos de estos valores límites. La fuerza máxima que puede aplicar un ciclista colocado de pie sobre los pedales podrá alcanzar e incluso superar su peso propio, pero nunca sería mayor que la necesaria para llegar a agotar la capacidad resistente de una cadena con todos sus eslabones en buenas condiciones. Hay que tener en cuenta, sin embargo, que en una cadena de 114 eslabones, es el más débil de todos ellos, el que limita su capacidad resistente. Además, las cargas que solicitan a la cadena serán de naturaleza dinámica, estarán amplificadas por coeficientes de impacto y por los de concentración de tensiones inherentes a su geometría. Pero, sobre todo, las cargas serán cíclicas y provocarán la fatiga del material, que suele ser la causa más habitual que provoca su rotura.
El análisis del equilibrio de la rueda trasera permite estimar los valores de las fuerzas que puede transferir la cadena y completa, además, la reflexión sobre el sistema de transmisión de una bicicleta.
A la rueda motriz trasera, a través de los piñones, llegará transformada la fuerza que transmite la cadena, que a su vez, proviene de la aplicada por el ciclista sobre el pedal y transferida a través del plato del pedalier a la cadena. Sobre la rueda actuará, además, su reacción de apoyo en el pavimento. El flujo de fuerzas que actúan y se auto equilibran en la estructura de la rueda trasera será la representada en los esquemas siguientes:
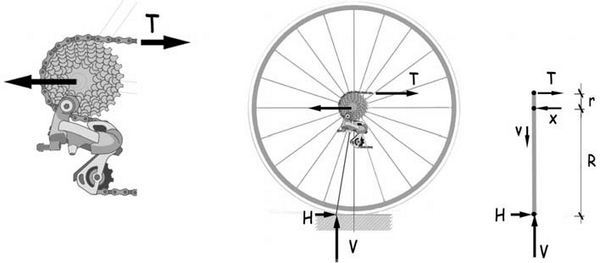
La fuerza horizontal que impulsa la bicicleta, y que se localiza en el área de contacto de la cubierta y el pavimento, será de acuerdo con la condición de equilibrio:
T · r = H · R
es decir
H = T · r / R
siendo T la tracción transmitida por la cadena; r, el radio del piñón asociado a la cadena y R el radio de la rueda.
Además, la reacción X que se genera en el buje de la rueda será
X = T + H = T · [1 + r / R]
Si, por ejemplo, consideramos un piñón de 18 dientes que tendrá un radio, aproximadamente, de r =18 · 12,7 / (2 · π) = 36,4 mm tendríamos, siendo R ≈ 350 mm,
H = T · 36,4 / 350 ≈ 0,10 · T
Si la tracción en la cadena fuese, como hemos visto anteriormente, de 1.750 N (que corresponde a la fuerza en los pedales de 1.000 N), el valor de H sería de 175 N. Dicho valor podría corresponder al esfuerzo puntual que se podría producir en una subida de pendiente pronunciada, porque asociada, pongamos, a una velocidad de 5 m/s correspondería a una potencia 175 N · 5 m/s = 875 W, que estará próximo al límite que puede generar un ciclista profesional en periodos muy cortos de tiempo.
De otra manera, si el valor de la fuerza tractora H fuese uno más habitual de 14 N (a lo que corresponderían potencias de 140 W para velocidades de 10 m/s) la fuerza de tracción en la cadena sería, del orden de
T ≈ H / 0,10 = 140 N
y en el pedal, de aproximadamente
F ≈ 140 N · 10 / 17,5 = 80 N
Todos estos valores son muy inferiores a la capacidad resistente que poseen todos los componentes del sistema de transmisión de una bicicleta. Lo que confirma que su dimensionamiento se basa en escenarios en los que se producen impactos, con fuerzas muy elevadas en periodos muy breves de tiempo, o para acciones repetidas que pueden provocarla fatiga del material para tensiones sensiblemente inferiores a las estáticas que podrían agotar su capacidad resistente.
Definir las fuerzas máximas que el ciclista puede introducir, a través de los pedales, en el sistema de transmisión de su bicicleta, es muy incierto. Por eso, la normativa establece ensayos específicos, para evaluar el comportamiento de bielas y pedales, en condiciones muy exigentes.