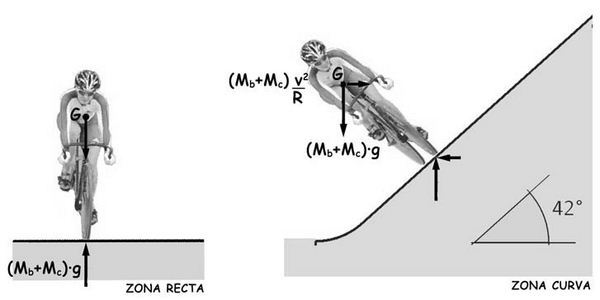
El equilibrio global de la bicicleta exige que las acciones que actúan sobre ella se equilibren con las reacciones, de signo contrario, que se sitúan en el contacto de las ruedas con el pavimento sobre el que se desplazan. Dicha condición suele permitir estimar los valores de las reacciones de apoyo de cualquier estructura, la bicicleta en nuestro caso. Y conocer dichas reacciones de apoyo ayuda a comprender y evaluar el comportamiento de la estructura en su conjunto y de cada una de sus partes. Es algo que todo ingeniero debería hacer instintivamente. En este texto se dedica especial atención, por ello, a determinar las reacciones de apoyo que provocan las diferentes acciones que pueden actuar sobre la bicicleta, lo que contribuye a plantear con claridad los esenciales conceptos de energía y potencia asociados al movimiento del ciclista y su bicicleta.
El comportamiento de todas las estructuras —tanto las creadas espontáneamente por la naturaleza o las que, con la ingeniería como comadrona, han nacido para dar respuesta a necesidades de los seres humanos— está gobernado por las tres sencillas y esenciales leyes descubiertas por Newton y expuestas en su libro Principios matemáticos de la filosofía natural, inicialmente escrito en latín y publicado en Londres el año 1687. Recordarlas bien merece la pena. La primera nos dice que un cuerpo permanece en reposo o se desplaza a velocidad constante, si no existe fuerza externa que se ejerza sobre él. La segunda, aunque expresada por el sabio universal en términos de constancia de la cantidad de movimiento, (m · v = cte) nos dice que una fuerza externa, F, provoca en un cuerpo de masa, m, una aceleración, a, tal que F = m · a. Y la tercera y última, expone que toda acción sobre un cuerpo es contrarrestada por una reacción igual pero de sentido contrario. Concepto que, de otra manera, ya había sido expuesto por Arquímedes muchos siglos antes y que, en definitiva, recuerda la exigencia del equilibrio, estático o dinámico, del conjunto de las fuerzas, acciones o reacciones, que actúan sobre un cuerpo o sobre cualquier parte que, virtualmente, podamos aislar de él.
La física newtoniana nos define, también, la energía que se necesita para poner en movimiento un cuerpo o para mantenerlo en movimiento, es decir, para asegurar su equilibrio dinámico. La energía es la fuerza por el espacio recorrido en la dirección de la fuerza. La potencia define la energía por unidad de tiempo. En un intervalo infinitesimal de tiempo, dt, el ciclista montado en su bicicleta, se habrá desplazado una distancia, dx, y su velocidad, será
V = dx/dt
Por tanto, las siguientes expresiones definen la energía, dE, y la potencia, P, en ese instante determinado:
dE = F · dx
P = F · dx/dt = F · v
La potencia será, por tanto, la fuerza por la velocidad. Cuando el ciclista pone la bicicleta en marcha genera un fuerza de inercia, F = m · a, e inocula la energía necesaria para que inicie el movimiento. De ello se trata en el apartado 10: «La energía del ciclista». No siendo su cuerpo una máquina perfecta, solamente aprovechará una parte de dicha energía para desplazarse. Habrá unas pérdidas de eficiencia debidas a las deformaciones elásticas de los componentes de la bicicleta (ruedas, manillar, cuadro,…), a los rozamientos internos de los mecanismos móviles (transmisión, bujes, dirección, pedales…) así como a las fuerzas de rozamiento entre los neumáticos de las ruedas y el pavimento por el que ruedan. Todo este conjunto de pérdidas se puede considerar equivalente a una fuerza global, a la que en bicicletas de alta gama, bien mantenidas, se le suele asignar un valor de 3 o 4 newtons, según sea la velocidad.
La energía necesaria para el movimiento es, asimismo, la que requiere el equilibrio dinámico del ciclista y su bicicleta, cuando acelera, o decelera, o mantiene su velocidad. Por eso, en lo que sigue, al identificar las fuerzas que actúan sobre una bicicleta se hace referencia a la energía y potencia asociadas al movimiento, en un diálogo que ayuda a cuantificarlas, y a comprenderlas, por tanto, mejor.
En adelante utilizaremos, naturalmente, el sistema internacional de unidades en el que se miden la masa en kilogramos (kg) y la fuerza en newtons (N). Cuando afirmamos que una persona pesa 80 kg, en realidad nos estamos refiriendo a su masa. Su peso, W, sería el resultado de multiplicar su masa por la aceleración de la gravedad g ≈ 9,8 m/s2 a la que, a efectos prácticos, consideraremos igual a 10 m/s2: W = 80 kg · 10 m/s2 = 800 N.
Analicemos en primer lugar, el equilibrio de la bicicleta, sola e inevitablemente estática, antes que el ciclista, montado sobre ella, la ponga en movimiento sobre una superficie, que supondremos horizontal.
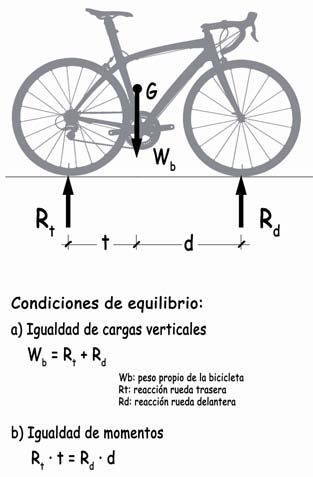
Condiciones de equilibrio:
a) Igualdad de cargas verticales: Wb = Rt + Rd
Wb: peso propio de la bicicleta,
aplicada en su centro de gravedad, Gb
Rt: reacción rueda trasera
Rd: reacción rueda delantera
b) Igualdad de momentos: Rt · t = Rd · d

Sobre la bicicleta, actuarán su peso propio Wb = Mb · g, que se puede suponer está concentrado en su centro de gravedad, Gb, y las reacciones Rt y Rd que se localizan en el contacto de las cubiertas de las ruedas con el pavimento y cuya suma igualará a Wb.
De la exigencia de igualdad de momentos de las acciones y reacciones en relación con el centro de gravedad, Gb, se deduce la segunda ecuación de equilibrio. Tendremos, por tanto, dos incógnitas, las reacciones de apoyo, Rt y Rd, y dos ecuaciones que nos permiten su deducción. La reacción Rt en la rueda trasera suele ser mayor por estar más próxima a la vertical del centro de gravedad. En una bici de 120 N de peso, por ejemplo, las reacciones de apoyo pueden ser del orden de 75 N en la rueda trasera y 45 N en la delantera.
Cuando el ciclista se coloca sobre la bicicleta, antes de ponerla en movimiento, las fuerzas del equilibrio, que continuará siendo estático, habrán cambiado. Al peso propio de la bicicleta se añadirá el del ciclista, que podría ser como seis veces mayor. El centro de gravedad de su masa corporal dependerá de la geometría que adopte sobre la máquina, pero se situará normalmente en el entorno del borde del sillín más próximo al manillar y por encima de éste.
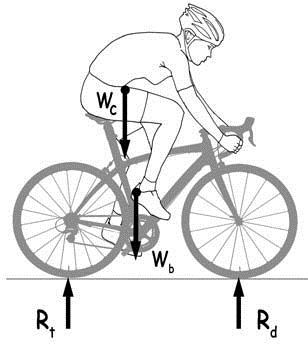
Las ecuaciones de equilibrio serán análogas al caso anterior, pero las reacciones en las ruedas traseras y delanteras habrán variado en proporción. Suponiendo que el peso conjunto de la bici (120 N) y del ciclista (680 N) alcanzase los 800 N, podríamos tener, como órdenes de magnitud:
Rt ≈ 75 + 500 = 575 N
Rd ≈ 45 + 180 = 225 N
Rt + Rd = 800 N
La rueda trasera soportará del orden del 70 al 75% del peso conjunto del ciclista y de la bicicleta y la delantera el 25 al 30% restante.
Cuando el ciclista pone su bicicleta en movimiento, se produce una aceleración a la que va asociada una fuerza de inercia, de sentido contrario al del movimiento, producto de la masa del conjunto ciclista-bicicleta por la aceleración en cada instante, aplicada en el centro de gravedad de la masa conjunta. Cuando se alcanza una velocidad uniforme, se anula la aceleración y, con ella, la fuerza de inercia.
Unas curvas posibles de desplazamientos-tiempo (x-t), velocidades-tiempo (v-t), y aceleraciones-tiempo (a-t), tendrían la apariencia de las representadas:
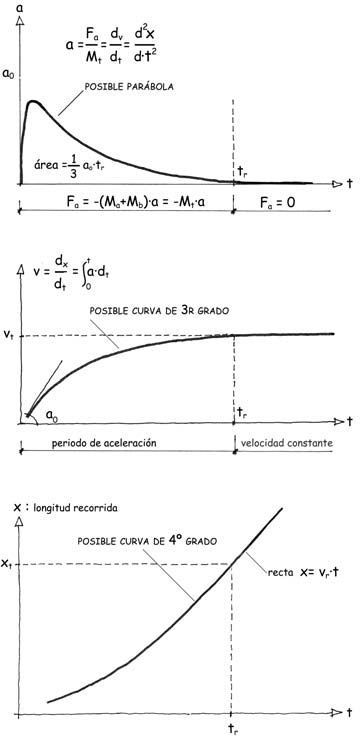
El periodo de aceleración duraría un tiempo, tr, y, por consiguiente, la curva correspondiente se iniciaría con una aceleración, a0, que se reduciría progresivamente hasta anularse en t = tr, haciéndose la curva tangente a la abcisa de tiempos. La parábola de ecuación
a = a0 · [1 – (t / tr)]2
sería una curva posible puesto que cumpliría las condiciones de contorno:
t = 0 ; a = a0
t = tr ; a = 0 ; da/dt = 0
Como a = dv/dt y, en consecuencia, v= ∫0t a · dt, la curva velocidad-tiempo será una ecuación de 3er grado con una pendiente en el origen que coincidirá con la aceleración inicial, a0, y con una tangente horizontal de ordenada v = vr, velocidad estabilizada a partir de t = tr.
Como el valor de vr debe coincidir con el área encerrada bajo la curva parabólica a-t, tendremos
vr = (1/3) · a0 · tr
Análogamente, como v = dx/dt y x = ∫0t v · dt, la curva de x-t, sería de 4º grado, con tangente nula en el origen y con tangente constante v = vr, a partir de t = tr.
Los gráficos anteriores no son adecuados para explicar lo que sucede en los momentos iniciales del movimiento. La aceleración no puede pasar instantáneamente de cero a un valor a0. Habrá un periodo de adaptación, el requerido para que los músculos del ciclista reciban instrucciones de su cerebro y transforme la energía química almacenada en su organismo en la energía mecánica que necesita el movimiento.
En el apartado 10, «La energía del ciclista» se trata con algún detalle esta compleja cuestión. Aquí nos limitaremos a plantear la influencia que tienen las aceleraciones en las reacciones de apoyo de la bicicleta, y pondremos ejemplos que nos permitan disponer de algunos órdenes de magnitud que nos ayuden a comprender mejor las fuerzas de inercia. Pero, antes de ello, conviene observar, también, que la aceleración máxima que puede impulsar la bicicleta nunca podrá superar la que, por insuficiencia de rozamiento estático, hiciese patinar la rueda trasera sobre el pavimento.
El equilibrio dinámico del ciclista y la bicicleta, supuesta su masa conjunta (MT = Mc + Mb) concentrada en un punto, G, sería la representada en el esquema.
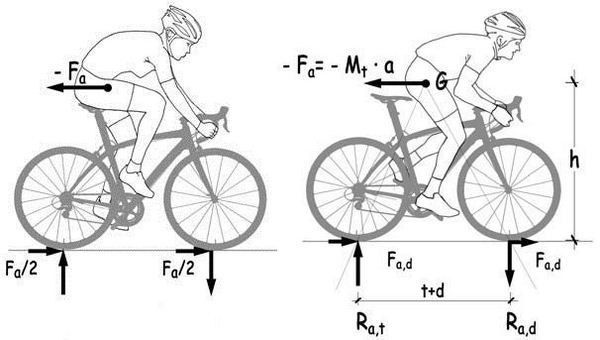
La fuerza de inercia, Fa, genera en el contacto de las ruedas delantera y trasera, las dos fuerzas Fa/2 de sentido contrario que la equilibran. La distancia, h, entre el centro de gravedad de la masa conjunta y el pavimento genera un momento Fa · h que se equilibra con un par de fuerzas verticales, iguales y contrarias, en las ruedas delantera y trasera. La aceleración provoca, por tanto, un aumento de la reacción de apoyo en la rueda trasera y una disminución en la rueda delantera, en proporciones que van cambiando a cada instante hasta que se estabiliza la velocidad, se anula la aceleración y la consiguiente fuerza de inercia.
Las ecuaciones de equilibrio serán, por tanto
Ra,d = –Ra,t
Fa · h = Rad · (t + d)
Para tener órdenes de magnitud, de estos conceptos, podemos imaginar la salida de una etapa individual de contrarreloj del Tour de Francia. Nuestro ciclista con sus 800 N de peso, incluido el de su ligera bicicleta (que no será la de menor peso entre todas las posibles porque el reglamento del Tour exige un peso mínimo y de ahí, el curioso ritual del pesaje de cada bicicleta, como si fuera un jamón, antes que el ciclista se coloque en la posición de salida) tardará unos 20 segundos en alcanzar su velocidad de crucero de unos 14 m/s, equivalentes a 50 km/h. La aceleración máxima podría ser —unas dos veces la aceleración media— del orden de 1,4 m/s2, 0,14 · g aproximadamente.
La fuerza de inercia valdría, en consecuencia,
Fa = (800 N/g) · 0,14 · g= 112 N
Si suponemos que la velocidad media en el periodo de aceleración es de 10 m/s, el ciclista necesitaría unos 10 m/s · 20 s = 200 metros de recorrido para alcanzar la velocidad estabilizada de 14 m/s.
La potencia que necesitaría nuestro ciclista hasta alcanzar la velocidad de crucero de 14 m/s en los 20 segundos iniciales de la contrarreloj, crecería desde 0, hasta una potencia de alrededor de 400 watios que es la que puede producir un ciclista profesional en excelente estado de forma durante una hora, el tiempo necesario para recorrer los 50 km de una etapa. Aunque, inicialmente, la potencia requerida habrá sido mayor.
Pero, además, en este tipo de competiciones, el corredor suele partir de una plataforma situada, tal vez, a 1,20 m de altura con una rampa de lanzamiento que podría tener una pendiente del 15% y una longitud de 8 m.
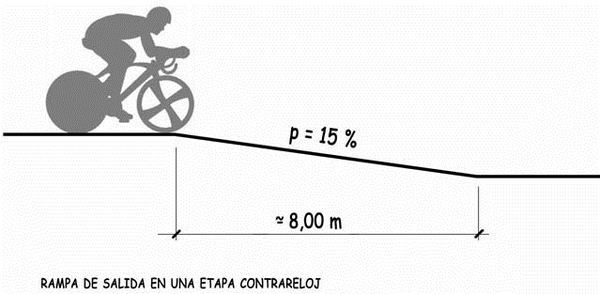

Debido al desnivel de 1,20 m de la rampa de salida, el ciclista y su bicicleta dispondrán de una energía potencial
Ep = m · g · h = 800 N · 1,20 m = 960 julios
Si los 8 metros de rampa se recorren en 1 segundo los watios aportados serían
P = 960 julios / 1 s = 960 watios
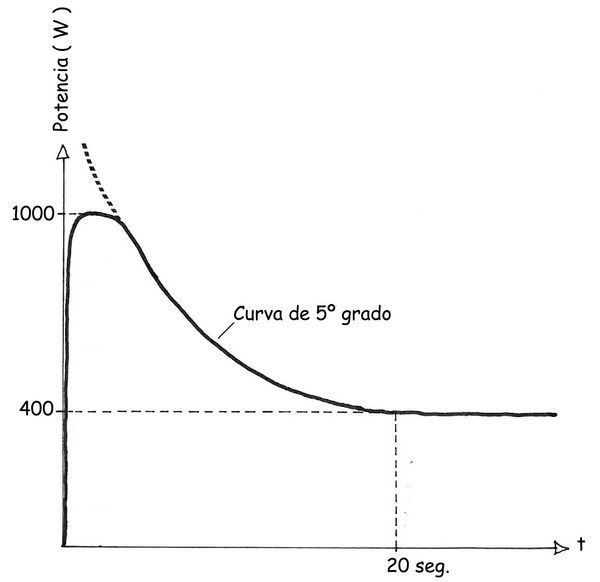
De manera que la curva de aportación de energía en función del tiempo del recorrido podría ser aproximadamente el representado en el gráfico adjunto.
Por otra parte, como se expondrá más adelante con más detalle, la pendiente de la rampa del 15% provoca una fuerza impulsiva paralela a ella, de
F = 0,15 · 800 N = 120 N
Si, al cabo de un segundo, al final de la rampa, la velocidad del ciclista alcanzan los 8,0 m/s, la potencia asociada sería
W = F · v = 120 N · 8 m/s = 960 W
lo que confirma el aspecto de la curva dibujada para la relación Potencia-tiempo de recorrido, que partirá lógicamente del origen de ordenadas, se elevará muy rápidamente hasta alcanzar un valor máximo próximo a los 1.000 W al cabo de un segundo y comenzará a descender por una curva que podría ser de 5º grado, hasta alcanzar al cabo de los 20 s, la potencia estabilizada de 400 W.
A partir de este momento la fuerza impulsiva debido al pedaleo del ciclista será
Fi = 400 W / 14 m/s = 28 N
De esta fuerza, una parte que se suele estimar en 4 N en la bicicleta bien mantenida de un profesional, permite compensar los rozamientos mecánicos y los debidos al contacto de las ruedas con el pavimento. Los 24 N restantes equilibrarían las fuerzas aerodinámicas generadas por el movimiento del ciclista y su bicicleta, a las que nos referiremos en el apartado siguiente. Pero, antes, evaluemos los cambios que se producen en las reacciones de apoyo de la bicicleta como consecuencia del movimiento. El equilibrio, a la velocidad estabilizada de 14 m/s sería el representado en la figura.
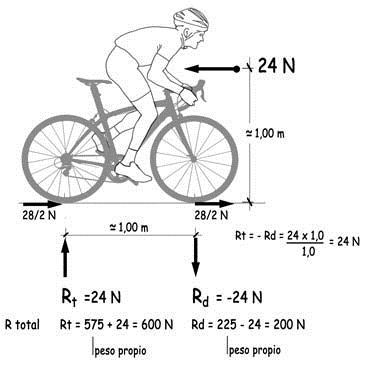
Las variaciones de las reacciones de apoyo de las ruedas traseras (+24 N) y delanteras (–24 N) no son relevantes. En el arranque, con la fuerza de inercia de 112 N (correspondiente a 0,14 · g), dichas variaciones serían de ±112 N. Recordando que habíamos estimado 225 N como reacción de la rueda delantera antes del inicio del movimiento, aún quedará margen para incrementar la aceleración.
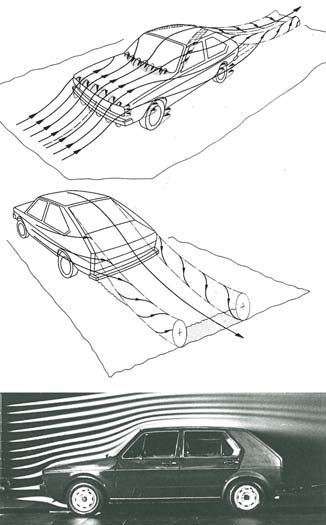
El ciclista y su bicicleta, al desplazarse, deben penetrar en un espacio ocupado por el aire que, aun estando quieto, se opone a la penetración. O, visto de otra manera, sucede como si sobre el ciclista inmóvil, incidiese un viento —el aire en movimiento— con la velocidad de su desplazamiento.
El flujo distorsionado del aire que alcanza al ciclista y su montura ejerce, por una parte, presiones perpendiculares a las superficies de contacto y, por otra, tensiones de rozamiento paralelas a dichas superficies. La resultante del conjunto de las presiones perpendiculares y de las tensiones tangenciales, es la fuerza aerodinámica —la «drag force» del lenguaje anglosajón— que se opone al movimiento y que determina el esfuerzo que ha de realizar el ciclista.
Ya en el siglo XVIII la física clásica, con los Bernouilli y otros sabios a la cabeza, estableció las bases de la mecánica de fluidos. Mucho más recientemente, con la invención de la aviación, se tuvo el estímulo decisivo para comprender y caracterizar la complejidad del viento y evaluar las fuerzas aerodinámicas que se generan en las superficies de objetos en movimiento o de aquellos fijos situados en una corriente de aire.
El viento actuando sobre el conjunto del ciclista y de la bicicleta provoca una fuerza aerodinámica, FD, que tiene por expresión
FD = ½ · Cv · ρ · A · v2
Cv es un coeficiente adimensional que depende de la geometría del obstáculo; ρ es la densidad del aire que se puede, en general, tomar como ρ =1,3 kg/m3, aunque varía entre otros factores con la altitud del lugar y con la temperatura; A es el área de la sombra proyectada por el cuerpo del ciclista y de la bicicleta sobre un plano perpendicular a la dirección del movimiento y v es la velocidad relativa del aire, que, en caso de ausencia de viento meteorológico, coincide con la del ciclista.
Unos valores característicos para un cicloturista circulando en posición erguida, en una bicicleta de paseo, a una velocidad de 5 m/s (18 km/h) pueden ser CD = 0,90, A = 0,45 m2. Por lo tanto, la fuerza aerodinámica provocada por el viento y opuesta al movimiento será:
Fa = ½ · 0,90 · 1,3 kg/m3 · 0,45 m2 · (5 m/s)2 ≈ 6,6 kg·m/s2 = 6,6 N
El valor de esta fuerza depende de la velocidad al cuadrado, y aumenta rápidamente cuando se incrementa dicha velocidad. Pero aún más significativo y relevante (aunque son conceptos íntimamente ligados) es que la potencia asociada al viento, varía con el cubo de la velocidad, puesto que
P = FD · v = ½ · CD · ρ · A · v3
Para los valores considerados de CD (0, 90), ρ (1,3 kg/m3) y A (0,45 m2) tendríamos, para diferentes velocidades, las siguientes fuerzas aerodinámicas opuestas al movimiento y las potencias asociadas los siguientes valores que aparecen en la tabla adjunta.
|
v (m/s) |
v (km/h) |
FD (N) |
P = FD · v (W) |
|---|---|---|---|
|
5,0 |
18,0 |
6,6 |
33 |
|
7,5 |
27,0 |
14,8 |
111 |
|
10,0 |
36,0 |
26,3 |
263 |
|
12,5 |
45,0 |
41,1 |
513 |
|
15,0 |
54,0 |
59,4 |
891 |
Y los gráficos correspondientes FD-v y P-v son los siguientes:
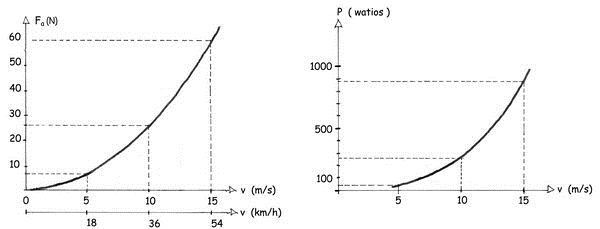
En la situación descrita, el cicloturista, con el torso erguido, difícilmente podría alcanzar velocidades de 10 m/s que requerirían potencias de 263 W disponibles, en todo caso, en periodos muy cortos de tiempo.
Se puede mejorar esta situación reduciendo el coeficiente Cd y minimizando, también, la superficie A, expuesta al viento. Una postura más aerodinámica del ciclista sobre la bicicleta reduce, simultáneamente, ambos factores.
Las características geométricas de la bicicleta influyen en mucha menor medida. En general su contribución a la fuerza aerodinámica opuesta al movimiento supone menos del 20% de la fuerza total, aunque, en todo caso puede marcar unas diferencias significativas, cuando se trata de la alta competición.
El coeficiente CD, que en el ejemplo anterior se ha tomado igual a 0,90, puede reducirse considerablemente. En algunas bicicletas carenadas, pseudobicicletas, se han conseguido valores de 0,1. La superficie expuesta al viento varía también según la posición del ciclista, entre un valor mínimo de 0,30 m2 (posición de contrarreloj, con el manillar de triatlón, los brazos recogidos sobre el cuerpo); 0,40 m2 para un ciclista con bici de carretera y las manos apoyadas en la parte inferior del manillar; y hasta 0,60 m2 y aún más para un cicloturista corpulento, erguido, en una bicicleta de paseo y con un equipamiento inadecuado.
Para el ciclista que disputaba, párrafos atrás, la etapa contrarreloj del Tour a una velocidad de 14 m/s, con su vestimenta, casco y ropaje aerodinámicos, su posición tumbada, brazos recogidos apoyados en un manillar de triatlón, rueda lenticular trasera y con pocos y aerodinámicos radios en la rueda delantera, podríamos tener un coeficiente de arrastre CD = 0,65 y un área expuesta de 0,30 m2 de manera que la fuerza aerodinámica que habría de vencer sería
FA = ½ · 0,65 · 1,3 kg/m3 · 0,30 m2 · (14 m/s)2 = 25 Newtons
a lo que corresponde una potencia
P = FA · v = 25 · 14 ≈ 350 watios
Añadiendo las debidas a las fuerzas de rozamientos internos y con el pavimento, estimados en 4 N, esto es
∂P = 4 N · 14 m/s = 56 watios
tendríamos,
PTOTAL = 350 + 56 = 404 watios
cifra que coincide aproximadamente con la considerada en el ejemplo.
El coeficiente de arrastre CD, fundamental para determinar la fuerza aerodinámica FD, que se opone al movimiento, suele ser de incierta definición si no se disponen de resultados de ensayos en túneles de viento. De hecho, cada vez es más frecuente que los fabricantes de bicicletas y componentes y los equipos profesionales con más recursos realicen ensayos en centros especializados, en los que se evalúan la influencia de la geometría de la bicicleta, del casco aerodinámico que suele portar el ciclista y de la posición del corredor sobre la bicicleta, en el coeficiente de arrastre CD, y en el área expuesta. Valores que, en todo caso, son una aproximación a la realidad más compleja de la competición, en la que influyen obviamente otros factores que difícilmente pueden ser ensayados. Aunque, el gran ensayo es el que proporciona los datos de la realidad, en una determinada carrera, que se pueden monitorizar con aparatos incorporados al cuerpo del atleta y a la bicicleta, y permiten conocer la potencia utilizada y la energía consumida en cada instante, la velocidad y las pulsaciones corporales entre otras informaciones. Se logra así dibujar un panorama preciso del rendimiento del atleta, compararlo con las expectativas y sacar las oportunas consecuencias de todo ello. Sabiendo, por otro lado, que no hay dos carreras iguales, aunque muchas puedan ser parecidas.
El término de velocidad (v2, para la estimación de la fuerza aerodinámica y v3 para la potencia) se refiere a la velocidad relativa. Cuando el viento meteorológico sople en contra, su velocidad se añadirá a la del ciclista. Y se restará en caso contrario, de manera que cuando sople a favor con suficiente fuerza el ciclista podría desplazarse sin pedalear. Cuando el viento meteorológico sea nulo, la velocidad a introducir en las fórmulas coincidirá con la del movimiento.
En los comentarios anteriores se ha supuesto que la huella imperceptible dejada por las ruedas en su recorrido es una recta perfecta y que el cuerpo del atleta se mantiene en un inalterable plano vertical. Pero ni siquiera en el caso de un trazado recto ideal será así, lo que influye en las fuerzas aerodinámicas que realmente se generan y que siempre tendrán componentes transversales, más aún en trazados con curvas, en los que además el ciclista se inclina e inclina la bicicleta para asegurar su estabilidad transversal.
La importancia práctica de las fuerzas aerodinámicas se manifiesta con toda claridad en el lugar en el que se ubican los ciclistas cuando se desplazan en grupo. El que se sitúa inmediatamente a rueda de quien lo lidera necesitará una potencia del orden del 30% inferior, reducción que puede alcanzar el 60% para los que discurren, protegidos, en el centro de un pelotón bien poblado.
Son numerosos, por otra parte, los estudios que se han hecho para evaluar la influencia que pueden tener la ropa del ciclista y la forma, más o menos ceñida, de portarla, la utilización de casco aerodinámico, el tipo de zapatillas utilizadas, la posición del cuerpo, la geometría del cuadro y de los tubos que lo conforman. La piel sin afeitar, por ejemplo, puede incrementar un 2% la fuerza aerodinámica.
Hay que recordar que como P = F · v, si se reduce la fuerza F, reduciendo su componente aerodinámica que a velocidades elevadas es, con mucho, la más significativa, para la misma potencia, se incrementará la velocidad del movimiento. Así, una reducción del 1% supondría un aumento de la velocidad y una reducción del tiempo en la contrarreloj de 50 km de 36 segundos (1% de una hora). Lo que separó a Contador de Andy Schleck en el Tour del 2010.
El ciclismo está lleno de sutilezas. Las ruedas de las bicicletas, por ejemplo, han evolucionado desde las que se configuraban con 36 radios cilíndricos, hacia otras con menor número de radios, de geometrías ovaladas más aerodinámicas, hasta llegar a las lenticulares, más pesadas, pero que oponen menos resistencia al viento longitudinal. Aunque, como importantísima contrapartida, al no ser permeables, son mucho más sensibles a la componente transversal de los vientos meteorológicos o a la originada por las curvas en los desplazamientos de la bicicleta.
Los numerosos estudios y ensayos realizados para evaluar y optimizar la tipología de las ruedas delanteras y traseras han puesto de manifiesto que si la bicicleta contribuye con un 20% como orden de magnitud, a la generación del total de las fuerzas aerodinámicas del conjunto ciclista-bicicleta, las dos ruedas son responsables, a su vez, hasta el 15% de dicha proporción, es decir hasta un 3% de la fuerza aerodinámica total. De ellos, el 65% corresponden a la rueda delantera. La trasera, que contribuye con el 35% restante, está protegida por el tubo vertical del cuadro, cuyos diseños más modernos y elaborados, aproximándose y adaptándose a la geometría de la rueda posterior pretenden subrayar este aspecto. A costa de modificar sustancialmente la tradicional y sencilla geometría tubular característica de los cuadros tradicionales por otras con secciones ovaladas y marcadamente variables. Para ruedas con 36 radios cilíndricos se han medido coeficientes de arrastre, CD, de 0,060 que se reducen a 0,025 para ruedas con 16 radios elípticos o de 12 radios aplanados que pueden tener hasta 6,4 mm de anchura y 0,6 mm de espesor. En una rueda lenticular CD se reduce hasta 0,018.
Cuando el viento incide sobre las ruedas lenticulares con una inclinación superior, digamos, a los 5° a 10° respecto al plano de la bicicleta, la fuerza longitudinal de arrastre puede aumentar un 18%, incremento al que una rueda lenticular delantera contribuiría el doble que una trasera. Lo que justifica la tendencia a disponer solamente ruedas lenticulares traseras. El ciclismo está lleno de sutilezas, porque cualquier mejora puede limar segundos preciosos.
El viento, fundamental en el rendimiento de un ciclista y en el comportamiento del conjunto que forma con su pareja la bicicleta —un matrimonio que no puede ser sólo de convivencia— tiene un carácter aleatorio y no determinista, y sólo se puede caracterizar con suficiente rigor recurriendo a los instrumentos que para ello pone a nuestra disposición la estadística. Es un dominio altamente especializado, aunque no se debería hacer inaccesible para nadie. Entre otras cosas porque el especialista puede comprender pero sólo el ciclista puede sentir y, además, si tiene quien se lo explique bien, podría llegar a comprender en sus rasgos generales lo que llega a sentir.
La mecánica de fluidos, con Bernouilli, Euler, Stokes, Navier y tantos otros, ha estudiado lo que ocurre cuando un objeto se sitúa en el flujo de un fluido, aire por ejemplo. En el entorno del obstáculo el flujo distorsionado puede ser laminar o, a determinadas velocidades y en determinadas condiciones que dependen también de su geometría y de la rugosidad de su superficie, se puede hacer turbulento, formándose, aguas abajo del obstáculo, remolinos característicos, con el fluido girando a gran velocidad.

La frontera entre el flujo laminar y el turbulento depende esencialmente del adimensional número de Reynolds. Para un cilindro de radio r, colocado con el eje perpendicular a la línea de corriente, tiene por expresión
NR = 2 · r · ρ · v / η
siendo v, la velocidad del aire; ρ, su densidad (≈ 1,3 kg/m3) y η su viscosidad, que con el aire a una temperatura de 20° C tiene por valor 1,8 · 105 Pa·s (Pascales por segundo o N/m2·s).
En el caso de la bicicleta esta transición se produce cuando su velocidad es del orden de 5 m/s, si la superficie de contacto es muy lisa. A velocidades más elevadas el flujo del aire que envuelve al ciclista y su montura se hace turbulento.
El número de Reynolds que señala la transición entre el régimen laminar y turbulento será, para v ≈ 5 m/s, y suponiendo que el ciclista y su bicicleta se puede representar por un cilindro de altura indefinida y de 0,60 m de diámetro.
NR = (2 · 0,60 m · 1,3 kg/m3 · 5 m/s) / 1,8 · 105 N/m2 · s
Para alejamos de estos escenarios, de fronteras inciertas y poco deseables, en las que se producen las vibraciones que perciben en ocasiones los ciclistas, cuando se desplazan a velocidades moderadas equipados con ropas de superficies muy lisas, se puede aumentar la rugosidad superficial de su vestimenta. Es lo que se pretende y se consigue, por ejemplo, con los hoyuelos característicos de las modernas pelotas de golf que incrementan su rugosidad superficial y aseguran el régimen turbulento del fluido que las envuelve, consiguiendo reducir significativamente las fuerzas aerodinámicas que se oponen a su movimiento.
Hasta ahora hemos supuesto que la bicicleta se desplazaba sobre una superficie perfectamente horizontal y hemos deducido las reacciones de apoyo, en posición estática y con el ciclista en movimiento. Las fuerzas que transmitiría un ciclista, hipotéticamente parado, en una rampa con una pendiente del p% se modifican en relación con las que se producen en un plano horizontal.
En el lenguaje cotidiano, la inclinación de carreteras, caminos o senderos se define por la pendiente, que es la tangente del ángulo que forma la rasante con la horizontal. La pendiente p, expresa, por tanto, la altura que se asciende o desciende por cada metro en planta recorrido. En una pendiente en subida del 10% se ascienden 10 cm por cada metro y en un kilómetro, 100 m.
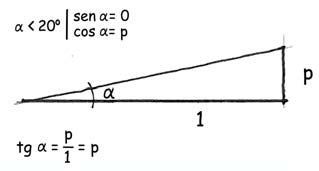
Como consecuencia de la pendiente p = tg α, el punto de encuentro, C, del vector que representa el peso del ciclista y su bicicleta, M · g, con la superficie de rodamiento horizontal se desplaza hacia la rueda trasera la magnitud
x = h · tg α = p · h
Si, sobre un plano horizontal, la distancia t0, del punto de encuentro C a la rueda trasera fuera de 40 cm, de 60 cm a la delantera y el centro de gravedad estuviese a un metro de altura, estos valores, en el caso del plano con 10% de pendiente, se convertirían en
tα = 40 – (10/100) · 100 = 40 – 10 = 30 cm
y
dα = 60 + 10 = 70 cm
con lo que variaría significativamente el reparto de peso entre las ruedas delanteras y traseras. Sobre una superficie horizontal las reacciones serían:
Rt = M · g · d / (r + d) = 60 / (40 + 60) · M · g = 0,60 M · g
Rd = 0,40 · M · g
mientras que en el caso de la pendiente p, pasarían a ser (sen α ≈ p y cos α ≈ 1)
Rtα = M · g · cos α · (dα + x) / (t + d) ≈ M · g · 70 / (40 + 60) = 0,70 M · g
Rdα = 0,30 · M · g
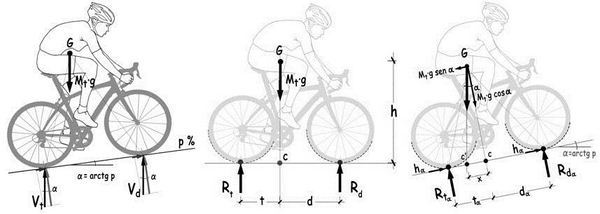
Además en el contacto de las ruedas con el pavimento se producirían unas fuerzas paralelas a la rasante de valor
Htα = Rtα · tg α = p · Rtα
Hdα = Rdα · tg α = p Rdα
cuya suma coincide, lógicamente, con el valor de p · M · g. Estas fuerzas, en subida, se oponen al movimiento y por lo tanto se añaden a las fuerzas motrices que necesita la bicicleta para desplazarse por carreteras llanas.
Para comprender bien la importancia de estas fuerzas, consideraremos un ciclista, que con su bicicleta pesa 800 N, tiene que subir una cuesta del 10% de diez kilómetros de longitud y, por tanto, salva un desnivel de 1.000 metros. Supongamos que la velocidad de desplazamiento en toda la ascensión sea de 4 m/s (14,4 km/h), y que, por consiguiente, necesitase
10.000 m / 4 m/s = 2.500 s (0,694 horas)
para completar la ascensión. Las fuerzas, paralelas a la pendiente, que intervienen en el movimiento, tendrán tres componentes:
• Fuerza equivalente a los rozamientos mecánicos y de los neumáticos con el pavimento, que a la moderada pero meritoria velocidad de 4 m/s, puede suponer 3 N.
• Fuerza aerodinámica, que suponiendo que no existe viento meteorológico, y considerando CD = 0,90 y A = 0,45 m2, valdría
FD = ½ · 0,90 · 1,3 kg/m3 · 0,45 m2 · (4 m/s)2 = 4,2 N
• Fuerza debida a la pendiente de la subida
FP = 0,10 · 800 = 80 N
En total,
FT = 3 + 4,2 + 80 = 87,2 N
Como sabe perfectamente cualquier ciclista, de las tres componentes, la debida a la pendiente es, con mucho, la más importante. Del orden del 92% del total en el ejemplo considerado. El ciclista con su pedaleo debe generar una fuerza de 87,2 N que iguale las anteriores y permita la velocidad constante de subida, de 4 m/s, que hemos supuesto. La potencia requerida para ello sería P = 87,2 N · 4 m/s = 348,8 W, a mantener durante los 2.500 segundos de duración de la ascensión; lo que solamente está al alcance de ciclistas profesionales en excelente estado de forma.
La energía restante, la que es necesaria para vencer los rozamientos y las fuerzas aerodinámicas, y que no se convierten en la energía potencial de la que el ciclista dispondrá para el descenso, se habrá perdido en forma de calor:
Ecalor = (3 + 4,2) N · 4 m/s · 2.500 s = 72.000 julios
Si suponemos, ahora, que se trata de descender por la misma carretera de montaña de diez kilómetros de longitud y con 10% dependiente continuada, en un trazado sin curvas, tendríamos que la inclinación produciría una fuerza favorable de 80 N (10% de 800 N) de las que habría que descontar 4 N debidos aproximadamente a los rozamientos, así como, las fuerzas aerodinámicas que se opondrían al movimiento y que crecerían con el cuadrado de la velocidad que fuese adquiriendo el ciclista en el descenso. El ciclista, tumbado sobre su bicicleta para reducir la superficie de exposición al viento y mejorar su coeficiente aerodinámico, aumentará progresivamente la velocidad, sin necesidad de pedalear, hasta alcanzar un valor tal que la fuerza aerodinámica se iguale con la debida a la pendiente (80 N) menos la estimada para los rozamientos (4 N), es decir 76 N. Suponiendo que, por la posición tumbada que adopten los ciclistas en estos descensos, el valor de CD se reduzca de 0,90 a 0,80 y la superficie expuesta de 0,45 m2 a 0,35 m2, tendríamos que la velocidad estable que alcanzaría el ciclista en el descenso sería tal que
½ · 0,80 · 1,3 · 0,35 · v2 = 76 N
y, en consecuencia,
v = [76 / (½ · 0,8 · 1,3 · 0,35)]½ = [76 / 0,182]½ = 20,4 m/s (73 km/h)
El descenso habría durado aproximadamente cinco veces menos que el ascenso y, teóricamente el ciclista, no habría necesitado aportar energía alguna. Metáfora de la vida.
Inicialmente, partiendo del reposo, la aceleración del ciclista sería
a = F / m = 76 N / (800 N / g) = 0,096 m/s2
un poco inferior al porcentaje de la pendiente, debido a los rozamientos. Progresivamente la aceleración se iría reduciendo hasta anularse, una vez alcanzada la velocidad de 20,4 m/s. El tiempo que tardaría en hacerlo sería inferior al minuto y la longitud recorrida no superaría los 500 m.

El frenado puede cambiar sustancialmente las fuerzas, tanto verticales como horizontales, que actúan sobre el tándem que forman la bicicleta y el ciclista. Provoca una deceleración en el movimiento y genera, por tanto, unas fuerzas de inercia que reducen su velocidad o pueden acabar anulándola. Por otra parte, un frenado brusco, puede hacer que deslicen las ruedas de las bicicletas, dejando de rodar, desequilibrando al ciclista. Por ello, para favorecer su equilibrio conviene activar prioritariamente el frenado de la rueda trasera, motivo por el que el freno correspondiente se suele situar a la derecha del manillar puesto que los usuarios diestros son mayoría. Los ciclistas zurdos suelen cambiar la posición de los frenos en el manillar.
Supongamos, a modo de referencia, que un ciclista circula a 10 m/s (36 km/h) y frena bruscamente, de manera que la bici se pare en 2 segundos. La deceleración media consiguiente sería
a = 10 m/s / 2 s = 5 m/s2 ≈ 0,5 · g.
Las fuerzas, en equilibrio, tendrán una resultante cuya línea de acción no debería sobrepasar el punto de contacto con el pavimento de la rueda delantera, para evitar el vuelco. De no ser así, la rueda trasera se levantaría, y todo el peso de la bicicleta y del ciclista se concentraría, como reacción de apoyo Rd, en la rueda delantera. Si suponemos que el centro de gravedad del conjunto de la bicicleta se sitúa a 1,20 m del nivel del suelo y su distancia horizontal al eje de la rueda delantera es de 0,80 m tendríamos el esquema aproximado de equilibrio representado en el gráfico adjunto.
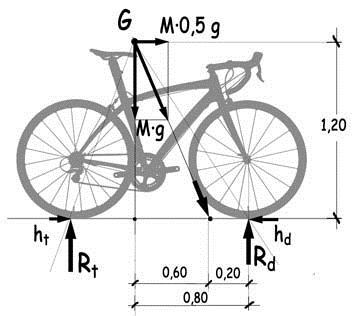
No hemos considerado en este ejercido elemental la fuerza aerodinámica que también interviene en el equilibrio durante el frenado. Como ya hemos visto, su valor para la velocidad supuesta de 10 m/s a la que se aplica el freno, es de unos 26,3 N, mientras que la fuerza de deceleración sería del orden de
(800 N / g) · 0,5 g = 400 N
muy superior. En términos cuantitativos, por tanto, no es relevante tomar aquella en consideración.
El elemental ejercicio, tal como se ha planteado, no es muy realista. Es probable que el rozamiento de las ruedas, que habrán dejado de girar con la aplicación brusca del freno, sea inferior al que necesitaría para producirse la fuerza teórica de deceleración de 400 N. No se produciría, por consiguiente, el vuelco por giro alrededor del punto de contacto de la rueda delantera con el pavimento.
Los vuelcos suelen ser consecuencia de impactos de la bicicleta con un obstáculo en la carretera, con el consiguiente destrozo en la rueda delantera debido al choque, que produciéndose en escasos instantes (el que tarda la rueda en destrozarse), habrá generado deceleraciones varias veces superiores a g, aceleración de la gravedad. En general, el frenado brusco de la bicicleta especialmente cuando se utiliza el freno delantero, provocaría el inmediato desplazamiento transversal de la rueda posterior y la caída del ciclista que en el golpe con el suelo y en su característico deslizamiento absorberá dolorosamente, la energía que hacía moverse a la bicicleta antes del frenado o del accidente. En las competiciones de motocicletas se aprecian con frecuencia este tipo de situaciones: vuelcos cuando se produce un choque y caídas, con aparatosos deslizamientos, debido a la incapacidad de las ruedas para generar los rozamientos necesarios para el equilibrio.
Simultáneamente a la aplicación de los frenos, el ciclista deja de pedalear y al hacerlo anula la fuerza motriz que provocaba el movimiento. Es evidente que, una bicicleta sobre una superficie de rodamiento horizontal puede llegar tranquilamente a pararse, sin aplicar los frenos a las ruedas, cuando el ciclista cesa el pedaleo. En estas circunstancias, las fuerzas horizontales que se opondrán al movimiento serían las equivalentes al conjunto de rozamientos de unos 3 o 4 newtons según la velocidad en cada instante, y la aerodinámica que iría rápidamente reduciéndose al disminuir la velocidad.
Los diagramas velocidad-tiempo de una bicicleta, que varía desplazándose a una velocidad constante, hasta su completa parada será la representada en el diagrama, para los dos casos extremos de aplicación brusca de los frenos o de ausencia de pedaleo.

El frenado brusco puede durar pocos segundos. Pero la aplicación progresiva de los frenos puede permitir que la rueda continúe girando y no se produzca el indeseable deslizamiento de las ruedas con el pavimento, preludio de inestabilidades y caídas laterales. Si se frena con suavidad aumentará el tiempo de parada, tal vez a unos 10 segundos, dependiendo de la velocidad inicial, mientras que la parada completa de una bicicleta sin utilización de frenos puede durar de 20 a 30 segundos, con un recorrido de unos 100 o 150 metros; cifras que serán tanto menores cuando más elevados sean los rozamientos internos y de las ruedas con el pavimento.
Para disponer de algunos órdenes de magnitud en relación con los conceptos asociados al frenado, supondremos una bicicleta de frenos tradicionales con los que se aplica la fuerza de frenado en la superficie lateral de las llantas. Supongamos que el ciclista circula a la velocidad constante de 10 m/s: la fuerza aerodinámica, considerando A = 0,45 m2, será
Fa = ½ · 0,90 · 1,3 · 0,45 · 102 = 26 N
Añadiendo 4 N por rozamientos equivalentes, tendremos la fuerza motriz de
Hm = 26 N + 4 N = 30 N
que estaría igualmente distribuida entre las dos ruedas.
Para que se inicie la deceleración por frenado, la fuerza inicial aplicada por las pastillas de los frenos a la llanta de las ruedas debería ser superior a los 15 N por rueda, y tanto mayor cuanto más brusca sea la frenada y menor el tiempo requerido para parar la bicicleta.
A medida que la bici reduzca su velocidad, la fuerza aerodinámica disminuirá rápidamente, al variar con v2. De manera que si se mantiene la fuerza de frenado la deceleración se irá haciendo mayor, o se mantendrá igual si se reduce progresivamente.
Si aplicamos brusca y simultáneamente en las dos ruedas, una fuerza de frenado de 130 N, por ejemplo, tendríamos que, inicialmente la deceleración, ad, sería
130 N – 30 N = (800/g) · ad
130 N, fuerza frenado
30 N, fuerza motriz (para v = 10 m/s)
800/g, masa del ciclista y el de la bicicleta
ad, deceleración
esto es
ad = (100/800) · g = 0,125 · g ≈ 1,25 m/s2
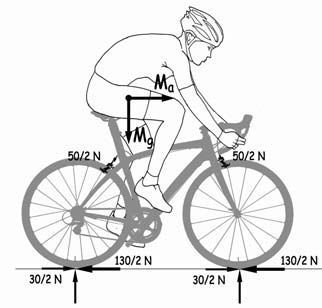
Suponiendo que se mantuviese esta deceleración inicial, porque la fuerza de frenada se fuese paulatinamente reduciendo, la bicicleta tardaría en pararse
t = 10 m/s / 1,25 m/s2 = 8 s
En este caso, el equilibrio de fuerzas de la rueda delantera, por ejemplo, será la representada en el esquema siguiente.
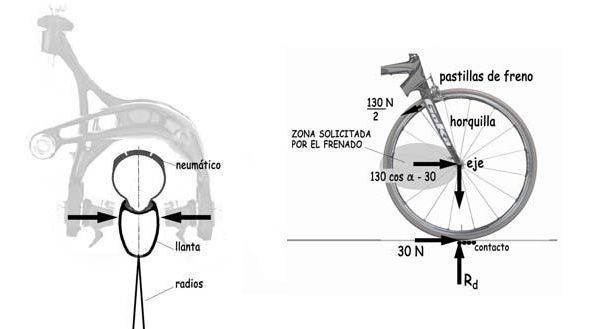
Las zapatas del freno provocarán unas compresiones transversales en la llanta, y consiguientemente, producirán las fuerzas de rozamiento necesarias para la frenada. Suponiendo un coeficiente de rozamiento de 0,50 con llantas secas, las fuerzas transversales de compresión serían, en el caso considerado, de 260 N = 130 N / 0,5.
La transferencia de las fuerzas de frenado hasta el punto de contacto de la rueda con el pavimento provocará la deformación de la llanta y de los radios de la bicicleta. Los más próximos a la horizontal, en la parte posterior del eje, serán los que se activarán prioritariamente para que se produzca dicha transferencia.
Si suponemos ahora que el frenado se realiza bruscamente, para que la bicicleta se pare, por ejemplo, en un solo segundo, la deceleración sería
a = 10 m/s / 1 s = 10 m/s2 ≈ g
La longitud de frenado consiguiente valdría,
Lf ≈ ½ · 10 m/s / 1 s = 5 m
y la fuerza de frenado tendría que valer 830 N para que se cumpla la igualdad
830 N – 30 N = (800 / g) · ad
Por tanto, ad sería igual a g.
Se trata de una fuerza considerable que provocaría la deformación de las ruedas y el teórico vuelco de la bicicleta, puesto que la resultante de fuerzas intersectaría al pavimento por delante de su punto de contacto con la rueda delantera.
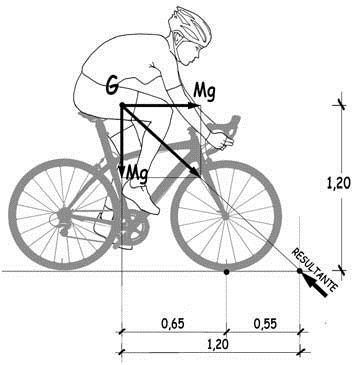
En vista de ello, resulta que el tiempo mínimo de frenado para que la deceleración no sobrepasase el valor de
(0,65 / 1,20) · g = 0,54 · g
tendría que ser de
tf = 1/(1 – 0,54) = 2,17 s
y la longitud consiguiente de parada
Lf = ½ · 10 m/s · 2,17 s = 10,85 m
En estas circunstancias, instintivamente, el ciclista se acomodará a la bici para bajar el centro de gravedad y desplazarlo hacia atrás. Además como la fuerza aerodinámica se reducirá notablemente al descender la velocidad, las fuerzas de frenado también podrán reducirse, lo que mejoraría la situación. Por otra parte, hay que recalcar que la fuerza horizontal nunca podrá superar a la del rozamiento por deslizamiento de la rueda, que habrá dejado de girar. De no ser así la bici deslizaría y el modelo de comportamiento del ciclista y de la bicicleta se haría más complejo. La situación será todavía más exigente y determinante, en el caso del frenado, en un sprint por ejemplo, a velocidades que pueden aproximarse a los 20 m/s.
Por otra parte, durante el hipotético frenado que estamos considerando (v = 10 m/s, t = 1 s) la potencia de frenado consiguiente sería de
P = 830 N · ½ · 10 m/s = 4.150 W
y la energía absorbida por la bicicleta sería
E= 4.150 W · 1 s = 4.150 julios
Es evidente que el frenado es uno de los escenarios en que los esfuerzos pueden ser los más importantes y que pueden determinar el dimensionamiento de la estructura de la bicicleta. Es una situación, por otra parte, en la que entra en juego el rozamiento estático de la rueda con el pavimento. En el cuadro siguiente en la primera columna se incluyen algunos valores de los coeficientes de rozamiento estático que suelen considerarse en las evaluaciones para diferentes superficies de rodadura y, en la segunda, los coeficientes de rozamiento por rodadura considerablemente más bajos.
|
Superficie de rodadura |
Coeficiente de rozamiento estático |
Coeficiente de rozamiento a la rodadura |
|---|---|---|
|
Hormigón o asfalto en seco |
0,8-0,9 |
0,014 |
|
Hormigón o asfalto, húmedos |
0,4-0,7 |
0,014 |
|
Grava |
0,6-0,7 |
0,02 |
|
Arena |
0,3-0,4 |
0,14-0,3 |
|
Hielo |
0,1-0,2 |
0,014 |
La bicicleta y el ciclista nunca permanecen en un plano perfectamente vertical, tal como se ha considerado hasta ahora. Aun cuando el trazado de la carretera sea perfectamente rectilíneo, y quiera serlo también el de la bicicleta, el ciclista se moverá transversalmente. Casi imperceptiblemente, en general. Pero a un observador atento no le pasa desapercibido el desplazamiento lateral, a derecha y a izquierda, del cuerpo del ciclista, al ritmo que marca su pedaleo. Aun cuando, visto de lado, su cuerpo, inclinado sobre el manillar, parezca transversalmente inmóvil. Es, también, frecuente ver al ciclista de pie y balanceándose sobre los pedales, moviendo ostensiblemente su cuerpo y su bicicleta, como sucede entre quienes compiten en una llegada al «sprint», o al cambiar de ritmo para iniciar una escapada, o al ascender un repecho o incluso para relajar los músculos.
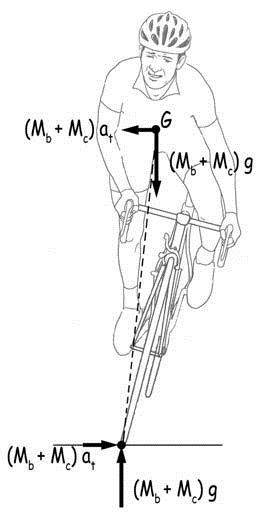
El esquema adjunto nos muestra una imagen muy característica. El ciclista, levantado del sillín, cargando sobre uno de los pedales, para impulsar su bicicleta. Se inclina primero hacia un lado y luego, al cargar sobre el otro pedal, se mueve hacia el otro. En este rítmico proceso, que se repite con la frecuencia del pedaleo, se generan fuerzas de inercia consecuencia de la aceleración transversal del ciclista y de la bicicleta. Y el conjunto de dichas fuerzas transversales y verticales deberá, también, estar, como siempre, en equilibrio con las reacciones de apoyo, que nacerán, como consecuencia de estos movimientos, en el contacto de las ruedas con el pavimento. La resultante de las fuerzas verticales debidas a la aceleración de la gravedad y a la del movimiento vertical, av, M · (g + av), y de las transversales M · at se equilibrarán con las reacciones de apoyo en el contacto de las ruedas con la carretera. Por simplicidad, no estamos considerando las fuerzas, de inercia o aerodinámicas, longitudinales.
El desplazamiento transversal del centro de gravedad del ciclista y su montura tendrá un valor máximo, en el que la velocidad transversal se anulará y cambiará de signo, cuando el movimiento del ciclista modifique su sentido.
Suponiendo que las huellas de las ruedas de la bicicleta dibujasen una línea recta (de ello se trata con más detalle en el apartado 7.2 «La geometría del desplazamiento»), los desplazamientos, velocidades y aceleraciones transversales del centro de gravedad del conjunto podrían representarse con curvas de geometría senoidal, que cortarían al eje del trazado en puntos definidos por el ritmo del pedaleo. Para cadencias de 90 pedaladas por minuto —periodo T = 60/90 = 0,66— los nodos de las curvas se producirán cada T/2 = 0,33 segundos.
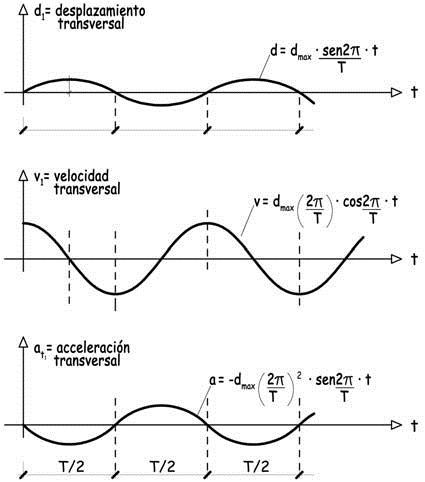
Las expresiones supuestas para las curvas de desplazamientos, velocidades y aceleraciones transversales en función del tiempo coinciden con las de los movimientos vibratorios armónicos de un péndulo, o de una masa suspendida de un muelle a la que se ha desplazado de su posición original.
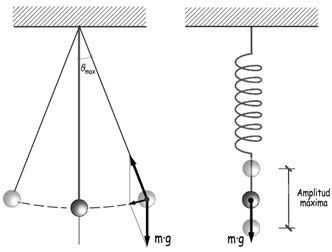
La fuerza de inercia asociada a la aceleración transversal, at, puede interpretarse como la correspondiente a la fuerza centrífuga generada en un movimiento curvilíneo
Fc = m · at = m · v2 / R
siendo R el radio de curvatura del movimiento transversal del centro de gravedad del conjunto bicicleta-ciclista y, v, la velocidad de desplazamiento longitudinal.
En un recorrido por una carretera sin curvas, la aceleración transversal máxima sería muy reducida, y la inclinación correspondiente del ciclista que asegura el equilibrio transversal, también. Si suponemos, a modo de ejemplo, que la velocidad longitudinal del ciclista es de 12 m/s (42,4 km/h), su cadencia de 90 pedaladas por minuto y su desplazamiento transversal máximo de 2 cm la aceleración transversal máxima sería (para t = T/4)
at,max = –dmax · (2 · π / T)2 · sen (2 · π / T · t) = –2 cm · (2 · π / 0,66)2 · sen (π / 2) = –180 cm/s2 = –0,18 · g
El cuerpo del ciclista se inclinaría para contribuir al equilibrio de esta fuerza centrífuga.
Hay que tener en cuenta, además, que en descensos con curvas en herradura de radios muy pequeños, el ciclista casi llega a parar la bicicleta, se inclina considerablemente e incluso suele extender hacia fuera la rodilla próxima al interior de la curva para generar una fuerza de inercia hacia adentro que le ayude a encontrar el equilibrio dinámico. En estas situaciones el valor del peralte de la curva determina la velocidad máxima a la que se puede trazar la curva, lo que depende asimismo del coeficiente de rozamiento entre la rueda que tiende a desplazarse transversalmente y el pavimento. Si éste está mojado o cubierto de gravilla, el rozamiento disminuye significativamente y el riesgo de caídas se incrementa a pesar de que el ciclista reduzca su velocidad. Si, por ejemplo, el ciclista y su bicicleta tuviesen que tomar una curva de 5 m de radio a una velocidad de 3 m/s (10,8 km/h), la fuerza centrífuga sería
Fc = M · v2 / R = M · (3 m/s)2 / 5 m = M · 32 / 5 = M · 1,8 m/s2 = M · 0,18 · g
El equilibrio dinámico transversal en este caso estaría reflejado en el esquema.
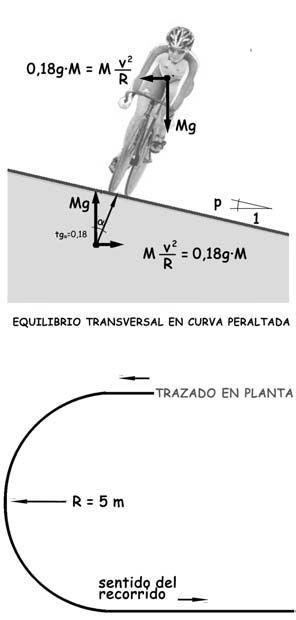
Si la carretera estuviese peraltada con una pendiente transversal del 18%, la resultante del peso y de la fuerza centrífuga, serían perpendiculares al pavimento y no aparecerían fuerzas transversales a contrarrestar por el rozamiento entre las ruedas y el suelo. Cuando el peralte es inferior a la inclinación de la resultante de las dos fuerzas, el equilibrio transversal exigiría la contribución del rozamiento, y la velocidad del ciclista al tomar esta curva estaría determinada por la condición de que la fuerza transversal correspondiente no superase la realmente disponible.
En el caso del ciclismo en pista, la superficie del pavimento es muy lisa para reducir al máximo el rozamiento a la rodadura, lo que exige peraltes muy pronunciados en las zonas curvas de manera que la inclinación de la bicicleta hace posible el equilibrio de fuerzas, sin necesidad de recurrir al rozamiento. En cambio, cuando un ciclista pedalea levantado y se mueve haciendo vaivenes sobre una superficie sin peralte, es imprescindible que exista rozamiento suficiente entre la rueda de la bicicleta y el pavimento para que se pueda generar la reacción horizontal de apoyo. Cuando no sucede así la bicicleta derrapará y el ciclista caerá lateralmente.