A pesar de tan sustantivas diferencias existen pautas de comportamiento que son comunes a todas las estructuras. Así ocurre con el universal criterio de equilibrio: la estructura globalmente y todas y cada una de las partes que virtualmente podemos aislar del conjunto, deben cumplir tan ineludible condición.
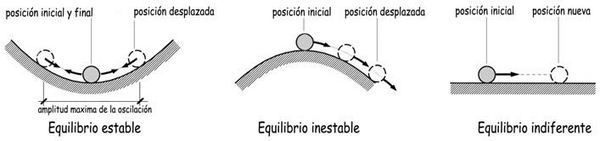
A los más privilegiados de mi generación nos explicaron en alguna dase de física de un bachillerato ya remoto, cuando éramos más o menos quinceañeros, que existían tres clases de equilibrio: el estable, el inestable y el indiferente.
Es probable que, para inculcarnos estos conceptos, el paciente profesor nos dibujase en una de aquellas enlutadas pizarras que por entonces presidían nuestras aulas, una bola situada en el punto más bajo de una superficie cóncava que tras ser ligeramente desplazada de su posición inicial de equilibrio, tras oscilar un cuantas veces con amplitudes progresivamente decrecientes, volvía a su posición inicial. Era una imagen característica del equilibrio estable.
Si la hipotética bola se situaba después en la cumbre de una superficie convexa sobre la que podía mantenerse «milagrosamente» quieta, cualquier desplazamiento, por mínimo que fuese, provocaba su movimiento irreversible y la bola no podía volver a su posición inicial. Elemental representación del equilibrio inestable. Si la misma bola se desplazaba sobre un plano perfectamente horizontal quedaba inmóvil en la nueva posición, lo que expresaba gráficamente el equilibrio indiferente.

Tuvieron que pasar muchos años para que quien esto escribe comprendiera mejor el significado de aquellos símbolos que habían quedado tranquilamente posados, y casi olvidados, en su memoria, y se atreviese a reelaborar los conceptos que, imprecisamente le había explicado aquel buen profesor de física que contribuyó a despertar mi perdurable interés por la disciplina que enseñaba.
La resultante de las acciones que actúan sobre un cuerpo o sobre una parte de él, debe ser igual y contraria a la resultante de las reacciones asociadas. Cuando las acciones, y consiguientemente las reacciones, varían con el tiempo, al equilibrio que debe existir entre unas y otras, y que irá cambiando a cada instante, se le puede considerar como dinámico. Y, por simplicidad, se puede aplicar también dicha denominación al equilibrio de todos los cuerpos en movimiento, aun cuando sean uniformes y no generen aceleraciones ni fuerzas de inercia. Por el contrario cuando un cuerpo no se mueve y las acciones y reacciones que actúan sobre él no varían con el tiempo, podemos considerar que estamos en un caso de «equilibrio estático».
En consecuencia, al equilibrio estable, con toda su aureola de prestigio, se le podría asociar con lo estático, con lo inmóvil, con la ausencia de vida. Por el contrario, al desasosegante equilibrio inestable, que provoca un rechazo social generalizado como todo cuanto es inestable e incierto, se le puede relacionar con lo dinámico, con el movimiento que es manifestación de vida. La posición, por ejemplo, de los brazos de una bailarina que gira como una peonza, asegura su equilibrio dinámico, siempre inestable, porque cambia a cada instante.
Y continuando con esta poco rigurosa pero expresiva analogía, nos queda, finalmente, el equilibrio indiferente que no es manifestación de vida ni expresión de su ausencia. Es la nada, lo que se denomina «pasotismo» en el lenguaje coloquial de hoy.
El mundo de la bicicleta, con el tiempo, ha ido acuñando expresiones que, a modo de proverbios, describen con precisión no exenta de encanto este dinamismo esencial. Así algunos atribuyen a Einstein aquel que asegura que la vida es como la bicicleta: si dejas de pedalear te caes. O aquel otro, tal vez de cosecha propia, que dice que cuando vas en bicicleta y parece que no sopla el viento es que sopla a favor. Y cuando sopla en contra hay que remar. Los pedales son los remos de la bicicleta.

Einstein montando en bicicleta.