El número áureo

Los brazos de una estrella de mar, la espiral de una caracola y los pétalos de una rosa tienen algo en común con el Partenón de Atenas y las pirámides de Giza: todos están estructurados alrededor de un número que se conoce como áureo (o fi, en honor al escultor griego Fidias, que lo utilizó artísticamente en sus obras). En la anotación matemática, fi se representa φ y corresponde, aproximadamente, a 1,618; no obstante, se trata de un número irracional, lo que significa que sus decimales continúan indefinidamente sin repetirse jamás.

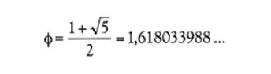
Así es como se calcula fi. Se dice que los dos lados de un rectángulo están en proporción áurea si la relación del lado más corto (C) y el más largo (L) es igual a la del lado largo y la suma de ambos.

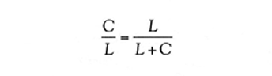
Si despejamos L utilizando la ecuación cuadrática, el resultado es el siguiente:

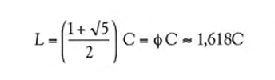
Los objetos que se construyen utilizando la razón áurea resultan agradables a la vista y aparecen sin cesar en el arte y en la naturaleza.

Examine los tres objetos que se muestran a continuación:

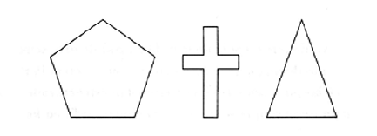
En el pentágono regular, los cinco lados tienen la misma longitud, por eso se dice que están en proporción áurea con las cinco diagonales que unen los puntos. El antiguo filósofo griego Pitágoras estaba tan impresionado con el pentágono regular que lo escogió como símbolo secreto de su escuela matemática, que adoraba a los números.

El primero en analizar la cruz fue el psicólogo alemán Gustav Fechner, que se dio cuenta de que la parte superior e inferior del brazo principal están en una perfecta proporción áurea.

En el triángulo, los lados más largos están en proporción áurea con el corto.