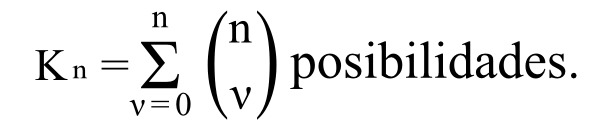
1^[60] El mundo es todo lo que es el caso.

1.1 El mundo es la totalidad de los hechos, no de las cosas.

1.11 El mundo viene determinado por los hechos, y por ser éstos todos los hechos.

1.12 Porque la totalidad de los hechos determina lo que es el caso y también todo cuanto no es el caso.

1.13 Los hechos en el espacio lógico son el mundo.

1.2 El mundo se descompone en hechos.

1.21 Algo puede ser el caso o no ser el caso, y todo lo demás permanecer igual.

2 Lo que es el caso, el hecho, es el darse efectivo de estados de cosas.

2.01 El estado de cosas es una conexión de objetos (cosas).

2.011 Poder ser parte integrante de un estado de cosas es esencial a la cosa.

2.012 En la lógica nada es casual: si la cosa puede ocurrir en el estado de cosas, la posibilidad del estado de cosas tiene que venir ya prejuzgada en la cosa.

2.0121 Parecería algo así como un azar que a la cosa capaz de darse de modo efectivo por sí misma le correspondiera posteriormente un estado de cosas.

Que las cosas puedan ocurrir en estados de cosas, es algo que debe radicar ya en ellas. (Algo lógico no puede ser meramente posible. La lógica trata de cualquier posibilidad y todas las posibilidades son sus hechos.)

Al igual que no podemos en absoluto representarnos objetos espaciales fuera del espacio, ni temporales fuera del tiempo, tampoco podemos representarnos objeto alguno fuera de la posibilidad de su conexión con otros.

Si puedo representarme el objeto en la trama del estado de cosas, no puedo representármelo fuera de la posibilidad de esa trama.

2.0122 La cosa es independiente en la medida en que puede ocurrir en todos los posibles estados de cosas, pero esta forma de independencia es una forma de interpelación con el estado de cosas, una forma de dependencia. (Es imposible que las palabras aparezcan de dos modos diferentes, solas y en la proposición.)

2.0123 Si conozco el objeto, conozco también todas las posibilidades de su ocurrencia en estados de cosas. (Cualquier posibilidad de este tipo debe radicar en la naturaleza del objeto.)

No cabe encontrar posteriormente una nueva posibilidad.

2.01231 Para conocer un objeto, no tengo ciertamente que conocer sus propiedades externas, pero sí debo conocer todas sus propiedades internas.

2.0124 Dados todos los objetos, vienen dados también con ello todos los posibles estados de cosas.

2.013 Cualquier cosa está, por así decirlo, en un espacio de posibles estados de cosas. Puedo representarme vacío ese espacio, pero no la cosa sin el espacio.

2.0131 El objeto espacial debe encontrarse en el espacio infinito. (El punto espacial es un lugar argumental.)

La mancha en el campo visual no tiene, ciertamente, por qué ser roja, pero ha de tener un color: tiene, por así decirlo, el espacio cromático en torno suyo. El tono ha de tener una altura, el objeto del sentido del tacto una dureza, etc.

2.014 Los objetos contienen la posibilidad de todos los estados de cosas.

2.0141 La forma del objeto es la posibilidad de su ocurrencia en estados de cosas.

2.02 El objeto es simple.

2.0201 Cualquier enunciado sobre complejos puede descomponerse en un enunciado sobre sus partes integrantes y en aquellas proposiciones que describen completamente los complejos.

2.021 Los objetos forman la sustancia del mundo. Por eso no pueden ser compuestos.

2.0211 Si el mundo no tuviera sustancia alguna, el que una proposición tuviera sentido dependería de que otra proposición fuera verdadera.

2.0212 Sería entonces imposible pergeñar una figura del mundo (verdadera o falsa).

2.022 Es manifiesto que por muy diferente del real que se piense un mundo ha de tener algo en común con él —una forma.

2.023 Lo que constituye esta forma fija son precisamente los objetos.

2.0231 La substancia del mundo sólo puede determinar una forma y no propiedades materiales. Porque éstas sólo vienen a ser representadas por las proposiciones, sólo vienen a ser formadas por la configuración de los objetos.

2.0232 Dicho sea incidentalmente, los objetos son incoloros.

2.0233 Dos objetos de la misma forma lógica sólo se diferencian entre sí —independientemente de sus propiedades externas— por el hecho de ser diferentes.

2.02331 O bien una cosa tiene propiedades que ninguna otra posee, en cuyo caso cabe distinguirla sin más de las otras mediante una descripción y remitir a ella; o bien, por el contrario, hay varias cosas que tienen todas sus propiedades en común, en cuyo caso es absolutamente imposible señalar una de ellas.

Porque si la cosa no viene distinguida por nada, entonces yo no puedo distinguirla, dado que si no ya estaría, en efecto, distinguida.

2.024 La substancia es lo que persiste independientemente de lo que es el caso.

2.025 Es forma y contenido.

2.0251 Espacio, tiempo y color (cromaticidad) son formas de los objetos.

2.026 Sólo si hay objetos puede haber una forma fija del mundo.

2.027 Lo fijo, lo persistente y el objeto son uno y lo mismo.

2.0271 El objeto es lo fijo, persistente; la configuración es lo cambiante, inestable.

2.0272 La configuración de los objetos forma el estado de cosas.

2.03 En el estado de cosas los objetos están unidos entre sí como los eslabones de una cadena.

2.031 En el estado de cosas los objetos se comportan unos con otros de un modo y manera determinados.

2.032 La estructura del estado de cosas es el modo y manera como los objetos se interrelacionan en él.

2.033 La forma es la posibilidad de la estructura.

2.034 La estructura del hecho viene constituida por las estructuras de los estados de cosas.

2.04 La totalidad de los estados de cosas que se dan efectivamente es el mundo.

2.05 La totalidad de los estados de cosas que se dan efectivamente determina también qué estados de cosas no se dan efectivamente.

2.06 El darse y no darse efectivos de estados de cosas es la realidad.

(Llamamos hecho positivo al darse efectivo de estados de cosas; al no darse efectivo, hecho negativo.)

2.061 Los estados de cosas son independientes unos de otros.

2.062 Del darse o no darse efectivos de un estado de cosas no puede deducirse el darse o no darse efectivos de otro.

2.063 La realidad total es el mundo.

2.1 Nos hacemos figuras de los hechos.

2.11 La figura representa el estado de cosas en el espacio lógico, el darse y no darse efectivos de estados de cosas.

2.12 La figura es un modelo de la realidad.

2.13 A los objetos corresponden en la figura los elementos de la misma.

2.131 Los elementos de la figura hacen en ella las veces de los objetos.

2.14 La figura consiste en que sus elementos se interrelacionan de un modo y manera determinados.

2.141 La figura es un hecho.

2.15 Que los elementos de la figura se comporten unos con otros de un modo y manera determinados, representa que las cosas se comportan así unas con otras.

Esta interrelación de los elementos de la figura se llama su estructura y la posibilidad de la misma, su forma de figuración.

2.151 La forma de figuración es la posibilidad de que las cosas se interrelacionen al igual que los elementos de la figura.

2.1511 La figura está enlazada así con la realidad; llega hasta ella.

2.1512 Es como un patrón de medida aplicado a la realidad.

2.15121 Sólo los puntos extremos de las marcas tocan el objeto a medir.

2.1513 Así pues, de acuerdo con esta concepción, a la figura pertenece también la relación figurativa que la convierte en figura.

2.1514 La relación figurativa consiste en las coordinaciones entre los elementos de la figura y los de las cosas.

2.1515 Estas coordinaciones son, por así decirlo, los tentáculos de los elementos de la figura con los que ésta toca la realidad.

2.16 Para ser figura, pues, el hecho ha de tener algo en común con lo figurado.

2.161 En la figura y en lo figurado tiene que haber algo idéntico en orden a que aquélla pueda siquiera ser figura de esto.

2.17 Lo que la figura ha de tener en común con la realidad para poder figurarla a su modo y manera —correcta o falsamente— es su forma de figuración.

2.171 La figura puede figurar cualquier realidad cuya forma tenga.

La figura espacial todo lo espacial, la cromática, todo lo cromático, etc.

2.172 Pero la figura no puede figurar su forma de figuración; la ostenta.

2.173 La figura representa su objeto desde fuera (su punto de vista es su forma de representación); por ello representa su objeto correcta o falsamente.

2.174 La figura no puede, sin embargo, situarse fuera de su forma de representación.

2.18 Lo que cualquier figura, sea cual fuere su forma, ha de tener en común con la realidad para poder siquiera —correcta o falsamente— figurarla, es la forma lógica, esto es, la forma de la realidad.

2.181 Si la forma de la figuración es la forma lógica, la figura se llama la figura lógica.

2.182 Cualquier figura es también una figura lógica. (Por el contrario, no toda figura es, pongamos por caso, espacial.)

2.19 La figura lógica puede figurar el mundo.

2.2 La figura tiene en común con lo figurado la forma lógica de la figuración.

2.201 La figura figura la realidad en la medida en que representa una posibilidad del darse y no darse efectivos de estados de cosas.

2.202 La figura representa un posible estado de cosas en el espacio lógico.

2.203 La figura contiene la posibilidad del estado de cosas que representa.

2.21 La figura concuerda o no con la realidad; es correcta o incorrecta, verdadera o falsa.

2.22 La figura representa lo que representa, independientemente de su verdad o falsedad, por la forma de la figuración.

2.221 Lo que la figura representa es su sentido.

2.222 Su verdad o falsedad consiste en el acuerdo o desacuerdo de su sentido con la realidad.

2.223 Para reconocer si la figura es verdadera o falsa, tenemos que compararla con la realidad.

2.224 Por la figura sólo no cabe reconocer si ella es verdadera o falsa.

2.225 No existe una figura verdadera a priori.

3 La figura lógica de los hechos es el pensamiento.

3.001 «Un estado de cosas es pensable» quiere decir: Podemos hacernos una figura de él.

3.01 La totalidad de los pensamientos verdaderos es una figura del mundo.

3.02 El pensamiento contiene la posibilidad del estado de cosas que piensa. Lo que es pensable es también posible.

3.03 No podemos pensar nada ilógico, porque de lo contrario tendríamos que pensar ilógicamente.

3.031 Se dijo en otro tiempo que Dios podría crearlo todo a excepción de cuanto fuera contrario a las leyes lógicas. De un mundo «ilógico» no podríamos, en rigor, decir qué aspecto tendría.

3.032 Representar en el lenguaje algo «que contradiga la lógica» es cosa tan escasamente posible como representar en la geometría mediante sus coordenadas una figura que contradiga las leyes del espacio; o dar las coordenadas de un punto que no existe.

3.0321 Podemos sin duda representar espacialmente un estado de cosas que vaya contra las leyes de la física, pero no uno que vaya contra las de la geometría.

3.04 Un pensamiento correcto a priori sería un pensamiento tal que su posibilidad condicionaría su verdad.

3.05 Sólo podríamos saber a priori que un pensamiento es verdadero si por el pensamiento mismo (sin objeto de comparación) resultara recognoscible su verdad.

3.1 En la proposición se expresa sensoperceptivamente el pensamiento.

3.11 Usamos el signo sensoperceptible (signo sonoro o escrito, etc.) de la proposición como proyección del estado de cosas posible.

El método de proyección es el pensar el sentido de la proposición.

3.12 Al signo mediante el que expresamos el pensamiento le llamo el signo proposicional. Y la proposición es el signo proposicional en su relación proyectiva al mundo.

3.13 A la proposición pertenece todo cuanto pertenece a la proyección; pero no lo proyectado.

Así pues, la posibilidad de lo proyectado, pero no esto mismo.

En la proposición, por tanto, aún no viene contenido su sentido, pero sí la posibilidad de expresarlo. («El contenido de la proposición» quiere decir el contenido de la proposición con sentido.)

En la proposición viene incluida la forma de su sentido, pero no su contenido.

3.14 El signo proposicional consiste en que sus elementos, las palabras, se comportan en él unos con otros de un modo y manera determinados.

El signo proposicional es un hecho.

3.141 La proposición no es un conglomerado de palabras. (Como tampoco el tema musical un conglomerado de tonos.)

La proposición es articulada.

3.142 Sólo hechos pueden expresar un sentido; una clase de nombres no puede.

3.143 Que el signo proposicional es un hecho es algo que viene velado por la forma expresiva corriente de la escritura o de la imprenta.

Porque en la proposición impresa, por ejemplo, el signo proposicional no aparece como esencialmente distinto de la palabra.

(Así fue posible que Frege llamara a la proposición un nombre compuesto.)

3.1431 Muy clara resulta la esencia del signo proposicional cuando, en lugar de imaginárnoslo compuesto de signos escritos, nos lo imaginamos compuesto de objetos espaciales (como, por ejemplo, mesas, sillas, libros).

La recíproca posición espacial de estas cosas expresa entonces el sentido de la proposición.

3.1432 No: «El signo complejo “aRb” dice que a está en la relación R con b» sino: Que “a” está en cierta relación con “b” dice que aRb.

3.144 Pueden describirse estados de cosas, no nombrarse. (Los nombres semejan puntos, las proposiciones flechas, tienen sentido.)

3.2 El pensamiento puede expresarse en la proposición de un modo tal que a los objetos del pensamiento correspondan elementos del signo proposicional.

3.201 Llamo «signos simples» a estos elementos, y a la proposición, «completamente analizada».

3.202 Los signos simples usados en la proposición se llaman nombres.

3.203 El nombre significa el objeto. El objeto es su significado. («A» es el mismo signo que «A».)

3.21 A la configuración del signo simple en el signo proposicional corresponde la configuración de los objetos en el estado de cosas.

3.22 En la proposición el nombre hace las veces del objeto.

3.221 A los objetos sólo puedo nombrarlos. Los signos hacen las veces de ellos. Sólo puedo hablar de ellos, no puedo expresarlos. Una proposición sólo puede decir cómo es una cosa, no lo que es.

3.23 La exigencia de la posibilidad de los signos simples es la exigencia de la precisión del sentido.

3.24 La proposición que trata del complejo está en relación interna con la proposición que trata de su parte integrante.

El complejo sólo puede venir dado por su descripción, y ésta será acertada o no. La proposición en la que se habla de un complejo no será absurda si éste no existe, será simplemente falsa.

Que un elemento proposicional designe un complejo es cosa que puede verse a partir de su carácter indeterminado en las proposiciones en las que aparece. Sabemos que no todo está aún determinado por esta proposición. (El signo de generalidad contiene ciertamente una figura primitiva.)

La contracción del símbolo de un complejo en un símbolo simple puede ser expresada mediante una definición.

3.25 Hay un análisis completo, y sólo uno, de la proposición.

3.251 La proposición expresa de un modo determinado y claramente especificable lo que expresa: la proposición es articulada.

3.26 El nombre no puede ya descomponerse más por definición alguna: es un signo primitivo.

3.261 Todo signo definido designa mediante los signos por los que fue definido; y las definiciones señalan el camino.

Dos signos, un signo primitivo y otro definido por signos primitivos, no pueden designar del mismo modo y manera. Los nombres no se pueden descomponer por definiciones. (Ningún signo que esté aislado tiene significado de forma independiente.)

3.262 Lo que no alcanza a expresarse en los signos es cosa que muestra su uso. Lo que los signos tragan es cosa que expresa su uso.

3.263 Los significados de los signos primitivos pueden ser explicados mediante aclaraciones. Aclaraciones son proposiciones que contienen signos primitivos. Sólo pueden ser, pues, comprendidas si los significados de estos signos son ya conocidos.

3.3 Sólo la proposición tiene sentido; sólo en la trama de la proposición tiene un nombre significado.

3.31 A cualquier parte de la proposición que caracterice su sentido la llamo una expresión (un símbolo). (La proposición misma es una expresión.)

Expresión es todo lo que, esencial para el sentido de la proposición, pueden tener en común entre sí las proposiciones.

La expresión caracteriza una forma y un contenido.

3.311 La expresión presupone las formas de todas las proposiciones en las que puede ocurrir. Es el distintivo característico común de una clase de proposiciones.

3.312 Viene, pues, representada por la forma general de las proposiciones que caracteriza.

Y, ciertamente, en esta forma la expresión será constante, y todo lo demás variable.

3.313 La expresión es representada, pues, mediante una variable cuyos valores son las proposiciones que contienen la expresión.

(En caso límite, la variable se convierte en constante, la expresión en proposición.)

Llamo a una variable así «variable proposicional».

3.314 La expresión sólo tiene significado en la proposición. Cualquier variable puede concebirse como variable proposicional.

(También el nombre variable.)

3.315 Si transformamos una parte integrante de una proposición en una variable, hay entonces una clase de proposiciones que son los valores todos de la proposición variable así surgida. Esta clase todavía depende, en general, de lo que, tras acuerdo arbitrario, mentemos con partes de aquella proposición. Pero si transformamos en variables todos aquellos signos cuyo significado fue fijado arbitrariamente, sigue habiendo aún una clase así. Sólo que ésta no depende ya de acuerdo alguno, sino únicamente de la naturaleza de la proposición. Corresponde a una forma lógica —a una figura lógica primitiva.

3.316 Qué valores puede asumir la variable proposicional es algo que se determina.

La determinación de los valores es la variable.

3.317 La determinación de los valores de las variables preposicionales es la especificación de las proposiciones cuyo distintivo común es la variable.

La determinación es una descripción de estas proposiciones.

La determinación tratará, pues, sólo de símbolos, no de su significado.

Y sólo esto es esencial a la determinación, que sólo es una descripción de símbolos y no dice nada sobre lo designado.

Cómo acontece la descripción de las proposiciones, es cosa inesencial.

3.318 Concibo la proposición —igual que Frege y Russell— como función de las expresiones contenidas en ella.

3.32 El signo es lo sensorialmente perceptible en el símbolo.

3.321 Dos símbolos distintos pueden tener, pues, en común el signo (signo escrito o sonoro, etc.) —designan entonces de modo y manera distintos.

3.322 Nunca puede ser el rasgo distintivo común de dos objetos el que los designemos con el mismo signo, pero con modos de designación distintos en cada caso. Porque el signo es ciertamente arbitrario. Cabría, pues, escoger también dos signos distintos, pero ¿dónde quedaría entonces lo común en la designación?

3.323 En el lenguaje ordinario sucede con singular frecuencia que la misma palabra designe de modo y manera distintos —esto es, que pertenezca a símbolos distintos—, o que dos palabras que designan de modo y manera distintos sean usados externamente de igual modo en la proposición.

Así la palabra «es» se presenta como cópula, como signo de igualdad y como expresión de existencia; «existir», como verbo intransitivo, parejo a «ir»; «idéntico», como adjetivo; hablamos de algo, pero también de que algo sucede.

(En la proposición «Verde es verde» —donde la primera palabra es el apellido de una persona y la última un adjetivo—, estas palabras no tienen tan sólo significado distinto, sino que son símbolos distintos.)

3.324 Surgen así fácilmente las confusiones más fundamentales (de las que está llena la filosofía entera).

3.325 Para eludir estos errores tenemos que usar un lenguaje sígnico que los excluya, en la medida en que no use el mismo signo en símbolos distintos, ni use externamente de igual manera signos que designen de modo diferente. Un lenguaje sígnico, pues, que obedezca a la gramática lógica —a la sintaxis lógica.

(La escritura conceptual de Frege y Russell es un lenguaje así, que, no obstante, no excluye aún todos los errores.)

3.326 Para reconocer el símbolo en el signo hay que atender al uso con sentido.

3.327 Sólo unido a su uso lógico-sintáctico determina el signo una forma lógica.

3.328 Si un signo no se usa, carece de significado. Éste es el sentido del lema de Occam.

(Si todo se comporta como si un signo tuviera significado, entonces tiene también significado.)

3.33 La sintaxis lógica no permite que el significado de un signo juegue en ella papel alguno; tiene que poder ser establecida sin mentar el significado de un signo; ha de presuponer sólo la descripción de las expresiones.

3.331 A partir de esta observación lancemos una mirada a la «Theory of types» de Russell: El error de Russell se muestra en que tuvo que hablar del significado de los signos al establecer las reglas sígnicas.

3.332 Ninguna proposición puede enunciar algo sobre sí misma, dado que el signo proposicional no puede estar contenido en él mismo (en esto consiste toda la «Theory of types»).

3.333 Una función no puede ser su propio argumento debido a que el signo funcional contiene ya la figura primitiva de su argumento y no puede contenerse a sí mismo.

Supongamos, por ejemplo, que la función F (fx) pudiera ser su propio argumento; habría, entonces, una proposición: «F(F(fx))» y en ella la función externa F y la función interna F deberían tener significados diferentes, dado que la interna tiene la forma φ(fx), la externa la forma ψ(φ(fx)). Común a ambas funciones es sólo la letra «F», que, sin embargo, sola nada designa.

Esto queda inmediatamente claro si en lugar de escribir «F(F(u))» escribimos «(Ǝφ): F(φu). ψu = Fu». Desaparece así la paradoja de Russell.

3.334 Las reglas de la sintaxis lógica tienen que comprenderse por sí mismas, con sólo saber cómo designa cada signo.

3.34 La proposición posee rasgos esenciales y casuales. Casuales son los rasgos que emanan del modo peculiar de elaboración del signo proposicional. Esenciales, sólo los que capacitan a la proposición para expresar su sentido.

3.341 Lo esencial en la proposición es, pues, lo común a todas las proposiciones que pueden expresar el mismo sentido.

Y asimismo, generalmente, lo esencial en el símbolo es lo que todos los símbolos que pueden cumplir el mismo fin tienen en común.

3.3411 Cabría, pues, decir: el nombre genuino es lo que tienen en común todos los símbolos que designan el objeto. Se seguiría así, sucesivamente, que ninguna clase de composición resulta esencial al nombre.

3.342 En nuestras notaciones hay, ciertamente, algo arbitrario, pero esto no es arbitrario: que si hemos determinado arbitrariamente algo, entonces algo diferente ha de ser el caso. (Esto depende de la esencia de la notación.)

3.3421 Puede que un modo peculiar de designación carezca de importancia, pero siempre es importante que se trate de un posible modo de designación. Y así sucede siempre en filosofía: lo individual se revela una y otra vez como no importante, pero la posibilidad de cada singular nos procura una ilustración sobre la esencia del mundo.

3.343 Definiciones son reglas de traducción de un lenguaje a otro. Cualquier lenguaje sígnico correcto ha de resultar traducible a cualquier otro de acuerdo con tales reglas: esto es lo que todos ellos tienen en común.

3.344 Lo que designa en el símbolo es lo común a todos aquellos símbolos por los que el primero puede ser sustituido de acuerdo con las reglas de la sintaxis lógica.

3.3441 Cabe expresar, por ejemplo, lo común a todas las notaciones para las funciones veritativas así: les es común el hecho de poder ser sustituidas todas ellas —p. ej.— por la notación de «~p» («no p») y «pvq» («poq»).

(Con ello queda caracterizado el modo y manera como una posible notación especial puede procurarnos ilustraciones generales.)

3.3442 El signo del complejo no se descompone a través del análisis arbitrariamente, de modo tal que, pongamos por caso, su descomposición fuera diferente en cada trama proposicional.

3.4 La proposición determina un lugar en el espacio lógico. La existencia de este espacio lógico viene garantizada únicamente por la existencia de las partes integrantes, por la existencia de la proposición con sentido.

3.41 El signo proposicional y las coordenadas lógicas: Esto es el lugar lógico.

3.411 El lugar geométrico y el lógico coinciden en que ambos son la posibilidad de una existencia.

3.42 Aunque a la proposición sólo le es dado determinar un lugar del espacio lógico, el espacio lógico total tiene, sin embargo, que venir dado ya por ella.

(De lo contrario, por la negación, la suma lógica, el producto lógico, etc., se introducirían siempre nuevos elementos —en coordinación.)

(El armazón lógico en torno a la figura determina el espacio lógico. La proposición atraviesa el espacio lógico entero.)

3.5 El signo proposicional usado, pensado, es el pensamiento.

4 El pensamiento es la proposición con sentido.

4.001 La totalidad de las proposiciones es el lenguaje.

4.002 El hombre posee la capacidad de construir lenguajes en los que cualquier sentido resulte expresable, sin tener la menor idea de cómo y qué significa cada palabra. Al igual que se habla sin saber cómo se producen los diferentes sonidos.

El lenguaje ordinario es una parte del organismo humano y no menos complicado que éste.

Es humanamente imposible extraer de él inmediatamente la lógica del lenguaje.

El lenguaje disfraza el pensamiento. Y de un modo tal, en efecto, que de la forma externa del ropaje no puede deducirse la forma del pensamiento disfrazado; porque la forma externa del ropaje está construida de cara a objetivos totalmente distintos que el de permitir reconocer la forma del cuerpo.

Las convenciones tácitas para la comprensión del lenguaje ordinario son enormemente complicadas.

4.003 La mayor parte de las proposiciones e interrogantes que se han escrito sobre cuestiones filosóficas no son falsas, sino absurdas. De ahí que no podamos dar respuesta en absoluto a interrogantes de este tipo, sino sólo constatar su condición de absurdos. La mayor parte de los interrogantes y proposiciones de los filósofos estriban en nuestra falta de comprensión de nuestra lógica lingüística. (Son del tipo del interrogante acerca de si lo bueno es más o menos idéntico que lo bello.)

Y no es de extrañar que los más profundos problemas no sean problema alguno.

4.0031 Toda filosofía es «crítica lingüística». (En todo caso, no en el sentido de Mauthner.) Mérito de Russell es haber mostrado que la forma aparente de la proposición no tiene por qué ser su forma real.

4.01 La proposición es una figura de la realidad.

La proposición es un modelo de la realidad tal como nos la pensamos.

4.011 A primera vista parece que la proposición —tal como viene impresa sobre el papel— no es figura alguna de la realidad de la que trata. Pero tampoco la notación musical parece ser a primera vista figura alguna de la música, ni nuestra escritura fonética (el alfabeto), figura alguna de nuestro lenguaje hablado. Y, sin embargo, estos lenguajes sígnicos se revelan también en el sentido corriente como figuras de lo que representan.

4.012 Es evidente que sentimos una proposición de la forma «aRb» como figura. Aquí el signo es evidentemente un símil de lo designado.

4.013 Y si penetramos en lo esencial de este carácter figurativo, vemos que éste no es perturbado por irregularidades aparentes (como el uso del # y del ^b en la notación musical).

Porque también estas irregularidades figuran lo que han de expresar; sólo que de otro modo y manera.

4.014 El disco gramofónico, el pensamiento musical, la notación musical, las ondas sonoras, están todos entre sí en esa relación interna figurativa que se da entre lenguaje y mundo.

A todos ellos les es común la factura lógica. (Como, en la fábula, los dos jóvenes, sus dos caballos y sus lirios. En cierta medida todos son uno.)

4.0141 En que haya una regla general que permita al músico sacar la sinfonía de la partitura, que haga posible deducir la sinfonía del surco del disco gramofónico y deducir de nuevo la partitura según la primera regla, consiste precisamente la semejanza interna de cosas aparentemente tan distintas. Y dicha regla es la ley de la proyección, que proyecta la sinfonía en el lenguaje de la notación musical. Es la regla de la traducción del lenguaje de la notación musical al del disco gramofónico.

4.015 La posibilidad de todos los símiles, del carácter figurativo entero de nuestro modo de expresión, descansa en la lógica de la figuración.

4.016 Para comprender la esencia de la proposición pensemos en la escritura jeroglífica, que figura los hechos que describe.

Y de ella, sin perder lo esencial de la figuración, surgió la escritura alfabética.

4.02 Vemos esto porque comprendemos el sentido del signo proposicional sin que nos haya sido explicado.

4.021 La proposición es una figura de la realidad: Pues conozco el estado de cosas representado por ella si comprendo la proposición. Y comprendo la proposición sin que me haya sido explicado su sentido.

4.022 La proposición muestra su sentido.

La proposición muestra cómo se comportan las cosas si es verdadera. Y dice que se comportan así.

4.023 La realidad tiene que quedar fijada por la proposición en orden al sí o al no.

Para ello ha de ser enteramente descrita por la misma. La proposición es la descripción de un estado de cosas.

Al igual que la descripción describe un objeto atendiendo a sus propiedades externas, así la proposición describe la realidad atendiendo a sus propiedades internas.

La proposición construye un mundo con ayuda de un armazón lógico, y por ello, puede verse en ella también cómo se comporta todo lo lógico, sí es verdadera. De una proposición falsa cabe extraer conclusiones.

4.024 Comprender una proposición quiere decir saber lo que es el caso si es verdadera.

(Cabe, pues, comprenderla sin saber si es verdadera.)

Se la comprende si se comprenden sus partes integrantes.

4.025 En la traducción de un lenguaje a otro no se procede traduciendo cada proposición del primero a una proposición del segundo; se traducen sólo las partes integrantes de las proposiciones.

(Y el diccionario no sólo traduce sustantivos, sino también verbos, adjetivos y conjunciones, etc.; y los trata a todos por igual.)

4.026 Los significados de los signos simples (de las palabras) deben sernos explicados para que nos sea posible entenderlos.

Pero con las proposiciones nos comprendemos.

4.027 Pertenece a la esencia de la proposición poder comunicarnos un sentido nuevo.

4.03 Una proposición debe comunicar un sentido nuevo con expresiones viejas.

La proposición nos comunica un estado de cosas; tiene, pues, que estar esencialmente conectada con el estado de cosas.

Y la conexión es, precisamente, que ella es su figura lógica.

La proposición sólo dice algo en la medida en que es una figura.

4.031 En la proposición, por así decirlo, se confecciona a modo de prueba un estado de cosas.

Cabe decir simplemente: en lugar de esta proposición tiene este y aquel sentido, esta proposición representa este y aquel estado de cosas.

4.0311 Un nombre está en lugar de una cosa, otro en lugar de otra y entre sí están unidos; así representa el todo —como una figura viva— el estado de cosas.

4.0312 La posibilidad de la proposición descansa sobre el principio de la representación de objetos por medio de signos.

Mi idea fundamental es que las «constantes lógicas» no representan nada. Que la lógica de los hechos no puede representarse.

4.032 Sólo en la medida en que está lógicamente articulada es la proposición una figura del estado de cosas.

(También la proposición «ambulo» es compuesta, porque su raíz con otra terminación y su terminación con otra raíz dan un sentido diferente.)

4.04 En la proposición tiene que poder distinguirse exactamente lo mismo que en el estado de cosas que representa.

Ambos deben poseer igual multiplicidad lógica (matemática). (Cfr. la mecánica de Hertz sobre modelos dinámicos.)

4.041 Esta multiplicidad matemática, a su vez, no puede, naturalmente, ser figurada de nuevo. Al figurar no cabe salir de ella.

4.0411 Si quisiéramos, p. ej., expresar lo que expresamos mediante «(x) fx» anteponiendo un índice a «fx» —algo así como: «Gen. fx»—, no bastaría, no sabríamos qué había sido generalizado. Si quisiéramos indicarlo mediante un índice «α» —algo así como: «f (x^α)»—, tampoco bastaría, no conoceríamos el ámbito del signo de generalidad.

Si quisiéramos intentarlo introduciendo una contraseña en los lugares argumentales —algo así como: «(A, A) . F (A, A)»—, no bastaría, no podríamos constatar la identidad de las variables. Etc.

Todos estos modos de designación no bastan porque no poseen la necesaria multiplicidad matemática.

4.0412 Por la misma razón no basta la explicación idealista de la visión de las relaciones espaciales mediante las «gafas espaciales», porque no puede explicar la multiplicidad de estas relaciones.

4.05 La realidad es comparada con la proposición.

4.06 Sólo en la medida en que es una figura de la realidad puede la proposición ser verdadera o falsa.

4.061 Si no se repara en que la proposición tiene un sentido independiente de los hechos, puede creerse fácilmente que verdadero y falso son relaciones equiparables entre signo y designado.

Cabría decir entonces, p. ej., que «p» designa de modo verdadero lo que «~p» de modo falso, etc.

4.062 ¿No es posible entenderse con proposiciones falsas como hasta ahora con verdaderas? Sólo mientras se sepa que son mentadas falsamente. ¡No! Porque una proposición es verdadera cuando las cosas se comportan como lo decimos con ella; y si con «p» mentamos «~p» y las cosas se comportan como lo mentamos, entonces «p» es, en la nueva concepción, verdadera y no falsa.

4.0621 Pero es importante que los signos «p» y «~p» puedan decir lo mismo. Porque ello muestra que en la realidad nada corresponde al signo «~».

Que en una proposición aparezca la negación no es aún un rasgo característico de su sentido (~~p = p).

Las proposiciones «p» y «~p» tienen sentido opuesto, pero les corresponde una y la misma realidad.

4.063 Una imagen para explicar el concepto de verdad: mancha negra sobre papel blanco; es posible describir la forma de la mancha diciendo de cada punto de la superficie si es blanco o negro. Al hecho de que un punto sea negro le corresponde un hecho positivo; al de que un punto sea blanco (no negro), un hecho negativo. Si designo un punto de la superficie (un valor fregeano de verdad), ello corresponde al supuesto sentado para el enjuiciamiento, etc., etc.

Pero para poder decir que un punto es negro o blanco, tengo que saber antes cuándo a un punto se le llama negro y cuándo se le llama blanco; para poder decir «p» es verdadero (o falso) tengo que haber determinado en qué circunstancias llamo verdadero a «p», y con ello determino el sentido de la proposición.

He aquí el punto en el que cojea el símil: podemos señalar un punto del papel sin saber qué es blanco y qué es negro; pero a una proposición sin sentido no le corresponde nada, puesto que no designa cosa alguna (valor veritativo) cuyas propiedades pudieran llevar por nombre «falso» o «verdadero», pongamos por caso; el verbo de una proposición no es «es verdadero» o «es falso» —como creía Frege—, sino que lo que «es verdadero» debe contener ya el verbo.

4.064 Cualquier proposición ha de tener un sentido; la afirmación no puede dárselo, puesto que es ella precisamente quien afirma el sentido. Y lo mismo vale para la negación, etc.

4.0641 Cabría decir: La negación se refiere ya al lugar lógico que determina la proposición negada. La proposición que niega determina otro lugar lógico que la negada.

La proposición que niega determina un lugar lógico con ayuda del lugar lógico de la proposición negada, en la medida en que describe éste como situado fuera de aquél.

Que pueda negarse de nuevo la proposición negada muestra ya que lo que es negado es ya una proposición y no sólo la preparación de una proposición.

4.1 La proposición representa el darse y no darse efectivos de los estados de cosas.

4.11 La totalidad de las proposiciones verdaderas es la ciencia natural entera (o la totalidad de las ciencias naturales).

4.111 La filosofía no es ninguna de las ciencias naturales.

(La palabra «filosofía» ha de significar algo que está por arriba o por debajo, pero no junto a las ciencias naturales.)

4.112 El objetivo de la filosofía es la clarificación lógica de los pensamientos.

La filosofía no es una doctrina, sino una actividad. Una obra filosófica consta esencialmente de aclaraciones.

El resultado de la filosofía no son «proposiciones filosóficas», sino el que las proposiciones lleguen a clarificarse. La filosofía debe clarificar y delimitar nítidamente los pensamientos, que de otro modo son, por así decirlo, turbios y borrosos.

4.1121 La psicología no tiene más parentesco con la filosofía que cualquier otra ciencia natural.

La teoría del conocimiento es la filosofía de la psicología. ¿Acaso no corresponde mi estudio del lenguaje sígnico al estudio de los procesos de pensamiento que los filósofos consideraban tan esencial para la filosofía de la lógica? Sólo que la mayoría de las veces se enredaron en investigaciones psicológicas inesenciales, y un peligro análogo corre también mi método.

4.1122 La teoría darwinista no tiene que ver con la filosofía más que cualquier otra hipótesis de la ciencia natural.

4.113 La filosofía delimita el ámbito disputable de la ciencia natural.

4.114 Debe delimitar lo pensable y con ello lo impensable.

Debe delimitar desde dentro lo impensable por medio de lo pensable.

4.115 Significará lo indecible en la medida en que representa claramente lo decible.

4.116 Cuanto puede siquiera ser pensado, puede ser pensado claramente. Cuanto puede expresarse, puede expresarse claramente.

4.12 La proposición puede representar la realidad entera, pero no puede representar lo que ha de tener en común con la realidad para poder representarla —la forma lógica.

Para poder representar la forma lógica, deberíamos situarnos con la proposición fuera de la lógica, es decir, fuera del mundo.

4.121 La proposición no puede representar la forma lógica; ésta se refleja en ella.

El lenguaje no puede representar lo que en él se refleja.

Lo que se expresa en el lenguaje no podemos expresarlo nosotros a través de él.

La proposición muestra la forma lógica de la realidad.

La ostenta.

4.1211 Así una proposición «fa» muestra que en su sentido aparece el objeto a; dos proposiciones «fa» y «ga», que en ambas se habla del mismo objeto. El que dos proposiciones se contradigan entre sí lo muestra su estructura; de igual modo, el que una se siga de la otra. Etc.

4.1212 Lo que puede ser mostrado, no puede ser dicho.

4.1213 Ahora comprendemos también nuestro sentimiento: que estamos en posesión de una concepción lógica correcta sólo si en nuestro lenguaje sígnico todo concuerda.

4.122 Podemos hablar, en cierto sentido, de propiedades formales de los objetos y estados de cosas o, respectivamente, de propiedades de la estructura de los hechos y, en el mismo sentido, de relaciones formales y relaciones de estructuras.

(En lugar de propiedad de la estructura digo también «propiedad interna»; en lugar de relación de las estructuras, «relación interna».

Introduzco estas expresiones para mostrar la raíz de la confusión, muy extendida entre los filósofos, entre las relaciones internas y las relaciones genuinas (externas).)

Pero el darse efectivo de tales propiedades y relaciones internas no puede ser afirmado mediante proposiciones, sino que se muestra en las proposiciones que representan aquellos estados de cosas y que tratan de aquellos objetos.

4.1221 A una propiedad interna de un hecho podemos llamarle también un rasgo de ese hecho. (En el sentido en que hablamos, por ejemplo, de rasgos faciales.)

4.123 Una propiedad es interna si resulta impensable que su objeto no la posea.

(Este color azul y aquél están eo ipso en la relación interna de más claro y más oscuro. Es impensable que estos dos objetos no estuvieran en esa relación.)

(Aquí corresponde al uso fluctuante de las palabras «propiedad» y «relación» el uso fluctuante de la palabra «objeto».)

4.124 El darse efectivo de una propiedad interna de un posible estado de cosas no viene expresado mediante una proposición, sino en la proposición que lo representa, por medio de una propiedad interna de la misma.

Sería tan absurdo atribuir a la proposición una propiedad formal como negársela.

4.1241 No es posible diferenciar las formas unas de otras diciendo que ésta tiene tal propiedad y aquélla tal otra; porque esto presupone que tiene algún sentido enunciar ambas propiedades de ambas formas.

4.125 El darse efectivo de una relación interna entre posibles estados de cosas se expresa lingüísticamente mediante una relación interna entre las proposiciones que los representan.

4.1251 Queda resuelta así la cuestión disputada de «si todas las relaciones son internas o externas».

4.1252 Llamo series de formas a las series que están ordenadas por relaciones internas.

La serie de los números no está ordenada por una relación externa, sino por una relación interna. Igualmente la serie de las proposiciones «aRb»,

«(Ǝx): aRx.xRb»,

«(Ǝx,y): aRx. xRy. yRb», etc.

(Si b está en una de estas relaciones con a, llamo a b un sucesor de a.)

4.126 En el sentido en el que hablamos de propiedades formales, podemos hablar ahora también de conceptos formales.

(Introduzco esta expresión para clarificar la raíz de la confusión de los conceptos formales con los conceptos propios que cruza toda la vieja lógica.)

Que algo caiga bajo un concepto formal como objeto suyo, no puede ser expresado mediante una proposición. Sino que se muestra en el signo de ese mismo objeto. (El nombre muestra que designa un objeto; el signo numérico, que designa un número; etc.).

Los conceptos formales, en efecto, no pueden ser representados, como los conceptos propios, por una función.

Porque sus rasgos distintivos, las propiedades formales, no se expresan mediante funciones.

La expresión del concepto formal es, pues, un rasgo de ciertos símbolos.

El signo de los rasgos distintivos de un concepto formal es, pues, un rasgo característico de todos los símbolos cuyos significados caen bajo el concepto.

Así pues, la expresión del concepto formal es una variable proposicional en la que sólo este rasgo característico es constante.

4.127 La variable proposicional designa el concepto formal, y sus valores, los objetos que caen bajo este concepto.

4.1271 Toda variable es el signo de un concepto formal. Porque cada variable representa una forma constante que poseen todos sus valores y que puede ser concebida como propiedad formal de estos valores.

4.1272 Así el nombre variable «x» es el signo genuino del pseudo-concepto objeto.

Siempre que la palabra «objeto» («cosa», etc.) es usada correctamente, se expresa en la escritura conceptual mediante el nombre variable.

Por ejemplo, en la proposición «hay 2 objetos, que…» mediante «(Ǝx, y)…».

Siempre que se usa de otro modo, es decir, como palabra conceptual genuina, surgen pseudoproposiciones absurdas.

Así, por ejemplo, no cabe decir «Hay objetos» como se dice, pongamos por caso, «Hay libros».

Como tampoco «Hay 100 objetos» o «Hay x objetos».

Y es absurdo hablar del número de todos los objetos.

Igual vale para las palabras «complejo», «hecho», «función», «número», etc.

Todas ellas designan conceptos formales y se representan en la escritura conceptual mediante variables, no mediante funciones o clases. (Como creían Frege y Russell.)

Expresiones como «1 es un número», «sólo hay un cero» y similares son absurdas.

(Tan absurdo es decir «sólo hay un 1» como absurdo sería decir: 2 x 2 es igual a 4 a las 3 horas.)

4.12721 El concepto formal viene ya dado con un objeto que cae bajo él. No cabe, pues, introducir objetos de un concepto formal y el concepto formal mismo como conceptos básicos. Así no cabe, por ejemplo, introducir el concepto de la función y también funciones especiales (al modo de Russell) como conceptos básicos; o el concepto de número y números determinados.

4.1273 Si queremos expresar la proposición general «b es un sucesor de a» en la escritura conceptual necesitamos una expresión para el miembro general de la serie de formas: aRb, (Ǝx): aRx . xRb, (Ǝx, y): aRx . xRy . yRb, … Sólo cabe expresar el miembro general de una serie de formas mediante una variable, porque el concepto: miembro de esta serie de formas, es un concepto formal. (Esto es algo que Frege y Russell pasaron por alto; de ahí la falsedad del modo y manera como quieren expresar proposiciones generales del tipo de las anteriores; ese modo y manera contiene un circulus vitiosus.)

Podemos determinar el miembro general de la serie de formas aduciendo su primer miembro y la forma general de la operación que genera el miembro siguiente a partir de la proposición precedente.

4.1274 La pregunta por la existencia de un concepto formal es absurda. Porque no hay proposición que pueda dar respuesta a tal pregunta.

(Así no cabe, p. ej., preguntar: «¿Hay proposiciones de sujeto-predicado inanalizables?»).

4.128 Las formas lógicas son anuméricas.

Por eso no hay en la lógica números prominentes, y por eso no hay monismo o dualismo filosóficos, etc.

4.2 El sentido de la proposición es su coincidencia y no coincidencia con las posibilidades del darse y no darse efectivos de los estados de cosas.

4.21 La proposición más sencilla, la proposición elemental, afirma el darse efectivo de un estado de cosas.

4.211 Un signo de la proposición elemental es que ninguna proposición elemental pueda entrar en contradicción con ella.

4.22 La proposición elemental consta de nombres. Es una trama, una concatenación de nombres.

4.221 Es manifiesto que en el análisis de las proposiciones hemos de llegar a proposiciones elementales que constan de nombres en conexión inmediata.

Se plantea aquí la cuestión de cómo se efectúa el nexo proposicional.

4.2211 Aunque el mundo sea infinitamente complejo, de modo que cada hecho conste de infinitos estados de cosas, y cada estado de cosas, de infinitos objetos, aún entonces tendría que haber objetos y estados de cosas.

4.23 El nombre aparece en la proposición sólo en la trama de la proposición elemental.

4.24 Los nombres son los símbolos simples; los denoto mediante letras sueltas («x», «y», «z»).

Escribo la proposición elemental como función de los nombres en la forma «fx», «x, y», etc.

O la denoto mediante las letras p, q, r.

4.241 Si uso dos signos en uno y el mismo significado, expreso esto colocando entre ambos el signo «=».

«a = b» quiere decir, pues: el signo «a» es sustituible por el signo «b».

(Si introduzco mediante una ecuación un nuevo signo «b», determinando que debe sustituir a un signo «a» ya conocido, escribo entonces la ecuación —definición— (como Russell) en la forma «a = b Def.». La definición es una regla sígnica.)

4.242 Así pues, expresiones de la forma «a = b» no son sino adminículos de la representación; nada expresan sobre el significado de los signos «a», «b».

4.243 ¿Podemos comprender dos nombres sin saber si designan la misma cosa o dos cosas distintas? ¿Podemos comprender una proposición en la que aparecen dos nombres sin saber si significan lo mismo o algo diferente?

Si conozco, p. ej., el significado de una palabra inglesa y de una palabra alemana que signifique lo mismo, entonces es imposible que ignore que ambas significan lo mismo; es imposible que no pueda traducir una a otra.

Expresiones como «a = a», o derivadas de éstas, no son ni proposiciones elementales ni signos con sentido. (Esto se mostrará después.)

4.25 Si la proposición elemental es verdadera, el estado de cosas se da efectivamente; si la proposición elemental es falsa, el estado de cosas no se da efectivamente.

4.26 La especificación de todas las proposiciones elementales verdaderas describe el mundo completamente. El mundo queda completamente descrito por la especificación de todas las proposiciones elementales más la especificación de las que de ellas son verdaderas y de las que de ellas son falsas.

4.27 Respecto al darse y no darse efectivos de n estados de cosas hay

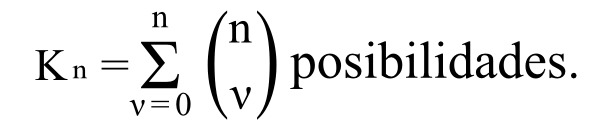
Pueden darse efectivamente todas las combinaciones de los estados de cosas y las otras no darse.

4.28 A estas combinaciones corresponde el mismo número de posibilidades de verdad —y falsedad— de n proposiciones elementales.

4.3 Las posibilidades veritativas de las proposiciones elementales significan las posibilidades del darse y no darse efectivos de los estados de cosas.

4.31 Podemos representar las posibilidades veritativas mediante esquemas del tipo siguiente («V» significa «verdadero»; «F», «falso». Las series de «V» y de «F» bajo la serie de las proposiciones elementales significan en un simbolismo fácilmente comprensible sus posibilidades veritativas):

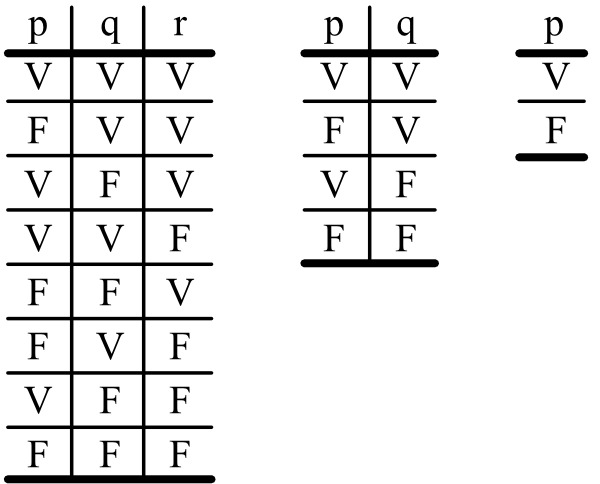
4.4 La proposición es la expresión de la coincidencia y no coincidencia con las posibilidades veritativas de las proposiciones elementales.

4.41 Las posibilidades veritativas de las proposiciones elementales son las condiciones de la verdad y falsedad de las proposiciones.

4.411 Es probable, en principio, que la introducción de las proposiciones elementales sea fundamental para la comprensión de todos los demás tipos de proposiciones. La comprensión de las proposiciones generales depende palpablemente, en efecto, de la de las proposiciones elementales.

4.42 Respecto de la coincidencia y no coincidencia de una proposición con las posibilidades veritativas de n proposiciones elementales hay

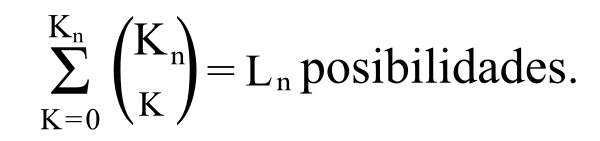
4.43 Podemos expresar la coincidencia con las posibilidades veritativas adscribiéndoles en el esquema el distintivo «V» (verdadero), p. ej.

La falta de este distintivo significa la no coincidencia.

4.431 La expresión de la coincidencia y no coincidencia con las posibilidades veritativas de las proposiciones elementales expresa las condiciones veritativas de la proposición.

La proposición es la expresión de sus condiciones veritativas. (Por ello, Frege las antepuso con todo acierto como explicación de los signos de su escritura conceptual. Sólo que la explicación del concepto de verdad es falsa en Frege: Si «lo verdadero» y «lo falso» fueran realmente objetos, y argumentos en ~p, etc., entonces, según la determinación fregeana, el sentido de «~p» no estaría en modo alguno determinado.)

4.44 El signo que surge de la correlación del citado distintivo «verdadero» y de las posibilidades veritativas, es un signo proposicional.

4.441 Está claro que al complejo de los signos «F» y «V» no corresponde objeto (o complejo de objetos) alguno; como tampoco a los trazos horizontales y verticales o a los paréntesis. No hay «objetos lógicos».

Cosa análoga vale, naturalmente, para todos los signos que expresan lo mismo que los esquemas de «V»y «F».

4.442 Esto:

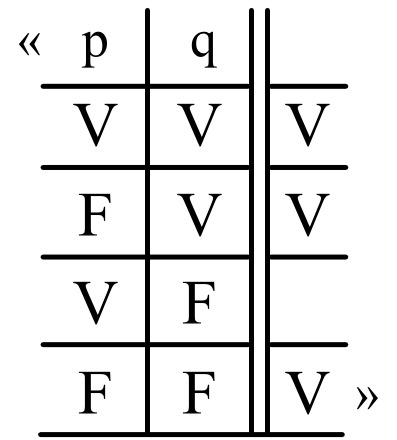
es, p. ej., un signo proposicional. (El «trazo judicativo» fregeano «^⊢» carece lógicamente de todo significado; lo único que muestra en Frege (y Russell) es que estos autores tenían por verdaderas las proposiciones así designadas. De ahí que «^⊢» no pertenezca a la trama proposicional, como tampoco el número de la proposición, pongamos por caso. Es imposible que una proposición diga de sí misma que es verdadera.) Si la secuencia serial de las posibilidades veritativas viene determinada de una vez por todas en el esquema por una regla combinatoria, entonces la última columna no es sino una expresión de las condiciones veritativas. Si escribimos esta columna como serie, entonces el signo proposicional se convierte en: «(VV—V) (p, q)» o más claramente: «(VVFV) (p, q)». (El número de sitios en el paréntesis izquierdo viene determinado por el número de miembros en el derecho.)

4.45 Para n proposiciones elementales hay L_n grupos posibles de condiciones veritativas.

Los grupos de condiciones veritativas que pertenecen a las posibilidades veritativas de un número de proposiciones elementales, pueden ordenarse en una serie.

4.46 Entre los grupos posibles de condiciones veritativas hay dos casos extremos.

En uno de ellos la proposición es verdadera para todas las posibilidades veritativas de las proposiciones elementales. Decimos que las condiciones veritativas son tautológicas.

En el segundo, la proposición es falsa para todas las posibilidades veritativas: Las condiciones veritativas son contradictorias.

En el primer caso llamamos a la proposición una tautología, en el segundo una contradicción.

4.461 La proposición muestra lo que dice; la tautología y la contradicción, que no dicen nada.

La tautología carece de posibilidades veritativas, dado que es incondicionalmente verdadera; y la contradicción no es verdadera en condición alguna.

Tautología y contradicción carecen de sentido.

(Como el punto del que parten dos flechas en dirección opuesta.)

(Nada sé, p. ej., sobre el tiempo si sé que llueve o no llueve.)

4.4611 Pero tautología y contradicción no son absurdas; pertenecen al simbolismo y ello de modo similar, ciertamente, a como el cero pertenece al simbolismo de la aritmética.

4.462 Tautología y contradicción no son figuras de la realidad. No representan ningún posible estado de cosas. Porque aquélla permite cualquier posible estado de cosas, ésta ninguno. En la tautología las condiciones de coincidencia con el mundo —las relaciones representativas— se neutralizan entre sí, de modo que no está en relación representativa alguna con la realidad.

4.463 Las condiciones veritativas determinan el espacio de juego que les es dejado a los hechos por la proposición.

(La proposición, la figura, el modelo, son, en sentido negativo, como un cuerpo sólido que limita la libertad de movimiento de los demás; en sentido positivo, como el espacio limitado por substancia sólida, en el que un cuerpo ocupa un lugar.) La tautología deja a la realidad el espacio lógico entero —infinito—; la contradicción llena todo el espacio lógico y no deja a la realidad punto alguno. De ahí que ninguna de las dos pueda determinar en modo alguno la realidad.

4.464 La verdad de la tautología es cierta; la de la proposición, posible; la de la contradicción, imposible. (Cierto, posible, imposible: He ahí los distintivos de la graduación que necesitamos en la teoría de la probabilidad.)

4.465 El producto lógico de una tautología y una proposición dice lo mismo que la proposición. Tal producto es, pues, idéntico a la proposición. Porque no cabe modificar lo esencial del símbolo sin modificar su sentido.

4.466 A una determinada conexión lógica de signos corresponde una determinada conexión lógica de sus significados; sólo a los signos inconexos corresponde una conexión arbitraria cualquiera.

Esto quiere decir que proposiciones que son verdaderas para cualquier estado de cosas no pueden ser en absoluto conexiones de signos, porque de lo contrario sólo podrían corresponderles determinadas conexiones de objetos. (Y a ninguna conexión lógica corresponde ninguna conexión de los objetos.)

Tautología y contradicción son los casos límites de la conexión sígnica, es decir, su disolución.

4.4661 Por supuesto que también en la tautología y en la contradicción los signos están aún unidos unos a otros, es decir, en relación mutua; pero estas relaciones carecen de significado, son inesenciales al símbolo.

4.5 Ahora parece posible dar la forma más general de la proposición: es decir, dar una descripción de las proposiciones de cualquier lenguaje sígnico, de modo que cualquier posible sentido pueda ser expresado mediante un símbolo al que convenga la descripción, y que cualquier símbolo al que convenga la descripción pueda expresar un sentido si los significados de los nombres son escogidos adecuadamente.

Está claro que en la descripción de la forma más general de la proposición sólo puede ser descrito lo esencial de ella; de lo contrario no sería, ciertamente, la más general.

Que haya una forma general de la proposición es cosa que viene probada por el hecho de que no puede haber proposición alguna cuya forma no hubiera podido ser prevista (esto es, construida).

La forma general de la proposición es: las cosas se comportan de tal y tal modo.

4.51 En el supuesto de que me fueran dadas todas las proposiciones elementales: entonces cabría preguntar simplemente: qué proposiciones puedo formar con ellas. Y éstas son todas las proposiciones, y así vienen delimitadas.

4.52 Las proposiciones son todo lo que se sigue de la totalidad de todas las proposiciones elementales (naturalmente también del hecho de que se trata de la totalidad de todas). (De ahí que, en cierto sentido, quepa decir que todas las proposiciones son generalizaciones de las proposiciones elementales.)

4.53 La forma general de la proposición es una variable.

5 La proposición es una función veritativa de las proposiciones elementales.

(La proposición elemental es una función veritativa de sí misma.)

5.01 Las proposiciones elementales son los argumentos veritativos de la proposición.

5.02 Hay una tendencia a confundir los argumentos de funciones con los índices de nombres. Reconozco, en efecto, tanto en el argumento como en el índice el significado del signo que los contiene.

En el «+_c» de Russell, p. ej., «c» es un índice que indica que el signo entero es el signo de adición para números cardinales. Pero esta designación descansa sobre una convención arbitraria, y en lugar de «+_c» cabría escoger también un signo simple; en «~p», sin embargo, «p» no es índice sino un argumento: el sentido de «~p» no puede ser comprendido sin que antes haya sido comprendido el sentido de «p». (En el nombre Julio César, «Julio» es un índice. El índice es siempre una parte de una descripción del objeto, a cuyo nombre lo adjuntamos. Por ejemplo, el César del linaje de los Julios.)

Si no me equivoco, la confusión de argumento e índice subyace a la teoría fregeana del significado de las proposiciones y funciones. Para Frege, las proposiciones de la lógica eran nombres, y sus argumentos, los índices de estos nombres.

5.1 Las funciones veritativas pueden ordenarse en series.

Éste es el fundamento de la teoría de la probabilidad.

5.101 Las funciones veritativas de un número cualquiera de proposiciones elementales pueden escribirse en un esquema del tipo siguiente:

A las posibilidades veritativas de los argumentos veritativos que hacen verdadera la proposición las llamo sus fundamentos veritativos.

5.11 Si todos los fundamentos veritativos que son comunes a un número de proposiciones son, al mismo tiempo, fundamentos veritativos de una determinada proposición, entonces decimos que la verdad de ésta se sigue de la verdad de aquéllas.

5.12 En particular, la verdad de una proposición «p» se sigue de la verdad de otra «q», si todos los fundamentos veritativos de la segunda lo son también de la primera.

5.121 Los fundamentos veritativos de una vienen contenidos en los de la otra; p se sigue de q.

5.122 Si p se sigue de q, entonces el sentido de «p» viene contenido en el sentido de «q».

5.123 Si un dios crea un mundo en el que determinadas proposiciones son verdaderas, con ello crea también ya un mundo en el que todas las proposiciones que se siguen de ellas son correctas. Y, de modo similar, no podría crear un mundo en el que la proposición «p» fuera verdadera sin crear todos sus objetos.

5.124 La proposición afirma cualquier proposición que se siga de ella.

5.1241 «p . q» es una de las proposiciones que afirman «p» y, a la vez, una de las proposiciones que afirman «q».

Dos proposiciones se oponen entre sí si no hay una proposición con sentido que afirme ambas.

Cualquier proposición que contradiga a otra la niega.

5.13 Que la verdad de una proposición se sigue de la verdad de otras proposiciones es cosa que percibimos a partir de la estructura de las proposiciones.

5.131 Si la verdad de una proposición se sigue de la verdad de otras, esto se expresa mediante relaciones en las que están las formas de aquellas proposiciones; y, ciertamente, no necesitamos ponerlas antes en aquellas relaciones, uniéndolas entre sí en una proposición, sino que estas relaciones son internas y se dan efectivamente tan pronto como aquellas proposiciones se dan efectivamente, y por ello.

5.1311 Si de pvq y ~p deducimos q, la relación de las formas preposicionales de «pvq» y «~p» queda oculta por el modo de designación. Pero si en lugar de «pvq» escribimos, por ejemplo, «p | q . | . p | q», y en lugar de «~p» escribimos «p | p» (p | q = ni p, ni q), entonces se hace evidente la trama interna.

(Que de (x) . fx pueda deducirse fa, muestra que la generalidad está presente también en el símbolo «(x) . fx».)

5.132 Si p se sigue de q, entonces puedo deducir p de q; inferir p de q.

El tipo de deducción sólo puede obtenerse sacándolo de ambas proposiciones.

Sólo ellas mismas pueden justificar la deducción. «Leyes deductivas» que —como en Frege y Russell— tienen que justificar las deducciones, carecen de sentido y serían superfluas.

5.133 Todo inferir sucede a priori.

5.134 De una proposición elemental no puede inferirse ninguna otra.

5.135 Del darse efectivo de un estado de cosas cualquiera no se puede, en modo alguno, deducir el darse efectivo de otro enteramente distinto.

5.136 No hay un nexo causal que justifique tal deducción.

5.1361 No podemos inferir los acaecimientos del futuro a partir de los actuales.

La creencia en el nexo causal es la superstición.

5.1362 La libertad de la voluntad consiste en que acciones futuras no pueden conocerse ahora. Sólo podríamos conocerlas de ser la causalidad una necesidad interna como la de la deducción lógica. La conexión entre saber y sabido es la de la necesidad lógica.

(«A sabe que p es el caso» carece de sentido si p es una tautología.)

5.1363 Si del hecho de que una proposición nos resulte evidente no se sigue que es verdadera, entonces la evidencia tampoco es justificación alguna para nuestra creencia en su verdad.

5.14 Si una proposición se sigue de otra, entonces ésta dice más que aquélla, aquélla menos que ésta.

5.141 Si p se sigue de q y q de p, entonces son una y la misma proposición.

5.142 La tautología se sigue de todas las proposiciones: no dice nada.

5.143 La contradicción es lo común de las proposiciones que ninguna proposición tiene en común con otra. La tautología es lo común de todas las proposiciones que nada tienen en común entre sí.

La contradicción, por así decirlo, desaparece fuera, la tautología, dentro de todas las proposiciones.

La contradicción es el límite externo de las proposiciones, la tautología es su centro insustancial.

5.15 Si V_r es el número de los fundamentos veritativos de la proposición «r», V_rs el de los fundamentos veritativos de la proposición «s», que lo son a la vez de «r», entonces llamamos a la relación: V_rs: V_r la medida de la probabilidad que la proposición «r» confiere a la proposición «s».

5.151 Sea, en una esquema como el anterior del número 5.101, V_r el número de los «V» en la proposición r; V_rs el número de los «V» en la proposición s que están en las mismas columnas con los «V» de la proposición r. La proposición r confiere entonces a la proposición s la probabilidad: V_rs: V_r.

5.1511 No hay objeto específico alguno, propio de las proposiciones de probabilidad.

5.152 A las proposiciones que carecen de argumentos veritativos en común las llamamos independientes entre sí.

Dos proposiciones elementales se confieren mutuamente la probabilidad 1/2.

Si p se sigue de q, entonces la proposición «q» confiere a la proposición «p» la probabilidad 1. La certeza de la deducción lógica es un caso límite de la probabilidad.

(Aplicación a la tautología y contradicción.)

5.153 Por sí misma una proposición no es probable ni improbable. Un evento ocurre o no ocurre, no hay un término medio.

5.154 Supongamos que en una urna hay igual número de bolas blancas y negras (y ninguna otra). Saco una bola tras otra y vuelvo a ponerlas en la urna. Por medio de este experimento, entonces, podré constatar que los números de las bolas negras y blancas extraídas se aproximan entre sí a medida que voy sacándolas.

Esto no es, pues, un hecho matemático.

Si ahora digo: es igualmente probable que saque una bola blanca que una negra, esto significa: todas las circunstancias que me son conocidas (incluidas las leyes de la naturaleza hipotéticamente admitidas) no confieren a la ocurrencia de un evento más probabilidad que a la ocurrencia de otro. Es decir, confieren —como fácilmente puede deducirse de las explicaciones anteriores— a cada uno la probabilidad 1/2.

Lo que confirmo por el experimento es que la ocurrencia de ambos eventos es independiente de las circunstancias de las que no tengo mayor conocimiento.

5.155 La unidad de la proposición de probabilidad es: las circunstancias —de las que, por lo demás, no tengo mayor conocimiento— confieren a la ocurrencia de un determinado evento tal y tal grado de probabilidad.

5.156 Así pues, la probabilidad es una generalización. Envuelve una descripción general de una forma proposicional.

Sólo a falta de certeza usamos la probabilidad.

Cuando, en efecto, no conocemos un hecho enteramente, pero sabemos algo sobre su forma.

(Una proposición puede ser, sin duda, una figura incompleta de un determinado estado de cosas, pero es siempre una figura completa.)

La proposición de probabilidad es, por así decirlo, un extracto de otras proposiciones.

5.2 Las estructuras de las proposiciones están en relaciones internas entre sí.

5.21 Podemos resaltar estas relaciones internas en nuestro modo de expresión representando una proposición como resultado de una operación que la obtiene a partir de otras proposiciones (las bases de la operación).

5.22 La operación es la expresión de una relación entre las estructuras de su resultado y de sus bases.

5.23 La operación es lo que ha de suceder con una proposición para hacer de ella otra.

5.231 Y esto dependerá, naturalmente, de sus propiedades formales, de la similitud interna de sus formas.

5.232 La relación interna que ordena una serie es equivalente a la operación por la que un miembro surge a partir de otro.

5.233 La operación sólo puede aparecer allí donde una proposición surge de otra de modo lógicamente significativo. O sea, allí donde comienza la construcción lógica de la proposición.

5.234 Las funciones veritativas de las proposiciones elementales son resultados de operaciones que tienen como bases las proposiciones elementales. (Llamo a estas operaciones, operaciones veritativas.)

5.2341 El sentido de una función veritativa de p es una función del sentido de p.

Negación, suma lógica, producto lógico, etcétera, son operaciones. (La negación invierte el sentido de la proposición.)

5.24 La operación se muestra en una variable; muestra cómo puede llegarse de una forma de proposiciones a otra.

Da expresión a la diferencia de las formas. (Y lo común entre las bases y el resultado de la operación son precisamente las bases.)

5.241 La operación no caracteriza forma alguna, sino sólo la diferencia de las formas.

5.242 La misma operación que de «p» hace «q», hace de «q» «r», y así sucesivamente. Esto sólo puede expresarse por el hecho de que «p», «q», «r», etc., son variables que expresan de modo general ciertas relaciones formales.

5.25 La ocurrencia de la operación no caracteriza el sentido de la proposición.

La operación no enuncia nada, sólo su resultado, y esto depende de las bases de la operación.

(Operación y función no deben confundirse una con otra.)

5.251 Una función no puede ser su propio argumento, pero el resultado de una operación puede convertirse, ciertamente, en su propia base.

5.252 Sólo así es posible la progresión miembro a miembro en una serie de formas (de tipo a tipo en las jerarquías de Russell y Whitehead). (Russell y Whitehead no admitieron la posibilidad de esta progresión, pero hicieron repetidamente uso de ella.)

5.2521 Llamo a la aplicación repetida de una operación a su propio resultado su aplicación sucesiva («O’ O’ O’ a» es el resultado de la triple aplicación sucesiva de «O’ξ» a «a»).

En sentido parecido hablo de la aplicación sucesiva de varias operaciones a un número de proposiciones.

5.2522 De ahí que escriba el miembro general de una serie de formas a, O’ a, O’ O’ a,… así: «[a, x, O’ x]». Esta expresión entre paréntesis es una variable. El primer miembro de la expresión entre paréntesis es el comienzo de la serie de formas; el segundo, la forma de un miembro cualquiera x de la serie, y el tercero, la forma del miembro de la serie que sigue inmediatamente a x.

5.2523 El concepto de la aplicación sucesiva de la operación es equivalente al concepto «y así sucesivamente».

5.253 Una operación puede anular el efecto de otra. Las operaciones pueden cancelarse entre sí.

5.254 La operación puede desaparecer (p. ej., la negación en «~~p», ~~p=p).

5.3 Todas las proposiciones son resultados de operaciones veritativas con las proposiciones elementales.

La operación veritativa es el modo y manera cómo a partir de las proposiciones elementales surge la función veritativa. De acuerdo con la esencia de la operación veritativa, del mismo modo que surge de las proposiciones elementales su función veritativa, surge de las funciones veritativas una nueva. Toda operación veritativa produce, a partir de funciones veritativas de proposiciones elementales, otra función veritativa de proposiciones elementales, una proposición. El resultado de toda operación veritativa con los resultados de operaciones veritativas con proposiciones elementales es nuevamente el resultado de una operación veritativa con proposiciones elementales.

Toda proposición es el resultado de operaciones veritativas con proposiciones elementales.

5.31 Los esquemas del núm. 4.31 tienen significado incluso cuando «p», «q», «r», etc., no son proposiciones elementales. Y es fácil de ver que el signo proposicional del núm. 4.442 expresa una función veritativa de proposiciones elementales incluso cuando «p» y «q» son funciones veritativas de proposiciones elementales.

5.32 Todas las funciones veritativas son resultados de la aplicación sucesiva de un número finito de operaciones veritativas a las proposiciones elementales.

5.4 Se muestra aquí que no hay «objetos lógicos», «constantes lógicas» (en el sentido de Frege y Russell).

5.41 Pues: son idénticos todos aquellos resultados de operaciones veritativas con funciones veritativas que son una y la misma función veritativa de proposiciones elementales.

5.42 Es evidente que v, ⊃, etc., no son relaciones en el sentido de derecha e izquierda, etcétera.

La posibilidad de la interdefinibilidad de los «signos primitivos» lógicos de Frege y Russell muestra ya que éstos no son signos primitivos y, propiamente ya, que no designan relaciones.

Y es evidente que el «⊃», que definimos mediante «~» y «v», es idéntico a aquel mediante el que definimos «v» con «~», y que éste «v» es idéntico al primero. Y así sucesivamente.

5.43 Que de un hecho p hayan de seguirse infinitos otros, a saber: ~~p, ~~~~p, etc., es cosa difícil de creer de antemano. Y no es menos extraño que el número infinito de las proposiciones de la lógica (de la matemática) se siga de media docena de «leyes fundamentales».

Pero todas las proposiciones de la lógica dicen lo mismo. Es decir, nada.

5.44 Las funciones veritativas no son funciones materiales.

Si se puede generar, p. ej., una afirmación mediante doble negación, ¿viene entonces contenida la negación —en algún sentido— en la afirmación? ¿«~~p» niega ~p, o afirma p, o ambas cosas?

La proposición «~~p» no trata de la negación como de un objeto; pero la posibilidad de la negación viene prejuzgada ya en la afirmación.

Y de haber un objeto que se llamara «~», entonces «~~p» debería decir otra cosa que «p». Porque una proposición trataría entonces precisamente de ~, la otra no.

5.441 Esta desaparición de las constantes lógicas aparentes tiene lugar también cuando «~(Ǝx) . ~fx» dice lo mismo que «(x) . fx», o «(Ǝx) . fx . x=a» dice lo mismo que «fa».

5.442 Si se nos da una proposición también se nos dan ya con ella los resultados de todas las operaciones veritativas que la tienen como base.

5.45 Si hay signos primitivos lógicos, entonces una lógica correcta ha de clarificar la posición de unos respecto a otros y justificar su existencia. La construcción de la lógica a partir de sus signos primitivos debe llegar a esclarecerse.

5.451 Si la lógica tiene conceptos fundamentales, éstos han de ser independientes entre sí. Una vez introducido un concepto primitivo, ha de estar introducido, en general, en todas las combinaciones en las que ocurra. No es posible, pues, introducirlo primero para una combinación y luego nuevamente para otra. P. ej.: una vez introducida una negación, tenemos que comprenderla ya tanto en proposiciones de la forma «~p» como en proposiciones como «~(pvq)», «(Ǝx) . ~fx» , entre otras. No podemos introducirla primero para una clase de casos, luego para otra, por cuanto que de proceder así quedaría dudoso si su significado sería el mismo en ambos casos, y no habría motivo alguno para utilizar en ambos casos el mismo tipo de combinación sígnica.

(En resumen, para la introducción de signos primitivos vale, mutatis mutandis, lo mismo que Frege («Grundgesetze der Arithmetik») dijo para la introducción de signos mediante definiciones.)

5.452 La introducción de un nuevo recurso en el simbolismo de la lógica ha de ser siempre un acontecimiento cargado de consecuencias. Ningún recurso nuevo puede introducirse en la lógica —con aire enteramente inocente, por así decirlo— entre paréntesis o a pie de línea.

(Así aparecen en los «Principia Mathematica» de Russell y Whitehead definiciones y leyes fundamentales en palabras. ¿Por qué aquí, de repente, palabras? Esto necesitaría una justificación. Tal justificación falta y ha de faltar, dado que el procedimiento no está, de hecho, permitido.)

Pero si la introducción de un nuevo adminículo en un lugar se ha revelado necesaria, entonces hay que preguntarse en seguida: ¿dónde habrá que usar siempre este adminículo a partir de ahora? Su posición en la lógica es lo que hay que explicar ahora.

5.453 Todos los números de la lógica han de resultar justificables.

O más bien: debe hacerse evidente que en la lógica no hay números.

No hay números prominentes.

5.454 En la lógica no hay relación de contigüidad, no puede haber clasificación alguna.

En la lógica no puede haber nada más general ni más especial.

5.4541 Las soluciones de los problemas lógicos han de ser simples, ya que imponen el standard de la simplicidad.

Los hombres han barruntado siempre que tiene que haber un ámbito de cuestiones cuyas respuestas yazcan unidas —a priori— simétricamente y en formación cerrada, regular.

Un ámbito en el que valga la proposición: simplex sigillum veri.

5.46 De haberse introducido correctamente los signos lógicos, se hubiera introducido también el sentido de todas sus combinaciones; o sea, no sólo «pvq», sino también ya «~(pv~q)», etc., etc. Con ello ya se habría introducido también el efecto de todas las combinaciones posibles, sin más, de paréntesis. Y con ello habría quedado claro que los signos primitivos propiamente generales no son los «pvq», «(Ǝx) . fx», etc., sino la forma más general de sus combinaciones.

5.461 Es significativo el hecho aparentemente sin importancia de que las pseudorrelaciones lógicas como v y ⊃ precisan de los paréntesis; contrariamente a las relaciones genuinas.

El uso de los paréntesis con aquellos signos primitivos aparentes remite ya, en efecto, al hecho de que éstos no son los signos primitivos genuinos. Y nadie creerá, desde luego, que los paréntesis tienen un significado autónomo.

5.4611 Los signos lógicos de operación son signos de puntuación.

5.47 Está claro que todo cuanto puede siquiera decirse de antemano sobre la forma de todas las proposiciones debe poder decirse de una vez.

En la proposición elemental vienen ya contenidas, en efecto, todas las operaciones lógicas. Puesto que «fa» dice lo mismo que «(Ǝx) . fx . x = a». Donde hay composición hay argumento y función, y donde están los dos últimos están ya todas las constantes lógicas.

Cabría decir: la única constante lógica es lo que todas las proposiciones tienen, por su naturaleza, en común unas con otras.

Pero esto es la forma general de la proposición.

5.471 La forma general de la proposición es la esencia de la proposición.

5.4711 Dar la esencia de la proposición quiere decir dar la esencia de toda descripción, o sea, la esencia del mundo.

5.472 La descripción de la forma más general de la proposición es la descripción del uno y único signo primitivo general de la lógica.

5.473 La lógica debe cuidarse de sí misma.

Un signo posible debe también poder designar. Todo lo que es posible en la lógica está también permitido. («Sócrates es idéntico» no quiere decir nada porque no hay ninguna propiedad que se llame «idéntico». La proposición es absurda porque no hemos establecido una determinación arbitraria, pero no porque el símbolo no estuviera permitido en y por sí mismo.)

En cierto sentido, no podemos equivocarnos en la lógica.

5.4731 La evidencia, de la que Russell tanto habló, sólo puede resultar superflua en la lógica en la medida en que el lenguaje mismo impide todo error lógico.— Que la lógica sea a priori consiste en que nada ilógico puede ser pensado.

5.4732 No podemos dar a un signo el sentido incorrecto.

5.47321 El lema de Occam no es, naturalmente, una regla arbitraria, ni una regla justificada por su éxito práctico: dice que unidades sígnicas innecesarias no significan nada.

Signos que cumplen un objetivo son lógicamente equivalentes, signos que no cumplen ningún objetivo son lógicamente asignificativos.

5.4733 Frege dice: cualquier proposición formada correctamente debe tener un sentido; y yo digo: cualquier proposición posible está correctamente formada y si carece de sentido ello sólo puede deberse a que no hemos dado significado a algunas de sus partes integrantes.

(Aunque creamos haberlo hecho.)

Así, «Sócrates es idéntico» no dice nada porque no hemos dado a la palabra «idéntico» ningún significado en cuanto adjetivo. Porque si aparece como signo de igualdad, entonces simboliza de un modo y manera totalmente distintos —la relación designante es otra diferente—, o sea, el símbolo es también en ambos casos de todo punto diferente; ambos símbolos sólo tienen casualmente uno con otro en común el signo.

5.474 El número de las operaciones fundamentales necesarias depende sólo de nuestra notación.

5.475 Lo único que importa es formar un sistema de signos de un determinado número de dimensiones de una multiplicidad matemática determinada.

5.476 Está claro que aquí no se trata de un número de conceptos fundamentales que deben ser designados, sino de la expresión de una regla.

5.5 Toda función veritativa es resultado de la aplicación sucesiva de la operación (-----V) (ξ, …) a proposiciones elementales.

Esta operación niega todas las proposiciones en el paréntesis derecho y la llamo la negación de esas proposiciones.

5.501 A una expresión entre paréntesis cuyos miembros sean proposiciones la denoto —si el orden serial de los miembros en el paréntesis es indiferente— por medio de un signo de la forma «(ξ)». «ξ» es una variable cuyos valores son los miembros de la expresión entre paréntesis; y el guión sobre la variable indica que representa todos sus valores en el paréntesis.

(Así pues, si tiene, pongamos por caso, los tres valores P, Q, R, entonces (ξ) = (P, Q, R)).

Los valores de la variable se estipulan.

La estipulación es la descripción de las proposiciones que representa la variable.

Cómo suceda la descripción de los miembros de la expresión entre paréntesis es inesencial.

Podemos distinguir tres tipos de descripción: 1.^a La enumeración directa. En este caso podemos colocar en lugar de la variable simplemente sus valores constantes. 2.^a Dando una función fx cuyos valores, para todos los valores de x, son las proposiciones a describir. 3.^a Dando una ley formal de acuerdo con la cual vienen formadas aquellas proposiciones. En este caso los miembros de la expresión entre paréntesis son los miembros todos de una serie de formas.

5.502 Escribo, pues, «N(ξ)» en lugar de «(-----V) (ξ, …)».

N(ξ) es la negación de todos los valores de la variable proposicional.

5.503 Puesto que, evidentemente, resulta fácil expresar cómo pueden formarse proposiciones con esta operación y cómo no pueden formarse proposiciones con ella, también esto ha de poder encontrar una expresión exacta.

5.51 Si ξ, sólo tiene un valor, entonces N(ξ) = ~p (no p); si tiene dos valores, entonces N(ξ) = ~p. ~q (ni p ni q).

5.511 ¿Cómo puede la lógica, que todo lo abarca y que refleja el mundo, utilizar garabatos y manipulaciones tan especiales? Sólo en la medida en que todos ellos se anudan formando una red infinitamente fina, el gran espejo.

5.512 «~p» es verdadera si «p» es falsa. Así pues, en la proposición verdadera «~p», «p» es una proposición falsa. ¿Pero cómo puedo ahora poner de acuerdo el guión «~» con la realidad?

Lo que niega en «~p» no es, sin embargo, el «~», sino lo que todos los signos de esta notación que niegan p tienen en común.

O sea, la regla común de acuerdo con la que se forman «~p», «~~~p», «~pv~p», «~p. ~ p», etc., etc., (ad inf.). Y esto común lo refleja la negación.

5.513 Cabría decir: lo común de todos los símbolos que afirman tanto p como q es la proposición «p . q». Lo común de todos los símbolos que afirman bien p o bien q es la proposición «pvq».

Y así cabe decir: dos proposiciones se oponen una a otra cuando no tienen nada en común. Y: cualquier proposición tiene sólo una negativa porque sólo hay una proposición que quede completamente fuera de ella.

También en la notación de Russell se muestra, así, que «q : pv~p» dice lo mismo que «q»; que «pv~p» no dice nada.

5.514 Una vez estipulada una notación hay en ella ya una regla de acuerdo con la cual se forman todas las proposiciones que niegan p; una regla de acuerdo con la cual se forman todas las proposiciones que afirman p o q, y así sucesivamente. Estas reglas son equivalentes a los símbolos y en ellos se refleja su sentido.

5.515 Tiene que mostrarse en nuestros símbolos que lo que viene unido mediante «v», «.», etc., han de ser proposiciones.

Y éste es ciertamente el caso, porque el símbolo «p» y «q» presupone ya por sí mismo el «v», «~», etc. Si el signo «p» no está en «pvq» por un signo complejo, no puede tener sentido por sí sólo; pero entonces tampoco pueden tener sentido las líneas «pvp», «p . p», etc., que tienen el mismo sentido que «p». Pero si «pvp» no tiene sentido, tampoco «pvq» puede tenerlo.

5.5151 ¿Tiene que formarse el signo de la proposición negativa con el signo de la positiva? ¿Por qué no cabría expresar la proposición negativa mediante un hecho negativo? (Por ejemplo: si «a» no está en una relación determinada con «b», ello podría expresar que aRb no es el caso.)

Pero también aquí la proposición negativa, a decir verdad, viene indirectamente formada mediante la positiva.

La proposición positiva debe presuponer la existencia de la proposición negativa, y viceversa.

5.52 Si los valores de ξ, son todos los valores de una función fx para todos los valores de x, entonces N(ξ) = ~(Ǝx) .fx.

5.521 Separo el concepto todo de la función veritativa.

Frege y Russell introdujeron la generalidad en conexión con el producto lógico o la suma lógica.

Se hizo difícil por eso comprender las proposiciones «(Ǝx) . fx» y «(x) . fx» en las que ambas ideas están encerradas.

5.522 Lo propio del signo de generalidad es, primero, que remite a una figura lógica primitiva y, segundo, que destaca las constantes.

5.523 El signo de generalidad aparece como argumento.

5.524 Si están dados los objetos, con ello nos vienen ya dados también todos los objetos.

Si están dadas las proposiciones elementales, con ello nos vienen ya dadas también todas las proposiciones elementales.

5.525 No es correcto reproducir la proposición «(Ǝx) .. fx» en palabras —como hace Russell— mediante «fx es posible».

Certeza, posibilidad e imposibilidad de un estado de cosas no vienen expresadas mediante una proposición, sino mediante el hecho de que una expresión sea una tautología, una proposición con sentido o una contradicción.

Aquel caso precedente al que uno quisiera remitirse siempre debe estar ya en el símbolo.

5.526 Cabe describir el mundo completamente mediante proposiciones enteramente generalizadas, lo que quiere decir, pues, sin adscribir de entrada a nombre alguno un objeto determinado.

Para llegar después al modo corriente de expresión hay que decir simplemente tras una expresión como «hay una y sólo una x tal que…»: y esta x es a.

5.5261 Una proposición enteramente generalizada es, como cualquier otra, una proposición compuesta.

(Esto se muestra en el hecho de que en «(Ǝx, φ) . φX» tenemos que mencionar separadamente «φ» y «x». Ambas están independientemente en relaciones designantes con el mundo, como en la proposición no generalizada.)

Distintivo del símbolo compuesto: tiene algo en común con otros símbolos.

5.5262 La verdad o falsedad de cualquier proposición cambia, ciertamente, algo en la trama general del mundo. Y el ámbito de juego que la totalidad de las proposiciones elementales deja a su trama es precisamente aquel que delimitan las proposiciones enteramente generalizadas. (Si una proposición elemental es verdadera, con ello, en cualquier caso, es verdadera una proposición elemental más.)

5.53 Expreso la igualdad del objeto mediante la igualdad del signo y no con ayuda de un signo de igualdad. La diversidad de los objetos, mediante la de los signos.

5.5301 Es evidente que la identidad no es una relación entre objetos. Esto queda muy claro si se considera, p. ej., la proposición «(x) : fx . ⊃ . x = a». Lo que esta proposición dice es simplemente que sólo a satisface la función f, y no que sólo satisfacen la función f aquellas cosas que están en una determinada relación con a.

Cabría decir, por supuesto, que sólo a está, efectivamente, en esa relación con a, pero para expresar esto necesitaríamos el propio signo de igualdad.

5.5302 La definición russelliana de « = » no basta; porque no puede decirse en orden a ella que dos objetos tengan todas las propiedades en común. (Aun cuando esta proposición jamás sea correcta, tiene, sin embargo, sentido.)

5.5303 Dicho sea de paso: es absurdo decir de dos cosas que son idénticas, y decir de una que es idéntica a sí misma no dice absolutamente nada.

5.531 Así pues, no escribo «f(a, b) . a = b», sino «f(a, a)» (o «f(b, b)»). Y no «f(a, b) . ~a = b», sino «f(a, b)».

5.532 Y análogamente: no «(Ǝx, y) . f(x,y) . x = y», sino «(Ǝx) . f(x, x)»; y no «(Ǝx, y) . f(x, y) . ~x = y», sino «(Ǝx, y) . f(x, y)».

(Esto es, en lugar del russelliano «(Ǝx, y) . f(x, y)»: «(Ǝx, y) . f(x, y) v . (Ǝx) . f(x, x)».)

5.5321 Así pues, en lugar de «(x) : fx ⊃ x = a» escribimos, p. ej., «(Ǝx) . fx. ⊃ . fa : ~(Ǝx, y) . fx fy». Y la proposición «sólo una x satisface f()» suena: «(Ǝx) . fx : ~(Ǝx, y) . fx . fy».

5.533 El signo de igualdad no es, pues, componente esencial alguno de la escritura conceptual.

5.534 Y ahora vemos que pseudoproposiciones como: «a=a», «a=b . b=c . ⊃ a=c», «(x) . x = x», «(Ǝx) . x = a», etc., no pueden escribirse en absoluto en una escritura conceptual correcta.

5.535 Con ello se solventan asimismo todos los problemas que venían vinculados a tales pseudoproposiciones.

Todos los problemas que lleva consigo el «Axiom of Infinity» de Russell pueden ser resueltos ya aquí.

Lo que ha de decir el Axiom of Infinity se expresaría en el lenguaje por la presencia de infinitos nombres con significado diferente.

5.5351 Hay ciertos casos en los que se tiene la tentación de utilizar expresiones de la forma «a = a» o «p ⊃ p», y similares. Y tal sucede, efectivamente, cuando se quiere hablar de la figura primitiva: proposición, cosa, etc. Así, Russell ha reproducido simbólicamente en los «Principies of Mathematics» el absurdo «p es una proposición» mediante «p ⊃ p», y lo ha puesto como hipótesis ante ciertas proposiciones, con el fin de que sus lugares argumentales no pudieran ser ocupados sino por proposiciones.

(Poner la hipótesis ante una proposición para asegurarle argumentos de la forma correcta es absurdo ya porque la hipótesis, para una no-proposición como argumento, no pasa a ser falsa, sino absurda, y porque la proposición misma se convierte en absurda por argumentos de tipo incorrecto, esto es, se preserva tan bien o tan mal a sí misma de los argumentos incorrectos como la hipótesis sin sentido añadida a tal efecto.)

5.5352 Igualmente querría expresarse «no hay cosas» mediante «~(Ǝx) . x = x». Pero, incluso siendo esto una proposición, ¿acaso no sería también verdadera si «hubiera cosas», sí, pero cosas que no fueran idénticas a sí mismas?

5.54 En la forma general de la proposición, la proposición no ocurre en la proposición sino como base de operaciones veritativas.

5.541 A primera vista parece como si una proposición pudiera ocurrir en otra también de otro modo. Especialmente en ciertas formas proposicionales de la psicología como «A cree que p es el caso», o «A piensa p», etc.

Aquí, a una mirada superficial puede parecer, ciertamente, como si la proposición p estuviera con un objeto A en una clase de relación.

(Y en la moderna teoría del conocimiento (Russell, Moore, etc.), dichas proposiciones, en efecto, han sido concebidas así.)

5.542 Pero está claro que «A cree que p», «A piensa p», «A dice p» son de la forma «“p” dice p»: y aquí no se trata de una coordinación de un hecho y un objeto, sino de la coordinación de hechos mediante la coordinación de sus objetos.

5.5421 Esto muestra también que el alma —el sujeto, etc.—, tal como es concebida en la actual psicología superficial, es una quimera.

Un alma compuesta no sería ya, ciertamente, un alma.

5.5422 La explicación correcta de la forma de la proposición «A juzga p» ha de mostrar que es imposible juzgar un absurdo. (La teoría de Russell no satisface esta condición.)

5.5423 Percibir un complejo quiere decir percibir que sus partes integrantes se comportan unas respecto de otras de tal y tal modo.

Esto explica asimismo, ciertamente, que la figura

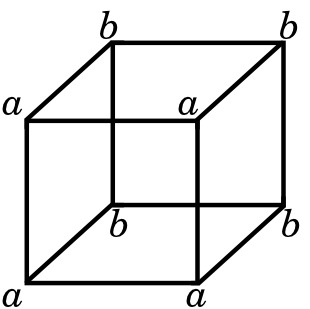
pueda ser vista de dos modos como cubo; y todos los fenómenos similares. Porque en realidad lo que vemos son dos hechos diferentes.

(Si miro primero a los ángulos a y sólo fugazmente a los b, entonces a aparece delante; y viceversa.)

5.55 Debemos responder ahora a priori a la pregunta por todas las formas posibles de proposiciones elementales.

La proposición elemental consta de nombres. Pero como no podemos aducir el número de nombres de significado diferente, tampoco podemos aducir la composición de la proposición elemental.

5.551 Nuestro principio fundamental es que cualquier interrogante que pueda resolverse en general mediante la lógica ha de poder resolverse sin más.

(Y si llegamos a la situación de tener que solucionar un problema de este tipo contemplando el mundo, ello mostraría que vamos por caminos radicalmente equivocados.)

5.552 La «experiencia» que necesitamos para comprender la lógica no es la de que algo se comporta de tal y tal modo, sino la de que algo es; pero esto, justamente, no es ninguna experiencia.

La lógica está antes de toda experiencia —de que algo es así. Está antes del cómo, no antes del qué.

5.5521 Y si esto no fuera así, ¿cómo podríamos aplicar la lógica? Cabría decir: si hubiera una lógica aunque no hubiera ningún mundo, ¿cómo podría entonces haber una lógica dado que hay un mundo?

5.553 Russell dijo que hay relaciones simples entre diferentes números de cosas (Individuáis). Pero ¿entre qué números? Y ¿cómo puede decidirse esto?

—¿Por la experiencia?

(No hay un número prominente.)

5.554 La determinación de cualquier forma especial sería enteramente arbitraria.

5.5541 Tiene que resultar determinable a priori, p. ej., si puedo llegar a encontrarme en la situación de tener que designar algo con el signo de una relación de 27 términos.

5.5542 Pero ¿podemos siquiera preguntar así? ¿Podemos establecer una forma sígnica y no saber si puede corresponder a algo?

¿Tiene sentido la pregunta: qué ha de ser para que algo pueda ser-el-caso?

5.555 Está claro que tenemos un concepto de la proposición elemental, prescindiendo de su forma lógica especial.

Pero donde pueden construirse símbolos de acuerdo a un sistema, allí lo lógicamente importante es este sistema y no cada uno de los símbolos particulares.

Cómo iba a ser posible que en lógica tuviera que habérmelas con fórmulas que puedo inventar; más bien tengo que habérmelas con aquello que me posibilita inventarlas.

5.556 No puede haber una jerarquía de las formas de las proposiciones elementales. Sólo podemos predecir lo que nosotros mismos construimos.

5.5561 La realidad empírica viene limitada por la totalidad de los objetos. El límite vuelve a mostrarse en la totalidad de las proposiciones elementales.

Las jerarquías son y tienen que ser independientes de la realidad.

5.5562 Si sabemos por motivos puramente lógicos que tiene que haber proposiciones elementales, entonces cualquiera que comprenda las proposiciones en su forma no analizada tiene que saberlo.

5.5563 Todas las proposiciones de nuestro lenguaje ordinario están de hecho, tal como están, perfectamente ordenadas desde un punto de vista lógico. Lo más simple que hemos de indicar aquí no es un símil de la verdad, sino la verdad misma.

(Nuestros problemas no son abstractos, sino acaso los más concretos que existen.)

5.557 La aplicación de la lógica decide qué proposiciones elementales hay.

Lo que pertenece a la aplicación es cosa que la lógica no puede anticipar.

Esto es claro: la lógica no puede chocar con su aplicación.

Pero la lógica ha de tocarse con su aplicación.

La lógica y su aplicación, pues, no pueden invadirse una a otra.

5.5571 Si no puedo especificar a priori las proposiciones elementales, querer especificarlas tendrá que llevar a un manifiesto absurdo.

5.6 Los límites de mi lenguaje significan los límites de mi mundo.

5.61 La lógica llena el mundo; los límites del mundo son también sus límites.

No podemos, por consiguiente, decir en lógica: en el mundo hay esto y esto, aquello no.

En efecto, esto presupondría, aparentemente, que excluimos ciertas posibilidades; y ello no puede ser el caso, porque, de otro modo, la lógica tendría que rebasar los límites del mundo: si es que, efectivamente, pudiera contemplar tales límites también desde el otro lado.

Lo que no podemos pensar no lo podemos pensar; así pues, tampoco podemos decir lo que no podemos pensar.

5.62 Esta observación ofrece la clave para resolver la cuestión de en qué medida es el solipsismo una verdad.

En rigor, lo que el solipsismo entiende es plenamente correcto, sólo que eso no se puede decir, sino que se muestra.

Que el mundo es mi mundo se muestra en que los límites del lenguaje (del lenguaje que sólo yo entiendo) significan los límites de mi mundo.

5.621 El mundo y la vida son una y la misma cosa.

5.63 Yo soy mi mundo. (El microcosmos.)

5.631 El sujeto pensante, representante no existe.

Si yo escribiera un libro «El mundo tal como lo encontré», debería informar en él también sobre mi cuerpo y decir qué miembros obedecen a mi voluntad y cuáles no, etc.; ciertamente esto es un método para aislar el sujeto o, más bien, para mostrar que en un sentido relevante no hay sujeto: de él solo, en efecto, no cabría tratar en este libro.

5.632 El sujeto no pertenece al mundo, sino que es un límite del mundo.

5.633 ¿Dónde descubrir en el mundo un sujeto metafísico?

Dices que ocurre aquí enteramente como con el ojo y el campo visual. Pero el ojo no lo ves realmente.

Y nada en el campo visual permite inferir que es visto por un ojo.

5.6331 El campo visual no tiene, en efecto, y por así decirlo, una forma como ésta:

5.634 Esto guarda relación con el hecho de que ninguna parte de nuestra experiencia es tampoco a priori.

Todo lo que vemos podría ser también de otra manera.

En general, todo lo que podemos describir podría ser también de otra manera.

No hay orden alguno a priori de las cosas.

5.64 Se ve aquí cómo, llevado a sus últimas consecuencias, el solipsismo coincide con el puro realismo.

El yo del solipsismo se contrae hasta convertirse en un punto inextenso y queda la realidad con él coordinada.

5.641 Existe, pues, realmente un sentido en el que en filosofía puede tratarse no-psicológicamente del yo.

El yo entra en la filosofía por el hecho de que el «mundo es mi mundo».

El yo filosófico no es el hombre, ni el cuerpo humano, ni el alma humana, de la que trata la psicología, sino el sujeto metafísico, el límite —no una parte del mundo.

6 La forma general de la función veritativa es: [p, ξ, N (ξ)]

Ésta es la forma general de la proposición.

6.001 Esto no dice otra cosa sino que toda proposición es un resultado de la aplicación sucesiva de la operación N’(ξ) a las proposiciones elementales.

6.002 Dada la forma general de cómo una proposición está construida, con ello viene dada asimismo la forma general según la cual a partir de una proposición cabe obtener otra por medio de una operación.

6.01 La forma general de la operación Ω’(η) es, pues: [ξ, N(ξ)] (η) (=[η, ξ, N(ξ)]).

Ésta es la forma más general de la transición de una proposición a otra.

6.02 Y así llegamos a los números: defino

x = Ω^0. x Def. y

Ω’Ω^v. x = Ω^v+1. x Def.

De acuerdo con estas reglas sígnicas escribimos, pues, la serie x, Ω’ x, Ω’Ω’ x, Ω’Ω’Ω’ x, …

así: Ω^0. x, Ω^0+1. x, Ω^0+1+1. x, Ω^0+1+1+1. x, …

O sea, en lugar de «[x, ξ, Ω’ ξ]», escribo: «[Ω^0. x, Ω^v. x, Ω^v+1. x]».

Y defino:

0 + 1 = 1 Def.

0 + 1 + 1 = 2 Def.

0 + 1 +1 + 1 = 3 Def.

(Y así sucesivamente.)

6.021 El número es el exponente de una operación.

6.022 El concepto de número no es otra cosa que lo común de todos los números, la forma general del número.

El concepto de número es el número variable.

Y el concepto de igualdad numérica es la forma general de todas las igualdades numéricas especiales.

6.03 La forma general del número entero es: [0, ξ, ξ + 1].

6.031 La teoría de las clases es enteramente superflua en la matemática.

Esto guarda relación con el hecho de que la generalidad que necesitamos en la matemática no es la casual.

6.1 Las proposiciones de la lógica son tautologías.

6.11 Las proposiciones de la lógica, pues, no dicen nada. (Son las proposiciones analíticas.)

6.111 Las teorías que presentan una proposición de la lógica como llena de contenido son siempre falsas. Cabría, p. ej., creer que las palabras «verdadero» y «falso» designan dos propiedades entre otras, en cuyo caso parecería un hecho curioso que cada proposición poseyera una de estas propiedades. Nada menos evidente ahora que esto; tan escasamente evidente como sonaría, por ejemplo, la proposición «todas las rosas son o bien amarillas o bien rojas», aunque fuera verdadera. En efecto, esta proposición asume ahora por entero el carácter de una proposición científico-natural, y esto es el indicio seguro de que fue concebida falsamente.

6.112 La explicación correcta de las proposiciones lógicas ha de conferirles un lugar exclusivo entre todas las proposiciones.

6.113 Que a la sola luz del símbolo pueda reconocerse que son verdaderas, es característica peculiar de las proposiciones lógicas, y este hecho encierra en sí toda la filosofía de la lógica. Y del mismo modo, que no pueda reconocerse en la sola proposición la verdad o falsedad de las proposiciones no lógicas, es también uno de los hechos más importantes.

6.12 Que las proposiciones de la lógica sean tautologías es cosa que muestra las propiedades formales —lógicas— del lenguaje, del mundo.

Que sus partes integrantes, así unidas, den una tautología, es cosa que caracteriza la lógica de sus partes integrantes.

Para que proposiciones, unidas de un determinado modo y manera, den una tautología, han de tener determinadas propiedades estructurales. Que así unidas den una tautología, es cosa, pues, que muestra que poseen esas propiedades estructurales.

6.1201 Que, por ejemplo, las proposiciones «p» y «~p» den una tautología en la combinación «p ⊃ q», «p» y «q» den una tautología combinadas entre sí en la forma «(p ⊃ q) . (p) : ⊃ : (q)», es cosa que muestra que q se sigue de p y de p ⊃ q. Que «(x) . fx: ⊃ : fa» sea una tautología, muestra que fa se sigue de (x) . fx. Etc., etc.

6.1202 Está claro que, para el mismo fin, en lugar de las tautologías podrían utilizarse también las contradicciones.

6.1203 Para reconocer como tal una tautología, en los casos en los que en la tautología no aparece signo de generalidad alguno, puede recurrirse al siguiente método visual: en lugar de «p», «q», «r», etc., escribo «VpF», «VqF», «VrF», etc. Expreso la combinación veritativa mediante corchetes. P. ej.:

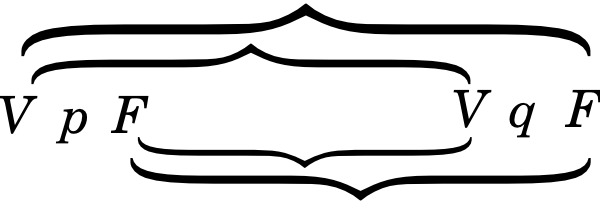
Y la coordinación de la verdad o falsedad de la proposición entera con las combinaciones veritativas de los argumentos veritativos, mediante rayas, del siguiente modo:

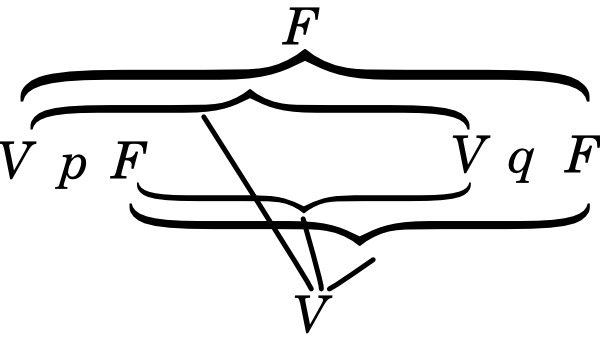
Así pues, este signo representaría, p. ej., la proposición p ⊃ q. Supongamos ahora que quiero investigar, p. ej., si la proposición ~(p . ~p) (principio de contradicción) es una tautología. En nuestra notación la forma «~ξ» se escribe:

La forma «ξ . η», así:

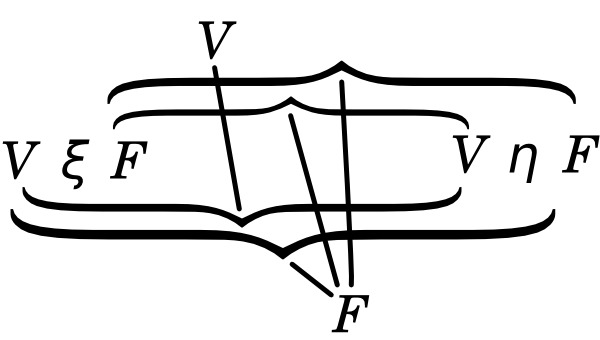
De ahí que la proposición ~(p. ~q) se exprese así:

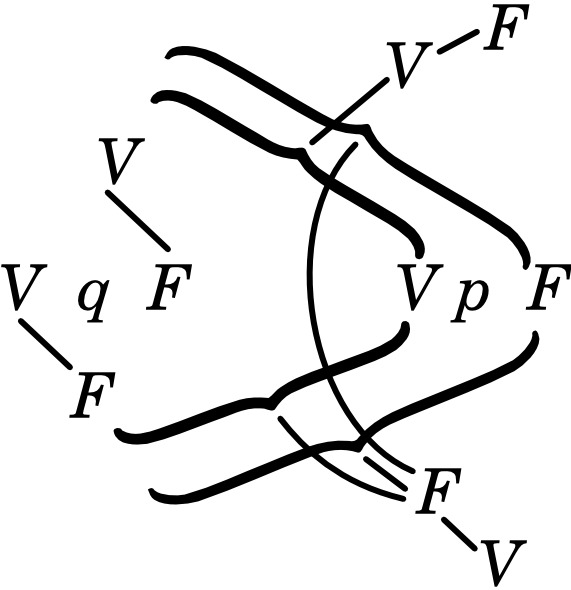
Si en lugar de «q» ponemos «p» e investigamos la conexión de las V y F más externas con las más internas, resulta entonces que la verdad de la proposición entera está coordinada con todas las combinaciones veritativas de su argumento; su falsedad, con ninguna.

6.121 Las proposiciones de la lógica demuestran las propiedades lógicas de las proposiciones combinándolas en proposiciones que no dicen nada.

Cabría llamar a este método un método-cero. En la proposición lógica se colocan proposiciones en equilibrio recíproco, y el estado de equilibrio muestra, entonces, cómo han de estar construidas lógicamente esas proposiciones.

6.122 De ello resulta que podemos pasar también sin las proposiciones lógicas, ya que en una notación adecuada podemos reconocer las propiedades formales de las proposiciones mirando simplemente esas proposiciones.

6.1221 Si dos proposiciones «p» y «q», p. ej., dan en la combinación «p ⊃ q» una tautología, está claro que q se sigue de p.

Que, p. ej., «q» se sigue de «p ⊃ q . p», es cosa que vemos a partir de las dos proposiciones mismas, pero podemos también mostrarlo así: combinándolas de modo que formen «p ⊃ q . p: ⊃ : q»; y entonces muestran que se trata de una tautología.

6.1222 Esto aclara la cuestión de por qué las proposiciones lógicas no pueden ser confirmadas por la experiencia, como tampoco pueden ser refutadas por ella. Una proposición de la lógica no sólo no puede ser refutada por experiencia posible alguna, sino que tampoco debe poder ser confirmada por ella.

6.1223 Ahora queda claro por qué se ha sentido a menudo como si las «verdades lógicas» pudieran ser «postuladas» por nosotros: podemos, en efecto, postularlas en la medida en que podemos postular una notación satisfactoria.

6.1224 Ahora queda claro también por qué se llamó a la lógica la teoría de las formas y de la deducción.

6.123 Está claro: las leyes lógicas no pueden estar sometidas a su vez a leyes lógicas.

(No hay, como creyó Russell, un principio de contradicción propio para cada «type», sino que basta uno, ya que no se aplica a sí mismo.)

6.1231 El distintivo de la proposición lógica no es la validez general.

Porque ser general quiere decir sólo: valer casualmente para todas las cosas. Ya que una proposición no generalizada puede ser tan tautológica como una generalizada.

6.1232 Cabría llamar esencial a la validez general lógica en contraposición a la casual de la proposición «todos los hombres son mortales», por ejemplo. Proposiciones como el «Axiom of reducibility» de Russell no son proposiciones lógicas, y esto explica nuestro sentimiento: que de ser verdaderas sólo podrían serlo por una feliz casualidad.

6.1233 Puede imaginarse un mundo en el que el Axiom of reducibility no tenga validez. Pero está claro que la lógica no tiene nada que ver con la cuestión de si nuestro mundo es realmente así o no.

6.124 Las proposiciones lógicas describen el armazón del mundo o, más bien, lo representan. No «tratan» de nada. Presuponen que los nombres tienen significado, y las proposiciones elementales, sentido; y ésta es su conexión con el mundo. Está claro que algo tiene que indicar sobre el mundo el hecho de que ciertas conexiones de símbolos —que tienen esencialmente un carácter determinado— sean tautologías. Aquí radica lo decisivo. Decíamos que algo hay de arbitrario en los símbolos que usamos y algo hay que no lo es. En la lógica sólo esto se expresa: Pero quiere decir que en la lógica no expresamos nosotros lo que queremos con ayuda de los signos, sino que en la lógica es la propia naturaleza de los signos naturalmente necesarios lo que se expresa: Si conocemos la sintaxis lógica de un lenguaje sígnico cualquiera, entonces ya están dadas todas las proposiciones de la lógica.

6.125 Es posible, y ciertamente también a la luz de la vieja concepción de la lógica, dar de antemano una descripción de todas las proposiciones lógicas «verdaderas».

6.1251 Por eso en la lógica tampoco puede haber nunca sorpresas.

6.126 Puede calcularse si una proposición pertenece a la lógica calculando las propiedades lógicas del símbolo.

Y esto lo hacemos cuando «demostramos» una proposición lógica. Porque formamos la proposición lógica a partir de otras según meras reglas sígnicas sin preocuparnos por un sentido y un significado.

La demostración de las proposiciones lógicas consiste en que las hacemos surgir a partir de otras proposiciones lógicas mediante la aplicación sucesiva de ciertas operaciones que a partir de las primeras generan una y otra vez tautologías. (Y, ciertamente, de una tautología sólo se siguen tautologías.) Naturalmente, este modo de mostrar que sus proposiciones son tautologías es enteramente inesencial a la lógica. Ya por el hecho de que las proposiciones de las que parte la demostración tienen, efectivamente, que mostrar sin demostración que son tautologías.

6.1261 En la lógica proceso y resultado son equivalentes.

(Ninguna sorpresa, en consecuencia.)

6.1262 En la lógica la demostración no es sino un medio mecánico auxiliar para un más fácil reconocimiento de la tautología, cuando ésta es complicada.

6.1263 Sería, en efecto, demasiado extraño que se pudiera demostrar lógicamente una proposición con sentido a partir de otra, y una proposición lógica también. Está claro de antemano que la demostración lógica de una proposición con sentido y la demostración en la lógica han de ser dos cosas de todo punto diferentes.

6.1264 La proposición con sentido enuncia algo, y su demostración muestra que ello es así; en la lógica toda proposición es la forma de una demostración. Toda proposición de la lógica es un modusponens representado en signos. (Y el modusponens no puede ser expresado mediante una proposición.)

6.1265 Siempre puede concebirse la lógica de modo que toda proposición sea su propia demostración.

6.127 Todas las proposiciones de la lógica son pariguales; no hay esencialmente entre ellas leyes fundamentales y proposiciones derivadas.

Toda tautología muestra por ella misma que es una tautología.

6.1271 Está claro que el número de las «leyes lógicas fundamentales» es arbitrario, puesto que la lógica podía, efectivamente, derivarse de una ley fundamental con sólo formar, p. ej., el producto lógico a partir de las leyes fundamentales de Frege. (Frege diría tal vez que esta ley fundamental ya no es inmediatamente evidente. Pero no deja de resultar curioso que un pensador tan exacto como Frege haya invocado el grado de evidencia como criterio de la proposición lógica.)

6.13 La lógica no es una teoría sino una figura especular del mundo.

La lógica es trascendental.

6.2 La matemática es un método lógico.

Las proposiciones de la matemática son ecuaciones, es decir, pseudoproposiciones.

6.21 La proposición matemática no expresa pensamiento alguno.

6.211 En la vida lo que necesitamos nunca es, ciertamente, la proposición matemática, sino que utilizamos la proposición matemática sólo para deducir de proposiciones que no pertenecen a la matemática otras proposiciones que tampoco pertenecen a ella.

(En la filosofía el interrogante «para qué usamos realmente tal palabra, tal proposición» lleva una y otra vez a valiosos esclarecimientos.)

6.22 La matemática muestra en las ecuaciones la lógica del mundo que las proposiciones de la lógica muestran en las tautologías.

6.23 Si dos expresiones vienen unidas por el signo de igualdad, ello quiere decir que son sustituibles una por otra. Pero si esto es el caso tiene que mostrarse en las dos expresiones mismas.

Que dos expresiones sean sustituibles una por otra, caracteriza su forma lógica.

6.231 Es una propiedad de la afirmación, que pueda ser concebida como doble negación. Es una propiedad de «1 + 1 + 1 + 1», que pueda concebirse como «(1 + 1) + (1 + 1)».

6.232 Frege dice que ambas expresiones tienen el mismo significado, pero diferente sentido. Pero lo esencial de la ecuación es que no resulta necesaria para mostrar que las dos expresiones unidas por el signo de igualdad tienen el mismo significado, ya que esto es algo que ambas expresiones mismas dejan ver.

6.2321 Y que las proposiciones de la matemática puedan ser probadas, no quiere decir otra cosa sino que su corrección puede ser percibida sin necesidad de que lo que expresan sea ello mismo comparado, en orden a su corrección, con los hechos.

6.2322 No es posible afirmar la identidad del significado de dos expresiones. Porque para poder afirmar algo de su significado tengo que conocer su significado; y en la medida en que conozco su significado sé si significan lo mismo o algo diferente.

6.2323 La ecuación caracteriza sólo el punto de vista desde el que considero ambas expresiones, es decir, el punto de vista de su igualdad de significado.

6.233 A la cuestión de si la intuición resulta necesaria para la resolución de los problemas matemáticos hay que responder que es precisamente el lenguaje el que procura aquí la necesaria intuición.

6.2331 Es precisamente el procedimiento del cálculo lo que proporciona esta intuición.

El cálculo no es un experimento.

6.234 La matemática es un método de la lógica.

6.2341 Lo esencial del método matemático es trabajar con ecuaciones. Que toda proposición de la matemática deba entenderse por sí misma, es cosa que descansa precisamente en este método.

6.24 El método de la matemática para llegar a sus ecuaciones es el método de sustitución.

Porque las ecuaciones expresan la sustituibilidad de dos expresiones, y nosotros avanzamos de un número de ecuaciones a ecuaciones nuevas sustituyendo unas expresiones por otras de acuerdo con las ecuaciones.

6.241 De ahí que la prueba de la proposición 2 X 2 = 4 se exprese así:

(Ω^v)^μ’ x = Ω^vXμ’ x Def.

Ω^2x2’ x = (Ω²)²’ x = (Ω²)¹⁺¹’ x = Ω²’Ω²’ x = Ω¹⁺¹’Ω¹⁺¹’

= (Ω’Ω)’(Ω’Ω) x = Ω’Ω’Ω’Ω’ x = Ω^1+1+1+1’ x = Ω⁴’ x.

6.3 La investigación de la lógica significa la investigación de toda legaliformidad. Y fuera de la lógica todo es casualidad.

6.31 En cualquier caso, la llamada ley de la inducción no puede ser una ley lógica, dado que es manifiestamente una proposición con sentido. Y por eso no puede ser tampoco una ley a priori.

6.32 La ley de causalidad no es una ley, sino la forma de una ley.

6.321 «Ley de causalidad» no es un nombre genérico. Y al igual que en la mecánica decimos que hay leyes del mínimum —tales como la ley de la mínima acción—, hay en la física leyes de causalidad, leyes de la forma de causalidad.

6.3211 Se ha sospechado, ciertamente, que tenía que haber una «ley de la mínima acción» antes de saber con exactitud cómo rezaba. (Aquí, como siempre, lo cierto a priori se revela como algo puramente lógico.)

6.33 No creemos a priori en una ley de conservación, sino que conocemos a priori la posibilidad de una forma lógica.

6.34 Todas aquellas proposiciones, como el principio de razón, de la continuidad en la naturaleza, del mínimo gasto en la naturaleza, etc., etc., todas ellas son intuiciones a priori sobre la posible conformación de las proposiciones de la ciencia.

6.341 La mecánica newtoniana, por ejemplo, lleva la descripción del mundo a una forma unitaria. Imaginémonos una superficie blanca con manchas negras irregulares. Diríamos entonces: cualquiera que sea la figura que toma cuerpo así, siempre puedo aproximarme arbitrariamente a su descripción, cubriendo la superficie con una red cuadriculada suficientemente fina y diciendo, acto seguido, de cada cuadrado que es blanco o que es negro. Habré llevado de este modo la descripción de la superficie a una forma unitaria. Esta forma es arbitraria, puesto que con igual éxito hubiera podido utilizar una red con aberturas triangulares o exagonales. Puede que la descripción con ayuda de una red triangulada hubiera resultado más sencilla; esto quiere decir que podríamos describir más exactamente la superficie con una red triangulada más burda que con una cuadriculada más fina (o al revés), etc. A las diferentes redes corresponden diferentes sistemas de descripción del mundo. La mecánica determina una forma de descripción del mundo al decir: todas las proposiciones de la descripción del mundo tienen que obtenerse de un modo y manera dados a partir de un número de proposiciones dadas —los axiomas mecánicos—. Procura así los materiales para la construcción del edificio científico y dice: cualquiera que sea el edificio que quieras levantar tendrás que construirlo de algún modo con estos y sólo estos materiales.

(Al igual que con el sistema numérico ha de poderse escribir un número arbitrario cualquiera, con el sistema de la mecánica, una proposición cualquiera de la física.)

6.342 Y ahora vemos la posición recíproca de lógica y mecánica. (Cabría hacer, también, que la red se compusiera de figuras de otro tipo, de triángulos y exágonos, por ejemplo.) Que una figura como la arriba citada pueda ser descrita mediante una red de una forma dada, es cosa que no dice nada sobre la figura. (Porque esto vale para cualquier figura de este tipo.) Pero lo que caracteriza a la figura es esto: que puede describirse enteramente mediante una determinada red de una determinada finura.

Así pues, tampoco enuncia nada sobre el mundo el hecho de que pueda ser descrito mediante la mecánica newtoniana; pero sí, ciertamente, el hecho de que se deje describir así mediante ella, como, en efecto, es el caso. También dice algo sobre el mundo el hecho de que pueda describirse más sencillamente mediante una mecánica que mediante otra.

6.343 La mecánica es un intento de construir de acuerdo con un plan todas las proposiciones verdaderas que necesitamos para la descripción del mundo.

6.3431 A través del aparato lógico entero, sin embargo, las leyes físicas hablan de los objetos del mundo.

6.3432 No debemos olvidar que la descripción del mundo mediante la mecánica es siempre enteramente general. En ella nunca se trata, p. ej., de puntos materiales determinados, sino de puntos cualesquiera.

6.35 Aunque en nuestra figura las manchas son figuras geométricas, la geometría no puede, sin embargo, obviamente, decir nada sobre su forma y posición efectivas. Pero la red es puramente geométrica, todas sus propiedades pueden indicarse a priori.

Leyes como el principio de razón, etc., tratan de la red, no de lo que la red describe.

6.36 Si hubiera una ley de causalidad podría rezar así:

«Hay leyes naturales». Pero, por supuesto, tal cosa no puede decirse; se muestra.

6.361 En el modo de expresión de Hertz cabría decir:

sólo sonpensables conexiones legaliformes.

6.3611 No podemos comparar ningún proceso con el «decurso del tiempo» —éste no existe—, sino sólo con otro proceso (con la marcha del cronómetro, por ejemplo).

De ahí que la descripción del decurso temporal sólo resulta posible apoyándonos en otro proceso.

Algo enteramente análogo vale para el espacio. Donde se dice, p. ej., que no podría suceder ninguno de dos acontecimientos (que se excluyen recíprocamente) porque no se da ninguna causa en orden a la que uno de ellos hubiera de suceder más bien que el otro, se trata en realidad de que no puede describirse en absoluto uno de ellos si no se da cierta asimetría. Y si tal asimetría está dada, entonces podemos concebirla como causa de la ocurrencia del uno y de la no-ocurrencia del otro.

6.36111 El problema kantiano de la mano derecha y de la mano izquierda, que no pueden hacerse coincidir superponiéndolas, se da ya en el plano, incluso en el espacio unidimensional, donde las dos figuras congruentes a y b tampoco pueden hacerse coincidir superponiéndolas sin sacarlas fuera de este espacio:

La mano derecha y la mano izquierda son, en efecto, enteramente congruentes. Y nada tiene que ver con ello el que no sea posible hacerlas coincidir superponiéndolas.

Sería posible calzar el guante derecho en la mano izquierda si cupiera darle la vuelta en el espacio cuatridimensional.

6.362 Lo que se puede describir puede ocurrir también, y lo que ha de excluir la ley de causalidad es cosa que tampoco puede describirse.

6.363 El procedimiento de la inducción consiste en que asumimos la ley más simple que cabe armonizar con nuestras experiencias.

6.3631 Pero ese procedimiento no tiene una fundamentación lógica, sino sólo psicológica.

Está claro que no hay fundamento alguno para creer que ocurrirá realmente el caso más simple.

6.36311 Que el sol vaya a salir mañana es una hipótesis; y esto quiere decir: no sabemos si saldrá.

6.37 No hay una necesidad por la que algo tenga que ocurrir porque otra cosa haya ocurrido. Sólo hay una necesidad lógica.

6.371 A toda la visión moderna del mundo subyace el espejismo de que las llamadas leyes de la naturaleza son las explicaciones de los fenómenos de la naturaleza.

6.372 Y así se aferran a las leyes de la naturaleza como a algo intocable, al igual que los antiguos a Dios y al destino.

Y ambos tienen razón y no la tienen. Pero los antiguos son, en cualquier caso, más claros en la medida en que reconocen un final claro, en tanto que en el nuevo sistema ha de parecer como si todo estuviera explicado.

6.373 El mundo es independiente de mi voluntad.

6.374 Y aunque todo lo que deseamos sucediera, esto sólo sería, por así decirlo, una gracia del destino, dado que no hay conexión lógica alguna entre voluntad y mundo capaz de garantizar tal cosa, ni nosotros mismos podríamos querer la hipotética conexión física.

6.375 Al igual que sólo hay una necesidad lógica, sólo hay también una imposibilidad lógica.

6.3751 Que, por ejemplo, dos colores estén a la vez en un lugar del campo visual es imposible y, a decir verdad, lógicamente imposible, puesto que ello viene excluido por la estructura lógica del color. Pensemos cómo se representa esta contradicción en la física; aproximadamente así: una partícula no puede tener al mismo tiempo dos velocidades; esto quiere decir que no puede estar al mismo tiempo en dos lugares; esto quiere decir que partículas en lugares diferentes, al mismo tiempo, no pueden ser idénticas.

(Está claro que el producto lógico de dos proposiciones elementales no puede ser una tautología ni una contradicción. El enunciado de que un punto del campo visual tiene al mismo tiempo dos colores diferentes es una contradicción.)

6.4 Todas las proposiciones valen lo mismo.

6.41 El sentido del mundo tiene que residir fuera de él. En el mundo todo es como es y todo sucede como sucede; en él no hay valor alguno, y si lo hubiera carecería de valor.

Si hay un valor que tenga valor ha de residir fuera de todo suceder y ser-así. Porque todo suceder y serasí son casuales.

Lo que los hace no-casuales no puede residir en el mundo; porque, de lo contrario, sería casual a su vez.

Ha de residir fuera del mundo.

6.42 Por eso tampoco puede haber proposiciones éticas. Las proposiciones no pueden expresar nada más alto.

6.421 Está claro que la ética no resulta expresable. La ética es trascendental.

(Ética y estética son una y la misma cosa.)

6.422 Cuando se asienta una ley ética de la forma «tú debes…» el primer pensamiento es: ¿y qué, si no lo hago? Pero está claro que la ética nada tiene que ver con el premio y el castigo en sentido ordinario. Esta pregunta por las consecuencias de una acción tiene que ser, pues, irrelevante. Al menos, estas consecuencias no deben ser acontecimientos. Porque algo correcto tiene que haber, a pesar de todo, en aquella interpelación. Tiene que haber, en efecto, un tipo de premio y de castigo éticos, pero éstos han de residir en la acción misma.

(Y está claro, asimismo, que el premio ha de ser algo agradable y el castigo algo desagradable.)

6.423 De la voluntad como soporte de lo ético no cabe hablar.

Y la voluntad como fenómeno sólo interesa a la psicología.

6.43 Si la voluntad buena o mala cambia el mundo, entonces sólo puede cambiar los límites del mundo, no los hechos; no lo que puede expresarse mediante el lenguaje.

En una palabra, el mundo tiene que convertirse entonces en otro enteramente diferente. Tiene que crecer o decrecer, por así decirlo, en su totalidad. El mundo del feliz es otro que el del infeliz.

6.431 Al igual que en la muerte el mundo no cambia sino que cesa.

6.4311 La muerte no es un acontecimiento de la vida. No se vive la muerte.

Si por eternidad se entiende, no una duración temporal infinita, sino intemporalidad, entonces vive eternamente quien vive en el presente.

Nuestra vida es tan infinita como ilimitado es nuestro campo visual.

6.4312 La inmortalidad temporal del alma del hombre, esto es, su eterno sobrevivir tras la muerte, no sólo no está garantizada en modo alguno, sino que, ante todo, tal supuesto no procura en absoluto lo que siempre se quiso alcanzar con él. ¿Se resuelve acaso un enigma porque yo sobreviva eternamente? ¿No es, pues, esta vida eterna, entonces, tan enigmática como la presente? La solución del enigma de la vida en el espacio y el tiempo reside fuera del espacio y del tiempo.

(No son problemas de la ciencia natural los que hay que resolver.)

6.432 Cómo sea el mundo es de todo punto indiferente para lo más alto. Dios no se manifiesta en el mundo.

6.4321 Los hechos pertenecen todos sólo a la tarea, no a la solución.

6.44 No cómo sea el mundo es lo místico sino que sea.

6.45 La visión del mundo sub specie aeterni es su visión como-todo-limitado. El sentimiento del mundo como todo limitado es lo místico.

6.5 Respecto a una respuesta que no puede expresarse, tampoco cabe expresar la pregunta.

El enigma no existe.

Si una pregunta puede siquiera formularse, también puede responderse.

6.51 El escepticismo no es irrebatible, sino manifiestamente absurdo, cuando quiere dudar allí donde no puede preguntarse.

Porque sólo puede existir duda donde existe una pregunta, una pregunta sólo donde existe una respuesta, y ésta, sólo donde algo puede ser dicho.

6.52 Sentimos que aun cuando todas las posibles cuestiones científicas hayan recibido respuesta, nuestros problemas vitales todavía no se han rozado en lo más mínimo. Por supuesto que entonces ya no queda pregunta alguna; y esto es precisamente la respuesta.

6.521 La solución del problema de la vida se nota en la desaparición de ese problema. (¿No es ésta la razón por la que personas que tras largas dudas llegaron a ver claro el sentido de la vida, no pudieran decir, entonces, en qué consistía tal sentido?)

6.522 Lo inexpresable, ciertamente, existe. Se muestra, es lo místico.

6.53 El método correcto de la filosofía sería propiamente éste: no decir nada más que lo que se puede decir, o sea, proposiciones de la ciencia natural —o sea, algo que nada tiene que ver con la filosofía—, y entonces, cuantas veces alguien quisiera decir algo metafísico, probarle que en sus proposiciones no había dado significado a ciertos signos. Este método le resultaría insatisfactorio —no tendría el sentimiento de que le enseñábamos filosofía—, pero sería el único estrictamente correcto.

6.54 Mis proposiciones esclarecen porque quien me entiende las reconoce al final como absurdas, cuando a través de ellas —sobre ellas— ha salido fuera de ellas. (Tiene, por así decirlo, que arrojar la escalera después de haber subido por ella.)

Tiene que superar estas proposiciones; entonces ve correctamente el mundo.

7 De lo que no se puede hablar hay que callar.